Exploration of Computational Approaches to Predict the Toxicity of Chemical Mixtures
Abstract
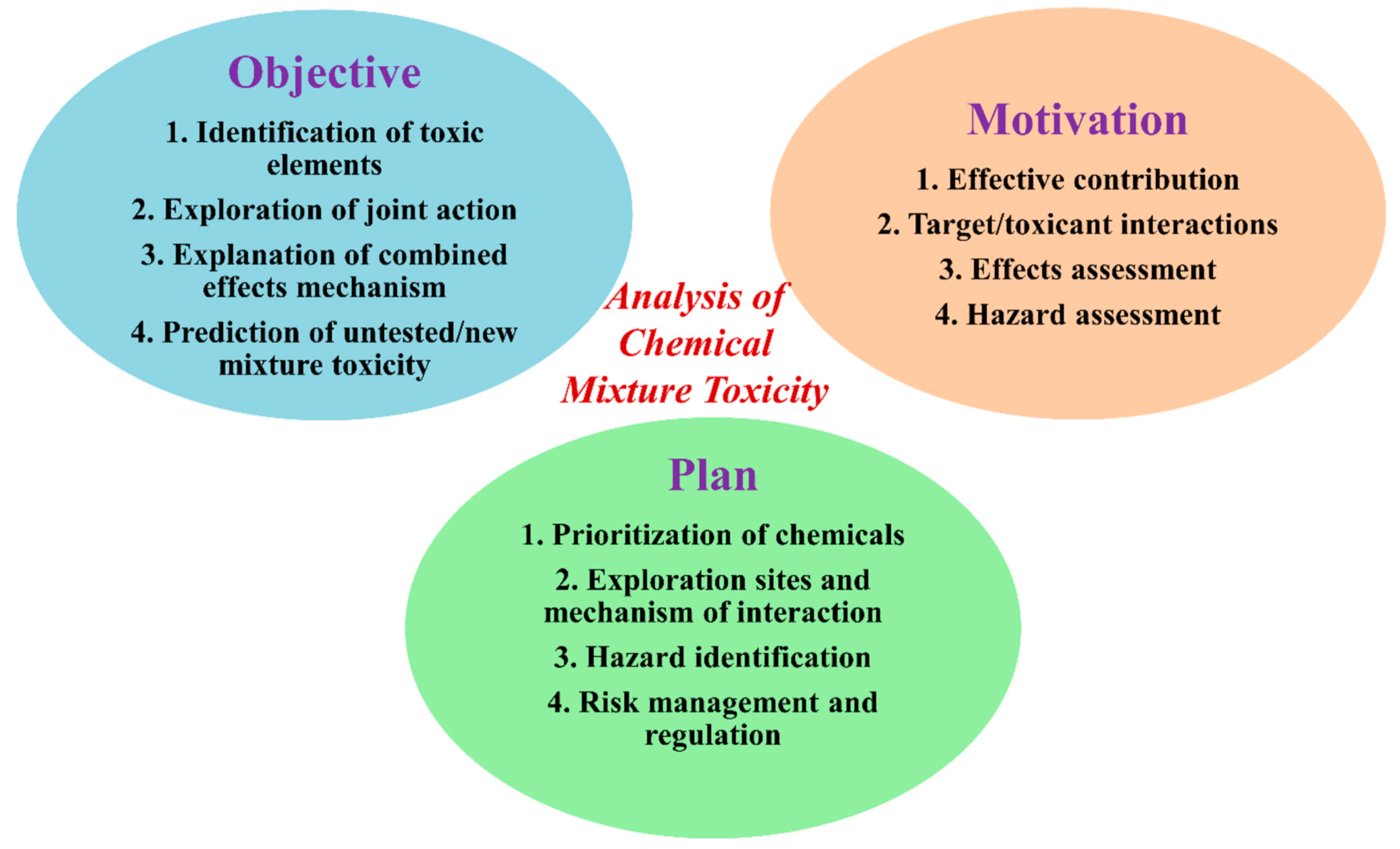
1. Introduction
- (a)
- toxicity data vary with different combinations of the same chemicals in a mixture;
- (b)
- form of exposure;
- (c)
- identification of each chemicals in a specific mixture is also difficult due to the presence of very small quantities; and
- (d)
- complex interactions among chemicals.
2. Why Exploration of Toxicity of Chemical Mixtures is Important?
3. Hypothesis for a Mixture’s Toxicity Exploration and Data for Computational Modeling
- (i)
- If chemicals in a mixture showed same mechanism of action for a specific response and act on same site of action, then there are chances of dilution of the response. This method is known as concentration addition (CA).
- (ii)
- If chemicals in mixtures act on different sites of action with dissimilar modes of action (MOA), this may disclose statistically independent responses without interaction. This method is known as independent action (IA).
- (iii)
- If chemicals are interactive in nature, then they may show synergistic or antagonistic effects.
3.1. Determination of Dosage Response Curves for All Chemicals in a Mixture
3.2. Determining the Effect of the Chemical Mixture
3.3. Modeling with Identified Hypothesis
3.3.1. Concentration Addition (CA)
3.3.2. Independent Action (IA)
3.3.3. Synergistic and Antagonistic Actions
3.3.4. Generalized Concentration Addition (GCA) Models
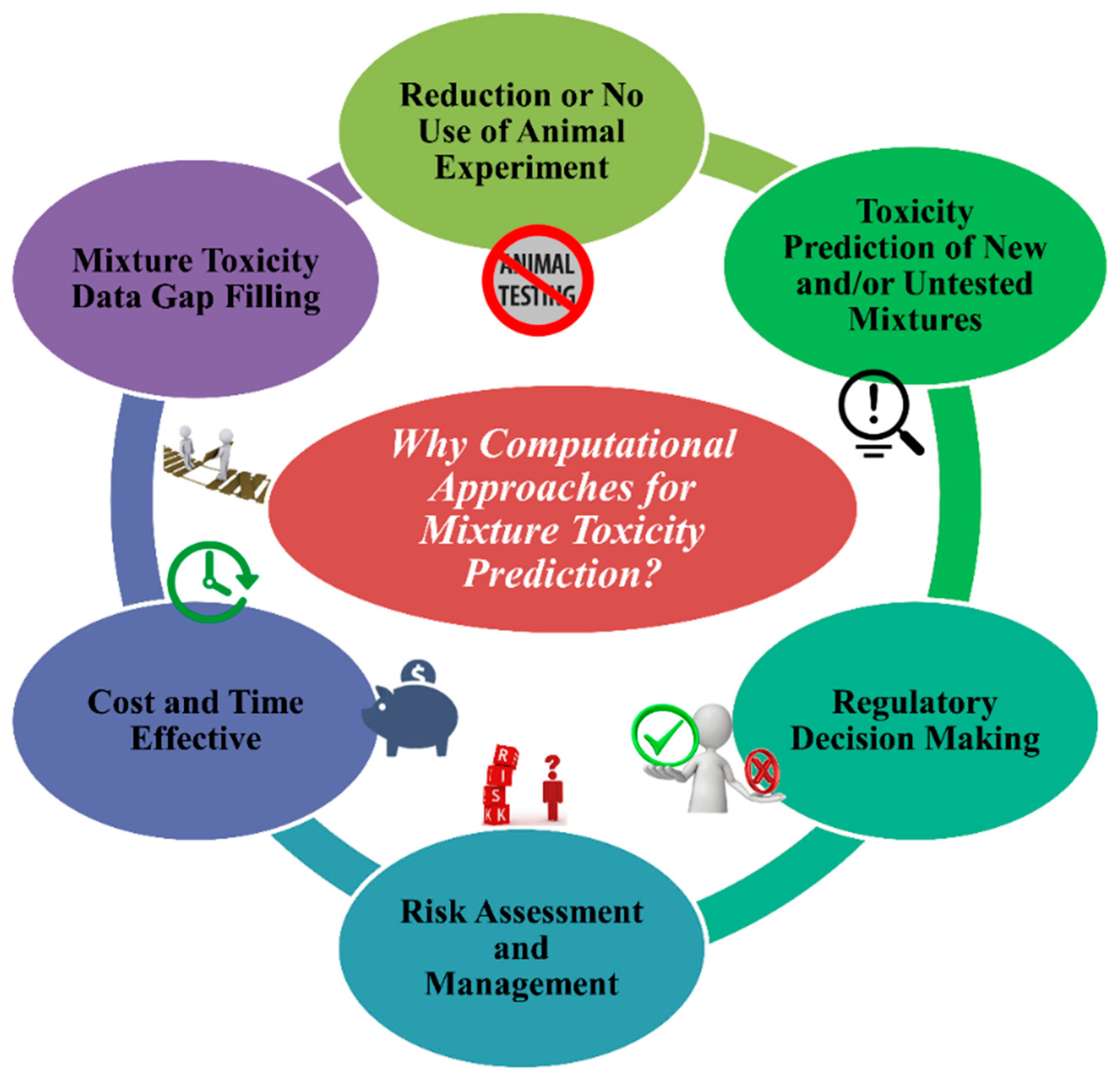
4. Importance of Computational Approaches to Determine the Toxicity of Chemical Mixtures
- (1.)
- To stop the unethical use of animal cruelty in the name of animal modeling. The application and acceptance of in silico approaches can decrease the use of animals in toxicity testing.
- (2.)
- Using in silico models from existing chemical mixtures, one can assess/predict the toxicity of untested and/or new different combinations of chemical mixtures for a specific species or systems if they fall under the applicability domain (AD).
- (3.)
- Regulatory agencies like United States Environmental Protection Agency (US EPA), European Union regulations like the Registration, Evaluation, Authorization and Restriction of Chemicals (REACH), and Health Canada consider and depend on in silico methods for toxicity and risk assessment followed by decision making.
- (4.)
- In silico methods are reliable tools to analyse the quantity of risk followed by methods to manage it.
- (5.)
- Without any doubt, in silico tools are cost- and time-effective compared to in vivo and in vitro methods.
- (6.)
- A reliable source of methods to fill gaps in mixture toxicity data as the majority of mixtures have no toxicity data at all.
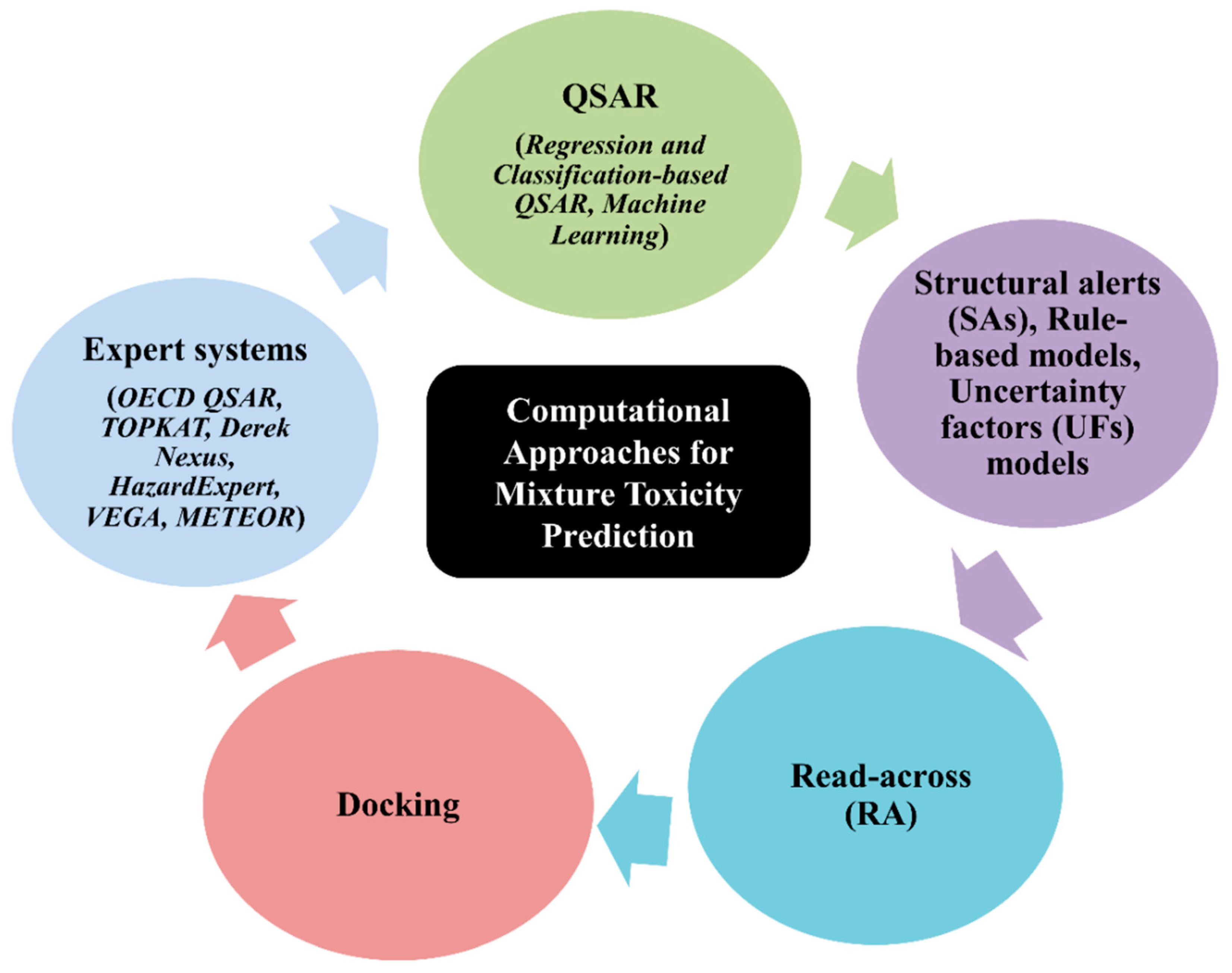
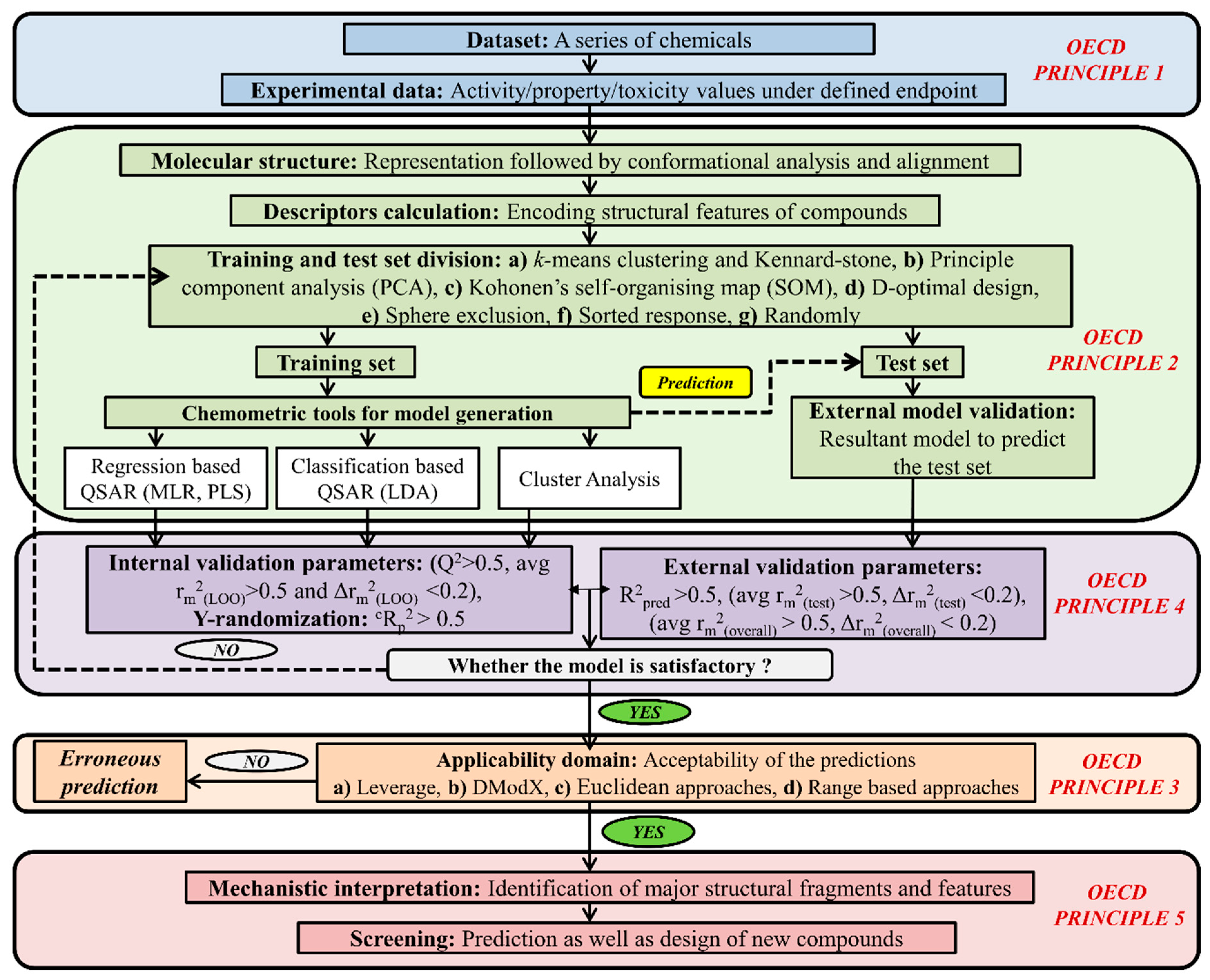
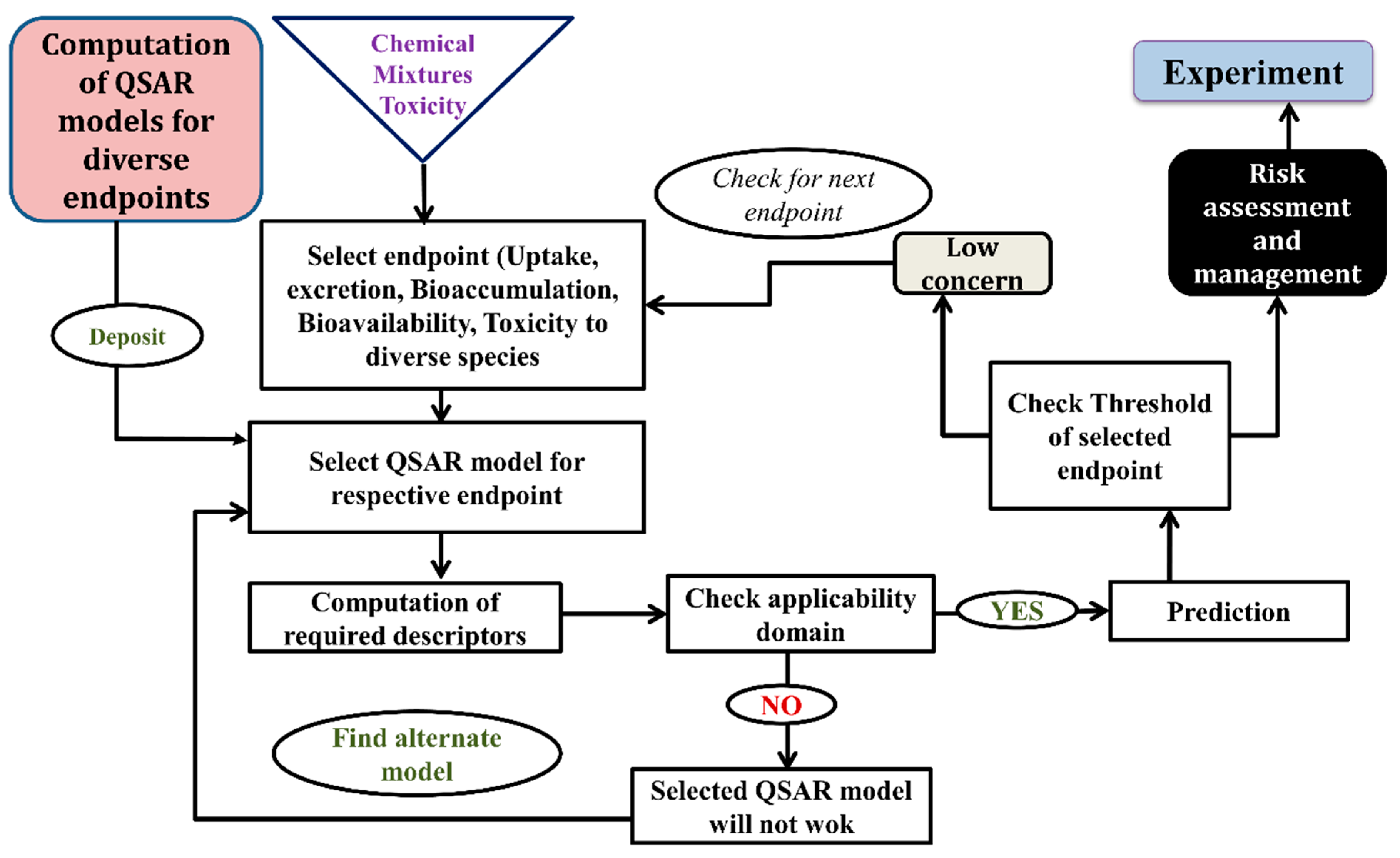
5. Types of Computational Approach for a Mixture’s Toxicity Prediction
- (1)
- Methods are easy to implement and interpret.
- (2)
- Help to determine how compounds should be transformed to decrease their toxicity.
- (3)
- Capable of categorizing the structure of likely metabolites.
- (1)
- The presence or absence of SAs does not offer understanding of the biological pathways of toxicity.
- (2)
- If all SAs are not identified properly, the method can increase false negatives.
6. Successful Application of Computational Modeling for Predicting a Mixture’s Toxicity
- Daphnia EC20 QSAR:
- Mesocosm NOEC QSAR:
7. Future Avenues of Chemical Mixture Toxicity Research
- (a)
- Mixture assessment should use low doses, for example up to the no-observed-adverse-effect level (NOAEL);
- (b)
- There is no ultimate or universal method, and one needs to develop new or modified approaches from case to case to address the complex issue of mixture, noting that old-style animal-based toxicology practices are insufficient for such a multifaceted issue;
- (c)
- Collaborative efforts between experimentalist and computational communities are must to address majority of issues and challenges related to mixture toxicity;
- (d)
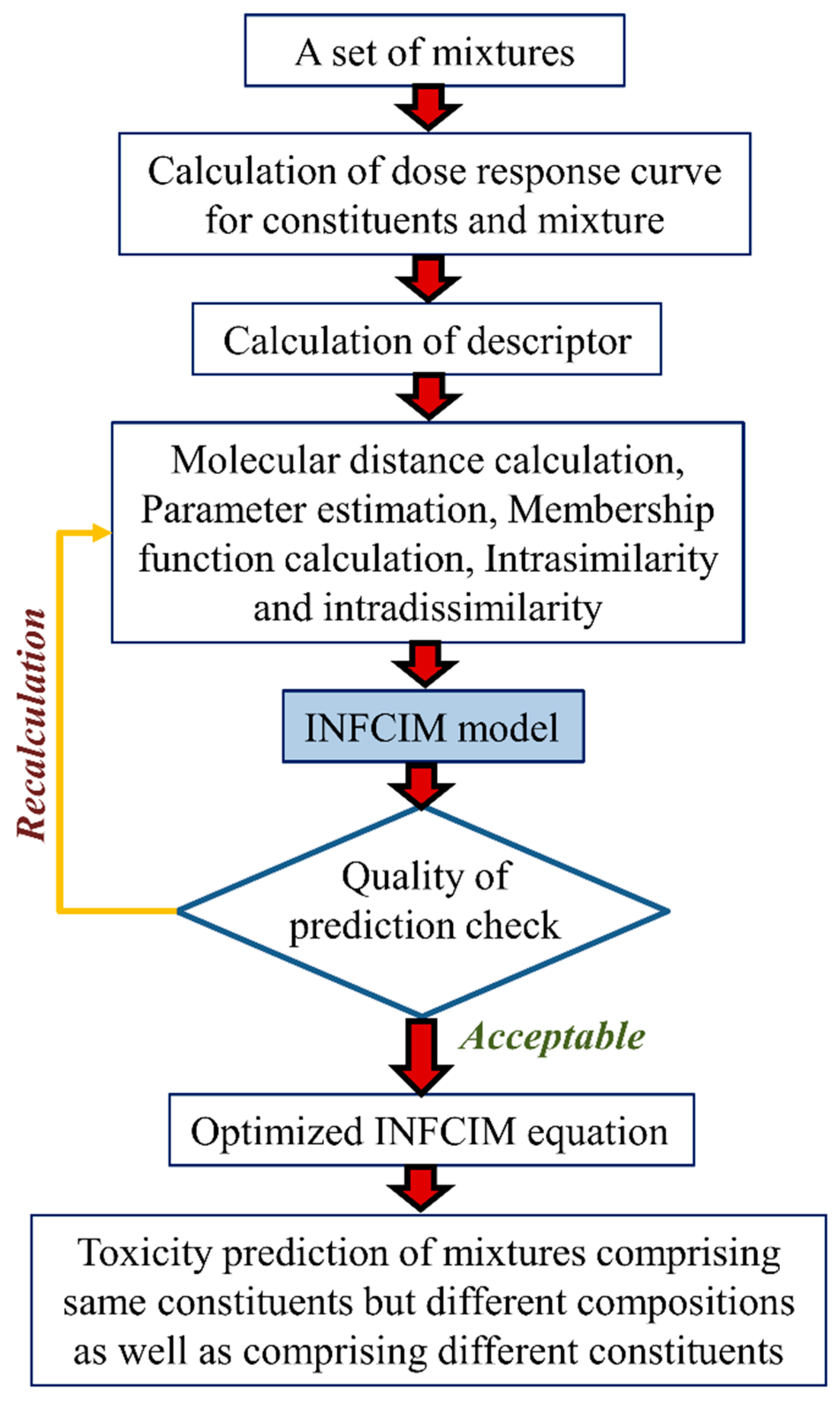
- A variant of the Hausdorff measure, called Hausdorff-like similarity (Hs), can be useful in modeling a complex system like mixtures [45]. To quantify the similarity degree between two systems, it is not suitable to account only for mutual or dissimilar features, but all the features of the systems have to be measured in the assessment. Hausdorff formula are capable of equally weighing both the existence of common/comparable elements. To measure the diversity relationship between the two sets X and Y, the Hausdorff formula can be defined as follows:from which the equivalent similarity measure can be calculated as:where the signs s and d denote the similarity and the distance measures, correspondingly.
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Teuschler, L.K.; Hertzberg, R.C. Current and future risk assessment guidelines, policy, and methods development for chemical mixtures. Toxicology 1995, 105, 137–144. [Google Scholar] [CrossRef]
- Logan, D.T.; Wilson, H.T. An ecological risk assessment method for species exposed to contaminant mixtures. Environ. Toxicol. Chem. 1995, 14, 351–359. [Google Scholar] [CrossRef]
- Henn, B.C.; Coull, B.A.; Wright, R.O. Chemical mixtures and children’s health. Curr. Opin. Pediatr. 2014, 26, 223–229. [Google Scholar] [CrossRef]
- Løkke, H.; Ragas, A.M.J.; Holmstrup, M. Tools and perspectives for assessing chemical mixtures and multiple stressors. Toxicology 2013, 313, 73–82. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Kechavarzi, C.; Li, X.; Wu, S.; Pollard, S.J.T.T.; Sui, H.; Coulon, F. Machine learning models for predicting PAHs bioavailability in compost amended soils. Chem. Eng. J. 2013, 223, 747–754. [Google Scholar] [CrossRef]
- Zou, X.; Lin, Z.; Deng, Z.; Yin, D.; Zhang, Y. The joint effects of sulfonamides and their potentiator on photobacterium phosphoreum: Differences between the acute and chronic mixture toxicity mechanisms. Chemosphere 2012, 86, 30–35. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A.; Benfenati, E.; Gini, G.; Leszczynska, D.; Leszczynski, J. Coral: Models of toxicity of binary mixtures. Chemom. Intell. Lab. Syst. 2012, 119, 39–43. [Google Scholar] [CrossRef]
- Tang, J.Y.M.; Mccarty, S.; Glenn, E.; Neale, P.A.; Warne, M.S.J.; Escher, B.I. Mixture effects of organic micropollutants present in water: Towards the development of effect-based water quality trigger values for baseline toxicity. Water Res. 2013, 47, 3300–3314. [Google Scholar] [CrossRef] [PubMed]
- Yao, Z.; Lin, Z.; Wang, T.; Tian, D.; Zou, X.; Gao, Y. Using molecular docking-based binding energy to predict toxicity of binary mixture with different binding sites. Chemosphere 2013, 92, 1169–1176. [Google Scholar] [CrossRef]
- Wang, T.; Wang, D.; Lin, Z.; An, Q.; Yin, C.; Huang, O. Prediction of mixture toxicity from the hormesis of a single chemical: A case study of combinations of antibiotics and quorum-sensing inhibitors with gram-negative bacteria. Chemosphere 2016, 150, 159–167. [Google Scholar] [CrossRef]
- Borzelleca, J. The art, the science and the seduction of toxicology. An evolutionary development. In Principles and Methods of Toxicology; Hayes, A., Ed.; Taylor and Francis: London, UK, 2001; pp. 1–22. [Google Scholar]
- Altenburger, R.; Backhaus, T.; Boedeker, W.; Faust, M.; Scholze, M.; Grimme, L.H. Predictability of the toxicity of multiple chemical mixtures to Vibrio fischeri: Mixtures composed of similarly acting chemicals. Environ. Toxicol. Chem. 2010, 19, 2341–2347. [Google Scholar] [CrossRef]
- Monosson, E. Chemical Mixtures: Considering the Evolution of Toxicology and Chemical Assessment. Environ. Health Perspect. 2005, 113, 383–390. [Google Scholar] [CrossRef] [PubMed]
- Bliss, C.I. The toxicity of poisons applied jointly. Ann. Appl. Biol. 1939, 26, 585–615. [Google Scholar] [CrossRef]
- Altenburger, R.; Nendza, M.; Schüürmann, G. Mixture Toxicity and Its Modeling by Quantitative Structure-Activity Relationships. Environ. Toxicol. Chem. 2003, 22, 1900–1915. [Google Scholar] [CrossRef] [PubMed]
- Howard, G.J.; Webster, T.F. Generalized concentration addition: A method for examining mixtures containing partial agonists. J. Theor. Biol. 2009, 259, 469–477. [Google Scholar] [CrossRef] [PubMed]
- Hadrup, N.; Taxvig, C.; Pedersen, M.; Nellemann, C.; Hass, U.; Vinggaard, A.M. Concentration addition, independent action and generalized concentration addition models for mixture effect prediction of sex hormone synthesis in vitro. PLoS ONE 2013, 8, e70490. [Google Scholar] [CrossRef]
- AltTox. Toxicity Testing Overview. Available online: http://alttox.org/mapp/toxicity-testing-overview/ (accessed on 15 January 2019).
- Valerio, L.G., Jr. In silico toxicology for the pharmaceutical sciences. Toxicol. Appl. Pharmacol. 2009, 241, 356–370. [Google Scholar] [CrossRef]
- Raies, A.B.; Bajic, V.B. In silico toxicology: Computational methods for the prediction of chemical toxicity. WIREs Comput. Mol. Sci. 2016, 6, 147–172. [Google Scholar] [CrossRef]
- Roy, K.; Kar, S.; Das, R.N. Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Roy, K.; Kar, S.; Das, R.N. A Primer on QSAR/QSPR Modeling: Fundamental Concepts (SpringerBriefs in Molecular Science); Springer: Berlin, Germany, 2015. [Google Scholar]
- Kar, S.; Roy, K. How far can virtual screening take us in drug discovery? Expert. Opin. Drug. Discov. 2013, 8, 245–261. [Google Scholar] [CrossRef]
- Kar, S.; Roy, K. Risk Assessment for Ecotoxicity of Pharmaceuticals—An Emerging Issue. Expert. Opin. Drug. Saf. 2012, 11, 235–274. [Google Scholar] [CrossRef]
- Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics; Wiley-VCH: New York, NY, USA, 2009. [Google Scholar]
- Guner, O.F. History and evolution of the pharmacophore concept in computer-aided drug design. Curr. Top. Med. Chem. 2002, 2, 1321–1332. [Google Scholar] [CrossRef] [PubMed]
- Hopfinger, A.; Wang, S.; Tokarski, J.; Baiqiang, J.; Albuquerque, M.; Madhav, P.; Duraiswami, C. Construction of 3D-QSAR Models Using the 4D-QSAR Analysis Formalism. J. Am. Chem. Soc. 1997, 119, 10509–10524. [Google Scholar] [CrossRef]
- Vedani, A.; Dobler, M. 5D-QSAR: The key for simulating induced fit? J. Med. Chem. 2002, 45, 2139–2149. [Google Scholar] [CrossRef]
- Vedani, A.; Dobler, M.; Lill, M.A. Combining protein modeling and 6D-QSAR. Simulating the binding of structurally diverse ligands to the estrogen receptor. J. Med. Chem. 2005, 48, 3700–3703. [Google Scholar] [CrossRef] [PubMed]
- Polanski, J. Receptor dependent multidimensional QSAR for modeling drug-receptor interactions. Curr. Med. Chem. 2009, 16, 3243–3257. [Google Scholar] [CrossRef] [PubMed]
- Venkatapathy, R.; Wang, N.C.Y. Developmental toxicity prediction. In Computational Toxicology; Reisfeld, B., Mayeno, A.N., Eds.; Humana Press: New York, NY, USA, 2013; Volume 930, pp. 305–340. [Google Scholar]
- Roncaglioni, A.; Toropov, A.A.; Toropova, A.P.; Benfenati, E. In silico methods to predict drug toxicity. Curr. Opin. Pharmacol. 2013, 13, 802–806. [Google Scholar] [CrossRef] [PubMed]
- Jeliazkova, N.; Jaworska, J.; Worth, A.P. Open source tools for read-across and category formation. In In Silico Toxicology: Principles and Applications; Cronin, M.T.D., Madden, J.C., Eds.; The Royal Society of Chemistry: Cambridge, UK, 2010; pp. 408–445. [Google Scholar]
- Roy, K.; Kar, S. In Silico Models for Ecotoxicity of Pharmaceuticals. In In Silico Methods for Predicting Drug Toxicity, Methods in Molecular Biology; Benfenati, E., Ed.; Springer: Berlin, Germany, 2016; Volume 1425. [Google Scholar]
- Tichý, M.; Cikrt, M.; Roth, Z.; Rucki, M. QSAR Analysis in Mixture Toxicity Assessment. SAR QSAR Environ. Res. 1998, 9, 155–169. [Google Scholar] [CrossRef]
- Mwense, M.; Wang, X.Z.; Buontempo, F.V.; Horan, N.; Young, A.; Osborn, D. Prediction of Noninteractive Mixture Toxicity of Organic Compounds Based on a Fuzzy Set Method. J. Chem. Inf. Comput. Sci. 2004, 44, 1763–1773. [Google Scholar] [CrossRef] [PubMed]
- Boeijea, G.M.; Canob, M.L.; Marshallc, S.J.; Belangerd, S.E.; Van Compernollee, R.; Dorne, P.B.; Gümbelf, H.; Toyg, R.; Wind, T. Ecotoxicity quantitative structure–activity relationships for alcohol ethoxylate mixtures based on substance-specific toxicity predictions. Ecotoxicol. Environ. Saf. 2006, 64, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Tian, D.; Lin, Z.; Yin, D. Quantitative Structure Activity Relationships (QSAR) for Binary Mixtures at Non-Equitoxic Ratios Based on Toxic Ratios-Effects Curves. Dose-Response Int. J. 2013, 11, 11. [Google Scholar] [CrossRef]
- Mo, L.; Zhu, Z.; Zhu, Y.; Zeng, H.; Li, Y. Prediction and Evaluation of the Mixture Toxicity of Twelve Phenols and Ten Anilines to the Freshwater Photobacterium Vibrio qinghaiensis sp.-Q67. J. Chem. 2014, 728254, 9. [Google Scholar]
- Wang, T.; Tang, L.; Luan, F.; Cordeiro, M.N.D.S. Prediction of the Toxicity of Binary Mixtures by QSAR Approach Using the Hypothetical Descriptors. Int. J. Mol. Sci. 2018, 19, 3423. [Google Scholar] [CrossRef] [PubMed]
- Kar, S.; Ghosh, S.; Leszczynski, J. Single or Mixture Halogenated Chemicals? Risk Assessment and Developmental Toxicity Prediction on Zebrafish Embryos Based on Weighted Descriptors Approach. Chemosphere 2018, 210, 588–596. [Google Scholar] [CrossRef] [PubMed]
- Qin, L.-T.; Chen, Y.-H.; Zhang, X.; Mo, L.-Y.; Zeng, H.-H.; Liang, Y.-P. QSAR prediction of additive and non-additive mixture toxicities of antibiotics and pesticide. Chemosphere 2018, 198, 122–129. [Google Scholar] [CrossRef] [PubMed]
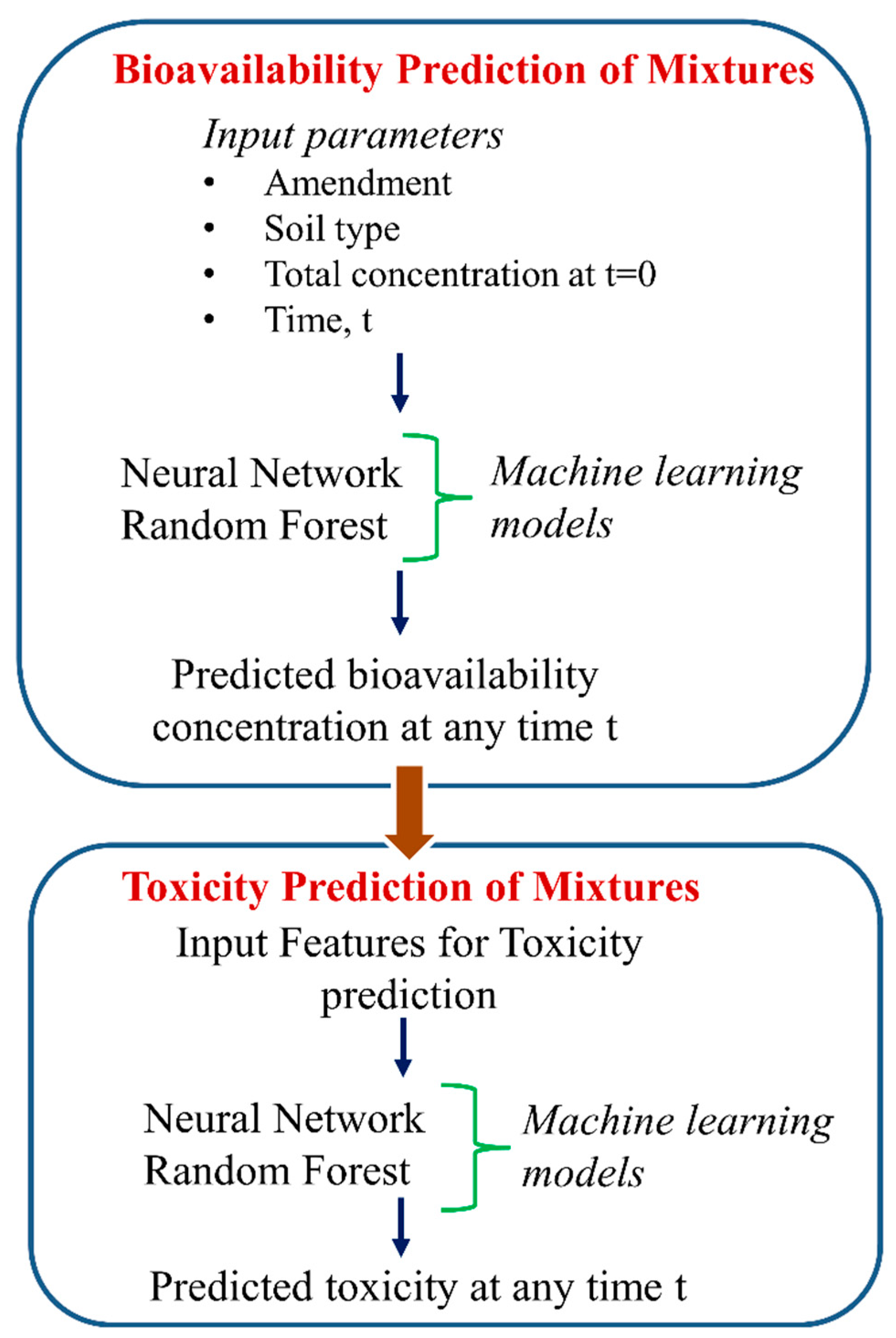
- Cipullo, S.; Snapir, B.; Prpich, G.; Campo, P.; Coulon, F. Prediction of bioavailability and toxicity of complex chemical mixtures through machine learning models. Chemosphere 2019, 215, 388–395. [Google Scholar] [CrossRef] [PubMed]
- Bucher, J.; Lucier, G. Current approaches toward chemical mixtures studies at the National Institute of Environmental Health Sciences and the U.S. National Toxicology Program. Environ. Health Perspect. 1998, 106, 1295–1298. [Google Scholar] [CrossRef] [PubMed]
- Mauri, A.; Ballabio, D.; Todeschini, R.; Consonni, V. Mixtures, metabolites, ionic liquids: A new measure to evaluate similarity between complex chemical systems. J. Cheminform. 2016, 8, 49. [Google Scholar] [CrossRef] [PubMed]
| Dimension | Description | Representative Example of Descriptors or Computational Method | Reference |
|---|---|---|---|
| 0D | Chemical formula derived descriptors | Constitutional indices (Molecular Weight (MW), sum of properties etc.), molecular property descriptors, count descriptors (count of bond, atom, non-hydrogen atom etc.) | [25] |
| 1D | Descriptors are derived using the representation of various sub-structural molecular fragments | Fingerprints, count of fragments, H-Bond acceptor/donor, Crippen AlogP98, PSA, SMARTS etc. | [25] |
| 2D | Descriptors are obtained from the graph theoretical representation of molecules including various structural and/or physicochemical property indices | Topological descriptors, eigenvalue-based descriptors, connectivity indices, descriptors containing topological and electronic information. | [25] |
| 3D | These independent variables encode various spatial as well as geometrical information of compounds and are derived using 3D representation of structure. Such parameters basically portray static representation of a ligand. | WHIM descriptors, MoRSE descriptors, Jurs parameters, GETAWAY descriptors, quantum-chemical descriptors, atomic coordinates, size, steric, surface and volume descriptors. Techniques e.g., Comparative Molecular Field Analysis (CoMFA), Comparative molecular similarity index analysis (CoMSIA) etc. | [25,26] |
| 4D | Depict multiple representation of the ligand molecule using various configurations, orientation, and protonation state representation. | Volsurf, GRID, Raptor etc. derived descriptors. | [27] |
| 5D | Descriptors consider the induced fit parameters and aim to establish a ligand-based virtual or pseudo receptor model. | Flexible-protein docking. | [28] |
| 6D | These are derived using the representation of various solvation circumstances along with the information obtained from 5D-descriptors. | Quasar. | [29] |
| 7D | Such analysis comprises real receptor or target-based receptor model data. | − | [30] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kar, S.; Leszczynski, J. Exploration of Computational Approaches to Predict the Toxicity of Chemical Mixtures. Toxics 2019, 7, 15. https://doi.org/10.3390/toxics7010015
Kar S, Leszczynski J. Exploration of Computational Approaches to Predict the Toxicity of Chemical Mixtures. Toxics. 2019; 7(1):15. https://doi.org/10.3390/toxics7010015
Chicago/Turabian StyleKar, Supratik, and Jerzy Leszczynski. 2019. "Exploration of Computational Approaches to Predict the Toxicity of Chemical Mixtures" Toxics 7, no. 1: 15. https://doi.org/10.3390/toxics7010015
APA StyleKar, S., & Leszczynski, J. (2019). Exploration of Computational Approaches to Predict the Toxicity of Chemical Mixtures. Toxics, 7(1), 15. https://doi.org/10.3390/toxics7010015






