The 1D Hybrid Material Allylimidazolium Iodoantimonate: A Combined Experimental and Theoretical Study
Abstract
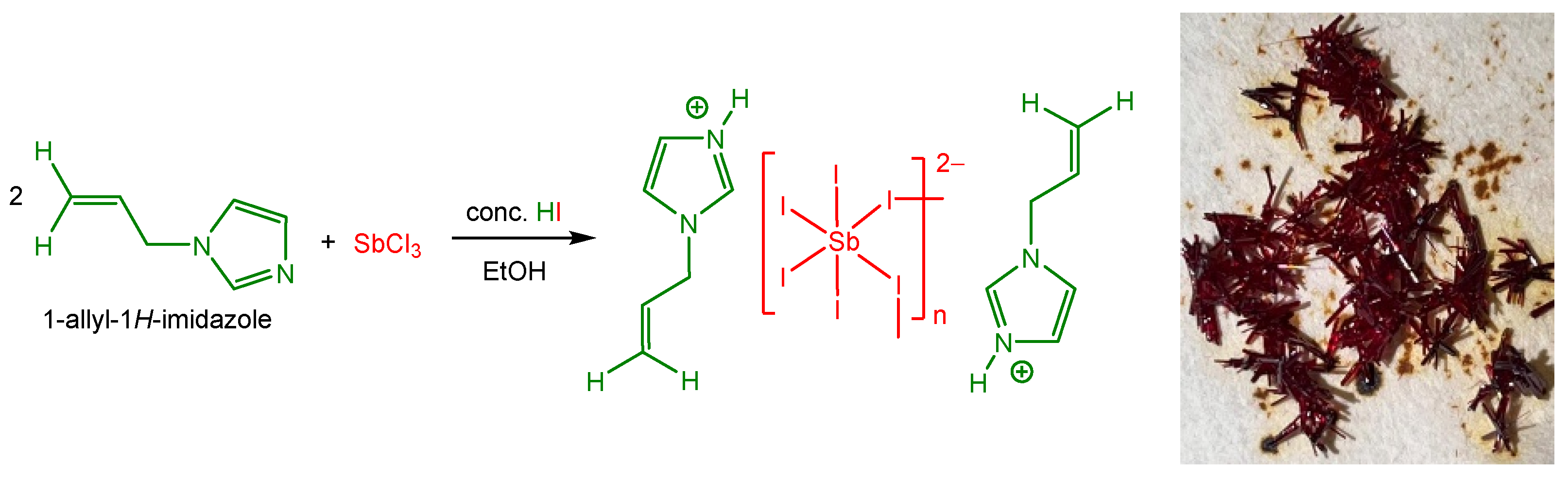
1. Introduction
2. Results and Discussion
2.1. Single-Crystal X-Ray Structure Determination
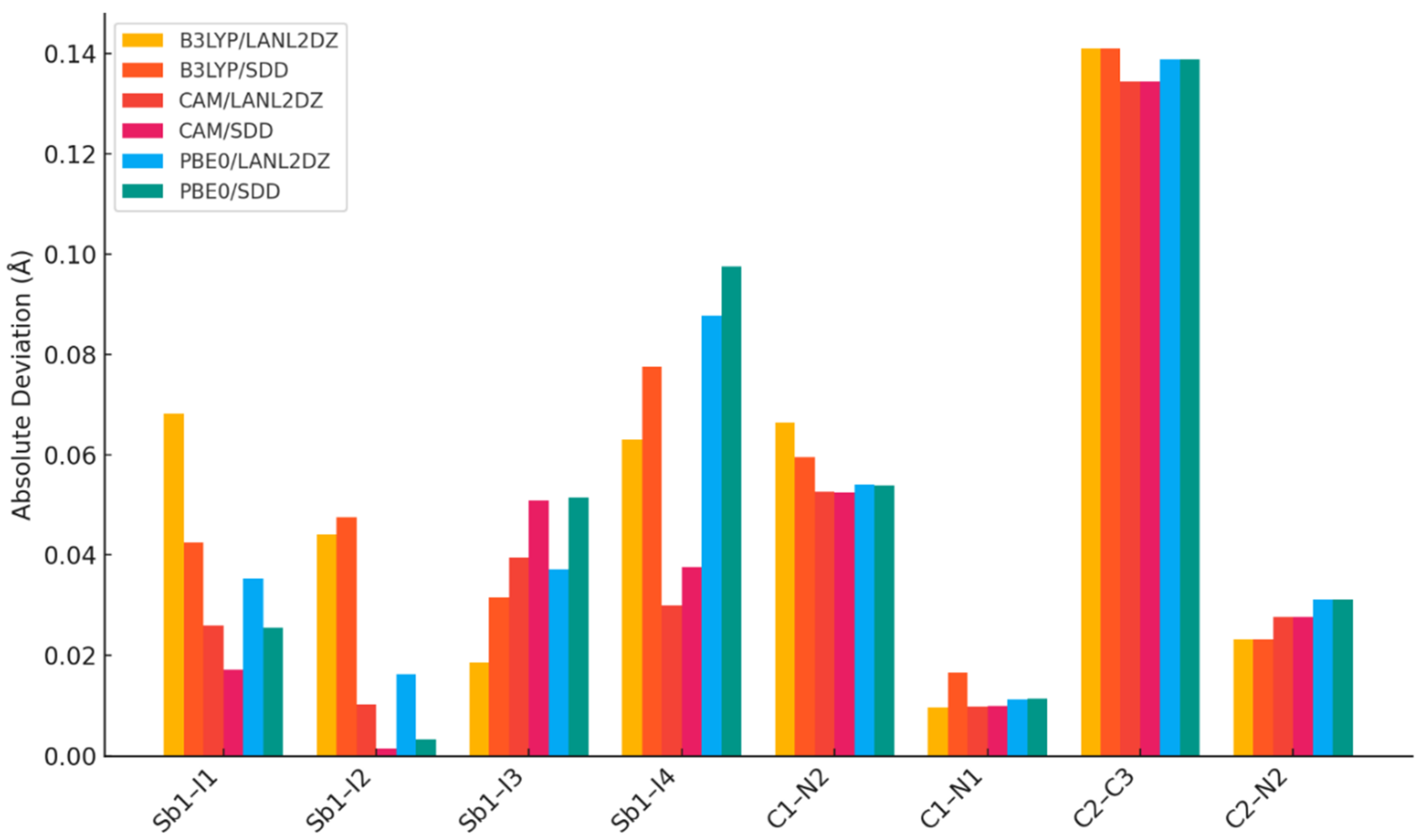
2.2. DFT Geometry Optimization
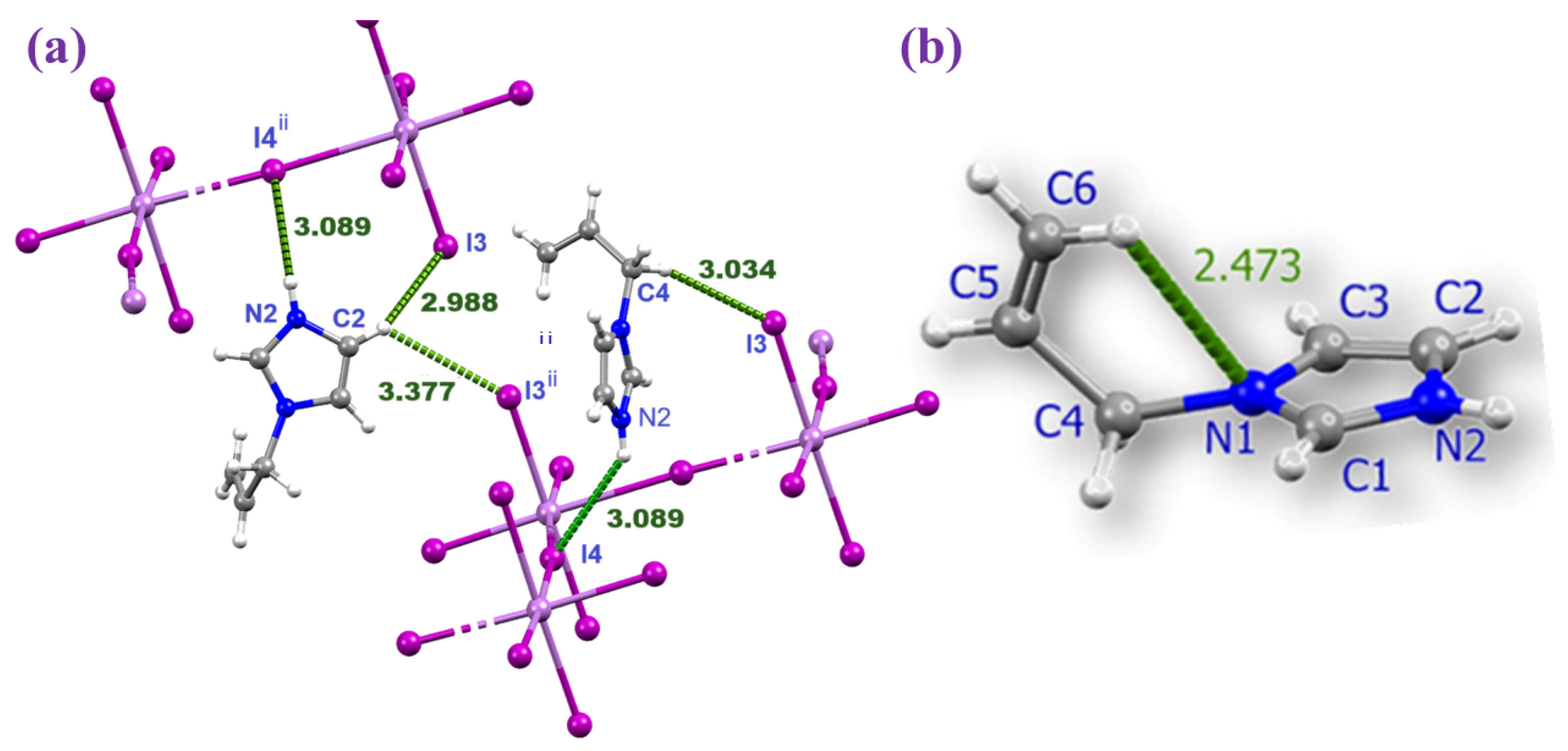
2.3. Computational Characterization of Non-Covalent Interactions
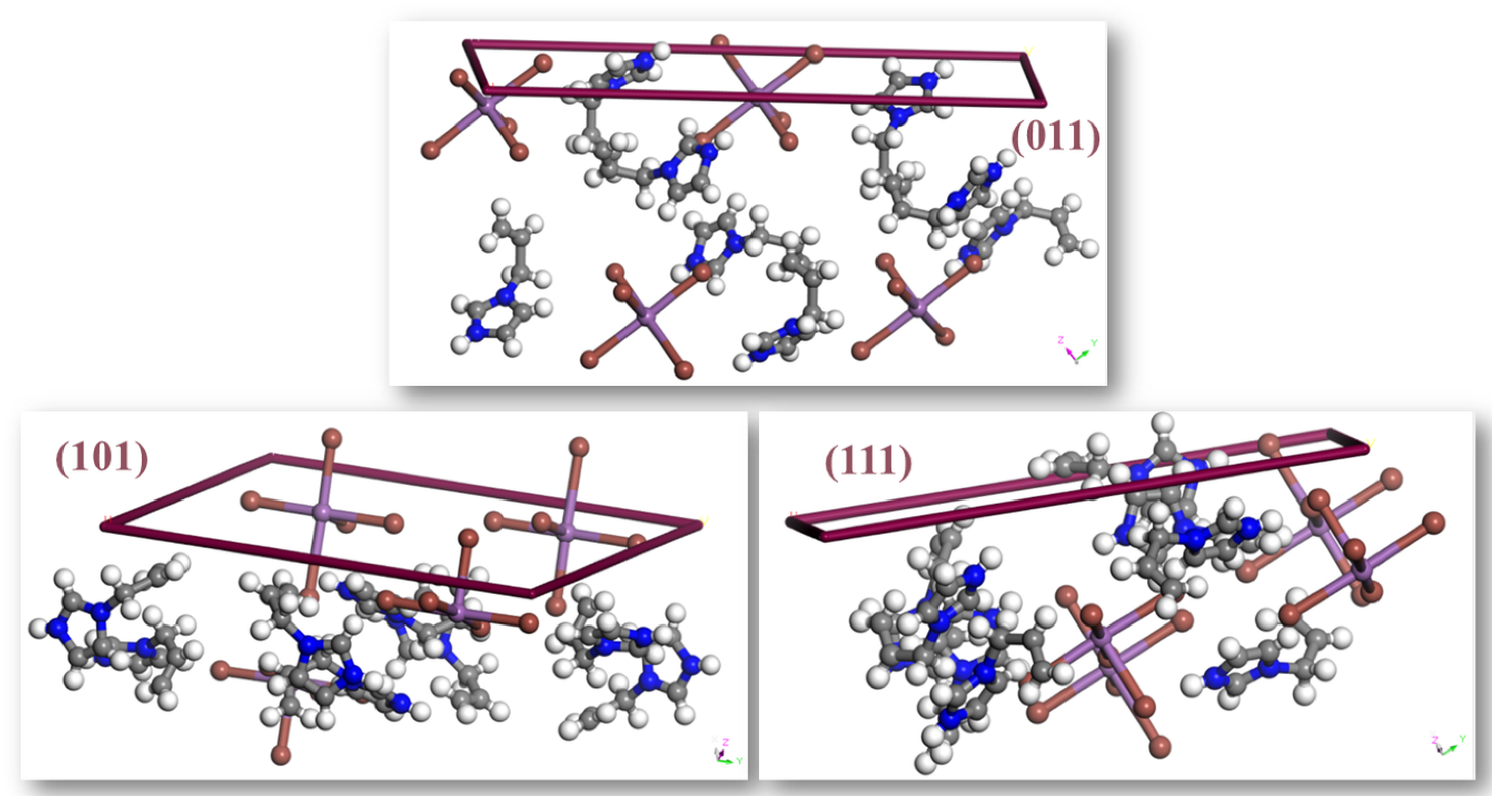
2.4. Crystal Habitus Simulation and Crystal Face Indexing
2.5. Void Analysis
2.6. FT-IR and Raman Spectroscopy
2.7. Optoelectronic Properties
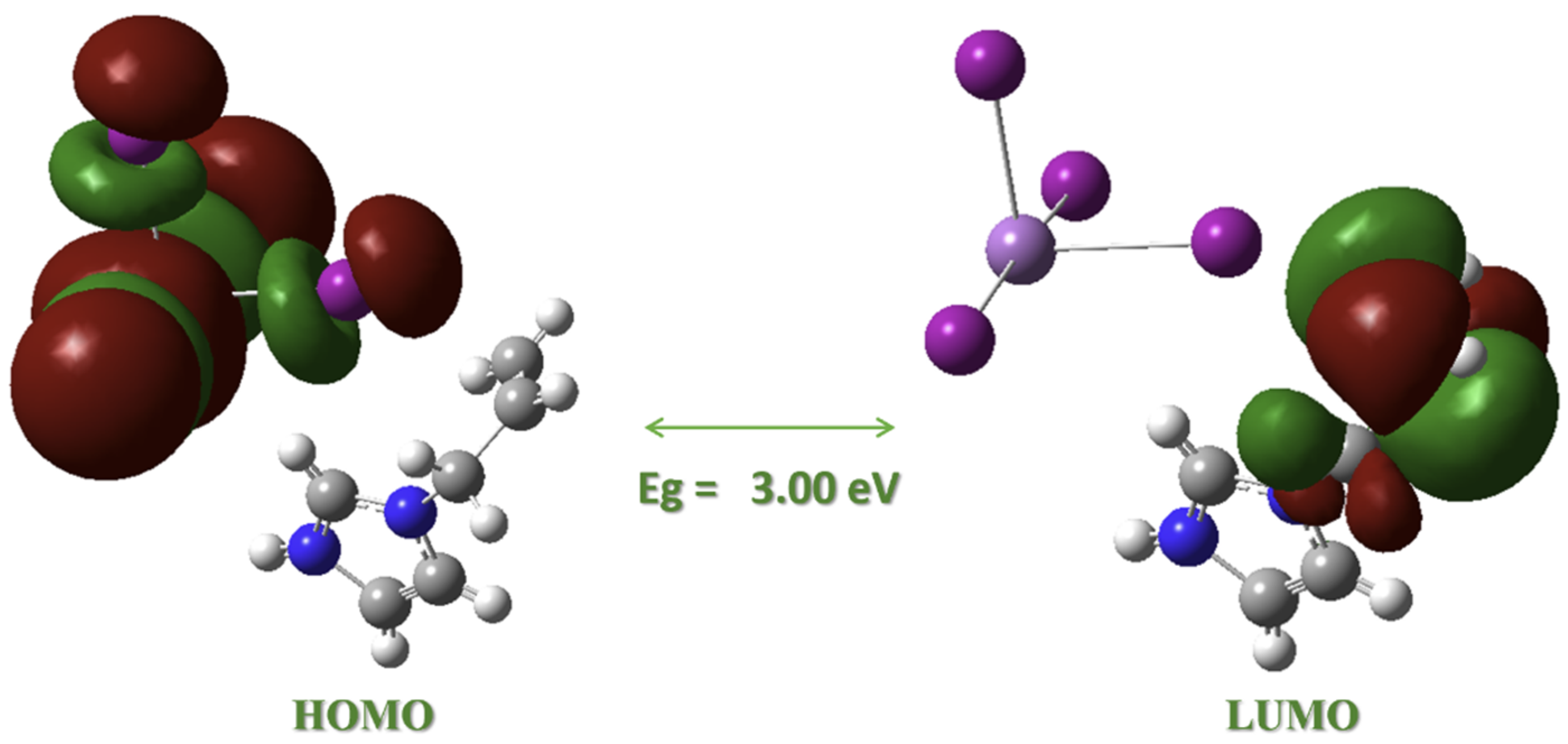
2.8. DFT-Calculated Frontier Orbital Character and Energies
Frontier Molecular Orbitals
3. Materials and Methods
3.1. Materials
3.2. Single Crystal Growth
3.3. Single-Crystal X-Ray Diffraction
3.4. Crystal Morphology Simulation
3.5. Spectroscopy
3.6. Computational Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, H.; Yang, X.; Bai, Y.; Meng, Q.; Wen, Z.; Sun, H.; Wei, Q.; Huang, D.; Yu, W.W.; Liu, F. Mechanoluminescence from Organic-Inorganic Metal Halide Perovskite Derivative. Adv. Sci. 2025, 12, e2414588. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Hamid, Z.; Babu, R.; Gómez-Graña, S.; Hu, X.; McCulloch, I.; Hoye, R.L.Z.; Rao, V.G.; Polavarapu, L. Halide Perovskite Photocatalysts for Clean Fuel Production and Organic Synthesis: Opportunities and Challenges. Adv. Mater. 2025, 2025, 2419603. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, A.D.; Yadav, H.M.; Sharma, K.K.; Shim, J.W.; Lee, J.-J.; Ghanem, M.A. Recent Advances in Innovative Device Designs and Engineering Strategies of Hybrid Perovskite Halides for Efficient Photoelectrochemical and Photocatalytic Applications. Small 2025, 2025, 2501570. [Google Scholar] [CrossRef] [PubMed]
- Berhe, T.A.; Su, W.-N.; Hwang, B.J. Halide Perovskites’ Multifunctional Properties: Coordination Engineering, Coordination Chemistry, Electronic Interactions and Energy Applications beyond Photovoltaics. Inorganics 2024, 12, 182. [Google Scholar] [CrossRef]
- Mao, L.; Chen, J.; Vishnoi, P.; Cheetham, A.K. The Renaissance of Functional Hybrid Transition-Metal Halides. Acc. Mater. Res. 2022, 3, 439–448. [Google Scholar] [CrossRef]
- Euvrard, J.; Yan, Y.; Mitzi, D.B. Electrical doping in halide perovskites. Nat. Rev. Mater. 2021, 6, 531–549. [Google Scholar] [CrossRef]
- Guo, X.; Burda, C. Coordination engineering toward high performance organic–inorganic hybrid perovskites. Coord. Chem. Rev. 2016, 320–321, 53–65. [Google Scholar] [CrossRef]
- Saparov, B.; Mitzi, D.B. Organic-Inorganic Perovskites: Structural Versatility for Functional Materials Design. Chem. Rev. 2016, 116, 4558–4596. [Google Scholar] [CrossRef]
- Huang, C.; Gajewiak, E.; Wright, A.; Rodriguez-Kazeem, W.; Heift, D.; Bear, J.C. A comparative meta-analysis of gains in efficiency in Pb and Sn-based perovskite solar cells over the last decade. Z. Anorg. Allg. Chem. 2023, 649, e202300045. [Google Scholar] [CrossRef]
- Nowsherwan, G.A.; Ali, Q.; Ali, U.F.; Ahmad, M.; Khan, M.; Hussain, S.S. Advances in Organic Materials for Next-Generation Optoelectronics: Potential and Challenges. Organics 2024, 5, 520–560. [Google Scholar] [CrossRef]
- Zhou, K.; Qi, B.; Liu, Z.; Wang, X.; Sun, Y.; Zhang, L. Advanced organic–inorganic hybrid materials for optoelectronic applications. Adv. Funct. Mater. 2024, 34, 2411671. [Google Scholar] [CrossRef]
- Morab, S.; Sundaram, M.M.; Pivrikas, A. Review on charge carrier transport in inorganic and organic semiconductors. Coatings 2023, 13, 1657. [Google Scholar] [CrossRef]
- Jonathan, L.; Diguna, L.J.; Samy, O.; Muqoyyanah, M.; Bakar, S.A.; Birowosuto, M.D.; El Moutaouakil, A. Hybrid Organic–Inorganic Perovskite Halide Materials for Photovoltaics towards Their Commercialization. Polymers 2022, 14, 1059. [Google Scholar] [CrossRef]
- Siegler, T.D.; Dawson, A.; Lobaccaro, P.; Ung, D.; Beck, M.E.; Nilsen, G.; Tinker, L.L. The Path to Perovskite Commercialization: A Perspective from the United States Solar Energy Technologies Office. ACS Energy Lett. 2022, 7, 1728–1734. [Google Scholar] [CrossRef]
- Xiang, W.; Liu, S.F.; Tress, W. A review on the stability of inorganic metal halide perovskites: Challenges and opportunities for stable solar cells. Energy Environ. Sci. 2021, 14, 2090–2113. [Google Scholar] [CrossRef]
- Zhuang, J.; Wang, J.; Yan, F. Review on Chemical Stability of Lead Halide Perovskite Solar Cells. Nano-Micro Lett. 2023, 15, 84. [Google Scholar] [CrossRef] [PubMed]
- Sakhatskyi, K.; John, R.A.; Guerrero, A.; Tsarev, S.; Sabisch, S.; Das, T.; Matt, G.J.; Yakunin, S.; Cherniukh, I.; Kotyrba, M.; et al. Assessing the Drawbacks and Benefits of Ion Migration in Lead Halide Perovskites. ACS Energy Lett. 2022, 7, 3401–3414. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.; Gondal, M.A.; Alzahrani, A.S.; Parvaz, M.; Ahmed, A.; Hussain, S. Recent Trends and Challenges in Lead-Free Perovskite Solar Cells: A Critical Review. ACS Appl. Energy Mater. 2024, 7, 1382–1397. [Google Scholar] [CrossRef]
- Yao, J.-Y.; Liu, H.; Chen, Z.-N.; Ma, B.; Xu, L.-J. Low-Dimensional Lead-Free Metal Halides for Efficient Electrically Driven Light-Emitting Diodes. Angew. Chem. Int. Ed. 2025, 64, e202423185. [Google Scholar] [CrossRef] [PubMed]
- EU Phasing Out Use of Pb. Available online: https://echa.europa.eu/hot-topics/lead (accessed on 27 May 2025).
- Li, Y.J.; Mu, B.H.; Li, H.B.; Tang, S.C.; Tian, J.; Li, Y.; Ji, Z.Y.; Wang, Y.J.; He, T.; Emeline, A.V.; et al. Bi-Based Metal Halide Perovskites and Their Photocatalytic Properties: A Review. Energy Fuels 2025, 39, 2986–3007. [Google Scholar] [CrossRef]
- Wang, X.; Hu, B.; Li, Y.; Zhang, G. Lead-Free Halide Perovskite Photocatalysts for Photocatalytic CO2 Reduction: A Review. Sol. RRL 2023, 7, 2300410. [Google Scholar] [CrossRef]
- Chen, X.; Jia, M.; Xu, W.; Pan, G.; Zhu, J.; Tian, Y.; Wu, D.; Li, X.; Shi, Z. Recent Progress and Challenges of Bismuth-Based Halide Perovskites for Emerging Optoelectronic Applications. Adv. Optical Mater. 2023, 11, 2202153. [Google Scholar] [CrossRef]
- Coccia, C.; Moroni, M.; Malavasi, L. Chiral Metal Halide Perovskites: Focus on Lead-Free Materials and Structure-Property Correlations. Molecules 2023, 28, 6166. [Google Scholar] [CrossRef] [PubMed]
- Priyadarshini, P.; Senapati, S.; Naik, R. Lead-free organic inorganic hybrid halide perovskites: An emerging candidate for bifunctional applications. Ren. Sust. Energy Rev. 2023, 186, 113649. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, Z.; Xiu, J.; Song, H.; Gatti, T.; He, Z. A critical review on bismuth and antimony halide based perovskites and their derivatives for photovoltaic applications: Recent advances and challenges. J. Mater. Chem. A 2020, 8, 16166–16188. [Google Scholar] [CrossRef]
- Hu, Y.-Q.; Hui, H.-Y.; Lin, W.-Q.; Wen, H.-Q.; Yang, D.-S.; Feng, G.-D. Crystal and Band-Gap Engineering of One-Dimensional Antimony/Bismuth-Based Organic−Inorganic Hybrids. Inorg. Chem. 2019, 58, 16346–16353. [Google Scholar] [CrossRef]
- Ganose, A.M.; Savory, C.N.; Scanlon, D.O. Beyond methylammonium lead iodide: Prospects for the emergent field on ns2 containing solar absorbers. Chem. Commun. 2017, 53, 20–44. [Google Scholar] [CrossRef]
- Jin, J.-C.; Shen, N.-N.; Wang, Z.-P.; Peng, Y.-C.; Huang, X.-Y. Photoluminescent ionic metal halides based on s2 typed ions and aprotic ionic liquid cations. Coord. Chem. Rev. 2021, 448, 214185. [Google Scholar] [CrossRef]
- Rowinska, M.; Stefanska, D.; Bednarchuk, T.J.; Zareba, J.K.; Jakubas, R.; Gagor, A. Polymorphism and Red Photoluminescence Emission from 5s2 Electron Pairs of Sb(III) in a New One-Dimensional Organic–Inorganic Hybrid Based on Methylhydrazine: MHy2SbI5. Molecules 2024, 29, 455. [Google Scholar] [CrossRef]
- Yao, L.; Xue, K.-H.; Tong, H.; Chen, C.; Niu, G.; Yang, W.; Tang, J. Dimensional Control of Chiral Antimony Halide Compounds for Enhanced Circular Dichroism. Cryst. Growth Des. 2022, 22, 5552–5558. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Sung, H.H.; Williams, I.D.; Lu, H. Structural Asymmetry and Chiroptical Activity of Chiral Antimony-Halide Hybrids. Eur. J. Inorg. Chem. 2022, 2022, e202200275. [Google Scholar] [CrossRef]
- Liu, K.; Deng, C.; Li, C.; Zhang, X.; Cao, J.; Yao, J.; Zhao, J.; Jiang, X.; Lin, Z.; Liu, Q. Hybrid Metal-Halide Infrared Nonlinear Optical Crystals of (TMEDA)MI5 (M = Sb, Bi) with High Stability. Adv. Opt. Mater. 2021, 9, 2101333. [Google Scholar] [CrossRef]
- Oswald, I.W.; Mozur, E.M.; Moseley, I.P.; Ahn, H.; Neilson, J.R. Hybrid Charge-Transfer Semiconductors:(C7H7)SbI4, (C7H7)BiI4, and Their Halide Congeners. Inorg. Chem. 2019, 58, 5818–5826. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.X.; Hua, X.N.; Chen, X.G.; Mei, G.Q.; Liao, W.Q. [C6N2H18][SbI5]: A Lead-free Hybrid Halide Semiconductor with Exceptional Dielectric Relaxation. Inorg. Chem. 2019, 58, 4337–4343. [Google Scholar] [CrossRef]
- Parmar, S.; Pal, S.; Biswas, A.; Gosavi, S.; Chakraborty, S.; Reddy, M.C.; Ogale, S. Designing a new family of oxonium-cation based structurally diverse organic-inorganic hybrid iodoantimonate crystals. Chem. Commun. 2019, 55, 7562–7565. [Google Scholar] [CrossRef]
- Dennington, A.J.; Weller, M.T. Synthesis, structure and optoelectronic properties of hybrid iodobismuthate & iodoantimonate semiconducting materials. Dalton Trans. 2018, 47, 3469–3484. [Google Scholar] [CrossRef]
- Mousdis, G.A.; Ganotopoulos, N.M.; Barkaoui, H.; Abid, Y.; Psycharis, V.; Savvidou, A.; Raptopoulou, C.P. One-Dimensional Organic–Inorganic Hybrid Materials Based on Antimony. Eur. J. Inorg. Chem. 2017, 2017, 3401–3408. [Google Scholar] [CrossRef]
- Qi, S.; Cheng, P.; Han, X.; Ge, F.; Shi, R.; Xu, L.; Li, G.; Xu, J. Organic–inorganic hybrid antimony(III) halides for second harmonic generation. Cryst. Growth Des. 2022, 22, 6545–6553. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Liang, P.; Zhou, T.; Wang, L.; Xie, R.-J. Dual-band luminescent lead-free antimony chloride halides with near-unity photoluminescence quantum efficiency. Chem. Mater. 2019, 31, 9363–9371. [Google Scholar] [CrossRef]
- Jridi, C.; Elleuch, N.; Shova, S.; Boujelbene, M. New lead-free Iodoantimonatehalide semiconductor: Synthesis, Structural characterization, DFT calculations, Hirshfeld surface, Thermal behavior, vibrational and optical properties. J. Mol. Struct. 2025, 1321, 139781. [Google Scholar] [CrossRef]
- Shestimerova, T.A.; Medved’ko, A.V.; Bykov, M.A.; Kalinin, M.A.; Metlin, M.T.; Taydakov, I.V.; Gontcharenko, V.E.; Wei, Z.; Dikarev, E.V.; Vatsadze, S.Z.; et al. A new supramolecular tecton: The crucial impact of the polycation charge and geometry of H-bonds on the structure and properties of halometallates in the solid state. Dalton Trans. 2025, 54, 6983–6992. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Song, Z.; Yang, C.; Wei, Y.; Liu, G.; Meng, L.; Wu, Q.; Dang, Y. Nonlinear Optical Effects of Hybrid Antimony(III) Halides Induced by Stereoactive 5s2 Lone Pairs and Trimethylammonium Cations. Inorg. Chem. 2024, 63, 10304–10311. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.; Zhang, G.; Wang, Y.; Zhang, M.; Tian, L.; Cheng, Z.; Lian, H.; Lin, J. Gradient Luminescence Enhancement in Organic Metal Halide Perovskites via the Suppression of [SbCln]3−n Unit Distortion. Inorg. Chem. 2024, 63, 24331–24341. [Google Scholar] [CrossRef] [PubMed]
- Hou, A.; Fan, L.; Xiong, Y.; Lin, J.; Liu, K.; Chen, M.; Guo, Z.; Zhao, J.; Liu, Q. Zero-Dimensional Halides with ns2 Electron (Sb3+) Activation to Generate Broad Photoluminescence. Inorg. Chem. 2023, 62, 12501–12509. [Google Scholar] [CrossRef]
- Rowinska, M.; Piecha-Bisiorek, A.; Medycki, W.; Durlak, P.; Jakubas, R.; Gagor, A. Structural, Electric and Dynamic Properties of (Pyrrolidinium)3[Bi2I9] and (Pyrrolidinium)3[Sb2I9]: New Lead-Free, Organic-Inorganic Hybrids with Narrow Band Gaps. Molecules 2023, 28, 3894. [Google Scholar] [CrossRef]
- Luo, J.B.; Wei, J.H.; Zhang, Z.Z.; Kuang, D.B. Water-Molecule-Induced Emission Transformation of Zero-Dimension Antimony-Based Metal Halide. Inorg. Chem. 2022, 61, 338–345. [Google Scholar] [CrossRef]
- Szklarz, P.; Jakubas, R.; Medycki, W.; Gagor, A.; Cichos, J.; Karbowiak, M.; Bator, G. (C3N2H5)3Sb2I9 and (C3N2H5)3Bi2I9: Ferroelastic lead-free hybrid perovskite-like materials as potential semiconducting absorbers. Dalton Trans. 2022, 51, 1850–1860. [Google Scholar] [CrossRef]
- Wu, Y.; Xiang, G.; Zhang, M.; Wei, D.; Cheng, C.; Leng, J.; Ma, H. Electronic Structures and Photoelectric Properties in Cs3Sb2X9 (X = Cl, Br, or I) under High Pressure: A First Principles Study. Nanomaterials 2022, 12, 2982. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Z.; Liu, X.; Tao, K.; Han, S.; Wang, Y.; Liu, Y.; Li, M.; Luo, J.; Sun, Z. Two Heteromorphic Crystals of Antimony-Based Hybrids Showing Tunable Optical Band Gaps and Distinct Photoelectric Responses. Inorg. Chem. 2019, 58, 6544–6549. [Google Scholar] [CrossRef]
- Cheng, J.; Qian, P.; Yang, M.; Huang, L.; Zeng, H.; Zou, G.; Lin, Z. Second-Harmonic Generation in Homochiral Antimony Halides Directed by L-Histidine. Inorg. Chem. 2023, 62, 16673–16676. [Google Scholar] [CrossRef]
- Gilday, L.C.; Robinson, S.W.; Barendt, T.A.; Langton, M.J.; Mullaney, B.R.; Beer, P.D. Halogen Bonding in Supramolecular Chemistry. Chem. Rev. 2015, 115, 7118–7195. [Google Scholar] [CrossRef] [PubMed]
- Ferjani, H.; Chebbi, H.; Fettouhi, M. One-Dimensional Organic–Inorganic Material (C6H9N2)2BiCl5: From Synthesis to Structural, Spectroscopic, and Electronic Characterizations. Int. J. Mol. Sci. 2021, 22, 2030. [Google Scholar] [CrossRef] [PubMed]
- Ferjani, H.; Lemine, O.; Ben Smida, Y.; Salah, N.; Kaouach, H.; Saadi, F.; Wahbi, H.I.; Almashnowi, M.Y.; Ramadan, R.; Onwudiwe, D.C. Visible emission from a zero-dimensional tin-based organic-inorganic metal halide for luminescent devices: Experimental and theoretical investigation. J. Mol. Struct. 2025, 1327, 141210. [Google Scholar] [CrossRef]
- Ferjani, H. Structural, Hirshfeld surface analysis, morphological approach, and spectroscopic study of new hybrid iodobismuthate containing tetranuclear 0D cluster Bi4I16·4(C6H9N2) 2(H2O). Crystals 2020, 10, 397. [Google Scholar] [CrossRef]
- Robinson, K.; Gibbs, G.V.; Ribbe, P.H. Quadratic elongation: A quantitative measure of distortion in coordination polyhedra. Science 1971, 172, 567–570. [Google Scholar] [CrossRef]
- Jiang, X.; Li, M.; Tao, Y.; Zhang, M.; Li, X.; Zhang, T.; Gu, J.; Bai, G.; Zheng, N.; Zhao, X.; et al. One-dimensional lead halide perovskite quantum ribbons with controllable edge terminations and ribbon widths. Chem 2025, 11, 102548. [Google Scholar] [CrossRef]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Zaib, S.; Khan, I.; Ibrar, A.; McAdam, C.J.; Abdou, S.N.; Ibrahim, M.M.; El-Bahy, S.M.; Frontera, A. Energetic Features of H-Bonded and Antiparallel π-Stacked Supramolecular Assemblies in Pyrazolones: Experimental, Computational and Biological Analyses. J. Mol. Struct. 2025, 1318, 139232. [Google Scholar] [CrossRef]
- Rocha, M.; Saeed, A.; Gil, D.M.; Echeverría, G.A.; Piro, O.E.; Khurshid, A.; Arshad, M.; Ali Shah, S.A.; Erben, M.F. Crystal Engineering with Novel Antipyride Derivatives: Insights from X-ray Diffraction, Hirshfeld Surface Analysis, and DFT Calculations on Intermolecular Interactions. J. Mol. Struct. 2025, 1319, 139450. [Google Scholar] [CrossRef]
- Woensdregt, C.F. Hartman-Perdok Theory: Influence of Crystal Structure and Crystalline Interface on Crystal Growth. Faraday Discuss. 1993, 95, 97–107. [Google Scholar] [CrossRef]
- Klein, J.; Kampermann, L.; Mockenhaupt, B.; Behrens, M.; Strunk, J.; Bacher, G. Limitations of the Tauc Plot Method. Adv. Funct. Mater. 2023, 33, 2304523. [Google Scholar] [CrossRef]
- Lin, F.; Yang, C.; Chen, R.; Wei, W.; Liu, M.; Wang, J.; Guo, F. Near-Unity Emission in Zero-Dimensional Sb(III)-Based Halides Intervened by Hydrogen Bonds towards Efficient Solid-State Lighting Technology. J. Alloys Compd. 2024, 976, 173054. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y.; Yin, H.; Chen, J.; Han, K.; Liu, F.; Zhang, R. Excitation-Dependent Emission in Sb3+-Doped All-Inorganic Rare-Earth Double Perovskites for Anticounterfeiting Applications. Inorg. Chem. 2024, 63, 10481–10489. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Rettig, A.; Feng, X.; Epifanovsky, E.; Head-Gordon, M. Faster Exact Exchange for Solids via occ-RI-K: Application to Combinatorially Optimized Range-Separated Hybrid Functionals for Simple Solids with Pseudopotentials Near the Basis Set Limit. J. Chem. Theory Comput. 2022, 18, 7336–7349. [Google Scholar] [CrossRef] [PubMed]
- Baer, R.; Livshits, E.; Salzner, U. Tuned Range-Separated Hybrids in Density Functional Theory. Annu. Rev. Phys. Chem. 2010, 12, 85–109. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Zheng, X.; Qiang Su, N.; Yang, W. Localized orbital scaling correction for systematic elimination of delocalization error in density functional approximations. Natl. Sci. Rev. 2018, 5, 203–215. [Google Scholar] [CrossRef]
- Möbs, J.; Stuhrmann, G.; Wippermann, S.; Heine, J. Optical Properties and Metal-Dependent Charge Transfer in Iodido Pentelates. ChemPlusChem 2023, 88, e202200403. [Google Scholar] [CrossRef]
- Koopmans, T. Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den Einzelnen Elektronen Eines Atoms. Physica 1934, 1, 104–113. [Google Scholar] [CrossRef]
- Janak, J.F. Proof that ∂E/∂ni = ε in density-functional theory. Phys. Rev. B 1978, 18, 7165–7168. [Google Scholar] [CrossRef]
- Tsuneda, T.; Song, J.-W.; Suzuki, S.; Hirao, K. On Koopmans’ theorem in density functional theory. J. Chem. Phys. 2010, 133, 174101. [Google Scholar] [CrossRef]
- Pearson, R.G. Absolute electronegativity and hardness: Application to inorganic chemistry. Inorg. Chem. 1988, 27, 734–740. [Google Scholar] [CrossRef]
- Wang, H.; Tal, A.; Bischoff, T.; Gono, P.; Pasquarello, A. Accurate and efficient band-gap predictions for metal halide perovskites at finite temperature. npj Comput. Mater. 2022, 8, 237. [Google Scholar] [CrossRef]
- Bruker AXS. SAINT Software Reference Manual; Bruker AXS Inc.: Madison, WI, USA, 1998. [Google Scholar]
- Sheldrick, G. SADABS; Bruker Axs Inc.: Madison, WI, USA, 2007. [Google Scholar]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXT–Integrated space-group and crystal-structure determination. Acta Crystallogr. C Found. Crystallogr. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Macrae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From visualization to analysis, design and prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef]
- Hobday, C.L.; Woodall, C.H.; Lennox, M.J.; Frost, M.; Kamenev, K.; Duren, T.; Morrison, C.A.; Moggach, S.A. Understanding the adsorption process in ZIF-8 using high pressure crystallography and computational modelling. Nat. Commun. 2018, 9, 1429. [Google Scholar] [CrossRef]
- Brekalo, I.; Lisac, K.; Ramirez, J.R.; Pongrac, P.; Xu, Y.; Ferguson, M.; Marrett, J.M.; Arhangelskis, M.; Friščić, T.; Holman, K.T. Mechanochemical Solid Form Screening of Zeolitic Imidazolate Frameworks using Structure-Directing Liquid Additives. ChemRxiv 2025. [Google Scholar] [CrossRef]
- Gao, Y.; Song, W.; Yang, J.; Ji, X.; Wang, N.; Huang, X.; Wang, T.; Hao, H. Crystal Morphology Prediction Models and Regulating Methods. Crystals 2024, 14, 484. [Google Scholar] [CrossRef]
- Donnay, J.D.H.; Harker, D. A new law of crystal morphology extending the law of Bravais. Amer Mineral. J. Earth Planet. Mater. 1937, 22, 446–467. [Google Scholar]
- Ferjani, H. Novel flucytosine salt: Structure, Hirshfeld surface analysis, morphology, FIMs, and computational studies. J. Mol. Graph. Model. 2025, 137, 109012. [Google Scholar] [CrossRef]
- Gasteiger, J.; Marsili, M. A new model for calculating atomic charges in molecules. Tetrahedron Lett. 1978, 19, 3181–3184. [Google Scholar] [CrossRef]
- Hartman, P.; Bennema, P. The attachment energy as a habit controlling factor: I. Theoretical considerations. J. Cryst. Growth 1980, 49, 145–156. [Google Scholar] [CrossRef]
- Hartman, P. The attachment energy as a habit controlling factor: III. Application to corundum. J. Cryst. Growth 1980, 49, 166–170. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+ G basis set for first-row elements, Li–F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. [Google Scholar] [CrossRef]
- Andrae, D.; Häußermann, U.; Dolg, M.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the second and third row transition elements. Theor. Chim. Acta 1990, 77, 123–141. [Google Scholar] [CrossRef]
- Cundari, T.R.; Stevens, W.J. Effective core potential methods for the lanthanides. J. Chem. Phys. 1993, 98, 5555–5565. [Google Scholar] [CrossRef]
- Dolg, M.; Stoll, H.; Preuss, H. A combination of quasirelativistic pseudopotential and ligand field calculations for lanthanoid compounds. Theor. Chim. Acta 1993, 85, 441–450. [Google Scholar] [CrossRef]
- Li, M.; Reimers, J.R.; Ford, M.J.; Kobayashi, R.; Amos, R.D. Accurate prediction of the properties of materials using the CAM-B3LYP Density Functional. J. Comput. Chem. 2021, 42, 1486–1497. [Google Scholar] [CrossRef]
- Kodikara, M.S.; Stranger, R.; Humphrey, M.G. Long-Range Corrected DFT Calculations of First Hyperpolarizabilities and Excitation Energies of Metal Alkynyl Complexes. ChemPhysChem 2018, 19, 1537–1546. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–556. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Bader, R.F. A bond path: A universal indicator of bonded interactions. J. Phys. Chem. A 1998, 102, 7314–7323. [Google Scholar] [CrossRef]
- Contreras-Garcia, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.P.; Beratan, D.N.; Yang, W. NCIPLOT: A program for plotting non-covalent interaction regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
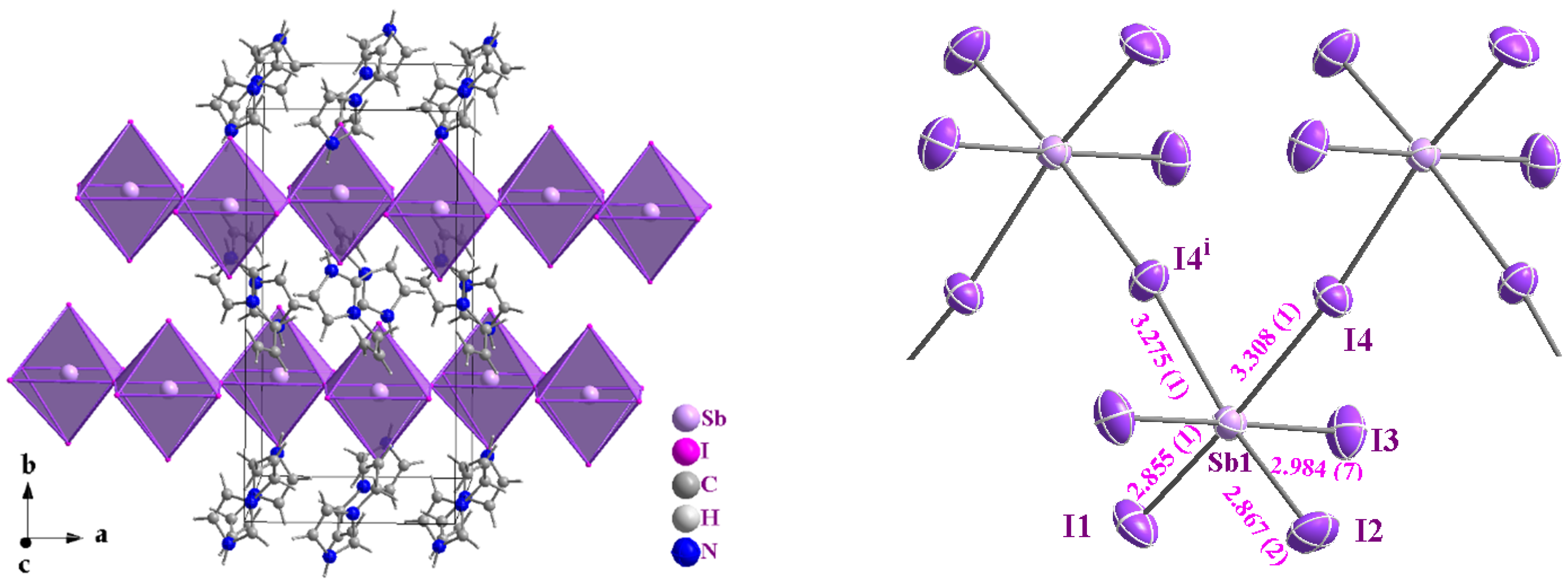
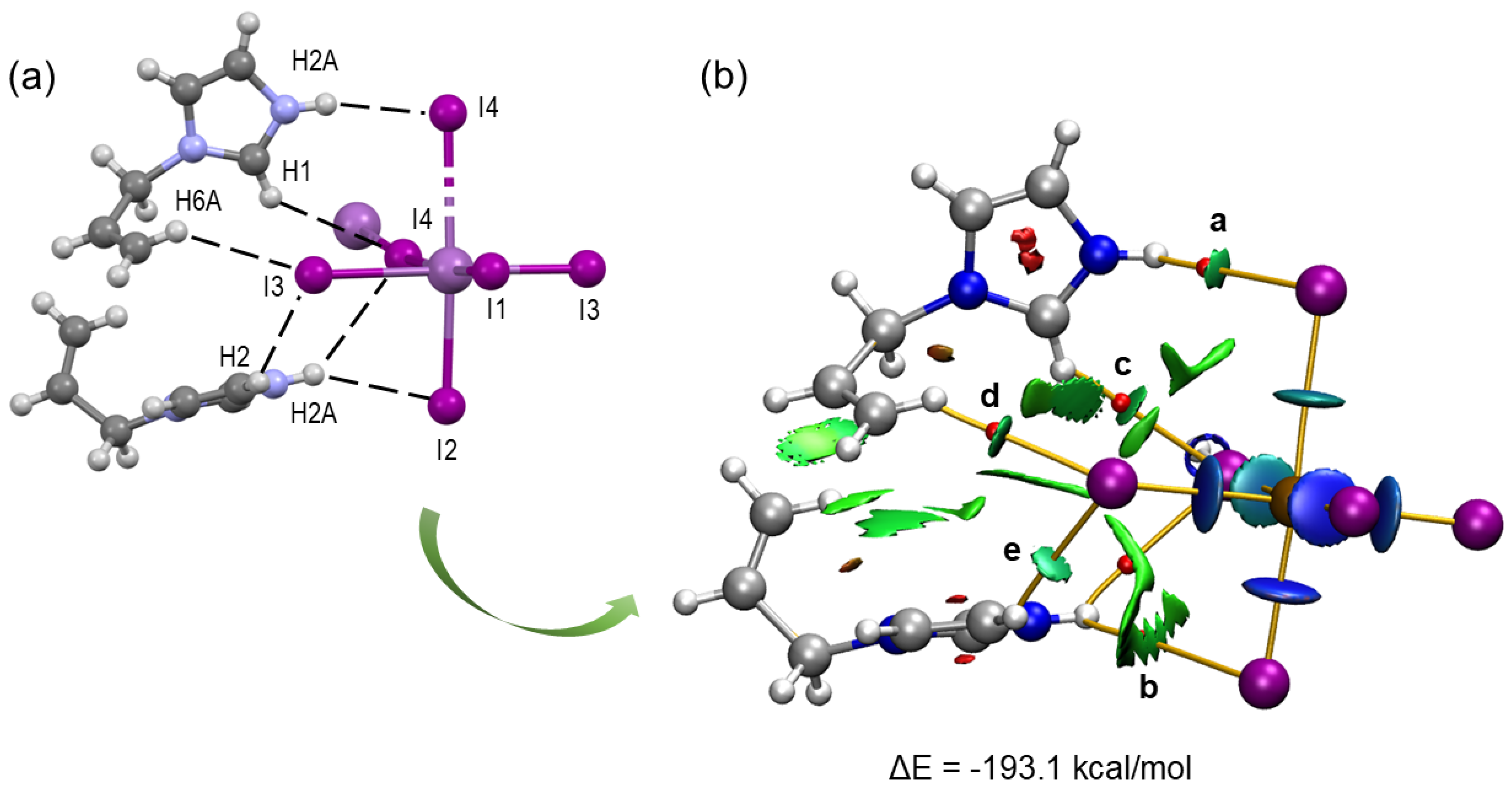


| Bond lengths (Å) | Sb1–I3 | 2.984(8) | |
| Sb1–I1 | 2.855(1) | Sb1–I3i | 2.984(8) |
| Sb1–I2 | 2.867(1) | Sb1–I4 | 3.308(1) |
| Bond angles (°) | |||
| I1–Sb1–I2 | 98.89(5) | I3–Sb1–I3i | 178.70(5) |
| I1–Sb1–I3 | 89.87(2) | I1–Sb1–I4 | 175.89(5) |
| I2–Sb1–I3 | 89.39(2) | I2–Sb1–I4 | 85.23(4) |
| I1–Sb1–I3i | 89.87(2) | I3–Sb1–I4 | 90.17(2) |
| I2–Sb1–I3i | 89.39(2) | I3i–Sb1–I4 | 90.17(2) |
| unit | distances (Å) | angles (°) | ||
| D–H···A | D–H | H···A | D···A | D–H···A |
| N2–H2A···I4 ii | 0.86 | 3.09 | 3.78(1) | 141 |
| C4–H4A···I3 iii | 0.97 | 3.03 | 3.91(3) | 152 |
| C2–H2···I3 ii | 0.93 | 2.99 | 3.73(2) | 138 |
| C1–H1···I4 iv | 0.93 | 3.17 | 3.93(2) | 141 |
| compound | Δoct | σoct2 | long Sb–I bond (Å) | d(H···I) Å | effect on structure | Ref. |
| (AImd)21∞[SbI5] | 0.0055 | 12.12 | 3.308 (1) | 3.09 | I4 displaced due to hydrogen bonding | This work |
| (2-MPDA)1∞[SbI5] | 0.0026 | 12.56 | 3.210 (1) | 2.93 | I4 displaced due to hydrogen bonding | [35] |
| (TMEDA)1∞[SbI5] | 0.0015 | 8.992 | 3.199 (9) | - | stereoactivity of 5s2 lone pair | [33] |
| (CH3SC(NH2)2)1∞[SbI5] | 0.0039 | 7.51 | 3.344 (3) | 2.94 | I1 displaced due to hydrogen bonding | [38] |
| (R-EBAH)21∞[SbI5] | 0.0659 | 18.746 | 3.255 (2) | 2.88 | I4 displaced due to hydrogen bonding | [32] |
| Exp | B3LYP/ LANL2DZ | B3LYP/ SDD | CAM/ LANL2DZ | CAM/ SDD | PBE0/ LANL2DZ | PBE0/ SDD | |
| Sb1–I1 | 2.855(1) | 2.92342 | 2.89780 | 2.88125 | 2.87243 | 2.89065 | 2.88086 |
| Sb1–I2 | 2.867(1) | 2.91104 | 2.91454 | 2.87727 | 2.86559 | 2.88333 | 2.87032 |
| Sb1–I3 | 2.984(1) | 2.96581 | 2.95290 | 2.94494 | 2.93347 | 2.94718 | 2.93301 |
| Sb1–I4 | 3.308(1) | 3.24489 | 3.23021 | 3.27784 | 3.27024 | 3.22004 | 3.21026 |
| C1–N2 | 1.27(3) | 1.33650 | 1.32956 | 1.32262 | 1.32247 | 1.32407 | 1.32384 |
| C1–N1 | 1.32(2) | 1.32961 | 1.33653 | 1.32984 | 1.32999 | 1.33121 | 1.33136 |
| C2–C3 | 1.22(3) | 1.36100 | 1.36107 | 1.35441 | 1.35447 | 1.35886 | 1.35890 |
| C2–N2 | 1.40(3) | 1.37680 | 1.37685 | 1.37228 | 1.37226 | 1.36888 | 1.36887 |
| experimental | models | ||||
| BFDH | GM | ||||
| h k l | multiplicity | dhkl (Å) | % total facet area | Eatt (total) (kcal∙mol−1) | % total facet area |
| (0 1 1) | 4 | 11.51 | 57.70 | −14.73 | 88.63 |
| (1 0 1) | 4 | 7.75 | 22.32 | −62.42 | 11.31 |
| (1 1 1) | 8 | 7.11 | 11.55 | −65.72 | 0.06 |
| (0 2 0) | 2 | 8.92 | 8.43 | – | – |
| compound | dimensionality | cation | Eg (eV) | Ref |
| (AImd)21∞[SbI5] | 1D | 1-allyl-1H-imidazolium | 3.15 | this work |
| (R-EBAH)21∞[SbI5] | 1D | (R)-(+)-α-ethylbenzyl-ammonium | 2.20 | [32] |
| (TMEDA)1∞[SbI5] | 1D | N,N,N′-trimethyl-ethylene-diammonium | 2.01 | [33] |
| (2-MPDA)1∞[SbI5] | 1D | 2-methyl-1,5-pentane-diammonium | 1.92 | [35] |
| (CH3SC(NH2)2)1∞[SbI5] | 1D | CH3SC(NH2)+ | 2.41 | [38] |
| (3A10)[SbI6]·3H2O | 0D | H3[6-amino-5,7-dimethyl-1,3-diazaadamantane]3+ a | 2.50 | [42] |
| (MHy)21∞[SbI5] | 1D | [NH2-NH2-CH3]+ | 2.12, 2.01 b | [30] |
| (AImd)21∞[BiCl5] | 1D | 1-allyl-1H-imidazolium | 3.26 | [53] |
| (AImd)2[SnCl6] | 0D | 1-allyl-1H-imidazolium | 3.72 | [54] |
| B3LYP/ LANL2DZ | B3LYP/ SDD | CAM/ LANL2DZ | CAM/ SDD | PBE0/ LANL2DZ | PBE0/ SDD | |
| EHOMO (eV) | −5.66 | −5.73 | −6.87 | −6.93 | −5.94 | −5.97 |
| ELUMO (eV) | −3.00 | −3.04 | −2.13 | −2.16 | −2.97 | −2.96 |
| Eg (eV) | 2.66 | 2.69 | 4.73 | 4.77 | 2.97 | 3.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferjani, H.; Bechaieb, R.; Gil, D.M.; Klein, A. The 1D Hybrid Material Allylimidazolium Iodoantimonate: A Combined Experimental and Theoretical Study. Inorganics 2025, 13, 243. https://doi.org/10.3390/inorganics13070243
Ferjani H, Bechaieb R, Gil DM, Klein A. The 1D Hybrid Material Allylimidazolium Iodoantimonate: A Combined Experimental and Theoretical Study. Inorganics. 2025; 13(7):243. https://doi.org/10.3390/inorganics13070243
Chicago/Turabian StyleFerjani, Hela, Rim Bechaieb, Diego M. Gil, and Axel Klein. 2025. "The 1D Hybrid Material Allylimidazolium Iodoantimonate: A Combined Experimental and Theoretical Study" Inorganics 13, no. 7: 243. https://doi.org/10.3390/inorganics13070243
APA StyleFerjani, H., Bechaieb, R., Gil, D. M., & Klein, A. (2025). The 1D Hybrid Material Allylimidazolium Iodoantimonate: A Combined Experimental and Theoretical Study. Inorganics, 13(7), 243. https://doi.org/10.3390/inorganics13070243








