Abstract
In photoacoustic spectroscopy, the signal is inversely proportional to the resonant cell volume. Photoacoustic spectroscopy (PAS) is an absorption spectroscopy technique that is suitable for detecting gases at low concentrations. This desirable feature has created a growing interest in miniaturizing PA cells in recent years. In this paper, a simulation of a miniaturized H-type photoacoustic cell consisting of two buffer holes and a resonator was performed in order to detect CO, NH3, NO, and CH4 pollutants. These gases are the main components of the air pollutants that are produced by the automotive industry. The linear forms of the continuity, Navier–Stokes equations, and the energy equation were solved using the finite element method in a gaseous medium. The generated pressure could be measured by a MEMS sensor. Photoacoustic spectroscopy has proven to be a sensitive method for detecting pollutant gases. The objectives of the measurements were: determining the proper position of the pressure gauge sensor; measuring the frequency response; measuring the frequency response changes at different temperatures; studying the local velocity at the resonant frequency; and calculating the quality factor. The acoustic quality coefficient, acoustic response (pressure), local velocity, frequency response, and the effect of different temperatures on the frequency response were investigated. A frequency response measurement represents the fact that different gases have different resonance frequencies, for which CO and NO gases had values of 23.131 kHz and 23.329 kHz, respectively. The difference between these gases was 200 Hz. NH3 and CH4 gases with values of 21.206 kHz and 21.106 kHz were separable with a difference of 100 Hz. In addition, CO and NO gases had a difference of 2000 Hz compared to NH3 and CH4, which indicates the characteristic fingerprint of the designed cell in the detection of different gases. Better access to high-frequency acoustic signals was the goal of the presented model in this paper.
1. Introduction
Nowadays, automotive industry pollution is considered a major threat to the planet. Concentrations of gases caused by human activities—for instance, transportation—lead to consequences from the local scale to the global scale that affect the climate, the environment, and human health [1,2,3,4]. As a result of increasing the number of automobiles on the roads, the transportation sector has become the second most considerable consumer of energy and has a major share in the production of air pollutants and greenhouse gas emissions [5,6].
Greenhouse gases have far–ranging environmental and health effects. They cause climate change by trapping heat. Climate change can disrupt the match between organisms and their local environment, reducing survival and reproduction, and causing subsequent impacts on populations and species distributions [7,8,9,10].
Emissions of materials such as carbon monoxide, nitrogen oxides, and hydrocarbons caused by the transportation sector have increased significantly in comparison to previous decades [11]. Carbon monoxide is a toxic gas that endangers human health and causes suffocation. The toxicity of carbon monoxide causes serious problems when it enters the car cabin, which can be avoided by installing a gas leak detector in the car [12]. Nitrogen oxides are important components of air pollution; in addition to helping to form acid rain and the greenhouse effect, at higher levels they have a great impact on human health and can lead to diseases of the respiratory system and, consequently, life-threatening diseases [13]. Ammonia and methane are also important pollutants in the atmosphere, and increasing amounts of them are emitted by road traffic [14]. NOX and CO are the two main pollutants emitted by vehicles, which cause serious environmental pollution as well as health problems and threats (Wang 2018) [15]. Scientists have found that global warming is related to an increment in carbon dioxide emissions, which is another result of gasoline combustion (Karol Tucki 2019) [16]. Optimizing gasoline formulations in order to ensure the best performance and minimal emissions of pollutants has always been a challenge for ages (I. Schifter 2020) [17]. Air contamination caused by energy consumption poses a significant ultimatum for the environment. The study of emission sources is of great importance for the improvement of environmental problems (Miao Zhang 2021) [18]. Identifying and quantifying the effects of gases plays a significant role in the development and improvement of gas-metering technology. One of the main methods of optical spectroscopy is photoacoustic spectroscopy, which utilizes sound and light to investigate materials in solid, liquid, and gas phases [19]. This method is considered an effective and inexpensive method for studying the properties of a substance [20]. Considering that transportation is responsible for most of the pollutants emitted by human resources, photoacoustic spectroscopy is an appropriate method for examining ambient gases due to meeting many needs related to gas detection, including: high sensitivity, spectral selection, and multi-component diagnosis [21]. Photoacoustic spectroscopy has been used to study greenhouse gases in recent years [22,23]. Currently, atmospheric gas sensors based on the principle of spectroscopy have become important, owing to their sensitivity and selectivity. These devices have the ability to quickly monitor and investigate pollutants, the presence in the atmosphere of which may have harmful consequences, such as acid rain, global climate change, and endangering human health [24]. Photoacoustic spectroscopy has various considerable benefits that differentiate this particular detection mechanism from other methods of absorption spectroscopy [25]:
- Photoacoustic spectroscopy does not need an optical detector. Accordingly, it has no choice for detecting wavelengths; therefore, it is possible to apply it to all wavelengths, from ultraviolet to infrared and terahertz.
- The zero-background feature lets the detector and preamplifier operate on a zero signal in a wide dynamic range.
These considerable advantages of photoacoustic spectroscopy have led to a competitive benefit over other absorption spectroscopy technologies. As shown in Figure 1, the photoacoustic effect on gases consists of four stages [26]: (i) modulation of the laser radiation (both amplitude and frequency) at a wavelength for which the target species shows high absorption; (ii) excitation of the target molecules by absorption of the incident radiation; (iii) non-radiative transfer of the absorbed radiation energy via collisions with other molecules, hence resulting in periodic heating at the modulation frequency; and (iv) detection of the acoustic waves produced by the periodic heating with sensitive microphones or pressure sensors.

Figure 1.
Schematic of the physical processes occurring in photoacoustic spectroscopy.
Advances in gas detection sensors for methane, propane, and other toxic gases in the automotive industry have been very promising. The use of detectors in cars in order to detect gas leakages has been considered due to an increase in mortality rates [27]. Optical gas sensors are powerful devices used to detect gases and monitor a variety of applications, such as environmental monitoring, industrial process control, medicine, and petrochemical industry applications [28]. Photoacoustic sensors use acoustic resonance to increase the signal level and improve the minimum concentration of detection [29]. In general, measures to control climate change or reduce air pollution have several advantages, comprising: improvements to energy efficiency, optimization of the environment, and improvements to social health and public benefits [30]. Here, the PS method was employed for the detection of pollutants in which a fingerprint feature was observed for gases. The investigation of toxic air pollutants emitted by vehicles was the main goal of this research. A miniaturized H-type photoacoustic cell was employed to the spectroscopy of CO, NH3, NO, and CH4 gases. The effects of important parameters such as the frequency response, the temperature, and the quality factor were numerically studied for the proposed system, and the results are presented in the Results and Discussion section.
2. Materials and Methods
2.1. Theory
This section explains the mathematical formulation of photoacoustic spectroscopy. The photoacoustic response was numerically investigated by solving the pressure field inside the cell, which is closely related to the acoustic waves produced by the photoacoustic effect [31,32]. Advances in numerical methods and the availability of user-friendly software allowing for the use of the finite element method (FEM) have paved the path for the direct solving of the Helmholtz equation and the optimization of the photoacoustic cell response [33]. Nowadays in general, it is accepted that the FEM is the most flexible numerical method [34]. The advantage of utilizing the FEM model is the potential to handle, in principle, any geometry of a photoacoustic cell. The essential equations for acoustics comprising thermal and viscous losses are applicable in the case where acoustic waves are produced by light absorption [35]:
where the quantities , and r represent the mass density, particle velocity, acoustic pressure, acoustic temperature, entropy, Gaussian spreading parameter, coefficient of shear viscosity, coefficient of bulk viscosity, and radial coordinate (the distance from the z-axis in the cylinders), respectively. Navier–Stokes linearized equations were used for modeling the sound wave propagation in the presence of viscous and thermal boundary layers. The harmonic changes were assumed to be negligible. In order to complete the partial differential equations, the continuity, motion, and energy conservation equations were used. As is obvious, the driving heat source was assumed to be of the Gaussian type. The heat source in a radial position respective to the center line of the resonator is expressed as Equation (4).
As discussed in [33,35], the produced heat in a PA cell by light absorption represents the source for a sound wave. Therefore, a corresponding source term has to be added to the Helmholtz equation:
where p is the Fourier transform, k = w/c, and c is the sound velocity. By considering that the absorbing transition is not saturated, and that the modulation frequency is significantly smaller than the relaxation rate of the molecular transition, the relation H(r, w) = aI(r, w) applies where I(r, w) is the Fourier-transformed intensity of the electromagnetic field. It is known that the solution of the inhomogeneous wave equation can be indicated by Equation (6):
The modes pj(r) and the corresponding eigenfrequencies wj = ckj can be established by solving the homogeneous Helmholtz equation:
2.2. Cell Design
The precision of a photoacoustic cell depends dramatically on its geometry. The H-type cell presented in the current study is simple in design and has two buffers that are connected to each other by a resonator. The buffer structure obviously affects the photoacoustic response. Selecting the dimensions of the buffer cylinders is a crucial issue in designing H-type photoacoustic cells [31,36]. Some advantages of investigating and using miniaturized photoacoustic cells are stated as follows:
- In photoacoustic spectroscopy, the signal is inversely related to the volume of the resonant cell, and this relation has led to the miniaturization of photoacoustic cells with great interest in recent years [37];
- Moreover, in photoacoustic spectroscopy, the detection limit is almost independent of the length of the laser–gas interaction, so this feature makes sensitivity and miniaturization possible in a photoacoustic spectroscopy system [38];
- Conventional photoacoustic gas analyzers mainly demand a large volume of the gas sample and are not suitable for detection applications in confined spaces [39].
Therefore, it is no wonder that a considerable portion of studies have focused on the design of miniaturized photo-acoustic sensors that can provide better portability and local detection without compromising the detection sensitivity. The cavity configuration was used because of the simple symmetry of the cylinder, which thoroughly matches the laser beam and propagates along the axis of the cylinder or one of its special modes, and also because of its easy processing [40]. The calculations were performed for a photoacoustic cell with a resonator length of Lres = 5 mm, a resonator radius of Rres = 2.5 mm, a buffer length of Lbuf = 2.5 mm, and a buffer radius of Rbuf = 2.5 × Rres. The geometrical dimensions of the parameters were chosen based on the MEMS-based microphone scales. Figure 2 represents a simulated photoacoustic cell.
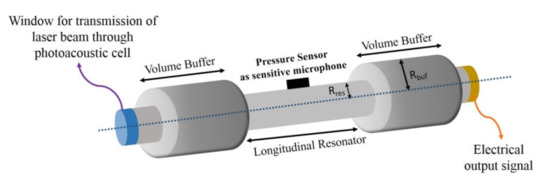
Figure 2.
H-cell model as the photoacoustic cell.
2.3. Numerical Modeling
FEM studies are widely used to probe the behavior of forthcoming devices and their optimization [41]. The simulation of the photoacoustic response in a miniaturized H-type photoacoustic cell is discussed in this section. It should be noted that the FEM simulation of a PS cell as a gas detector was validated using the experimental results from [32]. Various environmental parameters have an impact on the signal of a gas sensor—for instance, pressure, mechanical vibration, background noise, electromagnetic fields, and temperature. As the laser beam passes through the windows of the photoacoustic cell, some amount of light may be absorbed by the windows, which can produce acoustic waves; these undesirable waves are called window noise. In this case, the length of the buffer cylinder should be 1/4 acoustic wavelengths in order to minimize window noise [42]. The effects of mechanical vibrations or background noise are negligible at higher resonant frequencies because mechanical vibrations are usually at lower frequencies. Due to the optical readout, the effects of electromagnetic fields on the sensor signal are also negligible [43].
In general, two non-slip boundary conditions were applied to the velocity field and adiabatic conditions to temperature. These two conditions are known as standard boundary conditions for acoustic pressure. Standard boundary conditions of acoustic pressure were applied in order to prevent any thermal or adhesive boundary layers on the walls (layers are negligible) [44]. The other parameter that needed to be considered in the study of photoacoustic cells was the quality factor. The higher the loss rate, the lower the quality factor value [45]. The Q factor was determined as the ratio between the resonance frequency and the width of the resonance peak at half its resonance amplitude (FWHM). It was estimated using Equation (5) [46]:
where f0 represents the resonance frequency while fl and fh are the frequencies at which the value of the pressure amplitude has reduced to half of its value. Δf ( is the half width of the resonance peak. Therefore, Δf is also called the full width half maximum (FWHM) of the peak amplitude. The commercial FEM-based software COMSOL Multiphysics was utilized to model the miniaturized PA cell.
3. Results and Discussion
Due to the fact that vehicles are a major contributor to environmental pollution, in this study CO, NH3, NO, and CH4 gases were simulated. Then, the effect of various parameters was examined and analyzed when the miniaturized H-type photoacoustic cell was filled by these gases.
3.1. Acooustic Pressure
The acoustic pressure generated inside the cell was measured by a pressure sensor. Therefore, the first step in the study of gas was to detect the maximum amount of pressure in the photoacoustic cell. This maximum pressure is where the resonant frequency occurs, or in other words, it is the most suitable place for the pressure sensor to be located. COMSOL Multiphysics software was used to evaluate the distribution of acoustic pressure inside the miniaturized photoacoustic cell filled by CO, NH3, NO, and CH4 gases. The results are presented schematically in Figure 3.
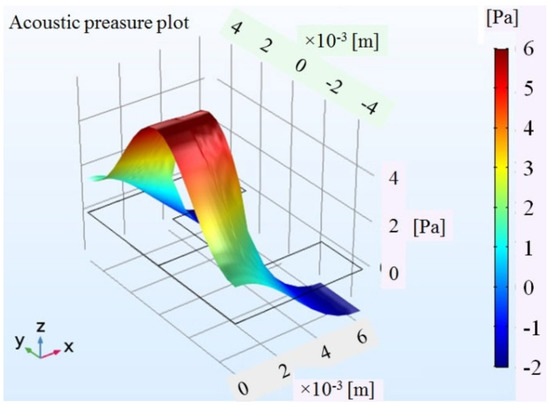
Figure 3.
Acoustic pressure distribution corresponding to the first longitudinal state in a miniaturized acoustic cell.
Figure 3 represents the acoustic pressure distribution for the first excited longitudinal state, where the strongest acoustic pressure occurred in the middle of the resonant cavity. Hence, the first natural frequency was assumed to be the resonant frequency. The technical principle of PAS is to detect the energy of the acoustic wave generated during the molecular de-excitation process, which can be detected with a microphone, a quartz tuning fork (QTF), or a micro-cantilever. In 2021, a multicomponent gas sensor was proposed to detect CH4, H2O, CO2, and C2H2 [47].
3.2. Frequency Response
Determining the frequency response of a photoacoustic cell is a common activity during cell design and examination [32]. The cell frequency response is examined in order to evaluate its suitability for specific measurements. A frequency analysis includes significant information for the design of a pressure sensor. The most important part of this information is determining the operation frequency of the sensor. The frequency of the acoustic wave, as stated in the previous section, is equal to the first natural frequency. Figure 4 shows the resonance frequencies for CO, NH3, NO, and CH4, which had values of 23.329, 21.206, 23.131, and 21.106 kHz, respectively.
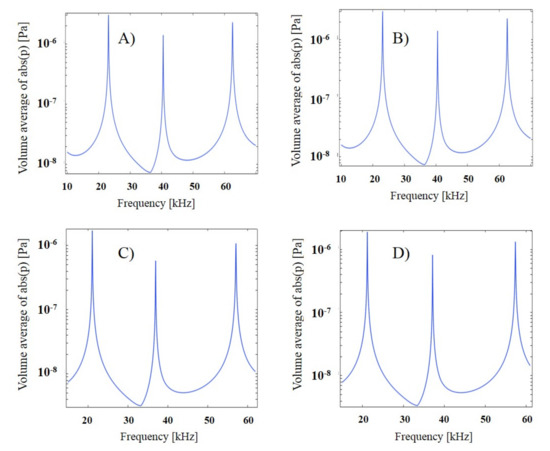
Figure 4.
Frequency response; the cell filled by (A) NO, (B) CO, (C) CH4, and (D) NH3.
3.3. Acoustic Velocity
Since the resonance frequency is directly related to the acoustic velocity, the local acoustic velocity at the resonant frequencies of the mentioned gases in Figure 4 were examined and the obtained results are shown in Figure 5. The r-coordinator in Figure 5 is the length of the resonator; the peaks are related to the frequency resonances of the resonators. The change in the peak of the frequency due to the change in acoustic velocity was different from the composition of the gas. It should be noted that the photoacoustic response of air components such as N2, O2, and CO2 was also simulated: 18.101 kHz for CO2; 23.684 kHz for N2; and 22.112 kHz for O2. Based on the results, these components have a frequency very different from the frequency of pollutants.
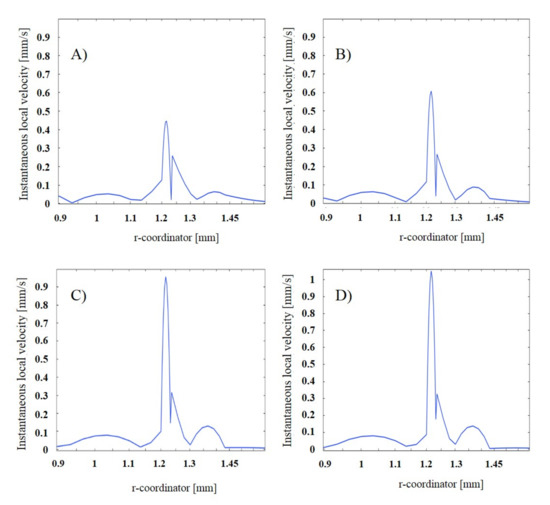
Figure 5.
Instantaneous local velocity (mm/s), with the cell filled by (A) NO, (B) CO, (C) CH4, or (D) NH3.
The obtained results show that the local acoustic velocity at the resonance frequencies had a maximum value in the center of the cell. This indicates the function of the cell in resonance mode.
3.4. Frequency Response Changes with Temperature Changes
Temperature was one of the factors that affected the resonance frequency, as the acoustic velocity increased with temperature T [48,49]. Therefore, temperature changes could cause a change in the resonant frequency of PA cells. The effects of temperature on the sensor in the temperature range of 243 to 303 degrees Kelvin were studied specifically to investigate their effects on the frequency response. Figure 6 shows the rate of change in the frequency response for temperature change. Temperature monitoring was necessary to ensure that the PS cell was working in resonance mode.
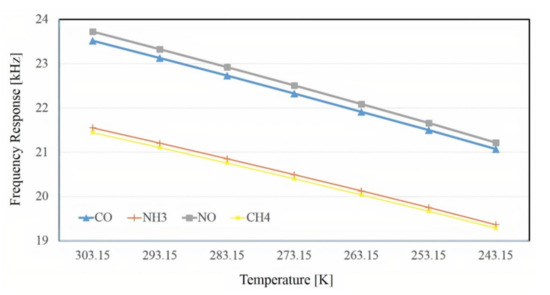
Figure 6.
Frequency response verses temperature variations.
3.5. Quality Factor
The quality factor expresses the amount of energy stored in the resonator relative to the energy lost during a complete period [50,51]. Low losses increase the quality factor. A high quality factor guarantees the sensitivity of the detection. When the resonance peaks are small, it means that the quality factor is lower. Table 1 shows the results for the quality factors of CO, NH3, NO, and CH4 gases. The results indicate that miniaturized photoacoustic cells have a high sensitivity and performance. The mechanical noise was reduced by miniaturizing the resonator’s diameter. Therefore, the QF increased significantly by decreasing the noise in the system. The achieved high QF indicates that the frequency response was highly sensitive for air pollutant gases.

Table 1.
Comparison of QF.
The laser photoacoustic spectroscopy method was an appropriate investigation technique which was capable of measuring gas concentrations at sub-ppb levels [52,53]. The smallest detectable concentration that could be detected with the system was calculated with the following equation:
where V = Vn is the voltage of the photoacoustic signal for a signal-to-noise ratio equal to 1 (SNR = 1), α (cm−1·atm−1) is the absorption coefficient for a given laser line, Pl (W) is the unmodulated peak value of the power laser, C (Pa.cm.W−1) is the cell constant, and SM (mV/Pa) is the total responsivity of the microphones.
4. Conclusions
In this paper, a simulation of a miniaturized photoacoustic cell is presented in order to investigate pollutants produced by the automotive industry. The main advantage of this cell is its size, which facilitates the generation of a proper resonance frequency and quality factor. The PAS method is employed for the detection of pollutants in which a fingerprint feature is observed for gases. The proposed cell has an acoustic response in the center of the resonator, which is the maximum pressure for different gases at different resonant frequencies, and the values for NO, NH3, CO, and CH4 were 23.329, 21.206, 23.131, and 21.106 kHz, respectively. It should be noted that frequency measurements are a common and simple electronic way to measure different mechanical variations, and 100–200 Hz is significant and can be easily measured by MEMS-based oscillators. The dependence of the frequency response on the temperature, as well as the effects of local changes in velocity on the resonance frequency, were investigated to ensure the cell performance in the resonance state. It was shown that the eigenfrequency of photoacoustic cells can be defined by the finite element method. The obtained results in the study of CO, NH3, NO, and CH4 gases had excellent measured frequencies. The suggested cell shows a remarkable QF for the detection of air pollutants. The results show a high potential for miniaturizing photoacoustic cells to expand sensitive laser sensors. The results are useful and well-organized for energy science and fuel cell studies.
Author Contributions
Conceptualization, R.H.V., R.S.P., A.M. (Ardashir Mohammadzadeh), J.H.A. and A.M. (Amir Mosavi); methodology, R.H.V., R.S.P., A.M. (Ardashir Mohammadzadeh), J.H.A. and A.M. (Amir Mosavi); formal analysis, R.H.V., R.S.P., A.M. (Ardashir Mohammadzadeh), J.H.A. and A.M. (Amir Mosavi); investigation, R.H.V., R.S.P., A.M. (Ardashir Mohammadzadeh), J.H.A. and A.M. (Amir Mosavi). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The paper presents no data.
Acknowledgments
This work has been supported by the Center for International Scientific Studies and Collaboration (CISSC) and the Ministry of Science Research and Technology. Also, the authors are grateful to Laurent Francis for fruitful discussions and technical assistance.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhao, Y.; Wang, Y.; Liang, C.; Wang, J.; Fang, J.; Zhou, M. Study of Mixed Pollution of Haze and Dust in Jinan Based on LiDAR. Photonics 2022, 9, 144. [Google Scholar] [CrossRef]
- Restaino, S.R.; Wilcox, C.C.; Andrews, J.R.; Santiago, F.; Martinez, T. Session V. Wavefront sensors, control systems and strategies.-Test Bed Systems for AO. In Proceedings of the 8th International Workshop on Adaptive Optics for Industry and Medicine, Padova, Italy, 3–10 July 2020. [Google Scholar]
- Yuan, Q.; Mirzajani, H.; Evans, B.; Greenbaum, E.; Wu, J. A disposable bulk-acoustic-wave microalga trapping device for real-time water monitoring. Sens. Actuators B Chem. 2020, 304, 127388. [Google Scholar] [CrossRef]
- Korwan, D.; Bevilacqua, R.; Restaino, S.; Bobak, J.; Santiago, F.; Hoppel, K.; Bailey, S.; Noel, S.; Carstins, J.; Randall, C.; et al. The GLO (GFCR Limb Occultation) sensor: A new sensor concept for upper troposphere and lower stratosphere (UTLS) composition and transport studies. In CubeSats and SmallSats for Remote Sensing III; SPIE: Bellingham, WA, USA, 2019; Volume 11131, pp. 154–163. [Google Scholar]
- Fulton, L.; Lah, O.; Cuenot, F. Transport Pathways for Light Duty Vehicles: Towards a 2 Scenario. Sustainability 2013, 5, 1863–1874. [Google Scholar] [CrossRef] [Green Version]
- Geiser, P.; Avetisov, V.; Espinoza-Nava, L.; Menegazzo, N.; Kaspersen, P. Continuous Emission Monitoring of Tetrafluoromethane Using Quantum Cascade Lasers. Photonics 2016, 3, 16. [Google Scholar] [CrossRef] [Green Version]
- Gadedjisso-Tossou, K.S.; Stoychev, L.I.; Mohou, M.A.; Cabrera, H.; Niemela, J.; Danailov, M.B.; Vacchi, A. Cavity ring-down spectros-copy for molecular trace gas detection using a pulsed DFB QCL emitting at 6.8 µm. Photonics 2020, 7, 74. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Hernández, J.C. Optimal selection and location of bess systems in medium-voltage rural dis-tribution networks for minimizing greenhouse gas emissions. Electronics 2020, 9, 2097. [Google Scholar] [CrossRef]
- El Shamy, R.S.; Swillam, M.A.; ElRayany, M.M.; Sultan, A.; Li, X. Compact Gas Sensor Using Silicon-on-Insulator Loop-Terminated Mach–Zehnder Interferometer. Photonics 2021, 9, 8. [Google Scholar] [CrossRef]
- Li, L.; Hao, H. Simulated Study of High-Sensitivity Gas Sensor with a Metal-PhC Nanocavity via Tamm Plasmon Polaritons. Photonics 2021, 8, 506. [Google Scholar] [CrossRef]
- Lopatin, O.P. Gas-diesel engine exhaust gas recirculation. IOP Conf. Ser. Earth Environ. Sci. 2020, 548, 062023. [Google Scholar] [CrossRef]
- Soh, A.C.; Hassan, M.K.; Ishak, A.J. Vehicle gas leakage detector. Pac. J. Sci. Technol. 2010, 11, 66–76. [Google Scholar]
- Pungjunun, K.; Chaiyo, S.; Praphairaksit, N.; Siangproh, W.; Ortner, A.; Kalcher, K.; Chailapakul, O.; Mehmeti, E. Electrochemical detection of NOx gas based on disposable paper-based analytical device using a copper nanoparticles-modified screen-printed graphene electrode. Biosens. Bioelectron. 2019, 143, 111606. [Google Scholar] [CrossRef] [PubMed]
- Cihelka, J.; Horká, V.; Civis, S. Diode laser photoacoustic detection of automobile exhaust emissions. In Proceedings of the 2005 7th International Conference Transparent Optical Networks, Barcelona, Spain, 7 July 2005; Volume 1, pp. 349–354. [Google Scholar]
- Wei, S.; Ding, T.; Zhang, S.; Tao, P.; Chen, J. Analysis of vehicle CO and NOx road emissions test based on PEMS. Energy Sources Part A Recover. Util. Environ. Eff. 2020, 1–15. [Google Scholar] [CrossRef]
- Tucki, K.; Mruk, R.; Orynycz, O.; Botwińska, K.; Gola, A.; Bączyk, A. Toxicity of Exhaust Fumes (CO, NOx) of the Compression-Ignition (Diesel) Engine with the Use of Simulation. Sustainability 2019, 11, 2188. [Google Scholar] [CrossRef] [Green Version]
- Schifter, I.; Díaz, L.; Sánchez-Reyna, G.; González-Macías, C.; González, U.; Rodríguez, R. Influence of gasoline olefin and aromatic content on exhaust emissions of 15% ethanol blends. Fuel 2020, 265, 116950. [Google Scholar] [CrossRef]
- Zhang, M.; Shi, L.; Ma, X.; Zhao, Y.; Gao, L. Study on Comprehensive Assessment of Environmental Impact of Air Pollution. Sustainability 2021, 13, 476. [Google Scholar] [CrossRef]
- Mohebbifar, M. The laser power effect on the performance of gas leak detector based on laser photo-acoustic spectroscopy. Sens. Actuators A Phys. 2020, 305, 111914. [Google Scholar] [CrossRef]
- Rück, T.; Bierl, R.; Matysik, F.M. Low-cost photoacoustic NO2 trace gas monitoring at the pptV-level. Sens. Actuators A Phys. 2017, 263, 501–509. [Google Scholar] [CrossRef]
- Dumitras, D.C.; Petrus, M.; Bratu, A.-M.; Popa, C. Applications of Near Infrared Photoacoustic Spectroscopy for Analysis of Human Respiration: A Review. Molecules 2020, 25, 1728. [Google Scholar] [CrossRef]
- Schmithausen, A.J.; Trimborn, M.; Büscher, W. Methodological comparison between a novel automatic sampling system for gas chromatography versus photoacoustic spectroscopy for measuring greenhouse gas emissions under field con-ditions. Sensors 2016, 16, 1638. [Google Scholar] [CrossRef] [Green Version]
- Hassouna, M.; Robin, P.; Charpiot, A.; Edouard, N.; Méda, B. Infrared photoacoustic spectroscopy in animal houses: Effect of non-compensated interferences on ammonia, nitrous oxide and methane air concentrations. Biosyst. Eng. 2013, 114, 318–326. [Google Scholar] [CrossRef]
- Zelinger, Z.; Střižı́k, M.; Kubát, P.; Jaňour, Z.; Berger, P.; Černý, A.; Engst, P. Laser remote sensing and photoacoustic spectrometry applied in air pollution investigation. Opt. Lasers Eng. 2004, 42, 403–412. [Google Scholar] [CrossRef]
- Yang, T.; Chen, W.; Wang, P. A review of all-optical photoacoustic spectroscopy as a gas sensing method. Appl. Spectrosc. Rev. 2020, 56, 143–170. [Google Scholar] [CrossRef]
- Marinov, D.; Sigrist, M.W. Monitoring of road-traffic emissions with a mobile photoacoustic system Dedicated to Professor Silvia Braslavsky to mark her great contribution to photochemistry and photobiology particularly in the field of photothermal methods. Photochem. Photobiol. Sci. 2003, 2, 774–778. [Google Scholar] [CrossRef]
- Routley, V. Motor vehicle exhaust gas suicide: Review of countermeasures. Crisis 2007, 28, 28–35. [Google Scholar] [CrossRef]
- Dayton, D.C.; Gonglewski, J.D.; Browne, S.L.; Restaino, S.R. MEMS adaptive optics: Field demonstration. In Optics in Atmospheric Propagation and Adaptive Systems V; SPIE: Bellingham, WA, USA , 2003; Volume 4884, pp. 186–195. [Google Scholar]
- Parvitte, B.; Risser, C.; Vallon, R.; Zeninari, V. Complete characterization of trace gas photoacoustic sensors using a finite element method. In Propagation Through and Characterization of Distributed Volume Turbulence; Optica Publishing Group: Washington, DC, USA, 2014; p. JTu4A-32. [Google Scholar]
- Alimujiang, A.; Jiang, P. Synergy and co-benefits of reducing CO2 and air pollutant emissions by promoting electric vehicles—A case of Shanghai. Energy Sustain. Dev. 2020, 55, 181–189. [Google Scholar] [CrossRef]
- Vafaie, R.H.; Nojavan, S.; Jermsittiparsert, K. Designing a miniaturized photoacoustic sensor for detecting hydrogen gas. Int. J. Hydrogen Energy 2020, 45, 21148–21156. [Google Scholar] [CrossRef]
- Mannoor, M.; Hwang, J.; Kang, S. Numerical study of geometrical effects on the performance of an H-type cylindrical resonant photoacoustic cell. J. Mech. Sci. Technol. 2018, 32, 5671–5683. [Google Scholar] [CrossRef]
- Parvitte, B.; Risser, C.; Vallon, R.; Zéninari, V. Quantitative simulation of photoacoustic signals using finite element modelling software. Appl. Phys. A 2013, 111, 383–389. [Google Scholar] [CrossRef]
- Baumann, B.; Kost, B.; Groninga, H.; Wolff, M. Eigenmode analysis of photoacoustic sensors via finite element method. Rev. Sci. Instruments 2006, 77, 044901. [Google Scholar] [CrossRef]
- Duggen, L.; Lopes, N.; Willatzen, M.; Rubahn, H.-G. Finite Element Simulation of Photoacoustic Pressure in a Resonant Photoacoustic Cell Using Lossy Boundary Conditions. Int. J. Thermophys. 2011, 32, 774–785. [Google Scholar] [CrossRef]
- Kost, B.; Baumann, B.; Germer, M.; Wolff, M.; Rosenkranz, M. Numerical shape optimization of photoacoustic resonators. Appl. Phys. A 2010, 102, 87–93. [Google Scholar] [CrossRef]
- Glière, A.; Rouxel, J.; Parvitte, B.; Boutami, S.; Zéninari, V. A Coupled Model for the Simulation of Miniaturized and Integrated Photoacoustic Gas Detector. Int. J. Thermophys. 2013, 34, 2119–2135. [Google Scholar] [CrossRef]
- Firebaugh, S.L.; Jensen, K.F.; Schmidt, M.A. Miniaturization and integration of photoacoustic detection. J. Appl. Phys. 2002, 92, 1555–1563. [Google Scholar] [CrossRef]
- Zhou, S.; Slaman, M.; Iannuzzi, D. Demonstration of a highly sensitive photoacoustic spectrometer based on a miniaturized all-optical detecting sensor. Opt. Express 2017, 25, 17541. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chen, W.; Yu, B. Recent Progress on Infrared Photoacoustic Spectroscopy Techniques. Appl. Spectrosc. Rev. 2011, 46, 440–471. [Google Scholar] [CrossRef]
- Durantin, C.; Rouxel, J.; Désidéri, J.A.; Gliere, A. Optimization of photoacoustics gas sensor using multifidelity RBF metamodeling. In Proceedings of the VII European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS Congress, Crete, Greece, 5–10 June 2016. [Google Scholar]
- Cai, Y.; Arsad, N.; Li, M.; Wang, Y. Buffer structure optimization of the photoacoustic cell for trace gas detection. Optoelectron. Lett. 2013, 9, 233–237. [Google Scholar] [CrossRef]
- Köhring, M.; Böttger, S.; Willer, U.; Schade, W. Temperature effects in tuning fork enhanced interferometric photoacoustic spec-troscopy. Opt. Express 2013, 21, 20911–20922. [Google Scholar] [CrossRef]
- Ishaku, L.; Hutson, D. A Resonant Photoacoustic CO 2 Sensor Based on MID-IR LED and MEMS Microphone Technology Op-erating at 4.3 µM. Innov. Syst. Des. Eng. 2016, 7. [Google Scholar]
- Bernd Baumann, M.; Kost, B.; Groninga, H. Calculation of Quality Factors and Amplitudes of Photoacoustic Resonators. Available online: https://www.academia.edu/download/42648873/Calculation_of_Quality_Factors_and_Ampli20160213-7343-wzqbds.pdf (accessed on 2 July 2022).
- El-Busaidy, S.A.S.; Baumann, B.; Wolff, M.; Duggen, L. Modelling of open photoacoustic resonators. Photoacoustics 2020, 18, 100161. [Google Scholar] [CrossRef]
- Yu, Y.; Tian, C.; Wang, Z.; Qian, S.; Yan, C.; Zhang, H. Multicomponent gas detection technology of FDM and TDM based on pho-toacoustic spectroscopy. Appl. Opt. 2021, 60, 838–843. [Google Scholar] [CrossRef]
- Ishaku, L.A.; Hutson, D.; Gibson, D. Temperature effects on photoacoustic carbon dioxide sensor developed using mid-IR LED. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar]
- Zhong, C.; Li, H.; Zhou, Y.; Lv, Y.; Chen, J.; Li, Y. Virtual synchronous generator of PV generation without energy storage for frequency support in autonomous microgrid. Int. J. Electr. Power Energy Syst. 2022, 134, 107343. [Google Scholar] [CrossRef]
- Cotterell, M.I.; Ward, G.P.; Hibbins, A.P.; Haywood, J.M.; Wilson, A.; Langridge, J.M. Optimizing the performance of aerosol photoa-coustic cells using a finite element model. Part 1: Method validation and application to single-resonator multipass cells. Aerosol Sci. Technol. 2019, 53, 1107–11027. [Google Scholar] [CrossRef] [Green Version]
- Wei, G.; Fan, X.; Xiong, Y.; Lv, C.; Li, S.; Lin, X. Highly disordered VO2 films: Appearance of electronic glass transition and potential for device-level overheat protection. Appl. Phys. Express 2022, 15, 043002. [Google Scholar] [CrossRef]
- Cernat, R.; Matei, C.; Bratu, A.M.; Popa, C.; Dutu, D.C.; Patachia, M.; Petrus, M.; Banita, S.; Dumitras, D.C. Laser photoacoustic spec-troscopy method for measurements of trace gas concentration from human breath. Rom. Rep. Phys. 2010, 62, 610–616. [Google Scholar]
- Luo, G.; Zhang, H.; Yuan, Q.; Li, J.; Wang, F.-Y. ESTNet: Embedded Spatial-Temporal Network for Modeling Traffic Flow Dynamics. IEEE Trans. Intell. Transp. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).