Abstract
The optical beam splitter is an essential device used for decoding in quantum key distribution. The impact of optical beam splitters on the security of quantum key distribution was studied, and it was found that the realistic device characteristics closely influence the error rate introduced by the wavelength-dependent attack on optical beam splitters. A countermeasure, combining device selection and error rate over-threshold alarms, is proposed to protect against such attacks. Beam splitters made of mirror coatings are recommended, and the variation of splitting ratio should be restricted to lower than 1 dB at 1260–1700 nm. For the partial attack scenario where the eavesdropper attacks only a portion of the quantum signal, a modified secure key rate formula is proposed to eliminate the revealed information of the attacked portion. Numerical results show that the QKD system adopting this countermeasure exhibits good performance with a secure key rate of over 10 kbps at 100 km and a maximum transmission distance of over 150 km, with only a small difference from the no-attack scenario. Additionally, a countermeasure to monitor the light intensity of different wavelengths is proposed to protect against the wavelength-dependent attack on optical beam splitters.
1. Introduction
With the rapid development of quantum computing technology, the security of classical encryption systems, which are based on computational complexity, has been challenged [1,2]. Quantum key distribution (QKD) provides another secure means for confidential communication and is attracting growing interest. QKD enables two separated communicating parties to establish secure keys, which can be used for confidential communication [3]. The security of quantum key distribution is guaranteed by the basic principles of quantum mechanics [4]. Since the BB84 protocol [5] was proposed, QKD has undergone fast development. Both theoretical descriptions [6,7,8,9] and experimental techniques [3,10] have matured, gradually moving from experimental verification [11,12,13,14,15,16,17,18,19,20,21,22] to the stage of large scale application [10,23,24].
Although QKD systems based on bulky optics have shown good performance, photonic integrated circuit technology holds promise for QKD, aiming at miniaturizing the device size [25,26,27,28]. The performance of various kinds of components on chip has been verified, such as sources [29], filters [30], beam splitters [31], and modulators [32]. Based on these advances, chip-based QKD has been developing rapidly. Optical transmitters on silicon photonics has been proposed for polarization-encoding QKD [33]. Multi-protocol compatible QKD has been realized using an indium phosphide-based transmitter and a silicon oxynitride-based receiver [32]. Measurement-device-independent QKD has been demonstrated on a silicon photonic chip operating at 1.25 GHz [34]. A complete quantum secure communication system has been presented with photonic integrated circuits, both the QKD chip and the quantum random number generator chip, assembled into compact modules [35]. Field tests of QKD with silicon photonics have been demonstrated in an intercity metropolitan range [36].
QKD has theoretically been proven to be information-theoretically secure. However, practical QKD systems do not necessarily reach the security level described in theory. This is mainly due to imperfect physical properties of the devices, which do not strictly match the abstraction of the device model in the theoretical proof [6]. Such imperfections may be used to design attacks against specific systems, which are known as quantum attacks [37]. For example, time-shift attacks [37,38] and blinding attacks [39] have been developed by exploiting the imperfections of single-photon detectors. In practical QKD systems, necessary countermeasures against known quantum attacks should be involved to ensure security of the system [40].
The basic QKD system can be divided into a transmitter, which is responsible for quantum state preparation and encoding, and a receiver, which is responsible for quantum state decoding and measurement. QKD based on polarization encoding is widely used in quantum communication [11,23]. In the polarization-encoded QKD system, the transmitter can use multiple lasers to represent different polarization states [11,23], or use a single laser to encode different quantum states with an additional modulator [23], while the receiver often uses passive decoding [11,23], where an optical beam splitter (BS) is used to split the quantum signal into two paths for measurements in two conjugate bases. Therefore, beam splitters are indispensable components in QKD. Bulky beam splitters made by fused biconical taper (FBT) or mirror-coating (MC) technology are commercial off-the-shelf products, and have been widely used in optical applications. Compact beam splitters can be achieved by integrated photonics. Both directional couplers [25] and multimode interference (MMI) couplers [32,33] have been used to act as beam splitters on silicon quantum chips. Beam splitters of other structures have also attracted much attention, such as non-uniform adiabatic couplers [31], photonic crystals [41], metamaterials [42], metasurface [43,44], polymers [26,45], and so on. The ideal BS in QKD should have a constant splitting ratio independent of external conditions. However, a realistic beam splitter is usually imperfect as the splitting ratio between the two ports is wavelength-dependent [46]. Adopting this imperfection, wavelength-dependent attacks on beam splitters were proposed [46], which are able to steal some information about the key and threaten the security of the actual system.
In this paper, by carefully looking into the wavelength-dependent characteristics of beam splitters and the features of such an attack, we propose two different kinds of countermeasures against the wavelength-dependent attack on beam splitters. The first countermeasure is to detect the qubit error rate and alert when it exceeds the pre-set threshold. The second countermeasure is to monitor the input light intensity of different wavelengths. These solutions can effectively protect against wavelength-dependent attacks and enhance the implementation security for QKD systems.
2. Wavelength-Dependent Attack of Beam Splitters
We first review the wavelength-dependent attack on optical beam splitters [46]. The schematic diagram of this attack is shown in Figure 1. Near the normal wavelength of the QKD system , the splitting ratio of the beam splitter is very close to 50:50, i.e., the splitting ratio , where and are the intensity of the different output ports of the beam splitter. However, if deviating far from the normal wavelength, the splitting ratio may change dramatically. Without loss of generality, we assume that . The extreme case is , where all incident light of wavelength exits from port 1 and all incident light of wavelength exits from port 2. Using this property, the following intercept-and-resend attack [46] can be designed to steal the key of the QKD system: (1) intercept the quantum signal emitted by the QKD system and randomly select the measurement basis and record the measurement results; and (2) select the attack wavelength according to the measurement basis, prepare the polarization state according to the measurement result, and then resend the signal to the QKD receiver. For example, if an eavesdropper chooses the Z basis and the measurement result is 0, then the horizontal polarized attacking signal of wavelength is prepared and sent to the receiver. Due to the characteristics of the optical beam splitter, all the attacking signals go to port 1 for measurement in the Z basis, leading to a certain result of 0. In this way, the eavesdropper can control the QKD receiver to be the same as their measurement result. This kind of attack is known as the wavelength-dependent attack on optical beam splitter [46].
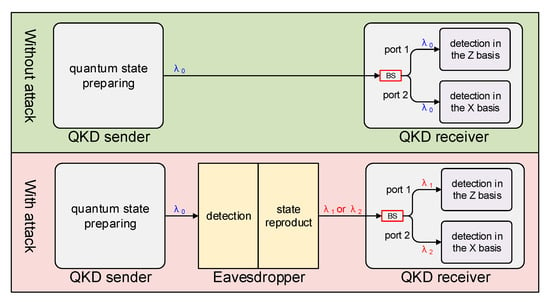
Figure 1.
Schemes of the wavelength-dependent attack on optical beam splitter. BS indicates optical beam splitter.
To achieve such an attack, stringent conditions are required. The first requirement is that the splitting ratio deviates severely from 0.5, and the ideal attack conditions are . It also requires that the attacking wavelength deviates far from the normal wavelength of the QKD system. For these two conditions, we propose two kinds of countermeasures, one provides protection by error rate alerting, and the other provides protection by light intensity monitoring.
3. Countermeasure of Error Rate Alerting
In practice, the beam splitter’s splitting ratio rarely equals to 1 or 0. For a BS made by fused biconical taper (FBT) technology in Ref. [46], , , i.e., 98.6% of the 1470 nm light is emitted from port 1 and 99.7% of the 1270 nm light is emitted from port 2. Thus, the above attack method will introduce an increase in the error rate detected between the QKD sender and receiver. The additional error rate introduced due to the wavelength-dependent attack on optical beam splitters can be calculated by the following equation [46]:
Near the wavelength , , the attack will cause an error rate of , which is too high to generate secure keys. In the extreme case, , the introduced error rate , and the eavesdropper obtains the same information as the receiver. The attacker will get 100% of the key’s information. We numerically simulated the additional error rate with different beam splitting ratios and present the results in Figure 2 below. Different colors in Figure 2 indicate different error rate ranges. The gray region in the upper left corner indicates that the additional error rate introduced by the attack has exceeded 11%, which will cause the QKD system to fail to generate secure keys. Thus, the attack will fail as it is impossible to steal information about the final keys, which means that the QKD system is secure. The colored area indicates that the attack introduces an error rate of less than 11%. Adjacent color blocks between them indicate a 1% increase in the error rate range. For example, the yellow area indicates an error rate of 7–8% and the orange range indicates an error rate of 8–9%. The objective of the attacker is to steal the key’s information, so the error rate introduced by the attack needs to be reduced as much as possible to hide the traces of the attack and maximize the information obtained. If the introduced error rate caused is limited to be less than 1%, the splitting ratio should meet and .
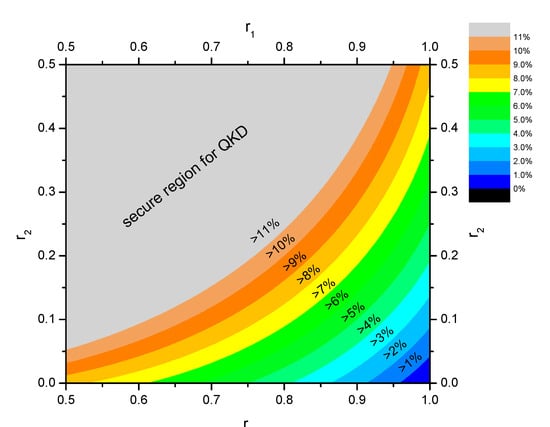
Figure 2.
Schemes of the wavelength-dependent attack on optical beam splitters. The horizontal axis indicates the splitting ratio , and the vertical axis indicates the splitting ratio . Different colors indicate the magnitude of the error rate introduced by the attack.
Since a severe deviation of the splitting ratio from 0.5 is necessary for the success of this attack, we propose a countermeasure by combining device selection and error rate over-threshold alarms to protect against this attack. Firstly, by selecting device types and device characteristics, we ensure that the beam splitters used feature a small variation of splitting ratio in a wide range of wavelength. The splitting ratios of the filtered BS are noted as and . Combining the single-mode cut-off wavelength of standard communication fibers [47] and the operating wavelength range of single-photon detectors [48], the spectral range for inspecting the splitting ratio of the BS can be determined as 1260–1700 nm. The two most commonly used beam splitters in optical communication are BS made by fused biconical taper (FBT) technology and BS made of mirror coatings (MC). The most commonly used integrated beam splitters are the MMI-type beam splitters on QKD chips. The FBT BS is generally wavelength dependent [46,49]. The splitting ratio of FBT BS exhibits an approximately periodic variation from nearly 0 to nearly 1 [46]. The splitting ratio of MMI-type BS features a similar variation pattern to that of FBT BS [50,51]. The variations in the splitting ratio of these two types of beam splitters are too large to ensure the safety of QKD systems. The MC BS can achieve a small change in splitting ratio over a wide wavelength range, as shown in Figure 3. Therefore, the MC BS is more suitable for the practical QKD system. Within current technology, we suggest selecting devices featuring wavelength dependence lower than 1 dB at 1260–1700 nm, i.e., and . denotes the minimum error rate that can be introduced by performing the wavelength-dependent attack under this spectral splitting ratio condition. According to Equation (1) and Figure 2, it is easy to conclude that the attack introduces the smallest error rate when and , and this minimum value can be easily calculated to be .
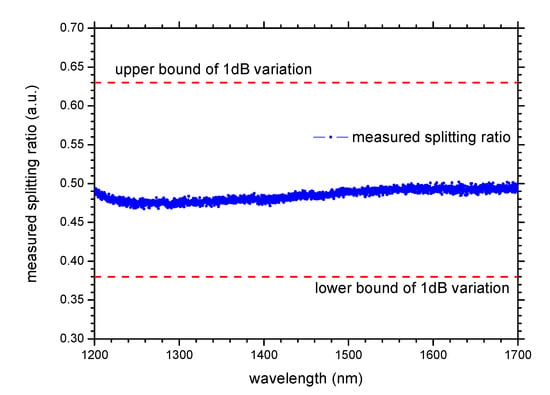
Figure 3.
The measured splitting ratio of the MC BS.
Secondly, we monitor the error rate of the QKD system in real-time and alert when a preset threshold is exceeded. As an alarm implies a likely attack, the system should stop QKD and discard relevant data to prevent information leakage. Considering the performance of commercial QKD devices, the monitoring threshold can be set to [23,52], which can effectively detect wavelength-dependent attacks of beam splitters.
The eavesdropper can further optimize the attack, to reduce the error rate caused, by only attacking part of the quantum signals. If the percentage of attacked signals is , the error rate caused by the attack is approximately . The eavesdropper may attack only a few signals to make , where the system cannot trigger an alarm. Fortunately, the amount of information that the attacker can obtain is also limited in this case. We can remove this amount of information to obtain the security key by modifying the secure key rate formula as follows:
where is the detection gain of a single photon state, is the error rate of a single photon state, is the binary Shannon function, and is the amount of information leaked in the error correction stage, is the efficiency of error correction, is the quantum bit error rate of the signal state under the decoy-state scheme.
We numerically simulated the performance of the QKD system after partial-attack modification, as shown in Figure 4. For simplicity, we calculated the secure key rate at infinite key size and ignored the detector’s dead time and the after-pulse effect. Low after-pulse or a key size more than 1 Mbit have little effect on the secure key rate [53,54]. The dead time effect significantly reduces the secure key rate at short-distance transmission, but has little impact for long-distance transmission. In our simulation, the model of signal state + decoy state + vacuum state was used [55]. The average photon number of the signal state, the decoy state, and the vacuum state was set to 0.4, 0.1, and 0, respectively. The probabilities of the signal state, the decoy state, and the vacuum state were set to 80%, 10%, and 10%, respectively. We assumed a balanced basis choice, i.e., 50% for choosing any basis for both the transmitter and the receiver. The repetition frequency at the transmitter was set to 625 MHz, and the insertion loss at the receiver side was set to 3 dB. The detection efficiency was set to 20%, and the dark count was set to 1000 cps. The error rate caused by the basis mismatch was set to 1%. The equations used in our simulation are presented in the Appendix A. The results showed that after partial-attack modification, the QKD system exhibited good performance, with a secure key rate of over 10 kbps at 100 km and a maximum transmission distance of over 150 km, which is of small difference from the no-attack scenario. Experimental demonstration is important to rate the simulated performance, which we would like to leave for future work.
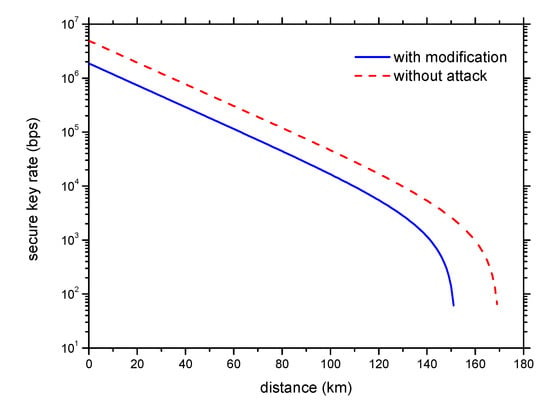
Figure 4.
Simulated key rate after partial-attack modification. The solid blue line indicates the secure key rate after partial-attack modification, and the red dashed line indicates the key rate in the no-attack scenario.
4. Countermeasure of Monitoring
As previously analyzed, to perform a successful wavelength-dependent attack on the optical beam splitter, it is necessary to select two attack wavelengths that are far from the normal operating wavelength of the QKD system, where the splitting ratio deviates severely from 0.5. We propose a countermeasure by monitoring the light intensity of different wavelengths to protect the optical beam splitter from wavelength-dependent attack. The principle of this protection scheme is shown in Figure 5. A filtering module is added at the QKD receiver before the quantum state decoding. The light of operating wavelength is used for the quantum state decoding. The light of non-operating wavelength is separated and measured by a monitoring detector. If the monitoring detector receives a strong light, an alarm is triggered as there is likely a wavelength-dependent attack from the channel. The system should stop QKD and discard relevant data to prevent information leakage. Commonly used fiber optic system filters are available for Wavelength Division Multiplexer (WDM) or Dense Wavelength Division Multiplexer (DWDM), the combination of which can effectively improve the filtering bandwidth and isolation of the filter. Filters also increase the isolation of the system in the non-operating wavelength region, making it necessary for an eavesdropper to increase the light intensity to conduct the attack, thus also increasing the probability of detecting the attack and reducing the sensitivity requirements for monitoring detectors.
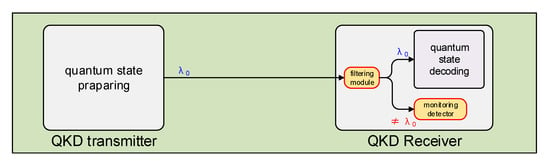
Figure 5.
Schemes of the countermeasure of monitoring.
5. Discussions
In addition to our proposed countermeasures, measurement-device-independent (MDI) QKD [56,57] or even device-independent (DI) QKD [58,59] can also be adopted to eliminate this vulnerability and avoid wavelength-dependent attacks on beam splitters. Our approach is easy to implement, cost-effective, compatible with commercial QKD systems, and has a relatively high secure key rate. The MDI scheme requires high stability to perform the single-photon interference during the measurement, and the secure key rate is relatively lower than our proposal. The DI approach, with better security, is a huge challenge for current technology, and the secure key rate is too low for practical usage. The recently proposed twin-field quantum key [60,61] is an improvement of the MDI scheme, which is expected to promote the transmission distance and the secure rate, thus being the key breakthrough route in MDI QKD research.
It is worth noting that the integrated beam splitters, such as the MMI-type BS commonly used in current QKD chips, show similar wavelength-dependent characteristics of splitting ratios with the FBT BS. Due to the large variation of the splitting ratio, QKD systems using integrated optical beam splitters alone are also affected by wavelength-dependent attacks and cannot guarantee safety. Thus, Figure 3 does not show the simulation results on the secure rate of the integrated BS. The security of the integrated chip-based QKD requires further study. QKD systems using integrated optical beams splitters require additional means to ensure their safety. The countermeasure of error rate alerting is not suitable for chip-based QKD system. Fortunately, the proposed countermeasure of monitoring is more applicable.
Although previous discussions focus on the security of optical beam splitters with unbiased basis choice, both proposed countermeasures apply to QKD systems using the biased basis choice [62]. It is natural for the splitting ratio to be unbalanced, as shown in Figure 2. In the biased scenario, the QKD system is required to monitor the error rates of the Z and X basis separately, rather than only focusing on the overall error rate [62]. Although the overall additional error rate caused by the attack can be lower, there will be a significant increase in the error rate of one of the two bases, which can be used to protect against the attack by the countermeasure of error rate alerting. Perhaps different thresholds should be set for the two bases respectively, and the secure key rate equation would need to be modified according to the biased basis choice.
6. Conclusions
First, we studied the necessary conditions for wavelength-dependent attacks of beam splitters, and numerically calculated the additional error rate introduced by the attack under different beam splitting ratios. Then, we proposed a countermeasure of error rate alerting to protect against this kind of attack. The MC BS was recommended, and devices with a splitting ratio variation of no more than 1 dB in the range of 1260–1700 nm were selected. Combined with an alerting threshold of 3% error rate, the system can effectively be protected against wavelength-dependent attacks of beam splitters. In the case of partial attack, a modified formula is given for estimating secure key rate. We also proposed a light intensity monitoring countermeasure to protect against wavelength-dependent attacks by measuring the incident light intensity at non-operating wavelengths. This work would help guide the design of QKD systems and improve the implementation security for practical systems.
Author Contributions
Conceptualization, D.-D.L., Y.-L.T. and Y.Z.; methodology, D.-D.L.; software, D.-D.L.; validation, Y.-L.T., Y.-K.Z. and L.Z.; formal analysis, D.-D.L. and Y.-L.T.; investigation, D.-D.L., Y.-K.Z., L.Z. and S.-B.T.; writing—original draft preparation, D.-D.L.; writing—review and editing, D.-D.L., Y.-L.T., Y.-K.Z., L.Z., Y.Z. and S.-B.T.; supervision, S.-B.T. and Y.Z.; funding acquisition, D.-D.L., Y.-L.T., Y.-K.Z. and S.-B.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Major Scientific and Technological Special Project of Anhui Province (Grant No. 202103a13010004), the Key R & D Plan of Shandong Province (Grant No. 2020CXGC010105), and the China Postdoctoral Science Foundation (Grant No. 2021M700315).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank our colleagues from QuantumCTek for delightful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
This appendix presents the equations used in the numerical simulation. The total efficiency can be expressed as , where denotes the transmission efficiency at the receiver, is the detection efficiency, is the transmission distance, and the fiber attenuation factor is set to 0.2 dB/km. and denotes the intensity of the signal state and the decoy state, respectively. is the probability of the signal state. is the dark count rate.
The percentage of the attacked photons can be estimated as
The gain of the signal state is
The gain of the decoy state can be calculated similarly.
The QBER of the signal state can be estimated as
The QBER of the decoy state can be calculated similarly.
The yield of the single-photon state can be expressed as
The gain of the single-photon state can be expressed as
The error rate of the single-photon state can be bounded as
Then the secure key rate can be expressed as
where is the repetition frequency of the QKD system.
References
- Wehner, S.; Elkouss, D.; Hanson, R. Quantum internet: A vision for the road ahead. Science 2018, 362, eaam9288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Y.; Bao, W.-S.; Cao, S.; Chen, F.; Chen, M.-C.; Chen, X.; Chung, T.-H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef] [PubMed]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef] [Green Version]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.; Dusek, M.; Lutkenhaus, M.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 10–12 December 1984; pp. 175–179. [Google Scholar]
- Gottesman, D.; Lo, H.-K.; Lutkenhaus, N.; Preskill, J. Security of quantum key distribution with imperfect devices. Quant. Inf. Comput. 2004, 4, 325–360. [Google Scholar]
- Hwang, W.Y. Quantum Key Distribution with High Loss: Toward Global Secure Communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.-B. Beating the Photon-Number-Splitting Attack in Practical Quantum Cryptography. Phys. Rev. Lett. 2005, 94, 230503. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.-K.; Ma, X.; Chen, K. Decoy State Quantum Key Distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Xu, F.; Chen, Y.-A.; Peng, C.-Z.; Pan, J.-W. Large scale quantum key distribution: Challenges and solutions. Opt. Express 2018, 26, 24260–24273. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.-Z.; Zhang, J.; Yang, D.; Gao, W.-B.; Ma, H.-X.; Yin, H.; Zeng, H.-P.; Yang, T.; Wang, X.-B.; Pan, J.-W. Experimental Long-Distance Decoy-State Quantum Key Distribution Based on Polarization Encoding. Phys. Rev. Lett. 2007, 98, 010505. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.-Y.; Wang, J.; Liang, H.; Liu, W.-Y.; Liu, Y.; Jiang, X.; Wang, Y.; Wan, X.; Cai, W.-Q.; Lei, J.; et al. Metropolitan all-pass and inter-city quantum communication network. Opt. Express 2010, 18, 27217–27225. [Google Scholar] [CrossRef]
- Zhou, F.; Yong, H.-L.; Li, D.-D.; Yin, J.; Ren, J.-G.; Peng, C.-Z. Study on quantum key distribution between different media. Acta Phys. Sin. 2014, 63, 140303. [Google Scholar] [CrossRef]
- Tang, Y.-L.; Yin, H.-L.; Zhao, Q.; Liu, H.; Sun, X.-X.; Huang, M.-Q.; Zhang, W.-J.; Chen, S.-J.; Zhang, L.; You, L.-X.; et al. Measurement-Device-Independent Quantum Key Distribution over Untrustful Metropolitan Network. Phys. Rev. X 2016, 6, 011024. [Google Scholar] [CrossRef] [Green Version]
- Liao, S.-K.; Yong, H.-L.; Liu, C.; Shentu, G.-L.; Li, D.-D.; Lin, J.; Dai, H.; Zhao, S.-Q.; Li, B.; Guan, J.-Y.; et al. Long-distance free-space quantum key distribution in daylight towards inter-satellite communication. Nat. Photonics 2017, 11, 509–513. [Google Scholar] [CrossRef]
- Boaron, A.; Boso, G.; Rusca, D.; Vullliez, C.; Autebert, C.; Caloz, M.; Perrenoud, M.; Gras, G.; Bussieres, F.; Li, M.-J.; et al. Secure Quantum Key Distribution over 421 km of Optical Fiber. Phys. Rev. Lett. 2018, 121, 190502. [Google Scholar] [CrossRef] [Green Version]
- Li, D.-D.; Gao, S.; Li, G.-C.; Xue, L.; Wang, L.-W.; Lu, C.-B.; Xiang, Y.; Zhao, Z.-Y.; Yan, L.-C.; Chen, Z.-Y.; et al. Field implementation of long-distance quantum key distribution over aerial fiber with fast polarization feedback. Opt. Express 2018, 26, 22793–22800. [Google Scholar] [CrossRef]
- Li, D.-D.; Shen, Q.; Chen, W.; Li, Y.; Han, X.; Yang, K.-X.; Xu, Y.; Lin, J.; Wang, C.-Z.; Yong, H.-L.; et al. Proof-of-principle demonstration of quantum key distribution with seawater channel: Towards space-to-underwater quantum communication. Opt. Commun. 2019, 452, 220–226. [Google Scholar] [CrossRef]
- Jiang, X.-L.; Deng, X.-Q.; Wang, Y.; Lu, Y.-F.; Li, J.-J.; Zhou, C.; Bao, W.-S. Weak Randomness Analysis of Measurement-Device-Independent Quantum Key Distribution with Finite Resources. Photonics 2022, 9, 356. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Y.; Yu, X.; Zhao, Y.; Zhang, J. Topology-Abstraction-Based Protection Scheme in Quantum Key Distribution Networks with Partially Trusted Relays. Photonics 2022, 9, 239. [Google Scholar] [CrossRef]
- Lu, Y.-F.; Wang, Y.; Jiang, M.-S.; Zhang, X.-X.; Liu, F.; Li, H.-W.; Zhou, C.; Tang, S.-B.; Wang, J.-Y.; Bao, W.-S. Sending or Not-Sending Twin-Field Quantum Key Distribution with Flawed and Leaky Sources. Entropy 2021, 23, 1103. [Google Scholar] [CrossRef]
- Lu, Y.-F.; Jiang, M.-S.; Wang, Y.; Zhang, X.-X.; Liu, F.; Zhou, C.; Li, H.-W.; Tang, S.-B.; Wang, J.-Y.; Bao, W.-S. Practical Analysis of Sending or Not-Sending Twin-Field Quantum Key Distribution with Frequency Side Channels. Appl. Sci. 2021, 11, 9560. [Google Scholar] [CrossRef]
- Chen, Y.-A.; Zhang, Q.; Chen, T.-Y.; Cai, W.-Q.; Liao, S.-K.; Zhang, J.; Chen, K.; Yin, J.; Ren, J.-G.; Chen, Z.; et al. An integrated space-to-ground quantum communication network over 4600 kilometers. Nature 2021, 589, 214–219. [Google Scholar] [CrossRef]
- Chen, T.-Y.; Jiang, X.; Tang, S.-B.; Zhou, L.; Yuan, X.; Zhou, H.; Wang, J.; Liu, Y.; Chen, L.-K.; Liu, W.-Y.; et al. Implementation of a 46-node quantum metropolitan area network. NPJ Quant. Inf. 2021, 7, 134. [Google Scholar] [CrossRef]
- Politi, A.; Matthews, J.C.F.; Thompson, M.G.; O’Brien, J.L. Integrated Quantum Photonics. IEEE J. Selected. Top. Quantum Electron. 2009, 20, 1077. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Felipe, D.; Katopodis, V.; Groumsa, P.; Kouloumentas, C.; Avramopoulos, H.; Dupuy, J.-Y.; Konczykowska, A.; Dede, A.; Beretta, A.; et al. Hybrid photonic integration on a Polymer Platform. Photonics 2015, 2, 1005–1026. [Google Scholar] [CrossRef]
- Wang, J.-W.; Sciarrino, F.; Laing, A.; Thompson, M.G. Integrated photonic quantum technologies. Nat. Photonics 2020, 14, 273–284. [Google Scholar] [CrossRef]
- Pelucchi, E.; Fagas, G.; Aharonovich, I.; Englund, D.; Figueroa, E.; Gong, Q.; Hannes, H.; Liu, J.; Lu, C.-Y.; Matsuda, N.; et al. The potential and global outlook of integrated photonics for quantum technologies. Nat. Rev. Phys. 2022, 4, 194–208. [Google Scholar] [CrossRef]
- Mazeas, F.; Traetta, M.; Bentivegna, M.; Kaiser, F.; Akatas, D.; Zhang, W.; Ramos, C.A.; Ngah, L.A.; Lunchi, T.; Picholle, E.; et al. High-quality photonic entanglement for wavelength-multiplexed quantum communication based on a silicon chip. Opt. Express 2016, 24, 28731–28738. [Google Scholar] [CrossRef]
- Brunetti, G.; Sasanelli, N.; Armenise, M.N.; Ciminelli, C. High performance and tunable optical pump-rejection filter for quantum photonic systems. Opt. Laser Technol. 2021, 139, 106987. [Google Scholar] [CrossRef]
- Akca, B.I.; Povazay, B.; Alex, A.; Worhoff, K.; Ridder, R.M.; Drexler, W.; Pollnau, M. Miniature spectrometer and beam splitter for an optical coherence tomography on a silicon chip. Opt. Express 2013, 21, 16648–16656. [Google Scholar] [CrossRef] [Green Version]
- Sibson, P.; Erven, C.; Godfrey, M.; Miki, S.; Yamashita, T.; Fujiwara, M.; Sasaki, M.; Terai, H.; Tanner, M.G.; Natarajan, C.M.; et al. Chip-based quantum key distribution. Nat. Commun. 2017, 8, 13984. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.; Sacher, W.D.; Tang, Z.-Y.; Mikkelsen, J.C.; Yang, Y.; Xu, F.; Thiessen, T.; Lo, H.-K.; Poon, J.K.S. Silicon photonic transmitter for polarization encoded quantum key distribution. Optica 2016, 3, 1274–1278. [Google Scholar] [CrossRef]
- Wei, K.-J.; Li, W.; Tan, H.; Li, Y.; Min, H.; Zhang, W.-J.; Li, H.; You, L.-X.; Wang, Z.; Jiang, X.; et al. High-Speed Measurement-Device-Independent Quantum Key Distribution with Integrated Silicon Photonics. Phys. Rev. X 2020, 10, 031030. [Google Scholar] [CrossRef]
- Paraiso, T.K.; Roger, T.; Marangon, D.G.; Marco, I.D.; Sanzaro, M.; Woodward, R.I.; Dynes J., F.; Yuan, Z.; Shields, A.J. A photonic integrated quantum secure communication system. Nat. Photonics 2021, 15, 850–856. [Google Scholar]
- Bunandar, D.; Lentine, A.; Lee, C.; Cai, H.; Long, C.M.; Boynton, N.; Martinez, N.; DeRose, C.; Chen, C.; Grein, M.; et al. Metropolitan Quantum Key Distribution with Silicon Photonics. Phys. Rev. X 2018, 8, 021009. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Fung, C.H.F.; Qi, B.; Chen, C.; Lo, H.-K. Quantum hacking: Experimental demonstration of time-shift attack against practical quantum-key-distribution systems. Phys. Rev. A 2008, 78, 042333. [Google Scholar] [CrossRef] [Green Version]
- Qi, B.; Fung, C.H.F.; Lo, H.-K.; Ma, X. Time-shift attack in practical quantum cryptosystems. Quant. Inf. Comput. 2007, 7, 73–82. [Google Scholar] [CrossRef]
- Lydersen, L.; Wiechers, C.; Wittmann, C.; Elser, D.; Skaar, J.; Makarov, V. Hacking commercial quantum cryptography systems by tailored bright illumination. Nat. Photonics 2010, 4, 686–689. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.-K.; Pan, J.-W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Tang, G.-Y.; Huang, H.-M.; Liu, Y.-Q.; Wang, H. Compact Photonic Crystal Polarization Beam Splitter Based on the Self-Collimation Effect. Photonics 2021, 8, 198. [Google Scholar]
- Chang, R.-J.; Huang, C.-C. Simulation of a High-Performance Polarization Beam Splitter Assisted by Two-Dimensional Metamaterials. Nanomaterials 2022, 12, 1852. [Google Scholar] [CrossRef]
- Li, J.; He, Y.-G.; Ye, H.; Wu, T.; Liu, Y.; He, X.; Li, J.; Cheng, J. High-Efficiency, Dual-Band Beam Splitter Based on an All-Dielectric Quasi-Continuous Metasurface. Materials 2021, 14, 3184. [Google Scholar] [CrossRef]
- He, Q.; Shen, Z. Polarization-Insensitive Beam Splitter with Variable Split Angles and Ratios Based on Phase Gradient Metasurfaces. Nanomaterials 2022, 12, 113. [Google Scholar]
- Prajzler, V.; Zazvorka, J. Polymer large core optical splitter 1 × 2 Y for high-temperature operation. Opt. Quantum Electron. 2019, 51, 216. [Google Scholar]
- Li, H.-W.; Wang, S.; Huang, J.-Z.; Chen, W.; Yin, Z.-Q.; Li, F.-Y.; Zhou, Z.; Liu, D.; Zhang, Y.; Guo, G.-C.; et al. Attacking a practical quantum-key-distribution system with wavelength-dependent beam-splitter and multiwavelength sources. Phys. Rev. A 2011, 84, 062308. [Google Scholar]
- ITU. Recommendation ITU-T G.652, Characteristics of a Single-Mode Optical Fibre and Cable. 2016. Available online: https://www.itu.int/itu-t/recommendations/rec.aspx?rec=13076&lang=en (accessed on 1 June 2022).
- Zhang, J.; Itzler, M.A.; Zbinden, H.; Pan, J.-W. Advances in InGaAs/InP single-photon detector systems for quantum communication. Light Sci. Appl. 2015, 4, e286. [Google Scholar] [CrossRef] [Green Version]
- Lin, W.; Zhang, H.; Song, B.; Miao, Y.; Liu, B.; Yan, D.; Liu, Y. Magnetically controllable wavelength-division multiplexing fiber coupler. Opt. Express 2015, 23, 11123–11134. [Google Scholar]
- Lee, Y.L.; Eom, T.J.; Shin, W.; Yu, B.-A.; Ko, D.-K.; Kim, W.-K.; Lee, H.-Y. Characteristics of a multi-mode interference device based on Ti:LiNbO3 channel waveguide. Opt. Express 2009, 17, 10718–10724. [Google Scholar] [CrossRef]
- Hua, P.-R.; Pun, E.Y.-B.; Yu, D.-Y.; Zhang, D.-L. Nonperiodic Oscillation with Wavelength of Mode Guided in a Special Ti-Diffused LiNbO3 Waveguide Structure. IEEE Photonics J. 2013, 5, 2202307. [Google Scholar]
- Liao, S.-K.; Cai, W.-Q.; Liu, W.-Y.; Zhang, L.; Li, Y.; Ren, J.-G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.-P.; et al. Satellite-to-ground quantum key distribution. Nature 2017, 549, 43–47. [Google Scholar] [CrossRef] [Green Version]
- Fung, C.H.F.; Ma, X.; Chau, H.F. Practical issues in quantum-key-distribution postprocessing. Phys. Rev. A 2010, 81, 012318. [Google Scholar] [CrossRef] [Green Version]
- Lim, C.C.W.; Curty, M.; Walenta, N.; Xu, F.; Zbinden, H. Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A 2014, 89, 022307. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Qi, B.; Zhao, Y.; Lo, H.-K. Practical decoy state for quantum key distribution. Phys. Rev. A 2005, 72, 012326. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.-K.; Curty, M.; Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Li, Y.-H.; Yang, K.-X.; Jiang, Y.-F.; Li, S.-L.; Hu, X.-L.; Abulizi, M.; Li, C.-L.; Zhang, W.-J.; Sun, Q.-C.; et al. Long-Distance Free-Space Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2020, 125, 260503. [Google Scholar] [CrossRef]
- Acin, A.; Brunner, N.; Gisin, N.; Massar, S.; Pironio, S.; Scarani, V. Device-Independent Security of Quantum Cryptography against Collective Attacks. Phys. Rev. Lett. 2007, 98, 230501. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.-H.; Zhang, Y.-Z.; Zhang, Q.; Pan, J.-W. Device-Independent Quantum Key Distribution with Random Postselection. Phys. Rev. Lett. 2022, 128, 110506. [Google Scholar] [CrossRef]
- Lucamarini, M.; Yuan, Z.; Dynes, J.; Shields, A. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 2018, 557, 400–403. [Google Scholar] [CrossRef]
- Fang, X.-T.; Zeng, P.; Liu, H.; Zou, M.; Wu, W.; Tang, Y.-L.; Sheng, Y.-J.; Xiang, Y.; Zhang, W.-J.; Li, H.; et al. Implementation of quantum key distribution surpassing the linear rate-transmittance bound. Nat. Photonics 2020, 14, 422–425. [Google Scholar] [CrossRef]
- Lo, H.-K.; Chau, H.F.; Ardehali, M. Efficient Quantum Key Distribution Scheme and Proof of its Security. J. Cryptol. 2005, 18, 133–165. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).