Optical Frequency Combs Generated in Silica Microspheres in the Telecommunication C-, U-, and E-Bands
Abstract
:1. Introduction
2. Methods
2.1. Fabrication of Microspheres
2.2. Numerical
2.2.1. Calculation of Dispersion and Nonlinear Coefficient
2.2.2. Calculation of Intracavity CW Power
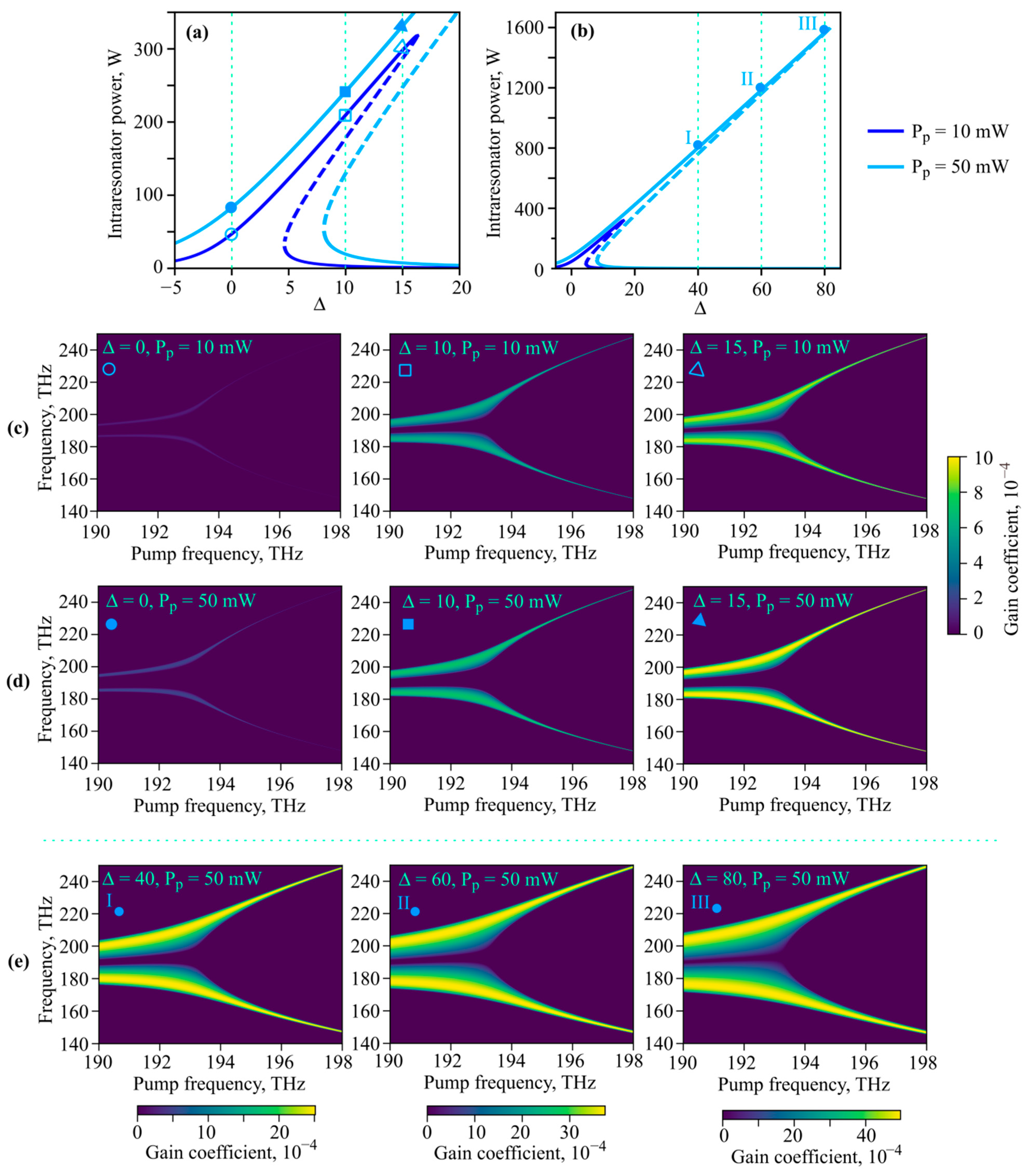
2.2.3. Calculation of Gain Coefficients for the Degenerate FWM Processes under the Strong Intracavity CW Field Approximation
2.2.4. Numerical Simulation Based on Lugiato–Lefever Equation with the Raman Nonlinearity Taken into Account
3. Results
3.1. The 1st Experimental Series
3.2. Theoretical Study of FWM
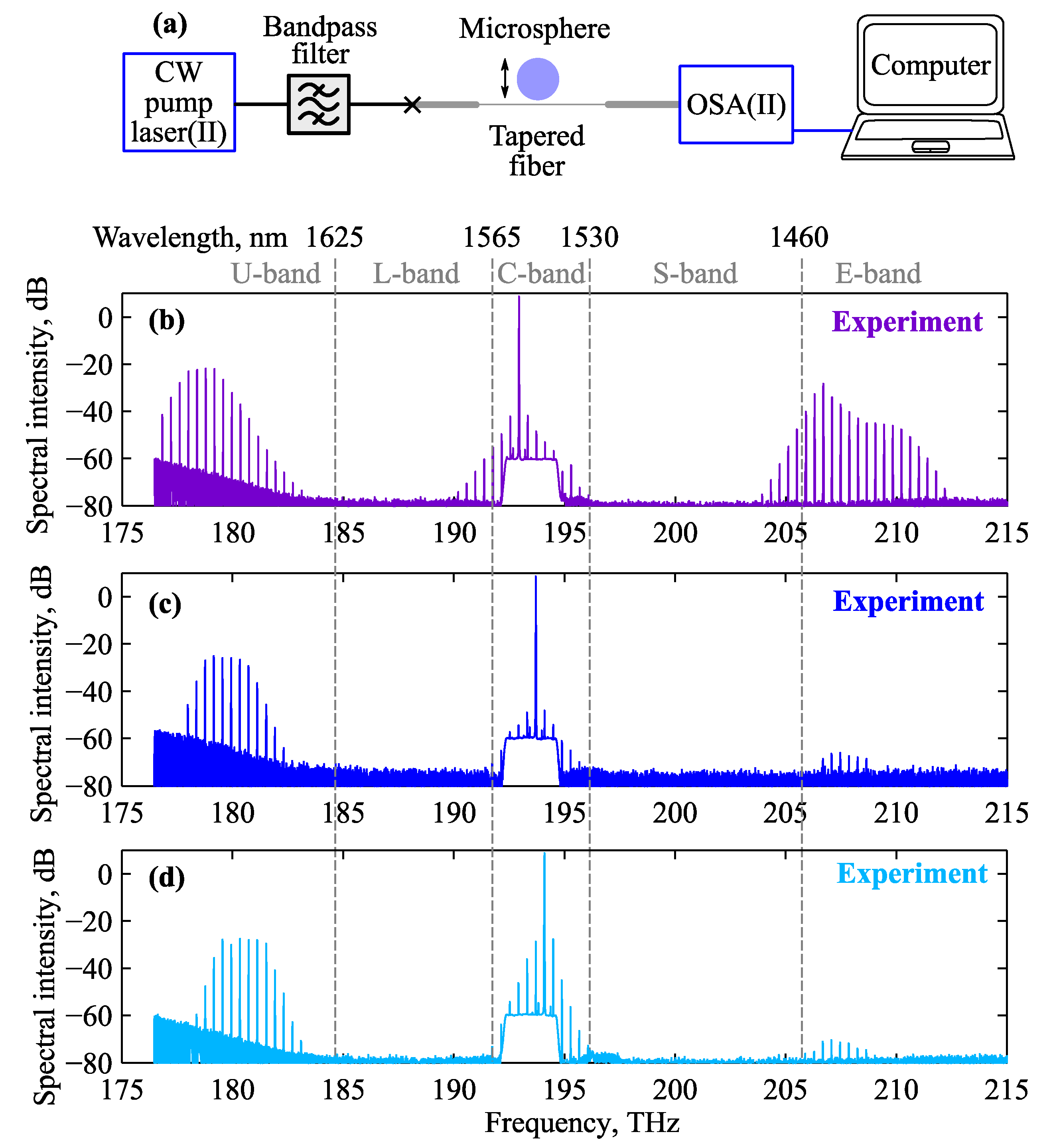
3.3. The 2nd Experimental Series
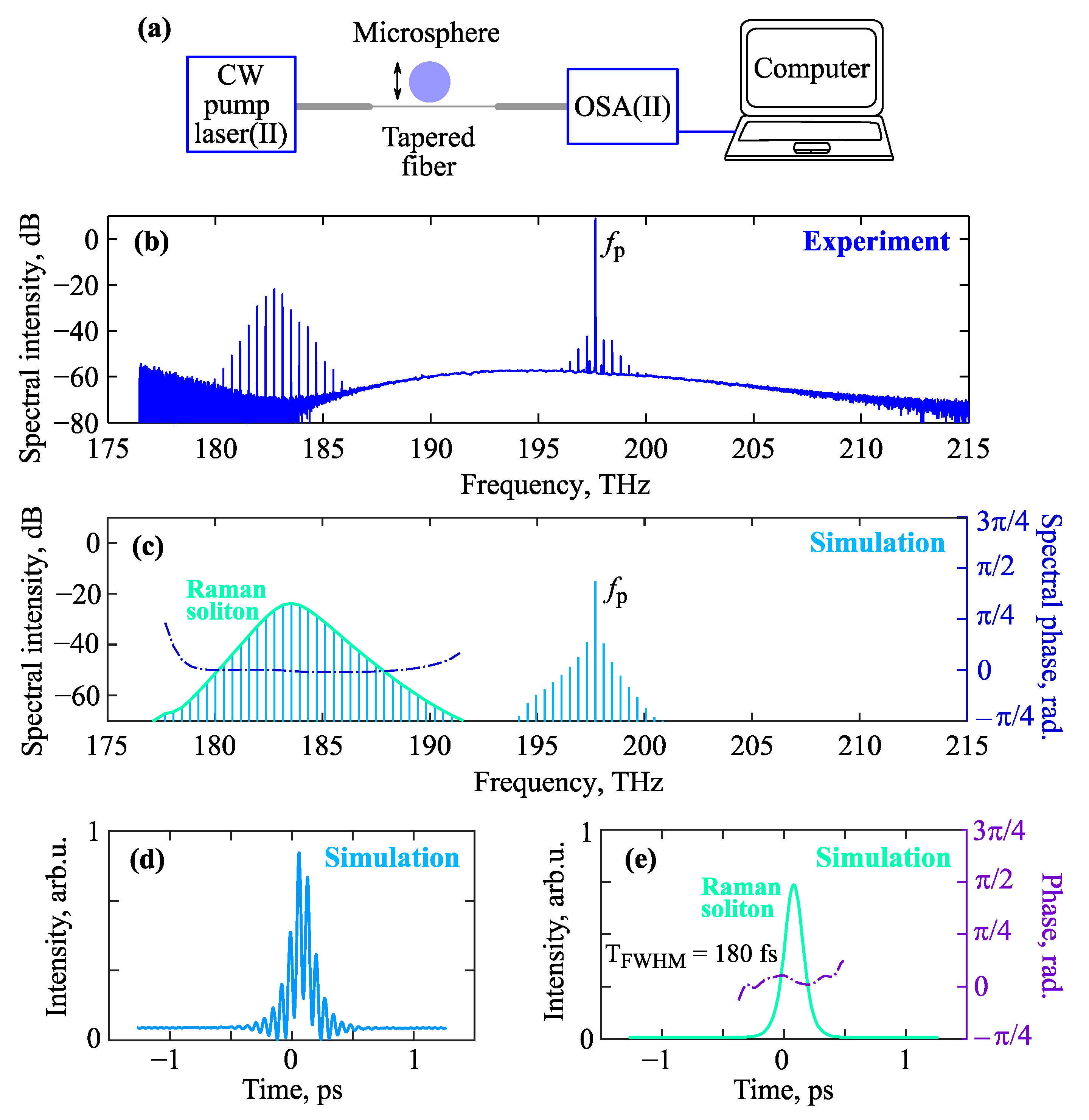
3.4. The 3rd Experimental Series and Its Interpretation
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Pasquazi, A.; Peccianti, M.; Razzari, L.; Moss, D.J.; Coen, S.; Erkintalo, M.; Chembo, Y.K.; Hansson, T.; Wabnitz, S.; Del’Haye, P.; et al. Micro-combs: A novel generation of optical sources. Phys. Rep. 2018, 729, 1–81. [Google Scholar] [CrossRef]
- Strekalov, D.V.; Marquardt, C.; Matsko, A.B.; Schwefel, H.G.L.; Leuchs, G. Nonlinear and quantum optics with whispering gallery resonators. J. Opt. 2016, 18, 123002. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, T.; Riesen, N.; Meldrum, A.; Fan, X.; Hall, J.M.; Monro, T.M.; François, A. Fluorescent and lasing whispering gallery mode microresonators for sensing applications. Laser Photonics Rev. 2017, 11, 1600265. [Google Scholar] [CrossRef]
- Brice, I.; Grundsteins, K.; Atvars, A.; Alnis, J.; Viter, R.; Ramanavicius, A. Whispering gallery mode resonator and glucose oxidase based glucose biosensor. Sens. Actuators B Chem. 2020, 318, 128004. [Google Scholar] [CrossRef]
- Zhivotkov, D.; Ristić, D.; Romanova, E.; Ivanda, M. Refractometric gas sensing using a whispering gallery mode microresonator coated with a supra-micron sol-gel layer. Opt. Mater. 2021, 118, 111286. [Google Scholar] [CrossRef]
- Soria, S.; Berneschi, S.; Brenci, M.; Cosi, F.; Nunzi Conti, G.; Pelli, S.; Righini, G.C. Optical Microspherical Resonators for Biomedical Sensing. Sensors 2011, 11, 785–805. [Google Scholar] [CrossRef] [PubMed]
- Toropov, N.; Cabello, G.; Serrano, M.P.; Gutha, R.R.; Rafti, M.; Vollmer, F. Review of biosensing with whispering-gallery mode lasers. Light Sci. Appl. 2021, 10, 42. [Google Scholar] [CrossRef]
- Peccianti, M.; Pasquazi, A.; Park, Y.; Little, B.E.; Chu, S.T.; Moss, D.J.; Morandotti, R. Demonstration of a stable ultrafast laser based on a nonlinear microcavity. Nat. Commun. 2012, 3, 765. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Soref, R. Reconfigurable optical directed-logic circuits using microresonator-based optical switches. Opt. Express 2011, 19, 5244–5259. [Google Scholar] [CrossRef]
- Han, Z.; Fast, S.S.; Klotz, E.; Vatnik, I.D.; Churkin, D.V. Optical filtering with axial whispering gallery modes on the surface of tapered optical fibers. Laser Phys. Lett. 2020, 17, 066201. [Google Scholar] [CrossRef]
- Liang, W.; Ilchenko, V.S.; Savchenkov, A.A.; Matsko, A.B.; Seidel, D.; Maleki, L. Whispering-gallery-mode-resonator-based ultranarrow linewidth external-cavity semiconductor laser. Opt. Lett. 2010, 35, 2822–2824. [Google Scholar] [CrossRef] [Green Version]
- Kondratiev, N.M.; Lobanov, V.E.; Cherenkov, A.V.; Voloshin, A.S.; Pavlov, N.G.; Koptyaev, S.; Gorodetsky, M.L. Self-injection locking of a laser diode to a high-Q WGM microresonator. Opt. Express 2017, 25, 28167–28178. [Google Scholar] [CrossRef]
- Cutrona, A.; Hanzard, P.-H.; Rowley, M.; Totero-Gongora, J.S.; Peccianti, M.; Malomed, B.A.; Oppo, G.-L.; Pasquazi, A. Temporal cavity solitons in a laser-based microcomb: A path to a self-starting pulsed laser without saturable absorption. Opt. Express 2021, 29, 6629–6646. [Google Scholar] [CrossRef]
- Del’Haye, P.; Schliesser, A.; Arcizet, O.; Wilken, T.; Holzwarth, R.; Kippenberg, T.J. Optical frequency comb generation from a monolithic microresonator. Nature 2007, 450, 1214–1217. [Google Scholar] [CrossRef] [Green Version]
- Pfeifle, J.; Brasch, V.; Lauermann, M.; Yu, Y.; Wegner, D.; Herr, T.; Hartinger, K.; Schindler, P.; Li, J.; Hillerkuss, D.; et al. Coherent terabit communications with microresonator Kerr frequency combs. Nat. Photon. 2014, 8, 375–380. [Google Scholar] [CrossRef] [Green Version]
- Fülöp, A.; Mazur, M.; Lorences-Riesgo, A.; Helgason, Ó.B.; Wang, P.-H.; Xuan, Y.; Leaird, D.E.; Qi, M.; Andrekson, P.A.; Weiner, A.M.; et al. High-order coherent communications using mode-locked dark-pulse Kerr combs from microresonators. Nat. Commun. 2018, 9, 1598. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, M.; Okawachi, Y.; Griffith, A.G.; Picqué, N.; Lipson, M.; Gaeta, A.L. Silicon-chip-based mid-infrared dual-comb spectroscopy. Nat. Commun. 2018, 9, 1869. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newman, Z.L.; Maurice, V.; Drake, T.; Stone, J.R.; Briles, T.C.; Spencer, D.T.; Fredrick, C.; Li, Q.; Westly, D.; Ilic, B.R.; et al. Architecture for the photonic integration of an optical atomic clock. Optica 2019, 6, 680–685. [Google Scholar] [CrossRef] [Green Version]
- Trocha, P.; Karpov, M.; Ganin, D.; Pfeiffer, M.H.P.; Kordts, A.; Wolf, S.; Krockenberger, J.; Marin-Palomo, P.; Weimann, C.; Randel, S.; et al. Ultrafast optical ranging using microresonator soliton frequency combs. Science 2018, 359, 887–891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gaeta, A.L.; Lipson, M.; Kippenberg, T.J. Photonic-chip-based frequency combs. Nat. Photonics 2019, 13, 158–169. [Google Scholar] [CrossRef]
- Crespo-Ballesteros, M.; Yang, Y.; Toropov, N.; Sumetsky, M. Four-port SNAP microresonator device. Opt. Lett. 2019, 44, 3498–3501. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Yang, Y.; Lu, Z.; Wang, W.; Zhang, W.; Xie, C.; Zhong, H.; Wu, L.; Wu, T.; Tan, Q.; et al. Experimental demonstration of nonlinear scattering processes in a microbottle resonator based on a robust packaged platform. J. Lightwave Technol. 2021. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Marisova, M.P.; Andrianov, A.V.; Akhmedzhanov, R.A.; Murnieks, R.; Tokman, M.D.; Skladova, L.; Oladyshkin, I.V.; Salgals, T.; Lyashuk, I.; et al. Microsphere-based optical frequency comb generator for 200 GHz spaced WDM data transmission system. Photonics 2020, 7, 72. [Google Scholar] [CrossRef]
- Spolitis, S.; Murnieks, R.; Skladova, L.; Salgals, T.; Andrianov, A.V.; Marisova, M.P.; Leuchs, G.; Anashkina, E.A.; Bobrovs, V. IM/DD WDM-PON communication system based on optical frequency comb generated in silica whispering gallery mode resonator. IEEE Access 2021, 9, 66335–66345. [Google Scholar] [CrossRef]
- Salgals, T.; Alnis, J.; Murnieks, R.; Brice, I.; Porins, J.; Andrianov, A.V.; Anashkina, E.A.; Spolitis, S.; Bobrovs, V. Demonstration of a fiber optical communication system employing a silica microsphere-based OFC source. Opt. Express 2021, 29, 10903–10913. [Google Scholar] [CrossRef]
- Hu, H.; Oxenløwe, L.K. Chip-based optical frequency combs for high-capacity optical communications. Nanophotonics 2021, 10, 1367–1385. [Google Scholar] [CrossRef]
- Spolitis, S.; Kurbatska, I.; Bobrovs, V. Comparison of C-band and L-band WDM-PON systems performance with PAM-4 modulation format. In Proceedings of the 2017 International Workshop on Fiber Optics in Access Network (FOAN), Munich, Germany, 6–8 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Spillane, S.M.; Kippenberg, T.J.; Vahala, K.J. Ultralow-threshold Raman laser using a spherical dielectric microcavity. Nature 2002, 415, 621–623. [Google Scholar] [CrossRef]
- Zhu, S.; Shi, L.; Ren, L.; Zhao, Y.; Jiang, B.; Xiao, B.; Zhang, X. Controllable Kerr and Raman-Kerr frequency combs in functionalized microsphere resonators. Nanophotonics 2019, 8, 2321–2329. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, R.; Kubota, A.; Hori, A.; Fujii, S.; Tanabe, T. Broadband gain induced Raman comb formation in a silica microresonator. J. Opt. Soc. Am. B 2018, 35, 933–938. [Google Scholar] [CrossRef] [Green Version]
- Andrianov, A.V.; Anashkina, E.A. Raman-assisted optical frequency combs generated in a silica microsphere in two whispering gallery mode families. Laser Phys. Lett. 2021, 18, 025403. [Google Scholar] [CrossRef]
- Yang, Q.-F.; Yi, X.; Yang, K.Y.; Vahala, K. Stokes solitons in optical microcavities. Nat. Phys. 2017, 13, 53–57. [Google Scholar] [CrossRef] [Green Version]
- Gorodetsky, M.L.; Savchenkov, A.A.; Ilchenko, V.S. Ultimate Q of optical microsphere resonators. Opt. Lett. 1996, 21, 453–455. [Google Scholar] [CrossRef]
- Webb, K.E.; Erkintalo, M.; Coen, S.; Murdoch, S.G. Experimental observation of coherent cavity soliton frequency combs in silica microspheres. Opt. Lett. 2016, 41, 4613–4616. [Google Scholar] [CrossRef] [Green Version]
- Sayson, N.L.B.; Webb, K.E.; Coen, S.; Erkintalo, M.; Murdoch, S.G. Widely tunable optical parametric oscillation in a Kerr microresonator. Opt. Lett. 2017, 42, 5190–5193. [Google Scholar] [CrossRef] [Green Version]
- ITU-T Recommendation G.694.1, Spectral Grids for WDM Applications: DWDM Frequency Grid; Telecommunication Standardization Sector of ITU; International Telecommunication Union: Geneva, Switzerland, 2012; pp. 1–7.
- Andrianov, A.V.; Anashkina, E.A. Single-mode silica microsphere Raman laser tunable in the U-band and beyond. Results Phys. 2020, 17, 103084. [Google Scholar] [CrossRef]
- Oraevsky, A.N. Whispering-gallery waves. Quantum Electron. 2002, 32, 377–400. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 6th ed.; Elsevier: London, UK, 2019. [Google Scholar]
- Fujii, S.; Tanabe, T. Dispersion engineering and measurement of whispering gallery mode microresonator for Kerr frequency comb generation. Nanophotonics 2020, 9, 1087–1104. [Google Scholar] [CrossRef] [Green Version]
- Coen, S.; Erkintalo, M. Universal scaling laws of Kerr frequency combs. Opt. Lett. 2013, 38, 1790–1792. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sayson, N.L.B.; Pham, H.; Webb, K.E.; Ng, V.; Trainor, L.S.; Schwefel, H.G.L.; Coen, S.; Erkintalo, M.; Murdoch, S.G. Origins of clustered frequency combs in Kerr microresonators. Opt. Lett. 2018, 43, 4180–4183. [Google Scholar] [CrossRef] [PubMed]
- Puzyrev, D.N.; Skryabin, D.V. Finesse and four-wave mixing in microresonators. Phys. Rev. A 2021, 103, 013508. [Google Scholar] [CrossRef]
- Godey, C.; Balakireva, I.V.; Coillet, A.; Chembo, Y.K. Stability analysis of the spatiotemporal Lugiato-Lefever model for Kerr optical frequency combs in the anomalous and normal dispersion regimes. Phys. Rev. A 2014, 89, 063814. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Karpov, M.; Lucas, E.; Kordts, A.; Pfeiffer, M.H.P.; Brasch, V.; Lihachev, G.; Lobanov, V.E.; Gorodetsky, M.L.; Kippenberg, T.J. Universal dynamics and deterministic switching of dissipative Kerr solitons in optical microresonators. Nat. Phys. 2017, 13, 94–102. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Bobrovs, V.; Salgals, T.; Brice, I.; Alnis, J.; Andrianov, A.V. Kerr optical frequency combs with multi-FSR mode spacing in silica microspheres. IEEE Photonics Technol. Lett. 2021, 33, 453–456. [Google Scholar] [CrossRef]
- Jung, H.; Gong, Z.; Liu, X.; Guo, X.; Zou, C.; Tang, H.X. Stokes and anti-Stokes Raman scatterings from frequency comb lines in poly-crystalline aluminum nitride microring resonators. Opt. Express 2019, 27, 22246–22253. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anashkina, E.A.; Marisova, M.P.; Salgals, T.; Alnis, J.; Lyashuk, I.; Leuchs, G.; Spolitis, S.; Bobrovs, V.; Andrianov, A.V. Optical Frequency Combs Generated in Silica Microspheres in the Telecommunication C-, U-, and E-Bands. Photonics 2021, 8, 345. https://doi.org/10.3390/photonics8090345
Anashkina EA, Marisova MP, Salgals T, Alnis J, Lyashuk I, Leuchs G, Spolitis S, Bobrovs V, Andrianov AV. Optical Frequency Combs Generated in Silica Microspheres in the Telecommunication C-, U-, and E-Bands. Photonics. 2021; 8(9):345. https://doi.org/10.3390/photonics8090345
Chicago/Turabian StyleAnashkina, Elena A., Maria P. Marisova, Toms Salgals, Janis Alnis, Ilya Lyashuk, Gerd Leuchs, Sandis Spolitis, Vjaceslavs Bobrovs, and Alexey V. Andrianov. 2021. "Optical Frequency Combs Generated in Silica Microspheres in the Telecommunication C-, U-, and E-Bands" Photonics 8, no. 9: 345. https://doi.org/10.3390/photonics8090345
APA StyleAnashkina, E. A., Marisova, M. P., Salgals, T., Alnis, J., Lyashuk, I., Leuchs, G., Spolitis, S., Bobrovs, V., & Andrianov, A. V. (2021). Optical Frequency Combs Generated in Silica Microspheres in the Telecommunication C-, U-, and E-Bands. Photonics, 8(9), 345. https://doi.org/10.3390/photonics8090345







