Nondegenerate Bright Solitons in Coupled Nonlinear Schrödinger Systems: Recent Developments on Optical Vector Solitons
Abstract
1. Introduction
2. Derivation of CNLS Equations and Other Integrable CNLS Type Models
3. Statement of the Problem
4. Nondegenerate Solitons and Their Collisions in Manakov System
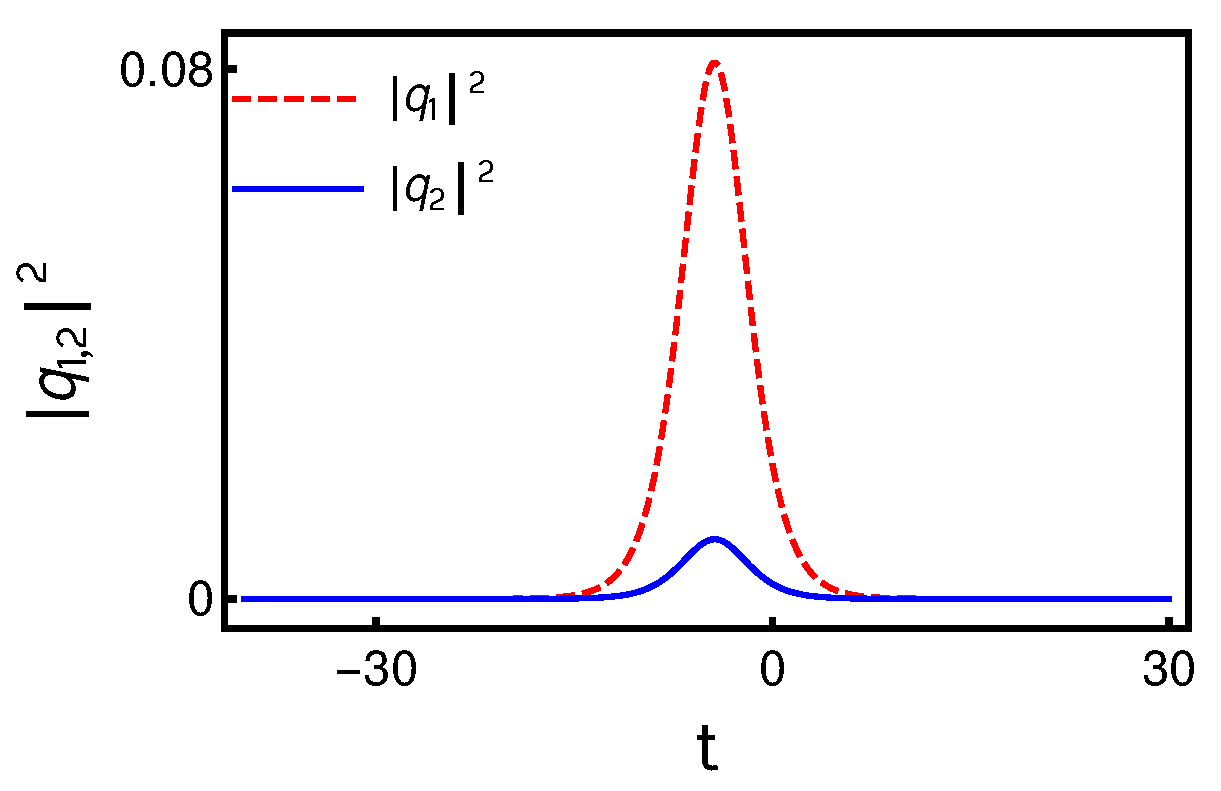
4.1. Nondegenerate Fundamental Soliton Solution of the Manakov System
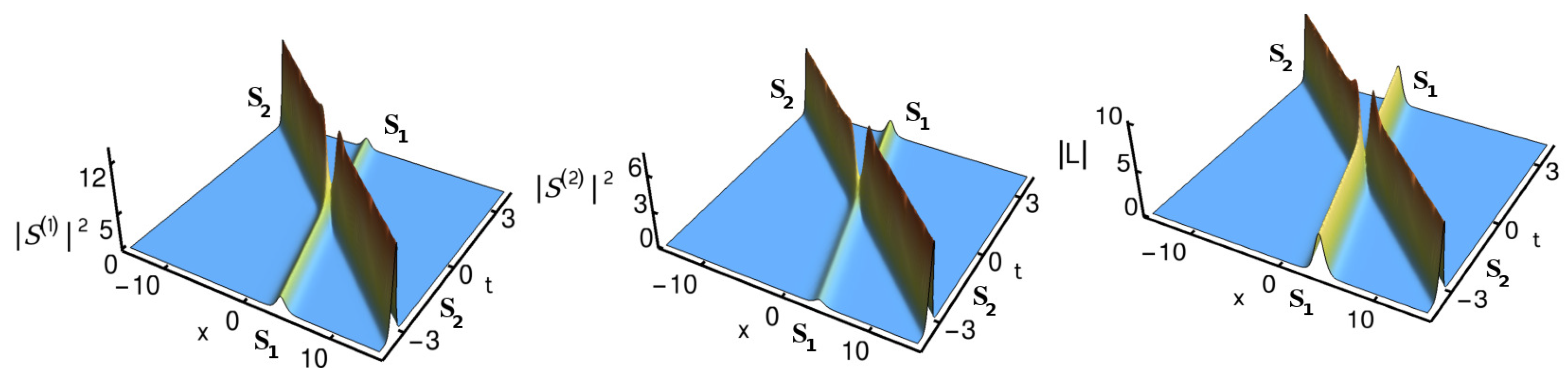
4.2. Nondegenerate Two-Soliton Solution
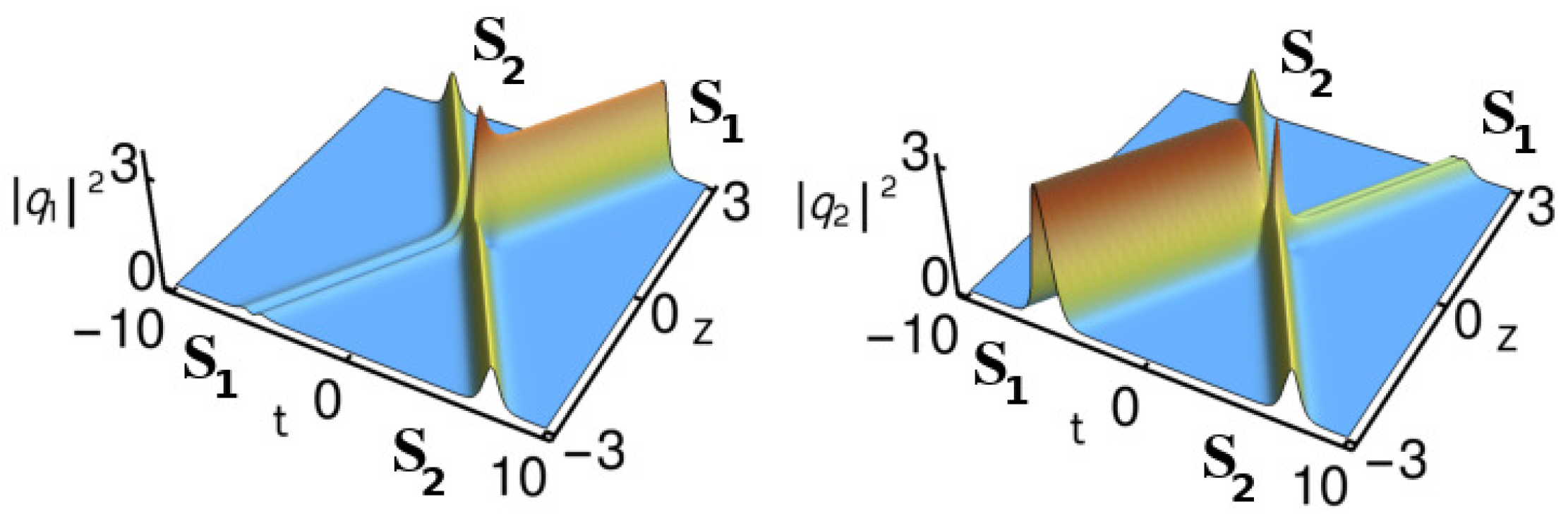
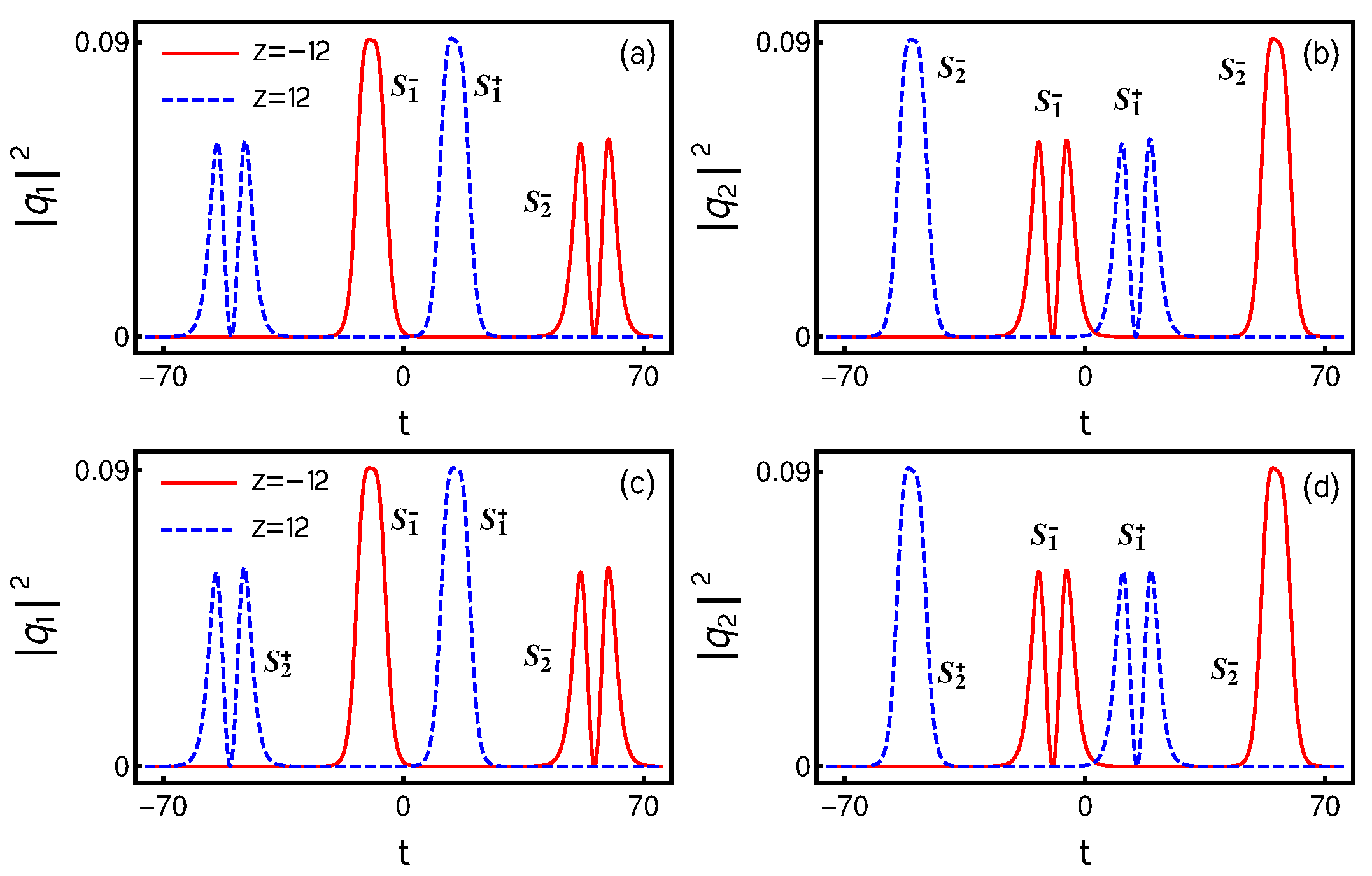
4.3. Various Types of Collision Dynamics of Nondegenerate Solitons
4.3.1. Asymptotic Analysis
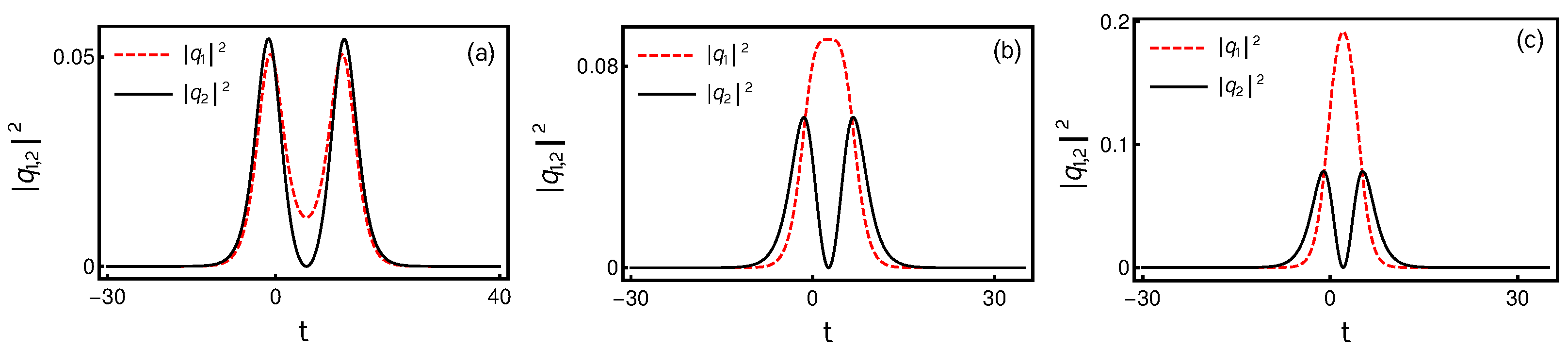
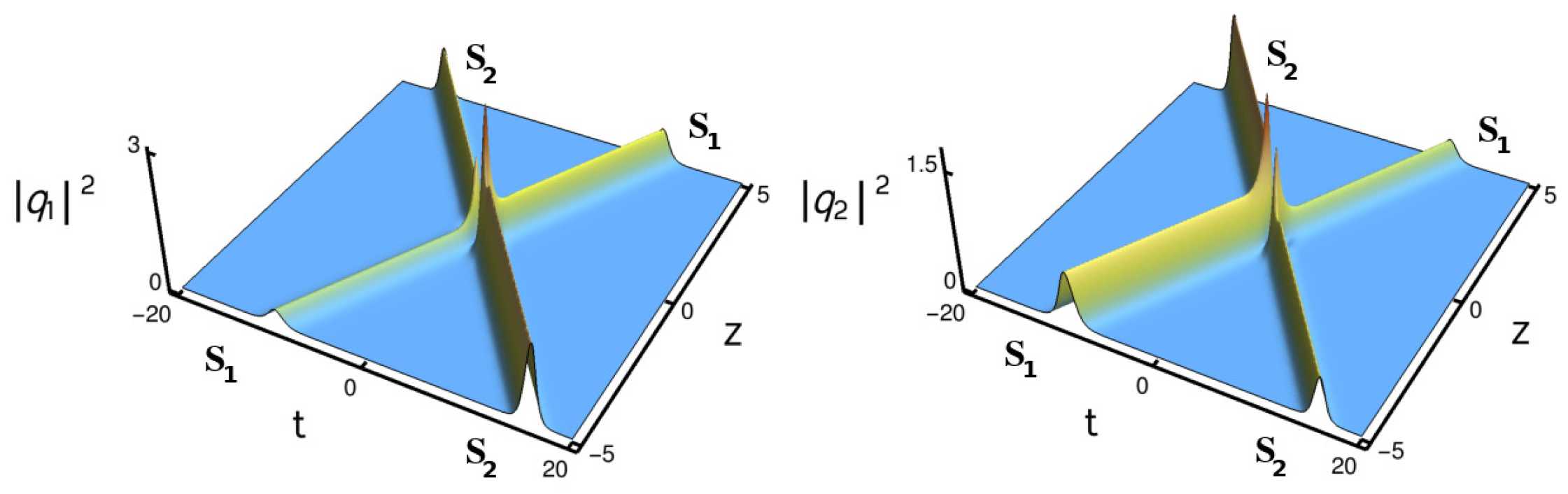
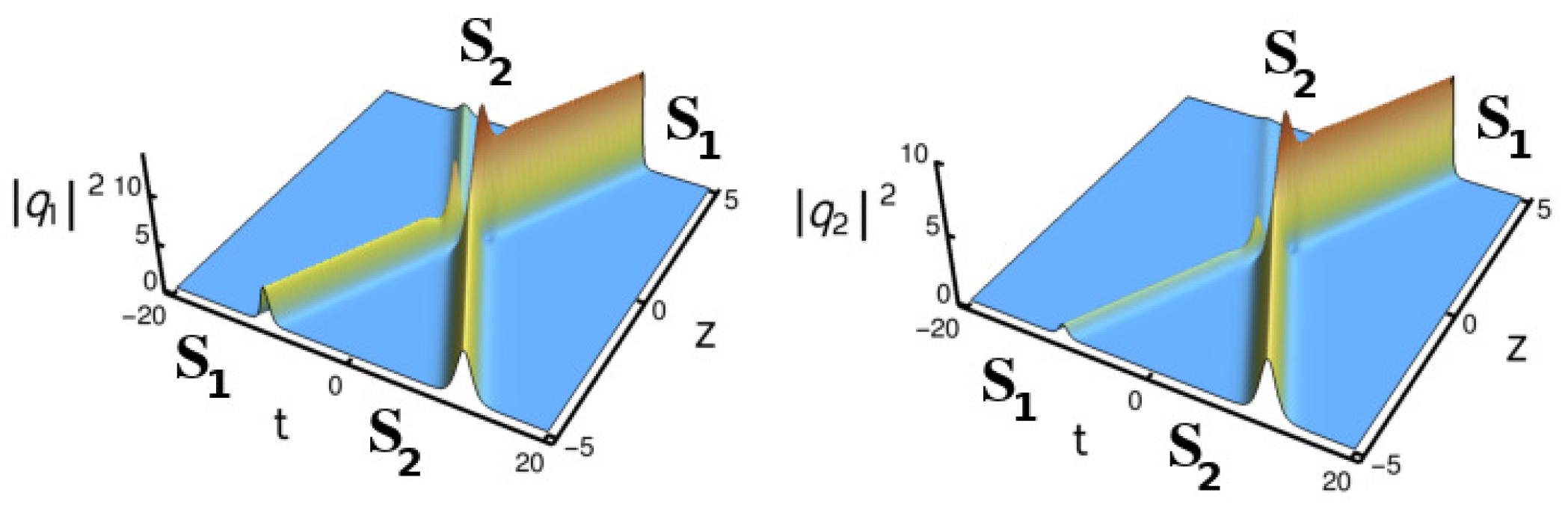
4.3.2. Elastic Collision: Shape Preserving, Shape Altering and Shape Changing Collisions
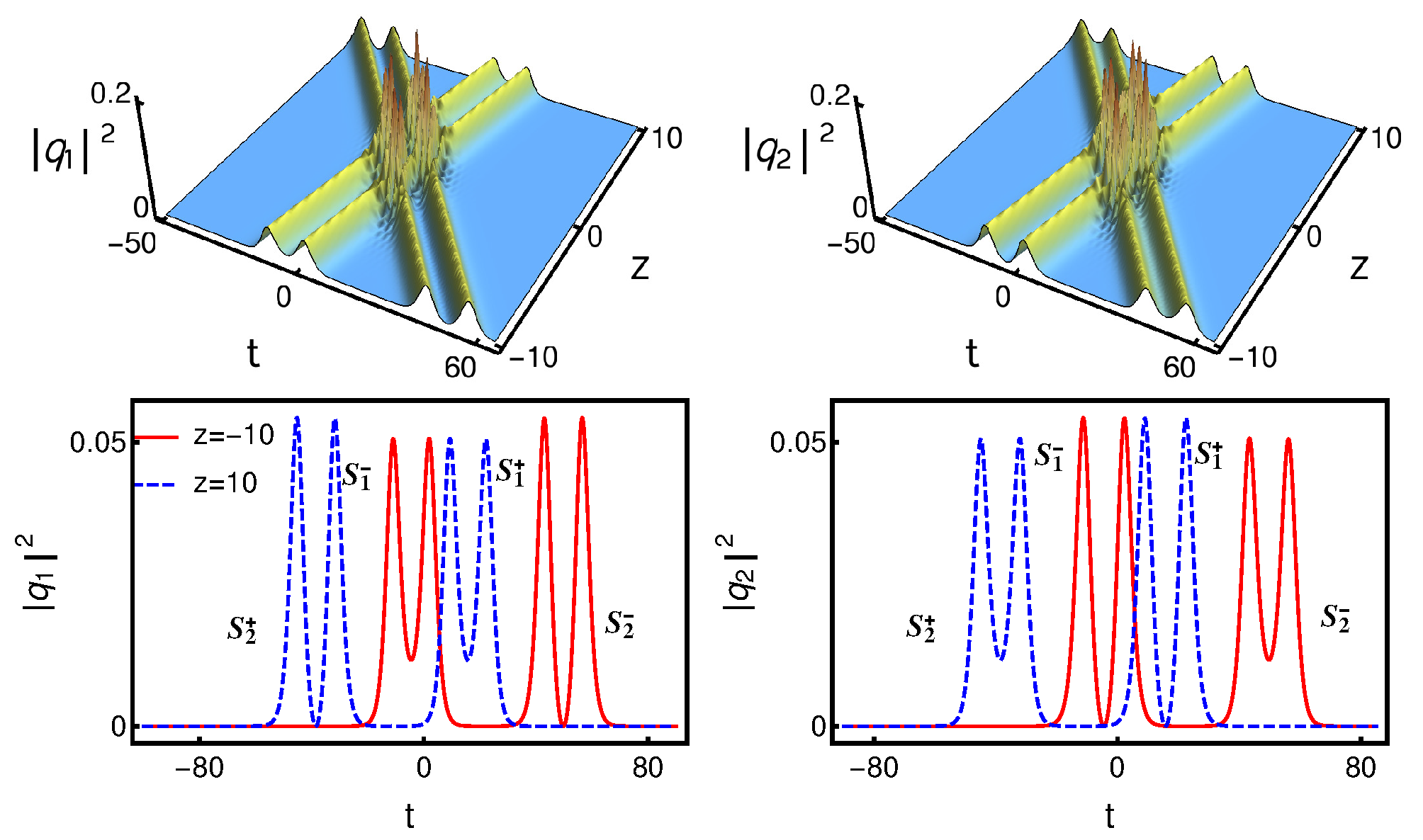
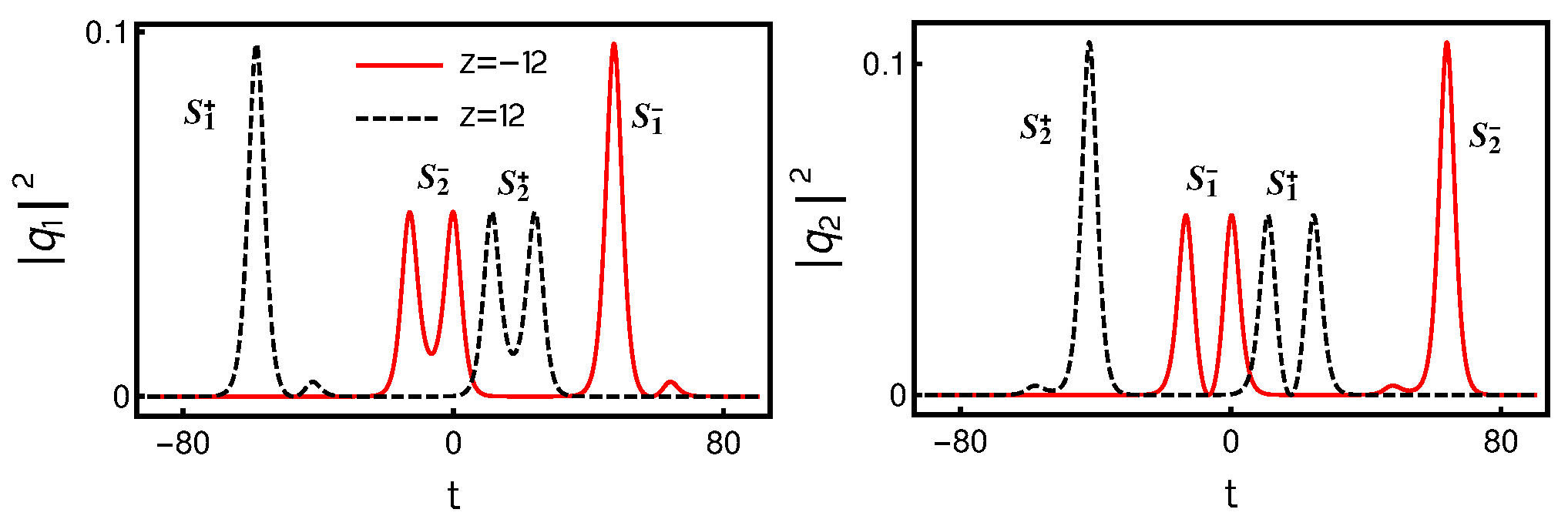
4.4. Collision between Nondegenerate and Degenerate Solitons
4.4.1. Asymptotic Analysis
4.5. Degenerate Soliton Collision Induced Shape Changing Scenario of Nondegenerate Soliton
4.6. Degenerate Bright Solitons and Their Shape Changing/Energy Redistribution Collision in the Manakov System
4.7. Possible Experimental Realization of Nondegenerate Solitons
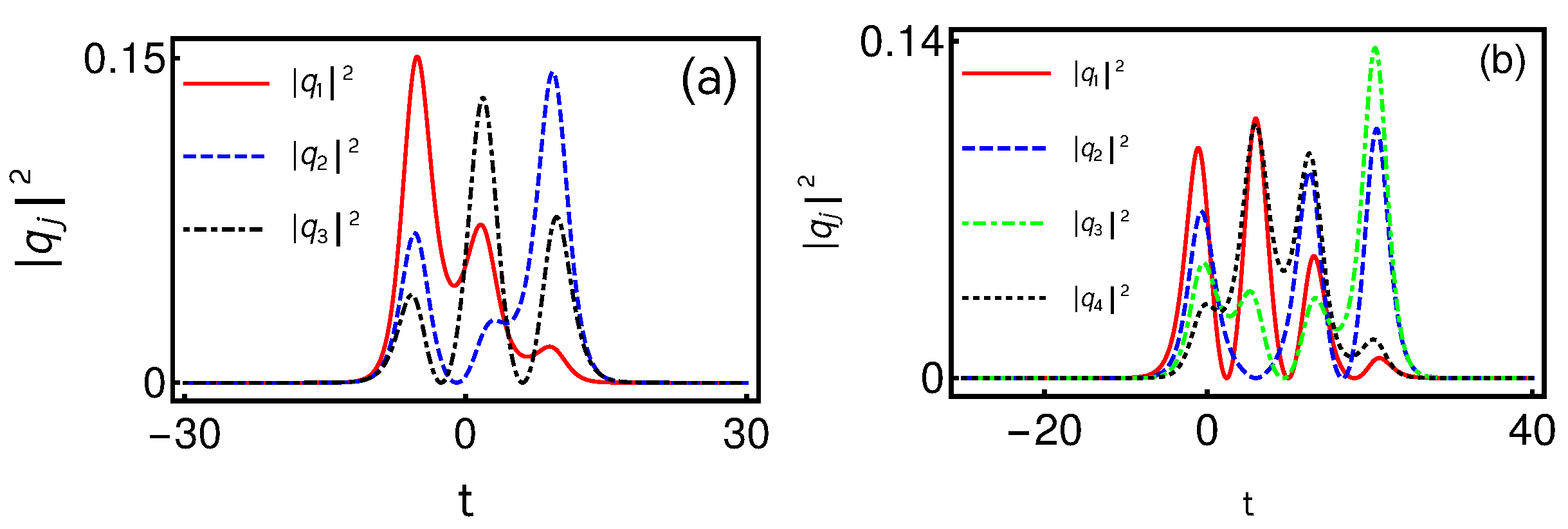
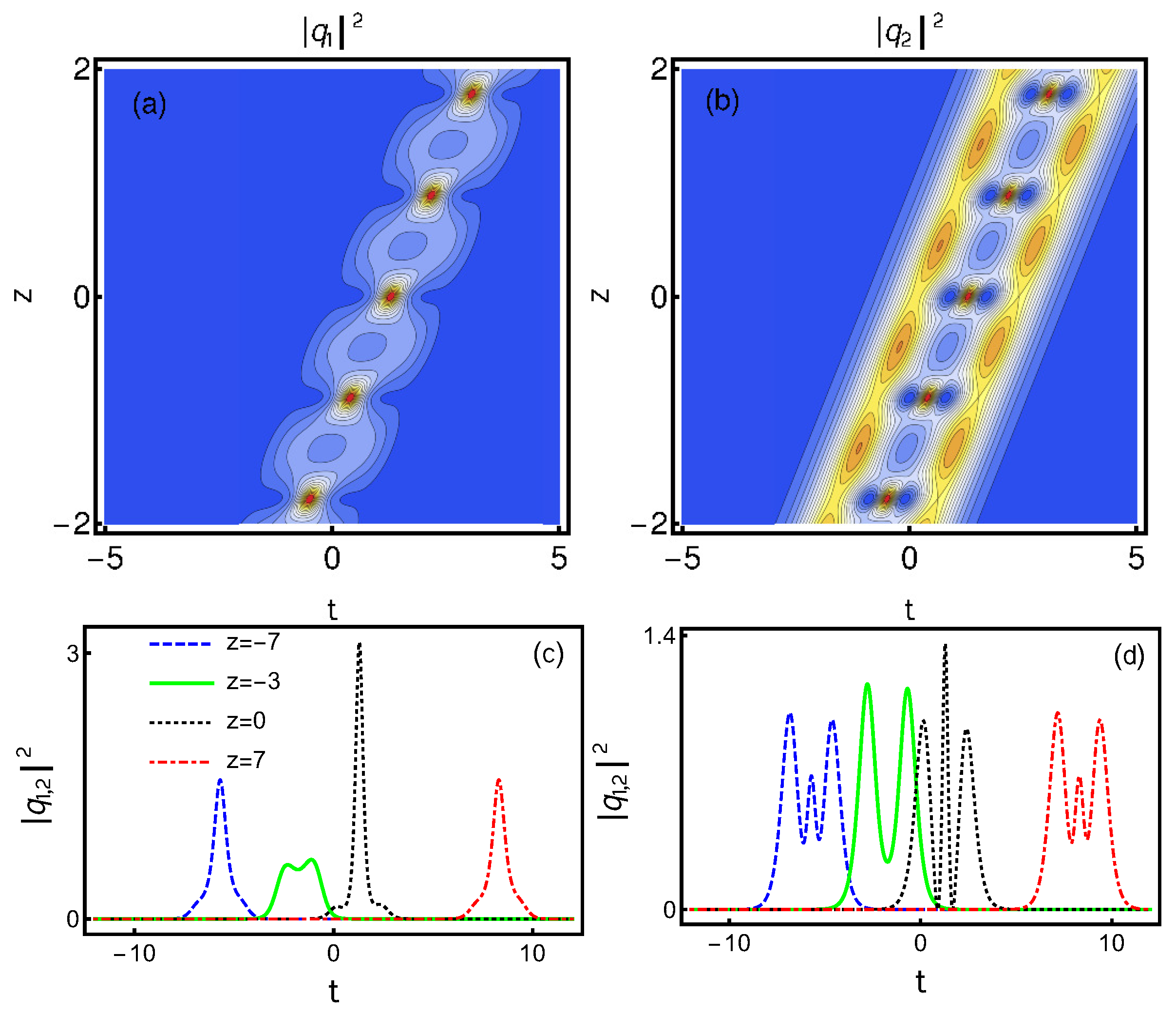
4.8. Multi-Humped Nondegenerate Fundamental Bright Soliton Solution in N-CNLS System
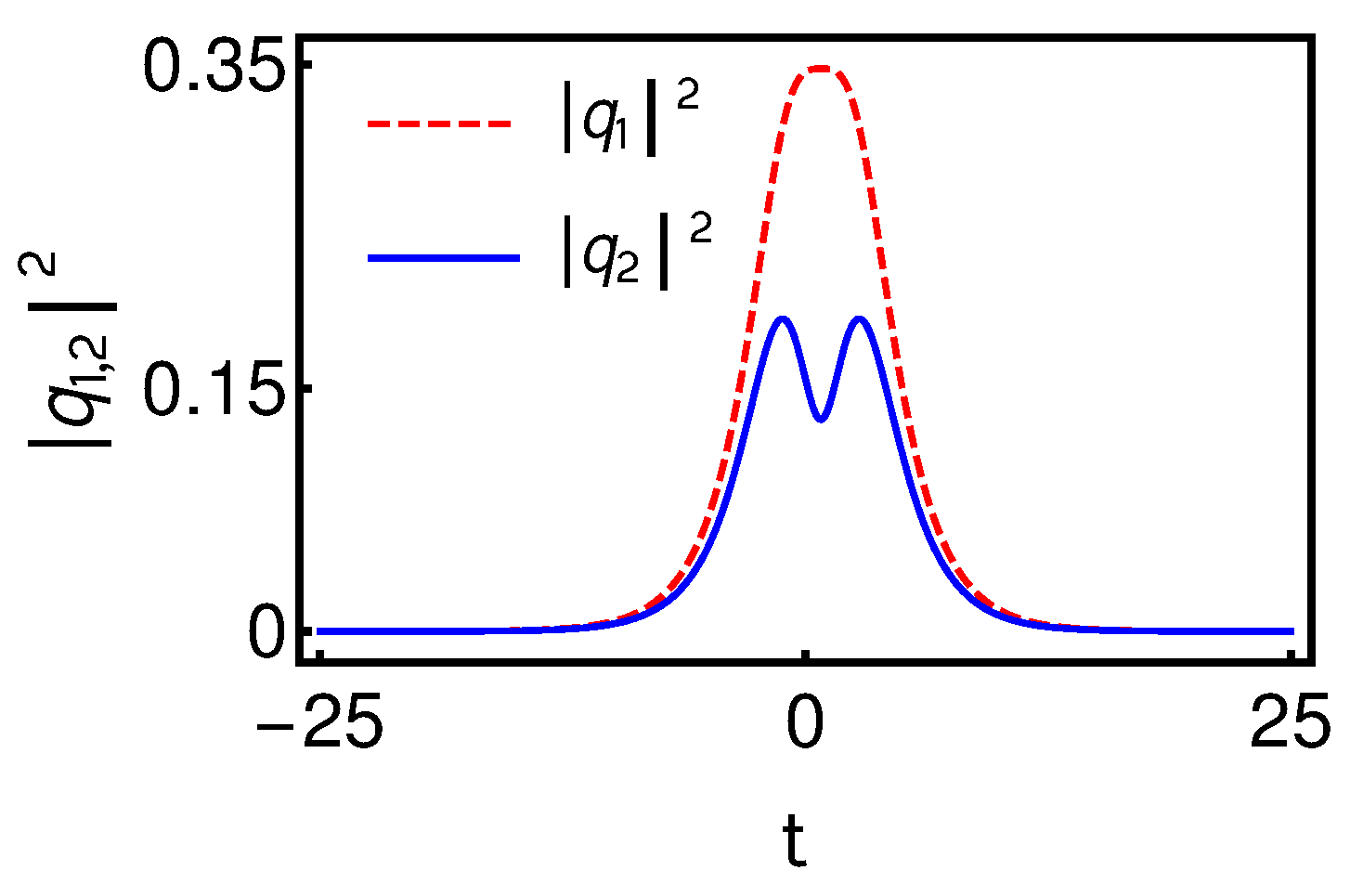
5. Nondegenerate and Degenerate Bright Solitons in the Mixed 2-CNLS System
6. Existence of Nondegenerate and Degenerate Bright Solitons in Two-Component Coherently Coupled Nonlinear Schrödinger System
7. Fundamental Vector Bright Solitons in a GCNLS System
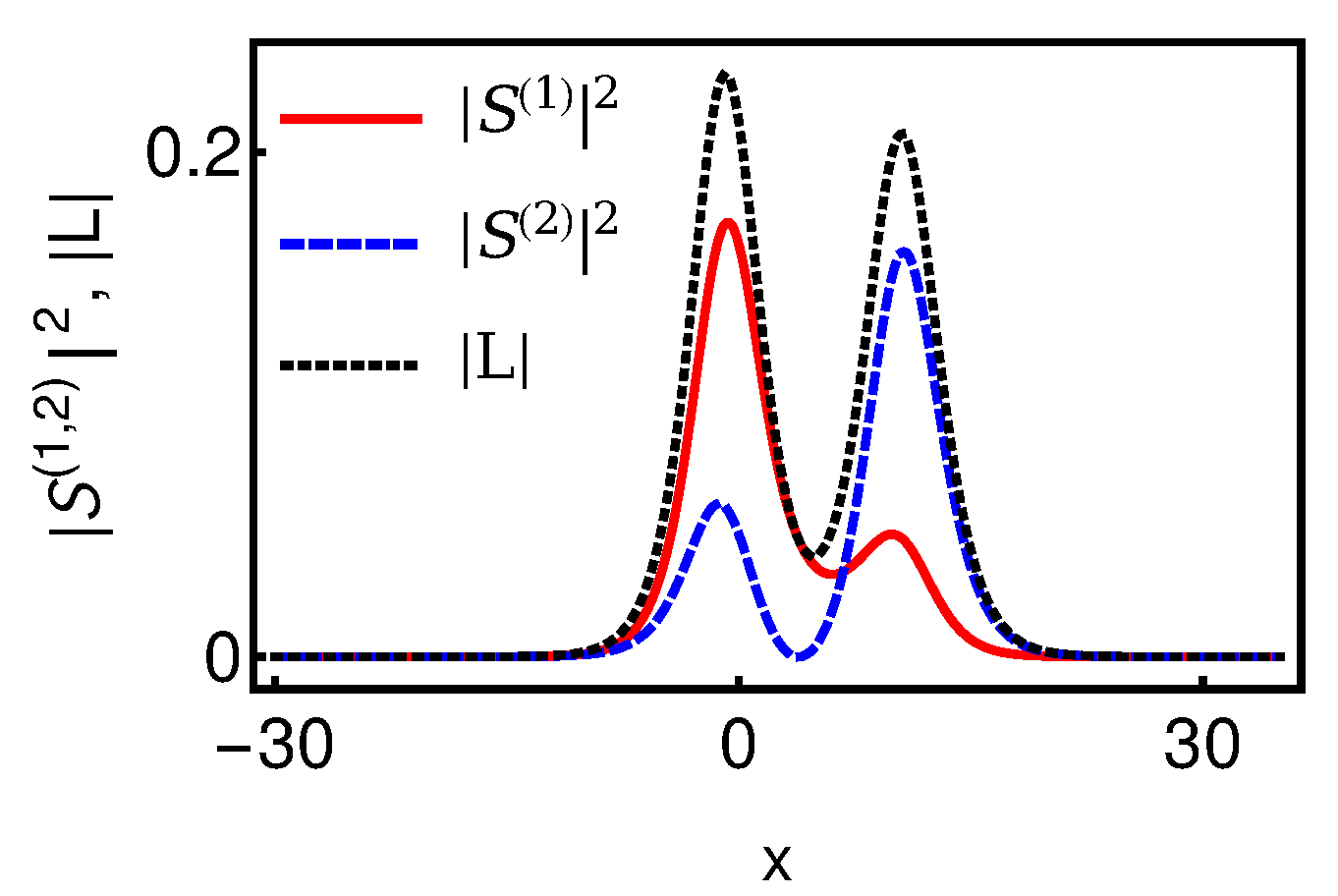
8. Nondegenerate and Degenerate Bright Solitons in Two Component LSRI System
9. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Constants That Appear in the Asymptotic Expressions in Section 4.4.1
References
- Zabusky, N.J.; Kruskal, M.D. Interaction of “Solitons” in a Collisionless Plasma and the Recurrence of Initial States. Phys. Rev. Lett. 1965, 15, 240–243. [Google Scholar] [CrossRef]
- Dauxois, T. Fermi, Pasta, Ulam and a mysterious lady. Phys. Today 2008, 61, 55–57. [Google Scholar] [CrossRef]
- Kivshar, Y.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals, 1st ed.; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optics, 5th ed.; Academic Press: Oxford, UK, 2013. [Google Scholar]
- Chen, Z.; Segev, M.; Christodoulides, D.N. Optical spatial solitons: Historical overview and recent advances. Rep. Prog. Phys. 2012, 75, 086401. [Google Scholar] [CrossRef]
- Malomed, B.A.; Mihalache, D.; Wise, F.; Torner, L. Spatiotemporal optical solitons. J. Opt. B Quantum Semiclass. Opt. 2005, 7, R53–R72. [Google Scholar] [CrossRef]
- Hasegawa, A.; Tappert, F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl. Phys. Lett. 1973, 23, 142. [Google Scholar] [CrossRef]
- Hasegawa, A.; Tappert, F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. II. Normal dispersion. Appl. Phys. Lett. 1973, 23, 171. [Google Scholar] [CrossRef]
- Mollenauer, L.F.; Stolen, R.H.; Gordon, J.P. Experimental Observation of Picosecond Pulse Narrowing and Solitons in Optical Fibers. Phys. Rev. Lett. 1980, 45, 1095. [Google Scholar] [CrossRef]
- Mollenauer, L.F.; Gordon, J.P. Nonlinear Fiber Optics, 1st ed.; Academic Press: San Diego, CA, USA, 2006. [Google Scholar]
- Zakharov, V.E.; Shabat, A.B. Interaction between solitons in a stable medium. Sov. Phys. JETP 1973, 37, 823–828. [Google Scholar]
- Gardner, C.S.; Green, G.; Kruskal, M.; Miura, R. Method for solving the Korteweg-deVries equation. Phys. Rev. Lett. 1967, 19, 1095. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering, 1st ed.; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Chabchoub, A.; Slunyaev, A.; Hoffmann, N.; Dias, F.; Kibler, B.; Genty, G.; Dudley, J.M.; Akhmediev, N. The Peregrine breather on the zero-background limit as the two-soliton degenerate solution: An experimental study. arXiv 2020, arXiv:2011.13252. [Google Scholar]
- Gordon, J.P. Interaction forces among solitons in optical fibers. Opt. Lett. 1983, 8, 596–598. [Google Scholar] [CrossRef]
- Mitschke, F.M.; Mollenauer, L.F. Experimental observation of interaction forces between solitons in optical fibers. Opt. Lett. 1987, 12, 355. [Google Scholar] [CrossRef] [PubMed]
- Stratmann, M.; Pagel, T.; Mitschke, F.M. Experimental Observation of Temporal Soliton Molecules. Phys. Rev. Lett. 2005, 95, 143902. [Google Scholar] [CrossRef]
- Hause, A.; Hartwig, H.; Böhm, M.; Mitschke, F.M. Binding mechanism of temporal soliton molecules. Phys. Rev. A 2008, 78, 063817. [Google Scholar] [CrossRef]
- Akhmediev, N.; Town, G.; Wabnitz, S. Soliton coding based on shape invariant interacting soliton packets: The three-soliton case. Opt. Commun. 1994, 104, 385. [Google Scholar] [CrossRef]
- Malomed, B.A. Bound solitons in the nonlinear Schrödinger/Ginzburg-Landau equation. In Large Scale Structures in Nonlinear Physics. Lecture Notes in Physics; Fournier, J.D., Sulem, P.L., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; p. 392. [Google Scholar]
- Afanasjev, V.V.; Malomed, B.A.; Chu, P.L. Stability of bound states of pulses in the Ginzburg-Landau equations. Phys. Rev. E 1997, 56, 6020. [Google Scholar] [CrossRef]
- Khawaja, U.A. Stability and dynamics of two-soliton molecules. Phys. Rev. E 2010, 81, 056603. [Google Scholar] [CrossRef] [PubMed]
- Grelu, P.; Soto-Crespo, J.M. Multisoliton states and pulse fragmentation in a passively mode-locked fibre laser. J. Opt. B Quantum SemiClass. Opt. 2004, 6, S271. [Google Scholar] [CrossRef]
- Tang, D.Y.; Zhao, B.; Shen, D.Y.; Lu, C.; Man, W.S.; Tam, H.Y. Compound pulse solitons in a fiber ring laser. Phys. Rev. A 2003, 68, 013816. [Google Scholar] [CrossRef]
- Akhmediev, N.N.; Ankiewicz, A.; Soto-Crespo, J.M. Stable soliton pairs in optical transmission lines and fiber lasers. J. Opt. Soc. Am. B 1998, 15, 515. [Google Scholar] [CrossRef]
- Melchert, O.; Willms, S.; Bose, S.; Yulin, A.; Roth, B.; Mitschke, F.M.; Morgner, U.; Babushkin, I.; Demircan, A. Soliton Molecules with Two Frequencies. Phys. Rev. Lett. 2019, 123, 243905. [Google Scholar] [CrossRef]
- Rohrmann, P.; Hause, A.; Mitschke, F. Solitons Beyond Binary: Possibility of Fibre-Optic Transmission of Two Bits per Clock Period. Sci. Rep. 2012, 2, 866. [Google Scholar] [CrossRef]
- Jakubowski, M.H.; Steiglitz, K.; Squier, R. State transformations of colliding optical solitons and possible application to computation in bulk media. Phys. Rev. E 1998, 58, 6752. [Google Scholar] [CrossRef]
- Steiglitz, K. Time-gated Manakov spatial solitons are computationally universal. Phys. Rev. E 2000, 63, 016608. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A. Multi-soliton complexes. Chaos 2000, 10, 600. [Google Scholar] [CrossRef] [PubMed]
- Mitschke, F. A Brief History of Fiber-Optic Soliton Transmission. In Handbook of Optical Fibers; Peng, G.-D., Ed.; Springer: Singapore, 2017; pp. 1–47. [Google Scholar]
- Radhakrishnan, R.; Sahadevan, R.; Lakshmanan, M. Integrability and singularity structure of coupled nonlinear Schródinger equations. Chaos Solitons Fractals 1995, 5, 2315. [Google Scholar] [CrossRef]
- Manakov, S.V. On the theory of two-dimensional stationary self-focusing of electromagnetic waves. Sov. Phys. JETP 1974, 38, 248. [Google Scholar]
- Menyuk, C.R. Pulse propagation in an elliptically birefringent Kerr medium. IEEE J. Quantum Electron. 1989, 25, 2674. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Lakshmanan, M.; Hietarinta, J. Inelastic collision and switching of coupled bright solitons in optical fibers. Phys. Rev. E 1997, 56, 2213. [Google Scholar] [CrossRef]
- Kanna, T.; Lakshmanan, M. Exact soliton solutions, shape changing collisions, and partially coherent solitons in coupled nonlinear Schrödinger equations. Phys. Rev. Lett. 2001, 86, 5043. [Google Scholar] [CrossRef] [PubMed]
- Anastassiou, C.; Segev, M.; Steiglitz, K.; Giordmaine, J.A.; Mitchell, M.; Shih, M.F.; Lan, S.; Martin, J. Energy-exchange interactions between colliding vector solitons. Phys. Rev. Lett. 1999, 83, 2332. [Google Scholar] [CrossRef]
- Kang, J.U.; Stegeman, G.I.; Aitchison, J.S.; Akhmediev, N. Observation of Manakov spatial solitons in AlGaAs planar waveguides. Phys. Rev. Lett. 1996, 76, 3699. [Google Scholar] [CrossRef]
- Rand, D.; Glesk, I.; Bres, C.S.; Nolan, D.A.; Chen, X.; Koh, J.; Fleischer, J.W.; Steiglitz, K.; Prucnal, P.R. Observation of temporal vector soliton propagation and collision in birefringent fiber. Phys. Rev. Lett. 2007, 98, 053902. [Google Scholar] [CrossRef] [PubMed]
- Soljacic, M.; Steiglitz, K.; Sears, S.M.; Segev, M.; Jakubowski, M.H.; Squier, R. Collisions of Two Solitons in an Arbitrary Number of Coupled Nonlinear Schrödinger Equations. Phys. Rev. Lett. 2003, 90, 254102. [Google Scholar] [CrossRef] [PubMed]
- Kanna, T.; Lakshmanan, M. Exact soliton solutions of coupled nonlinear Schrödinger equations: Shape-changing collisions, logic gates, and partially coherent solitons. Phys. Rev. E 2003, 67, 046617. [Google Scholar] [CrossRef] [PubMed]
- Vijayajayanthi, M.; Kanna, T.; Murali, K.; Lakshmanan, M. Harnessing energy-sharing collisions of Manakov solitons to implement universal NOR and OR logic gates. Phys. Rev. E 2018, 97, 060201(R). [Google Scholar] [CrossRef] [PubMed]
- Segev, M.; Crosignani, B.; Yariv, A.; Fischer, B. Spatial solitons in photorefractive media. Phys. Rev. Lett. 1992, 68, 923. [Google Scholar] [CrossRef] [PubMed]
- Duree, G.C.; Shultz, J.L.; Segev, M.; Yariv, A.; Crosignani, B.; Porto, P.D.; Sharp, E.J.; Neurgaonkar, R.R. Observation of self-trapping of an optical beam due to the photorefractive effect. Phys. Rev. Lett. 1993, 71, 533. [Google Scholar] [CrossRef]
- Segev, M.; Valley, G.C.; Crosignani, B.; DiPorto, P.; Yariv, A. Steady-State Spatial Screening Solitons in Photorefractive Materials with External Applied Field. Phys. Rev. Lett. 1994, 73, 3211. [Google Scholar] [CrossRef] [PubMed]
- Christodoulides, D.N.; Carvalho, M.I. Bright, dark, and gray spatial soliton states in photorefractive media. J. Opt. Soc. Am. B 1995, 12, 1628. [Google Scholar] [CrossRef]
- Christodoulides, D.N.; Singh, S.R.; Carvalho, M.I. Incoherently coupled soliton pairs in biased photorefractive crystals. Appl. Phys. Lett. 1996, 68, 1763. [Google Scholar] [CrossRef]
- Chen, Z.; Segev, M.; Coskun, T.H.; Christodoulides, D.N. Observation of incoherently coupled photorefractive spatial soliton pairs. Opt. Lett. 1996, 21, 1436. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Segev, M.; Coskun, T.H.; Christodoulides, D.N.; Kivshar, Y.S.; Afanasjev, V.V. Incoherently coupled dark–bright photorefractive solitons. Opt. Lett. 1996, 21, 1821. [Google Scholar] [CrossRef]
- Mitchell, M.; Segev, M.; Christodoulides, D.N. Observation of multihump multimode solitons. Phys. Rev. Lett. 1998, 80, 4657. [Google Scholar] [CrossRef]
- Akhmediev, N.; Królikowski, W.; Snyder, A.W. Partially coherent colitons of variable shape. Phys. Rev. Lett. 1998, 81, 4632. [Google Scholar] [CrossRef]
- Ankiewicz, A.; Królikowski, W.; Akhmediev, N. Partially coherent solitons of variable shape in a slow Kerr-like medium: Exact solutions. Phys. Rev. E 1999, 59, 6079. [Google Scholar] [CrossRef] [PubMed]
- Sukhorukov, A.A.; Akhmediev, N. Coherent and Incoherent Contributions to Multisoliton Complexes. Phys. Rev. Lett. 1999, 83, 4736. [Google Scholar] [CrossRef]
- Królikowski, W.; Akhmediev, N.; Luther-Davies, B. Collision-induced shape transformations of partially coherent solitons. Phys. Rev. E 1999, 59, 4654. [Google Scholar] [CrossRef]
- Christodoulides, D.N.; Joseph, R.I. Vector solitons in birefringent nonlinear dispersive media. Opt. Lett. 1988, 13, 53. [Google Scholar] [CrossRef]
- Akhmediev, N.N.; Buryak, A.V.; Soto-Crespo, J.M.; Andersen, D.R. Phase-locked stationary soliton states in birefringent nonlinear optical fibers. J. Opt. Soc. Am. B 1995, 12, 434. [Google Scholar] [CrossRef]
- Collings, B.C.; Cundiff, S.T.; Akhmediev, N.N.; Soto-Crespo, J.M.; Bergman, K.; Knox, W.H. Polarization-locked temporal vector solitons in a fiber laser: Experiment. J. Opt. Soc. Am. B 2000, 17, 354. [Google Scholar] [CrossRef]
- Tratnik, M.V.; Sipe, J.E. Bound solitary waves in a birefringent optical fiber. Phys. Rev. A 1988, 38, 2011. [Google Scholar] [CrossRef]
- Haelterman, M.; Sheppard, A.P.; Snyder, A.W. Bound-vector solitary waves in isotropic nonlinear dispersive media. Opt. Lett. 1993, 18, 1406. [Google Scholar] [CrossRef]
- Yang, J. Classification of the solitary waves in coupled nonlinear Schrödinger equations. Phys. D Nonlinear Phenom. 1997, 108, 92. [Google Scholar] [CrossRef]
- Elena, A.; Ostrovskaya, E.A.; Kivshar, Y.S.; Chen, Z.; Segev, M. Interaction between vector solitons and solitonic gluons. Opt. Lett. 1999, 24, 327. [Google Scholar]
- Ostrovskaya, E.A.; Kivshar, Y.S.; Skryabin, D.V.; Firth, W.J. Stability of Multihump Optical Solitons. Phys. Rev. Lett. 1999, 83, 296. [Google Scholar] [CrossRef]
- Pelinovsky, D.E.; Yang, J. Instabilities of multihump vector solitons in coupled nonlinear Schrödinger equations. Stud. Appl. Math. 2005, 115, 109. [Google Scholar] [CrossRef]
- Kanna, T.; Lakshmanan, M.; Dinda, P.T.; Akhmediev, N. Soliton collisions with shape change by intensity redistribution in mixed coupled nonlinear Schrödinger equations. Phys. Rev. E 2006, 73, 026604. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, A.P.; Kivshar, Y.S. Polarized dark solitons in isotropic Kerr media. Phys. Rev. E 1997, 55, 4773. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Aravinthan, K. Spatial vector soliton and its collisions in isotropic self-defocusing Kerr media. Phys. Rev. E 2007, 75, 066605. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Manikandan, N.; Aravinthan, K. Energy-exchange collisions of dark-bright-bright vector solitons. Phys. Rev. E 2015, 92, 062913. [Google Scholar] [CrossRef] [PubMed]
- Vijayajayanthi, M.; Kanna, T.; Lakshmanan, M. Bright-dark solitons and their collisions in mixed N-coupled nonlinear Schrödinger equations. Phys. Rev. A 2008, 77, 013820. [Google Scholar] [CrossRef]
- Feng, B.F. General N-soliton solution to a vector nonlinear Schrödinger equation. J. Phys. A Math. Theor. 2014, 47, 355203. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Lakshmanan, M. Bright and dark soliton solutions to coupled nonlinear Schrödinger equations. J. Phy. A Math. Gen. 1995, 28, 2683. [Google Scholar] [CrossRef]
- Ohta, Y.; Wang, D.S.; Yang, J. General N-Dark-Dark Solitons in the Coupled Nonlinear Schrödinger Equations. Stud. Appl. Math. 2011, 127, 345. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Frantzeskakis, D.J. Solitons in coupled nonlinear Schrödinger models: A survey of recent developments. Rev. Phys. 2016, 1, 140. [Google Scholar] [CrossRef]
- Song, Y.; Shi, X.; Wu, C.; Tang, D.; Zhang, H. Recent Progress of study on optical solitons in fiber lasers. Appl. Phys. Rev. 2019, 6, 021313. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A. Dissipative Solitons; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Stalin, S.; Ramakrishnan, R.; Senthilvelan, M.; Lakshmanan, M. Nondegenerate solitons in Manakov system. Phys. Rev. Lett. 2019, 122, 043901. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Stalin, S.; Lakshmanan, M. Nondegenerate solitons and their collisions in Manakov systems. Phys. Rev. E 2020, 102, 042212. [Google Scholar] [CrossRef] [PubMed]
- Stalin, S.; Ramakrishnan, R.; Lakshmanan, M. Nondegenerate soliton solutions in certain coupled nonlinear Schrödinger systems. Phys. Lett. A 2020, 384, 126201. [Google Scholar] [CrossRef]
- Qin, Y.H.; Zhao, L.C.; Ling, L. Nondegenerate bound-state solitons in multicomponent Bose-Einstein condensates. Phys. Rev. E 2019, 100, 022212. [Google Scholar] [CrossRef]
- Zhang, C.R.; Tian, B.; Qu, Q.X.; Liu, L.; Tian, H.Y. Vector bright solitons and their interactions of the couple Fokas-Lenells system in a birefringent optical fiber. Z. Angew. Math. Phys. 2020, 71, 18. [Google Scholar] [CrossRef]
- Ding, C.C.; Gao, Y.T.; Hu, L.; Deng, G.F.; Zhang, C.Y. Vector bright soliton interactions of the two-component AB system in a baroclinic fluid. Chaos Solitons Fractals 2021, 142, 110363. [Google Scholar] [CrossRef]
- Qin, Y.H.; Zhao, L.C.; Yang, Z.Q.; Ling, L. Multivalley dark solitons in multicomponent Bose-Einstein condensates with repulsive interactions. arXiv 2021, arXiv:2102.10507. [Google Scholar]
- Ramakrishnan, R.; Stalin, S.; Lakshmanan, M. Multihumped nondegenerate fundamental bright solitons in N-coupled nonlinear Schrödinger system. J. Phys. A Math. Theor. 2021, 54, 14LT01. [Google Scholar] [CrossRef]
- Lakshmanan, M.; Kanna, T. Shape changing collisions of optical solitons, universal logic gates and partially coherent solitons in coupled nonlinear Schrödinger equations. Pramana J. Phys. 2001, 57, 885. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Schulman, E.I. To the integrability of the system of two coupled nonlinear Schrödinger equations. Phys. D Nonlinear Phenom. 1982, 4, 270. [Google Scholar] [CrossRef]
- Kaup, D.J.; Malomed, B.A. Soliton trapping and daughter waves in the Manakov model. Phys. Rev. E 1993, 48, 599. [Google Scholar] [CrossRef] [PubMed]
- Lazarides, N.; Tsironis, G.P. Coupled nonlinear Schrödinger field equations for electromagnetic wave propagation in nonlinear left-handed materials. Phys. Rev. E 2005, 71, 036614. [Google Scholar] [CrossRef]
- Makhankov, V.G. Quasi-classical solitons in the Lindner-Fedyanin model-“hole”-like excitations. Phys. Lett. A 1981, 81, 156. [Google Scholar] [CrossRef]
- Makhankov, V.G.; Makhaldiani, N.V.; Pashaev, O.K. On the integrability and isotopic structure of the one-dimensional Hubbard model in the long wave approximation. Phys. Lett. A 1981, 81, 161. [Google Scholar] [CrossRef]
- Lindner, U.; Fedyanin, V. Solitons in a one-dimensional modified Hubbard model. Phys. Status Solidi B 1978, 89, 123. [Google Scholar] [CrossRef]
- Pérez-García, V.M.; Beitia, J.B. Symbiotic solitons in heteronuclear multicomponent Bose-Einstein condensates. Phys. Rev. A 2005, 72, 033620. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Prinari, B.; Trubatch, A.D. Soliton interactions in the vector NLS equation. Inverse Probl. 2004, 20, 1217. [Google Scholar] [CrossRef]
- Prinari, B.; Ablowitz, M.J.; Biondini, G. Inverse scattering transform for the vector nonlinear Schrödinger equation with nonvanishing boundary conditions. J. Math. Phys. 2006, 47, 063508. [Google Scholar] [CrossRef]
- Prinari, B.; Biondini, G.; Trubatch, A.D. Inverse scattering transform for the multi-component Nonlinear Schrödinger equation with nonzero boundary conditions. Stud. Appl. Math. 2011, 126, 245. [Google Scholar] [CrossRef]
- Biondini, G.; Kovacic, G. Inverse scattering transform for the focusing nonlinear Schrödinger equation with nonzero boundary conditions. J. Math. Phys. 2014, 55, 031506. [Google Scholar] [CrossRef]
- Biondini, G.; Kraus, D. Inverse Scattering transform for the defocusing Manakov system with nonzero boundary conditions. SIAM J. Math. Anal. 2015, 47, 706. [Google Scholar] [CrossRef]
- Prinari, B.; Vitale, F.; Biondini, G. Dark-bright soliton solutions with nontrivial polarization interactions for the three-component defocusing nonlinear Schrödinger equation with nonzero boundary conditions. J. Math. Phys. 2015, 56, 071505. [Google Scholar] [CrossRef]
- Biondini, G.; Kraus, D.K.; Prinari, B. The three-component defocusing nonlinear Schrödinger equation with nonzero boundary conditions. Commun. Math. Phys. 2016, 348, 475–533. [Google Scholar] [CrossRef]
- Park, Q.H.; Shin, H.J. Systematic construction of multicomponent optical solitons. Phys. Rev. E 2000, 61, 3093. [Google Scholar] [CrossRef]
- Degasperis, A.; Lombardo, S. Multicomponent integrable wave equations: I. Darboux-dressing transformation. J. Phys. A Math. Theor. 2007, 40, 961. [Google Scholar] [CrossRef]
- Degasperis, A.; Lombardo, S. Multicomponent integrable wave equations: II. Soliton solutions. J. Phys. A Math. Theor. 2009, 42, 385206. [Google Scholar] [CrossRef]
- Ling, L.; Zhao, L.C.; Guo, B. Darboux transformation and multi-dark soliton for N-component nonlinear Schrödinger equations. Nonlinearity 2015, 28, 3243. [Google Scholar] [CrossRef]
- Ling, L.; Zhao, L.C.; Guo, B. Darboux transformation and classification of solution for mixed coupled nonlinear Schrödinger equations. Commun. Nonlin. Sci. Numer. Simul. 2016, 32, 285. [Google Scholar] [CrossRef]
- Tsuchida, T. Exact solutions of multicomponent nonlinear Schrödinger equations under general plane-wave boundary conditions. arXiv 2013, arXiv:1308.6623v2. [Google Scholar]
- Crosignani, B.; Cutolo, A.; Porto, P.D. Coupled-mode theory of nonlinear propagation in multimode and single-mode fibers: Envelope solitons and self-confinement. J. Opt. Soc. Am. 1982, 72, 1136. [Google Scholar] [CrossRef]
- Park, Q.H.; Shin, H.J. Painlevé analysis of the coupled nonlinear Schrödinger equation for polarized optical waves in an isotropic medium. Phys. Rev. E 1999, 59, 2373. [Google Scholar] [CrossRef]
- Akhmediev, N.N.; Ostrovskaya, E.A. Elliptically polarized spatial solitons in cubic gyrotropic materials. Opt. Commun. 1996, 132, 190. [Google Scholar] [CrossRef]
- Kanna, T.M.; Vijayajayanthi, M.; Lakshmanan, M. Coherently coupled bright optical solitons and their collisions. J. Phys. A Math. Theor. 2010, 43, 434018. [Google Scholar] [CrossRef]
- Kanna, T.; Sakkaravarthi, K. Multicomponent coherently coupled and incoherently coupled solitons and their collisions. J. Phys. A Math. Theor. 2011, 44, 285211. [Google Scholar] [CrossRef]
- Kasamatsu, K.; Tsubota, M.; Ueda, M. Vortex molecules in coherently coupled two-component Bose-Einstein condensates. Phys. Rev. Lett. 2004, 93, 250406. [Google Scholar] [CrossRef] [PubMed]
- Congy, T.; Kamchatnov, A.M.; Pavloff, N. Nonlinear waves in coherently coupled Bose-Einstein condensates. Phys. Rev. A 2016, 93, 043613. [Google Scholar] [CrossRef]
- Babu Mareeswaran, R.; Kanna, T. Superposed nonlinear waves in coherently coupled Bose-Einstein condensates. Phys. Lett. A 2016, 380, 3244. [Google Scholar] [CrossRef]
- Ieda, J.; Miyakawa, T.; Wadati, M. Exact Analysis of Soliton Dynamics in Spinor Bose—Einstein Condensates. Phys. Rev Lett. 2004, 93, 194102. [Google Scholar] [CrossRef]
- Prinari, B.; Ortiz, A.K.; van der Mee, C.; Grabowski, M. Inverse Scattering Transform and Solitons for Square Matrix Nonlinear Schrödinger Equations. Stud. Appl. Math. 2018, 141, 308. [Google Scholar] [CrossRef]
- Li, L.; Li, Z.; Malomed, B.; Mihalache, D.; Liu, W. Exact Soliton Solutions and Nonlinear Modulation Instability in Spinor Bose-Einstein Condensates. Phys. Rev. A 2005, 72, 033611. [Google Scholar] [CrossRef]
- Wang, D.S.; Zhang, D.J.; Yang, J. Integrable properties of the general coupled nonlinear Schrödinger equations. J. Math. Phys. 2010, 51, 023510. [Google Scholar] [CrossRef]
- Lü, M.; Peng, M. Painlevé-integrability and explicit solutions of the general two-coupled nonlinear Schrödinger system in the optical fiber communications. Nonlinear. Dyn. 2013, 73, 405. [Google Scholar] [CrossRef]
- Vishnu Priya, N.; Senthilvelan, M. N-bright-bright and N-dark-dark solitons of the coupled generalized nonlinear Schrödinger equations. Commun. Nonlin. Sci. Numer. Simul. 2016, 36, 366. [Google Scholar] [CrossRef]
- Agalarov, A.; Zhulego, V.; Gadzhimuradov, T. Bright, dark, and mixed vector soliton solutions of the general coupled nonlinear Schrödinger equations. Phys. Rev. E 2015, 91, 042909. [Google Scholar] [CrossRef]
- Zakharov, V.E. Collapse of Langmuir waves. Sov. Phys. JETP 1972, 35, 908. [Google Scholar]
- Benny, D.J. A General Theory for Interactions Between Short and Long Waves. Stud. Appl. Math. 1977, 56, 81. [Google Scholar] [CrossRef]
- Kivshar, Y.S. Stable vector solitons composed of bright and dark pulses. Opt. Lett. 1992, 17, 1322. [Google Scholar] [CrossRef]
- Chowdhury, A.; Tataronis, J.A. Long wave–short wave resonance in nonlinear negative refractive index media. Phys. Rev. Lett. 2008, 100, 153905. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Biondini, G.; Blair, S. Nonlinear Schrödinger equations with mean terms in nonresonant multidimensional quadratic materials. Phys. Rev. E 2001, 63, 046605. [Google Scholar] [CrossRef] [PubMed]
- Sazonov, S.V.; Ustinov, N.V. Vector solitons generated by the long wave-short wave interaction. JETP Lett. 2011, 94, 610. [Google Scholar] [CrossRef]
- Nishikawa, K.; Hojo, H.; Mima, K.; Ikezi, H. Coupled nonlinear electron-plasma and ion-acoustic waves. Phys. Rev. Lett. 1974, 33, 148. [Google Scholar] [CrossRef]
- Yajima, N.; Oikawa, M. Formation and interaction of sonic-Langmuir solitons: Inverse scattering method. Prog. Theor. Phys. 1976, 56, 1719. [Google Scholar] [CrossRef]
- Kawahara, T. Nonlinear self-modulation of capillary-gravity waves on liquid layer. J. Phys. Soc. Jpn. 1975, 38, 265. [Google Scholar] [CrossRef]
- Kawahara, T.; Sugimoto, N.; Kakutani, T. Nonlinear interaction between short and long capillary-gravity waves. J. Phys. Soc. Jpn. 1975, 39, 1379. [Google Scholar] [CrossRef]
- Djordjevic, V.D.; Redekopp, L.G. On two-dimensional packets of capillary-gravity waves. J. Fluid Mech. 1977, 79, 703. [Google Scholar] [CrossRef]
- Kopp, C.G.; Redekopp, L.G. The interaction of long and short internal gravity waves: Theory and experiment. J. Fluid. Mech. 1981, 111, 367. [Google Scholar] [CrossRef]
- Boyd, J.P. Long wave/short wave resonance in equatorial waves. J. Phys. Oceanogr. 1982, 13, 450. [Google Scholar] [CrossRef]
- Zabolotskii, A.A. Resonant interaction between a localized fast wave and a slow wave with constant asymptotic amplitude. JETP 2009, 109, 859. [Google Scholar] [CrossRef]
- Aguero, M.; Frantzeskakis, D.J.; Kevrekidis, P.G. Asymptotic reductions of two coupled (2 + 1)-dimensional nonlinear Schrödinger equations: Application to Bose-Einstein condensates. J. Phys. A Math. Gen. 2006, 39, 7705. [Google Scholar] [CrossRef]
- Niztazakis, H.E.; Frantzeskakis, D.J.; Kevrekidis, P.G.; Malomed, B.A.; González, R.C. Bright-dark soliton complexes in spinor Bose-Einstein condensates. Phys. Rev. A 2008, 77, 033612. [Google Scholar] [CrossRef]
- Ma, Y.C.; Redekopp, L.G. Some solutions pertaining to the resonant interaction of long and short waves. Phys. Fluids 1979, 22, 1872. [Google Scholar] [CrossRef]
- Kanna, T.; Sakkaravarthi, K.; Tamilselvan, K. General multicomponent Yajima-Oikawa system: Painlevé analysis, soliton solutions, and energy-sharing collisions. Phys. Rev. E 2013, 88, 062921. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.; Feng, B.F.; Maruno, K.I. General mixed multi-soliton solutions to one-dimensional multicomponent Yajima-Oikawa system. J. Phys. Soc. Jpn. 2015, 84, 074001. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.; Feng, B.F.; Maruno, K.I. Multi-dark soliton solutions of the two-dimensional multi-component Yajima-Oikawa systems. J. Phys. Soc. Jpn. 2015, 84, 034002. [Google Scholar] [CrossRef][Green Version]
- Oikawa, M.; Okamura, M.; Funakoshi, M. Two-dimensional resonant interaction between long and short waves. J. Phys. Soc. Jpn. 1989, 58, 4416. [Google Scholar] [CrossRef]
- Ohta, Y.; Maruno, K.; Oikawa, M. Two-component analogue of two-dimensional long wave-short wave resonance interaction equations: A derivation and solutions. J. Phys. A Math. Theor. 2007, 40, 7659. [Google Scholar] [CrossRef]
- Radha, R.; Senthil Kumar, C.; Lakshmanan, M.; Gilson, C.R. The collision of multimode dromions and a firewall in the two-component long-wave-short-wave resonance interaction equation. J. Phys. A Math. Theor. 2009, 42, 102002. [Google Scholar] [CrossRef]
- Kanna, T.; Vijayajayanthi, M.; Sakkaravarthi, K.; Lakshmanan, M. Higher dimensional bright solitons and their collisions in a multicomponent long wave-short wave system. J. Phys. A Math.Theor. 2009, 42, 115103. [Google Scholar] [CrossRef]
- Sakkaravarthi, K.; Kanna, T.; Vijayajayanthi, M.; Lakshmanan, M. Multicomponent long-wave-short-wave resonance interaction system: Bright solitons, energy-sharing collisions, and resonant solitons. Phys. Rev. E 2014, 90, 052912. [Google Scholar] [CrossRef]
- Kanna, T.; Vijayajayanthi, M.; Lakshmanan, M. Mixed solitons in a (2 + 1)-dimensional multicomponent long-wave-short-wave system. Phys. Rev. E 2014, 90, 042901. [Google Scholar] [CrossRef]
- Chen, J.; Feng, B.F.; Chen, Y.; Ma, Z. General bright-dark soliton solution to (2 + 1)-dimensional multi-component long-wave-short-wave resonance interaction system. Nonlinear Dyn. 2017, 88, 1273. [Google Scholar] [CrossRef]
- Chow, K.W.; Chan, H.N.; Kedzioara, D.J.; Grimshaw, R.H.J. Rogue wave modes for the long wave-short wave resonance model. J. Phys. Soc. Jpn. 2013, 82, 074001. [Google Scholar] [CrossRef][Green Version]
- Chen, S.; Grelu, P.; Soto-Crespo, J.M. Dark-and bright-rogue-wave solutions for media with long-wave-short-wave resonance. Phys. Rev. E 2014, 89, 011201(R). [Google Scholar] [CrossRef] [PubMed]
- Chan, H.N.; Ding, E.; Kedzioara, D.J.; Grimshaw, R.H.J.; Chow, K.W. Rogue waves for a long wave–short wave resonance model with multiple short waves. Nonlinear Dyn. 2016, 85, 2827. [Google Scholar] [CrossRef]
- Chen, S.; Soto-Crespo, J.M.; Grelu, P. Coexisting rogue waves within the (2 + 1)-component long-wave-short-wave resonance. Phys. Rev. E 2014, 90, 033203. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.; Feng, B.F.; Maruno, K.I. Rational solutions to two-and one-dimensional multicomponent Yajima-Oikawa systems. Phys. Lett. A 2015, 379, 1510. [Google Scholar] [CrossRef]
- Rao, J.; Porsezian, K.; He, J.; Kanna, T. Dynamics of lumps and dark-dark solitons in the multi-component long-wave-short-wave resonance interaction system. Proc. R. Soc. A 2018, 474, 20170627. [Google Scholar] [CrossRef]
- Yang, J.W.; Gao, Y.T.; Sun, Y.H.; Shen, Y.J.; Su, C.Q. Higher-order rogue waves with new spatial distributions for the (2 + 1)-dimensional two-component long-wave-short-wave resonance interaction system. Eur. Phys. J. Plus 2016, 131, 416. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ablowitz, M.J.; Ohta, Y.; Trubatch, A.D. On discretizations of the vector nonlinear Schrödinger equation. Phys. Lett. A 1999, 253, 287. [Google Scholar] [CrossRef]
- Vijayajayanthi, M.; Kanna, T.; Lakshmanan, M. Multisoliton solutions and energy sharing collisions in coupled nonlinear Schrödinger equations with focusing, defocusing and mixed type nonlinearities. Eur. Phys. J. Spec. Top. 2009, 173, 57. [Google Scholar] [CrossRef]
- Gilson, C.; Hietarinta, J.; Nimmo, J.; Ohta, Y. Sasa-Satsuma higher-order nonlinear Schrödinger equation and its bilinearization and multisoliton solutions. Phys. Rev. E 2003, 68, 016614. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, H.; Malomed, B.A. Singular solitons. Phys. Rev. E 2020, 101, 012211. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishnan, R.; Stalin, S.; Lakshmanan, M. Dynamics of nondegenerate solitons in generalized coupled nonlinear Schrödinger system. 2021; Unpublished. [Google Scholar]
- Stalin, S.; Ramakrishnan, R.; Lakshmanan, M. Dynamics of nondegenerate solitons in long-wave short-wave resonance interaction system. 2021; Unpublished. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stalin, S.; Ramakrishnan, R.; Lakshmanan, M. Nondegenerate Bright Solitons in Coupled Nonlinear Schrödinger Systems: Recent Developments on Optical Vector Solitons. Photonics 2021, 8, 258. https://doi.org/10.3390/photonics8070258
Stalin S, Ramakrishnan R, Lakshmanan M. Nondegenerate Bright Solitons in Coupled Nonlinear Schrödinger Systems: Recent Developments on Optical Vector Solitons. Photonics. 2021; 8(7):258. https://doi.org/10.3390/photonics8070258
Chicago/Turabian StyleStalin, S., R. Ramakrishnan, and M. Lakshmanan. 2021. "Nondegenerate Bright Solitons in Coupled Nonlinear Schrödinger Systems: Recent Developments on Optical Vector Solitons" Photonics 8, no. 7: 258. https://doi.org/10.3390/photonics8070258
APA StyleStalin, S., Ramakrishnan, R., & Lakshmanan, M. (2021). Nondegenerate Bright Solitons in Coupled Nonlinear Schrödinger Systems: Recent Developments on Optical Vector Solitons. Photonics, 8(7), 258. https://doi.org/10.3390/photonics8070258