Optical Frequency Combs Generated in Silica Microspheres in the Telecommunication C-, U-, and E-Bands

Abstract

Optical frequency combs (OFCs) generated in microresonators with whispering gallery modes are demanded for different applications including telecommunications. Extending operating spectral ranges is an important problem for wavelength-division multiplexing systems based on microresonators. We demonstrate experimentally three spectrally separated OFCs in the C-, U-, and E-bands in silica microspheres which, in principle, can be used for telecommunication applications. For qualitative explanation of the OFC generation in the sidebands, we calculated gain coefficients and gain bandwidths for degenerate four-wave mixing (FWM) processes. We also attained a regime when the pump frequency was in the normal dispersion range and only two OFCs were generated. The first OFC was near the pump frequency and the second Raman-assisted OFC with a soliton-like spectrum was in the U-band. Numerical simulation based on the Lugiato–Lefever equation was performed to support this result and demonstrate that the Raman-assisted OFC may be a soliton.

1. Introduction

Microresonators with whispering gallery modes (WGMs) are attractive for various applications, including classical and non-classical ones [1,2]. Sensing [3,4,5] and biosensing [6,7], optical filtering and switching [8,9,10], frequency stabilization, and linewidth narrowing [11,12] are just a few of them. A possibility of developing a new class of optical sources with a controllable number of robust soliton pulses operating in self-starting regimes based on coupled resonators is discussed in [13], where stabilization is implemented by linear coupling without saturable absorption. The OFC generation in microresonators, demonstrated for the first time in 2007 [14], has greatly expanded the application range of such photonic devices [1]. They are used in coherent communication [15,16], dual-comb spectroscopy [17], optical atomic clock [18], ultrafast optical ranging [19], and in many more areas.

Although on-chip microresonators belong to one of the most actively developing areas [20], silica microresonators are also of great interest, since they are a very convenient platform for the development of micro-photonic devices. For example, a four-port microdevice based on an SNAP (surface nanoscale axial photonics) microresonator produced on the surface of a silica fiber was demonstrated in [21]. The silica microresonator technologies are easier and cheaper compared to the technologies of on-chip crystalline microresonators. The commonly used method of pump coupling into a microresonator through a tapered fiber also allows system parameters to be controlled in a wide range by varying the relative position between the resonator and the tapered fiber (while a similar adjustment is impossible for on-chip microresonators). To protect silica microresonators from air flows, dust, and high humidity, they are portably and robustly packaged [22].

Silica microresonators made of a standard optical fiber are suitable for application in the telecommunication range, since they can be pumped by narrow-linewidth C-band telecom lasers, and the corresponding experimental schemes are based on standard telecom components. Recently, we studied theoretically [23,24] and demonstrated experimentally [25] the implementation of wavelength division multiplexed-passive optical network (WDM-PON) in the C-band using an OFC generator based on a silica microsphere as a multiple light source. When several lasers (laser array) are replaced by a single OFC source, it improves the energy efficiency of the WDM fiber optical communication system, at the same time providing stable frequency spacing and strong phase relation between generated carriers (modes) [24,25,26]. Extending OFCs to the L-band is also a straightforward solution for WDM-PONs, when the use of the C-band is insufficient for satisfying the bandwidth demand. Particularly, it is of interest for next-generation passive optical network 2 (NG-PON2) or currently developing Super-PON networks, where frequencies of L-band are allocated for the downstream transmission [27]. U-band laser sources are mainly used for network monitoring purposes, so their development and investigation is also required.

It is known that, for Kerr OFC generation, the main mechanism is FWM, which can be readily applied for explanation of experiments. However, frequently, when generating OFCs, Raman nonlinearity plays an important role in silica microresonators. A Raman microsphere laser was demonstrated for the first time in [28]. Since then, Raman processes have been widely investigated. Many works were also devoted to study of Kerr–Raman OFCs (for example, [22,29,30,31]). However, the nonlinear dynamics of intracavity radiation can be so complex and diverse that it is still possible to discover new features or interesting regimes of nonlinear conversion of radiation.

Here, we demonstrate three experimental series on the generation of spectrally separated OFCs in silica microspheres. In the first series we obtained the first OFC near the pump frequency in the C-band, the second Stokes OFC in the U-band and beyond, and the third anti-Stokes OFC in the E-band. To give a qualitative explanation of OFC generation in the sidebands, we estimated gain coefficients and gain bandwidths for degenerate four-wave mixing (FWM) processes under the strong intracavity CW field approximation. To understand the opportunities for OFC generation in sidebands due to the degenerate FWM process within such an approximation, we analyzed in detail a pump frequency varying in the 190–198 THz range. In the second experimental series, by simple tuning of the pump frequency we attained frequency tunable Raman OFCs and E-band OFCs, as well as a C-band OFC. In the third experimental series, the pump frequency was in the normal dispersion range and we attained a Raman soliton-like spectrum without symmetric high-frequency sideband. To support this result, we performed numerical simulation based on the Lugiato–Lefever equation. We theoretically demonstrated Raman soliton generation in the anomalous dispersion range with the pump in the normal dispersion range, for the first time, to the best of our knowledge. Note that a Stokes (Raman-assisted) soliton co-existing with a fundamental dissipative Kerr soliton in the anomalous dispersion range was discovered in a silica on silicon microcavity [32], but this regime differs from ours.

2. Methods

2.1. Fabrication of Microspheres

Samples of silica microresonators were made of standard ITU-T G.652.D telecommunication fiber Corning SMF28e using the technology described in detail in [24]. In brief, it is based on repeated melting of a thinned fiber end with a fiber splicer. This fabrication process allows producing microspheres with reproducible and controllable diameters and similar Q-factors. Within a few hours after manufacturing, the Q-factors, regardless of the microsphere diameter, exceeded 5 × 10⁷ on average. Within a couple of days, the Q-factors dropped on the average to a value of 4 × 10⁷, and then this value remained unchanged for a long time. Two months after the preparation of the samples, the Q-factors were about 2 × 10⁷. Note that the record large value is Q = 8 × 10⁹ measured at 633 nm ~1 min after fabrication for a silica 750-μm microsphere [33]. However, typical Q-factors for silica microspheres at 1.55 μm used for OFC generation or Raman lasing are 10⁷–10⁸ [28,29,34,35], which agrees with our results. The reasons limiting Q-factors are discussed in [33].

We used microspheres with diameters d ≈ 165 μm and FSRs of about 400 GHz in all experiments and the corresponding numerical simulations. Note that the mode spacing 400 GHz = M × 100 GHz (M = 4) satisfies the ITU-T recommendation G.694.1 [36], which specifies the spectral grid for WDM systems. To excite WGMs in a microsphere, we used tapered fibers made of Corning SMF28e with gas burners [24,25,37].

2.2. Numerical

2.2.1. Calculation of Dispersion and Nonlinear Coefficient

To find a free spectral range (FSR) and to calculate dispersion of a microsphere, we numerically solved the characteristic equation for a fundamental TE mode family [38]:

$$n\frac{{\left[{(kd/2)}^{1/2}{J}_{l+1/2}(kd/2)\right]}^{\prime }}{{(kd/2)}^{1/2}{J}_{l+1/2}(kd/2)}=\frac{{\left[{(k_{0}d/2)}^{1/2}{H}_{l+1/2}^{(1)}(k_{0}d/2)\right]}^{\prime }}{{(k_{0}d/2)}^{1/2}{H}_{l+1/2}^{(1)}(k_{0}d/2)},$$

(1)

where the prime is the derivative with respect to the argument in parenthesis; J_l+1/2 and H_l+1/2⁽¹⁾ are the Bessel function and the Hankel function of the 1st kind of order l + 1/2, respectively; l is the azimuthal index; k₀ = 2∙π∙ν/c is the light propagation constant in vacuum; ν is the frequency; k = n(ν)·k₀; n(ν) is the linear refractive index of the silica glass (calculated using the Sellmeier formula given in [39]). We selected the first roots of Equation (1) for the fundamental mode family. The roots were localized using a well-known approximation formula for the eigenfrequencies presented, for example, in [38]. These approximate eigenfrequencies were used as the initial values for finding the roots of Equation (1). The iterative algorithm was implemented with the dispersion of the silica glass taken into account [39]. After finding eigenfrequencies for the fundamental TE mode family, we calculated the 2nd-order dispersion [40]:

$${\beta }_2=-\frac{1}{2{\pi }^{2}d}\frac{\Delta \left(\Delta {\nu }_l\right)}{{\left(\Delta {\nu }_l\right)}^3},$$

(2)

where

$$\Delta {\nu }_l=\frac{{\nu }_{l+1}-{\nu }_{l-1}}{2};\hspace{1em}\Delta (\Delta {\nu }_l)={\nu }_{l+1}-2{\nu }_l+{\nu }_{l-1}.$$

(3)

The electric field Ẽ(r) of the fundamental TE WGM was found as in [38], and after that, the effective WGM volume V_eff and nonlinear Kerr coefficient γ were calculated

$$V_{eff}=\frac{{\displaystyle \int n^2|\tilde{E}{|}^2{d}^{3}r}}{\max (n^2|\tilde{E}{|}^2)},$$

(4)

$$\gamma =\frac{2\pi }{\lambda }\frac{n_2}{V_{eff}/(\pi d)},$$

(5)

where n₂ = 2.2·10⁻²⁰ m²/W is the nonlinear refractive index of the silica glass [39]. We found γ = 6.2 (W∙km)⁻¹ for ν ≈ 193 THz and neglected its frequency dependence in the simulations below.

2.2.2. Calculation of Intracavity CW Power

Nonlinear dynamics of the intracavity radiation neglecting Raman contribution can be described by the Lugiato–Lefever equation in the following form [1]:

$$t_R\frac{\partial E(t,\tau )}{\partial t}=\left[-\alpha -i{\delta }_0+i\pi d{\displaystyle \sum _{k\ge 2}\frac{{\beta }_k}{k!}{\left(i\frac{\partial }{\partial \tau }\right)}^k+i\gamma \pi d|E(t,\tau ){|}^2}\right]E(t,\tau )+\sqrt{\theta }{E}_{in}$$

(6)

where Ε(t, τ) is the intracavity field; t_R is the round trip time; t and τ are slow and fast times, respectively; α is the loss coefficient including intrinsic and coupling losses; β_k is the dispersion of the k-th order; θ is the coupling coefficient; and δ₀ is the frequency detuning of the pump field Ε_in from the exact resonance.

Further, to find the intracavity CW power, we applied the commonly used approach [39,41]. For the CW solution, Equation (6) is reduced to the following algebraic equation in the standard dimensionless form [41]:

$$Y^3-2\Delta Y^2+({\Delta }^2+1)Y=X.$$

(7)

Here, X and Y are the normalized pump and intracavity powers, respectively; Δ is the normalized detuning (X = |E_in|²(π∙d∙γ∙θ/α³); Y = |E|²(π∙d∙γ/α); and Δ = δ₀/α). We found Y(Δ) from Equation (7), and in the case when this equation had three roots, we took the maximum value corresponding to the upper stable branch.

2.2.3. Calculation of Gain Coefficients for the Degenerate FWM Processes under the Strong Intracavity CW Field Approximation

To estimate the possibility of generating sidebands via degenerate FWM under the strong intracavity field approximation, we followed the approach developed in [35,42] (which can be extended taking into account the dispersion of finesse [43]). We assumed that the total intracavity field can be approximated as the sum of a strong CW field E₀ found from Equation (7) and two small-amplitude sidebands (|a_±| << |E₀|) symmetrically shifted by ±Ω from the pump frequency

$$E(t,\tau )\approx E_0+a_{+}\exp (i\Omega \tau )+a_{-}\exp (-i\Omega \tau ).$$

(8)

Next, we rewrote Equation (6), taking into account the expression (8), and linearized this equation. After algebraic transforms, the following system of equations was obtained

$$t_R\frac{d}{dt}\left(\begin{array}{c}{a}_{+}\\ a_{-}^{\ast }\end{array}\right)=\left(\begin{array}{cc}-\alpha +iB-i\pi d{D}_o(\Omega )& i\pi d\gamma {(E_0^{\ast })}^2\\ -i\pi d\gamma {(E_0^{\ast })}^2& -\alpha -iB-i\pi d{D}_o(\Omega )\end{array}\right)\left(\begin{array}{c}{a}_{+}\\ a_{-}^{\ast }\end{array}\right),$$

(9)

where B = −δ₀ + πd∙D_e(Ω) + 2πdγ|E₀|², D_o(Ω), and D_e(Ω) are odd and even dispersion, respectively

$$D_o(\Omega )={\displaystyle \sum _{k=1}^4{\beta }_{2k+1}{\Omega }^{2k+1}/(2k+1)!}.$$

(10)

$$D_e(\Omega )={\displaystyle \sum _{k=1}^4{\beta }_{2k}{\Omega }^{2k}/(2k)!}.$$

(11)

The eigenvalues of Equation (9) are

$${\lambda }_{\pm }(\Omega )t_R=-\alpha +i\pi d{D}_o(\Omega )\pm \sqrt{4\pi d\gamma P({\delta }_0-\pi d{D}_e(\Omega ))-{({\delta }_0-\pi d{D}_e(\Omega ))}^2-3{\pi }^2{d}^2{\gamma }^2{P}^2}$$

(12)

Here, P = |E₀|² is the intracavity power.

The instability (exponential increase of a_±) is observed if Re(λ_±(Ω) > 0). For this case, the gain coefficient is Re(λ_±(Ω)).

2.2.4. Numerical Simulation Based on Lugiato–Lefever Equation with the Raman Nonlinearity Taken into Account

To analyze the dynamics of the optical intracavity field taking the Raman nonlinearity into consideration, we used the generalized Lugiato–Lefever equation

$$t_R\frac{\partial E(t,\tau )}{\partial t}=\left[-\alpha -i{\delta }_0+i\pi d{\displaystyle \sum _{k\ge 2}\frac{{\beta }_k}{k!}{\left(i\frac{\partial }{\partial \tau }\right)}^k}\right]E(t,\tau )+i\gamma \pi d\cdot E(t,\tau ){\displaystyle \int R(s)|}E(t,\tau -s){|}^{2}ds+\sqrt{\theta }{E}_{in}.$$

(13)

with the added Raman response function R(t) [39]:

$$R(t)=(1-f_R)\delta (t)+f_R(T_1^{-2}+T_2^{-2})T_1\exp (-t/T_2)\sin (t/T_1),$$

(14)

where δ(t) is the Dirac delta function; f_R = 0.18 is the fraction of Raman contribution to the total nonlinear response; T₁ = 12.2 fs, and T₂ = 32 fs.

We used a home-made software based on the common symmetrized split-step Fourier method (SSFM) [39] for modeling intracavity light field dynamics.

3. Results

3.1. The 1st Experimental Series

In the 1st experimental series, we used the scheme shown in Figure 1a. The radiation from the output of a C-band tunable laser ‘CW pump laser (I)’ with a 4 mW power and a 100 kHz linewidth was amplified up to 220 mW using an erbium-doped fiber amplifier (EDFA). Next, the amplified signal passed a Faraday isolator (ISO), a polarization controller (PC), and was then coupled through a tapered fiber to a microsphere. Two CCD cameras were used for a rough control of the relative position between the tapered fiber and the microsphere and a piezo micro-positioner was used for precise control. We used a telecom Optical Spectrum Analyzer ‘OSA(I)’, which operates up to 1700 nm to record the output spectra. We varied the distance between the microsphere and the tapered fiber, thereby varying the effective coupling coefficient and the pump detuning from exact resonance (due to thermal mode pulling effect). It is well known that detuning is a very important parameter strongly affecting the nonlinear dynamics of intracavity radiation [44,45]. By changing the relative position between the tapered fiber and the microsphere, it is possible to obtain OFC in different regimes. Note that a similar scheme was previously used to generate a long-term stable OFC with 2∙FSR mode spacing [46]. Here, in the 1st experimental series, we pumped the microsphere at 193.4 THz near the zero dispersion frequency of about 193.3 THz. The calculated dispersion of the microsphere is shown in Figure 1b. We attained the first relatively weak OFC near the pump frequency and two spectrally separated OFCs in the sidebands (Figure 1c). The second low-frequency OFC was near 180 THz and the third high-frequency OFC is located symmetrically to the second OFC.

To qualitatively explain the OFC generation in the sidebands (Figure 1c), we estimated gain coefficients and gain bandwidths as described in Section 2.2.3. We took the pump power before the microsphere |E_in|² = 50 mW, assumed α = θ/2, and set the finesse π/α = 5 × 10⁴. Since detuning was not known for sure, we considered various values presented in Figure 1d. We found that the experimental sidebands shown in Figure 1c correspond to the gain bands for reasonable values of detuning. In addition, the Raman scattering may also affect the low-frequency OFC, but here we did not consider it for qualitative understanding of the FWM process.

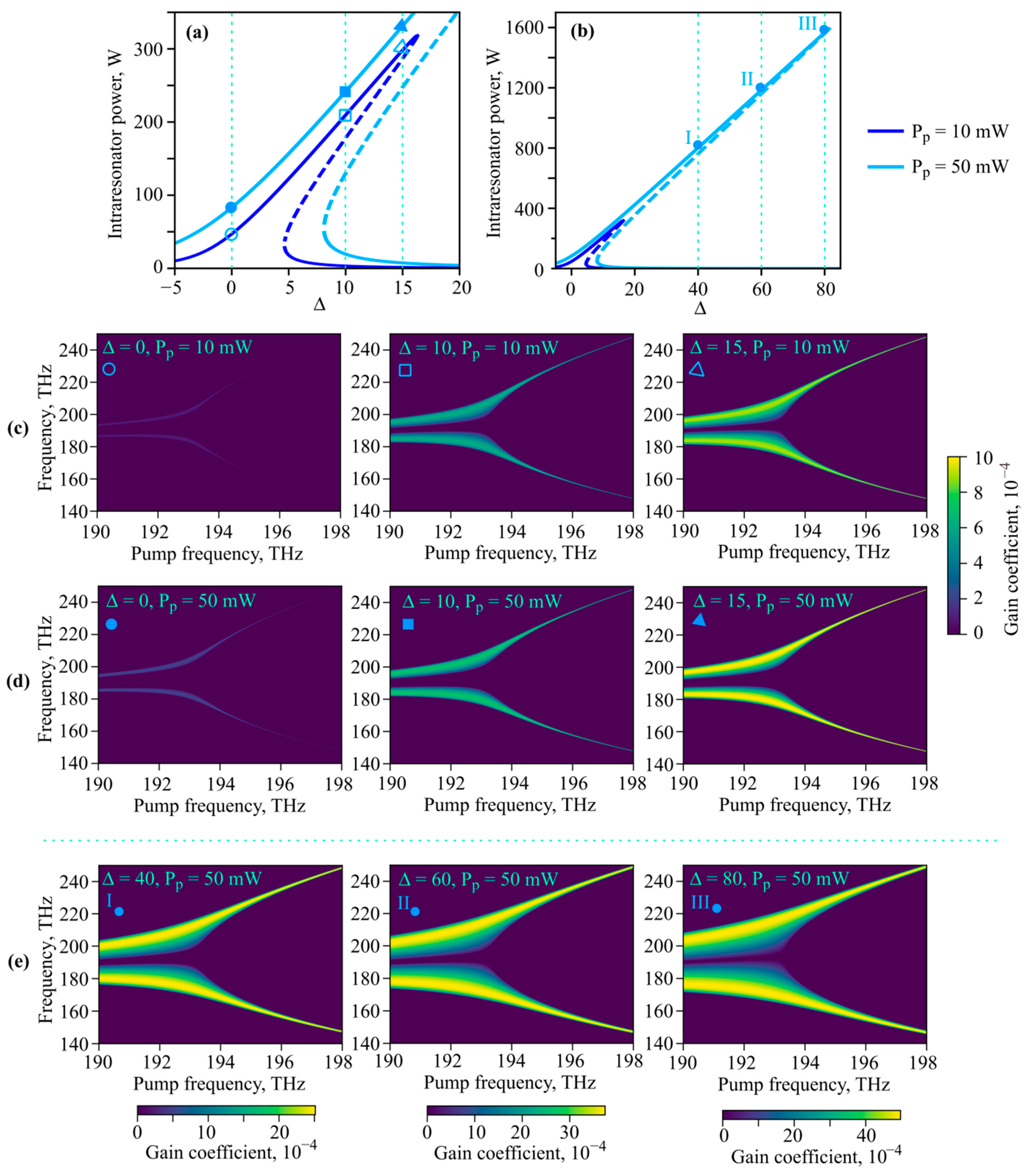
3.2. Theoretical Study of FWM

To understand the potential of OFC generation in sidebands due to the degenerate FWM process for a strong intracavity pump field, we analyzed the pump frequency varying in the 190–198 THz range. This frequency range can be obtained with commercially available tunable narrow-linewidth lasers. We considered pump powers P_p = 10 mW and P_p = 50 mW. We used the approach described in Section 2.2.2 for finding intracavity CW powers and the approach described in Section 2.2.3 for finding gain coefficients for a FWM process.

The calculated intracavity CW powers are shown in Figure 2a,b. For the marked points we calculated the gain coefficients as functions of the pump frequency and sideband frequencies. The numerical results are demonstrated in Figure 2c,d for pump powers of 10 mW and 50 mW, respectively, for dimensionless detuning Δ = 0, 10, 15 (see also the corresponding marked points in Figure 2a). Figure 2c,d are drawn for the same colormap scale. The sidebands are wider and located closer to the pump frequency when it is in the anomalous dispersion range. When the pump frequency is in the normal dispersion range, the sideband frequencies are shifted significantly from the pump frequency (which agrees with the results of the paper [35]). For the same detuning, maximum gain coefficients are slightly higher for P_p = 50 mW than for P_p = 10 mW due to a higher intracavity power (see Figure 1a). We also analyzed large values of detuning Δ = 40, 60, 80 for P_p = 50 mW (see also the corresponding marked points in Figure 2b). The calculated gain coefficients are given in Figure 2e (here, individual colormap scales are used for each value of detuning). The broadest gain-bands are obtained for the pump frequencies close to the zero dispersion frequency. Their spectral widths exceed 20 THz. The larger the detuning, the higher the gain coefficient.

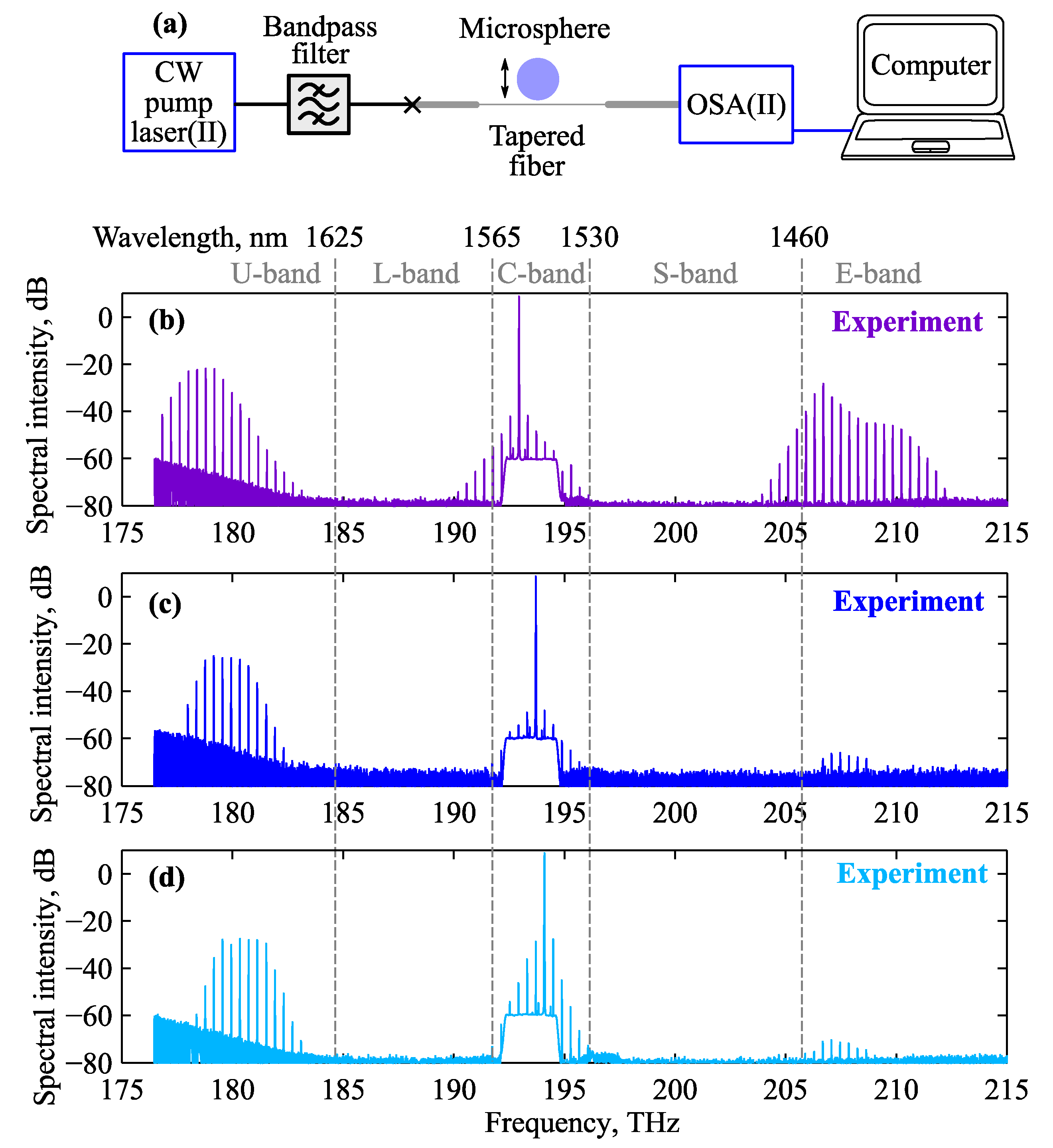
3.3. The 2nd Experimental Series

The 2nd experimental series was performed according to the schematic presented in Figure 3a. The microsphere was pumped by a CW laser ‘CW pump laser(II)’ tunable in the 190.3–197.9 THz range with a maximum power of 60 mW and a 10 kHz linewidth. A bandpass filter was placed before the tapered fiber for removing the background emission of the pump laser. Two CCD cameras and a piezo micro-positioner were also used for a rough and precise control of the relative position between the tapered fiber and the microsphere. The output spectra were measured with the Optical Spectrum Analyzer ‘OSA(II)’ which also operates up to 1700 nm. To obtain OFC generation, the regime of sweeping the CW laser frequency near a certain value was tuned on as in our previous works [31,37,46]. After a few sweeping periods, this regime was turned off (after that, the laser frequency was constant) and steady-state OFCs were generated due to thermal frequency pulling. Note that a similar scheme was previously used to generate Raman-assisted nested OFCs with soliton-like spectra belonging to two different mode families [31].

By adjusting the relative position between the microsphere and the tapered fiber, we attained three OFCs for the pump frequency of 192.9 THz (Figure 3b). The Raman-assisted OFC had a soliton-like shape (Figure 3b). Its low-frequency spectral wing extended beyond the OSA operating range. The E-band OFC contained more than 20 spectral lines with a relatively high intensity. For pump frequencies of 193.7 THz and 191.4 THz, the Raman-assisted OFCs in the U-band also had soliton-like shapes, while the E-band OFCs were very weak (Figure 3c,d). In these cases, the Raman OFCs were not weak in comparison with the pump, so the simple method of calculating gain coefficients for the FWM process described in Section 2.2.3 and applied in Section 3.1 and Section 3.2 could not be used.

It should be noted that in this experimental series, by simple tuning of the pump frequency we attained frequency tunable Raman soliton-like OFCs, which may be useful for applications.

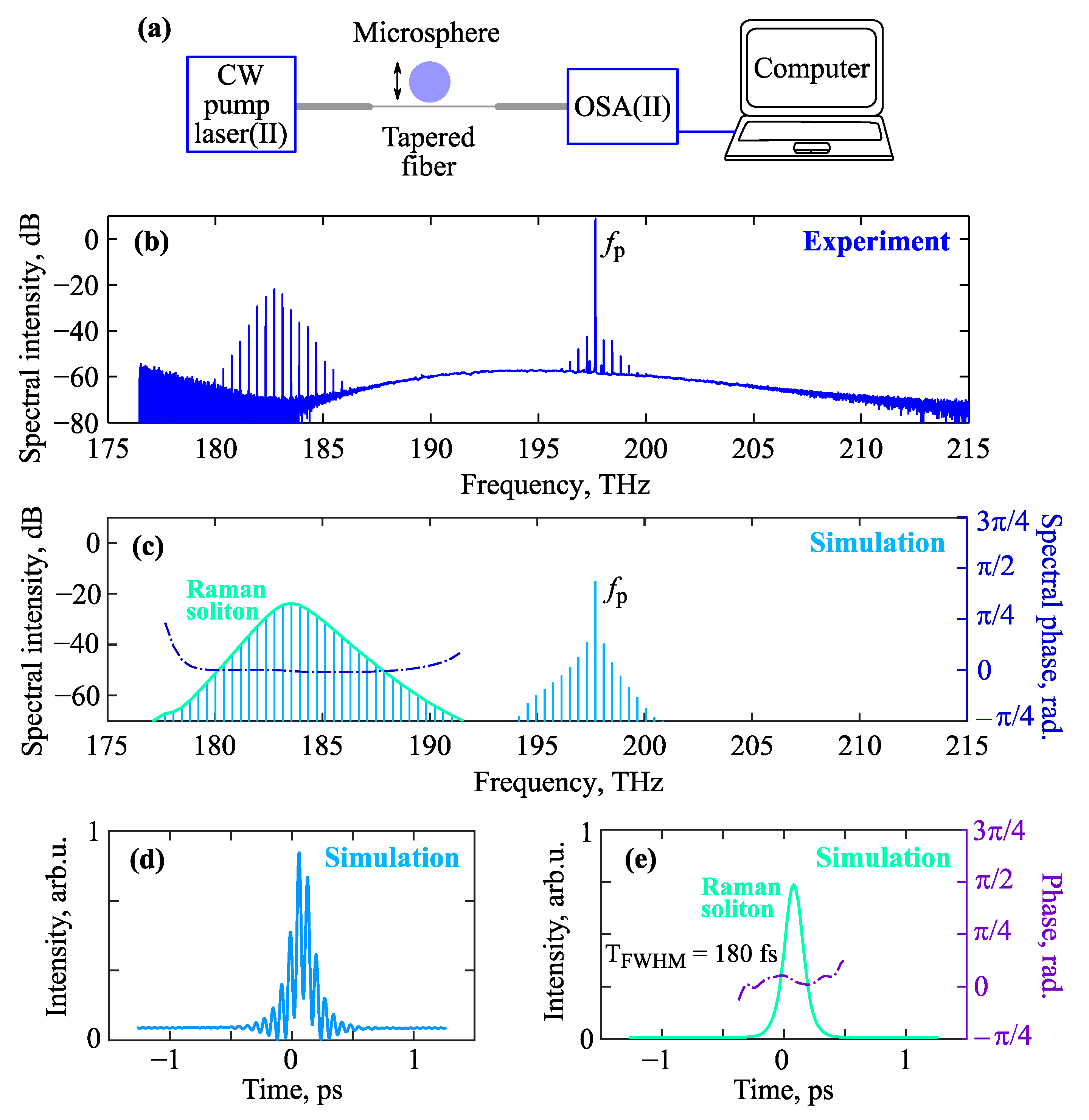
3.4. The 3rd Experimental Series and Its Interpretation

Next, we removed the bandpass filter from the scheme plotted in Figure 3a and operated with the scheme shown in Figure 4a. We set the pump frequency f_p = 197.7 THz and attained only two OFCs: the first one was near the pump frequency, and the second was the Raman-assisted OFC (Figure 4b). In this case, the pump frequency was in the normal dispersion range, while the soliton-like Raman-assisted OFC was in the anomalous dispersion range.

To demonstrate that the observed Raman OFC with a soliton-like spectrum may correspond to a “true” soliton (with localized unchangeable temporal profile), we performed numerical simulation in the framework of the Lugiato–Lefever equation with the Raman nonlinearity taken into account as described in Section 2.2.4. We considered 2⁹ modes. The numerically modeled stable spectrum and spectral phase of the Raman-assisted OFC are plotted in Figure 4c. Here, we set Δ = 6 and X = 25 to attain a sufficiently good agreement between the experimental and the simulated spectra (compare Figure 4b,c). The measured spectral intensity at the pump frequency f_p is higher than the calculated spectral intensity at f_p because in the experiment the transmitted unconverted pump is also measured. The slight difference in the shape of the experimental and measured spectra is explained by the fact that we did not exactly know several experimental parameters (for example, detuning and coupling coefficient). The simulated intensity distribution in the time domain is shown in Figure 4d. Next, we filtered out the Raman-assisted OFC in the spectral domain (using the super-Gaussian filter for the complex spectral envelope: exp(-(f_p + Δf_R)⁶/δf⁶), Δf_R = 15 THz, δf = 7 THz) and found its field distribution in the time domain. The temporal intensity and phase of the Raman soliton are plotted in Figure 4e. We indeed obtained the sech²-shape soliton demonstrated in Figure 4e. This soliton has almost flat spectral and temporal phases. Its duration is 180 fs (full width at half maximum, FWHM) and TBP = 0.315 (time-bandwidth product, TBP). Note that for the sech²-shape Fourier transform limited pulses, TBP is also 0.315.

4. Discussion

We have demonstrated three experimental series of spectrally separated OFC generation in different telecommunication bands in silica microspheres, with a diameter of about 165 μm and an FSR of about 400 GHz.

In the first series, we have obtained the first OFC near the pump frequency in the C-band, the second Stokes OFC in the U-band and beyond, and the third anti-Stokes OFC in the E-band. The qualitative explanation of OFC generation in the sidebands is based on degenerate four-wave mixing (FWM) processes under the strong intracavity CW field approximation. Note that similar spectra were previously demonstrated in different microresonators (for example, in [40,42,47]). We have also investigated the pump frequency varying in the 190–198 THz range. The sidebands are wider and are located closer to the pump frequency when the pump frequency is in the anomalous dispersion range. When the pump frequency is in the normal dispersion range, the sidebands’ frequencies are shifted significantly from the pump frequency (which agrees with the results of the paper [35]). For the same detuning, maximum gain coefficients are slightly higher for a higher pump power due to a higher intracavity power. The broadest gainbands are obtained for pump frequencies close to the zero dispersion frequency. Their spectral widths exceed 20 THz. The larger the detuning, the higher the gain coefficient.

In the second experimental series, by simple tuning of the pump frequency, we have attained frequency tunable Raman OFCs in the U-band and anti-Stokes OFCs in the E-band, and also OFCs in the C-band. In these cases, the Raman OFCs are not weak in comparison with the pump, so the simple method of calculating gain coefficients for the FWM process applied for the first series cannot be used here.

In the third experimental series, the pump frequency was in the normal dispersion range and we have attained a Raman soliton-like spectrum without symmetric high-frequency sideband. To demonstrate that the observed Raman OFC with a soliton-like spectrum can indeed correspond to a soliton with a localized unchangeable temporal profile, we have performed numerical simulation in the framework of the Lugiato–Lefever equation, with the Raman nonlinearity taken into account. Note that experimental and theoretical studies of the generation of Raman OFCs with bell-shaped spectra from a silica rod microresonator with controlled center frequency via detuning and coupling optimization were presented in [30]. However, the possibility of Raman soliton formation was not investigated in the work [30]. A Stokes soliton co-existing with a fundamental dissipative Kerr soliton in the anomalous dispersion range was discovered in a silica on silicon microcavity [32]. However, we could not find works reporting a Raman soliton in microresonators (in the anomalous dispersion range) when the pump with a weak OFC nearby was in the normal dispersion range (as in Figure 4). Thereforw, we believe that this found regime of the Raman soliton generation is novel.