Abnormal Fano Profile in Graphene-Wrapped Dielectric Particle Dimer
Abstract
1. Introduction
2. Materials and Methods
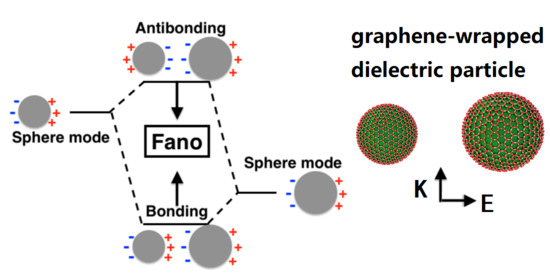
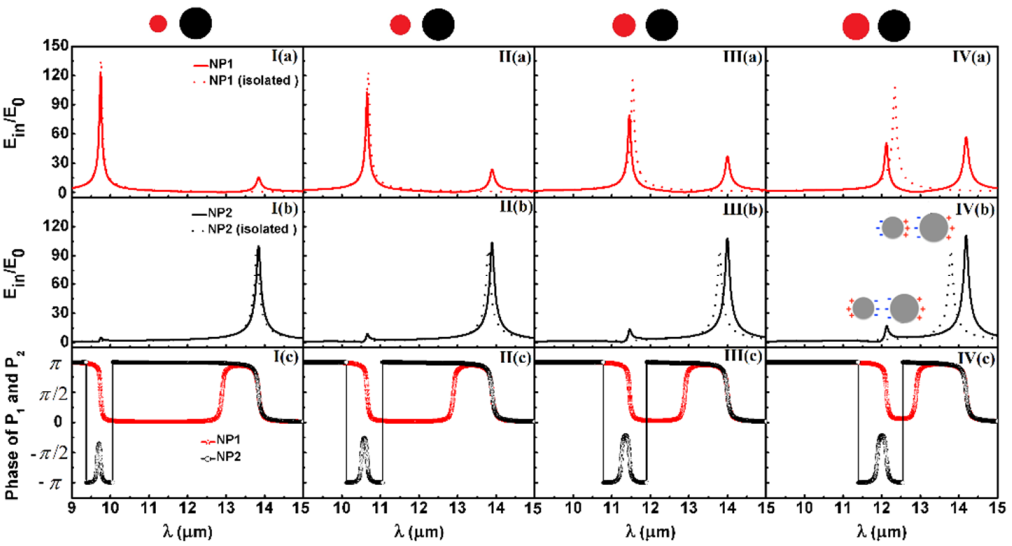
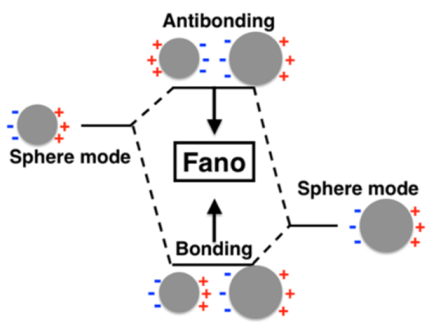
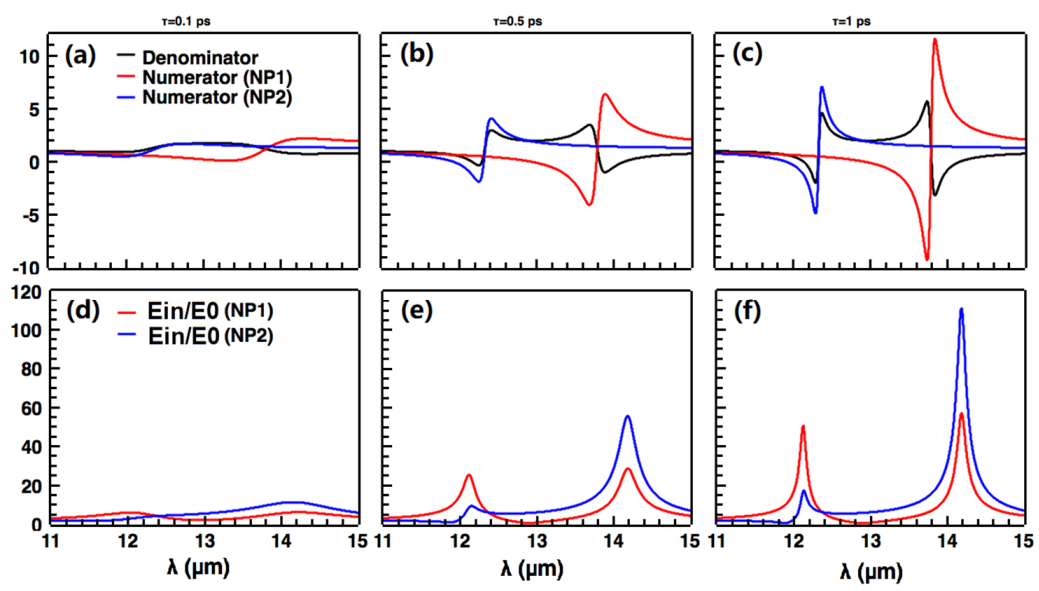
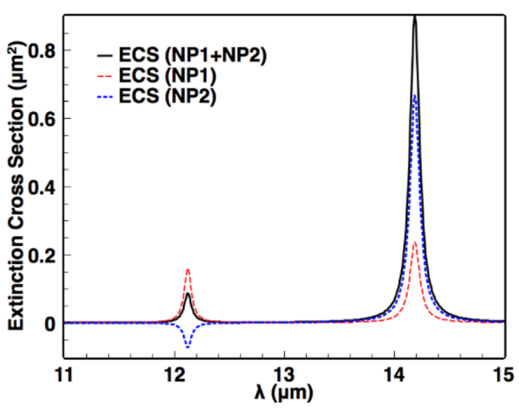
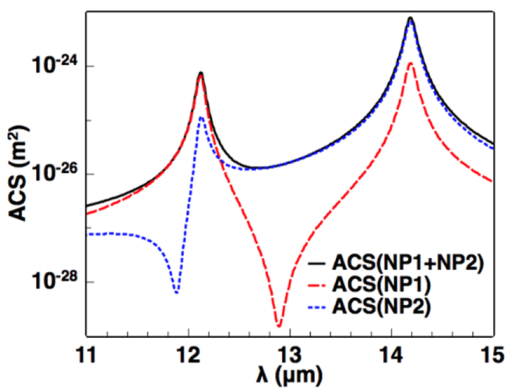
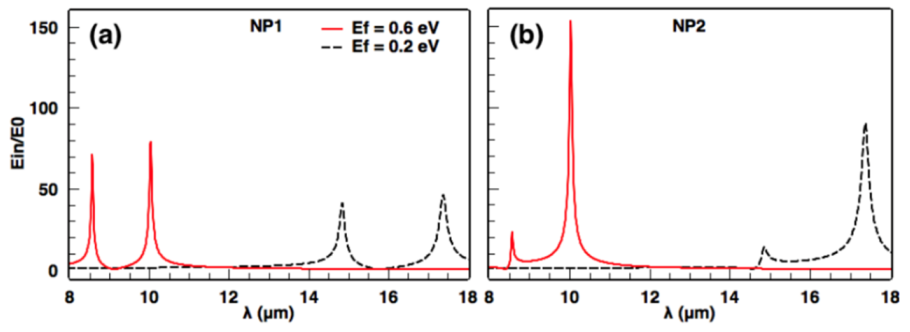
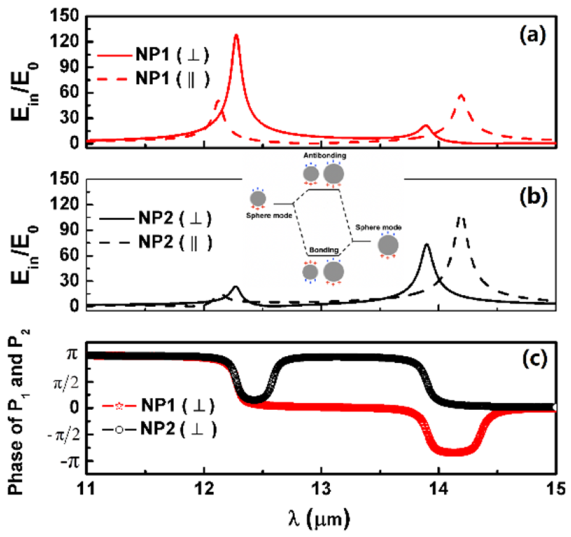
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Koppens, F.H.L.; Chang, D.E.; García de Abajo, F.J. Graphene Plasmonics: A Platform for Strong Light–Matter Interactions. Nano Lett. 2011, 11, 3370–3377. [Google Scholar] [CrossRef] [PubMed]
- Ju, L.; Geng, B.; Horng, J.; Girit, C.; Martin, M.; Hao, Z.; Bechtel, H.A.; Liang, X.; Zettl, A.; Shen, Y.R.; et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 2011, 6, 630–634. [Google Scholar] [CrossRef] [PubMed]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photonics 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Brar, V.W.; Jang, M.S.; Sherrott, M.; Lopez, J.J.; Atwater, H.A. Highly Confined Tunable Mid-Infrared Plasmonics in Graphene Nanoresonators. Nano Lett. 2013, 13, 2541–2547. [Google Scholar] [CrossRef] [PubMed]
- Low, T.; Avouris, P. Graphene Plasmonics for Terahertz to Mid-Infrared Applications. ACS Nano 2014, 8, 1086–1101. [Google Scholar] [CrossRef] [PubMed]
- Hendry, E.; Hale, P.J.; Moger, J.; Savchenko, A.K.; Mikhailov, S.A. Coherent Nonlinear Optical Response of Graphene. Phys. Rev. Lett. 2010, 105, 097401. [Google Scholar] [CrossRef] [PubMed]
- Constant, T.J.; Hornett, S.M.; Chang, D.E.; Hendry, E. All-optical generation of surface plasmons in graphene. Nat. Phys. 2016, 12, 124–127. [Google Scholar] [CrossRef]
- Jiang, T.; Huang, D.; Cheng, J.; Fan, X.; Zhang, Z.; Shan, Y.; Yi, Y.; Dai, Y.; Shi, L.; Liu, K.; et al. Gate-tunable third-order nonlinear optical response of massless Dirac fermions in graphene. Nat. Photonics 2018, 12, 430–436. [Google Scholar] [CrossRef]
- Soavi, G.; Wang, G.; Rostami, H.; Purdie, D.G.; De Fazio, D.; Ma, T.; Luo, B.; Wang, J.; Ott, A.K.; Yoon, D.; et al. Broadband, electrically tunable third-harmonic generation in graphene. Nat. Nanotechnol. 2018, 13, 583–588. [Google Scholar] [CrossRef]
- Ansell, D.; Radko, I.P.; Han, Z.; Rodriguez, F.J.; Bozhevolnyi, S.I.; Grigorenko, A.N. Hybrid graphene plasmonic waveguide modulators. Nat. Commun. 2015, 6, 8846. [Google Scholar] [CrossRef]
- Brar, V.W.; Sherrott, M.C.; Jang, M.S.; Kim, S.; Kim, L.; Choi, M.; Sweatlock, L.A.; Atwater, H.A. Electronic modulation of infrared radiation in graphene plasmonic resonators. Nat. Commun. 2015, 6, 7032. [Google Scholar] [CrossRef] [PubMed]
- García de Abajo, F.J. Graphene Plasmonics: Challenges and Opportunities. ACS Photonics 2014, 1, 135–152. [Google Scholar] [CrossRef]
- He, X.; Gao, P.; Shi, W. A further comparison of graphene and thin metal layers for plasmonics. Nanoscale 2016, 8, 10388–10397. [Google Scholar] [CrossRef] [PubMed]
- Jablan, M.; Soljacic, M.; Buljan, H. Plasmons in Graphene: Fundamental Properties and Potential Applications. Proc. IEEE 2013, 101, 1689–1704. [Google Scholar] [CrossRef]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; Garcia de Abajo, F.J.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. [Google Scholar] [CrossRef]
- Xia, S.-X.; Zhai, X.; Huang, Y.; Liu, J.-Q.; Wang, L.-L.; Wen, S.-C. Multi-band perfect plasmonic absorptions using rectangular graphene gratings. Opt. Lett. 2017, 42, 3052. [Google Scholar] [CrossRef]
- Halas, N.J.; Lal, S.; Chang, W.-S.; Link, S.; Nordlander, P. Plasmons in Strongly Coupled Metallic Nanostructures. Chem. Rev. 2011, 111, 3913–3961. [Google Scholar] [CrossRef]
- Deng, T.-S.; Parker, J.; Yifat, Y.; Shepherd, N.; Scherer, N.F. Dark Plasmon Modes in Symmetric Gold Nanoparticle Dimers Illuminated by Focused Cylindrical Vector Beams. J. Phys. Chem. C 2018, 122, 27662–27672. [Google Scholar] [CrossRef]
- Prodan, E. A Hybridization Model for the Plasmon Response of Complex Nanostructures. Science 2003, 302, 419–422. [Google Scholar] [CrossRef]
- Willets, K.A.; Van Duyne, R.P. Localized Surface Plasmon Resonance Spectroscopy and Sensing. Annu. Rev. Phys. Chem. 2007, 58, 267–297. [Google Scholar] [CrossRef]
- Lim, D.-K.; Jeon, K.-S.; Kim, H.M.; Nam, J.-M.; Suh, Y.D. Nanogap-engineerable Raman-active nanodumbbells for single-molecule detection. Nat. Mater. 2010, 9, 60–67. [Google Scholar] [CrossRef]
- Arroyo, J.O.; Kukura, P. Non-fluorescent schemes for single-molecule detection, imaging and spectroscopy. Nat. Photonics 2016, 10, 11–17. [Google Scholar] [CrossRef]
- Large, N.; Abb, M.; Aizpurua, J.; Muskens, O.L. Photoconductively Loaded Plasmonic Nanoantenna as Building Block for Ultracompact Optical Switches. Nano Lett. 2010, 10, 1741–1746. [Google Scholar] [CrossRef] [PubMed]
- Grigorenko, A.N.; Roberts, N.W.; Dickinson, M.R.; Zhang, Y. Nanometric optical tweezers based on nanostructured substrates. Nat. Photonics 2008, 2, 365–370. [Google Scholar] [CrossRef]
- Kawata, S.; Ono, A.; Verma, P. Subwavelength colour imaging with a metallic nanolens. Nat. Photonics 2008, 2, 438–442. [Google Scholar] [CrossRef]
- Christensen, T.; Jauho, A.-P.; Wubs, M.; Mortensen, N.A. Localized plasmons in graphene-coated nanospheres. Phys. Rev. B 2015, 91, 125414. [Google Scholar] [CrossRef]
- Smirnova, D.A.; Shadrivov, I.V.; Miroshnichenko, A.E.; Smirnov, A.I.; Kivshar, Y.S. Second-harmonic generation by a graphene nanoparticle. Phys. Rev. B 2014, 90. [Google Scholar] [CrossRef]
- Huang, Y.; Miroshnichenko, A.E.; Gao, L. Low-threshold optical bistability of graphene-wrapped dielectric composite. Sci. Rep. 2016, 6, 23354. [Google Scholar] [CrossRef]
- Zhang, K.; Huang, Y.; Miroshnichenko, A.E.; Gao, L. Tunable Optical Bistability and Tristability in Nonlinear Graphene-Wrapped Nanospheres. J. Phys. Chem. C 2017, 121, 11804–11810. [Google Scholar] [CrossRef]
- Lee, J.S.; You, K.H.; Park, C.B. Highly Photoactive, Low Bandgap TiO2 Nanoparticles Wrapped by Graphene. Adv. Mater. 2012, 24, 1133. [Google Scholar] [CrossRef]
- Lee, J.-S.; Kim, S.-I.; Yoon, J.-C.; Jang, J.-H. Chemical Vapor Deposition of Mesoporous Graphene Nanoballs for Supercapacitor. ACS Nano 2013, 7, 6047–6055. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Wang, H.; Tang, Y.; Zhou, Y.; Lu, T. Three-Dimensional Interconnected Network of Graphene-Wrapped Porous Silicon Spheres: In Situ Magnesiothermic-Reduction Synthesis and Enhanced Lithium-Storage Capabilities. ACS Appl. Mater. Interfaces 2014, 6, 3546–3552. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.; Jiang, L.; Xiang, Y. Tunable optical bistability of dielectric/nonlinear graphene/dielectric heterostructures. Opt. Express 2015, 23, 6497. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Stockman, M.I.; Bergman, D.J. Self-Similar Chain of Metal Nanospheres as an Efficient Nanolens. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef] [PubMed]
- Toroghi, S.; Kik, P.G. Cascaded plasmon resonant field enhancement in nanoparticle dimers in the point dipole limit. Appl. Phys. Lett. 2012, 100, 183105. [Google Scholar] [CrossRef]
- Bachelier, G.; Russier-Antoine, I.; Benichou, E.; Jonin, C.; Del Fatti, N.; Vallée, F.; Brevet, P.-F. Fano Profiles Induced by Near-Field Coupling in Heterogeneous Dimers of Gold and Silver Nanoparticles. Phys. Rev. Lett. 2008, 101, 197401. [Google Scholar] [CrossRef]
- Yang, Z.-J.; Zhang, Z.-S.; Zhang, W.; Hao, Z.-H.; Wang, Q.-Q. Twinned Fano interferences induced by hybridized plasmons in Au–Ag nanorod heterodimers. Appl. Phys. Lett. 2010, 96, 131113. [Google Scholar] [CrossRef]
- Lombardi, A.; Grzelczak, M.P.; Pertreux, E.; Crut, A.; Maioli, P.; Pastoriza-Santos, I.; Liz-Marzán, L.M.; Vallée, F.; Del Fatti, N. Fano Interference in the Optical Absorption of an Individual Gold–Silver Nanodimer. Nano Lett. 2016, 16, 6311–6316. [Google Scholar] [CrossRef]
- Ávalos-Ovando, O.; Besteiro, L.V.; Wang, Z.; Govorov, A.O. Temporal plasmonics: Fano and Rabi regimes in the time domain in metal nanostructures. Nanophotonics 2020, 9, 3587–3595. [Google Scholar] [CrossRef]
- Brown, L.V.; Sobhani, H.; Lassiter, J.B.; Nordlander, P.; Halas, N.J. Heterodimers: Plasmonic Properties of Mismatched Nanoparticle Pairs. ACS Nano 2010, 4, 819–832. [Google Scholar] [CrossRef]
- Sheikholeslami, S.; Jun, Y.; Jain, P.K.; Alivisatos, A.P. Coupling of Optical Resonances in a Compositionally Asymmetric Plasmonic Nanoparticle Dimer. Nano Lett. 2010, 10, 2655–2660. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Ma, P.; Wu, Y.M. Abnormal Fano Profile in Graphene-Wrapped Dielectric Particle Dimer. Photonics 2020, 7, 124. https://doi.org/10.3390/photonics7040124
Huang Y, Ma P, Wu YM. Abnormal Fano Profile in Graphene-Wrapped Dielectric Particle Dimer. Photonics. 2020; 7(4):124. https://doi.org/10.3390/photonics7040124
Chicago/Turabian StyleHuang, Yang, Pujuan Ma, and Ya Min Wu. 2020. "Abnormal Fano Profile in Graphene-Wrapped Dielectric Particle Dimer" Photonics 7, no. 4: 124. https://doi.org/10.3390/photonics7040124
APA StyleHuang, Y., Ma, P., & Wu, Y. M. (2020). Abnormal Fano Profile in Graphene-Wrapped Dielectric Particle Dimer. Photonics, 7(4), 124. https://doi.org/10.3390/photonics7040124