One-Way Zero Reflection in an Insulator-Metal-Insulator Structure Using the Transfer Matrix Method
Abstract
:1. Introduction
2. Simulation
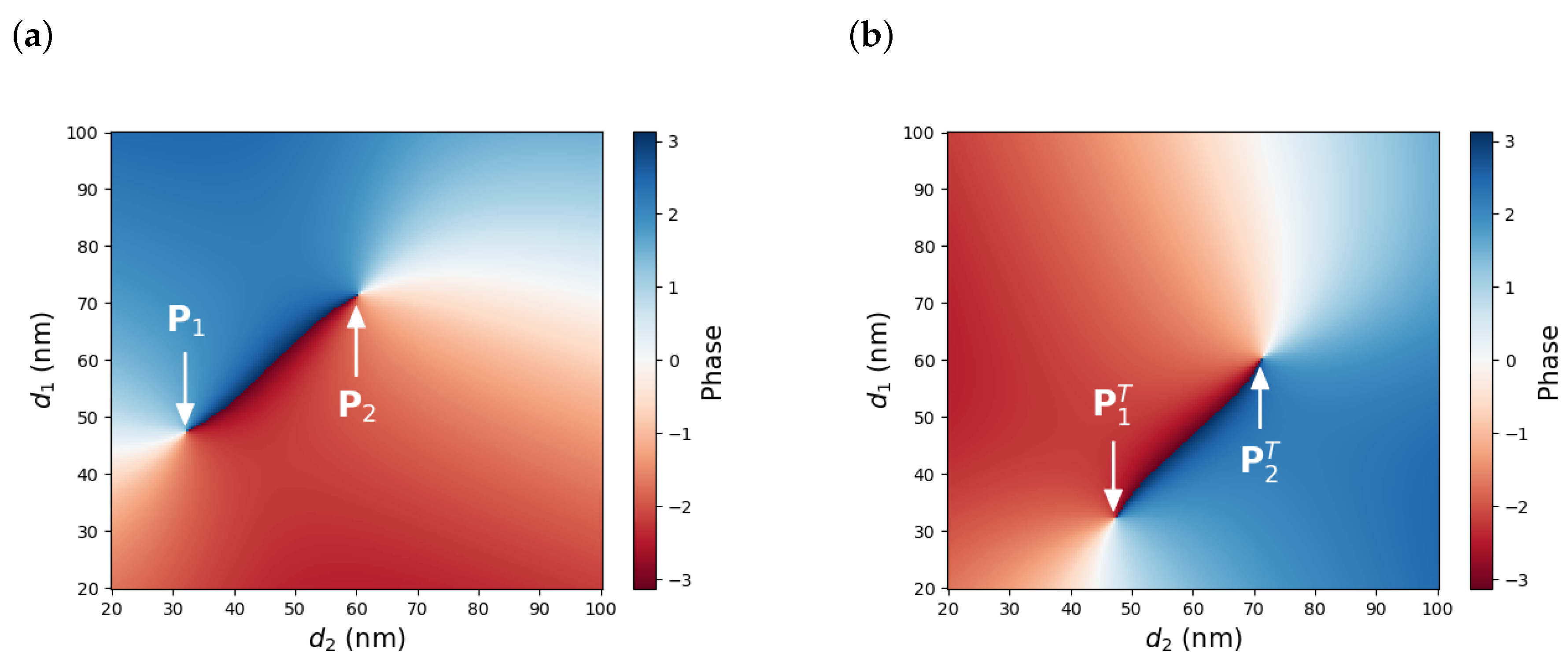
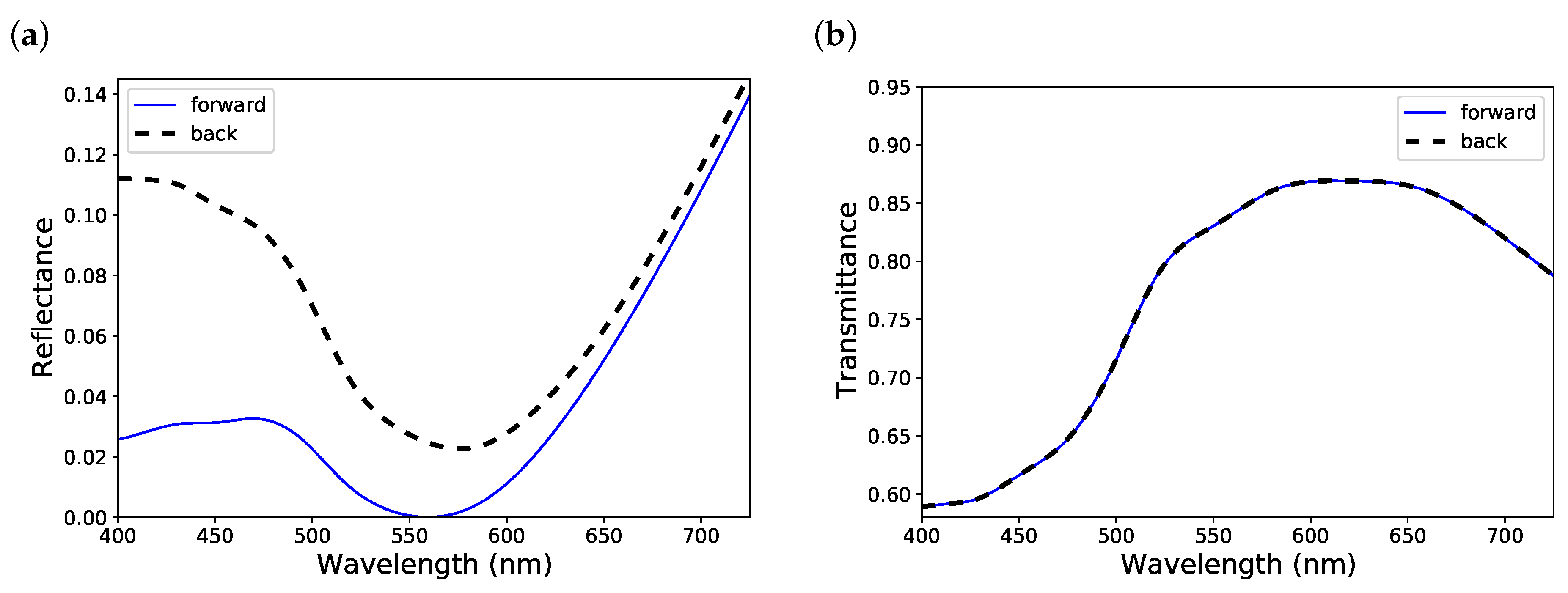
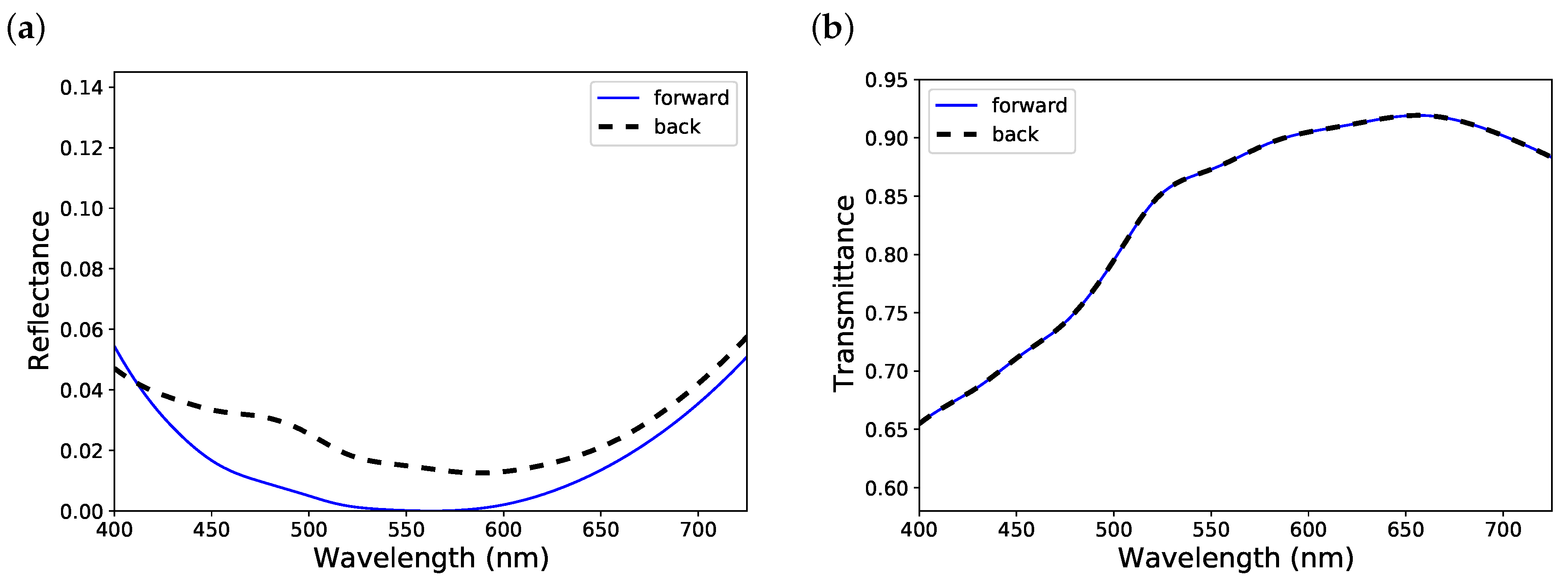
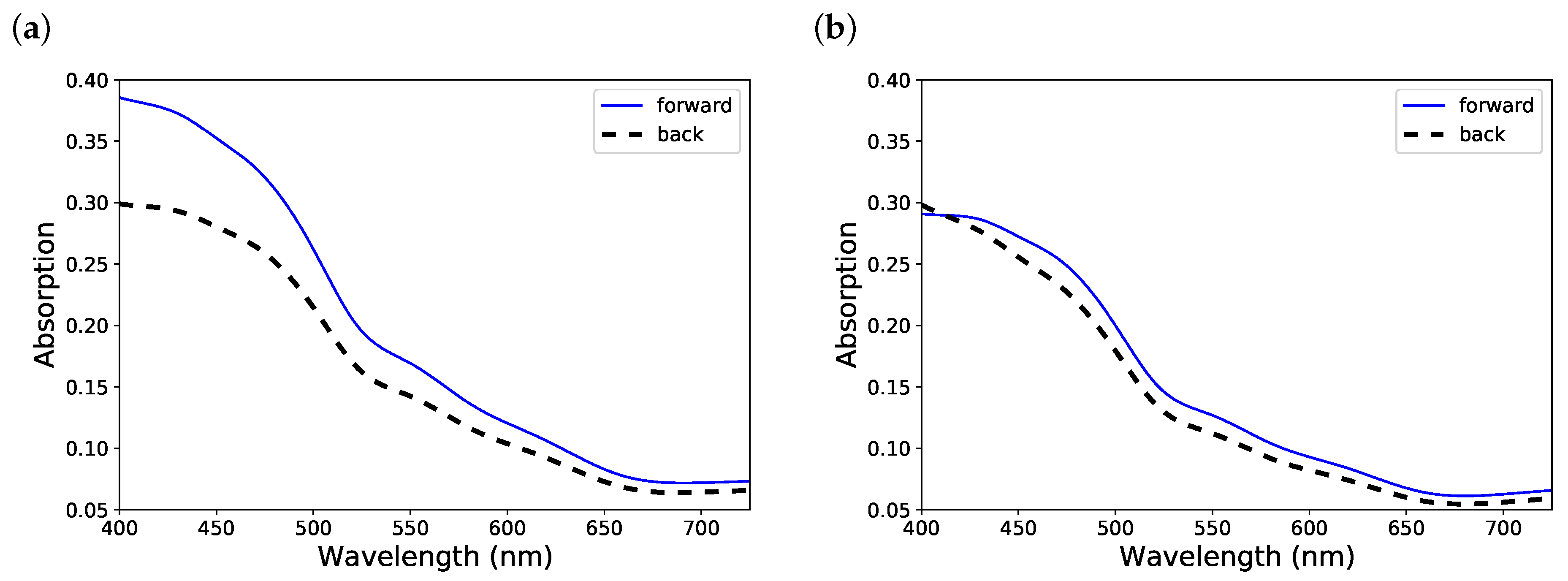
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef] [Green Version]
- Longhi, S.; Della Valle, G. Photonic Realization of PT-Symmetric Quantum Field Theories. Phys. Rev. A 2012, 85, 012112. [Google Scholar] [CrossRef]
- Bender, C.M. Making Sense of Non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1018. [Google Scholar] [CrossRef] [Green Version]
- Musslimani, Z.H.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N. Optical Solitons in PT Periodic Potentials. Phys. Rev. Lett. 2008, 100, 030402. [Google Scholar] [CrossRef] [PubMed]
- Guo, A.; Salamo, G.J.; Duchesne, D.; Morandotti, R.; Volatier-Ravat, M.; Aimez, V.; Siviloglou, G.A.; Christodoulides, D.N. Observation of PT-Symmetry Breaking in Complex Optical Potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of Parity-Time Symmetry in Optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef] [Green Version]
- Miri, M.-A.; LiKamWa, P.; Christodoulides, D.N. Large Area Single-Mode Parity–Time-Symmetric Laser Amplifiers. Opt. Lett. 2012, 37, 764. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Ramezani, H.; Eichelkraut, T.; Kottos, T.; Cao, H.; Christodoulides, D.N. Unidirectional Invisibility Induced by PT-Symmetric Periodic Structures. Phys. Rev. Lett. 2011, 106, 213901. [Google Scholar] [CrossRef] [Green Version]
- Liertzer, M.; Ge, L.; Cerjan, A.; Stone, A.D.; Türeci, H.E.; Rotter, S. Pump-Induced Exceptional Points in Lasers. Phys. Rev. Lett. 2012, 108, 173901. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; Xu, Y.L.; Fegadolli, W.S.; Lu, M.H.; Oliveira, J.E.B.; Almeida, V.R.; Chen, Y.F.; Scherer, A. Experimental Demonstration of a Unidirectional Reflectionless Parity-Time Metamaterial at Optical Frequencies. Nat. Mater. 2013, 12, 108–113. [Google Scholar] [CrossRef]
- Brandstetter, M.; Liertzer, M.; Deutsch, C.; Klang, P.; Schöberl, J.; Türeci, H.E.; Strasser, G.; Unterrainer, K.; Rotter, S. Reversing the Pump Dependence of a Laser at an Exceptional Point. Nat. Commun. 2014, 5, 4034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, L.; Wong, Z.J.; Ma, R.M.; Wang, Y.; Zhang, X. Single-Mode Laser by Parity-Time Symmetry Breaking. Science 2014, 346, 972–975. [Google Scholar] [CrossRef] [PubMed]
- Hodaei, H.; Miri, M.A.; Hassan, A.U.; Hayenga, W.E.; Heinrich, M.; Christodoulides, D.N.; Khajavikhan, M. Parity-Time-Symmetric Coupled Microring Lasers Operating around an Exceptional Point. Opt. Lett. 2015, 40, 4955. [Google Scholar] [CrossRef] [PubMed]
- Miri, M.-A.; Alú, A. Exceptional points in optics and photonics. Science 2019, 363, eaar7709. [Google Scholar] [CrossRef] [Green Version]
- Wiersig, J. Review of exceptional point-based sensors. Photonics Res. 2020, 8, 1457–1467. [Google Scholar] [CrossRef]
- Shen, Y.; Deng, X.H.; Chen, L. Unidirectional Invisibility in a Two-Layer Non-PT-Symmetric Slab. Opt. Express 2014, 22, 19440. [Google Scholar] [CrossRef]
- Feng, L.; Zhu, X.; Yang, S.; Zhu, H.; Zhang, P.; Yin, X.; Wang, Y.; Zhang, X. Demonstration of a Large-Scale Optical Exceptional Point Structure. Opt. Express 2014, 22, 1760. [Google Scholar] [CrossRef]
- Huang, Y.; Veronis, G.; Min, C. Unidirectional Reflectionless Propagation in Plasmonic Waveguide-Cavity Systems at Exceptional Points. Opt. Express 2015, 23, 29882. [Google Scholar] [CrossRef]
- Na, J.; Noh, H. Investigation of a Broadband Coherent Perfect Absorber in a Multi-Layer Structure by Using the Transfer Matrix Method. J. Korean Phys. Soc. 2018, 72, 66–70. [Google Scholar] [CrossRef]
- Ducourtieux, S.; Podolskiy, V.A.; Grésillon, S.; Buil, S.; Berini, B.; Gadenne, P.; Boccara, A.C.; Rivoal, J.C.; Bragg, W.D.; Banerjee, K.; et al. Near-Field Optical Studies of Semicontinuous Metal Films. Phys. Rev. B 2001, 64, 1654031–16540314. [Google Scholar] [CrossRef] [Green Version]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Andreasen, J.; Vanneste, C.; Ge, L.; Cao, H. Effects of Spatially Nonuniform Gain on Lasing Modes in Weakly Scattering Random Systems. Phys. Rev. A 2010, 81, 043818. [Google Scholar] [CrossRef] [Green Version]
- González-Vila, Á.; Debliquy, M.; Lahem, D.; Zhang, C.; Mégret, P.; Caucheteur, C. Molecularly imprinted electropolymerization on a metal-coated optical fiber for gas sensing application. Sens. Actuators B Chem. 2017, 244, 1145–1151. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, H.; Choi, J.-M. One-Way Zero Reflection in an Insulator-Metal-Insulator Structure Using the Transfer Matrix Method. Photonics 2021, 8, 8. https://doi.org/10.3390/photonics8010008
Noh H, Choi J-M. One-Way Zero Reflection in an Insulator-Metal-Insulator Structure Using the Transfer Matrix Method. Photonics. 2021; 8(1):8. https://doi.org/10.3390/photonics8010008
Chicago/Turabian StyleNoh, Heeso, and Jai-Min Choi. 2021. "One-Way Zero Reflection in an Insulator-Metal-Insulator Structure Using the Transfer Matrix Method" Photonics 8, no. 1: 8. https://doi.org/10.3390/photonics8010008




