Dynamic Scattering Approach for Solving the Radar Cross-Section of the Warship under Complex Motion Conditions
Abstract
1. Introduction
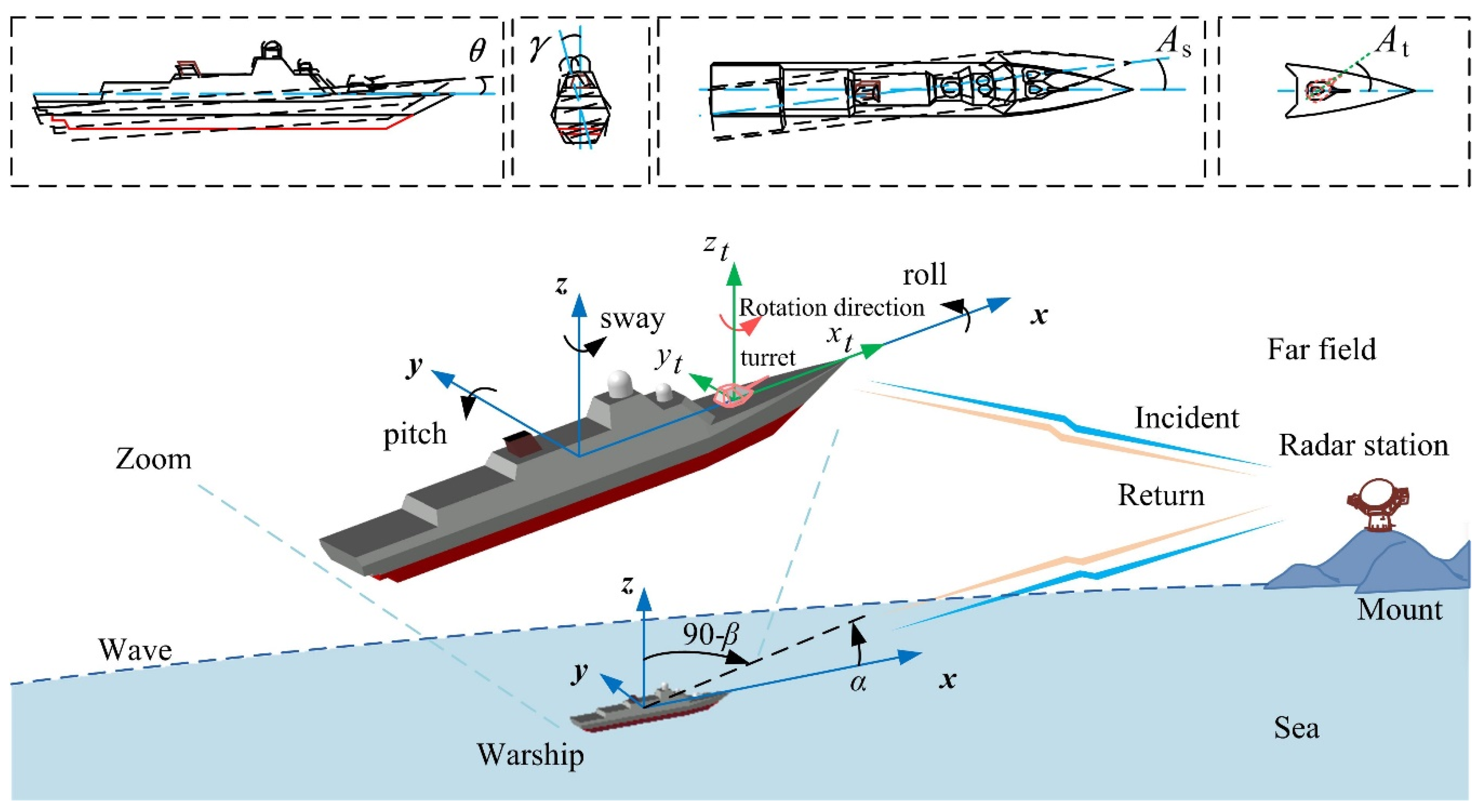
2. Dynamic Scattering Approach
2.1. Dynamic Simulation Method
2.2. Electromagnetic Scattering Calculation
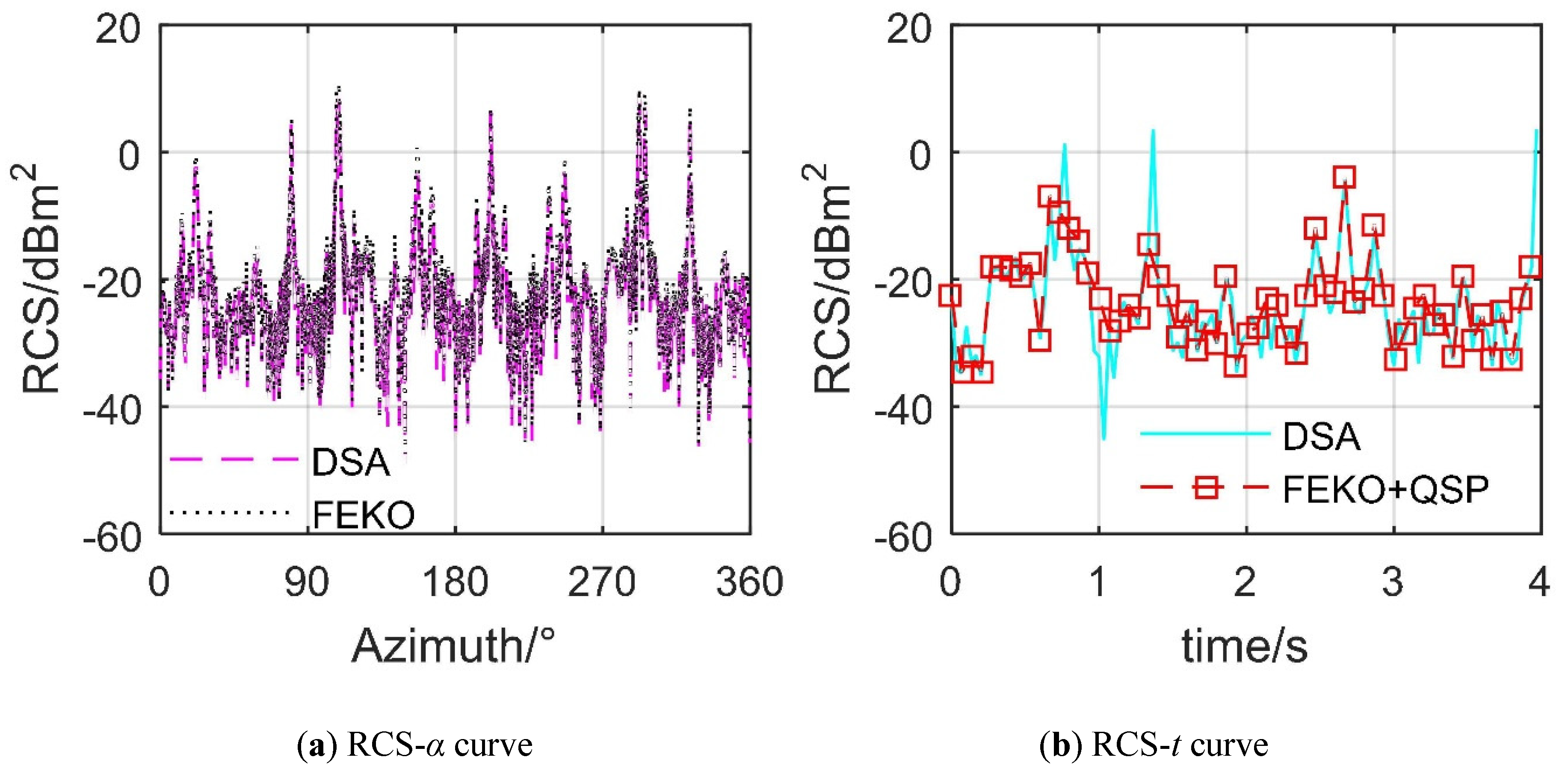
2.3. Method Validation
3. Model
4. Results and Discussion
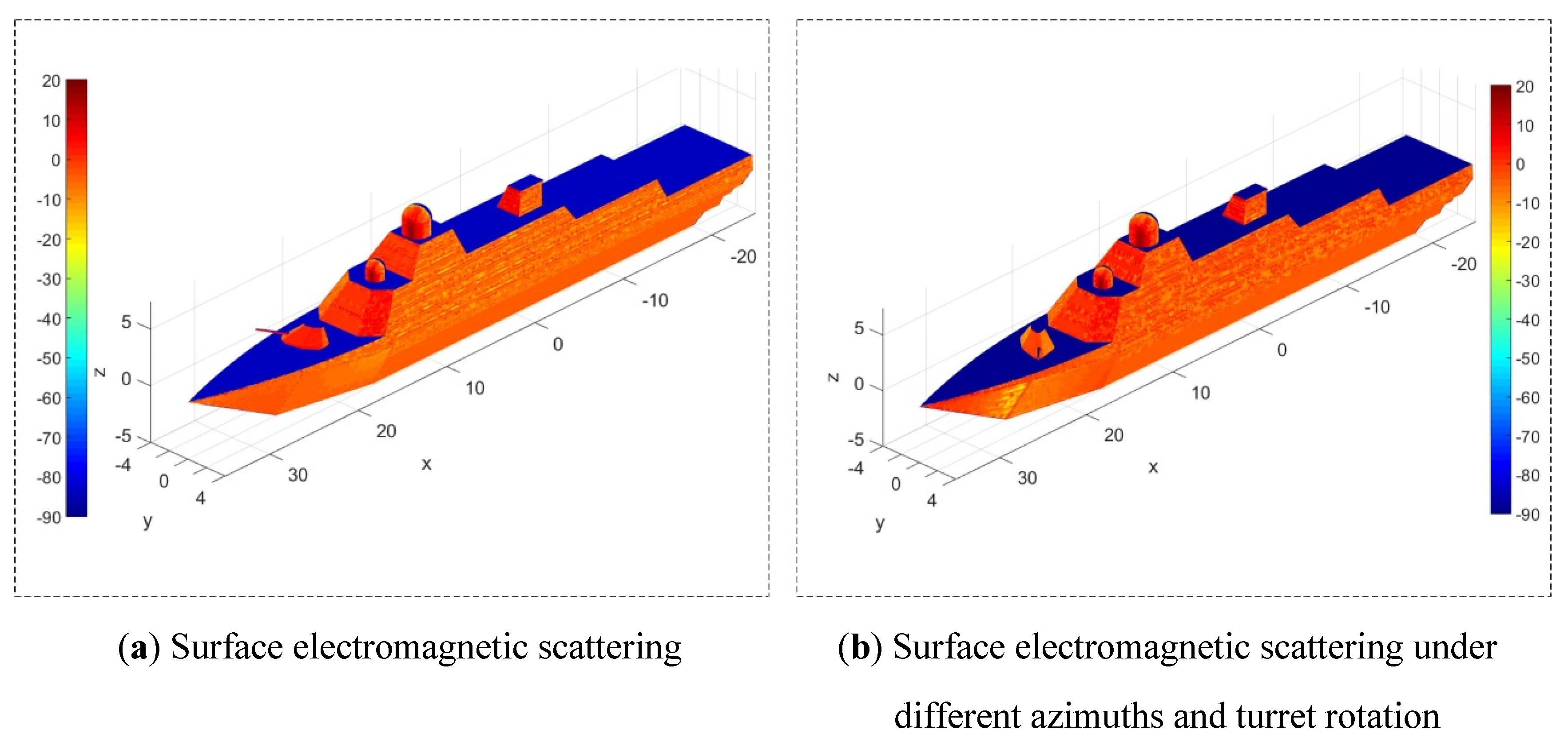
4.1. Effect of Turret Rotation
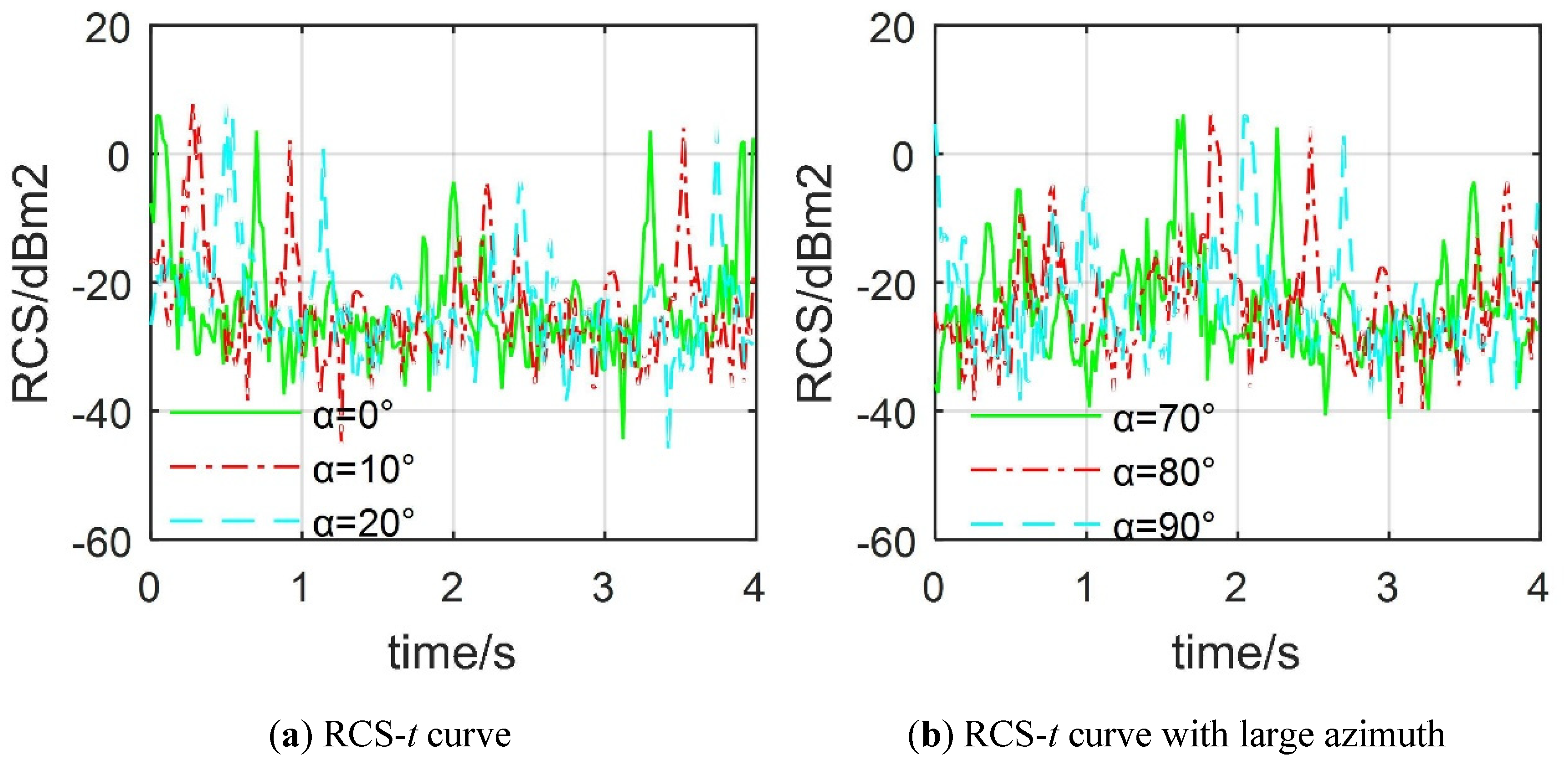
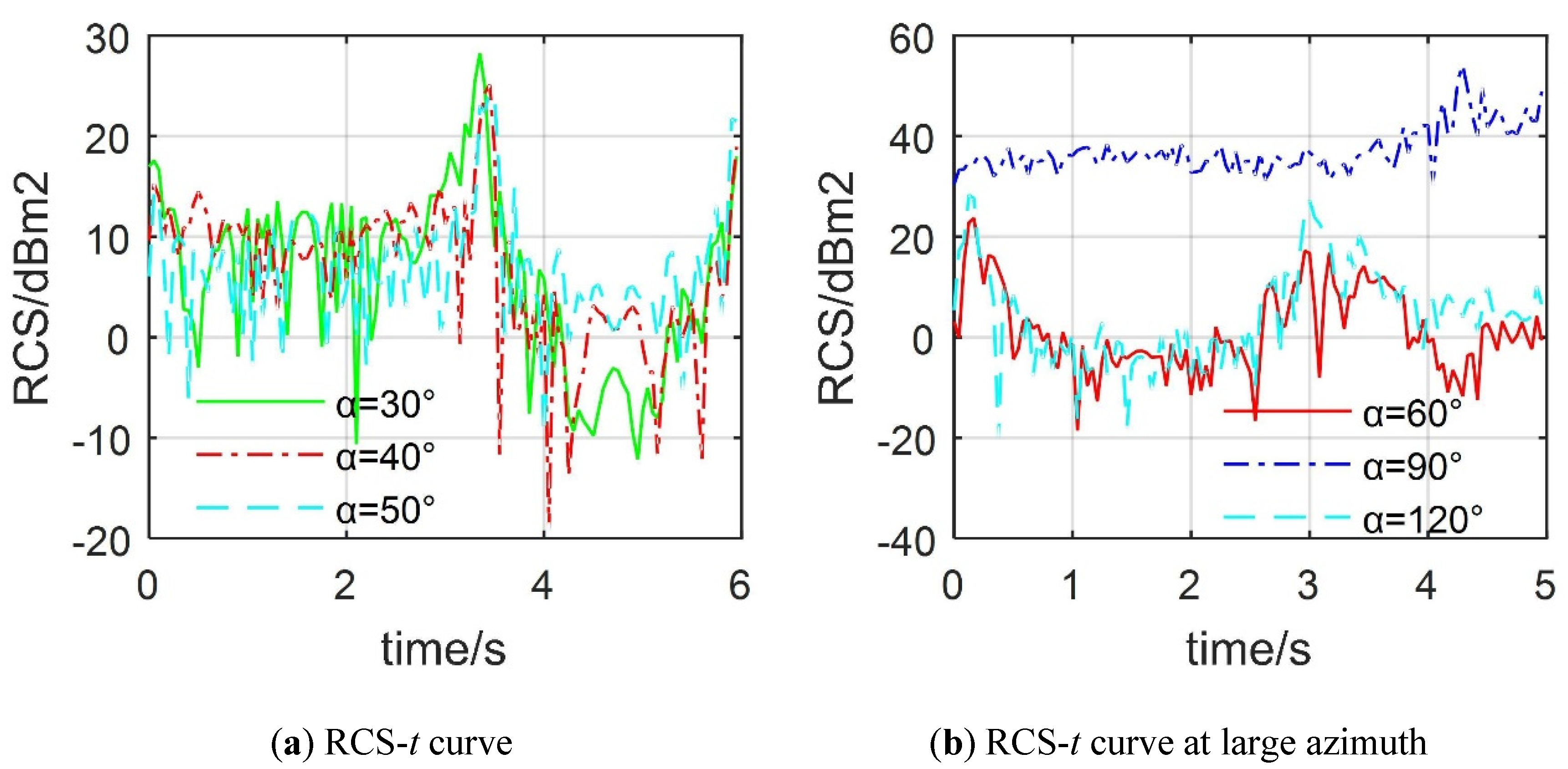
4.2. Effect of Observation Angles
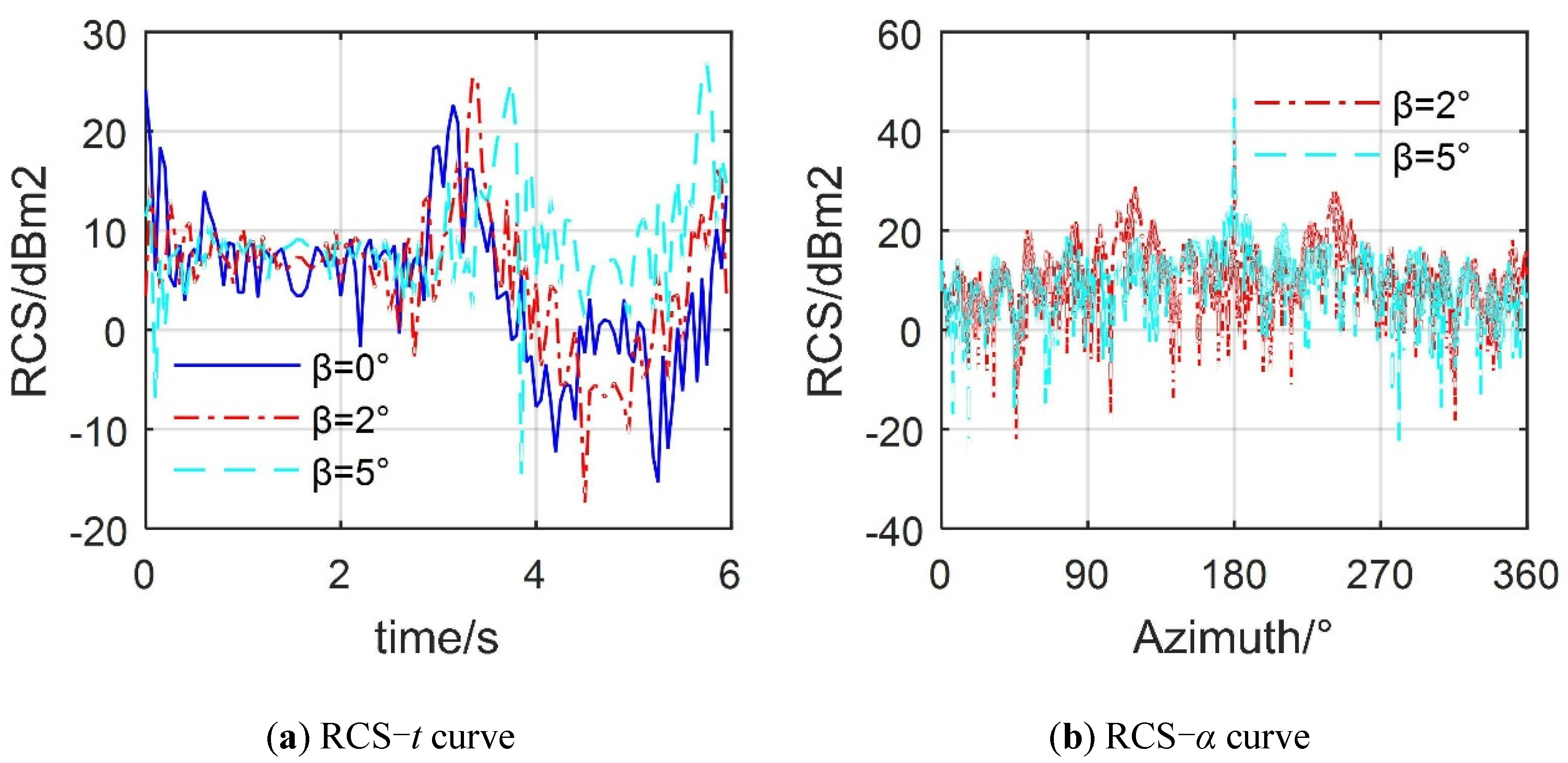
4.3. Effect of Attitude Changes
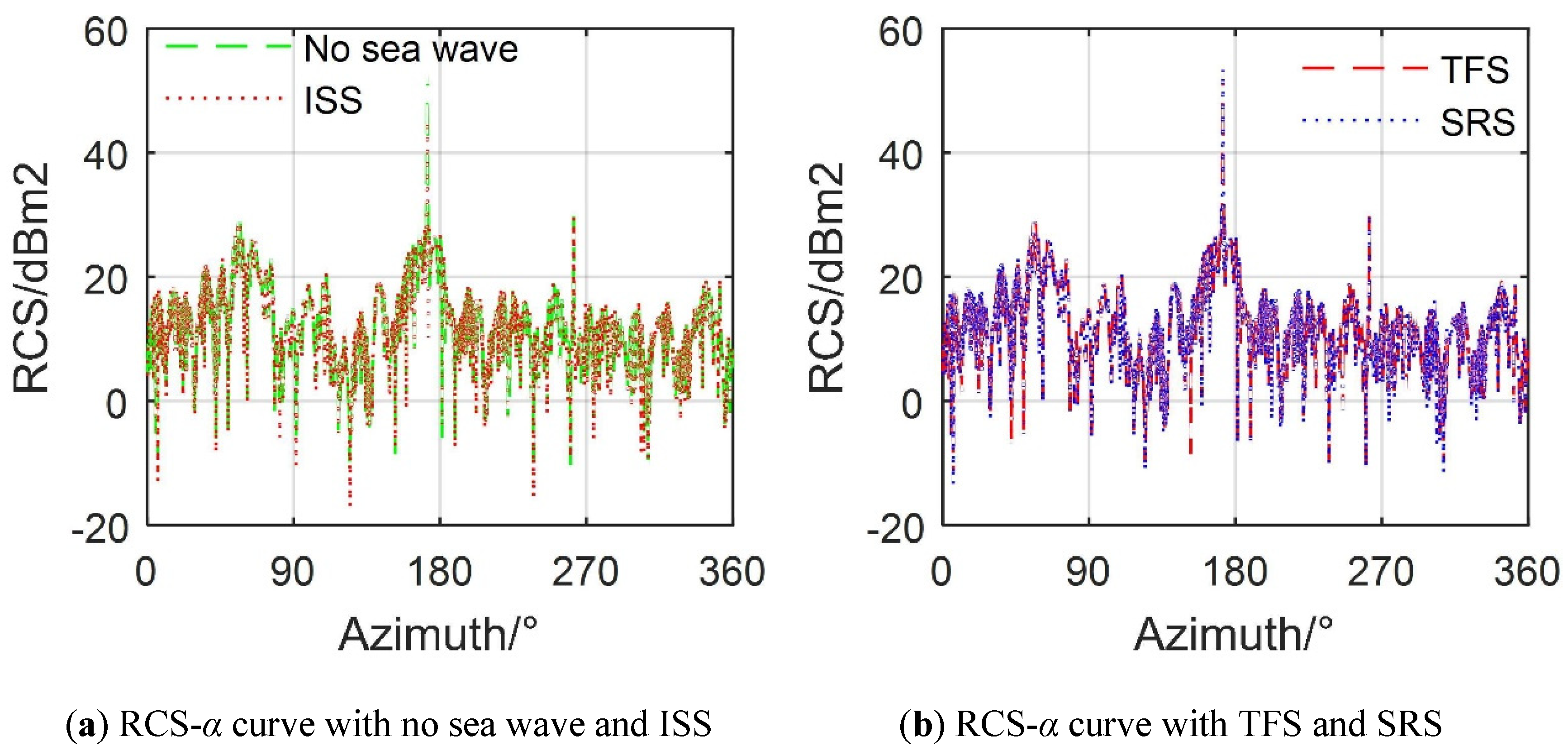
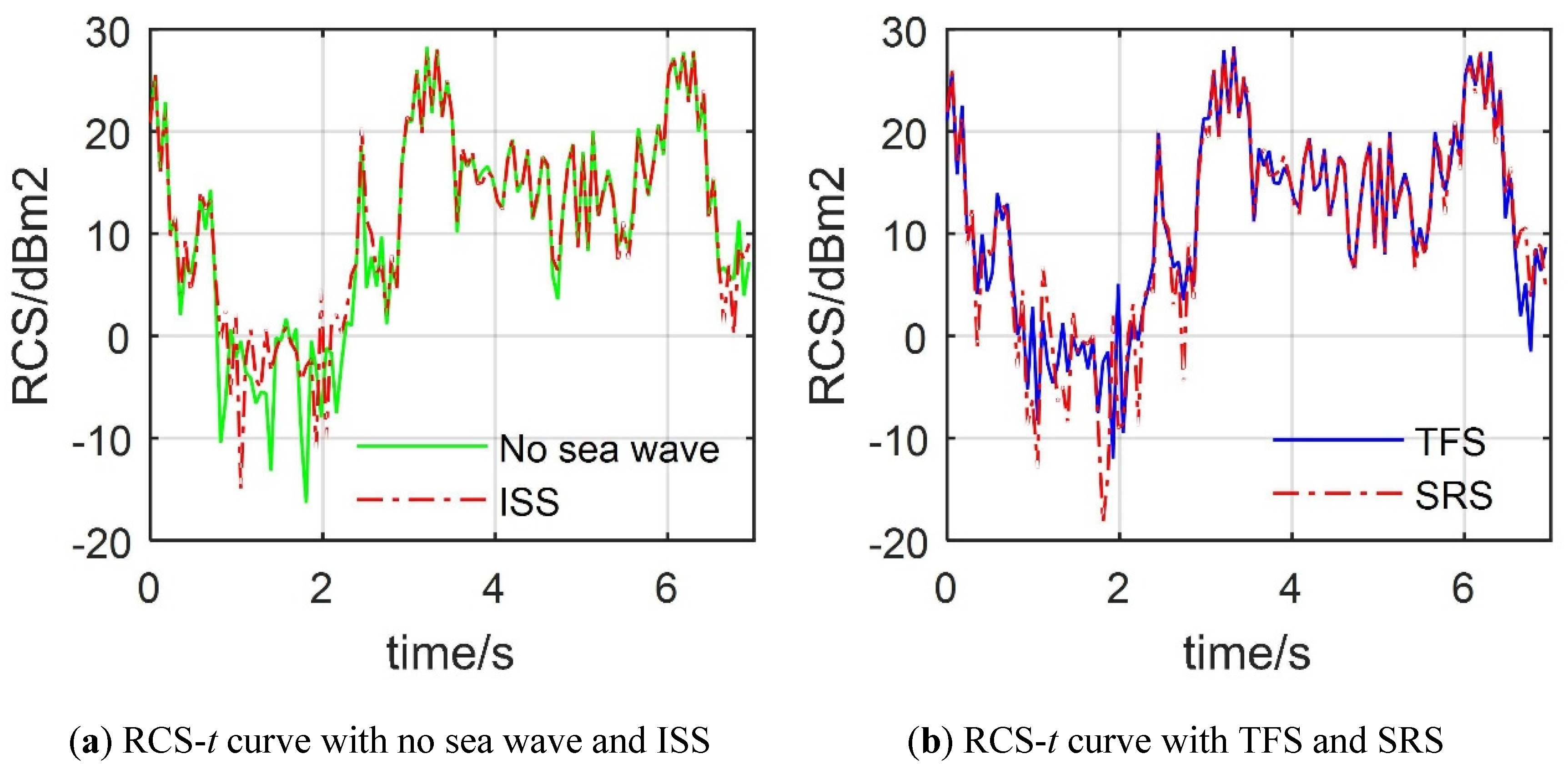
4.4. Effect of Sea Waves
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| α | azimuth between the warship and the radar station [°] |
| β | elevation angle between the warship and the radar station [°] |
| θ | pitch angle of the warship [°] |
| γ | roll angle of the warship [°] |
| As | sway angle of the warship [°] |
| At | rotation angle of the gun turret [°] |
| t | time [s] |
| mtur | model of gun turret |
| mhul | model of warship hull after removing the turret |
| mwars | model of warship |
| Xtur | distance from zt axis to z axis [m] |
| M(mtur) | grid matrix of the turret model |
| M(mhul) | grid matrix of the hull model |
| M(mwars) | grid matrix of the warship model |
| zwave | sea wave surface function |
| σ | radar cross-section [dBm2] |
| ZI | the illuminated area of warship |
| ZD | the dark area of warship |
| NF | the number of facets |
| NE | the number of edges |
Subscript
| tur | gun turret |
| hul | warship hull |
| wars | warship |
| wave | sea wave |
Appendix A
Appendix B
References
- Hopkins, B.; Miroshnichenko, A.E.; Poddubny, A.N.; Kivshar, Y.S. Fano resonance enhanced nonreciprocal absorption and scattering of light. Photonics 2015, 2, 745–757. [Google Scholar] [CrossRef]
- Feng, Y.; Zhu, W.; Huang, L.Y. Development and Assumption on Radar Stealth Technology of Surface Combat Ships. Ship Electron. Eng. 2018, 38, 5–8. [Google Scholar]
- Sun, B.; Yang, P.; Kattawar, G.W.; Zhang, X. Physical-geometric optics method for large size faceted particles. Opt. Express 2017, 25, 24044–24060. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.Q.; Chang, S.Y. The characteristic cross-section method on the shape radar stealthy design of naval vessels. Shipbuild. China 2008, 49, 113–120. [Google Scholar]
- Bogatskaya, A.; Schegolev, A.; Klenov, N.; Popov, A. Generation of Coherent and Spatially Squeezed States of an Electromagnetic Beam in a Planar Inhomogeneous Dielectric Waveguide. Photonics 2019, 6, 84. [Google Scholar] [CrossRef]
- Xiao, F.; Li, Y.X.; Li, M. Radar Stealth Techniques of Surface Warship. Shipboard Electron. Countermeas. 2009, 32, 35–37. [Google Scholar]
- Yalçin, U. Scattering from a cylindrical reflector: Modified theory of physical optics solution. JOSA A 2007, 24, 502–506. [Google Scholar] [CrossRef]
- Xiong, Y.; Ye, H.; Umeda, T.; Mizoguchi, S.; Morifuji, M.; Kajii, H.; Maruta, A.; Kondow, M. Photonic Crystal Circular Defect (CirD) Laser. Photonics 2019, 6, 54. [Google Scholar] [CrossRef]
- Bettle, M.C.; Gerber, A.G.; Watt, G.D. Unsteady analysis of the six DOF motion of a buoyantly rising submarine. Comput. Fluids 2009, 38, 1833–1849. [Google Scholar] [CrossRef]
- Tsai, C.C.; Tai, W.T.; Hsu, W.; Hsiao, S.C. Step approximation of water wave scattering caused by tension-leg structures over uneven bottoms. Ocean Eng. 2018, 166, 208–225. [Google Scholar] [CrossRef]
- Liu, Z.Z. Stealth and Anti-Stealth Techniques of Ships Radar. Ship Electron. Eng. 2008, 28, 33–36. [Google Scholar]
- Kim, K.; Kim, J.H.; Cho, D.S. Radar cross section analysis of marine targets using a combining method of physical optics/geometric optics and a Monte-Carlo simulation. Ocean Eng. 2009, 36, 821–830. [Google Scholar] [CrossRef]
- Yang, D.Q.; Chang, S.Y. The theory and method for naval vessel shape optimal design considering the radar stealthy performance. Ship Sci. Technol. 2006, 28, 42–47. [Google Scholar]
- Yao, T.; Zhu, D.; Ben, D.; Pan, S. Distributed MIMO chaotic radar based on wavelength-division multiplexing technology. Opt. Lett. 2015, 40, 1631–1634. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.Y.; Huang, J.; Yi, M.X. Comprehensive optimization of aerodynamic noise and radar stealth for helicopter rotor based on Pareto solution. Aerosp. Sci. Technol. 2018, 82, 607–619. [Google Scholar] [CrossRef]
- Shao, H.G. Application of radar stealth technology in surface ships. China Water Transp. 2017, 17, 79–80. [Google Scholar]
- Borovoi, A.; Grishin, I.; Naats, E.; Oppel, U. Backscattering peak of hexagonal ice columns and plates. Opt. Lett. 2000, 25, 1388–1390. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Huang, J.; Wu, N.N. Acoustic and radar integrated stealth design for ducted tail rotor based on comprehensive optimization method. Aerosp. Sci. Technol. 2019, 92, 244–257. [Google Scholar] [CrossRef]
- Sun, A.L.; Li, C.Q.; Liu, D.X.; Zhou, Y.H.; Dong, G.X. Study on Assessment of Shipping Water for Determination of Freeboard of Open-Top Containership. Shipbuild. China 2019, 60, 168–178. [Google Scholar]
- Surendran, S.; Lee, S.K.; Kim, S.Y. Studies on an algorithm to control the roll motion using active fins. Ocean Eng. 2007, 34, 542–551. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J. FDTD for hydrodynamic electron fluid Maxwell equations. Photonics 2015, 2, 459–467. [Google Scholar] [CrossRef]
- de Tomasi, F.; Torsello, G.; Perrone, M.R. Water-vapor mixing-ratio measurements in the solar-blind region. Opt. Lett. 2000, 25, 686–688. [Google Scholar] [CrossRef]
- Chen, G.J.; Zhang, Z.; Mao, P. Research on U.S. Army Carrier Aircraft Approach Procedures and Standardized Design. Aviat. Stand. Qual. 2019, 5, 8–11,18. [Google Scholar]
- Vijayaraghavan, D.; Keith, T.G. Grid transformation and adaption techniques applied in the analysis of cavitated journal bearings. J. Tribol. 1990, 112, 52–59. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Huang, J. Target head direction far field radar cross section reduction based on narrow surface element method. Optik 2020, 200, 163230. [Google Scholar] [CrossRef]
- Bueno, L.C.; Borge, J.C.N.; Alexandre, E.; Hessner, K.; Sanz, S.S. Accurate estimation of significant wave height with support vector regression algorithms and marine radar images. Coast. Eng. 2016, 114, 233–243. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, H. The engineering arithmetic of transforming grid coordinates into radar measure coordinates. Fire Control Command Control 2007, 32, 73–77. [Google Scholar]
- Memos, C.D.; Karambas, T.V.; Avgeris, I. Irregular wave transformation in the nearshore zone: Experimental investigations and comparison with a higher order Boussinesq model. Ocean Eng. 2005, 32, 1465–1485. [Google Scholar] [CrossRef]
- Zuo, X.S.; Wang, L.X.; Liu, H.L.; Wang, Y.; Zhang, Y. Research on similarity for simulating automatic carrier landing process of full-scale aircraft with scaled-model. Acta Aeronaut. Et Astronaut. Sin. 2019, 41, 123005. [Google Scholar]
- Ouyang, K.; Lin, R.K.; Wu, S.J.; Sheu, W.H. The Numerical Analysis of Flow Field on Warship Deck. Int. J. Eng. Res. 2015, 4, 118–122. [Google Scholar] [CrossRef]
- Mittapalli, V.; Khan, H. Excitation Schemes of Plasmonic Angular Ring Resonator-Based Band-Pass Filters Using a MIM Waveguide. Photonics 2019, 6, 41. [Google Scholar] [CrossRef]
- Ezhilsabareesh, K.; Suchithra, R.; Samad, A. Performance enhancement of an impulse turbine for OWC using grouped grey wolf optimizer based controller. Ocean Eng. 2019, 190, 106425. [Google Scholar] [CrossRef]
- Zhu, H.W.; Shao, Y.L.; Liu, Y.S. Chordal axis transformation based on mid-surface generation approach for thin-walled model. Comput. Integr. Manuf. Syst. 2018, 24, 649–659. [Google Scholar]
- Wu, P.F.; Shi, Z.S.; Wu, Z.H.; Hao, L.J. Estimation and Compensation Method of Deck Motion for Unmanned Helicopter Landing on Ship. Electron. Opt. Control 2019, 26, 22–27. [Google Scholar]
- Karam, M.A. Bridging the quasi-static and the physical optics approximations: An elliptic disk case. Appl. Opt. 1998, 37, 1666–1673. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.F.; Shi, Z.G.; Guo, J.; Li, J.C. Sea Surface Modeling Based on the Spectrum of Ocean Waves Modeling and the FFT. J. Chongqing Univ. Technol. (Nat. Sci.) 2014, 28, 77–82. [Google Scholar]
- Pan, H.Y.; Zhao, J.C.; Wang, Z.L. Research on Modeling and Simulation of Virtual Sea Surface. Tonghua Teach. Coll. (Nat. Sci.) 2018, 39, 5–8. [Google Scholar]
- Aşırım, Ö.E.; Kuzuoğlu, M. Numerical study of resonant optical parametric amplification via gain factor optimization in dispersive microresonators. Photonics 2020, 7, 5. [Google Scholar] [CrossRef]
- Fei, C.J.; Wu, P.L.; Zhang, Q.Y.; Fang, G.Y.; Zhu, W.H. Improved Model of Ocean Wave Induced Magnetic Field Based on the First Order Stokes Equations. J. Electron. Inf. Technol. 2017, 39, 2007–2013. [Google Scholar]
- Liu, W.L.; Zhang, J. Optimization of the Wave Particle Mode Based on SPH by the MC Algorithm. J. Ocean Technol. 2017, 36, 41–45. [Google Scholar]
- Gao, L.; Reno, J.L.; Kumar, S. Short barriers for lowering current-density in terahertz quantum cascade lasers. Photonics 2020, 7, 7. [Google Scholar] [CrossRef]

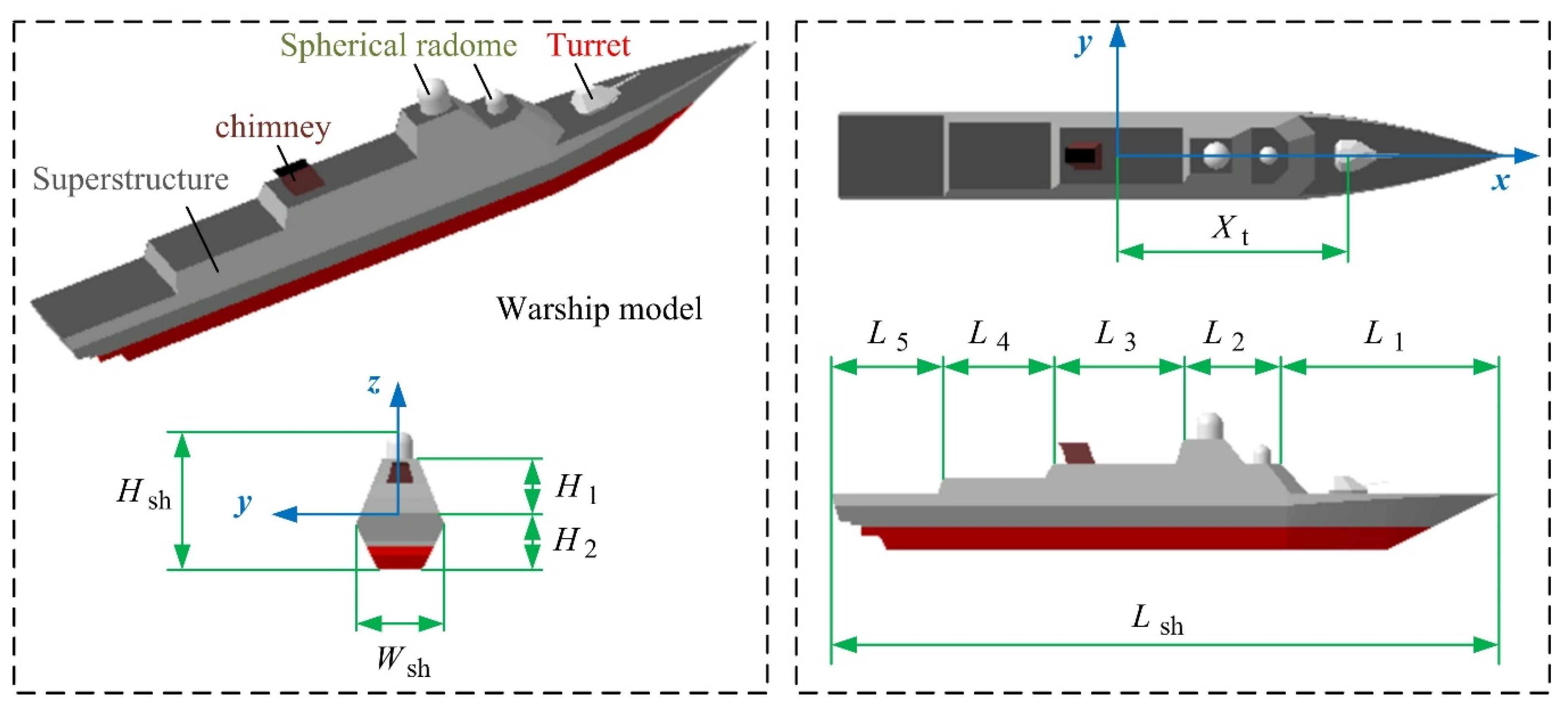





| Parameter | Lsh | L1 | L2 | L3 | L4 | L5 |
| Value/m | 60 | 19.5 | 8.74 | 11.7 | 9.95 | 10.11 |
| Parameter | Hsh | H1 | H2 | Wsh | Xt | |
| Value/m | 12.4 | 4.98 | 5 | 8 | 21.3 |
| Area | Maximum Value/mm | Area | Maximum Value/mm |
|---|---|---|---|
| Global minimum size | 3 | Gun barrel | 4 |
| Gun mount | 8 | Turret | 20 |
| Bow edge | 25 | Stern edge | 30 |
| Spherical radar | 30 | Chimney | 35 |
| Hull side ridge | 40 | Warship body | 50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Huang, J. Dynamic Scattering Approach for Solving the Radar Cross-Section of the Warship under Complex Motion Conditions. Photonics 2020, 7, 64. https://doi.org/10.3390/photonics7030064
Zhou Z, Huang J. Dynamic Scattering Approach for Solving the Radar Cross-Section of the Warship under Complex Motion Conditions. Photonics. 2020; 7(3):64. https://doi.org/10.3390/photonics7030064
Chicago/Turabian StyleZhou, Zeyang, and Jun Huang. 2020. "Dynamic Scattering Approach for Solving the Radar Cross-Section of the Warship under Complex Motion Conditions" Photonics 7, no. 3: 64. https://doi.org/10.3390/photonics7030064
APA StyleZhou, Z., & Huang, J. (2020). Dynamic Scattering Approach for Solving the Radar Cross-Section of the Warship under Complex Motion Conditions. Photonics, 7(3), 64. https://doi.org/10.3390/photonics7030064







