Abstract
In optical communication systems, frame synchronization is essential for subsequent operations, such as error correction and payload extraction. Various methods, so far, have been proposed in the published literature, but the performance is unsatisfactory under high bit error rate (BER) conditions. We present, in this work, a novel data-aided frame synchronization technique for optical packet transmission systems, in which the transmitter sends a sequence of packets with a specific synchronization word periodically inserted, and the receiver blindly recognizes the synchronization word to attain frame synchronization. The proposed algorithm detects the synchronization word based on Hough transform (HT), a classic method for line detection in digital image processing. The core principle of the algorithm is to exploit the periodicity of the frame synchronization word, which appears as black-and-white spaced stripes on a binary image when the frames are all aligned. Simulations are conducted over a 56Gbps optical QPSK transmission system, and the results show that our algorithm is still effective in attaining frame synchronization at a BER of 0.3. A comparison is also made between our algorithm and existed autocorrelation (AC)-based algorithm. The results demonstrate that our algorithm has a better error resilience performance. When the BER is higher than 0.03, our algorithm outperforms an AC-based algorithm significantly.
1. Introduction
In optical communication systems, frame synchronization is indispensable to subsequent signal processing, such as error correction and information extraction [1,2]. It can be considered as a type of reverse engineering problem in the field of information theory, which has received increased attention over the past few decades [3]. There are mainly two categories of frame synchronization techniques: data-aided frame synchronization and code-aided frame synchronization. For the former, synchronization is attained through recognizing the synchronization word, while for the latter, synchronization is achieved through exploiting the properties of error correction code.
In cooperative communications, data-aided frame synchronization is commonly applied, and there are two main types of methods, correlation rule and maximum-likelihood (ML) rule [4]. In 1953, Barker first proposed a correlation-based recognizer to detect the given frame synchronization sequence in received bit stream [5]. This method is simple to implement, but it has a poor performance and a narrow application scope. Some improved schemes have also been put forward in succession, such as double correlation [6,7], which is robust to carrier frequency and phase errors. A method based on the ML rule for frame synchronization was first proposed by Massey in 1972 over additive white Gaussian noise (AWGN) channel [8], and he concluded that ML-based detection has a better performance than traditional correlation detection. The conclusion was subsequently confirmed in the environment of high SNR by Nielsen [9], and was further extended to the M-ary phase shift keying modulation by Liu and Tan [10]. Later, ML-based frame synchronization algorithms for flat fading channels and frequency-selective channels were proposed successively [11,12,13]. In addition to the correlation and ML rule, some other schemes have also been offered in recent years. Chiani and Martini applied the likelihood ratio test (LRT) in the hypothesis test theory to frame synchronization detection [14,15,16], and their method performs better than correlation in AWGN channels. Kim exploited post-detection integration (PDI) to provide coarse frame alignment with limited complexity with respect to ML solutions [17]. More recently, another novel algorithm called balanced generalized PDI (B-GPDI), which combines the ML rule and PDI for synchronization detection, was reported in [18].
In non-cooperative communications, a synchronization word needs to be recognized blindly for data-aided frame synchronization. Yang proposed a blind recognition algorithm based on the peak characteristic of the partial third-order correlation function for the synchronization word being m-sequence [19]. A joint recognition algorithm based on correlation filtering and Hadamard transform is proposed in [20], and it performs well with a high bit error rate. Naseri used the auto-correlation function to blindly recover the synchronization word and frame length in a satellite system, and proposed another two algorithms based on hardware equipment, in case auto-correlation cannot determine the exact frame length [21]. The blind recognition algorithm of the synchronization word based on soft-decision for QPSK signals was proposed in [22], and it can clearly enhance the accuracy of blind recognition. Guo proposed a cumulative filtering algorithm to identify the frame header [23], but it is difficult to determine the decision threshold with a complex frame structure or uncertain synchronization word length. To resolve this issue, an improved algorithm based on autocorrelation (AC) was proposed by Xu [24]. Peak-to-average ratio (PAR) is calculated in his algorithm to overcome high bit-error-rate (BER). In recent years, code-aided frame synchronization has received considerable attention, due to the advantages of saving bandwidth and high spectral efficiency [25,26,27,28].
In this paper, we propose a novel frame synchronization method based on Hough transform, in which synchronization is achieved through blindly recognizing the synchronization word. In our work, we build an interception matrix filled with intercepted bit stream. When frames are all aligned in the interception matrix, the columns of synchronization word appear as black and white stripes, if we consider the matrix as a binary image. Hence, Hough transform, which is a classic method for line detection in digital image processing, is applied in this work to detect the stripes in the interception matrix. Simulations are carried out in the optical QPSK transmission system, and the results show that the new method can efficiently recognize the synchronization word and attain frame synchronization. The proposed method is also compared with the AC-based algorithm and simulation results demonstrate that our HT-based algorithm performs better at high BER.
The remainder of this paper is organized as follows. Section 2 briefly introduces the existing AC-based frame synchronization algorithm. In Section 3, principles of Hough transform are first introduced in detail and an example of its application is given. Then, the data-aided frame synchronization algorithm based on Hough transform is presented. Simulation experiments are carried out in Section 4, and the HT-based synchronization algorithm is compared with the AC-based algorithm. Finally, Section 5 provides the conclusion.
2. Fundamental of AC-Based Frame Synchronization Algorithm
Information is usually transmitted using frames as basic unit in the optical transmission systems. Figure 1a gives a schematic diagram of frame sequence with synchronization word inserted centrally. It can be shown that an intact frame, the length of which is L, contains two parts, fixed frame synchronization word (S) and varying payload (D). The length of them are M and N, respectively, and L = M + N. In the data received by receiver, the synchronization word is periodic emergence, while the payload is random. Through locating the synchronization word, frame synchronization is attained, and the payload can be extracted further for subsequent operations.
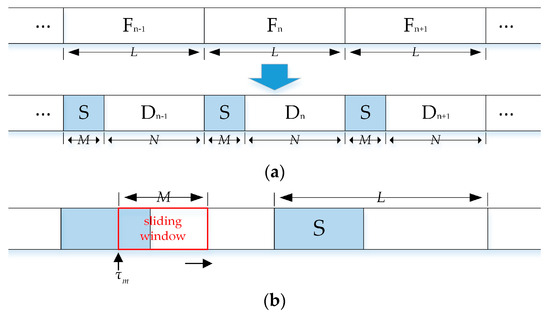
Figure 1.
Received frame sequence. F, frame; S, frame synchronization word; D, payload; L, frame length; M, synchronization word length; N, payload length; (a) diagram of frame sequence with fixed synchronization word inserted.; (b) sliding window starting from .
In cooperative communications, S is known to the receiver and synchronization is achieved through finding the optimal delay that maximizes the cross-correlation of received sequence and S. The high SNR approximation of this method is given in [8]:
where is the ith element of S and is the ith element of received sequence in the sliding window, starting from , as shown in Figure 1b.
However, in the context of non-cooperative communications, S is unknown to the receiver. Hence, the cross-correlation in Equation (1) is not computable. An alternative option using auto-correlation is given in [24]:
where and are the ith element of received sequence in the sliding window starting from and , respectively, l is the length of sliding window and is an estimate of the frame length.
Specifically, a sampling data storage matrix is built in the AC-based synchronization algorithm, and is sequentially filled into the matrix. Since the probability distributions of 0 and 1 in S and D are different, the synchronization word can be detected through calculating the probability distributions of 0 and 1 at each position of the sliding window, with and the l constant.
3. HT-Based Frame Synchronization Algorithm
3.1. Hough Transform
In 1962, Hough devised an ingenious method, popularly called Hough transform (HT), which efficiently identifies lines in images [29,30]. It is still an important tool for digital image processing nowadays. The core idea of Hough transform is to establish a dual relationship between points and lines, image space and Hough space. The principle of detecting straight lines based on Hough transform is briefly introduced as follows.
The equation representation of a straight line in cartesian coordinates (we call it xy-space in this paper) can be expressed by slope (k) and intercept (b) as follows.
If the parameter space, kb-space is established, the straight line in xy-space actually corresponds to a point in kb-space. Similarly, a straight line in kb-space corresponds to a point in xy-space. This is a so-called dual relationship mentioned above. It can be easily drawn that intersecting position relationship in kb-space corresponds to collinear position relationship in xy-space. However, there is a parameter problem with the established kb-space. The vertical lines in xy-space, whose slope is infinite, do not have corresponding points in kb-space. To this end, space is established and the correspondence can be written as.
As shown in Figure 2, is the algebraic distance from the origin to the line and is the angle between x-axis and the vector perpendicular to the line. If we restrict to the interval , the dual relationship between xy-space and -space exists in any cases. However, the curve in -space corresponding to the point in xy-space is not a straight line, but a sinusoid.
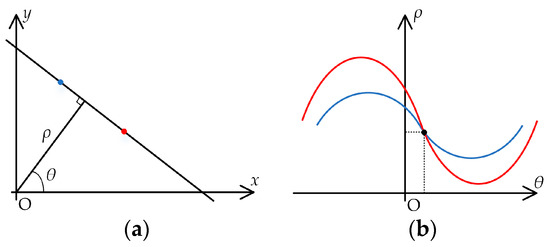
Figure 2.
Dual relationship between xy-space and -space. (a) xy-space; (b) -space.
The xy-space is the image space while the -space is sometimes called Hough space. The properties of point-to-line dual relationship between image space and Hough space can be summarized as follows.
- A point in image space corresponds to a sinusoid in Hough space;
- A point in Hough space corresponds a straight line in image space;
- The collinear position relationship of points in image space corresponds to the intersecting position relationship of curves in Hough space.
However, it is essentially exhaustive that we map all the points in image space into their corresponding curves in Hough space, without any restrictions for straight line detection, and the computation required grows quadratically with the number of points [31]. To this end, Hough space is quantized into grids, and accumulator cells are created. For each non-background point in image space, the corresponding curve given by Equation (4) is entered in the grids by incrementing the count in each accumulator cell along the curve. Eventually, a given cell records the total number of curves passing through it, which means that these points in image space are collinear. Figure 3 gives an example for a thorough understanding.
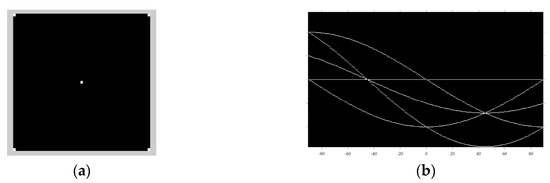
Figure 3.
Example of line detection based on Hough transform (HT). (a) Image space with five points in a black background; (b) Hough space.
There are five points in the image space with a black background, which corresponds to five curves in Hough space, respectively. is quantified at 1-degree intervals and the interval for is also one. Hough space is divided into accumulator cells. It can be seen from Hough space that the two points at are generated by the intersection of the three curves, which means that there are two sets of three collinear points in the image space. The four sets of collinear points on the vertical and horizontal lines in image space corresponds to four points generated by the intersection of two curves in Hough space.
3.2. Algorithm
In the context of non-cooperative communications, M, N, and the type of S are all unknown, which require to be recognized blindly for frame synchronization [32]. Blind recognition of frame parameters can be implemented through the properties of frame synchronization word, which are fixed and cyclical. To achieve this, the interception matrix C, with r rows and l columns, is built by filling it with the intercepted bit stream from top left to bottom right. As shown in Equation (5), Y is the intercepted bit stream.
There are two cases for the number of columns of interception matrix C, and . In case of , all elements of certain columns are either 0 or 1, which are called synchronization-word columns in this paper, while elements of other columns are random, and we call these non-synchronization-word columns. In the case of , there do not exist synchronization-word columns yet. Based on this property, all we need to do is to go through all possible values of l to estimate the frame length L and synchronization word position.
As we all know, , which means the interception matrix C is filled with 0 and 1. If we consider C as the image space, in which 0 is black and 1 is white, it can be displayed as a binary image in Figure 4. The two cases, that and , are shown in Figure 4a,b, respectively. The synchronization-word columns appear as black and white straight stripes in a binary image, while the non-synchronization-word columns appear as snowflake noise.

Figure 4.
Binary image of interception matrix C. (a) ; (b) .
To identify the case that when going through all possible values of l, line detection based on Hough transform can be applied. However, there practically exist collinear points at any angle in the image space C, which means straight lines can be detected with taking any values. Considering that the number of collinear points in the synchronization-word columns is the largest in the vertical direction, we just need to simply find the accumulator cells with the most counts at in Hough space for all . The recognition algorithm is summarized as follows.
Step1. Set the search range of l and initialize it. (Assume that );
Step2. Fill the image space with the intercepted bit stream Y from top left to bottom right;
Step3. Perform edge extraction on image space;
Step4. Quantify and . For each non-background point in image space , calculate its corresponding sinusoid according to Equation (4) and fill the curve into Hough space by incrementing the count in each accumulator cell along the curve;
Step5. Record the largest counts among all the accumulator cells at in Hough space. Let it be .
Step6. If , let and return to Step2. Otherwise, execute Step 6;
Step7. Fill all the into vector X and find the maximum value. Let it be ;
Step8. Extract the elements greater than from the vector X, and find the one with the smallest subscript from them, and use the subscript value as the estimate of the frame length L, which is recorded as . ( will be determined in the simulation next);
Step9. Let and fill the image matrix with the intercepted bit stream Y;
Step10. Record the count of each accumulator cell at in Hough space and recognize the synchronization word.
4. Simulation Results and Discussion
In this section, the performance of HT-based data-aided frame synchronization method is analyzed. Simulations are conducted over a 56 Gbps QPSK coherent optical transmission system built in Optisystem. The BER of received bit stream is first calculated at the receiver, and then the frame synchronization algorithm is applied to attain synchronization before payload extraction.
The frame length L in simulation is set to 1024 bits, while the frame synchronization word S is 0xA53C, 16 bits in length. The payload D is generated randomly. Details of how the proposed algorithm works are shown first, and then its performance in different situations is analyzed. Finally, a comparison between our proposed algorithm and the algorithm proposed in [24] is made.
First, the workflow of HT-based blind recognition algorithm is presented at BER = 2 × 10−2. r, the rows of image space, is set to 100 and the search range of l is [500,5000]. Figure 5 above gives the running results of Step2–Step4 of the algorithm at l = 1024. It can be seen from the Step 2-result that there is obvious image noise in the synchronization-word columns, which is circled with a red frame. From the Step3-result, we can find that the noise is eliminated after edge extraction, and the characteristics of the synchronization-word columns are retained. Apparently, our algorithm can suppress the effects of noise to some extent, thus improving the error resilience performance.
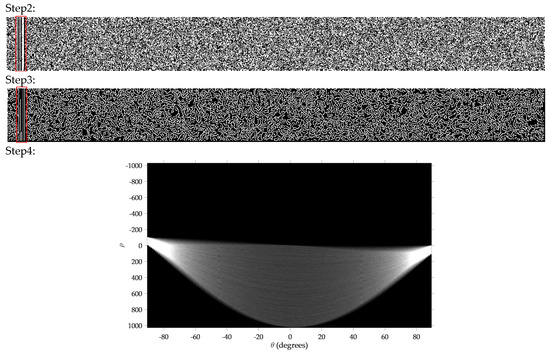
Figure 5.
Running results of Step2–Step4. Result of Step2 is the binary image of image matrix C and the result of Step3 is the binary image after edge extraction; the result of Step4 is the Hough space.
Figure 6 gives the running result of frame length search in Step7. It can be seen that the case that l = kL (k = 1,2,3,4) is effectively identified. Considering that the one with the smallest subscript among those greater than is taken as in Step8, should be greater than (0.77) so that . Result of synchronization-word recognition in Step10 is shown in Figure 7. The synchronization-word columns are recognized and since 0 is background point, it can be seen from the figure that the synchronization word is 1010,0101,0011,1100 (0xA53C). From Figure 5, Figure 6 and Figure 7, we can find that HT-based blind recognition algorithm can effectively recognize the frame parameters, including frame length L, frame synchronization word S and its length M, under the BER condition of the error correction limit (BER = 2 × 10−2).
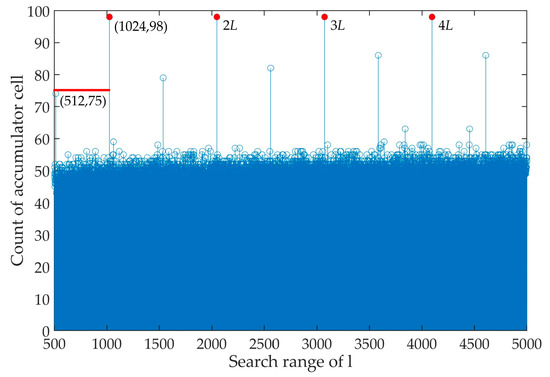
Figure 6.
Result of frame length search in Step7. (l∈[500,5000] and L = 1024)
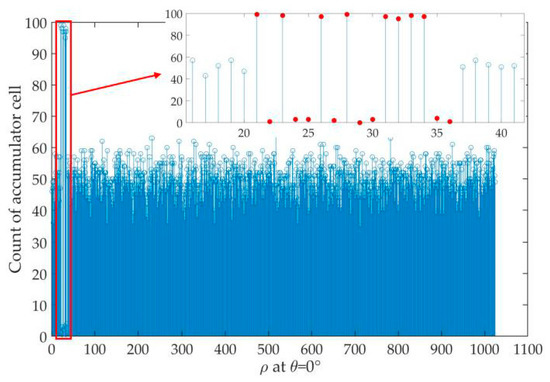
Figure 7.
Result of frame synchronization word recognition in Step10. The enlarged part is the synchronization-word columns.
Then, the value of is discussed at different BER, and we have also explored the influence of the selection of r on the value of . For each BER level, 20 simulations are conducted, and takes the mean. The curves of versus BER for different values of r are shown in Figure 8. When r takes 20, the value of is greater than 1, as BER exceeds 0.2, which means that the frame parameters cannot be recognized correctly. When r exceeds 50, our algorithm still works at BER = 0.3. On the other hand, when r exceeds 200, the value of r has little influence on . Hence, the optimal value of r should be between 100 and 200, taking into account both the amount of calculation and the accuracy of identification. In addition, it can be seen from Figure 8 that the value of decreases first, and then turns to increase as BER increases, which reflects the ability of our algorithm to suppress noise from another aspect. When the value of r increases, the turning point of moves towards higher BER.
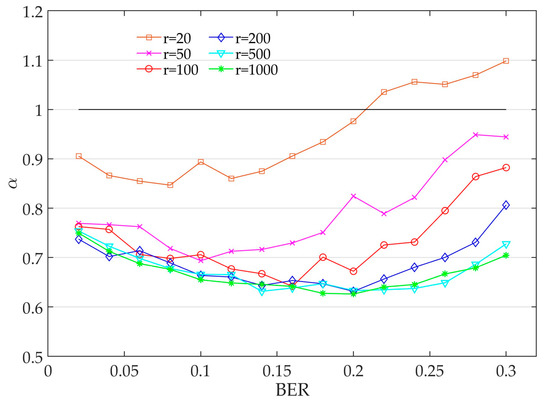
Figure 8.
Value of versus bit error rate (BER) under different r. r, the columns of interception matrix C.
Finally, the recognition accuracy, which is defined as the ratio of the times of recognizing correctly to the total times, is compared between our proposed algorithm and the autocorrelation-based recognition algorithm proposed in [24]. A total of 100 simulations are carried out for each BER level. The value of takes 0.8 and r is set to 100 in the comparison simulation, according to Figure 8. The results are shown in Figure 9.
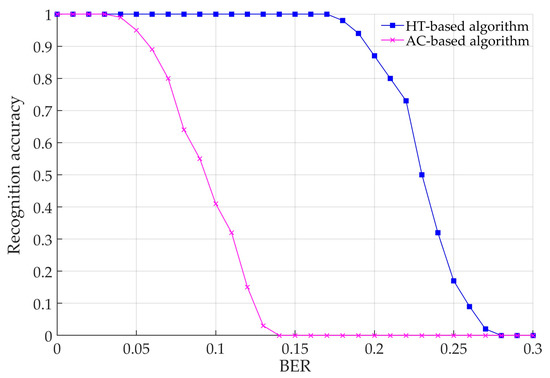
Figure 9.
Comparison between HT-based recognition algorithm and AC-based algorithm. HT, Hough Transform; AC, autocorrelation.
As shown in Figure 9, the HT-based blind recognition algorithm outperforms the autocorrelation-based blind algorithm. When the BER is over 0.1, the recognition accuracy of the AC-based algorithm is lower than 0.5, while that of the HT-based algorithm is still 1. The recognition accuracy of HT-based algorithm starts to gradually decrease at BER = 0.18 and deteriorates sharply at BER = 0.22. Actually, the recognition accuracy is related to the value of . Apparently, our algorithm has a better error resilience performance.
5. Conclusions
In this work, we have conducted a detailed investigation on the techniques of frame synchronization, and give a brief review of some previous works. A typical frame synchronization method based on auto-correlation was introduced as a comparison. Our proposed algorithm based on Hough transform was finally presented. Simulations were carried out over a 56Gbps QPSK coherent optical transmission system.
The workflow of our algorithm was shown first and some key parameters were analyzed, including r, the columns of interception matrix C, and , a threshold set for recognizing frame length. The results show that our algorithm still works well at BER = 0.3, and the optimal value for r is between 100 and 200, considering both the computation and bit-error resilience. The trend of the value of with the growth of BER reflects the suppression effect on noise of our algorithm. A comparison of recognition performance between our algorithm and an existing autocorrelation-based algorithm was also made. The results demonstrate that our algorithm outperforms the AC-based algorithm significantly, as the BER exceeds 0.03. It is noteworthy that our algorithm is also effective for the recognition of the frame synchronization word inserted in the frame at intervals.
However, the proposed algorithm requires the frame synchronization word to be inserted periodically in the receiving frames, which does not apply to code-aided frame synchronization. On the other hand, the computation of our algorithm is not compared with other algorithms, which will be further studied.
Author Contributions
Conceptualization, H.Y.; methodology, J.C.; software, H.Y.; supervision, Z.H.; validation, S.L.; writing (original draft), H.Y.; writing, review and editing, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (General Program), Grant No. 51575517.
Acknowledgments
The authors would like to acknowledge Qiquan Zheng for providing high-performance computer as a simulation platform, and the authors also would like to thank editors and anonymous reviewers for giving valuable suggestions that have helped to improve the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wozencraft, J.M.; Jacobs, I.M. Principles of Communication Engineering; Wiley: New York, NY, USA, 1965. [Google Scholar]
- TM Synchronization and Channel Coding; Blue Book; Issue 1; CCSDS: Washington, DC, USA, 2003.
- Mehdi, T.; Hamidreza, M. Reverse Engineering of Communications Networks: Evolution and Challenges. arXiv, 2017; arXiv:1704.05432. [Google Scholar]
- Guangzu, L.; Jianxin, W.; Tian, B. Frame Detection Based on Cyclic Autocorrelation and Constant False Alarm Rate in Burst Communication Systems. China Commun. 2015, 12, 55–63. [Google Scholar]
- Barker, R.H. Group Synchronization of Binary Digital Systems. Commun. Theory 1953, 20, 273–287. [Google Scholar]
- Choi, Z.Y.; Lee, Y.H. On the Use of Double Correlation for Frame Synchronization in the Presence of Frequency Offset. In Proceedings of the 1999 IEEE International Conference on Communications, Vancouver, BC, Canada, 6–10 June 2019; pp. 958–962. [Google Scholar]
- Choi, Z.Y.; Lee, Y.H. Frame synchronization in the presence of frequency offset. IEEE Trans. Commun. 2002, 50, 1062–1065. [Google Scholar] [CrossRef]
- Massey, J.L. Optimum Frame Synchronization. IEEE Trans. Commun. 1972, 20, 115–119. [Google Scholar] [CrossRef]
- Nielsen, P.T. Some Optimum and Suboptimum Frame Synchronizers for Binary Data in Gaussian Noise. IEEE Trans. Commun. 1973, 21, 770–772. [Google Scholar] [CrossRef]
- Lui, G.L.; Tan, H.H. Frame synchronization for Gaussian channels. IEEE Trans. Commun. 1987, 35, 818–829. [Google Scholar]
- Robertson, P. Maximum likelihood frame synchronization for flat fading channels. In Proceedings of the 1992 IEEE International Conference on Communications, Chicago, IL, USA, 14–18 June 1992; pp. 1426–1430. [Google Scholar]
- Wang, Y.; Shi, K.; Serpedin, E. Continuous Mode Frame Synchronization for Frequency Selective Channels. IEEE Trans. Commun. 2004, 53, 865–871. [Google Scholar] [CrossRef]
- Kopansky, A.; Bystrom, M. Frame Synchronization for Noncoherent Demodulation on Flat Fading Channels. In Proceedings of the 2000 IEEE International Conference on Communications, New Orleans, LA, USA, 18–22 June 2000; pp. 312–316. [Google Scholar]
- Chiani, M.; Martini, M. Optimum synchronization of frames with unknown, variable lengths on Gaussian channels. In Proceedings of the IEEE Global Telecommunications Conference, Dallas, TX, USA, 29 November–3 December 2004; Volume 6, pp. 4087–4091. [Google Scholar]
- Chiani, M.; Martini, M. Practical frame synchronization for data with unknown distribution on AWGN channels. IEEE Commun. Lett. 2005, 9, 456–458. [Google Scholar] [CrossRef]
- Chiani, M.; Martini, M. On sequential frame synchronization in AWGN channels. IEEE Trans. Commun. 2006, 54, 339–348. [Google Scholar] [CrossRef]
- Kim, P.; Pedone, R.; Villanti, M.; Vanelli-Coralli, A.; Corazza, G.E.; Chang, D.I.; Oh, D.G. Robust frame synchronization for the DVB-S2 system with large frequency offsets. Int. J. Satell. Commun. Netw. 2009, 27, 35–52. [Google Scholar] [CrossRef]
- Pedone, R.; Villanti, M.; Vanelli-Coralli, A.; Corazza, G.; Mathiopoulos, P.T. Frame Synchronization in Frequency Uncertainty. IEEE Trans. Commun. 2010, 58, 1235–1246. [Google Scholar] [CrossRef]
- Bai, Y.; Yang, J.X.; Zhang, Y. A Recognition Method of m-sequence Synchronization Codes using Higher-order statistical Processing. J. Electrinics Inf. Technol. 2012, 34, 33–37. (In Chinese) [Google Scholar] [CrossRef]
- Bai, Y.; Yang, J.X.; Zhang, Y. Recognition Method of Fame Synchronization Codes based on Relativity Filter and Hadamard transformation Algorithm. J. Detect. Contol. 2011, 33, 69–72. (In Chinese) [Google Scholar]
- Naseri, A.; Salemm, J.; Hajimohammadii, M. Improving the blind recovering algorithm and synchronization word in satellite communication systems. Indian J. Sci. Res. 2014, 1, 15–19. [Google Scholar]
- Qin, J.Y.; Huang, Z.P. Novel Blind Recognition Algorithm of Frame Synchronization Words Based on Soft-Decision in Digital Communication Systems. PLoS ONE 2015, 10, e0132114. [Google Scholar] [CrossRef]
- Guo, F.K.; Wang, M. Research on Detection of Frame Head on Fixed Frame Length. J. Signal Inf. Process. 2014, 44, 33–36. (In Chinese) [Google Scholar]
- Xu, Y.Y.; Zhong, Y.; Huang, P.Z. An Improved Blind Recognition Algorithm of Frame Parameters Based on Self-Correlation. Information 2019, 10, 64. [Google Scholar] [CrossRef]
- Imad, R.; Sicot, G.; Houcke, S. Blind frame synchronization for error correcting codes having a sparse parity check matrix. IEEE Trans. Commun. 2009, 57, 1574–1577. [Google Scholar] [CrossRef]
- Xia, T.; Wu, H. Joint Blind Frame Synchronization and Encoder Identification for Low-Density Parity-Check Codes. IEEE Commun. Lett. 2014, 18, 353–355. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, Z.; Su, S. Blind Frame Synchronization of Reed-Solomon Coded Optical Transmission Systems. OPTIK 2013, 124, 998–1002. [Google Scholar]
- Qi, Y.; Wang, B.; Rong, M.; Liu, T. Comments on “Theoretical Analysis of a MAP Based Blind Frame Synchronizer. IEEE Trans. Wirel. Commun. 2011, 10, 3127–3132. [Google Scholar]
- Hough, P.V.C. A Method and Means for Recognizing Complex Patterns. U.S. Patent 3,069,654, 18 December 1962. [Google Scholar]
- Mukhopadhyay, P.; Chaudhuri, B. A survey of Hough Transform. Pattern Recognit. 2014, 48, 993–1010. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Imad, R.; Houcke, S. Theoretical Analysis of a MAP Based Blind Frame Synchronizer. IEEE Trans. Wirel. Commun. 2009, 8, 5472–5476. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).