Abstract
Mueller matrix polarimetry is a potentially powerful technique for obtaining microstructural information of biomedical specimens. Thus, it has found increasing application in both backscattering imaging of bulk tissue samples and transmission microscopic imaging of thin tissue slices. Recently, we proposed a technique to transform the 4 × 4 Mueller matrix elements into a group of parameters, which have explicit associations with specific microstructural features of samples. In this paper, we thoroughly analyze the relationships between the Mueller matrix transformation parameters and the characteristic microstructures of tissues by using experimental phantoms and Monte Carlo simulations based on different tissue mimicking models. We also adopt quantitative evaluation indicators to compare the Mueller matrix transformation parameters with the Mueller matrix polar decomposition parameters. The preliminary imaging results of bulk porcine colon tissues and thin human pathological tissue slices demonstrate the potential of Mueller matrix transformation parameters as biomedical diagnostic indicators. Also, this study provides quantitative criteria for parameter selection in biomedical Mueller matrix imaging.
1. Introduction
Polarization imaging techniques are sensitive to microstructural changes in tissues, and can therefore be regarded as potential tools for biomedical diagnosis [1,2,3]. As a comprehensive description of polarization characteristics of scattering samples, Mueller matrices have recently been widely used in abnormal tissue detection for both backward imaging of bulk tissue sample scattering and transmission imaging of thin tissue slices [4,5,6,7,8,9,10,11]. However, although a Mueller matrix contains rich structural information about tissues, such information is difficult to obtain from the 16 elements directly. To deal with this problem, several methods have been proposed to transform these 16 Mueller matrix elements into different groups of derived parameters with clearer physical and structural meaning [12,13,14,15].
For instance, the Mueller matrix polar decomposition (MMPD) [12] and the Mueller matrix transformation (MMT) [14,15] methods have both shown that the derived parameters can distinguish dysplasia and normal areas of investigated tissue samples [16,17,18]. The MMPD method decomposes a Mueller matrix into a set of sub-matrices representing a depolarizer, a retarder, and a diattenuator, respectively. After the decomposition, the three sub-matrices can be transformed into specific parameters related to the depolarization, retardance, and diattenuation properties. Meanwhile, in our previous studies, we have found that the Mueller matrix elements of anisotropic media can be fitted to trigonometric functions. Based on these functions, the MMT parameters can be obtained and provide several indicators of anisotropy, depolarization, and direction of fibrous structures [3]. Besides, there are some other recent studies in the Mueller matrix analysis, where the Mueller matrix images of tissues were also analyzed in the frame of groups of parameters [19,20,21,22].
Recent applications of various cancerous tissues have demonstrated the diagnostic potential of Mueller matrix-derived parameters [6,8,17,23]. However, a quantitative analysis of the Mueller matrix parameters is still needed to help select a specific group of parameters suitable for a specific biomedical polarization measurement. In this paper, we compare the MMPD and MMT methods, focusing on their quantitative characterization capabilities of tissue properties, especially the depolarization and anisotropy. Firstly, we use a silk phantom and a birefringent gradient-index (GRIN) lens [24] to reveal the distinct effects of cylindrical scatterers and birefringence on Mueller matrix elements. Then, based on the sphere-cylinder-birefringence model (SCBM) [25,26] and the Monte Carlo simulation program [27], we generate the Mueller matrices of different tissue models, and calculate their corresponding MMPD and MMT parameters. Lastly, two indicators are adopted to evaluate the characterization capabilities of these parameters. The preliminary imaging results of porcine colon and human pathological tissues demonstrate quantitative criteria for parameter selection in biomedical Mueller matrix imaging.
2. Methods and Materials
2.1. Experimental Setup and Materials
The Mueller matrix measurement setup used in this study is based on a dual-rotating retarder polarimeter, as shown in Figure 1a. The light source is a diode laser (3 W, 632 nm, Δλ = 20 nm, Cree, Shenzhen, China). The polarization state generator (PSG) is composed of a lens (L1, Thorlabs, Newton, NJ, USA), a fixed linear polarizer (P1, GCM-0902M, extinction ratio 500:1, Daheng Optics, Beijing, China), and a rotatable quarter-wave plate (R1, Daheng Optics, China). Similarly, the polarization state analyzer (PSA) is also composed of a lens (L2/L3, focal lengths 5 cm, Thorlabs, USA), a fixed linear polarizer (P2/P3, GCM-0902M, extinction ratio 500:1, Daheng Optics, China), and a rotatable quarter-wave plate (R2/R3, Daheng Optics, China). The polarization images of the sample are recorded by a 12-bit CCD camera (CCD1/CCD2, QImaging 74-0107A, Canada). During the measurement, the polarizers (P1, P2, P3) are fixed in the horizontal direction, while the quarter-wave plates (R1, R2, R3) rotate with the fixed rates ω2 = 5ω1. Then, the Mueller matrix elements can be calculated by using the Fourier coefficients [28,29]. The setup was calibrated by measuring the Mueller matrices of standard samples, including air and retarders, and the experimental results demonstrated that the maximum error of the setup is about 1%. It can be noticed from Figure 1a that by changing the position of the PSA arm, the backward and forward Mueller matrices of the sample can be obtained.
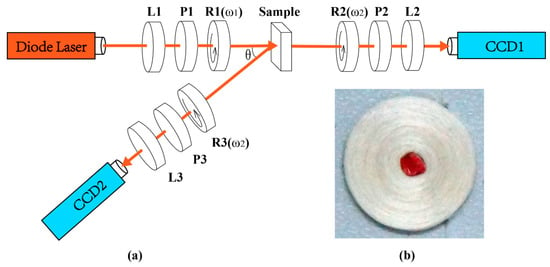
Figure 1.
(a) Schematic of the Mueller matrix configuration for both backscattering and transmission measurements. L1, L2, L3: lens; P1, P2, P3: polarizer; R1, R2, R3: quarter-wave plate. (b) Silk phantom; the diameter of the silk fiber is 1.5 μm and its refractive index is 1.56; the scattering coefficient of the silk layer is 70 cm−1, the outer diameter of the phantom is 1.5 cm and its thickness is 2 mm.
As shown in Figure 1b, here we use a silk phantom to initially observe the effects of cylindrical scatterers on Mueller matrix elements. Since the silk phantom is made of natural silk fibers neatly wound around a plastic pillar, it can be approximated as an anisotropic cylindrical scatterer [25]. We also use a GRIN lens to observe the effects of birefringence on Mueller matrix elements. For the GRIN lens, its anisotropic properties mainly come from birefringence along its radius. The GRIN lens is provided by Femto Technology Co. Ltd. It is 6.0 cm in length, 2 mm in diameter, and its birefringence (Δn) along the radius is from 0 to 10−5. Considering that the scattering property of the silk phantom is strong, while it is limited for the GRIN lens, we measure the backscattering Mueller matrix of the silk phantom and the transmission Mueller matrix of the GRIN lens.
To test the biomedical application of the Mueller matrix-derived parameters, we also measure two different tissue samples: (1) ex vivo porcine colon tissue (imaged from serosa side) in reflection geometry, and (2) human pathological tissue sections in transmission direction. The human tissue samples were provided by Shenzhen Sixth People’s (Nanshan) hospital. The use of human tissue samples in this study was approved by the Ethics Committee of the Shenzhen Sixth People’s (Nanshan) Hospital.
2.2. Mueller Matrix Polar Decomposition (MMPD) and Mueller Matrix Transformation (MMT) Parameters
The MMPD method proposed by Lu and Chipman regards the Mueller matrix as a combination of three main factors: depolarizer, retarder, and diattenuator.
Using Equation (1) the MMPD parameters Δ, R, and D can be calculated, representing depolarization, retardance, and diattenuation properties of the sample, respectively. It should be noted that the retardance is composed of linear retardance and circular retardance. In this paper, we mainly analyze the linear retardance of tissues as represented by Equation (2):
In our previous studies, both experiments and Monte Carlo simulations have confirmed that the azimuthal angular-dependent Mueller matrix elements can be fitted to trigonometric functions. Using these functions, several independent MMT parameters can be obtained shown, as in Equation (3).
Here we use the MMT parameters formulas according to a previous study [15], in which t2 and t3 are represented as PL and qL. Each MMT parameter is calculated using a group of Mueller matrix elements, while the MMPD parameters are obtained from a relatively complex decomposition process of all 16 Mueller matrix elements. Hence, the calculation of the MMT parameters is faster than that of the MMPD parameters [8]. Previous studies have shown that: (1) the MMT parameter b and the MMPD parameter Δ are both sensitive to the depolarization property of samples [6]; (2) for the MMT method, both parameters t1 and t2 are sensitive to the anisotropy degree of scattering media, and t3 is an indicator of birefringence of tissues [3]; (3) for the MMPD method, retardance R and diattenuation D are both related to the anisotropy of samples. Besides, the orientation of anisotropic structures can also be revealed using different Mueller matrix elements, as discussed in our previous study [30,31]. However, a quantitative comparison between the MMT and MMPD methods is still needed to help select a specific group of Mueller matrix derived parameters that are highly sensitive and computationally applicable for different biomedical polarization measurement and imaging scenarios.
2.3. Monte Carlo Simulation and Evaluation Indicators
To compare the MMPD and MMT parameters quantitatively, in this study we use the Monte Carlo (MC) simulation programs based on different models to track the interaction between polarized photons and tissue microstructures [25,26,27]. Here in this study, the sphere model (SM) is considered to be an effective simulation of isotropic tissues, whose characteristic features are mainly reflected in depolarization [17]. In our previous work, the sphere-cylinder model (SCM) was proposed to simulate the anisotropic tissues containing fibrous scatterers [25,27], whose anisotropic structural features can be described approximately by the density, direction, and diameter of the cylinders. The sphere-birefringence model (SBM) was used to simulate anisotropic tissues containing birefringence effects [6,7,8,26], whose characteristic features can be described by the value and orientation of birefringence. Based on the sphere-cylinder-birefringence model and the Monte Carlo simulation program, we can generate the Mueller matrices of tissues with different structural features. In our previous studies, we compared the MC simulated Mueller matrices with the corresponding experimental Mueller matrix images. The results shown as Figures 4 and 8 in [26], Figures 6 and 7 in [25], Figures 2 and 3 in [32], and Figure 2 in [33] demonstrated that the MC simulation can be used as a powerful tool to analyze the experimental Mueller matrix images of tissues quantitatively.
For biomedical imaging, the parameters are required to have a high image contrast and a good correlation with the changes in characteristic structural features of tissues. Here we introduce two evaluation indicators to clarify the relationship between the parameters and tissue properties, shown as Equation (4):
T represents the variation range normalized by the codomain of a certain parameter (represented by y) as a certain structural feature varies. A larger value of T means a better image contrast for that polarization parameter; r2, whose codomain is [0,1], is a coefficient of determination, which is the square of the correlation coefficient between a parameter (represented by y) and a structural feature (represented by x). A larger value of r2 means a better linear relationship between a parameter and a structural feature. Thus, r2 can be used as an indicator to evaluate the sensitivity of a parameter to a certain tissue characteristic feature.
3. Results and Discussion
3.1. Comparison between the Mueller Matrices of the Silk Phantom and GRIN Lens
To analyze the different effects of cylindrical scatterers and birefringence, we measured the backscattering 2D Mueller matrix of the silk phantom and the transmission 2D Mueller matrix of the birefringent GRIN lens, as shown in Figure 2a,b. It can be observed from the experimental results that the upper left 3 × 3 elements of the silk phantom represent periodic intensity variations, while for the GRIN lens similar periodic variations are observed for the lower right 3 × 3 elements. To show the relationship between the intensity variation of each element and the anisotropy orientation (alignment of cylinders or fast axis of birefringence), we plot their azimuthally dependent curves in Figure 2c,d. We choose the element values from the range of radii as 0.42 cm to 0.54 cm for silk phantom curves and 0.8 mm to 0.9 mm for GRIN lens curves.
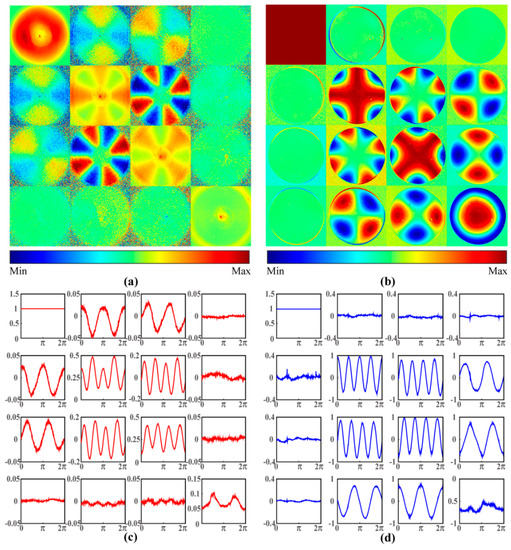
Figure 2.
(a) A 2D backscattering Mueller matrix image of silk phantom. The color code for m12, m13, m21, and m31 is from −0.1 to 0.1. The color code for m23 and m32 is from −0.2 to 0.2. The color code for other elements is from −1 to 1. (b) A 2D transmission Mueller matrix image of birefringent gradient-index (GRIN) lens. The color code for all 16 elements is from −1 to 1. Azimuthal dependent curves of the Mueller matrix elements for (c) the silk phantom and (d) the GRIN lens. All the Mueller matrix elements are normalized by m11.
It can be concluded from Figure 2c,d that: (1) For both the silk phantom and the GRIN lens, the middle four elements m22, m33, m23, and m32 have very similar characteristics. As the anisotropy axes change from 0 to 2π, the m22 and m33 elements show cosinusoidal variations, while the m23 and m32 elements represent sinusoidal changes. Also we observe that the middle elements have 4 periods in (0, 2π). The main difference of the middle four elements between the silk phantom and GRIN lens is that the m22 and m33 shown in Figure 2c have a DC offset compared to Figure 2d. This means that the cylindrical scattering and birefringence result in a similar periodic intensity change for these elements, however, the scattering of the silk phantom also induces depolarization, which results in the DC offset to the diagonal elements; (2) for the silk phantom, the upper left m12, m13, m21, and m31 elements show two periods in (0, 2π), indicating that cylindrical scatterers cause diattenuation; (3) for the GRIN lens, the lower right m24, m34, m42, and m43 elements represent a similar variation as for the upper left elements of the silk phantom. More precisely, the m12 and m21 for the silk phantom and the m34 andm43 elements for the GRIN lens have cosinusoidal forms, while the m13 and m31 for the silk phantom and the m24, m42 elements for the GRIN lens show sinusoidal forms.
In summary, Figure 2 shows that the different origins of anisotropy have different effects on Mueller matrix elements. The anisotropy originated from cylindrical scatterers mainly results in the periodic intensity variations of the upper left 3 × 3 elements of Mueller matrix, while the anisotropy originated from birefringence mainly leads to the periodic intensity variations of the lower right 3 × 3 elements of Mueller matrix [3,6]. By analyzing different groups of elements, the anisotropic scattering and birefringence may be distinguished.
The Mueller matrix derived parameters of the silk phantom and the GRIN lens are shown in Figure 3a,b. We can see from Figure 3a that the structural properties of the silk phantom are mainly reflected in the parameters Δ, b, t1, and t2, or in other words the depolarization and the diattenuation. The values of retardance related parameters δ, t3 are close to zero, which confirms that the linear retardance induced by cylindrical scatterers is very limited. It should be noticed that there is some radial non-uniformity in Figure 3a due to the oblique incidence of the illuminating light in backscattering measurements. Simulations have shown that the non-uniformity decreases as the oblique incident angle is reduced [34]. As shown in Figure 3b, the birefringence of the GRIN lens is mainly reflected in the parameters δ, t1, and t3. Moreover, the small value of Δ and the large value of b demonstrate that the depolarization of the GRIN lens is very limited. It can be concluded that the effect of anisotropic scattering is mainly reflected in parameters t1, t2, and D, while the effect of birefringence can be detected by parameters t1, t3, and δ. However, for biomedical applications, further quantitative comparisons between these different groups of parameters are needed for: (1) t1, t2, and D; (2) t1, t3, and δ; and (3) Δ and b.
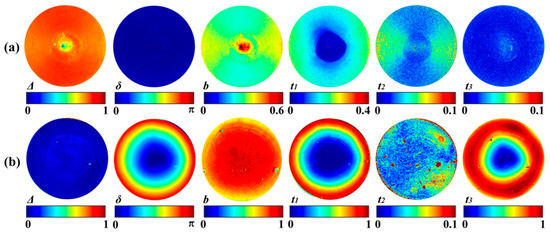
Figure 3.
Mueller matrix derived parameters of the samples: (a) Mueller matrix polar decomposition (MMPD) and Mueller matrix transformation (MMT) parameters of the silk phantom. (b) MMPD and MMT parameters of the GRIN lens. Since the m14 values for both samples are close to 0 (Figure 2a–d), the images of D (not shown) and t2 are almost the same.
3.2. Parameters for Depolarizing Isotropic Tissues
Firstly, we compare the MMPD parameter Δ and the MMT parameter b for an isotropic scattering medium—assumed to be mainly composed of cells of different sizes—using MC simulation. Pathological changes result in variation in the characteristic features of cells, and our previous studies have demonstrated that isotropic tissues, such as human skin basal cell carcinoma samples, can be approximately described by a bi-component spherical scattering model, in which the large spheres represent cell nuclei, while the small ones mimic organelles [17]. In the absence of fibrous structures, changes are mainly reflected in depolarization rather than retardance and diattenuation. Here we use the sphere model (SM) with no birefringence and the two evaluation indicators proposed in Section 2.3 to compare Δ and b for isotropic scattering media. The simulation parameters are set approximately according to real tissues: the large and small spheres have 4 μm diameter and 0.2 μm diameter, respectively. We analyze isotropic media with three different large-small sphere ratios of 1:4, 1:1, 4:1, and the total scattering coefficient (total μs) is set from 50 cm−1 to 450 cm−1. The refractive indices of large and small spheres are both 1.45. The refractive index of interstitial medium is 1.33 [35,36].
We can observe from Figure 4a,b that as the scattering coefficient increases, the curves of Δ and b have contrary trends, confirming that Δ and b are correlated to depolarization positively and negatively, respectively. For any μs, the tissue with a 1:4 large-small sphere ratio has the most prominent depolarization (the largest Δ and the smallest b). From Figure 4c it is observed that a larger large-small sphere ratio means a smaller T. These simulation results (Figure 4a–c) demonstrate that changes in number of small spheres (organelles) is the main factor leading to the depolarization image contrast for isotropic tissues, which is consistent with our previous observations [17]. It can also be observed from Figure 4c that for depolarizing samples, the MMPD parameter Δ has a slightly better image contrast than the MMT parameter b. Moreover, it can be seen from Figure 4d that the r2 of Δ and b are almost equal to 1, which means they are strongly related to proliferation of particles. The similar characteristic features of the evaluation indicators T and r2 shown in Figure 4c,d reveal that the MMPD parameter Δ and the MMT parameter b can both be used to obtain the depolarization information.
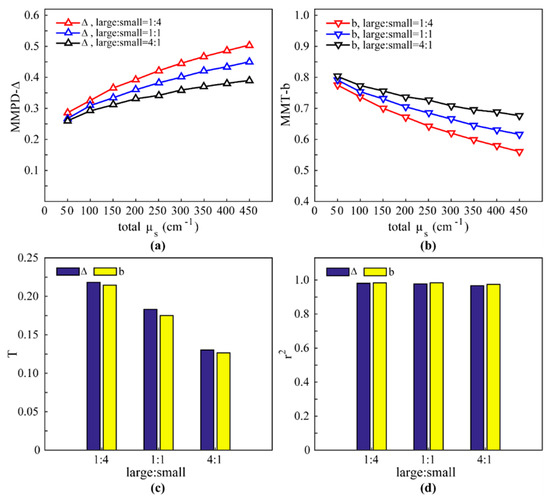
Figure 4.
Monte Carlo (MC) simulation results of bi-component sphere model in the backward direction: (a) MMPD parameter Δ. (b) MMT parameter b. (c) T of Δ and b; the codomains of both parameters are [0,1]. (d) The r2 of Δ and b.
3.3. Parameters for Anisotropic Tissues with Cylindrical Scatterers
As discussed above, the anisotropic properties of tissues may come from cylindrical scatterers or birefringence. Here we use the sphere-cylinder model (SCM) to simulate the interactions between polarized photons and cylinders.
To simulate the process of fibrosis, the proportion of the cylindrical scatterers was varied from 0 to 100%, while the alignment of fibers did not change. The total scattering coefficients of the spherical and cylindrical scatterers were set as 50 cm−1, 210 cm−1, and 350 cm−1. The diameters of the spheres and cylinders are both 1.5 μm [37]. The refractive index of the interstitial medium is 1.33. As shown in Figure 5a,b, both the MMPD parameter D and the MMT parameter t2 have good linear correlations with the increase in cylindrical scatterers, whereas the variation in MMPD parameter δ and MMT parameter t3 are very limited. Also, the r2 values of the parameters D and t2 are both close to 1, as shown in Figure 5d, confirming a strong relationship between the cylindrical scatterers and these two parameters (D and t2). Moreover, it can be noticed that for different total scattering coefficients, the values of D and t2 are almost the same, indicating that the proportion of cylindrical scatterers is the main contribution to the image contrast of these parameters. In addition, the expression of parameter t2 is very similar to that of parameter D, which additionally takes into account the m14 element. However, the m14 is often very small for tissues. Therefore, the T and r2 values are almost the same as shown in Figure 5c,d. The MC simulation results demonstrate that the effect of cylindrical scatterers can be detected using the diattenuation related parameters D and t2, which is in consistent with the observations of the 2D Mueller matrix images above (Figure 3).
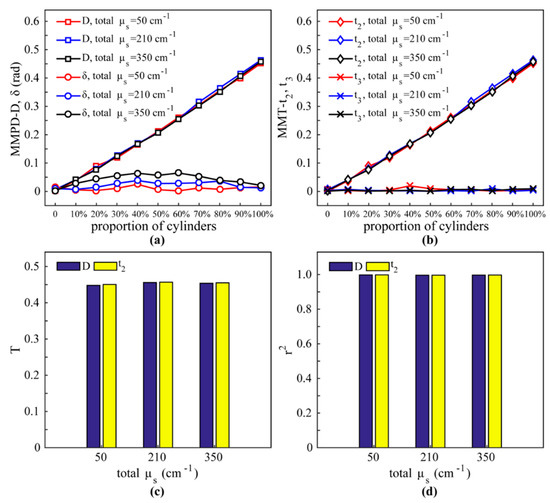
Figure 5.
MC simulation results of sphere-cylinder model in backward direction: (a) MMPD parameters D and δ. (b) MMT parameters t2 and t3. (c) T of D and t2; the codomains of D and t2 are [0,1]. (d) The r2 of D and t2.
3.4. Parameters for Anisotropic Tissues with Birefringence
The sphere-birefringence model was adapted to simulate tissues whose anisotropy mainly comes from birefringence. Recently, we have found that the value of linear retardance can be used to detect various abnormal tissues, such as cervical cancer [6], liver cirrhosis [8] and breast cancer [23]. The pathological fibrosis can result in an increase of birefringence in tissues, leading to image contrast of the Mueller matrix derived parameters between normal and abnormal areas. Here the birefringence (Δn) is changed from 0 to 0.004 [38]. The diameters of small and large spheres are 0.2 μm and 4 μm, respectively. The scattering coefficient ratio between the large and small spheres is 1:4. The total scattering coefficient is 125 cm−1. The refractive index of the interstitial medium is 1.33.
It can be seen from Figure 6a,b that as Δn increases from 0 to 0.004, the MMPD parameter δ and the MMT parameter t3 increase monotonically in both the forward and backward scattering directions, whereas the parameters D and t2 are close to zero. This phenomenon is consistent with what we observed in the images of GRIN lens parameters (Figure 3b), indicating the parameters δ and t3 are correlated to birefringence. More details can be found in Figure 6c that show that in the forward direction, the T value of t3 is much larger than that of δ. This means that in the forward direction the MMT parameter t3 is a better indicator of birefringence than the MMPD parameter δ. It is shown in Figure 6d that the r2 values of δ in both the forward and backward directions are closer to 1 than that of t3, indicating that the MMPD parameter δ has a better correlation with birefringence changes in tissues. In general, both the MMPD parameter δ and the MMT parameter t3 have potential to detect birefringence features in tissues. In transmission, when the image contrast is primarily considered, using t3 may achieve a better result, while parameter δ should be chosen to obtain a better correlation with tissue birefringence.
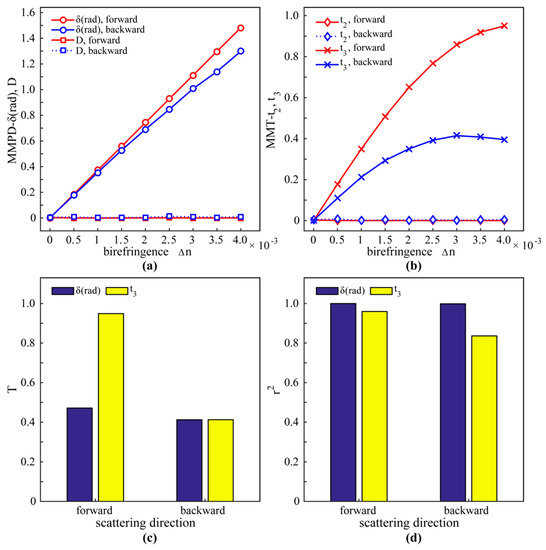
Figure 6.
MC simulation results of a sphere-birefringence model in both forward and backward scattering directions: (a) MMPD parameters D and δ. (b) MMT parameter t2 and t3. (c) T of δ and t3; the codomain of δ is [0, π]; the codomain of t3 is [0,1]. (d) The r2 of δ and t3.
To further test the conclusions above, we measured the Mueller matrix derived parameters of tissues samples: (1) ex vivo porcine colon tissue (imaged from serosa side) in reflection geometry, and (2) a human breast carcinoma tissue section in transmission direction. The images of Mueller matrix parameters are shown in Figure 7. It can be observed from the experimental results that: (1) Figure 7a shows relatively high values for parameters Δ and b (the value of Δ is in (0.7, 1), the value of b is in (0, 0.3)), and lower values for the other parameters. This confirms that for bulk tissues with strong depolarization, the tissue properties can be observed by the Mueller matrix derived parameters Δ and b; (2) in Figure 7b, for the human breast invasive ductal carcinoma section, the fibrous hyperplasia leads to an increase in the birefringence as seen in a previous study [23], thus the images of retardance related parameters δ, t3 contrast the fibrous structures. More specifically, the image contrast of parameter t3 is better than that of parameter δ, which is consistent with the simulation result in Figure 6c. However, the images of parameters D and t2 have barely noticeable textures, meaning that the fibrosis structures may cause little diattenuation in tissues and these two parameters (D and t2) may not be suitable for detecting fibrosis for thin tissue slices. Additionally, because of the limited scattering, the value of parameter Δ is almost 0 and the value of b is close to 1.
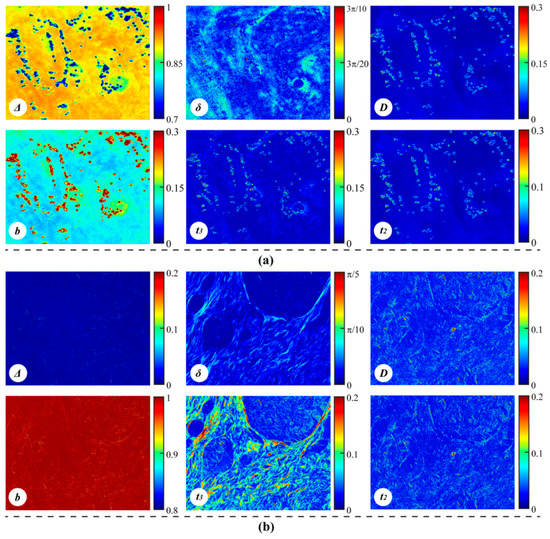
Figure 7.
Mueller matrix derived parameters of: (a) ex vivo porcine colon tissue; all the color scales are set to 0.3 times the codomains of the parameters. It should be noticed that there are areas with abnormally small values of Δ and large values of b, which result from the specular reflection induced pixel saturation. (b) Human breast invasive ductal carcinoma tissue: 12 μm-thick, unstained, and dewaxed; all the color scales are 0.2 times the codomains of the parameters.
In the MC simulation results shown in Figure 6c, it can be found that the T value of t3 (Tt3) is larger than that of δ (Tδ). In order to test whether the result above is stable or not for different tissues, we measured the transmission Mueller matrices of 90 human pathological tissue slices: 30 Crohn disease tissue samples, 30 intestinal tuberculosis tissue samples, and 30 breast ductal carcinoma tissue samples. We then compared the T values of the parameters δ and t3, as shown in Figure 8. All the Crohn disease tissues (red circles), intestinal tuberculosis tissues (blue asterisks), and breast carcinoma tissues (green triangles) have prominent fibrosis structures. It can be seen from Figure 8 that the T values of t3 are about 2.8 times larger than those of δ, confirming that the image contrast of parameter t3 is better than that of parameter δ. The coefficients of determination r2 of the T values between δ and t3 for three types of tissues are 0.994, 0.932, and 0.973, respectively, indicating the significant linear correlations.
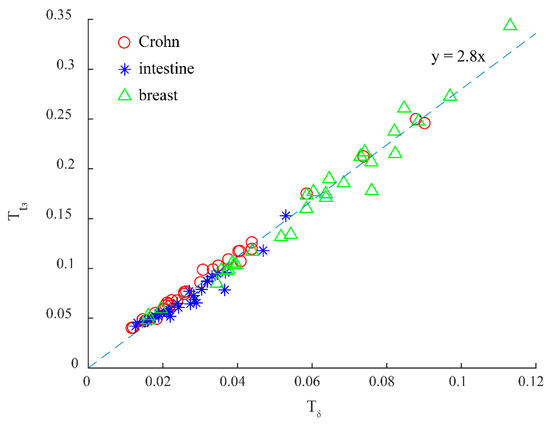
Figure 8.
Comparison between Tδ: T values of the MMPD parameter δ, and Tt3: T values of the MMT parameter t3 for 90 human pathological tissue slices. X-axis: Tδ. Y-axis: Tt3. Red circles: Crohn-Crohn disease tissues. Blue asterisks: intestine-intestinal tuberculosis tissues. Green triangles: breast-breast carcinoma tissues.
In summary, for imaging anisotropic tissue slices in transmission and detection of the retardance related parameters δ, t3 has the potential to reveal dysplasia or cancer induced birefringence change quantitatively. Besides, we used the MATLAB tic-toc function to count the computing time of Mueller matrix-derived parameters used in this study, showing that the MMT method is ten times faster than the MMPD method (0.0016 s versus 0.0179 s for 160 Mueller matrices) under the same hardware condition (2.5 GHz Intel® CoreTM i7, MATLAB 2014).
4. Conclusions
Here we compared different Mueller matrix-derived parameters focusing on their quantitative characterization capabilities of tissue properties, especially the depolarization and anisotropy. We used a silk phantom and a birefringent gradient-index lens to reveal the distinct effects of cylindrical scatterers and birefringence on different Mueller matrix elements. Then, based on the sphere-cylinder-birefringence model and the Monte Carlo simulation program, we generated the Mueller matrices of different tissue models, and calculated their corresponding MMPD and MMT parameters. Using two indicators, we evaluated the characterization capabilities of these parameters quantitatively. The preliminary imaging results of porcine colon tissues and thin human pathological tissue slides demonstrated the potential of Mueller matrix transformation parameters as biomedical diagnostic indicators. Also, this study provides quantitative criteria for parameters selection in biomedical Mueller matrix imaging.
Author Contributions
Conceptualization, H.H., D.S.E., and H.M.; data curation, W.S., W.L., J.Q., T.L., and S.L.; methodology, J.Q., Y.D., and J.W.; supervision, H.M.; writing—original draft, W.S. and W.L.; writing—review and editing, H.H., D.S.E., and H.M.
Funding
This study was supported by National Natural Science Foundation of China (NSFC) (No. 61527826, 11611130168), the Royal Society International Exchange Scheme Award IE150970, and the Science and Technology Project of Shenzhen (No. JCYJ20170412170814624).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ghosh, N.; Vitkin, I.A. Tissue polarimetry: Concepts, challenges, applications, and outlook. J. Biomed. Opt. 2011, 16, 110801. [Google Scholar] [CrossRef] [PubMed]
- Kunnen, B.; Macdonald, C.; Doronin, A.; Jacques, S.; Eccles, M.; Meglinski, I. Application of circularly polarized light for non-invasive diagnosis of cancerous tissues and turbid tissue-like scattering media. J. Biophotonics 2015, 8, 317–323. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Liao, R.; Zeng, N.; Li, P.; Chen, Z.; Liu, X.; Ma, H. Mueller matrix polarimetry—An emerging new tool for characterizing the microstructural feature of complex biological specimen. J. Lightwave Technol. 2018. [Google Scholar] [CrossRef]
- Alali, S.; Vitkin, I.A. Polarized light imaging in biomedicine: Emerging Mueller matrix methodologies for bulk tissue assessment. J. Biomed. Opt. 2015, 20, 061104. [Google Scholar] [CrossRef] [PubMed]
- Pierangelo, A.; Nazac, A.; Benali, A.; Validire, P.; Cohen, H.; Novikova, T.; Ibrahim, B.H.; Manhas, S.; Fallet, C.; Antonelli, M.R.; et al. Polarimetric imaging of uterine cervix: A case study. Opt. Express 2013, 21, 14120–14130. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; He, H.; Zeng, N.; Du, E.; Guo, Y.; Liu, S.; Wu, J.; He, Y.; Ma, H. Characterizing the microstructures of biological tissues using Mueller matrix and transformed polarization parameters. Biomed. Opt. Express 2014, 5, 4223–4234. [Google Scholar] [CrossRef] [PubMed]
- He, C.; He, H.; Chang, J.; Dong, Y.; Liu, S.; Zeng, N.; He, Y.; Ma, H. Characterizing microstructures of cancerous tissues using multispectral transformed Mueller matrix polarization parameters. Biomed. Opt. Express 2015, 6, 2934–2945. [Google Scholar] [CrossRef]
- Wang, Y.; He, H.; Chang, J.; He, C.; Liu, S.; Li, M.; Zeng, N.; Wu, J.; Ma, H. Mueller matrix microscope: A quantitative tool to facilitate detections and fibrosis scorings of liver cirrhosis and cancer tissues. J. Biomed. Opt. 2016, 21, 071112. [Google Scholar] [CrossRef] [PubMed]
- He, H.; He, C.; Chang, J.; Lv, D.; Wu, J.; Duan, C.; Zhou, Q.; Zeng, N.; He, Y.; Ma, H. Monitoring microstructural variations of fresh skeletal muscle tissues by Mueller matrix imaging. J. Biophotonics 2017, 10, 664–673. [Google Scholar] [CrossRef] [PubMed]
- Qi, J.; Ye, M.; Singh, M.; Clancy, N.T.; Elson, D.S. Narrow band 3×3 Mueller polarimetric endoscopy. Biomed. Opt. Express 2013, 4, 2433–2449. [Google Scholar] [CrossRef] [PubMed]
- Qi, J.; Elson, D.S. A high definition Mueller polarimetric endoscope for tissue characterization. Sci. Rep. 2016, 6, 25953. [Google Scholar] [CrossRef]
- Lu, S.Y.; Chipman, R.A. Interpretation of Mueller matrix based on polar decomposition. J. Opt. Soc. Am. A 1996, 13, 1106–1113. [Google Scholar] [CrossRef]
- Ossikovski, R. Analysis of depolarizing Mueller matrices through a symmetric decomposition. J. Opt. Soc. Am. A 2009, 26, 1109–1118. [Google Scholar] [CrossRef]
- He, H.; Chang, J.; He, C.; Ma, H. Transformation of full 4×4 Mueller matrices: A quantitative technique for biomedical diagnosis. Proc. SPIE 2016, 9707, 97070K. [Google Scholar]
- Li, P.; Lv, D.; He, H.; Ma, H. Separating azimuthal orientation dependence in polarization measurements of anisotropic media. Opt. Express 2018, 26, 3791–3800. [Google Scholar] [CrossRef] [PubMed]
- Dubreuil, M.; Babilotte, P.; Martin, L.; Sevrain, D.; Rivet, S.; Grand, Y.L.; Brun, G.L.; Turlin, B.; Jeune, B.L. Mueller matrix polarimetry for improved liver fibrosis diagnosis. Opt. Lett. 2012, 37, 1061–1063. [Google Scholar] [CrossRef] [PubMed]
- Du, E.; He, H.; Zeng, N.; Sun, M.; Guo, Y.; Wu, J.; Liu, S.; Ma, H. Mueller matrix polarimetry for differentiating characteristic features of cancerous tissues. J. Biomed. Opt. 2014, 19, 076013. [Google Scholar] [CrossRef]
- Liu, T.; Sun, T.; He, H.; Liu, S.; Dong, Y.; Wu, J.; Ma, H. Comparative study of the imaging contrasts of Mueller matrix derived parameters between transmission and backscattering polarimetry. Biomed. Opt. Express 2018, 9, 4413–4428. [Google Scholar] [CrossRef] [PubMed]
- Das, N.K.; Dey, R.; Chakraborty, S.; Panigrahi, P.K.; Meglinski, I.; Ghosh, N. Quantitative assessment of submicron scale anisotropy in tissue multifractality by scattering Mueller matrix in the framework of Born approximation. Opt. Commun. 2018, 413, 172–178. [Google Scholar] [CrossRef]
- Ushenko, A.; Sdobnov, A.; Dubolazov, A.; Gritsuk, M.; Ushenko, Y.; Bykov, A.; Meglinski, I. Stokes-correlometry analysis of biological tissues with polycrystalline structure. IEEE J. Sel. Top. Quant. 2019, 25, 1–12. [Google Scholar] [CrossRef]
- Borovkova, M.; Peyvasteh, M.; Dubolazov, O.; Ushenko, Y.; Ushenko, V.; Bykov, A.; Deby, S.; Rehbinder, J.; Novikova, T.; Meglinski, I. Complementary analysis of Mueller-matrix images of optically anisotropic highly scattering biological tissues. J. Eur. Opt. Soc.-Rapid 2018, 14, 20. [Google Scholar] [CrossRef]
- Ushenko, V.; Sdobnov, A.; Syvokorovskaya, A.; Dubolazov, A.; Vanchulyak, O.; Ushenko, A.; Ushenko, Y.; Gorsky, M.; Sidor, M.; Bykov, A.; et al. 3D Mueller-matrix diffusive tomography of polycrystalline blood films for cancer diagnosis. Photonics 2018, 5, 54. [Google Scholar] [CrossRef]
- Dong, Y.; Qi, J.; He, H.; He, C.; Liu, S.; Wu, J.; Elson, D.S.; Ma, H. Quantitatively characterizing the microstructural features of breast ductal carcinoma tissues in different progression stages by Mueller matrix microscope. Biomed. Opt. Express 2017, 8, 3643–3655. [Google Scholar] [CrossRef]
- Chang, J.; Zeng, N.; He, H.; Guo, Y.; Ma, H. Removing the polarization artifacts in Mueller matrix images recorded with a birefringent gradient-index lens. J. Biomed. Opt. 2014, 19, 095001. [Google Scholar] [CrossRef]
- He, H.; Zeng, N.; Liao, R.; Yun, T.; Li, W.; He, Y.; Ma, H. Application of sphere-cylinder scattering model to skeletal muscle. Opt. Express 2010, 18, 15104–15112. [Google Scholar] [CrossRef]
- Du, E.; He, H.; Zeng, N.; Guo, Y.; Liao, R.; He, Y.; Ma, H. Two-dimensional backscattering Mueller matrix of sphere–cylinder birefringence media. J. Biomed. Opt. 2012, 17, 126016. [Google Scholar] [CrossRef] [PubMed]
- Yun, T.; Zeng, N.; Li, W.; Li, D.; Jiang, X.; Ma, H. Monte Carlo simulation of polarized photon scattering in anisotropic media. Opt. Express 2009, 17, 16590–16602. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, D.H.; Chipman, R.A. Mueller matrix ellipsometry with imperfect compensators. J. Opt. Soc. Am. A 1978, 68, 1519–1528. [Google Scholar]
- Goldstein, D.H.; Chipman, R.A. Error analysis of a Mueller matrix polarimeter. J. Opt. Soc. Am. A 1990, 7, 693–700. [Google Scholar] [CrossRef]
- Sun, T.; Liu, T.; He, H.; Wu, J.; Ma, H. Distinguishing anisotropy orientations originated from scattering and birefringence of turbid media using Mueller matrix derived parameters. Opt. Lett. 2018, 43, 4092–4095. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Sun, M.; Zeng, N.; Du, E.; Liu, S.; Guo, Y.; Wu, J.; He, Y.; Ma, H. Mapping local orientation of aligned fibrous scatterers for cancerous tissues using backscattering Mueller matrix imaging. J. Biomed. Opt. 2014, 19, 106007. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Zeng, N.; Li, W.; Yun, T.; Liao, R.; He, Y.; Ma, H. Two-dimensional backscattering Mueller matrix of sphere-cylinder scattering medium. Opt. Lett. 2010, 35, 2323–2325. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Zeng, N.; Du, E.; Guo, Y.; Li, D.; Liao, R.; Ma, H. A possible quantitative Mueller matrix transformation technique for anisotropic scattering media. Photon. Lasers Med. 2013, 2, 129–137. [Google Scholar] [CrossRef]
- Sun, M.; He, H.; Zeng, N.; Du, E.; Guo, Y.; Peng, C.; He, Y.; Ma, H. Probing microstructural information of anisotropic scattering media using rotation-independent polarization parameters. Appl. Opt. 2014, 53, 2949–2955. [Google Scholar] [CrossRef] [PubMed]
- Hidovic-Rowe, D.; Claridge, E. Modelling and validation of spectral reflectance for the colon. Phys. Med. Biol. 2005, 50, 1071–1093. [Google Scholar] [CrossRef] [PubMed]
- Maeda, T.; Arakawa, N.; Takahashi, M.; Aizu, Y. Monte Carlo simulation of spectral reflectance using a multilayered skin tissue model. Opt. Rev. 2010, 17, 223–229. [Google Scholar] [CrossRef]
- He, C.; He, H.; Li, X.; Chang, J.; Wang, Y.; Liu, S.; Zeng, N.; He, Y.; Ma, H. Quantitatively differentiating microstructures of tissues by frequency distributions of Mueller matrix images. J. Biomed. Opt. 2015, 20, 105009. [Google Scholar] [CrossRef] [PubMed]
- Pasquesi, J.J.; Schlachter, S.C.; Boppart, M.D.; Chaney, E.; Kaufman, S.J.; Boppart, S.A. In vivo detection of exercised-induced ultrastructural changes in genetically-altered murine skeletal muscle using polarization-sensitive optical coherence tomography. Opt. Express 2006, 14, 1547–1556. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).