Improving Diagnosis of Cervical Pre-Cancer: Combination of PCA and SVM Applied on Fluorescence Lifetime Images
Abstract
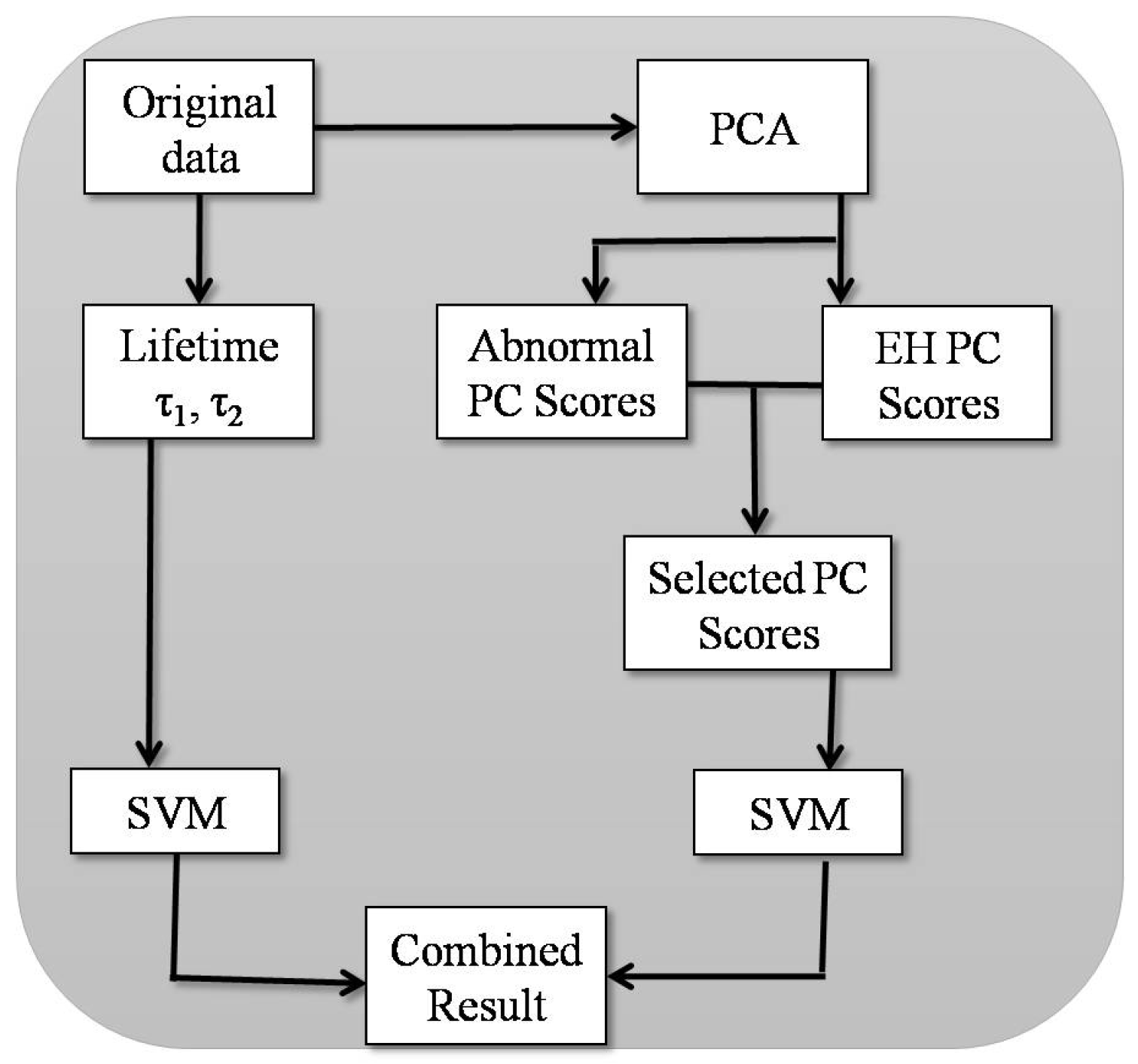
1. Introduction
2. Results
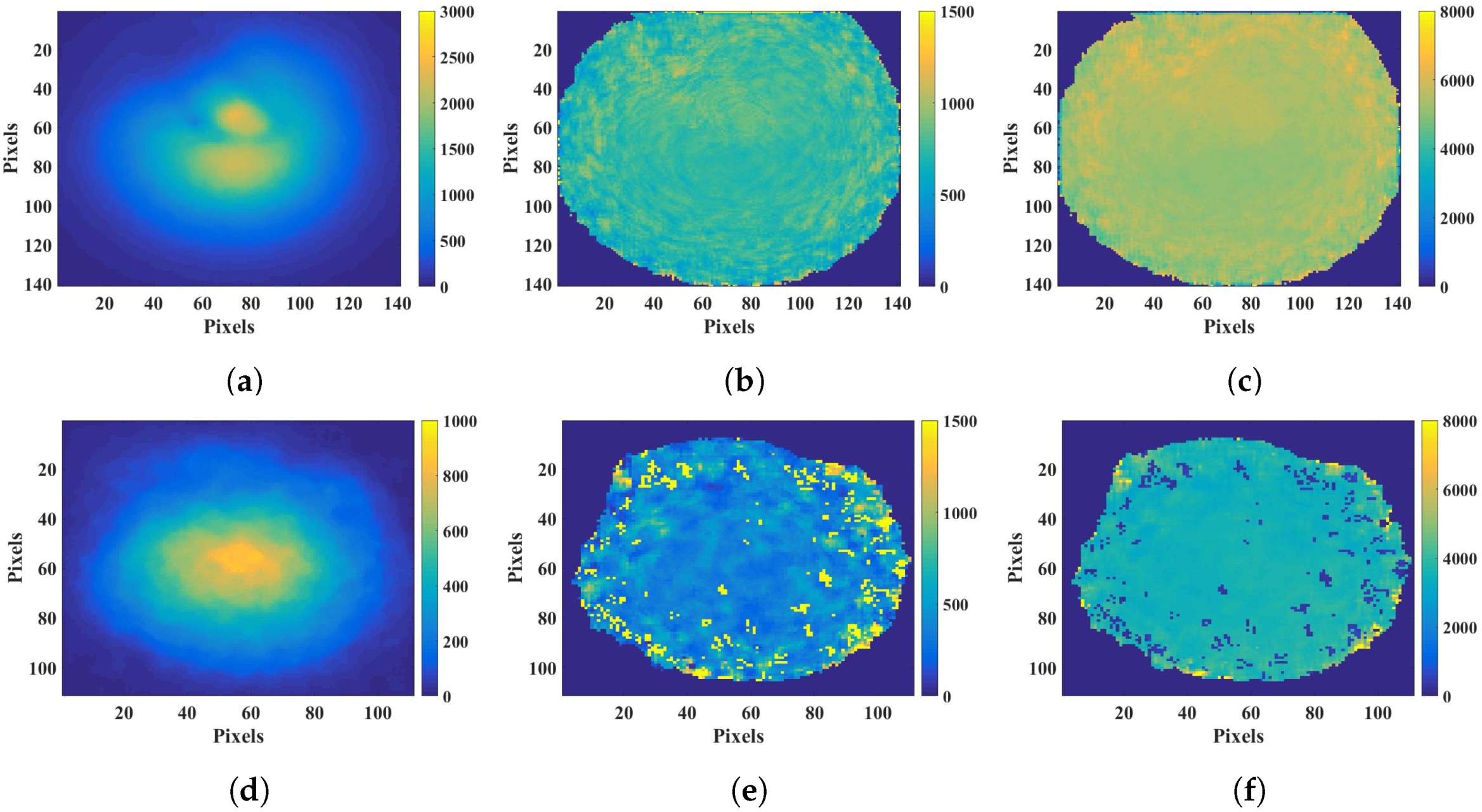
2.1. Fluorescence Lifetime
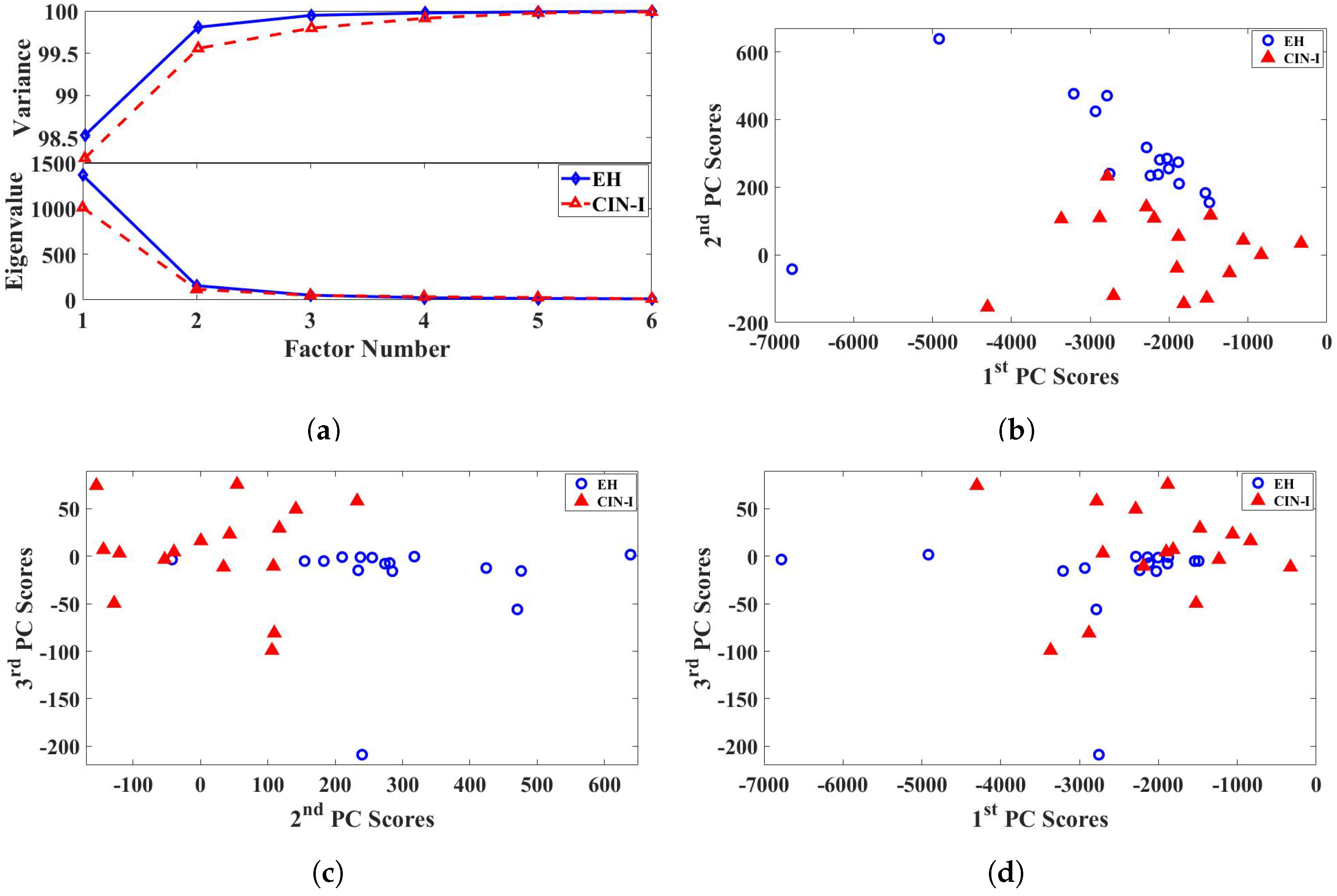
2.2. Principal Component Analysis
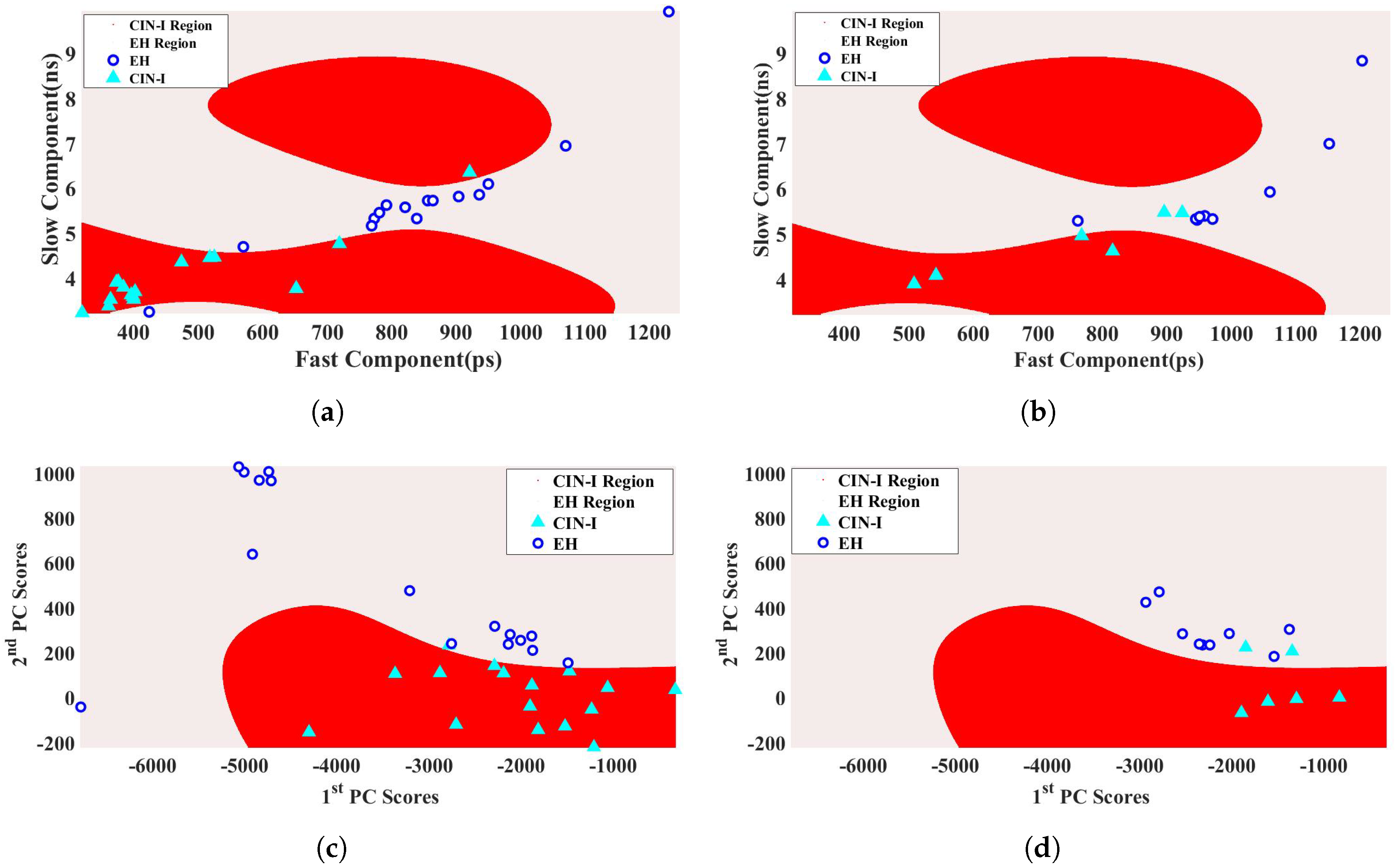
2.3. Support Vector Machine
3. Discussion
3.1. Fluorescence Lifetime
3.2. Principal Component Analysis
3.3. Support Vector Machine
4. Materials and Methods
4.1. Sample Collection
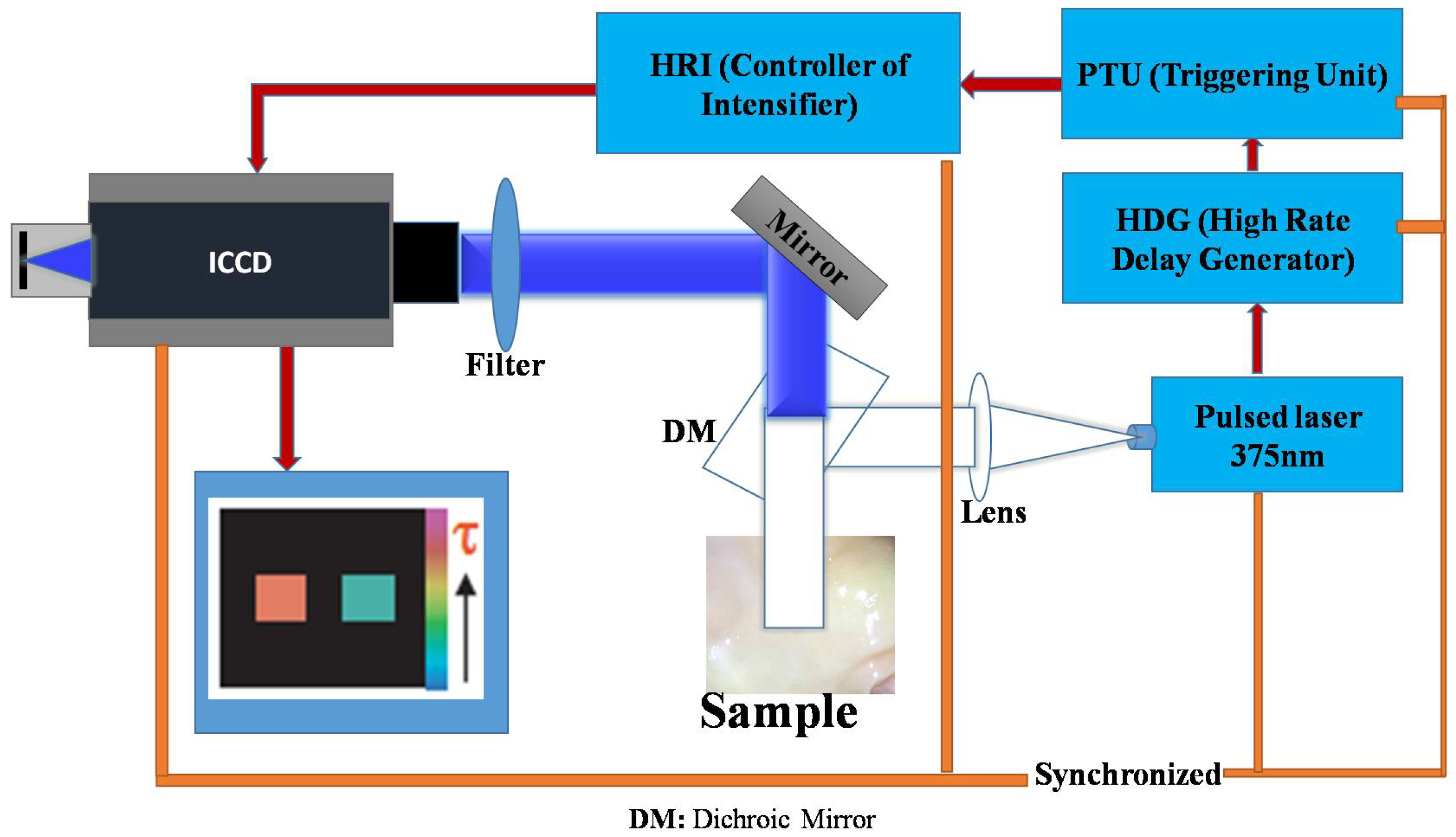
4.2. Data Collection
4.3. Data Analysis
4.3.1. Fluorescence Lifetime
4.3.2. Principal Component Analysis (PCA)
4.3.3. Support Vector Machine (SVM)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alfano, R.R.; Tata, D.B.; Cordero, J.; Tomashefsky, P.; Longo, F.; Alfano, M. Laser induced fluorescence spectroscopy from native cancerous and normal tissue. IEEE J. Quantum Electron. 1984, 20, 1507–1511. [Google Scholar] [CrossRef]
- Alfano, R.R.; Tang, G.C.; Pradhan, A.; Lam, W.; Choy, D.; Opher, E. Fluorescence spectra from cancerous and normal human breast and lung tissues. IEEE J. Quantum Electron. 1987, 23, 1806–1811. [Google Scholar] [CrossRef]
- Alfano, R.R.; Pradhan, A.; Tang, G.C.; Wahl, S.J. Optical spectroscopic diagnosis of cancer and normal breast tissues. JOSA B 1989, 6, 1015–1023. [Google Scholar] [CrossRef]
- Pu, Y.; Wang, W.; Yang, Y.; Alfano, R.R. Stokes shift spectroscopy highlights differences of cancerous and normal human tissues. Opt. Lett. 2012, 37, 3360–3362. [Google Scholar] [CrossRef] [PubMed]
- Heintzelman, D.L.; Utzinger, U.; Fuchs, H.; Zuluaga, A.; Gossage, K.; Gillenwater, A.M.; Jacob, R.; Kemp, B.; Richards-Kortum, R.R. Optimal Excitation Wavelengths for In Vivo Detection of Oral Neoplasia Using Fluorescence Spectroscopy. Photochem. Photobiol. 2000, 72, 103–113. [Google Scholar] [CrossRef]
- Brookner, C.K.; Utzinger, U.; Staerkel, G.; Richards-Kortum, R.R.; Mitchell, M.F. Cervical fluorescence of normal women. Lasers Surg. Med. 1999, 24, 29–37. [Google Scholar] [CrossRef]
- Grossman, N.; Ilovitz, E.; Chaims, O.; Salman, A.; Jagannathan, R.; Mark, S.; Cohen, B.; Gopas, J.; Mordechai, S. Fluorescence spectroscopy for detection of malignancy: H-ras overexpressing fibroblasts as a model. J. Biochem. Biophys. Methods 2001, 50, 53–63. [Google Scholar] [CrossRef]
- Pu, Y.; Wang, W.; Yang, Y.; Alfano, R.R. Stokes shift spectroscopic analysis of multifluorophores for human cancer detection in breast and prostate tissues. J. Biomed. Opt. 2013, 18, 017005. [Google Scholar] [CrossRef]
- Ramanujam, N.; Mitchell, M.F.; Mahadevan, A.; Warren, S.; Thomsen, S.; Silva, E.; Kortum, R.R. In vivo diagnosis of cervical intraepithelial neoplasia using 337-nm-excited laser-induced fluorescence. Proc. Natl. Acad. Sci. USA 1994, 91, 10193–10197. [Google Scholar] [CrossRef]
- Chidananda, S.M.; Satyamoorthy, K.; Rai, L.; Manjunath, A.P.; Kartha, V.B. Optical diagnosis of cervical cancer by fluorescence spectroscopy technique. Int. J. Cancer 2006, 119, 139–145. [Google Scholar] [CrossRef]
- Chang, S.K.; Mirabal, Y.N.; Atkinson, E.N.; Cox, D.D.; Malpica, A.; Mitchell, M.F.; Kortum, R.R. Combined reflectance and fluorescence spectroscopy for in vivo detection of cervical pre-cancer. J. Biomed. Opt. 2005, 10, 024031. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Papaioannou, T.; Jo, J.A.; Vaitha, R.; Shastry, K.; Marcu, L. Time-domain laser-induced fluorescence spectroscopy apparatus for clinical diagnostics. Rev. Sci. Instrum. 2004, 75, 151–162. [Google Scholar] [CrossRef]
- Pitts, J.D.; Mycek, M.A. Design and development of a rapid acquisition laser-based fluorometer with simultaneous spectral and temporal resolution. Rev. Sci. Instrum. 2001, 72, 3061–3072. [Google Scholar] [CrossRef]
- Mycek, M.A.; Schomacker, K.T.; Nishioka, N.S. Colonic polyp differentiation using time-resolved autofluorescence spectroscopy. Gastrointest. Endosc. 1998, 48, 390–394. [Google Scholar] [CrossRef]
- Elson, D.; Requejo-Isidro, J.; Munro, I.; Reavell, F.; Siegel, J.; Suhling, K.; Tadrous, P.; Benninger, R.; Lanigan, P.; McGinty, J.; et al. Time-domain fluorescence lifetime imaging applied to biological tissue. Photochem. Photobiol. Sci. 2004, 3, 795–801. [Google Scholar] [CrossRef] [PubMed]
- Vishwanath, K.; Pogue, B.; Mycek, M.A. Quantitative fluorescence lifetime spectroscopy in turbid media: Comparison of theoretical, experimental and computational methods. Phys. Med. Biol. 2002, 47, 3387. [Google Scholar] [CrossRef]
- Pradhan, A.; Das, B.B.; Yoo, K.M.; Cleary, J.; Prudente, R.; Celmer, E.; Alfano, R.R. Time-resolved UV photoexcited fluorescence kinetics from malignant and non-malignant human breast tissues. Lasers Life Sci. 1992, 4, 225–234. [Google Scholar]
- Tata, D.B.; Foresti, M.; Cordero, J.; Tomashefsky, P.; Alfano, M.A.; Alfano, R.R. Fluorescence polarization spectroscopy and time-resolved fluorescence kinetics of native cancerous and normal rat kidney tissues. Biophys. J. 1986, 50, 463–469. [Google Scholar] [CrossRef]
- Tadrous, P.J.; Siegel, J.; French, P.M.; Shousha, S.; Lalani EN Stamp, G.W. Fluorescence lifetime imaging of unstained tissues: Early results in human breast cancer. J. Pathol. 2003, 199, 309–317. [Google Scholar] [CrossRef]
- Das, B.; Shi, L.; Budansky, Y.; Rodriguez-Contreras, A.; Alfano, R. Alzheimer mouse brain tissue measured by time resolved fluorescence spectroscopy using single-and multi-photon excitation of label free native molecules. J. Biophotonics 2018, 11, 201600318. [Google Scholar] [CrossRef]
- Sun, Y.; Phipps, J.; Elson, D.S.; Stoy, H.; Tinling, S.; Meier, J.; Poirier, B.; Chuang, F.S.; Farwell, D.G.; Marcu, L. Fluorescence lifetime imaging microscopy: In vivo application to diagnosis of oral carcinoma. Opt. Lett. 2009, 34, 2081–2083. [Google Scholar] [CrossRef] [PubMed]
- Kalaivani, R.; Masilamani, V.; AlSalhi, M.S.; Devanesan, S.; Ramamurthy, P.; Palled, S.R.; Ganesh, K.M. Cervical cancer detection by time-resolved spectra of blood components. J. Biomed. Opt. 2014, 19, 057011. [Google Scholar] [CrossRef]
- Gu, J.; Fu, C.Y.; Ng, B.K.; Liu, L.B.; Lim-Tan, S.K.; Lee, C.G.L. Enhancement of early cervical cancer diagnosis with epithelial layer analysis of fluorescence lifetime images. PLoS ONE 2015, 10, 0125706. [Google Scholar] [CrossRef] [PubMed]
- Evan Gerard, I.; Karen, H.V. Proliferation, cell cycle and apoptosis in cancer. Nature 2001, 411, 342. [Google Scholar] [CrossRef] [PubMed]
- Drezek, R.A.; Guillaud, M.; Collier, T.G.; Boiko, I.; Malpica, A.; MacAulay, C.E.; Richards-Kortum, R.R. Light scattering from cervical cells throughout neoplastic progression: Influence of nuclear morphology, DNA content, and chromatin texture. J. Biomed. Opt. 2003, 8, 7–17. [Google Scholar] [CrossRef] [PubMed]
- Devi, S.; Panigrahi, P.K.; Pradhan, A. Detecting cervical cancer progression through extracted intrinsic fluorescence and principal component analysis. J. Biomed. Opt. 2014, 19, 127003. [Google Scholar] [CrossRef] [PubMed]
- Georgakoudi, I.; Jacobson, B.C.; Müller, M.G.; Sheets, E.E.; Badizadegan, K.; Carr-Locke, D.L.; Crum, C.P.; Boone, C.W.; Dasari, R.R.; Van Dam, J.; et al. NAD (P) H and collagen as in vivo quantitative fluorescent biomarkers of epithelial precancerous changes. Cancer Res. 2002, 62, 682–687. [Google Scholar]
- Alfano, R.R. Advances in ultrafast time resolved fluorescence physics for cancer detection in optical biopsy. AIP Adv. 2012, 2, 011103. [Google Scholar] [CrossRef]
- Singh, P.; Sahoo, G.R.; Pradhan, A. Spatio-temporal map for early cancer detection: Proof of concept. J. Biophotonics 2018. [Google Scholar] [CrossRef]
- Drezek, R.A.; Sokolov, K.V.; Utzinger, U.; Boiko, I.; Malpica, A.; Mitchell, M.F.; Richards-Kortum, R.R. Understanding the contributions of NADH and collagen to cervical tissue fluorescence spectra: Modeling, measurements, and implications. J. Biomed. Opt. 2001, 6, 385–397. [Google Scholar] [CrossRef]
- Kamath, S.D.; Bhat, R.A.; Ray, S.; Mahato, K.K. Autofluorescence of normal, benign, and malignant ovarian tissues: A pilot study. Photomed. Laser Surg. 2009, 27, 325–335. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.; An, Y.; Lee, J.; Ku, T.; Kang, Y.; Ahn, C.W.; Choi, C. Principal component analysis of dynamic fluorescence images for diagnosis of diabetic vasculopathy. J. Biomed. Opt. 2016, 21, 046003. [Google Scholar] [CrossRef]
- Pu, H.; He, W.; Zhang, G.; Zhang, B.; Liu, F.; Zhang, Y.; Luo, J.; Bai, J. Separating structures of different fluorophore concentrations by principal component analysis on multispectral excitation-resolved fluorescence tomography images. Biomed. Opt. Express 2013, 4, 1829–1845. [Google Scholar] [CrossRef] [PubMed]
- Hillman, E.M.; Moore, A. All-optical anatomical co-registration for molecular imaging of small animals using dynamic contrast. Nat. Photonics 2007, 1, 526. [Google Scholar] [CrossRef]
- Welshe, K.; Sherlock, S.P.; Dai, H. Deep-tissue anatomical imaging of mice using carbon nanotube fluorophores in the second near-infrared window. Appl. Phys. Sci. 2011, 108, 8943–8948. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D.; Liu, F.; Bai, J. Principal component analysis of dynamic fluorescence diffuse optical tomography images. Opt. Express 2010, 18, 6300–6314. [Google Scholar] [CrossRef]
- Cortes, C.; Vladimir, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chapelle, O.; Vapnik, V.; Bengio, Y. Model selection for small sample regression. Mach. Learn. 2002, 48, 9–23. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, Y.F. FS SFS A novel feature selection method for support vector machines. Common. Comput. Inf. Sci. 2006, 39, 1333–1345. [Google Scholar] [CrossRef]
- Acir, N. A support vector machine classifier algorithm based on a perturbation method and its application to ECG beat recognition systems. Expert Syst. Appl. 2006, 31, 150–158. [Google Scholar] [CrossRef]
- Rejani, Y.; Selvi, S.T. Early detection of breast cancer using SVM classifier technique. Int. J. Comput. Sci. Eng. 2009, 1, 127–130. [Google Scholar]
- Majumder, S.K.; Ghosh, N.; Gupta, P.K. Support vector machine for optical diagnosis of cancer. J. Biomed. Opt. 2005, 10, 024034. [Google Scholar] [CrossRef] [PubMed]
- Mukhopadhyay, S.; Kurmi, I.; Dey, R.; Das, N.K.; Pradhan, S.; Pradhan, A.; Ghosh, N.; Panigrahi, P.K.; Mohanty, S. Optical diagnosis of colon and cervical cancer by support vector machine. In Biophotonics: Photonic Solutions for Better Health Care V; SPIE Photonics Europe: Brussels, Belgium, 2016; Volume 9887. [Google Scholar]
- Girosi, F.; Jones, M.; Poggio, T. Regularization theory and neural networks architectures. Neural Comput. 1995, 7, 219–269. [Google Scholar] [CrossRef]
- Smola, A.J.; Scholkopf, B.; Muller, K.R. The connection between regularization operators and support vector kernels. Neural Netw. 1998, 11, 637–649. [Google Scholar] [CrossRef]
- Lee, K.C.; Siegel, J.; Webb, S.E.D.; Leveque-Fort, S.; Cole, M.J.; Jones, R.; Dowling, K.; Lever, M.J.; French, P.M.W. Application of the stretched exponential function to fluorescence lifetime imaging. Biophys. J. 2001, 81, 1265–1274. [Google Scholar] [CrossRef]

| Linear | Polynomial Kernel (Order-3) | RBF Kernel | |
|---|---|---|---|
| Accuracy | 81 | 84 | 84 |
| Precission | 92 | 100 | 100 |
| Sensitivity | 92 | 100 | 100 |
| Specificity | 93 | 100 | 100 |
| Sensitivity Training | Specificity Training | Sensitivity Validation | Specificity Validation | |
|---|---|---|---|---|
| Lifetime | 100 | 100 | 60 | 100 |
| PCA | 100 | 100 | 67 | 100 |
| Combined result | 100 | 100 | 87 | 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahoo, G.R.; Singh, P.; Pandey, K.; Kala, C.; Pradhan, A. Improving Diagnosis of Cervical Pre-Cancer: Combination of PCA and SVM Applied on Fluorescence Lifetime Images. Photonics 2018, 5, 57. https://doi.org/10.3390/photonics5040057
Sahoo GR, Singh P, Pandey K, Kala C, Pradhan A. Improving Diagnosis of Cervical Pre-Cancer: Combination of PCA and SVM Applied on Fluorescence Lifetime Images. Photonics. 2018; 5(4):57. https://doi.org/10.3390/photonics5040057
Chicago/Turabian StyleSahoo, Gyana Ranjan, Pankaj Singh, Kiran Pandey, Chayanika Kala, and Asima Pradhan. 2018. "Improving Diagnosis of Cervical Pre-Cancer: Combination of PCA and SVM Applied on Fluorescence Lifetime Images" Photonics 5, no. 4: 57. https://doi.org/10.3390/photonics5040057
APA StyleSahoo, G. R., Singh, P., Pandey, K., Kala, C., & Pradhan, A. (2018). Improving Diagnosis of Cervical Pre-Cancer: Combination of PCA and SVM Applied on Fluorescence Lifetime Images. Photonics, 5(4), 57. https://doi.org/10.3390/photonics5040057





