Propagation of Cylindrical Vector Laser Beams in Turbid Tissue-Like Scattering Media
Abstract
1. Introduction
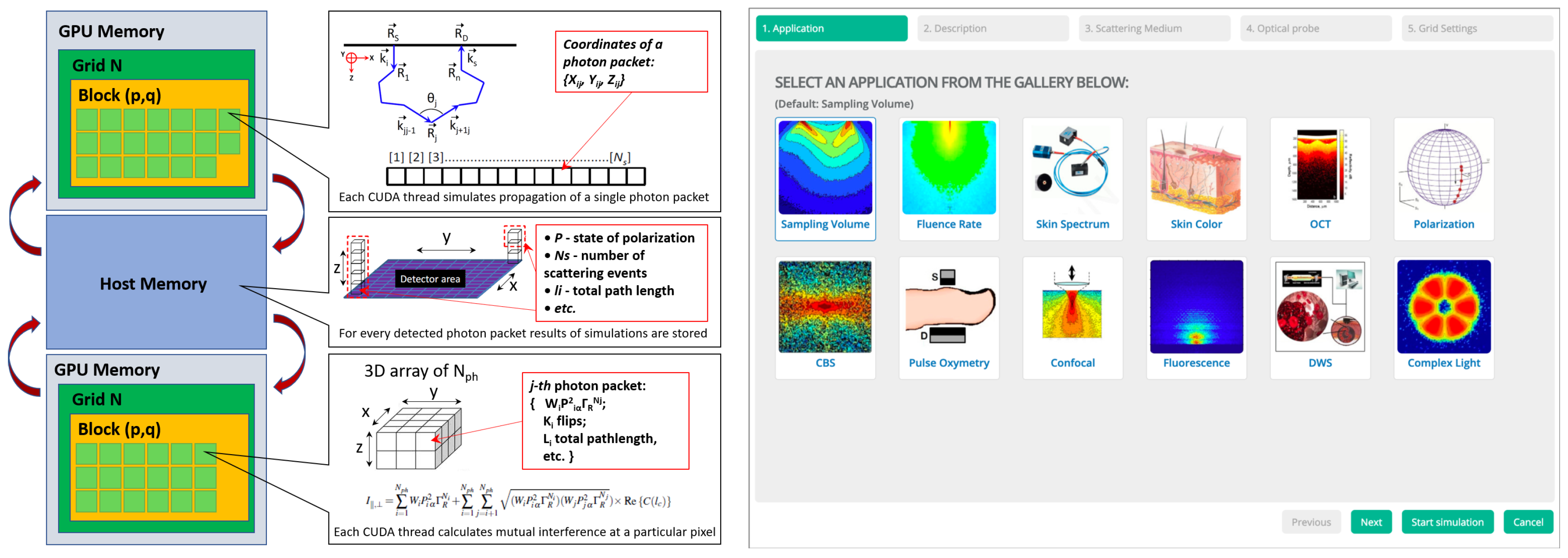
2. Online GPU-Accelerated Monte Carlo Modeling of Photon Migration in Scattering Media
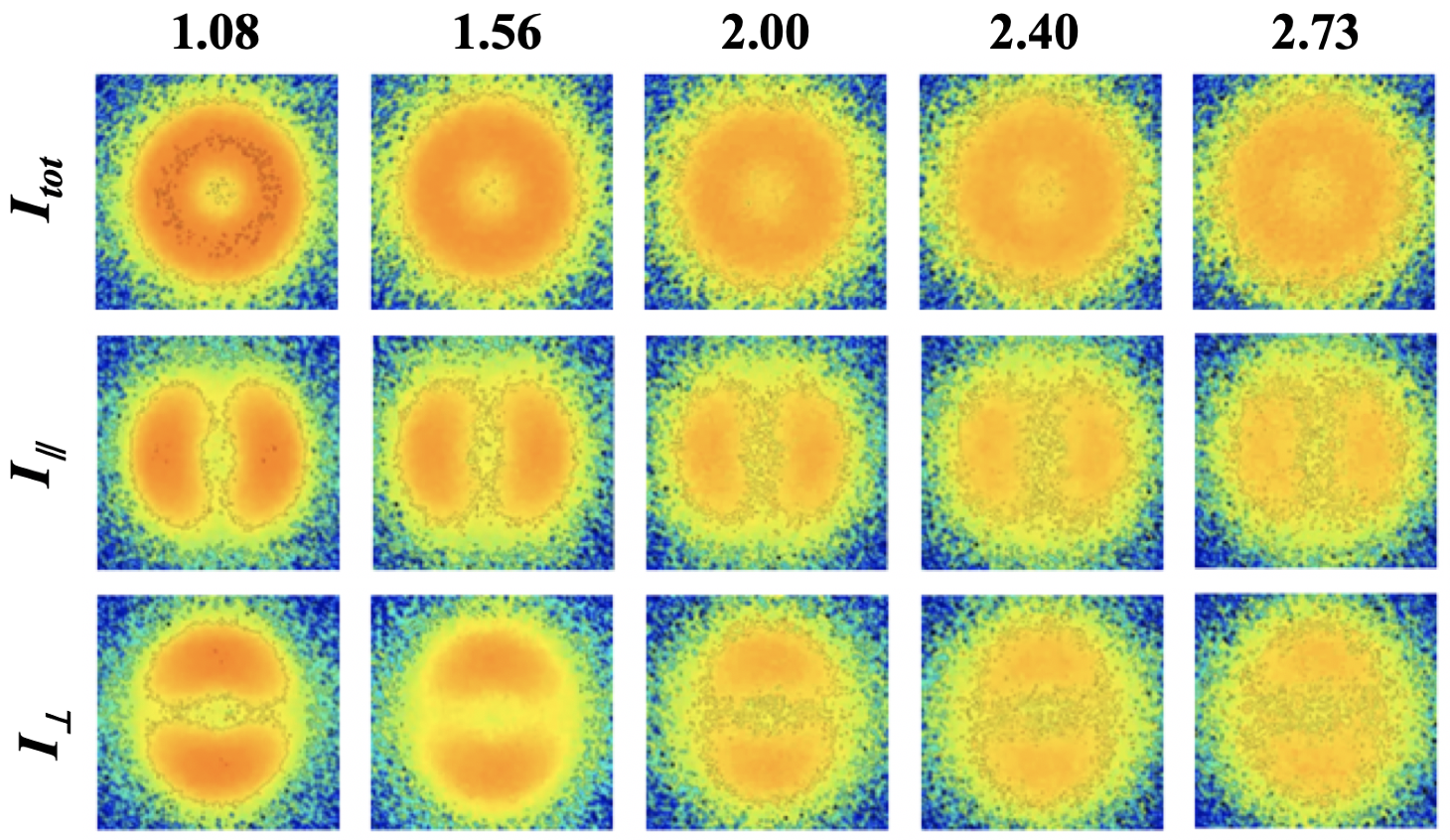
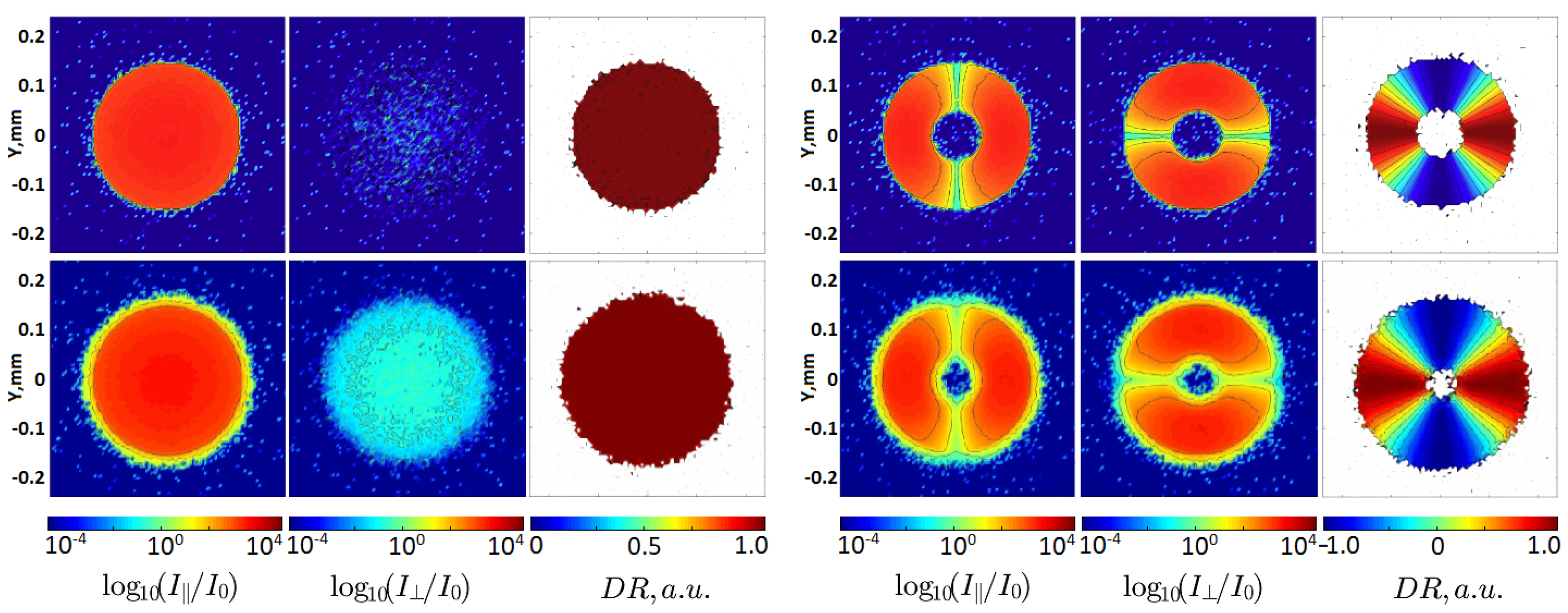
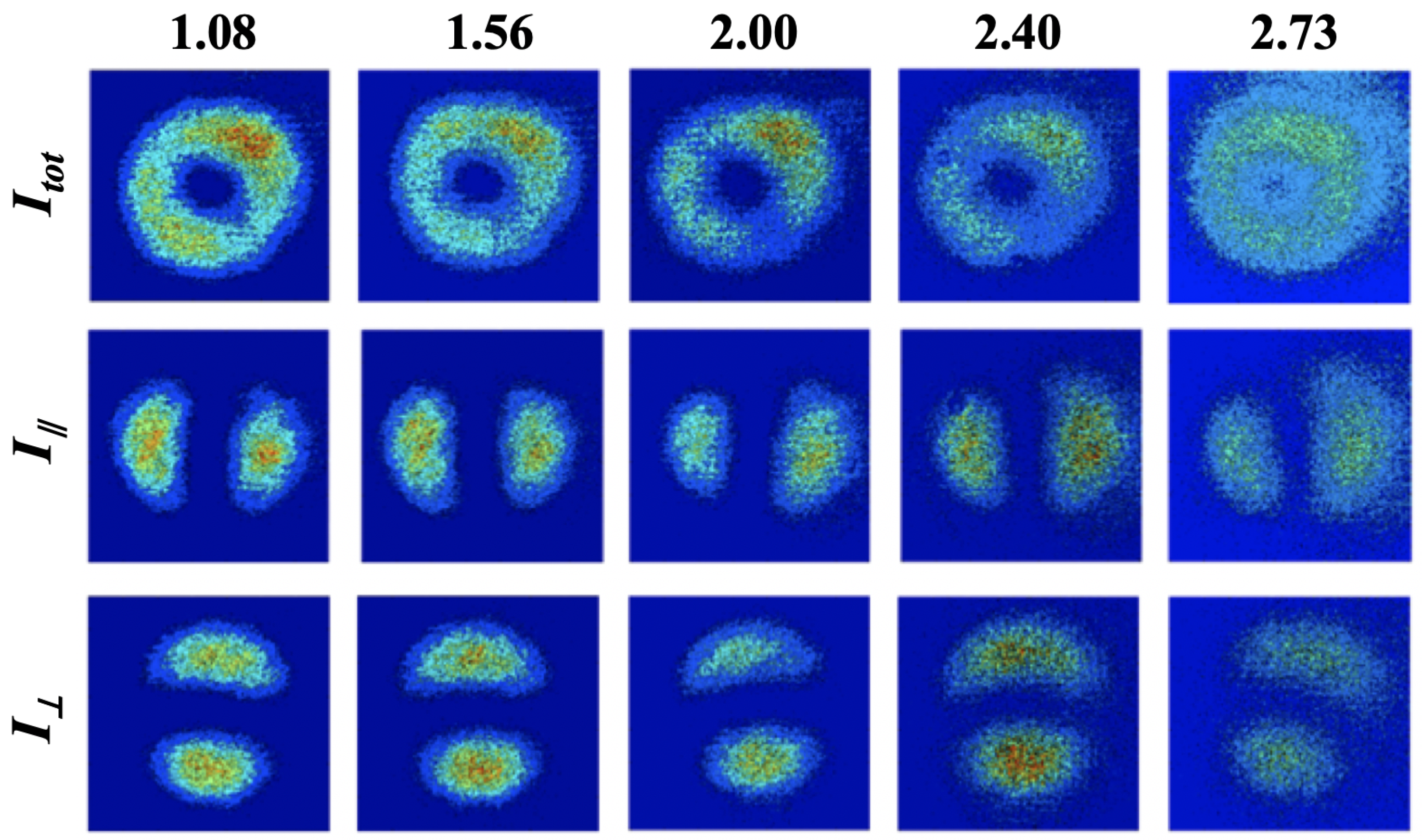
3. Results and Discussion
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tuchin, V. (Ed.) Handbook of Optical Biomedical Diagnostics; SPIE Press: Washington, DC, USA, 2002; Volume PM107. [Google Scholar]
- Evers, D.; Hendriks, B.; Lucassen, G.; Ruers, T. Optical spectroscopy: Current advances and future applications in cancer diagnostics and therapy. Future Oncol. 2012, 8, 307–320. [Google Scholar] [CrossRef] [PubMed]
- Alfano, R.; Tata, D.; Cordero, J.; Tomashefsky, P.; Longo, F.; Alfano, M. Laser induced fluorescence spectroscopy from native cancerous and normal tissue. IEEE J. Quantum Electron. 1984, 20, 1507–1511. [Google Scholar] [CrossRef]
- Alfano, R.; Tang, G.; Pradhan, A.; Lam, W.; Choy, D.; Opher, E. Fluorescence spectra from cancerous and normal human breast and lung tissues. IEEE J. Quantum Electron. 1987, 23, 1806–1811. [Google Scholar] [CrossRef]
- Liu, C.H.; Alfano, R.R.; Sha, W.L.; Zhu, H.R.; Akins, D.L.; Cleary, J.; Prudente, R.; Cellmer, E. Human breast tissues studied by IR Fourier-transform Raman spectroscopy. In Proceedings of the Conference on Lasers and Electro-Optics, Baltimore, MD, USA, 12–17 May 1991; p. CWF51. [Google Scholar]
- Abramczyk, A.; Brozek-Pluska, B.; Surmacki, J.; Jablonska-Gajewicz, J.; Kordek, R. Raman optical biopsy of human breast cancer. Prog. Biophys. Mol. Biol. 2012, 108, 74–81. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zhou, Y.; Sun, Y.; Li, J.Y.; Zhou, L.X.; Boydston-White, S.; Masilamani, V.; Zhu, K.; Pu, Y.; Alfano, R.R. Resonance Raman and Raman Spectroscopy for Breast Cancer Detection. Technol. Cancer Res. Treat. 2013, 12, 371–382. [Google Scholar] [CrossRef]
- Wu, B.; Smith, J.; Zhang, L.; Gao, X.; Alfano, R.R. Characterization and discrimination of human breast cancer and normal breast tissues using resonance Raman spectroscopy. Proc. SPIE 2018, 10489, 104890X. [Google Scholar]
- Lu, L.; Shi, L.; Secor, J.; Alfano, R. Resonance Raman scattering of beta-carotene solution excited by visible laser beams into second singlet state. J. Photochem. Photobiol. B Biol. 2018, 179, 18–22. [Google Scholar] [CrossRef]
- Ghosh, N.; Vitkin, I. Tissue polarimetry: Concepts, challenges, applications and outlook. J. Biomed. Opt. 2011, 16, 110801. [Google Scholar] [CrossRef]
- Tuchin, V.; Wang, L.; Zimnyakov, D. (Eds.) Optical Polarization in Biomedical Applications; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Tuchin, V. Handbook of Coherent-Domain Optical Methods, Biomedical Diagnostics, Environmental Monitoring and Material Science; Springer: New York, NY, USA, 2013. [Google Scholar]
- Mishchenko, M.; Yatskiv, Y.; Rosenbush, V.; Videen, G. Polarimetric Detection, Characterization and Remote Sensing. In Mueller Matrix Characterization of Biological Tissues; Svaenkov, S., Ed.; NATO Science for Peace and Security Series C: Environmental Security; Springer: Dordrecht, The Netherlands, 2011; pp. 437–472. [Google Scholar]
- Pierangelo, A.; Nazac, A.; Benali, A.; Validire, P.; Cohen, H.; Novikova, T.; Ibrahim, B.H.; Manhas, S.; Fallet, C.; Antonelli, M.R.; et al. Polarimetric imaging of uterine cervix: A case study. Opt. Express 2013, 21, 14120–14130. [Google Scholar] [CrossRef]
- Kunnen, B.; Macdonald, C.; Doronin, A.; Jacques, S.; Eccles, M.; Meglinski, I. Application of circularly polarized light for non-invasive diagnosis of cancerous tissues and turbid tissue-like scattering media. J. Biophotonics 2015, 8, 317–323. [Google Scholar] [CrossRef]
- Torres, J.; Torner, L. Twisted Photons: Applications of Light with Orbital Angular Momentum, 1st ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2011. [Google Scholar]
- Cheng, W.; Haus, J.W.; Zhan, Q. Propagation of vector vortex beams through a turbulent atmosphere. Opt. Express 2009, 17, 17829–17836. [Google Scholar] [CrossRef] [PubMed]
- Han, W.; Yang, Y.; Cheng, W.; Zhan, Q. Vectorial optical field generator for the creation of arbitrarily complex fields. Opt. Express 2013, 21, 20692–20706. [Google Scholar] [CrossRef]
- Milione, G.; Nguyen, T.; Leach, J.; Nolan, D.; Alfano, R. Using the nonseparability of vector beams to encode information for optical communication. Opt. Lett. 2015, 40, 4887–4890. [Google Scholar] [CrossRef]
- Mamani, S.; Shi, L.; Ahmed, T.; Karnik, R.; Rodríguez-Contreras, A.; Nolan, D.; Alfano, R. Transmission of classically entangled beams through mouse brain tissue. J. Biophotonics 2018, 11, e201800096. [Google Scholar] [CrossRef] [PubMed]
- Milione, G.; Sztul, H.I.; Nolan, D.A.; Alfano, R.R. Higher-Order Poincaré Sphere, Stokes Parameters, and the Angular Momentum of Light. Phys. Rev. Lett. 2011, 107, 053601. [Google Scholar] [CrossRef]
- Milione, G.; Sztul, H.I.; Nolan, D.A.; Alfano, R.R. Higher Order Pancharatnam-Berry Phase and the Angular Momentum of Light. Phys. Rev. Lett. 2012, 108, 190401. [Google Scholar] [CrossRef]
- Brosseau, C. Fundamentals of Polarized Light: A Statistical Optics Approach; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Kuzmin, V.; Meglinski, I. Numerical simulation of coherent back-scattering and temporal intensity correlations in random media (Overview). Quantum Electron. 2006, 36, 990–1002. [Google Scholar] [CrossRef]
- Rojas-Ochoa, L.; Lacoste, D.; Lenke, R.; Schurtenberger, P.; Schefford, F. Depolarization of backscattered linearly polarized light. J. Opt. Soc. Am. A 2004, 21, 1799–1804. [Google Scholar] [CrossRef]
- Sawicki, J.; Kastor, N.; Xu, M. Electric field Monte Carlo simulation of coherent backscattering of polarized light by a turbid medium containing Mie scatterers. Opt. Express 2008, 16, 5728–5738. [Google Scholar] [CrossRef]
- Radosevich, A.; Rogers, J.; Capoglu, I.; Mutyal, N.; Pradhan, P.; Backman, V. Open source software for electric field Monte Carlo simulation of coherent backscattering in biological media containing birefringence. J. Biomed. Opt. 2012, 17, 115001. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.; Zheng, L. MCML—Monte Carlo modelling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L. Propagation of polarized light in birefringent turbid media: A Monte Carlo study. J. Biomed. Opt. 2002, 7, 279–290. [Google Scholar] [CrossRef]
- Gangnus, S.; Matcher, S.; Meglinski, I. Monte Carlo modeling of polarized light propagation in biological tissues. Laser Phys. 2004, 14, 1–6. [Google Scholar]
- Ramella-Roman, J.; Prahl, S.; Jacques, S. Three Monte Carlo programs of polarized light transport into scattering media: Part I. Opt. Express 2005, 13, 4420–4438. [Google Scholar] [CrossRef]
- Doronin, A.; Radosevich, A.; Backman, V.; Meglinski, I. Two electric field Monte Carlo models of coherent backscattering of polarized light. J. Opt. Soc. Am. A 2014, 31, 2394–2400. [Google Scholar] [CrossRef]
- Doronin, A.; Meglinski, I. Online object oriented Monte Carlo computational tool for the needs of biomedical optics. Biomed. Opt. Express 2011, 2, 2461–2469. [Google Scholar] [CrossRef]
- Doronin, A.; Meglinski, I. Peer-to-Peer Monte Carlo simulation of photon migration in topical applications of biomedical optics. J. Biomed. Opt. 2012, 17, 090504. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Alfano, R.R. Circular polarization memory of light. Phys. Rev. E 2005, 72, 065601. [Google Scholar] [CrossRef]
- Sobol’, I. The Monte Carlo Method; The University of Chicago Press: Chicago, IL, USA, 1974. [Google Scholar]
- Wilson, B.; Adam, G. A Monte Carlo model for the absorption and flux distributions of light in tissue. Med. Phys. 1983, 10, 824–830. [Google Scholar] [CrossRef]
- Prahl, S.; Keijzer, M.; Jacques, S.; Welch, A. A Monte Carlo model of light propagation in tissue. In SPIE Proceedings of Dosimetry of Laser Radiation in Medicine and Biology; Muller, G., Sliney, D., Eds.; Plenum Press: New York, NY, USA, 1989; Volume IS 5, pp. 102–111. [Google Scholar]
- Keijzer, M.; Jacques, S.; Prahl, S.; Welch, A. Light distributions in artery tissue: Monte Carlo simulations for finite-diameter laser beams. Lasers Surg. Med. 1989, 9, 148–154. [Google Scholar] [CrossRef]
- Feng, S.; Fanan, Z.; Chance, B. Monte Carlo simulations of photon migration path distributions in multiple scattering media. Proc. SPIE 1993, 1888, 78–89. [Google Scholar]
- Zhu, C.; Liu, Q. Review of Monte Carlo modeling of light transport in tissues. J. Biomed. Opt. 2013, 18, 050902. [Google Scholar] [CrossRef]
- Henyey, L.; Greenstein, J. Diffuse radiation in the galaxy. Astrophys. J. 1941, 93, 70–83. [Google Scholar] [CrossRef]
- Kirk, D.B.; Hwu, W. Programming Massively Parallel Processors: A Hands-On Approach; MK Publishers: Burlington, MA, USA, 2010. [Google Scholar]
- Jones, R. A new calculus for the treatment of optical systems. I. Description and discussion of the new calculus. J. Opt. Soc. Am. 1941, 31, 488–493. [Google Scholar] [CrossRef]
- Jones, R. A new calculus for the treatment of optical systems. II. Description and discussion of the new calculus. J. Opt. Soc. Am. 1941, 31, 493–499. [Google Scholar] [CrossRef]
- Gerald, A.; Burch, J. Introduction to Matrix Methods in Optics, 1st ed.; John Wiley & Sons: London, UK, 1975. [Google Scholar]
- Collett, E. The Essential Guide to Image Processing, 2nd ed.; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Rossum, M.; Nieuwenhuizen, T. Multiple scattering of classical waves: Microscopy, mesoscopy, and diffusion. Rev. Mod. Phys. 1999, 71, 313–370. [Google Scholar] [CrossRef]
- Case, K.; Zweifel, P. Mesoscopic Physics of Electrons and Photons; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Carney, P.; Wolf, E.; Agarwal, G. Statistical generalizations of the optical cross-section theorem with application to inverse scatter. J. Opt. Soc. Am. A 1997, 14, 3366–3371. [Google Scholar] [CrossRef]
- Kuzmin, V.; Meglinski, I. Coherent effects of multiple scattering for scalar and electromagnetic fields: Monte-Carlo simulation and Milne-like solutions. Opt. Commun. 2007, 273, 307–310. [Google Scholar] [CrossRef]
- Churmakov, D.; Meglinski, I.; Greenhalgh, D. Influence of refractive index matching on the photon diffuse reflectance. Phys. Med. Biol. 2002, 47, 4271–4285. [Google Scholar] [CrossRef]
- Al-Qasimi, A.; Korotkova, O.; James, D.; Wolf, E. Definitions of the Degree of Polarization of a Light Beam. Opt. Lett. 2007, 32, 1015–1016. [Google Scholar] [CrossRef]
- Pedrotti, F.; Pedrotti, L.; Pedrotti, L. Introduction to Optics, 3rd ed.; Pearson: London, UK, 2007. [Google Scholar]
- Berrocal, E.; Meglinski, I.V.; Greenhalgh, D.A.; Linne, M.A. Image transfer through the complex scattering turbid media. Laser Phys. Lett. 2006, 3, 464–468. [Google Scholar] [CrossRef]
- Wang, W.; Gozali, R.; Shi, L.; Lindwasser, L.; Alfano, R. Deep transmission of Laguerre-Gaussian vortex beams through turbid scattering media. Opt. Lett. 2016, 41, 2069–2072. [Google Scholar] [CrossRef]
- Amic, E.; Luck, J.; Nieuwenhuizen, T.M. Anisotropic multiple scattering in diffusive media. J. Phys. A Math. Gen. 1996, 29, 4915–4955. [Google Scholar] [CrossRef]
- Nieuwenhuizen, T.; Luck, J. Skin layer of diffusive media. Phys. Rev. E 1993, 48, 569–588. [Google Scholar] [CrossRef]
- Kuzmin, V.; Aksenova, E. A generalized Milne solution for the correlation effects of multiple light scattering with polarization. J. Exp. Theor. Phys. 2003, 96, 816–831. [Google Scholar] [CrossRef]
- Kuzmin, V. The Milne problem solution for the temporal correlation function of an electromagnetic field. Opt. Spectrosc. 2002, 93, 439–448. [Google Scholar] [CrossRef]
- Rosalez-Guzmán, C.; Bhebhe, N.; Forbes, A. Simultaneous generation of multiple vector beams on a single SLM. Opt. Express 2017, 25, 25697. [Google Scholar] [CrossRef] [PubMed]


| References | |||
|---|---|---|---|
| Milne solution [57,58] | 3.025 | 1.563 | 1.935 |
| Kuzmin et al. [59,60] | 3.029 | 1.570 | 1.929 |
| Our MC model | 3.023 | 1.565 | 1.931 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doronin, A.; Vera, N.; Staforelli, J.P.; Coelho, P.; Meglinski, I. Propagation of Cylindrical Vector Laser Beams in Turbid Tissue-Like Scattering Media. Photonics 2019, 6, 56. https://doi.org/10.3390/photonics6020056
Doronin A, Vera N, Staforelli JP, Coelho P, Meglinski I. Propagation of Cylindrical Vector Laser Beams in Turbid Tissue-Like Scattering Media. Photonics. 2019; 6(2):56. https://doi.org/10.3390/photonics6020056
Chicago/Turabian StyleDoronin, Alexander, Nicolás Vera, Juan P. Staforelli, Pablo Coelho, and Igor Meglinski. 2019. "Propagation of Cylindrical Vector Laser Beams in Turbid Tissue-Like Scattering Media" Photonics 6, no. 2: 56. https://doi.org/10.3390/photonics6020056
APA StyleDoronin, A., Vera, N., Staforelli, J. P., Coelho, P., & Meglinski, I. (2019). Propagation of Cylindrical Vector Laser Beams in Turbid Tissue-Like Scattering Media. Photonics, 6(2), 56. https://doi.org/10.3390/photonics6020056







