The Influence of Traps on the Self-Heating Effect and THz Response of GaN HEMTs
Abstract
1. Introduction
2. Materials and Methods
- Under-thinned layers (<25 nm) yield weak built-in fields, reducing 2DEG concentration and degrading conduction;
- Over-thickened layers (>25 nm) diminish gate control efficacy, attenuating the terahertz response.
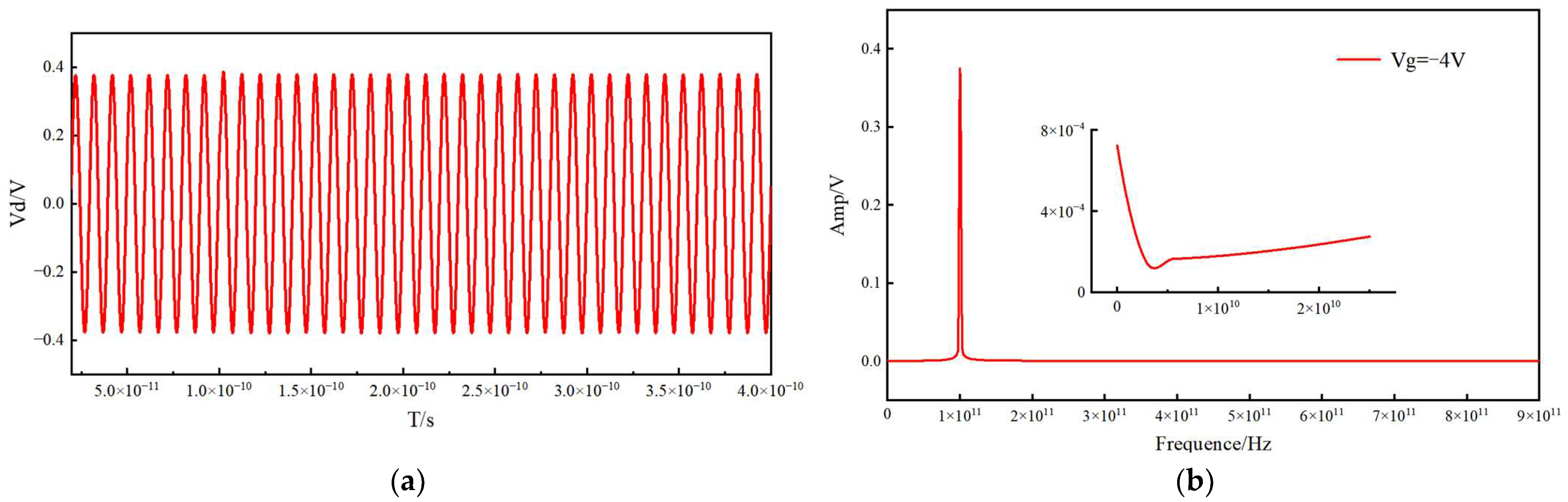
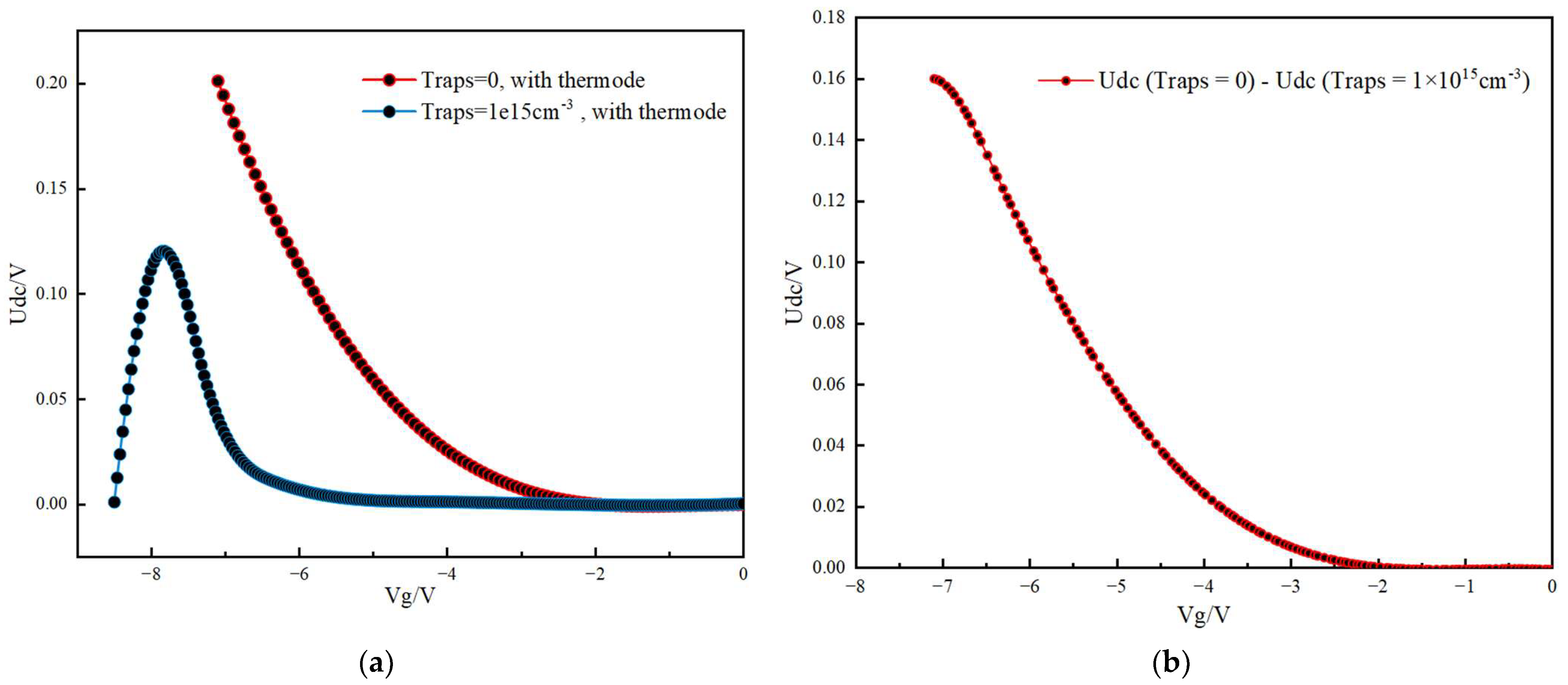
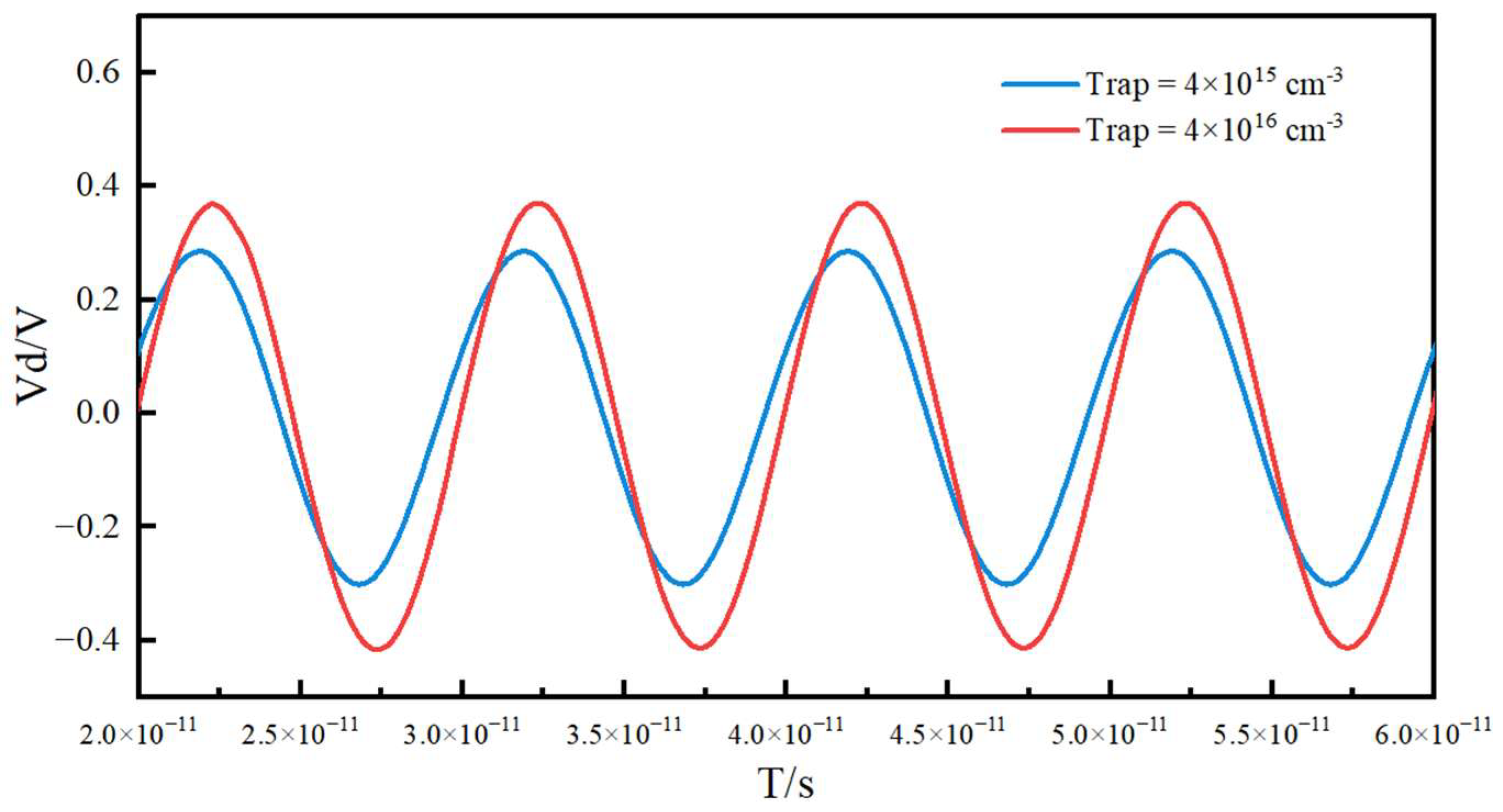
3. Results and Discussion
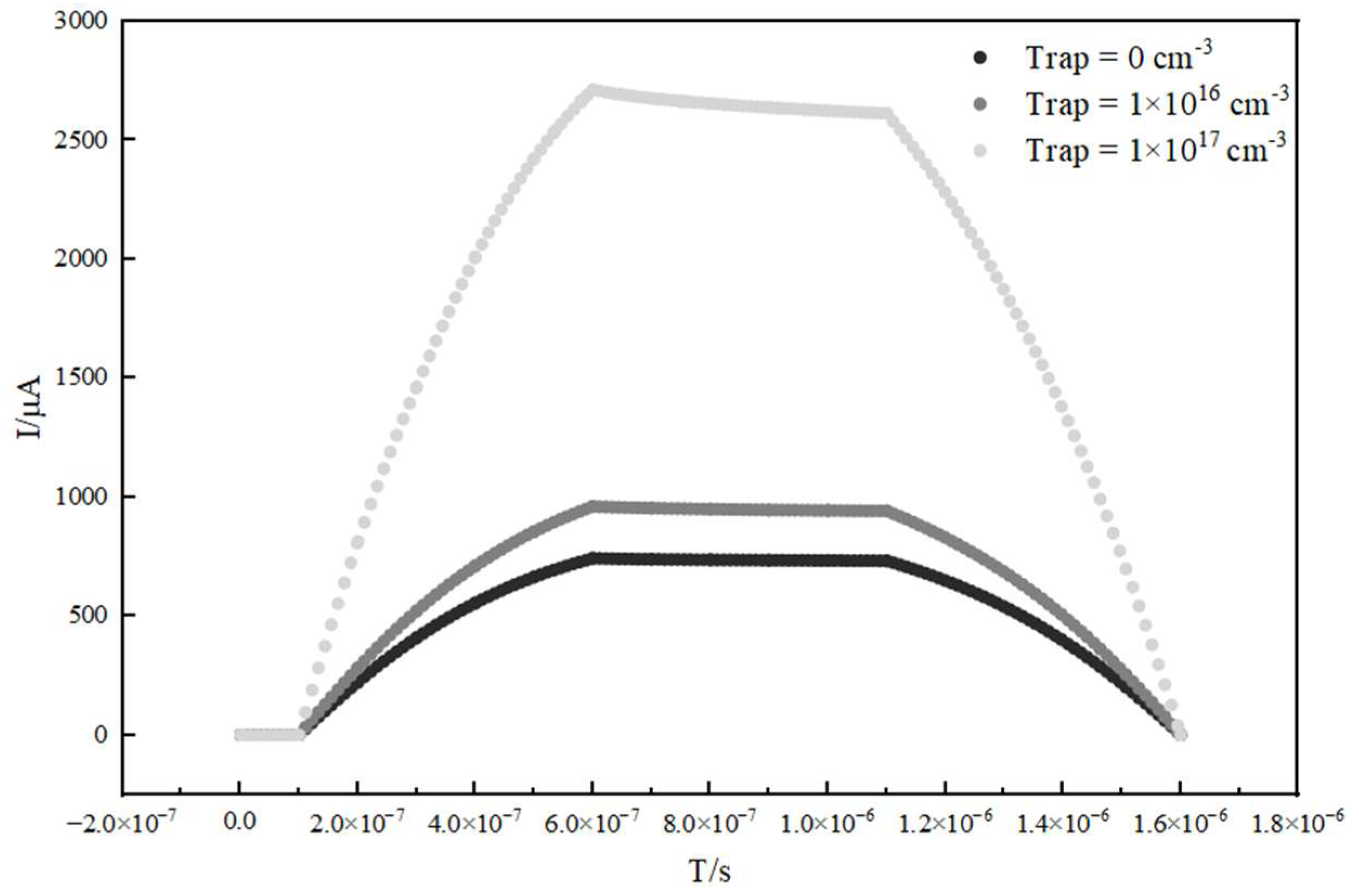
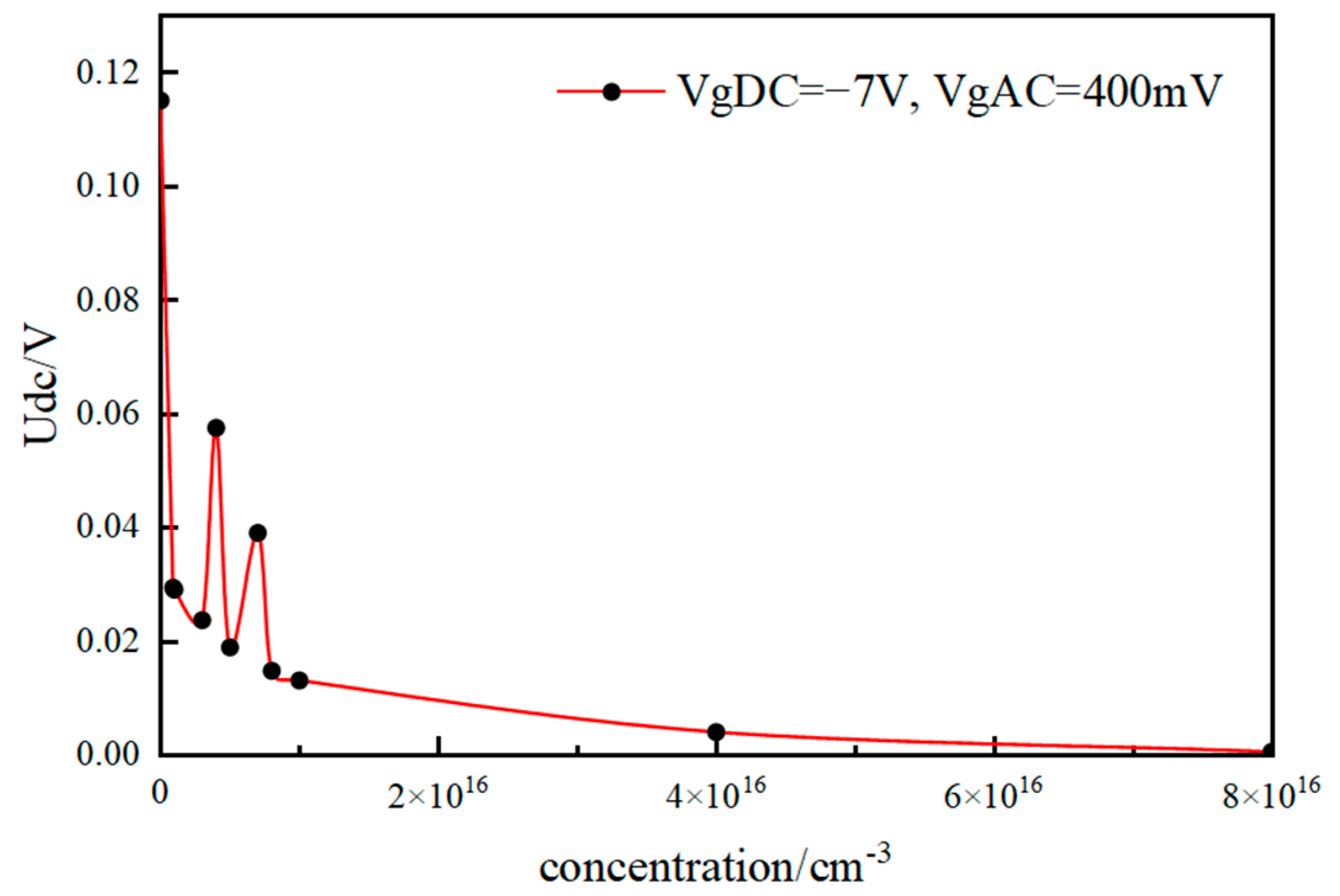
- In a low concentration range (0 to ), the current collapse trend is negligible;
- In an intermediate concentration range ( to ), the current collapse fluctuates, peaking at a trap concentration of ;
- In a high concentration range (), the current collapse intensifies significantly, showing a clear degradation trend.
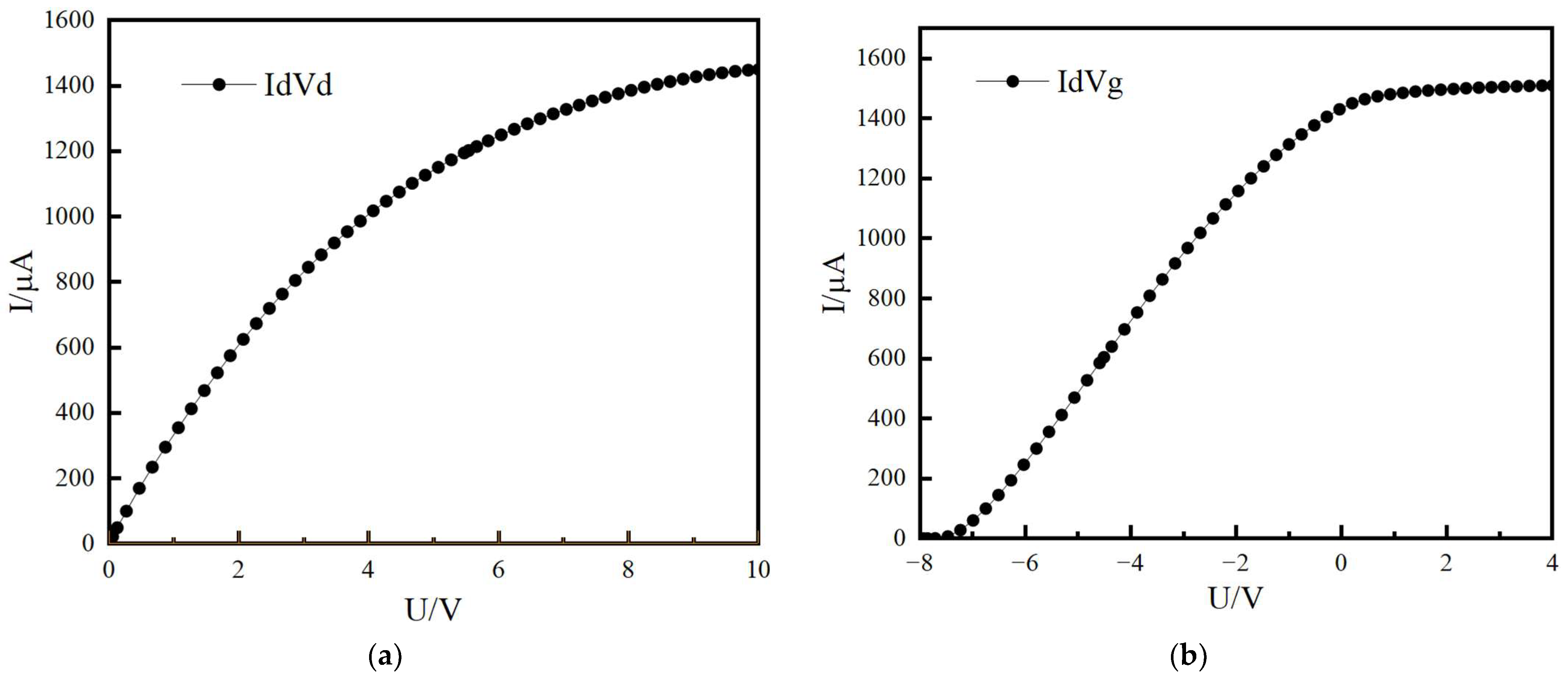
- A larger trap density leads to more sever degradation in ;
- Two maximum values are observed at trap densities of 4 and 7 .
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Quast, H.; Loffler, T. 3D-terahertz-tomography for material inspection and security. In Proceedings of the 2009 34th International Conference on Infrared, Millimeter, and Terahertz Waves, Busan, Republic of Korea, 21–25 September 2009. [Google Scholar]
- Liu, J.; Dai, J.; Chin, S.L.; Zhang, X.-C. Broadband terahertz wave remote sensing using coherent manipulation of fluorescence from asymmetrically ionized gases. Nat. Photonics 2010, 4, 627–631. [Google Scholar] [CrossRef]
- Yang, Y.; Yamagami, Y.; Yu, X.; Pitchappa, P.; Webber, J.; Zhang, B.; Fujita, M.; Nagatsuma, T.; Singh, R. Terahertz topological photonics for on-chip communication. Nat. Photonics 2020, 14, 446–451. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Li, Y.; Ozcan, A.; Jarrahi, M. High-throughput terahertz imaging: Progress and challenges. Light Sci. Appl. 2023, 12, 233. [Google Scholar] [CrossRef]
- Hou, H.W.; Liu, Z.; Teng, J.H.; Palacios, T.; Chua, S.J. High Temperature Terahertz Detectors Realized by a GaN High Electron Mobility Transistor. Sci. Rep. 2017, 7, 46664. [Google Scholar] [CrossRef]
- Bauer, M.; Ramer, A.; Chevtchenko, S.A.; Osipov, K.Y.; Cibiraite, D.; Pralgauskaite, S.; Ikamas, K.; Lisauskas, A.; Heinrich, W.; Krozer, V.; et al. A High-Sensitivity AlGaN/GaN HEMT Terahertz Detector with Integrated Broadband Bow-Tie Antenna. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 430–444. [Google Scholar] [CrossRef]
- An, N.; Li, L.; Wang, W.; Xu, X.; Zeng, J. High-Efficiency D-Band Monolithically Integrated GaN SBD-Based Frequency Doubler with High Power Handling Capability. IEEE Trans. Electron Devices 2022, 69, 4843–4847. [Google Scholar] [CrossRef]
- Wang, C.; Luo, J.; Zhang, Z.; Gu, C.; Zhu, H.; Zhang, L. A 2.0–3.0 GHz GaN HEMT-Based High-Efficiency Rectifier Using Class-EFJ Operating Mode. Electronics 2024, 13, 2786. [Google Scholar] [CrossRef]
- Saidi, I.; Gassoumi, M.; Maaref, H.; Mejri, H.; Gaquière, C. Self-heating and trapping effects in AlGaN/GaN heterojunction field-effect transistors. J. Appl. Phys. 2009, 106, 054511. [Google Scholar] [CrossRef]
- Arivazhagan, L.; Jarndal, A.H.M.; Chander, S.; Godfrey, D.; Kumar, J.R.; Bhagyalakshmi, S.; Reddy, P.K.; Nirmal, D. Self-Heating Analysis of GaN-HEMT for Various Ambient Temperature and Substrate Thickness. In Proceedings of the 2020 5th International Conference on Devices, Circuits and Systems (ICDCS), Coimbatore, India, 5–6 March 2020. [Google Scholar]
- Chen, X.; Boumaiza, S.; Wei, L. Modeling Bias Dependence of Self-Heating in GaN HEMTs Using Two Heat Sources. IEEE Trans. Electron Devices 2020, 67, 3082–3087. [Google Scholar] [CrossRef]
- Kebir, M.E.; Bri, S. Self-Heating in the HEMT AlGaN/GaN transistor. In Proceedings of the 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 2–3 December 2020. [Google Scholar]
- Tang, Z.L.; Shen, Y.; Cao, B.Y. Modulating Self-Heating Effects in GaN HEMTs Using Slant Field Plate. IEEE Trans. Electron Devices 2025, 72, 1907–1911. [Google Scholar] [CrossRef]
- Kalavagunta, A.; Mukherjee, S.; Reed, R.; Schrimpf, R. Comparison between trap and self-heating induced mobility degradation in AlGaN/GaN HEMTs. Microelectron. Reliab. 2014, 54, 570–574. [Google Scholar] [CrossRef]
- Zhang, Y.; Shiwei, F.; Hui, Z.; Xueqin, G.; Bing, D.; Lin, M. Self-heating and traps effects on the drain transient response of AlGaN/GaN HEMTs. J. Semicond. 2014, 35, 104003. [Google Scholar] [CrossRef]
- Maryam, S.; Peiman, A. Influence of the Passivation Layers on the Self-Heating Effect in the Double Channel AlGaN/GaN MOS-HEMT Device. Russ. Microelectron. 2023, 52, 112–118. [Google Scholar] [CrossRef]
- Nasir, A.; Zhang, X.; Lu, L.; Zhang, J.; Lyu, J.; Cui, Y. Enhanced crystalline quality of non-polar a-plane AlGaN epitaxial film grown with Al-composition-graded AlGaN intermediate layer. Mater. Res. Express 2021, 8, 055901. [Google Scholar] [CrossRef]
- Zou, X.; Yang, J.; Qiao, Q.; Zou, X.; Chen, J.; Shi, Y.; Ren, K. Trap Characterization Techniques for GaN-Based HEMTs: A Critical Review. Micromachines 2023, 14, 2044. [Google Scholar] [CrossRef]
- He, X.-G.; Zhao, D.-G.; Jiang, D.-S. Formation of two-dimensional electron gas at AlGaN/GaN heterostructure and the derivation of its sheet density expression*. Chin. Phys. B 2015, 24, 067301. [Google Scholar] [CrossRef]
- Lingaparthi, R.; Dharmarasu, N.; Radhakrishnan, K.; Ranjan, A.; Seah, T.L.A.; Huo, L. Source of two-dimensional electron gas in unintentionally doped AlGaN/GaN multichannel high-electron-mobility transistor heterostructures. Appl. Phys. Lett. 2021, 118, 122105. [Google Scholar] [CrossRef]
- Greco, G.; Iucolano, F.; Roccaforte, F. Ohmic contacts to Gallium Nitride materials. Appl. Surf. Sci. 2016, 383, 324–345. [Google Scholar] [CrossRef]
- Kim, H. Vertical Schottky Contacts to Bulk GaN Single Crystals and Current Transport Mechanisms: A Review. J. Electron. Mater. 2021, 50, 6688–6707. [Google Scholar] [CrossRef]
- Ha, M.-W.; Seok, O.; Lee, H.; Lee, H.H. Mobility Models Based on Forward Current-Voltage Characteristics of P-type Pseudo-Vertical Diamond Schottky Barrier Diodes. Micromachines 2020, 11, 598. [Google Scholar] [CrossRef]
- Nasir, A.; Xu, B.; Ali, I.; Akbar, J. Improvements in structural and optical properties of nonpolar a-plane AlGaN epilayers with nanoscale island-like SiNx interlayer. J. Mater. Sci. Mater. Electron. 2023, 34, 60. [Google Scholar] [CrossRef]
- Sani, H.; Khosroabadi, S. Improving Thermal Effects and Reduction of Self-heating Phenomenon in AlGaN/GaN/Si Based HEMT. J. Electron. Mater. 2021, 50, 2295–2304. [Google Scholar] [CrossRef]
- Kumar, A.; Gupta, A.; Rai, S. Reduction of self-heating effect using selective buried oxide (SELBOX) charge plasma based junctionless transistor. AEU-Int. J. Electron. Commun. 2018, 95, 162–169. [Google Scholar] [CrossRef]
- Dyakonov, M.; Shur, M. Detection, mixing, and frequency multiplication of terahertz radiation by two-dimensional electronic fluid. IEEE Trans. Electron Devices 1996, 43, 380–387. [Google Scholar] [CrossRef]
- Dyakonov, M.; Shur, M. Shallow water analogy for a ballistic field effect transistor: New mechanism of plasma wave generation by dc current. Phys. Rev. Lett. 1993, 71, 2465–2468. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Lin, Q.; Jing, W.; Han, F.; Zhao, M.; Jiang, Z. TCAD Simulation for Nonresonant Terahertz Detector Based on Double-Channel GaN/AlGaN High-Electron-Mobility Transistor. IEEE Trans. Electron Devices 2018, 65, 4807–4813. [Google Scholar] [CrossRef]
- Nasir, A.; Zhang, X.; Zakria, M.; Zhang, J.; Hu, G.; Cui, Y. Effect of NH3-flow modulation on the morphological properties of nonpolar a-plane AlGaN epilayers. Superlattices Microstruct. 2021, 159, 107045. [Google Scholar] [CrossRef]
- Zhu, Y.; Ji, X.; Liao, Y.; Wu, F.; Yan, F. TCAD simulation of gate-enclosed MOSFET for terahertz detector. In Proceedings of the 2014 12th IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT), Guilin, China, 28–31 October 2014. [Google Scholar]
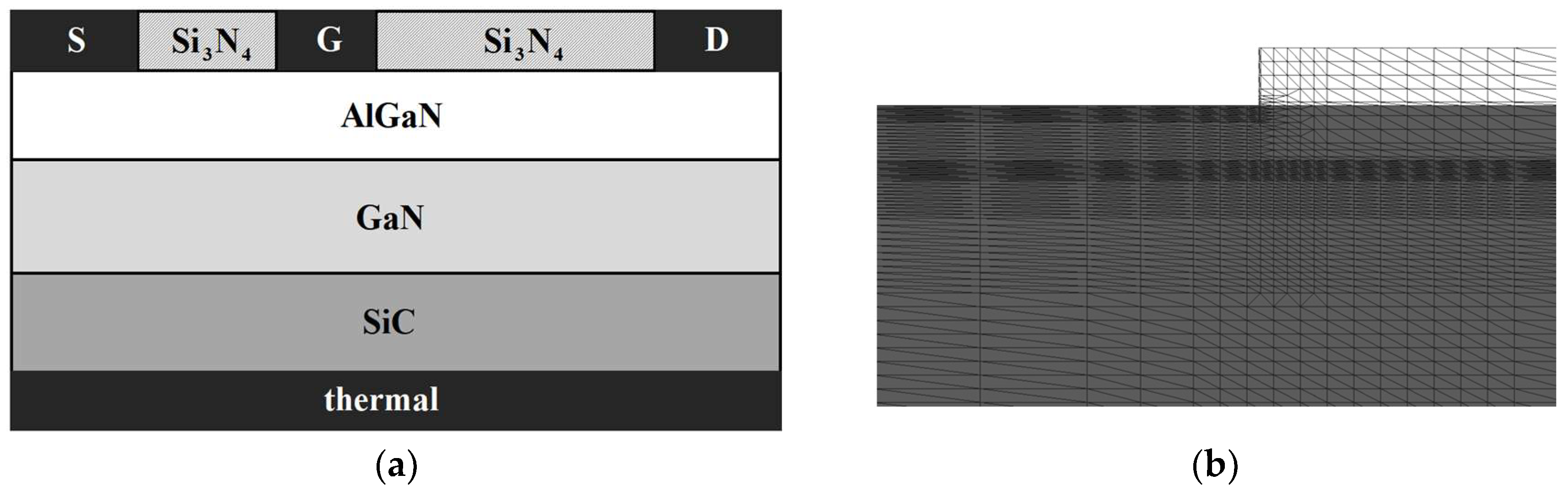


| Material/Contact | Thickness () | Width () |
|---|---|---|
| (S side) | 0.025 | 1.5 |
| (D side) | 0.025 | 2.2 |
| 0.025 | 5.9 | |
| 2 | 5.9 | |
| 10 | 5.9 | |
| Electrode S | — | 0.5 |
| Electrode G | — | 1 |
| Electrode D | — | 0.5 |
| thermal | — | 5.9 |
| Symbol | Electrons | Holes | Unit |
|---|---|---|---|
| 1417 | 470.5 | ||
| ζ | 2.5 | 2.2 | 1 |
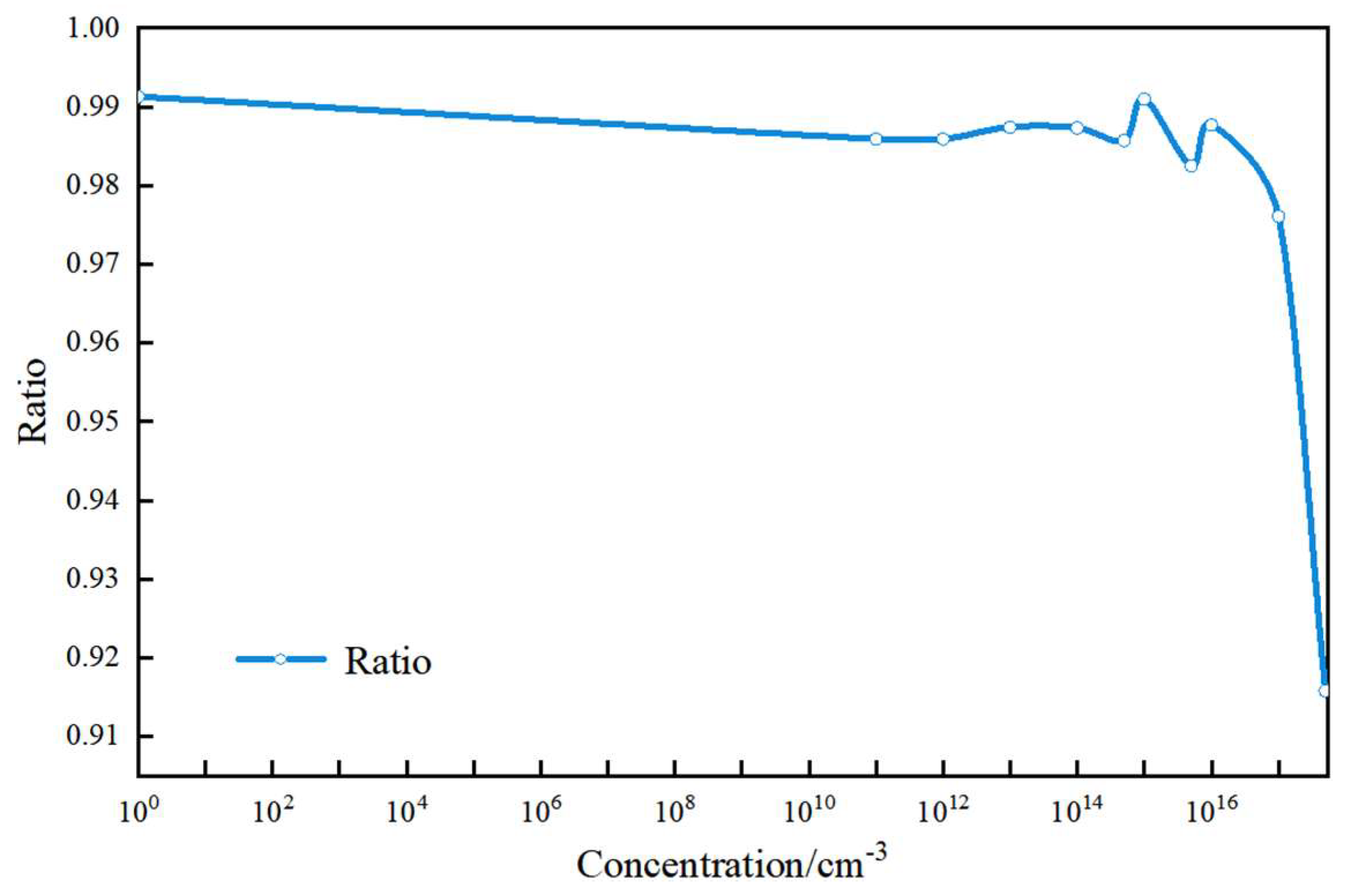
| Trap Concentration () | () | () | |
|---|---|---|---|
| 0 | 738.7534 | 732.3348 | 0.9913 |
| 742.8229 | 732.3365 | 0.9859 | |
| 742.8384 | 732.3516 | 0.9859 | |
| 742.9932 | 733.6027 | 0.9874 | |
| 744.5444 | 735.1205 | 0.9873 | |
| 5 | 751.5934 | 740.8572 | 0.9857 |
| 756.6317 | 749.8305 | 0.9910 | |
| 848.5516 | 833.7205 | 0.9825 | |
| 953.7343 | 942.0889 | 0.9877 | |
| 2677.808 | 2613.827 | 0.9761 | |
| 5 | 8478.159 | 7763.949 | 0.9158 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, H.; Wang, X.; Wang, X.; Wang, L. The Influence of Traps on the Self-Heating Effect and THz Response of GaN HEMTs. Photonics 2025, 12, 719. https://doi.org/10.3390/photonics12070719
Fan H, Wang X, Wang X, Wang L. The Influence of Traps on the Self-Heating Effect and THz Response of GaN HEMTs. Photonics. 2025; 12(7):719. https://doi.org/10.3390/photonics12070719
Chicago/Turabian StyleFan, Huichuan, Xiaoyun Wang, Xiaofang Wang, and Lin Wang. 2025. "The Influence of Traps on the Self-Heating Effect and THz Response of GaN HEMTs" Photonics 12, no. 7: 719. https://doi.org/10.3390/photonics12070719
APA StyleFan, H., Wang, X., Wang, X., & Wang, L. (2025). The Influence of Traps on the Self-Heating Effect and THz Response of GaN HEMTs. Photonics, 12(7), 719. https://doi.org/10.3390/photonics12070719






