MEMS-Integrated Tunable Fabry–Pérot Microcavity for High-Quality Single-Photon Sources
Abstract
1. Introduction
2. Device Design and Simulation
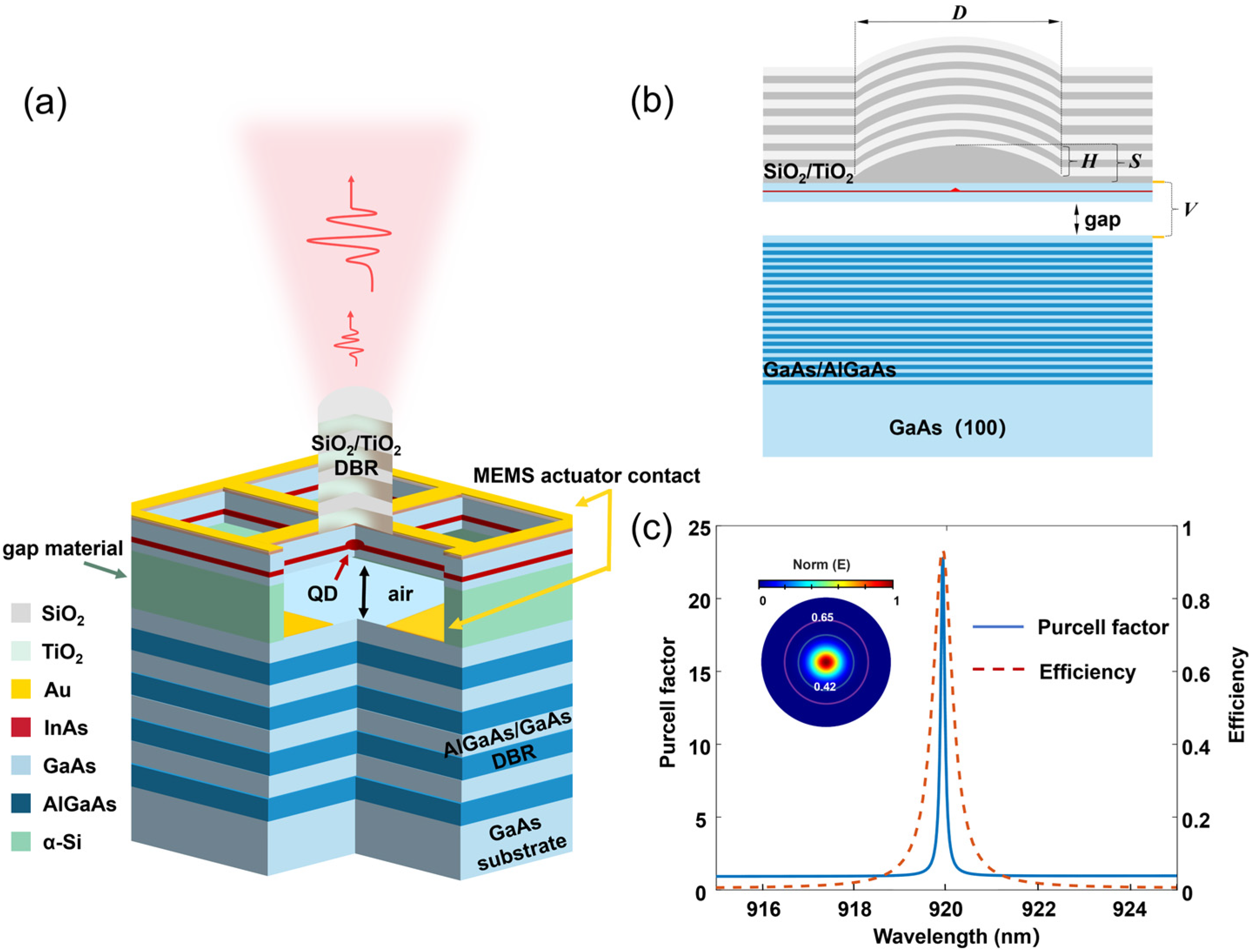
2.1. MEMS-Integrated Tunable Fabry–Pérot Cavity Design
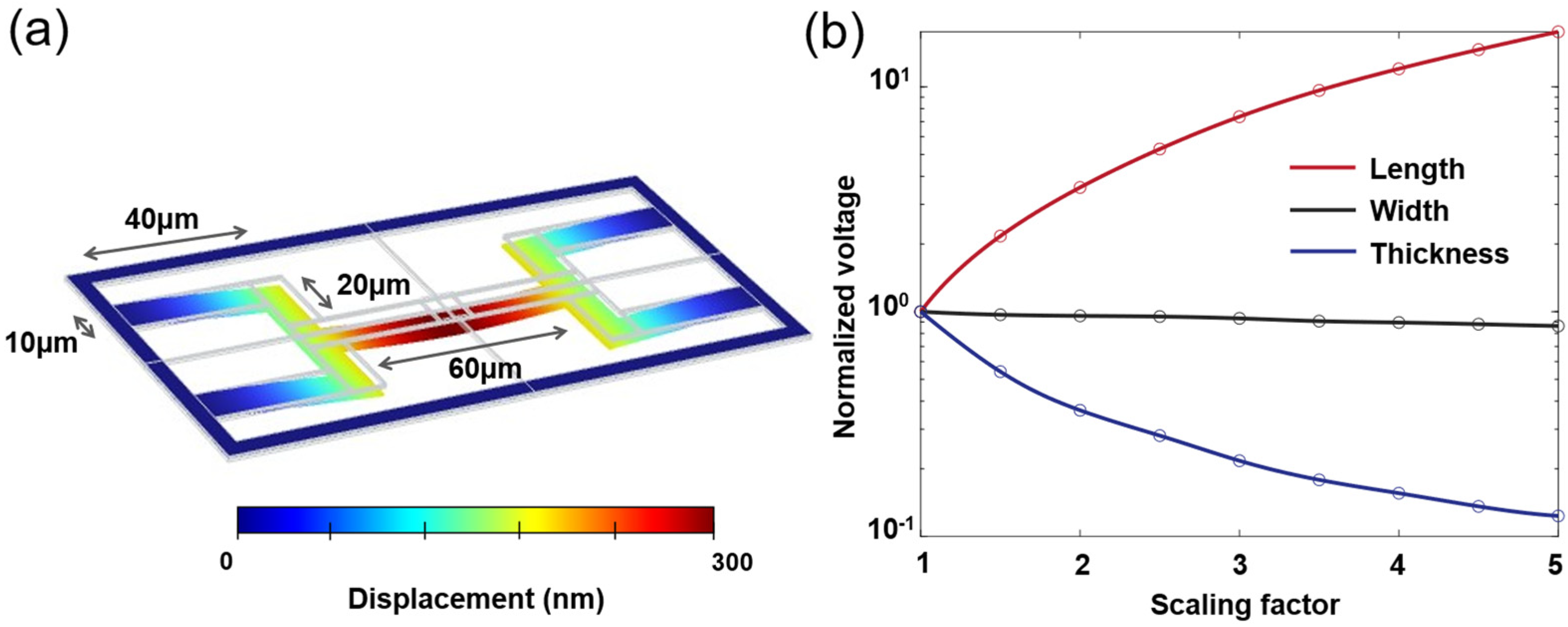
2.2. Optical and Mechanical Co-Design
3. Device Fabrication and Characterization
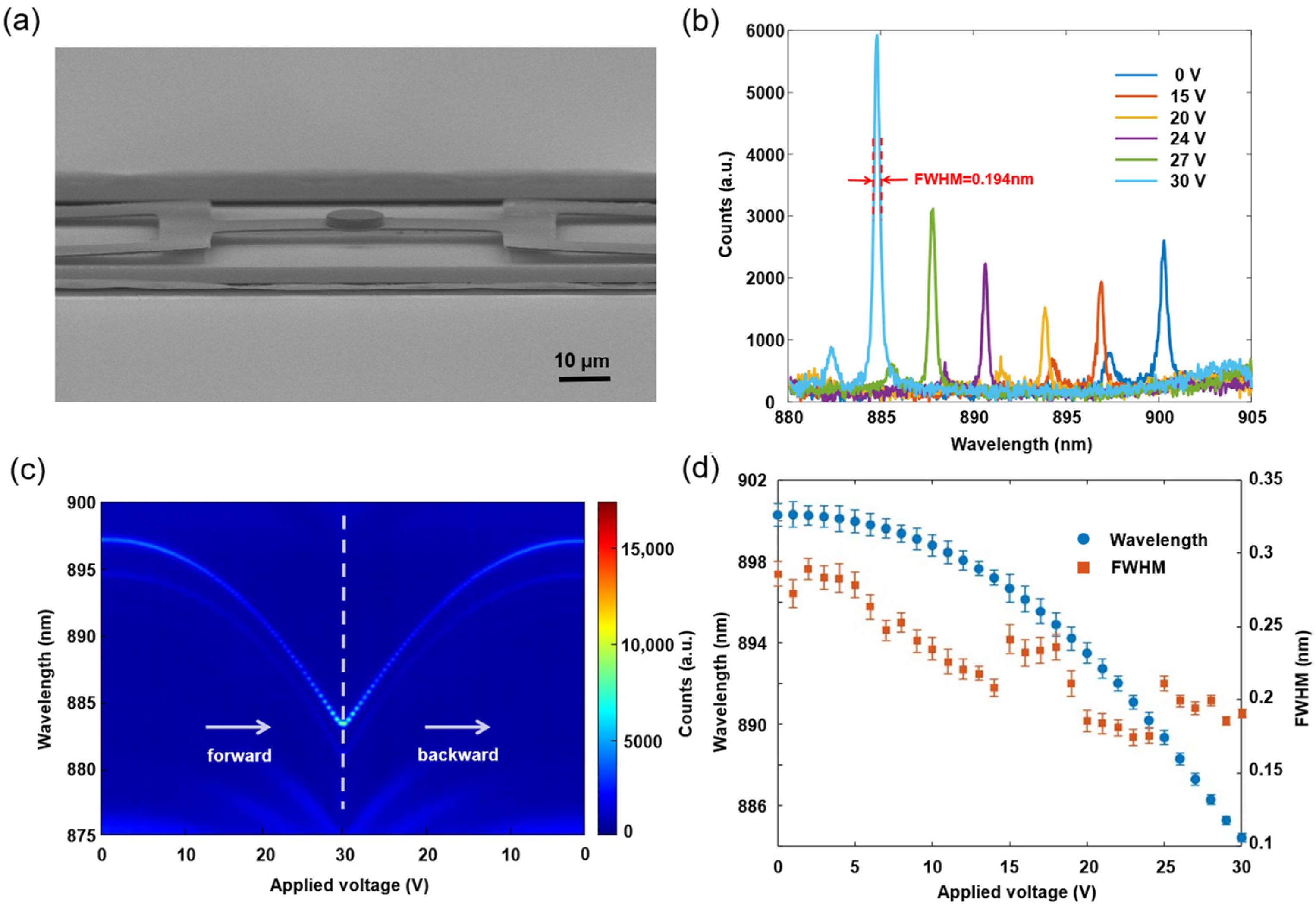
3.1. Fabrication Process
3.2. Microavity Tunability
4. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, J.; Cao, Y.; Li, Y.H.; Liao, S.K.; Zhang, L.; Ren, J.G.; Cai, W.Q.; Liu, W.Y.; Li, B.; Dai, H.; et al. Satellite-Based Entanglement Distribution over 1200 Kilometers. Science 2017, 356, 1140–1144. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Qin, J.; Ding, X.; Chen, M.C.; Chen, S.; You, X.; He, Y.M.; Jiang, X.; You, L.; Wang, Z.; et al. Boson Sampling with 20 Input Photons and a 60-Mode Interferometer in a 1014-Dimensional Hilbert Space. Phys. Rev. Lett. 2019, 123, 250503. [Google Scholar] [CrossRef] [PubMed]
- Peniakov, G.; Su, Z.-E.; Beck, A.; Cogan, D.; Amar, O.; Gershoni, D. Towards Supersensitive Optical Phase Measurement Using a Deterministic Source of Entangled Multiphoton States. Phys. Rev. B 2020, 101, 245406. [Google Scholar] [CrossRef]
- Bradac, C.; Gao, W.; Forneris, J.; Trusheim, M.E.; Aharonovich, I. Quantum Nanophotonics with Group IV Defects in Diamond. Nat. Commun. 2020, 11, 5625. [Google Scholar] [CrossRef]
- Santori, C.; Fattal, D.; Vuckovic, J.; Solomon, G.S.; Yamamoto, Y. Indistinguishable Photons from a Single-Photon Device. Nature 2002, 419, 594–597. [Google Scholar] [CrossRef]
- Meraner, M.; Mazloom, A.; Krutyanskiy, V.; Krcmarsky, V.; Schupp, J.; Fioretto, D.A.; Sekatski, P.; Northup, T.E.; Sangouard, N.; Lanyon, B.P. Indistinguishable Photons from a Trapped-Ion Quantum Network Node. Phys. Rev. A 2020, 102, 052614. [Google Scholar] [CrossRef]
- McKeever, J.; Boca, A.; Boozer, A.D.; Miller, R.; Buck, J.R.; Kuzmich, A.; Kimble, H.J. Deterministic Generation of Single Photons from One Atom Trapped in a Cavity. Science 2004, 303, 1992–1994. [Google Scholar] [CrossRef]
- He, Y.-M.; Clark, G.; Schaibley, J.R.; He, Y.; Chen, M.-C.; Wei, Y.-J.; Ding, X.; Zhang, Q.; Yao, W.; Xu, X.; et al. Single Quantum Emitters in Monolayer Semiconductors. Nat. Nanotechnol. 2015, 10, 497–502. [Google Scholar] [CrossRef]
- Chen, Y.; Zopf, M.; Keil, R.; Ding, F.; Schmidt, O.G. Highly-Efficient Extraction of Entangled Photons from Quantum Dots Using a Broadband Optical Antenna. Nat. Commun. 2018, 9, 2994. [Google Scholar] [CrossRef]
- Liu, S.F.; Wei, Y.M.; Li, X.S.; Yu, Y.; Liu, J.; Yu, S.Y.; Wang, X.H. Dual-Resonance Enhanced Quantum Light-Matter Interactions in Deterministically Coupled Quantum-Dot-Micropillars. Light Appl. 2021, 10, 158. [Google Scholar] [CrossRef]
- Liu, J.; Su, R.B.; Wei, Y.M.; Yao, B.M.; da Silva, S.F.C.; Yu, Y.; Iles-Smith, J.; Srinivasan, K.; Rastelli, A.; Li, J.T.; et al. A Solid-State Source of Strongly Entangled Photon Pairs with High Brightness and Indistinguishability. Nat. Nanotechnol. 2019, 14, 586–593. [Google Scholar] [CrossRef] [PubMed]
- Purcell, E.M. Spontaneous Emission Probabilities at Radio Frequencies BT—Confined Electrons and Photons: New Physics and Applications; Burstein, E., Weisbuch, C., Eds.; Springer: Boston, MA, USA, 1995; p. 839. ISBN 978-1-4615-1963-8. [Google Scholar]
- Kaganskiy, A.; Gschrey, M.; Schlehahn, A.; Schmidt, R.; Schulze, J.H.; Heindel, T.; Strittmatter, A.; Rodt, S.; Reitzenstein, S. Advanced in-Situ Electron-Beam Lithography for Deterministic Nanophotonic Device Processing. Rev. Sci. Instrum. 2015, 86, 073903. [Google Scholar] [CrossRef] [PubMed]
- Dousse, A.; Lanco, L.; Suffczyński, J.; Semenova, E.; Miard, A.; Lemaître, A.; Sagnes, I.; Roblin, C.; Bloch, J.; Senellart, P. Controlled Light-Matter Coupling for a Single Quantum Dot Embedded in a Pillar Microcavity Using Far-Field Optical Lithography. Phys. Rev. Lett. 2008, 101, 267404. [Google Scholar] [CrossRef] [PubMed]
- Gschrey, M.; Thoma, A.; Schnauber, P.; Seifried, M.; Schmidt, R.; Wohlfeil, B.; Krüger, L.; Schulze, J.-H.; Heindel, T.; Burger, S.; et al. Highly Indistinguishable Photons from Deterministic Quantum-Dot Microlenses Utilizing Three-Dimensional in Situ Electron-Beam Lithography. Nat. Commun. 2015, 6, 7662. [Google Scholar] [CrossRef]
- Thon, S.M.; Rakher, M.T.; Kim, H.; Gudat, J.; Irvine, W.T.M.; Petroff, P.M.; Bouwmeester, D. Strong Coupling through Optical Positioning of a Quantum Dot in a Photonic Crystal Cavity. Appl. Phys. Lett. 2009, 94, 111115. [Google Scholar] [CrossRef]
- Sapienza, L.; Davanco, M.; Badolato, A.; Srinivasan, K. Nanoscale Optical Positioning of Single Quantum Dots for Bright and Pure Single-Photon Emission. Nat. Commun. 2015, 6, 7833. [Google Scholar] [CrossRef]
- Unsleber, S.; He, Y.-M.; Gerhardt, S.; Maier, S.; Lu, C.-Y.; Pan, J.-W.; Gregersen, N.; Kamp, M.; Schneider, C.; Hoefling, S. Highly Indistinguishable On-Demand Resonance Fluorescence Photons from a Deterministic Quantum Dot Micropillar Device with 74% Extraction Efficiency. Opt. Express 2016, 24, 8539–8546. [Google Scholar] [CrossRef]
- Finley, J.J.; Sabathil, M.; Vogl, P.; Abstreiter, G.; Oulton, R.; Tartakovskii, A.I.; Mowbray, D.J.; Skolnick, M.S.; Liew, S.L.; Cullis, A.G.; et al. Quantum-Confined Stark Shifts of Charged Exciton Complexes in Quantum Dots. Phys. Rev. B 2004, 70. [Google Scholar] [CrossRef]
- Wang, H.; He, Y.-M.; Chung, T.-H.; Hu, H.; Yu, Y.; Chen, S.; Ding, X.; Chen, M.-C.; Qin, J.; Yang, X.; et al. Towards Optimal Single-Photon Sources from Polarized Microcavities. Nat. Photonics 2019, 13, 770–775. [Google Scholar] [CrossRef]
- Nowak, A.K.; Portalupi, S.L.; Giesz, V.; Gazzano, O.; Dal Savio, C.; Braun, P.-F.; Karrai, K.; Arnold, C.; Lanco, L.; Sagnes, I.; et al. Deterministic and Electrically Tunable Bright Single-Photon Source. Nat. Commun. 2014, 5, 3240. [Google Scholar] [CrossRef]
- Ding, X.; He, Y.; Duan, Z.C.; Gregersen, N.; Chen, M.C.; Unsleber, S.; Maier, S.; Schneider, C.; Kamp, M.; Höfling, S.; et al. On-Demand Single Photons with High Extraction Efficiency and Near-Unity Indistinguishability from a Resonantly Driven Quantum Dot in a Micropillar. Phys. Rev. Lett. 2016, 116, 020401. [Google Scholar] [CrossRef] [PubMed]
- He, Y.-M.; He, Y.; Wei, Y.-J.; Wu, D.; Atatuere, M.; Schneider, C.; Hoefling, S.; Kamp, M.; Lu, C.-Y.; Pan, J.-W. On-Demand Semiconductor Single-Photon Source with Near-Unity Indistinguishability. Nat. Nanotechnol. 2013, 8, 213–217. [Google Scholar] [CrossRef] [PubMed]
- Tomm, N.; Javadi, A.; Antoniadis, N.O.; Najer, D.; Löbl, M.C.; Korsch, A.R.; Schott, R.; Valentin, S.R.; Wieck, A.D.; Ludwig, A.; et al. A Bright and Fast Source of Coherent Single Photons. Nat. Nanotechnol. 2021, 16, 399. [Google Scholar] [CrossRef] [PubMed]
- Somaschi, N.; Giesz, V.; De Santis, L.; Loredo, J.C.; Almeida, M.P.; Hornecker, G.; Portalupi, S.L.; Grange, T.; Antón, C.; Demory, J.; et al. Near-Optimal Single-Photon Sources in the Solid State. Nat. Photonics 2016, 10, 340–345. [Google Scholar] [CrossRef]
- Bennett, A.J.; Pooley, M.A.; Stevenson, R.M.; Ward, M.B.; Patel, R.B.; De Giroday, A.B.; Sköld, N.; Farrer, I.; Nicoll, C.A.; Ritchie, D.A.; et al. Electric-Field-Induced Coherent Coupling of the Exciton States in a Single Quantum Dot. Nat. Phys. 2010, 6, 947–950. [Google Scholar] [CrossRef]
- Lettner, T.; Gyger, S.; Zeuner, K.D.; Schweickert, L.; Steinhauer, S.; Hedlund, C.R.; Stroj, S.; Rastelli, A.; Hammar, M.; Trotta, R.; et al. Strain-Controlled Quantum Dot Fine Structure for Entangled Photon Generation at 1550 Nm. NANO Lett. 2022, 22, 4285. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, J.; Zopf, M.; Jung, K.; Zhang, Y.; Keil, R.; Ding, F.; Schmidt, O.G. Wavelength-Tunable Entangled Photons from Silicon-Integrated III–V Quantum Dots. Nat. Commun. 2016, 7, 10387. [Google Scholar] [CrossRef]
- Yang, J.; Chen, Y.; Rao, Z.; Zheng, Z.; Song, C.; Chen, Y.; Xiong, K.; Chen, P.; Zhang, C.; Wu, W.; et al. Tunable Quantum Dots in Monolithic Fabry-Perot Microcavities for High-Performance Single-Photon Sources. Light Appl. 2024, 13, 33. [Google Scholar] [CrossRef]
- Cole, G.D.; Behymer, E.; Bond, T.C.; Goddard, L.L. Short-Wavelength MEMS-Tunable VCSELs. Opt. Express 2008, 16, 16093–16103. [Google Scholar] [CrossRef]
- Wang, M.; PENG, H.; Hao, C.; Zhou, X.; Zheng, W.; Liu, A. Detector-Integrated Vertical-Cavity Surface-Emitting Laser with a Movable High-Contrast Grating Mirror. Photonics Res. 2024, 12, 1437–1448. [Google Scholar] [CrossRef]
- Li, K.; Chase, C.; Rao, Y.; Chang-Hasnain, C.J. Widely Tunable 1060-Nm High-Contrast Grating VCSEL. In Proceedings of the 2016 Compound Semiconductor Week (CSW) [Includes 28th International Conference on Indium Phosphide & Related Materials (IPRM) & 43rd International Symposium on Compound Semiconductors (ISCS), Toyama, Japan, 26–30 June 2016; pp. 1–2. [Google Scholar] [CrossRef]
- Chase, C.; Zhou, Y.; Chang-Hasnain, C.J. Size Effect of High Contrast Gratings in VCSELs. Opt. Express 2009, 17, 24002. [Google Scholar] [CrossRef] [PubMed]
- Ding, F.; Stoeferle, T.; Mai, L.; Knoll, A.; Mahrt, R.F. Vertical Microcavities with High Q and Strong Lateral Mode Confinement. Phys. Rev. B 2013, 87, 161116(R). [Google Scholar] [CrossRef]
- Ferrara, J.E. High Contrast Metastructures on Silicon for Optoelectronic Devices, University of California. 2015. Available online: https://www2.eecs.berkeley.edu/Pubs/TechRpts/2017/EECS-2017-12.pdf (accessed on 7 April 2023).
- Cole, G.D.; Björlin, E.S.; Chen, Q.; Chan, C.Y.; Wu, S.M.; Wang, C.S.; MacDonald, N.C.; Bowers, J.E. MEMS-Tunable Vertical-Cavity SOAs. IEEE J. Quantum Electron. 2005, 41, 390–407. [Google Scholar] [CrossRef]
- Mateus, C.F.R.; Huang, M.C.Y.; Chang-Hasnain, C.J. Micromechanical Tunable Optical Filters: General Design Rules for Wavelengths from near-IR up to 10μm. Sensors Actuators A Phys. 2005, 119, 57–62. [Google Scholar] [CrossRef]
- Gayral, B.; Gérard, J.M. Strong Purcell Effect for InAs Quantum Boxes in High-Q Wet-Etched Microdisks. Phys. E 2000, 7, 641–645. [Google Scholar] [CrossRef]
- Vyshnevyy, A.A. Gain-Dependent Purcell Enhancement, Breakdown of Einstein’s Relations, and Superradiance in Nanolasers. Phys. Rev. B 2022, 105, 085116. [Google Scholar] [CrossRef]
- Krasnok, A.; Alu, A. Active Nanophotonics. Proc. IEEE 2020, 108, 628–654. [Google Scholar] [CrossRef]
- Barbour, R.J.; Dalgarno, P.A.; Curran, A.; Nowak, K.M.; Baker, H.J.; Hall, D.R.; Stoltz, N.G.; Petroff, P.M.; Warburton, R.J. A Tunable Microcavity. J. Appl. Phys. 2011, 110, 053107. [Google Scholar] [CrossRef]
- Goyvaerts, J.; Kumari, S.; Uvin, S.; Zhang, J.; Baets, R.; Gocalinska, A.; Pelucchi, E.; Corbett, B.; Roelkens, G. Transfer-Print Integration of GaAs p-i-n Photodiodes onto Silicon Nitride Waveguides for Near-Infrared Applications. Opt. Express 2020, 28, 21275–21285. [Google Scholar] [CrossRef]
- Larson, M.C. Microelectromechanical Wavelength-Tunable Vertical-Cavity Light-Emitters and Lasers, Stanford University. 1996. Available online: https://www.proquest.com/pqdtglobal (accessed on 20 July 2024).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Yang, J.; Peng, X.; Yu, Y. MEMS-Integrated Tunable Fabry–Pérot Microcavity for High-Quality Single-Photon Sources. Photonics 2025, 12, 315. https://doi.org/10.3390/photonics12040315
Zheng Z, Yang J, Peng X, Yu Y. MEMS-Integrated Tunable Fabry–Pérot Microcavity for High-Quality Single-Photon Sources. Photonics. 2025; 12(4):315. https://doi.org/10.3390/photonics12040315
Chicago/Turabian StyleZheng, Ziyang, Jiawei Yang, Xuebin Peng, and Ying Yu. 2025. "MEMS-Integrated Tunable Fabry–Pérot Microcavity for High-Quality Single-Photon Sources" Photonics 12, no. 4: 315. https://doi.org/10.3390/photonics12040315
APA StyleZheng, Z., Yang, J., Peng, X., & Yu, Y. (2025). MEMS-Integrated Tunable Fabry–Pérot Microcavity for High-Quality Single-Photon Sources. Photonics, 12(4), 315. https://doi.org/10.3390/photonics12040315





