Combating Antimicrobial Resistance: Spectroscopy Meets Machine Learning
Abstract
1. Introduction
2. Spectroscopic Methods in AMR Detection
2.1. Raman Spectroscopy
2.2. Fourier Transform Infrared Spectroscopy (FTIR)
2.3. Nuclear Magnetic Resonance (NMR)
2.4. Near-Infrared Spectroscopy (NIR)
2.5. Other Emerging Spectroscopic Techniques
3. Machine Learning Methods in AMR Research
3.1. Supervised Learning
3.1.1. Partial Least Squares Methods (PLS)
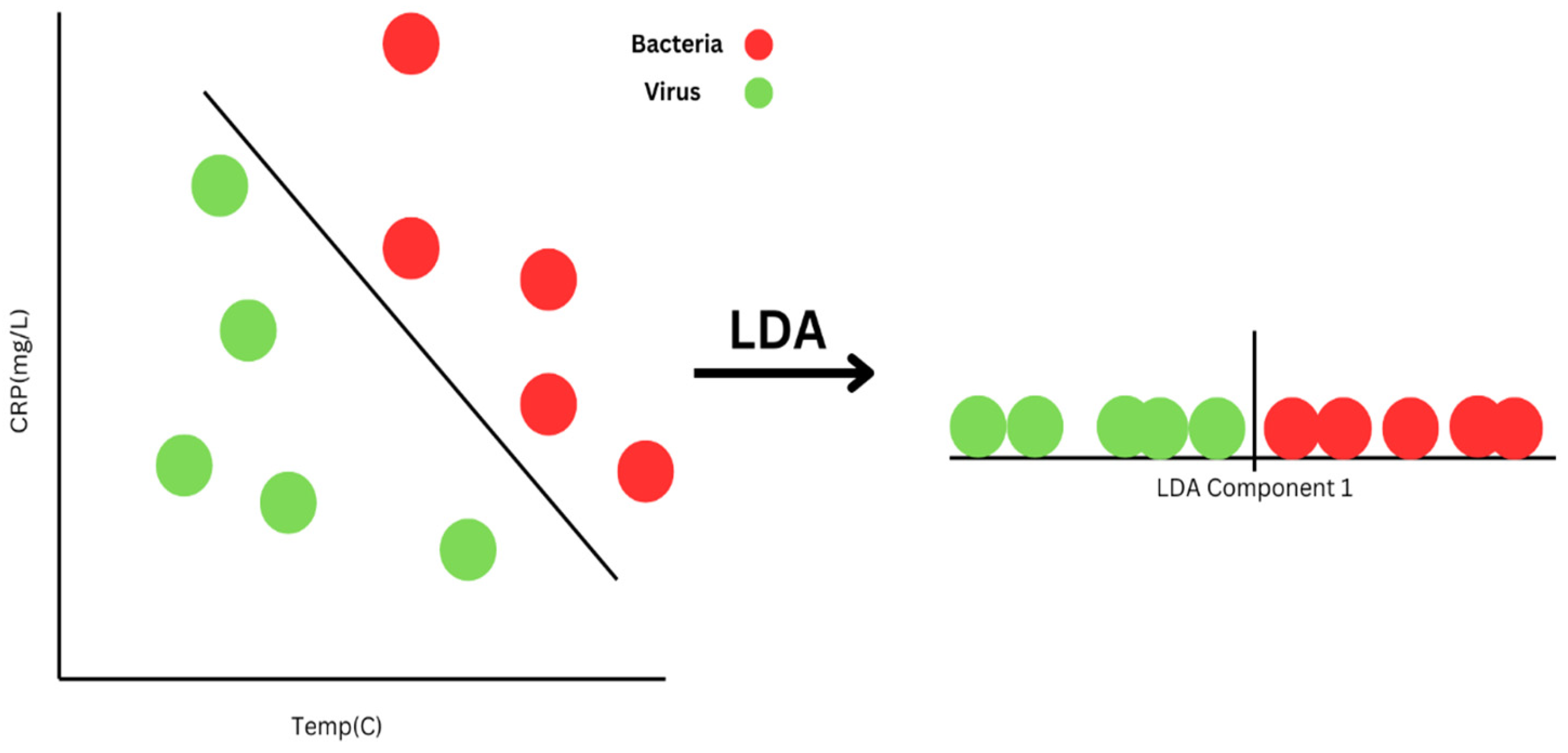
3.1.2. Linear Discriminant Analysis (LDA)
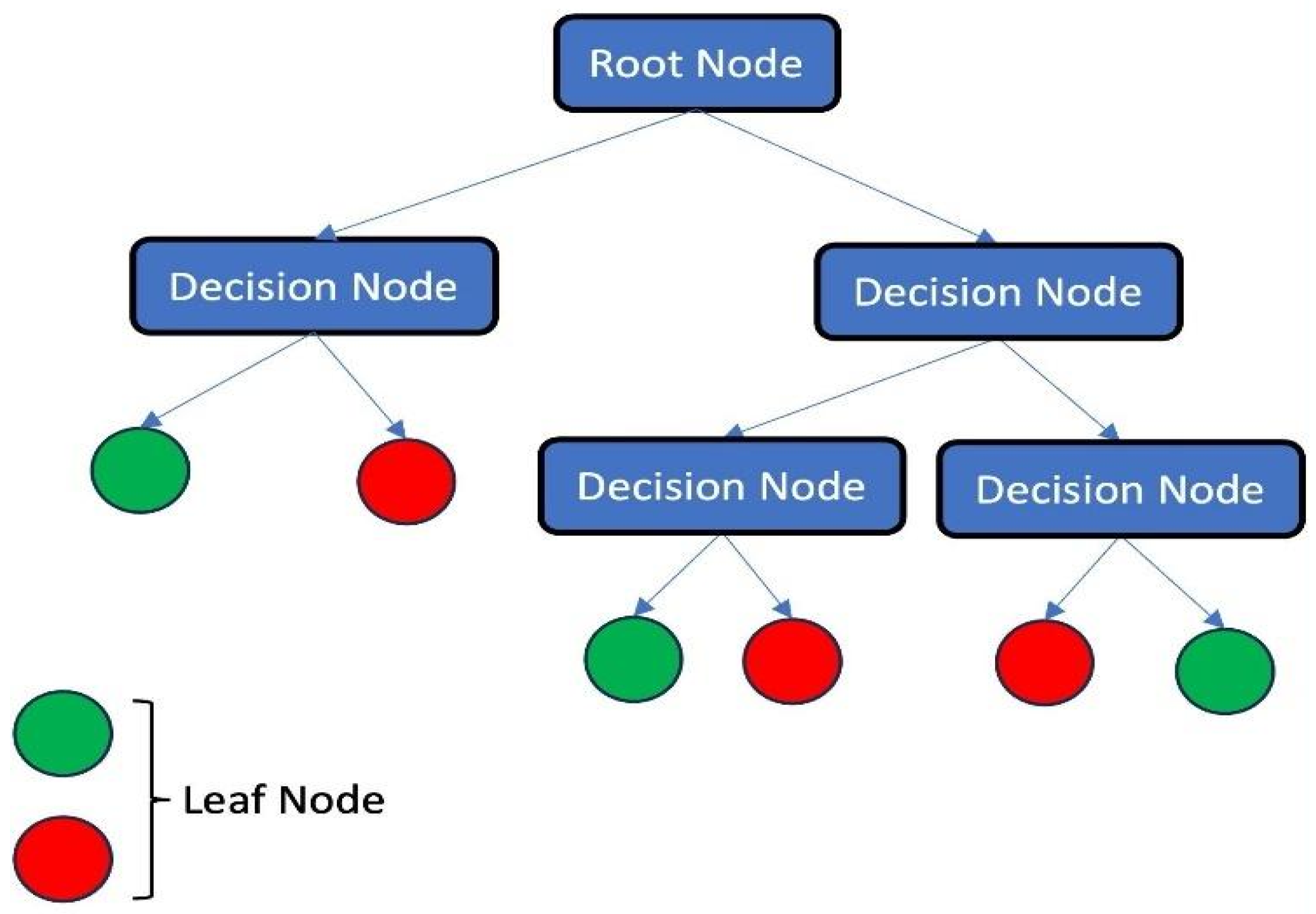
3.1.3. Decision Tree (DT)
- Entropy:
- Gini Index:
- Variance:
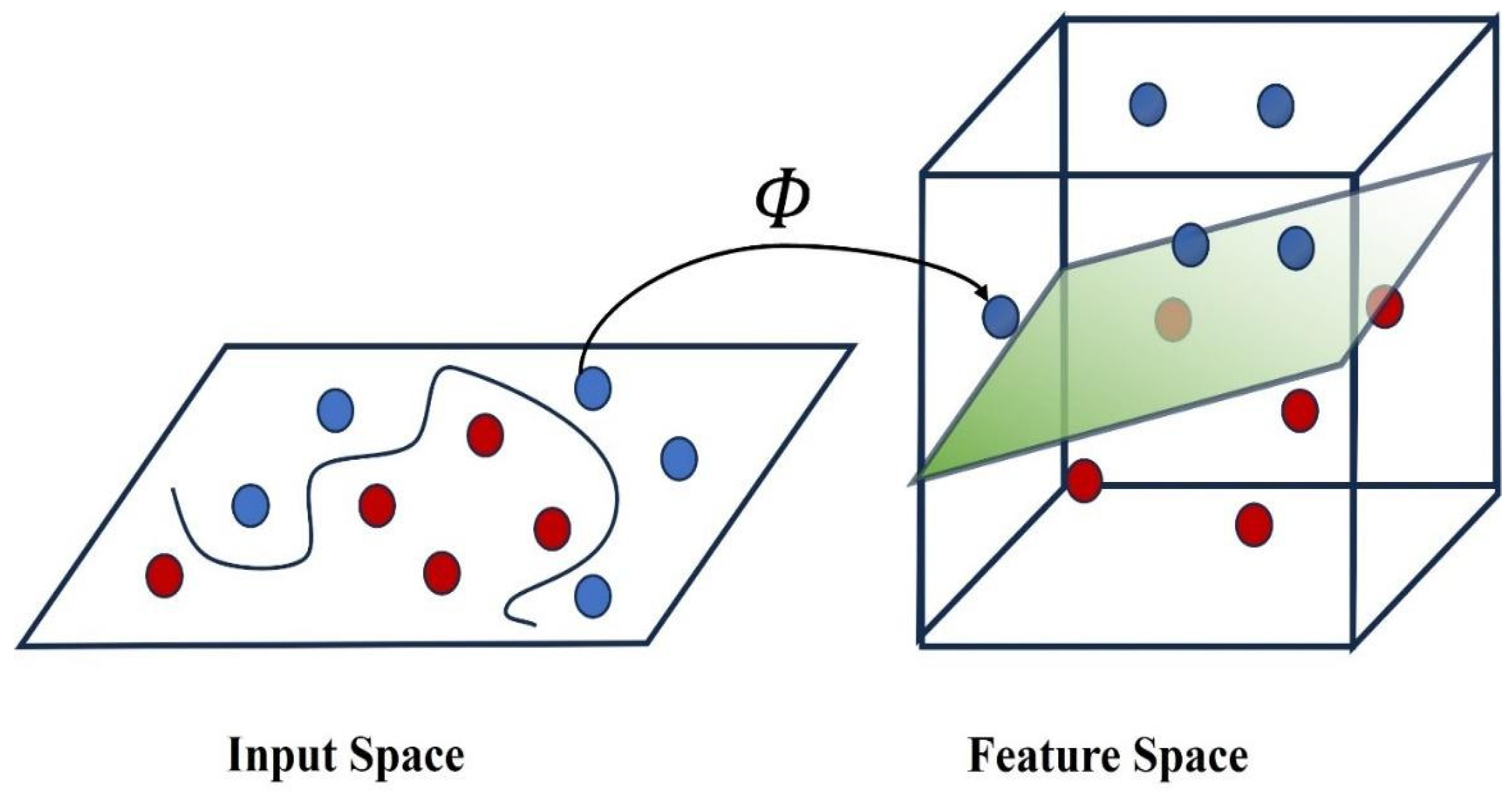
3.1.4. Support Vector Machines (SVMs)
- Minimize
- Subject towhere there are l data points, is a vector of l Lagrange multipliers, C is a constant, and is defined as follows:where is the ith data point with a dimensional vector. In this way, by solving the above minimization, we will have the value of . In addition, from the derivation of these equations, the equation of optimal hyperplane can be written as
- Gaussian Radial Basis:
- Exponential Radial Basis:
- Multi-layer Perceptron:
3.1.5. Random Forests
3.1.6. Logistic Regression (LR)
3.1.7. Gradient Boosting (GB)
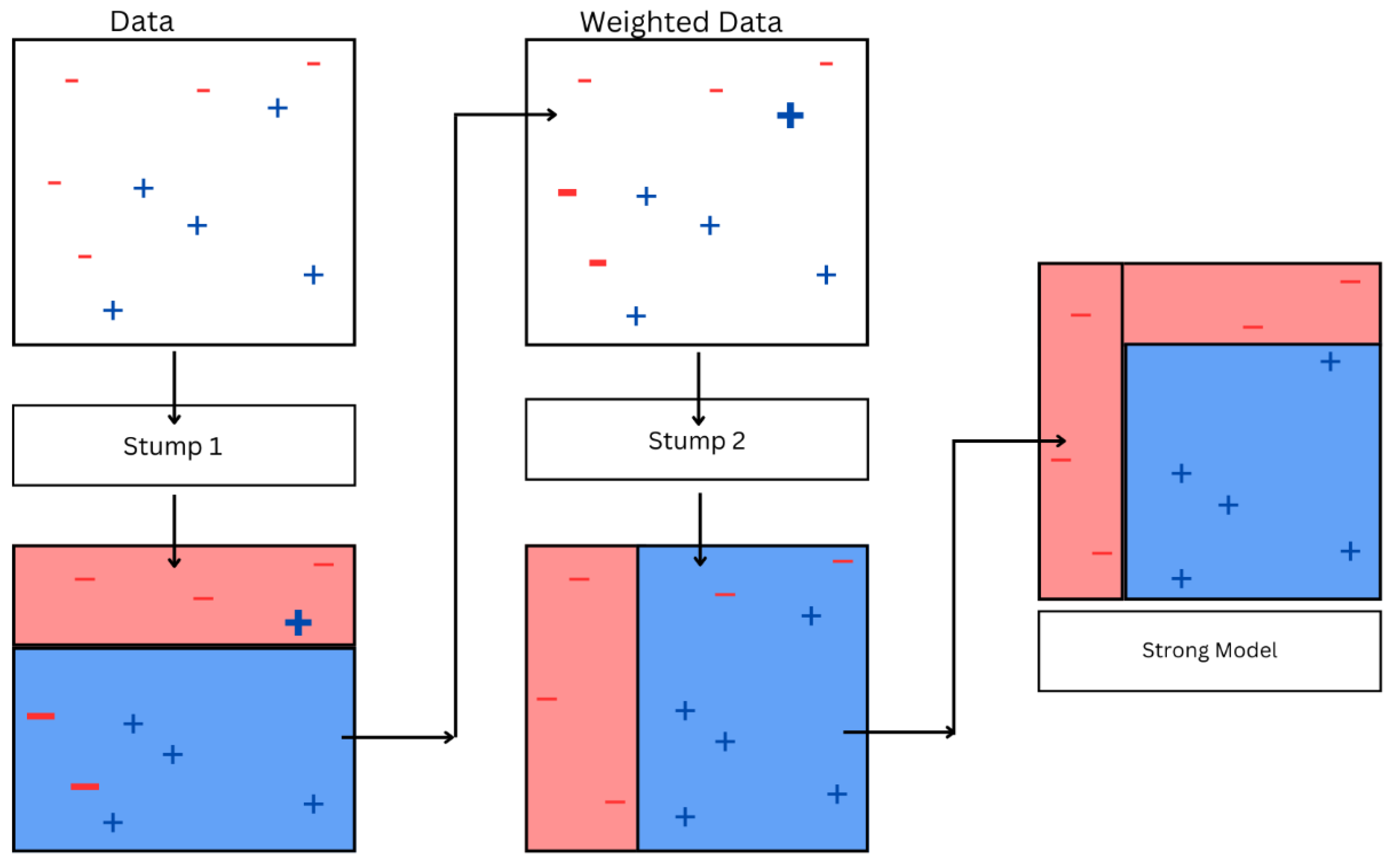
3.1.8. AdaBoost
- (a)
- Initialize equal weights for each data point. For example, if there are N data points, then each data point is assigned weight.
- (b)
- A weak classifier is trained on these weighted data points. The classifier tries to minimize weighted error, where the error for each incorrect prediction is weighted by the weight of the data point for which the prediction was made.
- (c)
- The learner’s error rate, ϵ, is determined by evaluating the weighted sum of incorrectly predicted samples. This error rate indicates how effectively the learner performs on the weighted data.
- (d)
- Calculate the weight of by using
- (e)
- This weight signifies the participation of this learner in the end prediction of the ensemble. Better-performing learners will have a higher weight, representing a higher contribution in the final prediction.Update the weights of the data points using the following formula:where is the weight of ith sample, is the true label, and is the prediction of the weak learner, followed by normalizing the weights of the data points to ensure that they add up to one, ensuring fairness for the data points in the next iteration. Repeat the steps until the specified number of iterations or certain criteria are satisfied. In this process, each iteration introduces a new weak learner to the model ensemble.
- (f)
- The end model is constructed by summing the outputs of multiple weak learners using the calculated weights. When the model is used for predicting the label of a new sample, each weak classifier contributes to the prediction with a weight, and the ultimate prediction is calculated by taking a weighted mean of the estimates made by each and every weak classifier.
3.1.9. Neural Networks
- (a)
- Mean Squared Error Loss Function:
- (b)
- Cross Entropy Loss Function:
- (c)
- Mean Absolute Percentage Error/Deviation:
- (a)
- Binary step function:
- (b)
- Linear activation function:
- (c)
- Sigmoid/logistic function:
- (d)
- Tanh function:
- (e)
- Rectified Linear Unit, popularly known as ReLU function:
- (f)
- Leaky Rectified Linear Unit function (Leaky ReLU):
- (g)
- Parametric ReLU function:
- (h)
- Exponential Linear Unit (ELU) function:
- (i)
- Softmax function:where n defines the quantity of neurons in the output layer used.
- (j)
- Swish function:
- (k)
- Gaussian Error Linear Unit (GELU) function:
- (l)
- Scaled Exponential Linear Unit, also called SELU function:
3.2. Unsupervised Learning
3.2.1. Principal Component Analysis (PCA)
3.2.2. Hierarchical Cluster Analysis (HCA)
3.2.3. K-Means Clustering
- (a)
- Euclidean distance:
- (b)
- Manhattan distance:
- (c)
- Mahalanobis distance:
- (d)
- Hamming distance:
- (e)
- Cosine distance:
3.3. Deep Learning
3.4. Transfer Learning
3.5. Reinforcement Learning (RL)
4. Case Studies and Applications of ML in AMR Research
5. Discussion and Future Directions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sharma, A.; Sarin, S. Indian Priority Pathogen List 2019. Available online: https://cdn.who.int/media/docs/default-source/searo/india/antimicrobial-resistance/ippl_final_web.pdf?sfvrsn=9105c3d1_6 (accessed on 10 September 2022).
- Ventola, C.L. The Antibiotic Resistance Crisis Part 1: Causes and Threats. Pharm. Ther. 2015, 40, 277. [Google Scholar]
- Kardas, P. Patient compliance with antibiotic treatment for respiratory tract infections. J. Antimicrob. Chemother. 2002, 49, 897–903. [Google Scholar] [CrossRef] [PubMed]
- Van Boeckel, T.P.; Brower, C.; Gilbert, M.; Grenfell, B.T.; Levin, S.A.; Robinson, T.P.; Teillant, A.; Laxminarayan, R. Global trends in antimicrobial use in food animals. Proc. Natl. Acad. Sci. USA 2015, 112, 5649–5654. [Google Scholar] [CrossRef] [PubMed]
- Laxminarayan, R.; Duse, A.; Wattal, C.; Zaidi, A.K.; Wertheim, H.F.; Sumpradit, N.; Vlieghe, E.; Hara, G.L.; Gould, I.M.; Goossens, H.; et al. Antibiotic resistance-the need for global solutions. Lancet Infect. Dis. 2013, 13, 1057–1098. [Google Scholar] [CrossRef]
- Lack of Innovation Set to Undermine Antibiotic Performance and Health Gains. Available online: https://www.who.int/news/item/22-06-2022-22-06-2022-lack-of-innovation-set-to-undermine-antibiotic-performance-and-health-gains#:~:text=Lack%20of%20innovation%20set%20to%20undermine%20antibiotic%20performance%20and%20health%20gains,-22%20June%202022&text=Development%20of%20new%20antibacterial%20treatments,by%20the%20World%20Health%20Organization (accessed on 22 June 2022).
- Ericsson, H.M.; Sherris, J.C. Antibiotic sensitivity testing. Report of an international collaborative study. Acta Pathol. Microbiol. Scand. B Microbiol. Immunol. 1971, 90. [Google Scholar]
- Jorgensen, J.H.; Ferraro, M.J.; McElmeel, M.L.; Spargo, J.; Swenson, J.M.; Tenover, F.C. Detection of penicillin and extended-spectrum cephalosporin resistance among Streptococcus pneumoniae clinical isolates by use of the E test. J. Clin. Microbiol. 1994, 32, 159–163. [Google Scholar] [CrossRef]
- di Toma, A.; Brunetti, G.; Chiriacò, M.S.; Ferrara, F.; Ciminelli, C. A Novel Hybrid Platform for Live/Dead Bacteria Accurate Sorting by On-Chip DEP Device. Int. J. Mol. Sci. 2023, 24, 7077. [Google Scholar] [CrossRef]
- Brunetti, G.; Conteduca, D.; Armenise, M.N.; Ciminelli, C. Novel micro-nano optoelectronic biosensor for label-free real-time biofilm monitoring. Biosensors 2021, 11, 361. [Google Scholar] [CrossRef]
- Kim, D.; Jun, S.R.; Hwang, D. Employing Machine Learning for the Prediction of Antimicrobial Resistance (AMR) Phenotypes. In SoutheastCon; IEEE: Piscataway, NJ, USA, 2024; pp. 1519–1524. [Google Scholar]
- Ho, C.S.; Jean, N.; Hogan, C.A.; Blackmon, L.; Jeffrey, S.S.; Holodniy, M.; Banaei, N.; Saleh, A.A.; Ermon, S.; Dionne, J. Rapid identification of pathogenic bacteria using Raman spectroscopy and deep learning. Nat. Commun. 2019, 10, 4927. [Google Scholar] [CrossRef]
- Kochan, K.; Nethercott, C.; Taghavimoghaddam, J.; Richardson, Z.; Lai, E.; Crawford, S.A.; Peleg, A.Y.; Wood, B.R.; Heraud, P. Rapid Approach for Detection of Antibiotic Resistance in Bacteria Using Vibrational Spectroscopy. Anal. Chem. 2020, 92, 8235–8243. [Google Scholar] [CrossRef]
- Hollas, J.M. Modern Spectroscopy; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Carey, P.R. Raman spectroscopy, the sleeping giant in structural biology, awakes. J. Biol. Chem. 1999, 274, 26625–26628. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.S.; Landry, Z.; Pereira, F.C.; Wagner, M.; Berry, D.; Huang, W.E.; Taylor, G.T.; Kneipp, J.; Popp, J.; Zhang, M.; et al. Raman microspectroscopy for microbiology. Nat. Rev. Methods Primers 2021, 1, 80. [Google Scholar] [CrossRef]
- Ramesh, G.; Paul, W.; Valparambil Puthanveetil, V.; Raja, K.; Embekkat Kaviyil, J. Raman spectroscopy as a novel technique for the identification of pathogens in a clinical microbiology laboratory. Spectrosc. Lett. 2022, 55, 546–551. [Google Scholar] [CrossRef]
- Dewachter, L.; Maarten, F.; Jan, M. Bacterial heterogeneity and antibiotic survival: Understanding and combatting persistence and heteroresistance. Mol. Cell 2019, 76, 255–267. [Google Scholar] [CrossRef]
- Barzan, G.; Sacco, A.; Mandrile, L.; Giovannozzi, A.M.; Brown, J.; Portesi, C.; Alexander, M.R.; Williams, P.; Hardie, K.R.; Rossi, A.M. New frontiers against antibiotic resistance: A Raman-based approach for rapid detection of bacterial susceptibility and biocide-induced antibiotic cross-tolerance. Sens. Actuators B Chem. 2020, 309, 127774. [Google Scholar] [CrossRef]
- Yu, Y.; Xue, J.; Zhang, W.; Ru, S.; Liu, Y.; Du, K.; Jiang, F. Antibiotic heteroresistance: An important factor in the failure of Helicobacter Pylori eradication. Crit. Rev. Microbiol. 2025, 1–16. [Google Scholar] [CrossRef]
- Kerr, L.T.; Byrne, H.J.; Hennelly, B.M. Optimal choice of sample substrate and laser wavelength for Raman spectroscopic analysis of biological specimen. Anal. Methods 2015, 7, 5041–5052. [Google Scholar] [CrossRef]
- Butler, H.J.; Ashton, L.; Bird, B.; Cinque, G.; Curtis, K.; Dorney, J.; Esmonde-White, K.; Fullwood, N.J.; Gardner, B.; Martin-Hirsch, P.L.; et al. Using Raman spectroscopy to characterize biological materials. Nat. Protoc. 2016, 11, 664–687. [Google Scholar] [CrossRef]
- Das, S.; Saxena, K.; Tinguely, J.C.; Pal, A.; Wickramasinghe, N.L.; Khezri, A.; Dubey, V.; Ahmad, A.; Perumal, V.; Ahmad, R.; et al. SERS Nanowire Chip and Machine Learning-Enabled Classification of Wild-Type and Antibiotic-Resistant Bacteria at Species and Strain Levels. ACS Appl. Mater. Interfaces 2023, 15, 24047–24058. [Google Scholar] [CrossRef]
- Rohman, A.; Windarsih, A.; Lukitaningsih, E.; Rafi, M.; Betania, K.; Fadzillah, N.A. The use of FTIR and Raman spectroscopy in combination with chemometrics for analysis of biomolecules in biomedical fluids: A review. Biomed. Spectrosc. Imaging 2019, 8, 55–71. [Google Scholar] [CrossRef]
- Novais, Â.; Gonçalves, A.B.; Ribeiro, T.G.; Freitas, A.R.; Méndez, G.; Mancera, L.; Read, A.; Alves, V.; López-Cerero, L.; Rodríguez-Baño, J.; et al. Development and validation of a quick, automated, and reproducible ATR FT-IR spectroscopy machine-learning model for Klebsiella pneumoniae typing. J. Clin. Microbiol. 2024, 62, e01211-23. [Google Scholar] [CrossRef] [PubMed]
- Abu-Aqil, G.; Lapidot, I.; Salman, A.; Huleihel, M. Quick Detection of Proteus and Pseudomonas in Patients’ Urine and Assessing Their Antibiotic Susceptibility Using Infrared Spectroscopy and Machine Learning. Sensors 2023, 23, 8132. [Google Scholar] [CrossRef] [PubMed]
- Kochan, K.; Jiang, J.H.; Kostoulias, X.; Lai, E.; Richardson, Z.; Pebotuwa, S.; Heraud, P.; Wood, B.R.; Peleg, A.Y. Fast and Accurate Prediction of Antibiotic Susceptibility in Clinical Methicillin-Resistant S. aureus Isolates Using ATR-FTIR Spectroscopy: A Model Validation Study. Anal. Chem. 2025, 97, 6041–6048. [Google Scholar] [CrossRef] [PubMed]
- Barrera Patiño, C.P.; Soares, J.M.; Blanco, K.C.; Bagnato, V.S. Machine Learning in FTIR Spectrum for the Identification of Antibiotic Resistance: A Demonstration with Different Species of Microorganisms. Antibiotics 2024, 13, 821. [Google Scholar] [CrossRef]
- Abu-Aqil, G.; Sharaha, U.; Suleiman, M.; Riesenberg, K.; Lapidot, I.; Salman, A.; Huleihel, M. Culture-independent susceptibility determination of E. coli isolated directly from patients’ urine using FTIR and machine-learning. Analyst 2022, 147, 4815–4823. [Google Scholar] [CrossRef]
- Klages, J. Structure and Dynamics Using NMR Spectroscopy. Doctoral Dissertation, Technische Universität München, Munich, Germany, 2008. [Google Scholar]
- Aries, M.L.; Cloninger, M.J. NMR metabolomic analysis of bacterial resistance pathways using multivalent quaternary ammonium functionalized macromolecules. Metabolomics 2020, 16, 1–11. [Google Scholar] [CrossRef]
- Medeiros-Silva, J.; Jekhmane, S.; Paioni, A.L.; Gawarecka, K.; Baldus, M.; Swiezewska, E.; Breukink, E.; Weingarth, M. High-resolution NMR studies of antibiotics in cellular membranes. Nat. Commun. 2018, 9, 3963. [Google Scholar] [CrossRef]
- Romaniuk, J.A.; Cegelski, L. Bacterial cell wall composition and the influence of antibiotics by cell-wall and whole-cell NMR. Philos. Trans. R. Soc. B Biol. Sci. 2015, 370, 20150024. [Google Scholar] [CrossRef]
- Kaprou, G.D.; Bergšpica, I.; Alexa, E.A.; Alvarez-Ordóñez, A.; Prieto, M. Rapid methods for antimicrobial resistance diagnostics. Antibiotics 2021, 10, 209. [Google Scholar] [CrossRef]
- Liu, Z.; Davies, P.B. Infrared laser absorption spectroscopy of rotational and vibration rotational transitions of HeH+ up to the dissociation threshold. J. Chem. Phys. 1997, 107, 337–341. [Google Scholar] [CrossRef]
- Jin, N.; Semple, K.T.; Jiang, L.; Luo, C.; Zhang, D.; Martin, F.L. Spectrochemical analyses of growth phase-related bacterial responses to low (environmentally relevant) concentrations of tetracycline and nanoparticulate silver. Analyst 2018, 143, 768–776. [Google Scholar] [CrossRef] [PubMed]
- Jin, N.; Paraskevaidi, M.; Semple, K.T.; Martin, F.L.; Zhang, D. Infrared Spectroscopy Coupled with a Dispersion Model for Quantifying the Real-Time Dynamics of Kanamycin Resistance in Artificial Microbiota. Anal. Chem. 2017, 89, 9814–9821. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Kasun, L.C.; Wang, Q.J.; Zheng, Y.; Lin, Z. A review of machine learning for near-infrared spectroscopy. Sensors 2022, 22, 9764. [Google Scholar] [CrossRef] [PubMed]
- Chakkumpulakkal Puthan Veettil, T.; Kochan, K.; Williams, G.C.; Bourke, K.; Kostoulias, X.; Peleg, A.Y.; Lyras, D.; De Bank, P.A.; Perez-Guaita, D.; Wood, B.R. A multimodal spectroscopic approach combining mid-infrared and near-infrared for discriminating gram-positive and gram-negative bacteria. Anal. Chem. 2024, 96, 18392–18400. [Google Scholar] [CrossRef]
- Gao, L.; Smith, R.T. Optical hyperspectral imaging in microscopy and spectroscopy–a review of data acquisition. J. Biophotonics 2015, 8, 441–456. [Google Scholar] [CrossRef]
- Wang, Y.; Reardon, C.P.; Read, N.; Thorpe, S.; Evans, A.; Todd, N.; Van Der Woude, M.; Krauss, T.F. Attachment and antibiotic response of early-stage biofilms studied using resonant hyperspectral imaging. NPJ Biofilms. Microbiomes. 2020, 6, 57. [Google Scholar] [CrossRef]
- Elbehiry, A.; Marzouk, E.; Abalkhail, A.; Abdelsalam, M.H.; Mostafa, M.E.; Alasiri, M.; Ibrahem, M.; Ellethy, A.T.; Almuzaini, A.; Aljarallah, S.N.; et al. Detection of antimicrobial resistance via state-of-the-art technologies versus conventional methods. Front. Microbiol. 2025, 16, 1549044. [Google Scholar] [CrossRef]
- Globus, T.; Igor, S.; Boris, G. Teraherz vibrational spectroscopy of E. coli and molecular constituents: Computational modeling and experiment. Adv. Biosci. Biotechnol. 2013, 4, 493–503. [Google Scholar] [CrossRef]
- Colbaugh, R.; Glass, K. Predicting Antimicrobial Resistance via Lightly-Supervised Learning. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2428–2433. [Google Scholar]
- Goodswen, S.J.; Barratt, J.L.; Kennedy, P.J.; Kaufer, A.; Calarco, L.; Ellis, J.T. Machine learning and applications in microbiology. FEMS Microbiol. Rev. 2021, 45, fuab015. [Google Scholar] [CrossRef]
- Abdi, H. Partial least squares regression and projection on latent structure regression (PLS Regression). Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 97–106. [Google Scholar] [CrossRef]
- Truong, V.K.; Chapman, J.; Cozzolino, D. Monitoring the Bacterial Response to Antibiotic and Time Growth Using Near-infrared Spectroscopy Combined with Machine Learning. Food Anal. Methods 1994, 14, 1394–1401. [Google Scholar] [CrossRef] [PubMed]
- Tahir, F.; Kamran, A.; Majeed, M.I.; Alghamdi, A.A.; Javed, M.R.; Nawaz, H.; Iqbal, M.A.; Tahir, M.; Tariq, A.; Rashid, N.; et al. Surface-Enhanced Raman Scattering (SERS) in Combination with PCA and PLS-DA for the Evaluation of Antibacterial Activity of 1-Isopentyl-3-pentyl-1H-imidazole-3-ium Bromide against Bacillus subtilis. ACS Omega 2024, 9, 6861–6872. [Google Scholar] [CrossRef] [PubMed]
- Dourou, D.; Grounta, A.; Argyri, A.A.; Froutis, G.; Tsakanikas, P.; Nychas, G.J.E.; Doulgeraki, A.I.; Chorianopoulos, N.G.; Tassou, C.C. Rapid Microbial Quality Assessment of Chicken Liver Inoculated or Not With Salmonella Using FTIR Spectroscopy and Machine Learning. Front. Microbiol. 2021, 11, 623788. [Google Scholar] [CrossRef]
- Xanthopoulos, P.; Pardalos, P.M.; Trafalis, T.B.; Xanthopoulos, P.; Pardalos, P.M.; Trafalis, T.B. Linear discriminant analysis. In Robust Data Mining; Springer: Berlin/Heidelberg, Germany, 2013; pp. 27–33. [Google Scholar]
- Balakrishnama, S.; Ganapathiraju, A. Linear discriminant analysis-a brief tutorial. Inst. Signal Inf. Process. 1998, 18, 1–8. [Google Scholar]
- Ciloglu, F.U.; Caliskan, A.; Saridag, A.M.; Kilic, I.H.; Tokmakci, M.; Kahraman, M.; Aydin, O. Drug-resistant Staphylococcus aureus bacteria detection by combining surface-enhanced Raman spectroscopy (SERS) and deep learning techniques. Sci. Rep. 2021, 11, 18444. [Google Scholar] [CrossRef]
- Liu, W.; Tang, J.W.; Lyu, J.W.; Wang, J.J.; Pan, Y.C.; Shi, X.Y.; Liu, Q.H.; Zhang, X.; Gu, B.; Wang, L. Discrimination between Carbapenem-Resistant and Carbapenem-Sensitive Klebsiella Pneumoniae Strains through Computational Analysis of Surface-Enhanced Raman Spectra: A Pilot Study. Microbiol. Spectr. 2022, 10, e02409-21. [Google Scholar] [CrossRef]
- Nakar, A.; Pistiki, A.; Ryabchykov, O.; Bocklitz, T.; Rösch, P.; Popp, J. Detection of multi-resistant clinical strains of E. coli with Raman spectroscopy. Anal. Bioanal. Chem. 2022, 414, 1481–1492. [Google Scholar] [CrossRef]
- Fernández-Manteca, M.G.; Ocampo-Sosa, A.A.; de Alegría-Puig, C.R.; Roiz, M.P.; Rodríguez-Grande, J.; Madrazo, F.; Calvo, J.; Rodríguez-Cobo, L.; López-Higuera, J.M.; Fariñas, M.C.; et al. Automatic classification of Candida species using Raman spectroscopy and machine learning. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2023, 290, 122270. [Google Scholar] [CrossRef]
- Yamamoto, T.; Taylor, J.N.; Koseki, S.; Koyama, K. Prediction of growth/no growth status of previously unseen bacterial strain using Raman spectroscopy and machine learning. LWT 2023, 174, 114449. [Google Scholar] [CrossRef]
- Song, Y.Y.; Ying, L.U. Decision tree methods: Applications for classification and prediction. Shanghai Arch. Psychiatry 2015, 27, 130. [Google Scholar]
- Lu, W.; Li, H.; Qiu, H.; Wang, L.; Feng, J.; Fu, Y.V. Identification of pathogens and detection of antibiotic susceptibility at single-cell resolution by Raman spectroscopy combined with machine learning. Front. Microbiol. 2023, 13, 1076965. [Google Scholar] [CrossRef] [PubMed]
- Ciloglu, F.U.; Saridag, A.M.; Kilic, I.H.; Tokmakci, M.; Kahraman, M.; Aydin, O. Identification of methicillin-resistant: Staphylococcus aureus bacteria using surface-enhanced Raman spectroscopy and machine learning techniques. Analyst 2020, 145, 7559–7570. [Google Scholar] [CrossRef] [PubMed]
- Lowie, T.; Callens, J.; Maris, J.; Ribbens, S.; Pardon, B. Decision tree analysis for pathogen identification based on circumstantial factors in outbreaks of bovine respiratory disease in calves. Prev. Vet. Med. 2021, 196, 105469. [Google Scholar] [CrossRef] [PubMed]
- Burges, C.J. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Zhu, H.; Luo, J.; Liao, J.; He, S. High-Accuracy Rapid Identification and Classification of Mixed Bacteria Using Hyperspectral Transmission Microscopic Imaging and Machine Learning. Prog. Electromagn. Res. 2023, 178, 49–62. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, X.D.; Tang, J.W.; Ma, Z.W.; Usman, M.; Liu, Q.H.; Wu, C.Y.; Li, F.; Zhu, Z.B.; Gu, B. Machine learning analysis of SERS fingerprinting for the rapid determination of Mycobacterium tuberculosis infection and drug resistance. Comput. Struct. Biotechnol. J. 2022, 20, 5364–5377. [Google Scholar] [CrossRef]
- Gutiérrez, P.; Godoy, S.E.; Torres, S.; Oyarzún, P.; Sanhueza, I.; Díaz-García, V.; Contreras-Trigo, B.; Coelho, P. Improved antibiotic detection in raw milk using machine learning tools over the absorption spectra of a problem-specific nanobiosensor. Sensors 2020, 20, 4552. [Google Scholar] [CrossRef]
- Rigatti, S.J. Random Forest. J. Insur. Med. 2017, 47, 31–39. [Google Scholar] [CrossRef]
- Kleinbaum, D.G. Logistic Regression; Springer: New York, NY, USA, 2002. [Google Scholar]
- Lu, J.; Chen, J.; Liu, C.; Zeng, Y.; Sun, Q.; Li, J.; Shen, Z.; Chen, S.; Zhang, R. Identification of antibiotic resistance and virulence-encoding factors in Klebsiella pneumoniae by Raman spectroscopy and deep learning. Microb. Biotechnol. 2022, 15, 1270–1280. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, Y.; Liu, W.; Yuan, C.; Luo, X.; Xie, F.; Chen, X.; de la Chapelle, M.L.; Tian, H.; Yang, X.; et al. Evaluation of classification ability of logistic regression model on SERS data of miRNAs. J. Biophotonics 2022, 15, e202200108. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
- Bühlmann, P.; Yu, B. Boosting with the L 2 loss: Regression and classification. J. Am. Stat. Assoc. 2003, 98, 324–339. [Google Scholar] [CrossRef]
- Tang, J.W.; Liu, Q.H.; Yin, X.C.; Pan, Y.C.; Wen, P.B.; Liu, X.; Kang, X.X.; Gu, B.; Zhu, Z.B.; Wang, L. Comparative Analysis of Machine Learning Algorithms on Surface Enhanced Raman Spectra of Clinical Staphylococcus Species. Front. Microbiol. 2021, 12, 696921. [Google Scholar] [CrossRef] [PubMed]
- Zeng, W.; Wang, C.; Xia, F. Classification and identification of foodborne pathogenic bacteria by Raman spectroscopy based on PCA and LightGBM algorithm. In Proceedings of the International Conference on Algorithms, High Performance Computing, and Artificial Intelligence (AHPCAI 2023), Yinchuan, China, 8–19 August 2023; SPIE: Washington, DC, USA, 2023; Volume 12941. [Google Scholar]
- Macgregor-Fairlie, M.; De Gomes, P.; Weston, D.; Rickard, J.J.S.; Goldberg Oppenheimer, P. Hybrid use of Raman spectroscopy and artificial neural networks to discriminate Mycobacterium bovis BCG and other Mycobacteriales. PLoS ONE 2023, 18, e0293093. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.W.; Li, J.Q.; Yin, X.C.; Xu, W.W.; Pan, Y.C.; Liu, Q.H.; Gu, B.; Zhang, X.; Wang, L. Rapid Discrimination of Clinically Important Pathogens Through Machine Learning Analysis of Surface Enhanced Raman Spectra. Front. Microbiol. 2022, 13, 843417. [Google Scholar] [CrossRef]
- Xu, J.; Luo, Y.; Wang, J.; Tu, W.; Yi, X.; Xu, X.; Song, Y.; Tang, Y.; Hua, X.; Yu, Y.; et al. Artificial intelligence-aided rapid and accurate identification of clinical fungal infections by single-cell Raman spectroscopy. Front. Microbiol. 2023, 14, 1125676. [Google Scholar] [CrossRef]
- Goodacre, R.; Timmins, E.M.; Burton, R.; Kaderbhai, N.; Woodward, A.M.; Kell, D.B.; Rooney, P.J. Rapid Identification of Urinary Tract Infection Bacteria Using Hyperspectral Whole-Organism Fingerprinting and Artificial Neural Networks. Microbiology 1998, 144, 1157–1170. [Google Scholar] [CrossRef]
- Ma, L.; Chen, L.; Chou, K.C.; Lu, X. Campylobacter jejuni antimicrobial resistance profiles and mechanisms determined using a raman spectroscopy-based metabolomic approach. Appl. Environ. Microbiol. 2021, 87, e00388-21. [Google Scholar] [CrossRef]
- Sharaha, U.; Rodriguez-Diaz, E.; Riesenberg, K.; Bigio, I.J.; Huleihel, M.; Salman, A. Using infrared spectroscopy and multivariate analysis to detect antibiotics’ resistant Escherichia coli bacteria. Anal. Chem. 2017, 89, 8782–8790. [Google Scholar] [CrossRef]
- Thomsen, B.L.; Christensen, J.B.; Rodenko, O.; Usenov, I.; Grønnemose, R.B.; Andersen, T.E.; Lassen, M. Accurate and fast identification of minimally prepared bacteria phenotypes using Raman spectroscopy assisted by machine learning. Sci. Rep. 2022, 12, 16436. [Google Scholar] [CrossRef]
- Chia, C.; Sesia, M.; Ho, C.S.; Jeffrey, S.S.; Dionne, J.; Candes, E.J.; Howe, R.T. Interpretable classification of bacterial Raman spectra with knockoff wavelets. IEEE J. Biomed. Health Inform. 2021, 26, 740–748. [Google Scholar] [CrossRef] [PubMed]
- Tewes, T.J.; Welle, M.C.; Hetjens, B.T.; Tipatet, K.S.; Pavlov, S.; Platte, F.; Bockmühl, D.P. Understanding Raman Spectral Based Classifications with Convolutional Neural Networks Using Practical Examples of Fungal Spores and Carotenoid-Pigmented Microorganisms. AI 2023, 4, 114–127. [Google Scholar] [CrossRef]
- Al-Shaebi, Z.; Uysal Ciloglu, F.; Nasser, M.; Aydin, O. Highly accurate identification of bacteria’s antibiotic resistance based on raman spectroscopy and U-net deep learning algorithms. ACS Omega 2022, 7, 29443–29451. [Google Scholar] [CrossRef]
- Kanter, I.; Yaari, G.; Kalisky, T. Applications of community detection algorithms to large biological datasets. Methods Mol. Biol. 2021, 2243, 59–80. [Google Scholar]
- Rodriguez, L.; Zhang, Z.; Wang, D. Recent advances of Raman spectroscopy for the analysis of bacteria. Anal. Sci. Adv. 2023, 4, 81–95. [Google Scholar] [CrossRef]
- Shlens, J. A Tutorial on Principal Component Analysis. arXiv 2014, arXiv:1404.1100. [Google Scholar]
- Berrazeg, M.; Drissi, M.; Medjahed, L.; Rolain, J.M. Hierarchical clustering as a rapid tool for surveillance of emerging antibiotic-resistance phenotypes in Klebsiella pneumoniae strains. J. Med. Microbiol. 2013, 62, 864–874. [Google Scholar] [CrossRef]
- Sinaga, K.P.; Yang, M.S. Unsupervised K-means clustering algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Mushtaq, A.; Nawaz, H.; Majeed, M.I.; Rashid, N.; Tahir, M.; Nawaz, M.Z.; Shahzad, K.; Dastgir, G.; Bari, R.Z.A.; ul Haq, A.; et al. Surface-enhanced Raman spectroscopy (SERS) for monitoring colistin-resistant and susceptible E. coli strains. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 278, 121315. [Google Scholar] [CrossRef]
- Sakagianni, A.; Koufopoulou, C.; Koufopoulos, P.; Kalantzi, S.; Theodorakis, N.; Nikolaou, M.; Paxinou, E.; Kalles, D.; Verykios, V.S.; Myrianthefs, P.; et al. Data-driven approaches in antimicrobial resistance: Machine learning solutions. Antibiotics 2024, 13, 1052. [Google Scholar] [CrossRef]
- Signoroni, A.; Savardi, M.; Pezzoni, M.; Guerrini, F.; Arrigoni, S.; Turra, G. Combining the use of CNN classification and strength-driven compression for the robust identification of bacterial species on hyperspectral culture plate images. IET Comput. Vis. 2018, 12, 941–949. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Y.; Mehmood, A.; Liu, Y.; Qin, X.; Dong, Q. Intelligent identification of foodborne pathogenic bacteria by self-transfer deep learning and ensemble prediction based on single-cell Raman spectrum. Talanta 2025, 285, 127268. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Xue, Y.; Yang, C.; Li, B.; Zhang, Y. Rapid identification and drug resistance screening of respiratory pathogens based on single-cell Raman spectroscopy. Front. Microbiol. 2023, 14, 1065173. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Chakraborty, T.; Doijad, S.; Falgenhauer, L.; Falgenhauer, J.; Goesmann, A.; Schwengers, O.; Heider, D. Deep transfer learning enables robust prediction of antimicrobial resistance for novel antibiotics. Antibiotics 2022, 11, 1611. [Google Scholar] [CrossRef]
- Yao, H.; Wei, L.; Xue, W. Adversarial contrastive domain-generative learning for bacteria Raman spectrum joint denoising and cross-domain identification. Eng. Appl. Artif. Intell. 2025, 148, 110426. [Google Scholar] [CrossRef]
- Weaver, D.T.; King, E.S.; Maltas, J.; Scott, J.G. Reinforcement Learning informs optimal treatment strategies to limit antibiotic resistance. Proc. Natl. Acad. Sci. USA 2024, 121, e2303165121. [Google Scholar] [CrossRef]
- Dumont, A.P.; Fang, Q.; Patil, C.A. A computationally efficient Monte-Carlo model for biomedical Raman spectroscopy. J. Biophotonics 2021, 14, e202000377. [Google Scholar] [CrossRef]
- Marangoni-Ghoreyshi, Y.G.; Franca, T.; Esteves, J.; Maranni, A.; Portes, K.D.P.; Cena, C.; Leal, C.R. Multi-resistant diarrheagenic Escherichia coli identified by FTIR and machine learning: A feasible strategy to improve the group classification. RSC Adv. 2023, 13, 24909–24917. [Google Scholar] [CrossRef]
- Ribeiro da Cunha, B.; Fonseca, L.P.; Calado, C.R. Simultaneous elucidation of antibiotic mechanism of action and potency with high-throughput Fourier-transform infrared (FTIR) spectroscopy and machine learning. Appl. Microbiol. Biotechnol. 2021, 105, 1269–1286. [Google Scholar] [CrossRef]
- Chasse, J. New Analytical Tools for Biomedical Applications Using Machine Learning and Spectroscopy. Spectroscopy 2023, 38, 8–9. [Google Scholar] [CrossRef]
- Schröder, U.C.; Kirchhoff, J.; Hübner, U.; Mayer, G.; Glaser, U.; Henkel, T.; Pfister, W.; Fritzsche, W.; Popp, J.; Neugebauer, U. On-chip spectroscopic assessment of microbial susceptibility to antibiotics within 3.5 hours. J. Biophotonics 2017, 10, 1547–1557. [Google Scholar] [CrossRef] [PubMed]
- Barrera-Patiño, C.P.; Soares, J.M.; Branco, K.C.; Inada, N.M.; Bagnato, V.S. Spectroscopic Identification of Bacteria Resistance to Antibiotics by Means of Absorption of Specific Biochemical Groups and Special Machine Learning Algorithm. Antibiotics 2023, 12, 1502. [Google Scholar] [CrossRef]
- Saikia, D.; Jadhav, P.; Hole, A.R.; Krishna, C.M.; Singh, S.P. Unraveling the Secrets of Colistin Resistance with Label-Free Raman Spectroscopy. Biosensors 2022, 12, 749. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Chakraborty, T.; Doijad, S.; Falgenhauer, L.; Falgenhauer, J.; Goesmann, A.; Hauschild, A.C.; Schwengers, O.; Heider, D. Prediction of antimicrobial resistance based on whole-genome sequencing and machine learning. Bioinformatics 2022, 38, 325–334. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, D.; Kamoshida, G.; Kawakubo, S.; Azuma, S.; Tsuji, T.; Kitada, N.; Saito-Moriya, R.; Yamada, N.; Tanaka, R.; Okuda, A.; et al. Near-infrared in vivo imaging system for dynamic visualization of lung-colonizing bacteria in mouse pneumonia. Microbiol. Spectr. 2024, 12, e00828-24. [Google Scholar] [CrossRef]
- Maguire, F.; Rehman, M.A.; Carrillo, C.; Diarra, M.S.; Beiko, R.G. Identification of primary antimicrobial resistance drivers in agricultural nontyphoidal Salmonella enterica serovars by using machine learning. Msystems 2019, 4, 10–1128. [Google Scholar] [CrossRef]
- Jiang, P.; Sun, S.; Goh, S.G.; Tong, X.; Chen, Y.; Yu, K.; He, Y.; Gin, K.Y.H. A rapid approach with machine learning for quantifying the relative burden of antimicrobial resistance in natural aquatic environments. Water Res. 2024, 262, 122079. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, J.; Duan, Q.; Feng, Y.; Luo, R.; Wang, W.; Liu, F.; Bi, S.; Lee, J. A fast antibiotic detection method for simplified pretreatment through spectra-based machine learning. Front. Environ. Sci. Eng. 2022, 16, 1–12. [Google Scholar] [CrossRef]
- Shams, S.; Ahmed, S.; Smaje, D.; Tengsuttiwat, T.; Lima, C.; Goodacre, R.; Muhamadali, H. Application of infrared spectroscopy to study carbon-deuterium kinetics and isotopic spectral shifts at the single-cell level. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2025, 327, 125374. [Google Scholar] [CrossRef]
- Muehlethaler, C.; Leona, M.; Lombardi, J.R. Towards a validation of surface-enhanced Raman scattering (SERS) for use in forensic science: Repeatability and reproducibility experiments. Forensic Sci. Int. 2016, 268, 1–13. [Google Scholar] [CrossRef]
- Fan, T.W.M.; Lane, A.N. Applications of NMR spectroscopy to systems biochemistry. Prog. Nucl. Magn. Reson. Spectrosc. 2016, 92, 18–53. [Google Scholar] [CrossRef] [PubMed]
- Zahra, A.; Qureshi, R.; Sajjad, M.; Sadak, F.; Nawaz, M.; Khan, H.A.; Uzair, M. Current advances in imaging spectroscopy and its state-of-the-art applications. Expert Syst. Appl. 2024, 238, 122172. [Google Scholar] [CrossRef]
- Kang, R.; Park, B.; Eady, M.; Ouyang, Q.; Chen, K. Classification of foodborne bacteria using hyperspectral microscope imaging technology coupled with convolutional neural networks. Appl. Microbiol. Biotechnol. 2020, 104, 3157–3166. [Google Scholar] [CrossRef] [PubMed]
- Ennab, M.; Hamid, M. Designing an interpretability-based model to explain the artificial intelligence algorithms in healthcare. Diagnostics 2022, 12, 1557. [Google Scholar] [CrossRef] [PubMed]
- Popa, S.L.; Pop, C.; Dita, M.O.; Brata, V.D.; Bolchis, R.; Czako, Z.; Saadani, M.M.; Ismaiel, A.; Dumitrascu, D.I.; Grad, S.; et al. Deep Learning and Antibiotic Resistance. Antibiotics 2022, 11, 1674. [Google Scholar] [CrossRef]
- Van Duijn, S.; Barsosio, H.C.; Omollo, M.; Milimo, E.; Akoth, I.; Aroka, R.; De Sanctis, T.; K’Oloo, A.; June, M.J.; Houben, N.; et al. Public-private partnership to rapidly strengthen and scale COVID-19 response in Western Kenya. Front. Public Health 2023, 10, 837215. [Google Scholar] [CrossRef]
- MacLean, E.L.; Villa-Castillo, L.; Ruhwald, M.; Ugarte-Gil, C.; Pai, M. Integrated testing for TB and COVID-19. Med 2022, 3, 162–166. [Google Scholar] [CrossRef]
- Available online: https://globalamrhub.org/ (accessed on 30 June 2025).
- Available online: https://gardp.org/ (accessed on 30 June 2025).
- Available online: https://carb-x.org/ (accessed on 30 June 2025).



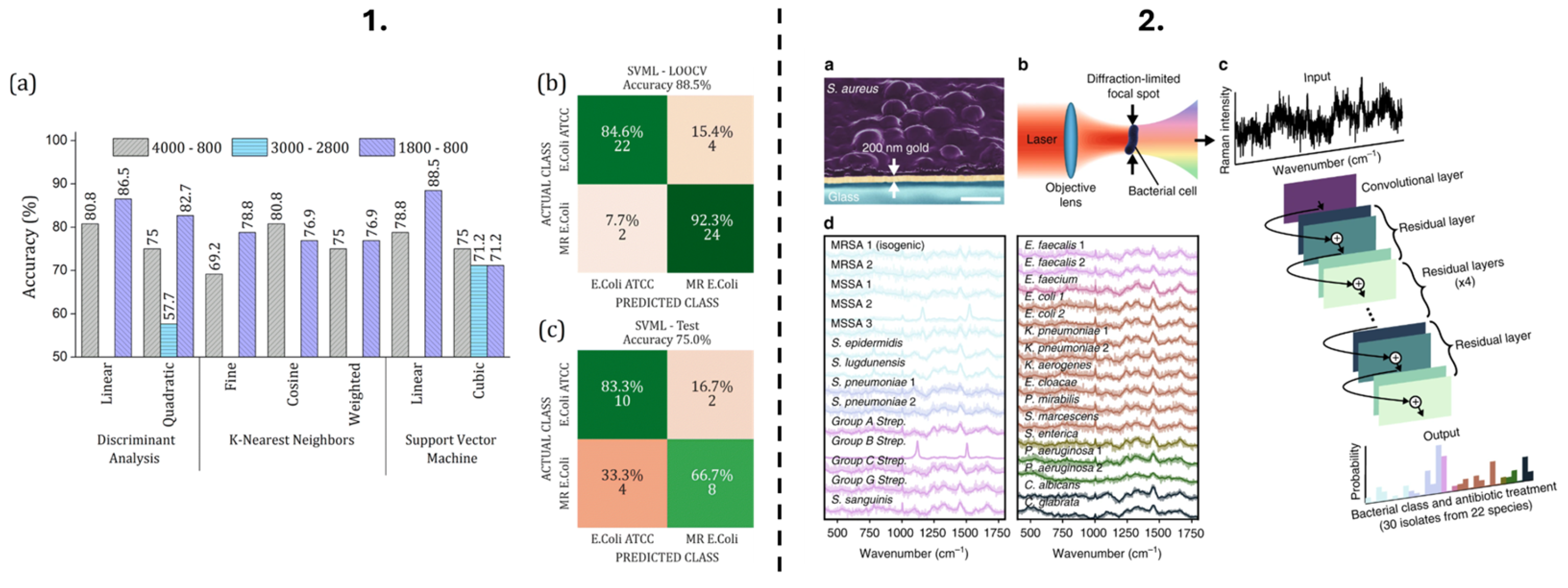
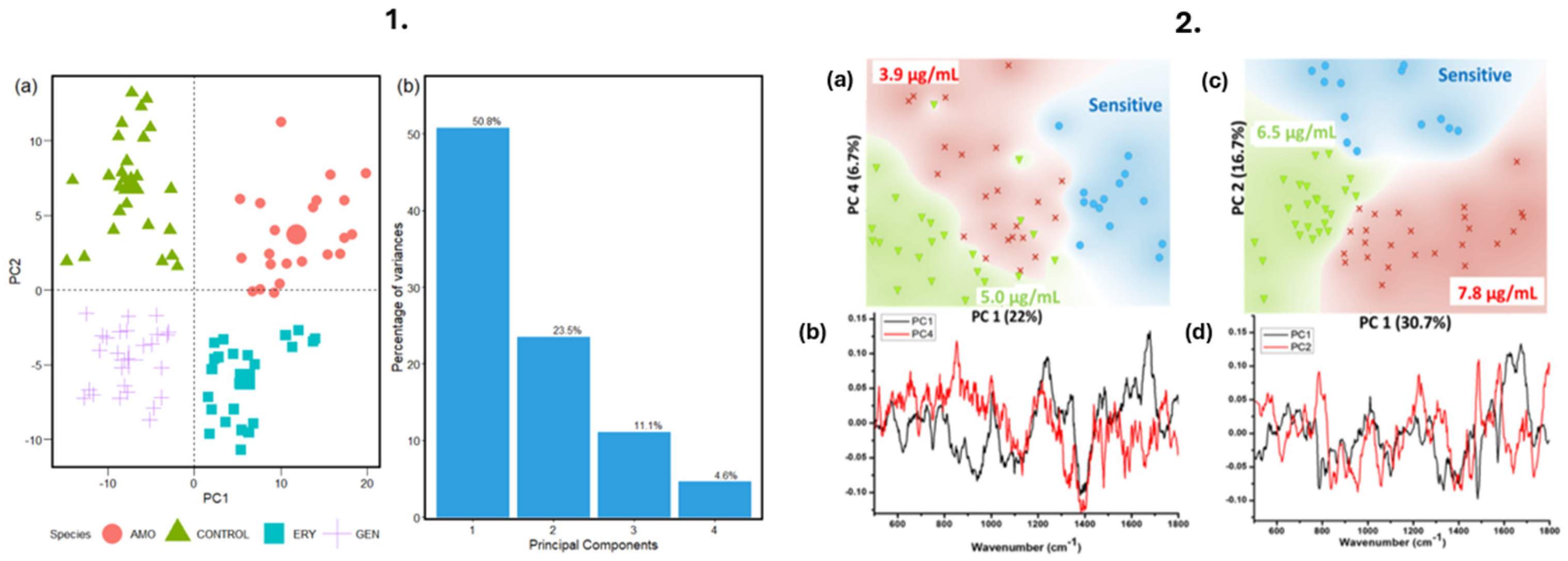
| Method | Output | Time to Result | Automated Compatibility | Limitations |
|---|---|---|---|---|
| Microdilution | MIC | 16–24 h | High | Labor-intensive, requires incubation |
| Gradient Diffusion (E-test) | MIC | 16–24 h | Medium | Higher cost, subjective MIC reading |
| Disk Diffusion | Zone Diameter | 16–24 h | Low | Qualitative, no MIC |
| Dielectrophoresis (DEP) | Viability | <1 h | Medium | Device complexity, sensitive to the ionic environment |
| Optoelectronic Sensors | Metabolic/Structural Changes | <1 h | High | Environmental sensitivity, complex fabrication |
| Technique | Molecular Target | Sample Prep | Strengths | Limitations |
|---|---|---|---|---|
| Raman | Vibrational bonds (C-H, C=C, etc.) | Dried bacterial film on slide (e.g., quartz or CaF2) | Label-free, chemical-specific, single-cell capable | Fluorescence background, low signal without enhancement |
| FTIR | IR-active bonds (e.g., C=O, N-H, O-H) | Thin dried film or pellet on an IR-transparent surface | Broad chemical fingerprint, minimal reagents needed | Lower spatial resolution, needs a dry sample |
| SERS | Same as Raman + signal amplification | Bacteria coated with silver/gold nanoparticles | Ultra-sensitive, works on low-concentration samples | Nanoparticle prep can be complex with reproducibility issues |
| NMR | Nucleus environment (e.g., H, C, P nuclei) | Requires high sample concentration in solution or solid-state | Detailed structural info, label-free | Expensive, long time, needs high sample volume |
| NIR | Overtones and combinations (C-H, N-H, O-H) | Little prep; works in aqueous solution | Fast, works in real-time, easy setup | Low specificity, overlapping spectra |
| HIS | Whole spectra per pixel (multiband imaging) | Grow bacteria on a flat transparent surface | High spatial info, detects heterogeneity | Complex hardware, lots of data |
| THz | Weak molecular bonds, water dynamics | Film or biofilm layer, hydrated samples | Good for hydration and membrane properties | Costly, not common yet |
| Method | Description | Applications in Antimicrobial Resistance |
|---|---|---|
| PLS | A linear regression model that transforms predictors and responses into a new domain. Useful when the target variable is continuous or categorical. | Raman spectroscopy coupled with PLSR successfully identified Campylobacter species in mixed samples of C. jejuni, E. coli, C. upsaliensis, and C. fetus [77]. |
| LDA | Projects data to a lower-dimensional space for class separation, enhancing interpretability. | PCA-LDA models combined with IR spectroscopy differentiated between resistant and sensitive E. coli strains [78]. Also applied to SERS data to classify clinical pathogens [52]. |
| SVM | Projects data into a higher-dimensional space and creates hyperplanes for classification. | SVM with Raman spectra enabled accurate identification of infectious fungi with 100% sensitivity and specificity using single-cell Raman spectroscopy (SCRS) [75]. |
| RF | An ensemble of decision trees trained on different dataset subsets and features. Provides robust classification and handles overfitting well. | Combined with spectroscopy for classification of antibiotic-resistant bacterial strains; improved feature importance interpretation [79]. |
| Logistic Regression | Uses a sigmoid function to predict categorical outcomes; particularly effective in binary classification problems. | Used as a baseline classifier in AMR studies; interpretable and efficient in small-scale Raman datasets [80]. |
| AdaBoost | Similar to GB but increases weight for misclassified points. Focuses learners on difficult cases to improve accuracy. | Boosts weak classifiers on spectroscopy datasets; useful in settings with class imbalance. |
| Neural Network | Inspired by the human brain; consists of interconnected layers for learning non-linear patterns. Supports classification and regression tasks. | Neural networks, including ANN and CNN, were used for bacterial and fungal infection classification from Raman and IR databases with >90% accuracy [12,81]. CNNs also identified MRSA vs. MSSA with 89% accuracy [12]. |
| U-Net (CNN architecture) | Specialized CNN architecture for image-like data; ideal for segmentation and feature extraction. | U-Net architecture achieved high accuracy in classifying antibiotic resistance from Raman spectra of 30 bacterial and yeast isolates [82]. |
| Method | Description | Applications in Antimicrobial Resistance |
|---|---|---|
| PCA | A dimensionality reduction technique widely used in spectroscopy to reduce features into principal components for easier visualization and interpretation. | Raman spectroscopy was used to find spectral differences between colistin-sensitive and resistant E. coli strains using PCA [88]. PCA and clustering were applied to identify similar spectral patterns among Mycobacterium bovis and Mycobacteriales strains [73]. |
| HCA | Groups similar data points into clusters using a tree-like dendrogram, which helps identify relationships among observations. | Used in conjunction with Raman spectroscopy to classify bacterial strains and monitor structural similarities across resistant and non-resistant species [77]. |
| K-Means Clustering | A centroid-based algorithm that partitions data into a predefined number of clusters based on distance metrics. | Applied in spectral data to differentiate microbial strains by their biochemical signatures, especially in unsupervised analysis settings [89]. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saikia, D.; Dadhara, R.; Tanan, C.; Avati, P.; Verma, T.; Pandey, R.; Singh, S.P. Combating Antimicrobial Resistance: Spectroscopy Meets Machine Learning. Photonics 2025, 12, 672. https://doi.org/10.3390/photonics12070672
Saikia D, Dadhara R, Tanan C, Avati P, Verma T, Pandey R, Singh SP. Combating Antimicrobial Resistance: Spectroscopy Meets Machine Learning. Photonics. 2025; 12(7):672. https://doi.org/10.3390/photonics12070672
Chicago/Turabian StyleSaikia, Dimple, Ritam Dadhara, Cebajel Tanan, Prajwal Avati, Tushar Verma, Rishikesh Pandey, and Surya Pratap Singh. 2025. "Combating Antimicrobial Resistance: Spectroscopy Meets Machine Learning" Photonics 12, no. 7: 672. https://doi.org/10.3390/photonics12070672
APA StyleSaikia, D., Dadhara, R., Tanan, C., Avati, P., Verma, T., Pandey, R., & Singh, S. P. (2025). Combating Antimicrobial Resistance: Spectroscopy Meets Machine Learning. Photonics, 12(7), 672. https://doi.org/10.3390/photonics12070672





