Efficient Design of a Terahertz Metamaterial Dual-Band Absorber Using Multi-Objective Firefly Algorithm Based on a Multi-Cooperative Strategy
Abstract
1. Introduction
2. Structure
3. Method
- (1)
- When firefly Fj has no dominance relationship with others, the update equation is as follows:
- (2)
- When firefly Fj is dominated by firefly Fi, the update equation is as follows:
4. Result Analysis
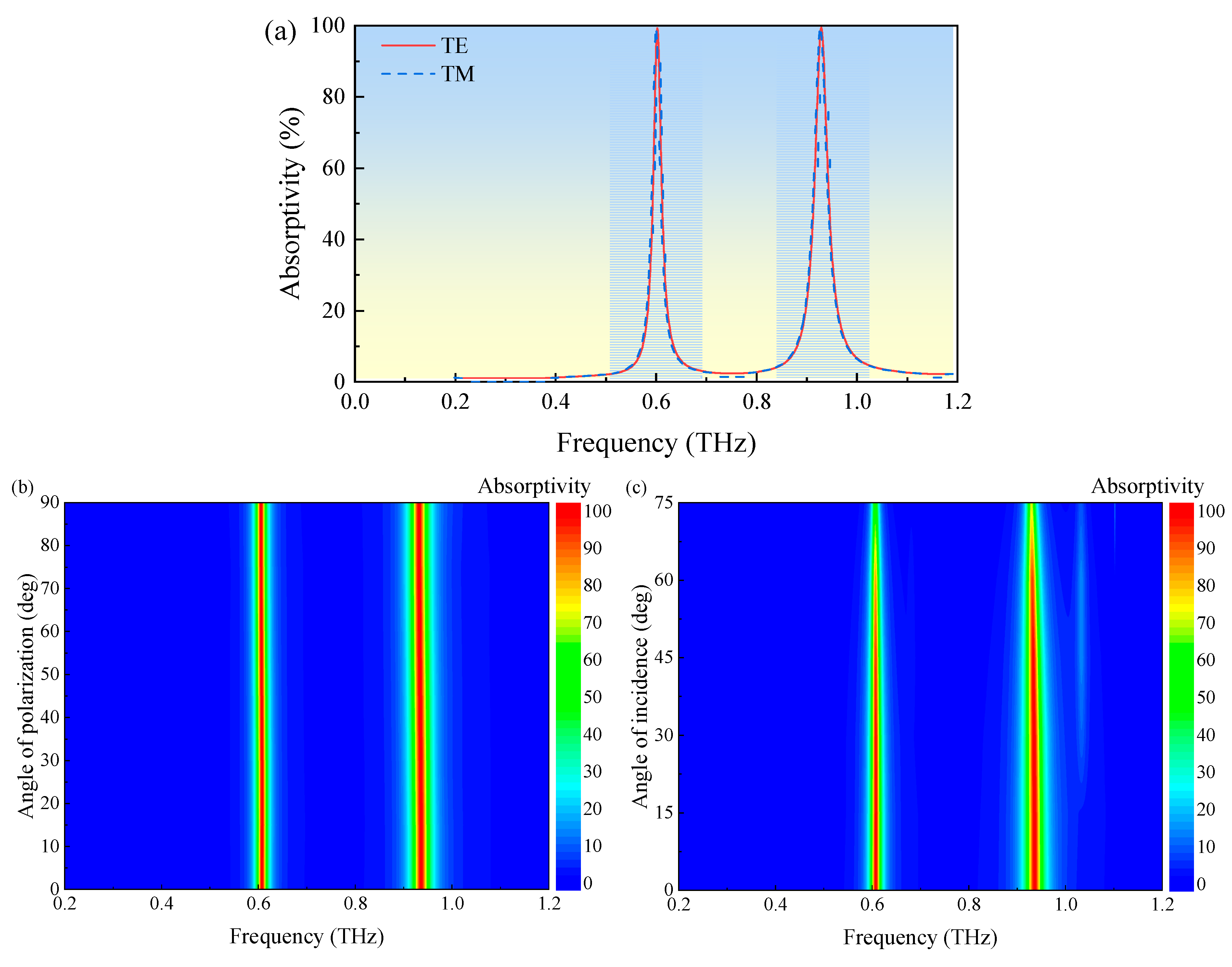
4.1. Analysis of Absorption Spectral Performance
4.2. Analysis of Electromagnetic Characteristics
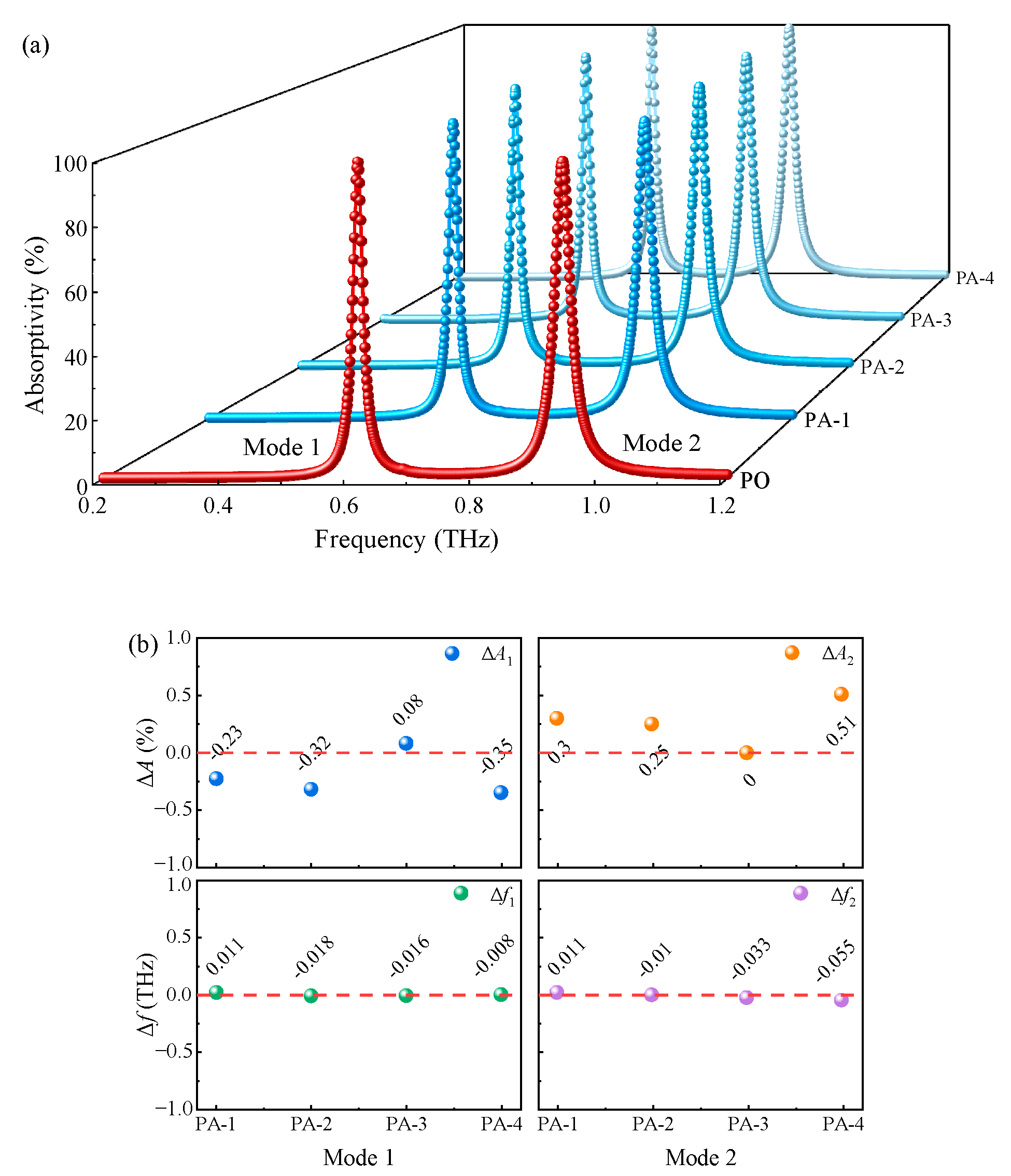
4.3. Stability Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Siegel, P.H. Terahertz technology. IEEE Trans. Microw. Theory Tech. 2002, 50, 910–928. [Google Scholar] [CrossRef]
- Pacheco-Peña, V. Terahertz Technologies and Its Applications. Electronics 2021, 10, 268. [Google Scholar] [CrossRef]
- Lu, X.Y.; Venkatesh, S.; Saeidi, H. A Review on Applications of Integrated Terahertz Systems. China Commun. 2021, 18, 175–201. [Google Scholar] [CrossRef]
- Jain, P.K.; Luther, J.; Ewers, T.; Alivisatos, A.P. Localized surface plasmon resonances (LSPRs) arising from free carriers in doped quantum dots. Nat Mater. 2011, 10, 361–366. [Google Scholar]
- Kim, J.B.; Lee, J.H.; Moon, C.K.; Kim, S.Y.; Kim, J.J. Highly Enhanced Light Extraction from Surface Plasmonic Loss Minimized Organic Light-Emitting Diodes. Adv. Mater. 2013, 25, 3571–3577. [Google Scholar] [CrossRef]
- Saadeldin, A.S.; Hameed, M.F.O.; Elkaramany, E.M.A.; Obayya, S.S.A. Highly Sensitive Terahertz Metamaterial Sensor. IEEE Sens. J. 2019, 19, 7993–7999. [Google Scholar] [CrossRef]
- Wang, D.X.; Luo, S.Y.; Xu, K.D. A Flexible Terahertz Metamaterial Sensor for Pesticide Sensing and Detection. Acs Appl. Mater. Interfaces 2024, 16, 27969–27978. [Google Scholar] [CrossRef]
- Wei, Q.; Bi, D.; Qi, X.; Ren, M.; Wu, F. Angle-independent topological interface states in one-dimensional photonic crystal heterostructures containing hyperbolic metamaterials. Opt. Lett. 2025, 50, 451–454. [Google Scholar] [CrossRef]
- Wei, M.G.; Long, Y.; Wu, F.; Liu, G.G.; Zhang, B.L. Abrupt lateral beam shifts from terahertz quasi-bound states in the continuum. Sci. Bull. 2025, 70, 882–888. [Google Scholar] [CrossRef]
- Lu, X.Y.; Wan, R.G.; Zhang, T.Y. Metal-dielectric-metal based narrow band absorber for sensing applications. Opt. Express 2015, 23, 29842–29847. [Google Scholar] [CrossRef]
- Liu, X.L.; Tyler, T.; Starr, T.; Starr, A.; Jokerst, N.M.; Padilla, W.J. Taming the blackbody with infrared metamaterials as selective thermal emitters. Phys. Rev. Lett. 2011, 107, 045901. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Li, J.; Yang, H.; Wang, J.; Li, B.; Zhang, H.; Yi, Y. TiN-Only Metasurface Absorber for Solar Energy Harvesting. Photonics 2025, 12, 443. [Google Scholar] [CrossRef]
- Cheng, S.; Li, W.; Zhang, H.; Akhtar, M.N.; Yi, Z.; Zeng, Q.; Ma, C.; Sun, T.; Wu, P.; Ahmad, S. High sensitivity five band tunable metamaterial absorption device based on block like Dirac semimetals. Opt. Commun. 2024, 569, 130816. [Google Scholar] [CrossRef]
- Zeng, Z.; Liu, H.; Zhang, H.; Cheng, S.; Yi, Y.; Yi, Z.; Wang, J.; Zhang, J. Tunable ultra-sensitive four-band terahertz sensors based on Dirac semimetals. Photonics Nanostruct.-Fundam. Appl. 2025, 63, 101347. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Pang, H.-Z.; Wang, X.; Wang, J.-L.; Wang, Z.-L.; Liu, S.-Y.; Tian, H.-Q. Sensing characteristics of dual band terahertz metamaterial absorber sensor. Acta Phys. Sin. 2021, 70, 168101. [Google Scholar] [CrossRef]
- Darsi, L.; Rana, G. A Refractive Index-Based Dual-Band Metamaterial Sensor Design and Analysis for Biomedical Sensing Applications. Sensors 2025, 25, 232. [Google Scholar] [CrossRef]
- Ma, L.M.; Liu, Y.H.; Zhu, Y.K.; Gu, W.H. Sensing Performance of Triple-Band Terahertz Metamaterial Absorber Based on Snowflake-Shaped Resonators. Photonics 2022, 9, 777. [Google Scholar] [CrossRef]
- Zhu, A.J.; Bu, P.C.; Cheng, L.; Hu, C.; Mahapatra, R. High-Q Multiband Narrowband Absorbers Based on Two-Dimensional Graphene Metamaterials. Photonics 2024, 11, 469. [Google Scholar] [CrossRef]
- Ding, Z.P.; Su, W.; Luo, Y.L.; Ye, L.P.G.; Li, W.L.; Zhou, Y.H.; Tang, B.; Yao, H.B. Artificial neural network-based inverse design of metasurface absorber with tunable absorption window. Mater. Des. 2023, 234, 112331. [Google Scholar] [CrossRef]
- Ding, K.G.; Zhao, Z.N.; Ma, S.Y.; Qiu, Y.Q.; Lang, T.T.; Chen, T. Accelerating optimization of terahertz metasurface design using principal component analysis in conjunction with deep learning networks. Phys. Commun. 2024, 66, 102452. [Google Scholar] [CrossRef]
- Min, X.T.; Hao, X.Y.; Chen, Y.P.; Liu, M.; Cheng, X.M.; Huang, W.; Li, Y.F.; Xu, Q.; Zhang, X.Q.; Ye, M.; et al. Deep learning-enhanced prediction of terahertz response of metasurfaces. Opt. Laser Technol. 2024, 179, 111321. [Google Scholar] [CrossRef]
- Li, J.; Cai, R.; Chen, H.Y.; Ma, B.Y.; Wu, Q.N.; Li, M.W. Deep neural network-enabled multifunctional switchable terahertz metamaterial devices. Sci. Rep. 2024, 14, 19868. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Ong, J.R.; Chu, H.S.; Chen, V.H.J.; Zhu, A.Y.T.; Genevet, P. Freestanding dielectric nanohole array metasurface for mid-infrared wavelength applications. Opt. Lett. 2017, 42, 2639–2642. [Google Scholar] [CrossRef]
- Zhang, B.H.; Chen, W.W.; Wang, P.J.; Dai, S.X.; Li, H.X.; Lu, H.; Ding, J.; Li, J.; Li, Y.; Fu, Q.; et al. Particle swarm optimized polarization beam splitter using metasurface-assisted silicon nitride Y-junction for mid-infrared wavelengths. Opt. Commun. 2019, 451, 186–191. [Google Scholar] [CrossRef]
- Mokhtari, A.; Rezaei, M.H.; Zarifkar, A. Ultra-broadband absorber based on metamaterial resonators utilizing particle swarm optimization algorithm. Photonics Nanostruct.-Fundam. Appl. 2023, 53, 101105. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.H.; Meng, Y.L.; Li, Y.; Li, Y.S.; Pan, G.M.; Kang, J.; Zhan, C.L.; Wang, Z.D.; Hu, S.T.; et al. Ultra-broadband, high-efficiency metamaterial absorber based on particle swarm optimization algorithm. Opt. Mater. 2024, 150, 115140. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural And Artificial Systems; MIT Press: Cambridge, UK, 1975; Volume 1, pp. 159–170. [Google Scholar]
- Liu, C.X.; Maier, S.A.; Li, G.X. Genetic-Algorithm-Aided Meta-Atom Multiplication for Improved Absorption and Coloration in Nanophotonics. ACS Photonics 2020, 7, 1716–1722. [Google Scholar] [CrossRef]
- Cai, H.G.; Srinivasan, S.; Czaplewski, D.A.; Martinson, A.B.F.; Gosztola, D.J.; Stan, L.; Loeffler, T.; Sankaranarayanan, S.; López, D. Inverse design of metasurfaces with non-local interactions. Npj Comput. Mater. 2020, 6, 116. [Google Scholar] [CrossRef]
- Lin, C.H.; Chen, Y.S.; Lin, J.T.; Wu, H.C.; Kuo, H.T.; Lin, C.F.; Chen, P.; Wu, P.C. Automatic Inverse Design of High-Performance Beam-Steering Metasurfaces via Genetic-type Tree Optimization. Nano Lett. 2021, 21, 4981–4989. [Google Scholar] [CrossRef]
- Donda, K.D.; Hegde, R.S. Rapid Design of Wide-Area Heterogeneous Electromagnetic Metasurfaces beyond the Unit-Cell Approximation. Prog. Electromagn. Res. M 2017, 60, 1–10. [Google Scholar] [CrossRef]
- Zhu, D.Z.; Whiting, E.B.; Campbell, S.D.; Burckel, D.B.; Werner, D.H. Optimal High Efficiency 3D Plasmonic Metasurface Elements Revealed by Lazy Ants. ACS Photonics 2019, 6, 2741–2748. [Google Scholar] [CrossRef]
- Zhang, J.H.; Zhang, S.J.; Dong, J.; Wang, M.; Luo, H.; Wu, R.G.; Xiao, C.W. Design of Pixel Terahertz Metamaterial Absorber Sensor Based on an Improved Ant Colony Algorithm. IEEE Sens. J. 2024, 24, 40801–40810. [Google Scholar] [CrossRef]
- Chen, N.; Yang, S.; An, S. A New Hybrid Algorithm based on PSO and Fireworks Algorithm for Optimal Design of Metasurface Absorber in RF Energy Harvesting. In Proceedings of the 2024 IEEE 21st Biennial Conference on Electromagnetic Field Computation (CEFC), Jeju, Republic of Korea, 2–5 June 2024; pp. 1–2. [Google Scholar]
- Qu, W.W.; Wang, Y.R.; Li, G.L.; Xie, Z.H.; Li, Z.R.; Deng, H.; Shang, L.P. An adaptive assisted method based on MOPSO for THz MMA effective designing. J. Phys. D Appl. Phys. 2024, 58, 035103. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Beckington, UK, 2010; Volume 2, pp. 1–49. [Google Scholar]
- Xie, C.W.; Zhang, F.L.; Lu, J.B.; Xiao, C.; Long, G.L. Multi-Objective Firefly Algorithm Based on Multiply Cooperative Strategies. Acta Electron. Sin. 2019, 47, 2359–2367. [Google Scholar]
- Wang, Y.R.; Qu, W.W.; Li, G.L.; Deng, H.; Shang, L.P. An optimization method for terahertz metamaterial absorber based on multi-objective particle swarm optimization. Acta Phys. Sin. 2025, 74, 057801. [Google Scholar] [CrossRef]
- Chen, X.; Grzegorczyk, T.M.; Wu, B.-I.; Pacheco, J., Jr.; Kong, J.A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 2004, 70 Pt 2, 016608. [Google Scholar] [CrossRef]
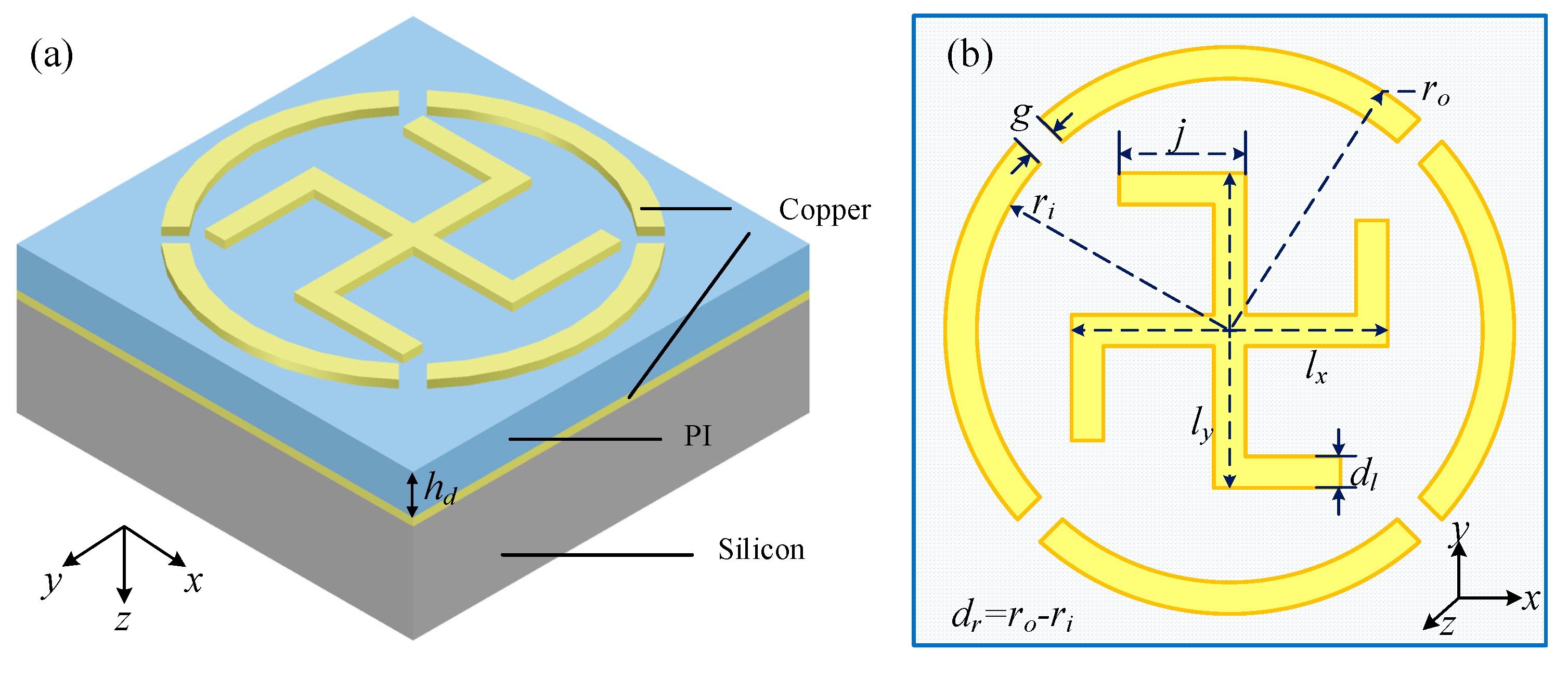
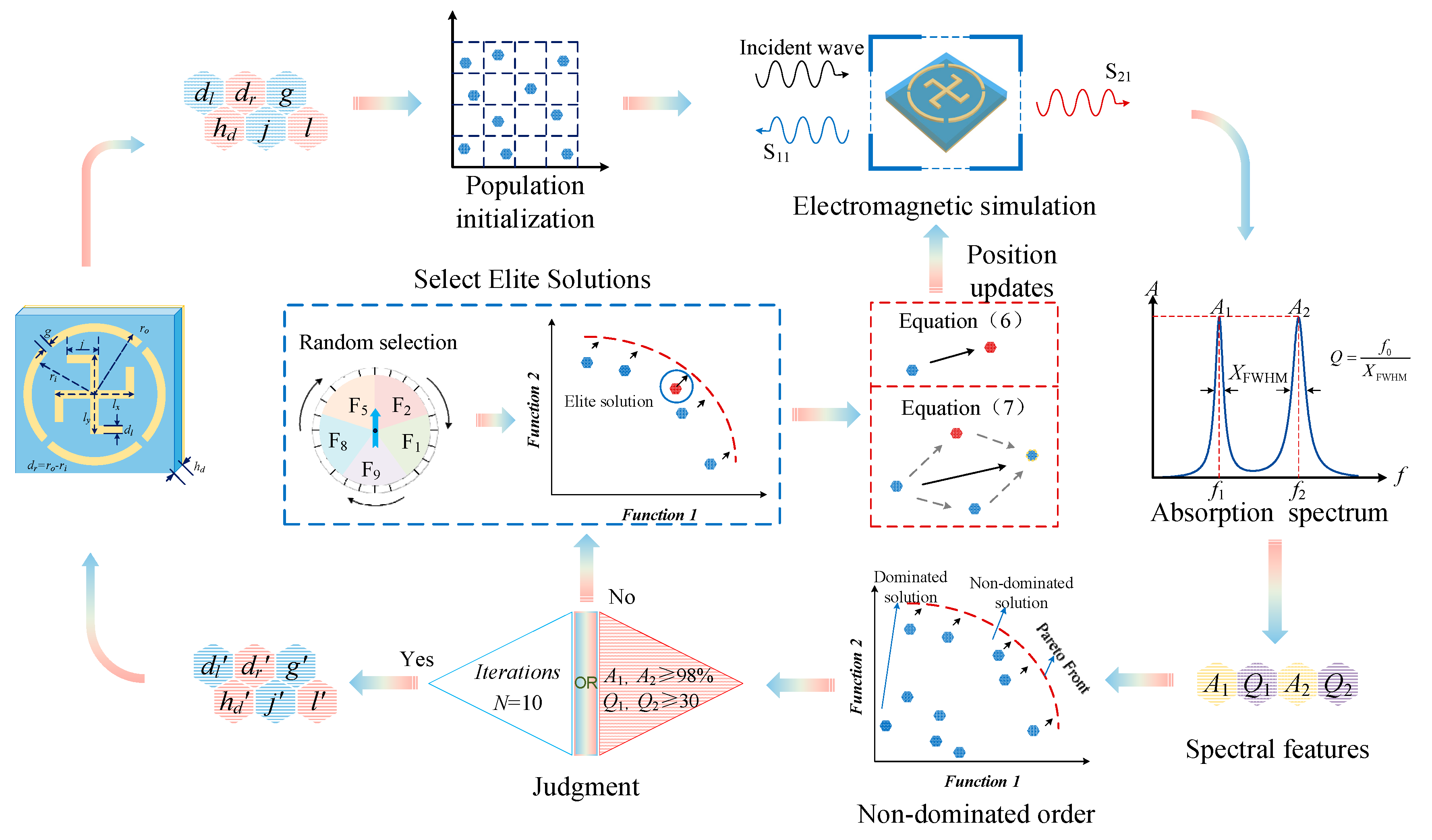

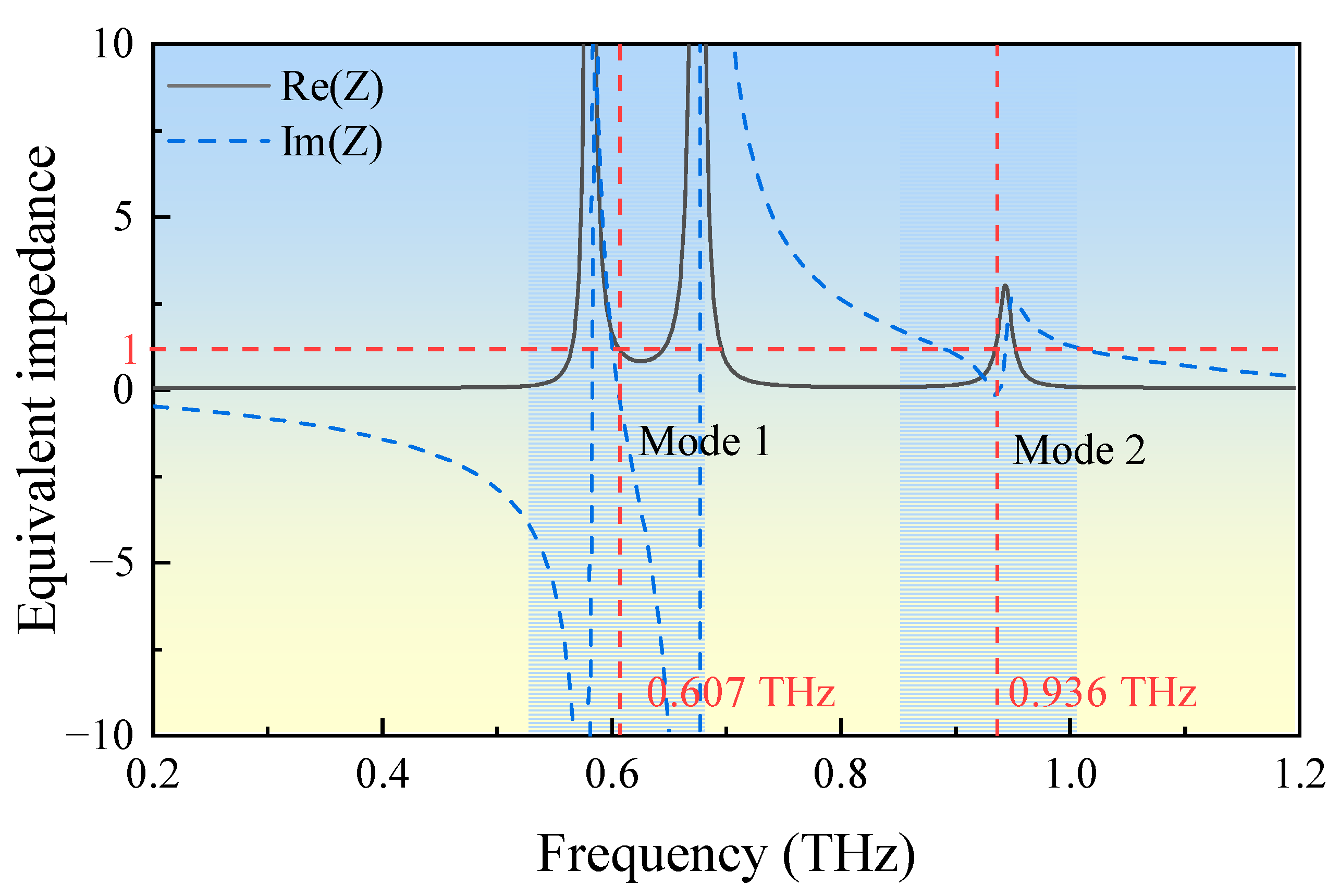
| Constraint Name | Constraint Equation | Range of Constraint |
|---|---|---|
| m1 | m1 < 0 | |
| m2 | m2 < 0 | |
| m3 | m3 < 0 | |
| m4 | m4 < 0 | |
| m5 | m5 < 0 | |
| m6 | m6 < 0 |
| Method | f0 (THz) | A (%) | Q-Factor | Population Size | Iterations | Total Time (h) |
|---|---|---|---|---|---|---|
| MOPSO | 0.617 | 99.92 | 33.11 | 15 | 14 | 12.22 |
| 0.869 | 98.26 | 30.13 | ||||
| MOFA-MCS | 0.607 | 99.14 | 31.48 | 15 | 8 | 6.98 |
| 0.936 | 99.42 | 30.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Huang, Y.; Wang, Y.; Qu, W.; Deng, H.; Shang, L. Efficient Design of a Terahertz Metamaterial Dual-Band Absorber Using Multi-Objective Firefly Algorithm Based on a Multi-Cooperative Strategy. Photonics 2025, 12, 637. https://doi.org/10.3390/photonics12070637
Li G, Huang Y, Wang Y, Qu W, Deng H, Shang L. Efficient Design of a Terahertz Metamaterial Dual-Band Absorber Using Multi-Objective Firefly Algorithm Based on a Multi-Cooperative Strategy. Photonics. 2025; 12(7):637. https://doi.org/10.3390/photonics12070637
Chicago/Turabian StyleLi, Guilin, Yan Huang, Yurong Wang, Weiwei Qu, Hu Deng, and Liping Shang. 2025. "Efficient Design of a Terahertz Metamaterial Dual-Band Absorber Using Multi-Objective Firefly Algorithm Based on a Multi-Cooperative Strategy" Photonics 12, no. 7: 637. https://doi.org/10.3390/photonics12070637
APA StyleLi, G., Huang, Y., Wang, Y., Qu, W., Deng, H., & Shang, L. (2025). Efficient Design of a Terahertz Metamaterial Dual-Band Absorber Using Multi-Objective Firefly Algorithm Based on a Multi-Cooperative Strategy. Photonics, 12(7), 637. https://doi.org/10.3390/photonics12070637




