Topological Rainbow Trapping with Expanded Bandwidth in Valley Photonic Crystals
Abstract
1. Introduction
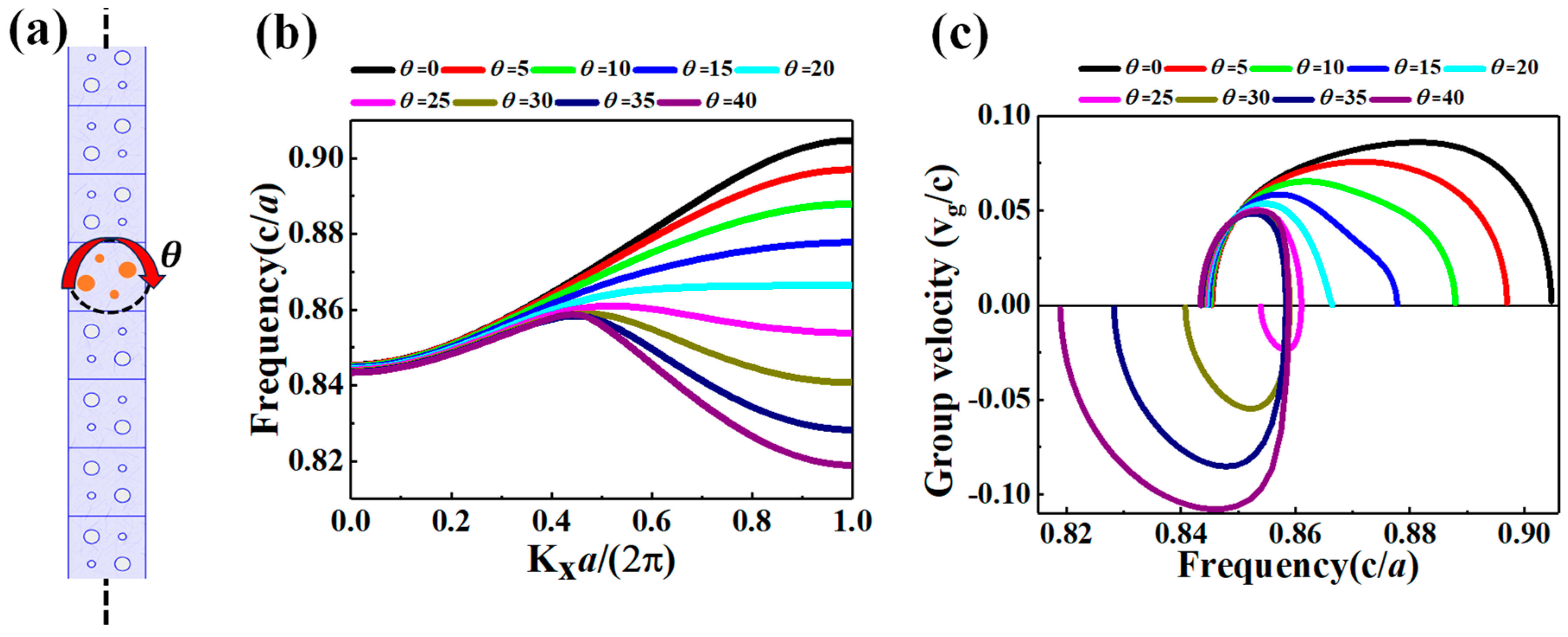
2. Valley Topological PC and Photonic Band Structures
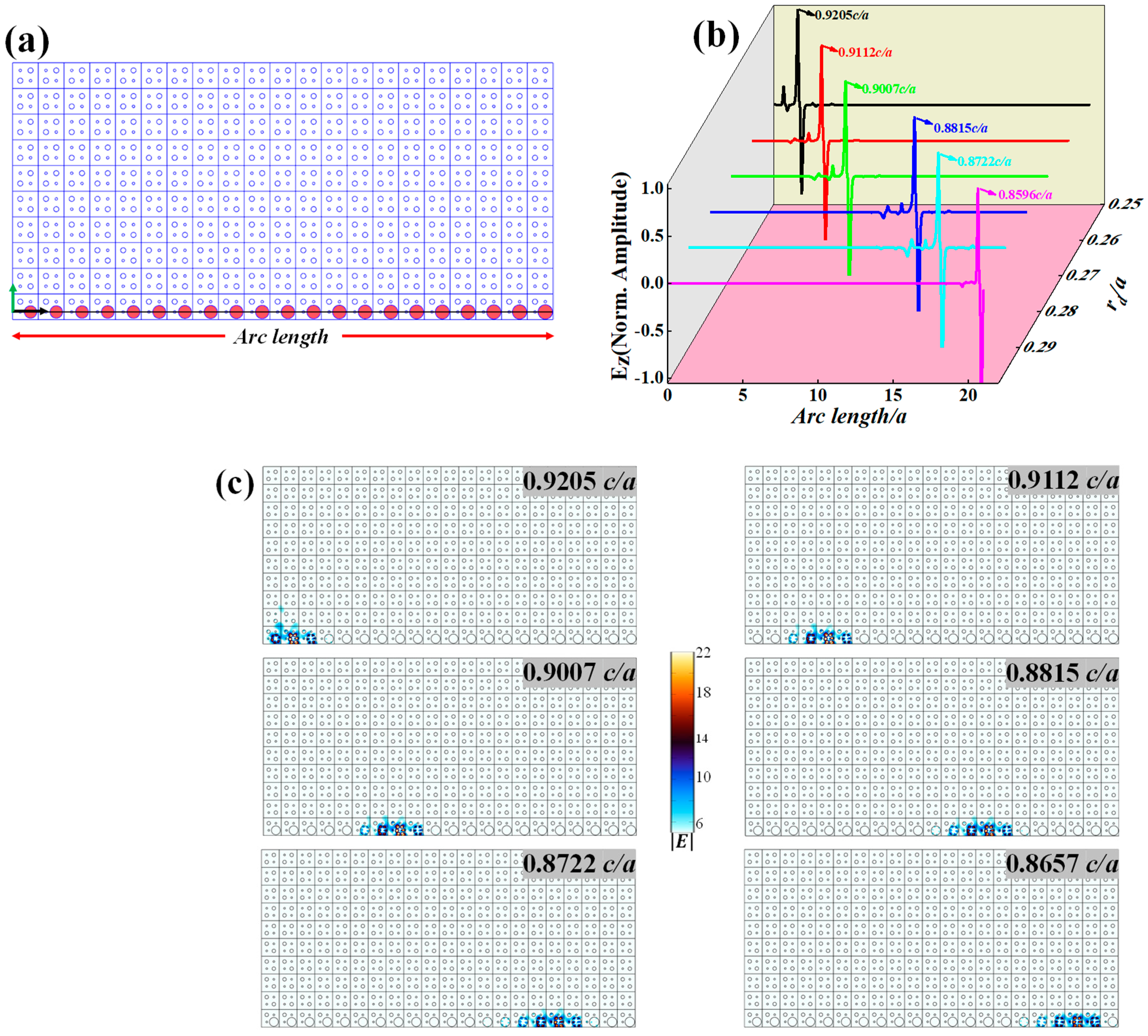
3. Rainbow Trapping Structures
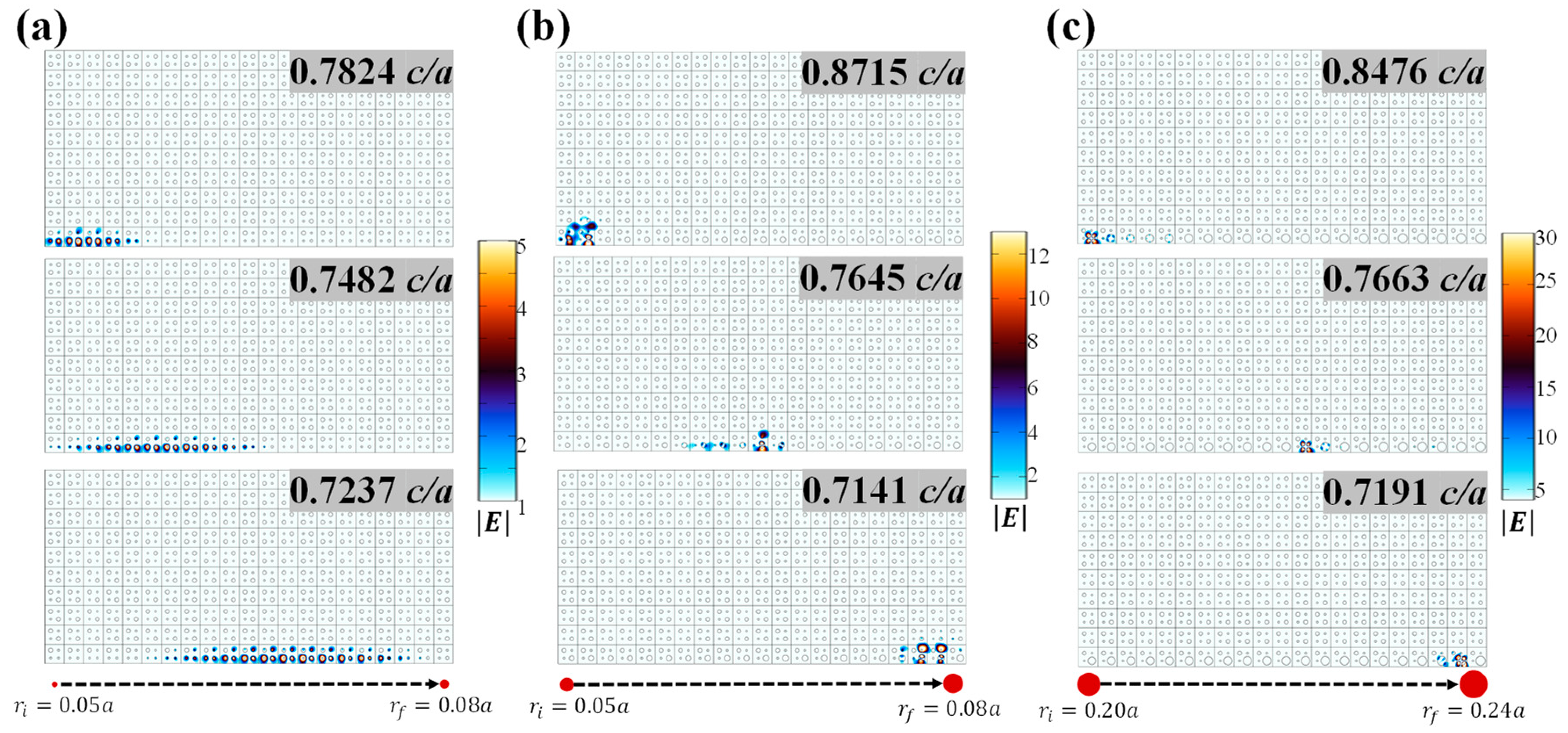
4. Verification of Robustness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Z.-Y. Optics and photonics at nanoscale: Principles and perspectives. Europhys. Lett. 2015, 110, 14001. [Google Scholar] [CrossRef]
- You, J.; Ma, Q.; Zhang, L.; Liu, C.; Zhang, J.; Liu, S.; Cui, T. Electromagnetic metamaterials: From classical to quantum. Electromagn. Sci. 2023, 1, 1–33. [Google Scholar] [CrossRef]
- Ai, X.-C.; Pan, S.-C.; Wang, Y.-H.; Tian, S.-C. Optimization Design of Photonic-Crystal Surface-Emitting Lasers: Toward Large Bandwidth and Single-Lane 200G Optical Transmission. Prog. Electromagn. Res. 2024, 180, 89–101. [Google Scholar] [CrossRef]
- Firouzjaei, A.S.; Afghahi, S.S.; Valmoozi, A.-A.E. Emerging Trends, Applications, and Fabrication Techniques in Photonic Crystal Technology. In Recent Advances and Trends in Photonic Crystal Technology; IntechOpen: London, UK, 2024. [Google Scholar]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton Univ. Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Hou, C.-H.; Tseng, S.-Z.; Chan, C.-H.; Chen, T.-J.; Chien, H.-T.; Hsiao, F.-L.; Chiu, H.-K.; Lee, C.-C.; Tsai, Y.-L.; Chen, C.-C. Output power enhancement of light-emitting diodes via two-dimensional hole arrays generated by a monolayer of microspheres. Appl. Phys. Lett. 2009, 95, 133105. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Cai, D.P.; Chen, C.C.; Chan, C.H.; Lee, C.C.; Tsai, Y.L. Photonic Crystal Cavity with Double Heterostructure in GaN Bulk. IEEE Photonics J. 2013, 5, 2202606. [Google Scholar] [CrossRef]
- Hsiao, F.-L.; Ni, C.-Y.; Tsai, Y.-P.; Chiang, T.-W.; Yang, Y.-T.; Fan, C.-J.; Chang, H.-M.; Chen, C.-C.; Lee, H.-F.; Lin, B.-S.; et al. Design of Waveguide Polarization Convertor Based on Asymmetric 1D Photonic Crystals. Nanomaterials 2022, 12, 2454. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.-Y.; Huang, H.-C.; Chen, C.-W.; Hsiao, F.-L.; Cheng, Y.-C.; Chen, C.-C. Design of Reflective Polarization Rotator in Silicon Waveguide. Nanomaterials 2022, 12, 3694. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.-H.; Cai, D.-P.; Tsai, Y.-L.; Chen, C.-C.; Lin, C.-E.; Yen, T.-J. Genetic algorithms optimization of photonic crystal fibers for half diffraction angle reduction of output beam. Opt. Express 2014, 22, 22590–22597. [Google Scholar] [CrossRef]
- Chen, C.-C. Design of ultra-short polarization convertor with enhanced birefringence by photonic crystals. Results Phys. 2021, 24, 104138. [Google Scholar] [CrossRef]
- Price, H.; Chong, Y.; Khanikaev, A.; Schomerus, H.; Maczewsky, L.J.; Kremer, M.; Heinrich, M.; Szameit, A.; Zilberberg, O.; Yang, Y. Roadmap on topological photonics. J. Phys. Photonics 2022, 4, 032501. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photonics 2014, 8, 821–829. [Google Scholar] [CrossRef]
- Ota, Y.; Takata, K.; Ozawa, T.; Amo, A.; Jia, Z.; Kante, B.; Notomi, M.; Arakawa, Y.; Iwamoto, S. Active topological photonics. Nanophotonics 2020, 9, 547–567. [Google Scholar] [CrossRef]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef]
- Liu, J.-W.; Shi, F.-L.; He, X.-T.; Tang, G.-J.; Chen, W.-J.; Chen, X.-D.; Dong, J.-W. Valley photonic crystals. Adv. Phys. X 2021, 6, 1905546. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.-X.; Liang, L.; Zhu, W.; Fan, L.; Lin, Z.-K.; Li, F.; Zhang, X.; Luan, P.-G.; Poo, Y.; et al. Hybrid topological photonic crystals. Nat. Commun. 2023, 14, 4457. [Google Scholar] [CrossRef]
- Zeng, Y.; Chattopadhyay, U.; Zhu, B.; Qiang, B.; Li, J.; Jin, Y.; Li, L.; Davies, A.G.; Linfield, E.H.; Zhang, B.; et al. Electrically pumped topological laser with valley edge modes. Nature 2020, 578, 246–250. [Google Scholar] [CrossRef]
- Liu, J.-W.; Liu, G.-G.; Zhang, B. Three-Dimensional Topological Photonic Crystals. Prog. Electromagn. Res. 2024, 181, 99–112. [Google Scholar] [CrossRef]
- Zheng, J.; Guo, Z.; Sun, Y.; Jiang, H.; Li, Y.; Chen, H. Topological Edge Modes in One-Dimensional Photonic Artificial Structures. Prog. Electromagn. Res. 2023, 177, 1–20. [Google Scholar] [CrossRef]
- Elshahat, S.; Wang, C.; Zhang, H.; Lu, C. Perspective on the topological rainbow. Appl. Phys. Lett. 2021, 119, 230505. [Google Scholar] [CrossRef]
- Lu, C.; Sun, Y.-Z.; Wang, C.; Zhang, H.; Zhao, W.; Hu, X.; Xiao, M.; Ding, W.; Liu, Y.-C.; Chan, C.T. On-chip nanophotonic topological rainbow. Nat. Commun. 2022, 13, 2586. [Google Scholar] [CrossRef]
- Xu, Q.; Peng, Y.; Shi, A.; Peng, P.; Liu, J. Dual-band topological rainbows in Penrose-triangle photonic crystals. J. Opt. Soc. Am. A 2024, 41, 366–370. [Google Scholar] [CrossRef] [PubMed]
- AbdelAll, N.; Almokhtar, M.; Khouqeer, G.; Soliman, S.E. Realizing the topological rainbow based on cavity-coupled topological edge state. Opt. Laser Technol. 2024, 171, 110351. [Google Scholar] [CrossRef]
- Elshahat, S.; Esmail, M.S.M.; Yuan, H.; Feng, S.; Lu, C. Broadband Multiple Topological Rainbows. Ann. Der Phys. 2022, 534, 2200137. [Google Scholar] [CrossRef]
- Elshahat, S.; Zhang, H.; Lu, C. Topological rainbow based on coupling of topological waveguide and cavity. Opt. Express 2023, 31, 20187–20199. [Google Scholar] [CrossRef]
- Sakoda, K. Optical Properties of Photonic Crystals; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Liang, L.; Zhou, X.; Hu, J.-H.; Wang, H.-X.; Jiang, J.-H.; Hou, B. Rainbow trapping based on higher-order topological corner modes. Opt. Lett. 2022, 47, 1454–1457. [Google Scholar] [CrossRef]
- Ezawa, M. Higher-order topological insulators and semimetals on the breathing kagome and pyrochlore lattices. Phys. Rev. Lett. 2018, 120, 026801. [Google Scholar] [CrossRef]
- Lera, N.; Torrent, D.; San-Jose, P.; Christensen, J.; Alvarez, J.V. Valley Hall phases in kagome lattices. Phys. Rev. B 2019, 99, 134102. [Google Scholar] [CrossRef]
- Shen, S.-l.; Li, C.; Wu, J.-F. Investigation of corner states in second-order photonic topological insulator. Opt. Express 2021, 29, 24045–24055. [Google Scholar] [CrossRef]
- Kim, K.-H.; Om, K.-K. Multiband Photonic Topological Valley-Hall Edge Modes and Second-Order Corner States in Square Lattices. Adv. Opt. Mater. 2021, 9, 2001865. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, W.; Elshahat, S.; Lu, C. Topological rainbow trapping based on gradual valley photonic crystals. Front. Phys. 2023, 11, 1141997. [Google Scholar] [CrossRef]
- Xi, X.; Ye, K.-P.; Wu, R.-X. Topological photonic crystal of large valley Chern numbers. Photonics Res. 2020, 8, B1–B7. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, Y.; Zhang, Y.; Zheng, Y.; Jiang, X. Topological Properties of a Two-Dimensional Photonic Square Lattice without C4 and Mx(y) Symmetries. ACS Photonics 2022, 9, 2448–2454. [Google Scholar] [CrossRef]
- Skirlo, S.A.; Lu, L.; Soljačić, M. Multimode One-Way Waveguides of Large Chern Numbers. Phys. Rev. Lett. 2014, 113, 113904. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Meng, Y.; Tian, J.; Huang, Y.; Xiang, H.; Han, D.; Wen, W. Direct observation of valley-polarized topological edge states in designer surface plasmon crystals. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Mei, J.; Wu, Y.; Chan, C.T.; Zhang, Z.-Q. First-principles study of Dirac and Dirac-like cones in phononic and photonic crystals. Phys. Rev. B 2012, 86, 035141. [Google Scholar] [CrossRef]
- Tang, G.-J.; Chen, X.-D.; Shi, F.-L.; Liu, J.-W.; Chen, M.; Dong, J.-W. Frequency range dependent topological phases and photonic detouring in valley photonic crystals. Phys. Rev. B 2020, 102, 174202. [Google Scholar] [CrossRef]
- Chen, X.-D.; Zhao, F.-L.; Chen, M.; Dong, J.-W. Valley-contrasting physics in all-dielectric photonic crystals: Orbital angular momentum and topological propagation. Phys. Rev. B 2017, 96, 020202. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, R.; Tao, X.; Gao, J. Topological valley-locked waveguides with C4 impurity. Nanophotonics 2024, 13, 3727–3736. [Google Scholar] [CrossRef]
- Tang, G.-J.; He, X.-T.; Shi, F.-L.; Liu, J.-W.; Chen, X.-D.; Dong, J.-W. Topological Photonic Crystals: Physics, Designs, and Applications. Laser Photonics Rev. 2022, 16, 2100300. [Google Scholar] [CrossRef]
- Ma, T.; Shvets, G. All-Si valley-Hall photonic topological insulator. New J. Phys. 2016, 18, 025012. [Google Scholar] [CrossRef]
- Gong, Y.; Wong, S.; Bennett, A.J.; Huffaker, D.L.; Oh, S.S. Topological Insulator Laser Using Valley-Hall Photonic Crystals. ACS Photonics 2020, 7, 2089–2097. [Google Scholar] [CrossRef]
- He, L.; Addison, Z.; Mele, E.J.; Zhen, B. Quadrupole topological photonic crystals. Nat. Commun. 2020, 11, 3119. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.-Z.; Zhang, Z.; Chen, H.; Gao, F. Polarization-wavelength locked plasmonic topological states. Polarization 2023, 2023, 9–25. [Google Scholar] [CrossRef]
- Noh, J.; Huang, S.; Chen, K.P.; Rechtsman, M.C. Observation of photonic topological valley Hall edge states. Phys. Rev. Lett. 2018, 120, 063902. [Google Scholar] [CrossRef]
- Chaplain, G.J.; De Ponti, J.M.; Aguzzi, G.; Colombi, A.; Craster, R.V. Topological Rainbow Trapping for Elastic Energy Harvesting in Graded Su-Schrieffer-Heeger Systems. Phys. Rev. Appl. 2020, 14, 054035. [Google Scholar] [CrossRef]
- Wang, G.; Wei, Y.; Chen, Z.; Lim, C.W. Controllable subwavelength topological rainbow trapping in water-filling acoustic metamaterials. Appl. Acoust. 2023, 207, 109366. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, N. Multimode resonator technique in antennas: A review. Electromagn. Sci. 2023, 1, 1–17. [Google Scholar] [CrossRef]
- Tian, F.; Wang, Y.; Huang, W.; Fang, X.; Guo, S.; Zhou, T. Ultra-compact topological photonic crystal rainbow nanolasers operating in the 1550 nm telecom band with wavelength-scale mode volumes. arXiv 2024, arXiv:2411.11009. [Google Scholar]
- AbdelAll, N.; Almokhtar, M.; Khouqeer, G.; Esmail, M.S.M.; Abood, I.; El Soliman, S. Multifunctional topological photonic crystal device for multichannel frequency routing and highly sensitive refractive index sensing. Phys. Scr. 2024, 99, 055539. [Google Scholar] [CrossRef]
- Soliman, S.E.; Abood, I.; Lu, C. Robust multi-mode rainbow trapping with ultra-high-Q Fano resonances. Opt. Express 2024, 32, 1010–1019. [Google Scholar] [CrossRef]
- Abood, I.; El Soliman, S.; Wenlong, H.; Ouyang, Z. Multi-Fano resonances by TCS and resonance-enhanced TES in hybrid photonic crystals for ultracompact sensing. Opt. Laser Technol. 2025, 180, 111513. [Google Scholar] [CrossRef]
- Luo, Z.-Y.; Zhang, T.; Ye, Y.-T.; Wang, Y.-F.; Yu, C.-C.; Luo, Z.-C.; Zhang, Y.-J.; Xu, M.-C.; Sanders, B.C.; Wang, H.; et al. On-Demand Photon Storage and Retrieval with a Solid-State Photon Molecule at Room Temperature. Electromagn. Sci. 2024, 2, 1–10. [Google Scholar] [CrossRef]
- Ma, K. Regulation and control of electromagnetic field in radio-frequency circuits and systems. Electromagn. Sci. 2023, 1, 1–28. [Google Scholar] [CrossRef]
- Li, M.X.; Wang, Y.K.; Lu, M.J.; Sang, T. Dual-mode of topological rainbow in gradual photonic heterostructures. J. Phys. D Appl. Phys. 2022, 55, 095103. [Google Scholar] [CrossRef]
- Asghari, M.; Krishnamoorthy, A.V. Silicon photonics: Energy-efficient communication. Nat. Photonics 2011, 5, 268–270. [Google Scholar] [CrossRef]
- Loncar, M.; Doll, T.; Vuckovic, J.; Scherer, A. Design and fabrication of silicon photonic crystal optical waveguides. J. Light. Technol. 2000, 18, 1402–1411. [Google Scholar] [CrossRef]
- Feng, J.; Chen, Y.; Blair, J.; Kurt, H.; Hao, R.; Citrin, D.S.; Summers, C.J.; Zhou, Z. Fabrication of annular photonic crystals by atomic layer deposition and sacrificial etching. J. Vac. Sci. Technol. B 2009, 27, 568–572. [Google Scholar] [CrossRef]
- Baba, T.; Matsuzaki, T. Fabrication and Photoluminescence Studies of GaInAsP/InP 2-Dimensional Photonic Crystals. Jpn. J. Appl. Phys. 1996, 35, 1348–1352. [Google Scholar] [CrossRef]
- Tavousi, A.; Rakhshani, M.R.; Mansouri-Birjandi, M.A. High sensitivity label-free refractometer based biosensor applicable to glycated hemoglobin detection in human blood using all-circular photonic crystal ring resonators. Opt. Commun. 2018, 429, 166–174. [Google Scholar] [CrossRef]
- Xu, W.; Li, Y. The effect of anisotropy on light extraction of organic light-emitting diodes with photonic crystal structure. J. Nanomater. 2013, 2013, 7. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, D. The research and progress of micro-fabrication technologies of two-dimensional photonic crystal. Chin. Sci. Bull. 2007, 52, 865–876. [Google Scholar] [CrossRef]
- Chong, T.C.; Hong, M.H.; Shi, L.P. Laser precision engineering: From microfabrication to nanoprocessing. Laser Photonics Rev. 2010, 4, 123–143. [Google Scholar] [CrossRef]
- Trifonov, T.; Marsal, L.F.; Rodriguez, A.; Pallares, J.; Alcubilla, R. Two-dimensional photonic crystals of rods with a dielectric cladding. In Proceedings of the Microtechnologies for the New Millennium 2005, Sevilla, Spain, 9–11 May 2005; Volume 5840, pp. 746–757. [Google Scholar]
- Lehmann, V.; Foll, H. Formation Mechanism and Properties of Electrochemically Etched Trenches in n-Type Silicon. J. Electrochem. Soc. 1990, 137, 653–659. [Google Scholar] [CrossRef]
- Gruning, U.; Lehmann, V.; Ottow, S.; Busch, K. Macroporous silicon with a complete two-dimensional photonic band gap centered at 5 μm. Appl. Phys. Lett. 1996, 68, 747–749. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El. Soliman, S.; Abood, I.; All, N.A.; Chen, C.-C. Topological Rainbow Trapping with Expanded Bandwidth in Valley Photonic Crystals. Photonics 2025, 12, 487. https://doi.org/10.3390/photonics12050487
El. Soliman S, Abood I, All NA, Chen C-C. Topological Rainbow Trapping with Expanded Bandwidth in Valley Photonic Crystals. Photonics. 2025; 12(5):487. https://doi.org/10.3390/photonics12050487
Chicago/Turabian StyleEl. Soliman, Sayed, Israa Abood, Naglaa Abdel All, and Chii-Chang Chen. 2025. "Topological Rainbow Trapping with Expanded Bandwidth in Valley Photonic Crystals" Photonics 12, no. 5: 487. https://doi.org/10.3390/photonics12050487
APA StyleEl. Soliman, S., Abood, I., All, N. A., & Chen, C.-C. (2025). Topological Rainbow Trapping with Expanded Bandwidth in Valley Photonic Crystals. Photonics, 12(5), 487. https://doi.org/10.3390/photonics12050487






