Spectral Tuning and Angular–Gap Interrogation of Terahertz Spoof Surface Plasmon Resonances Excited on Rectangular Subwavelength Grating Using Attenuated Total Reflection in Otto Configuration
Abstract
1. Introduction
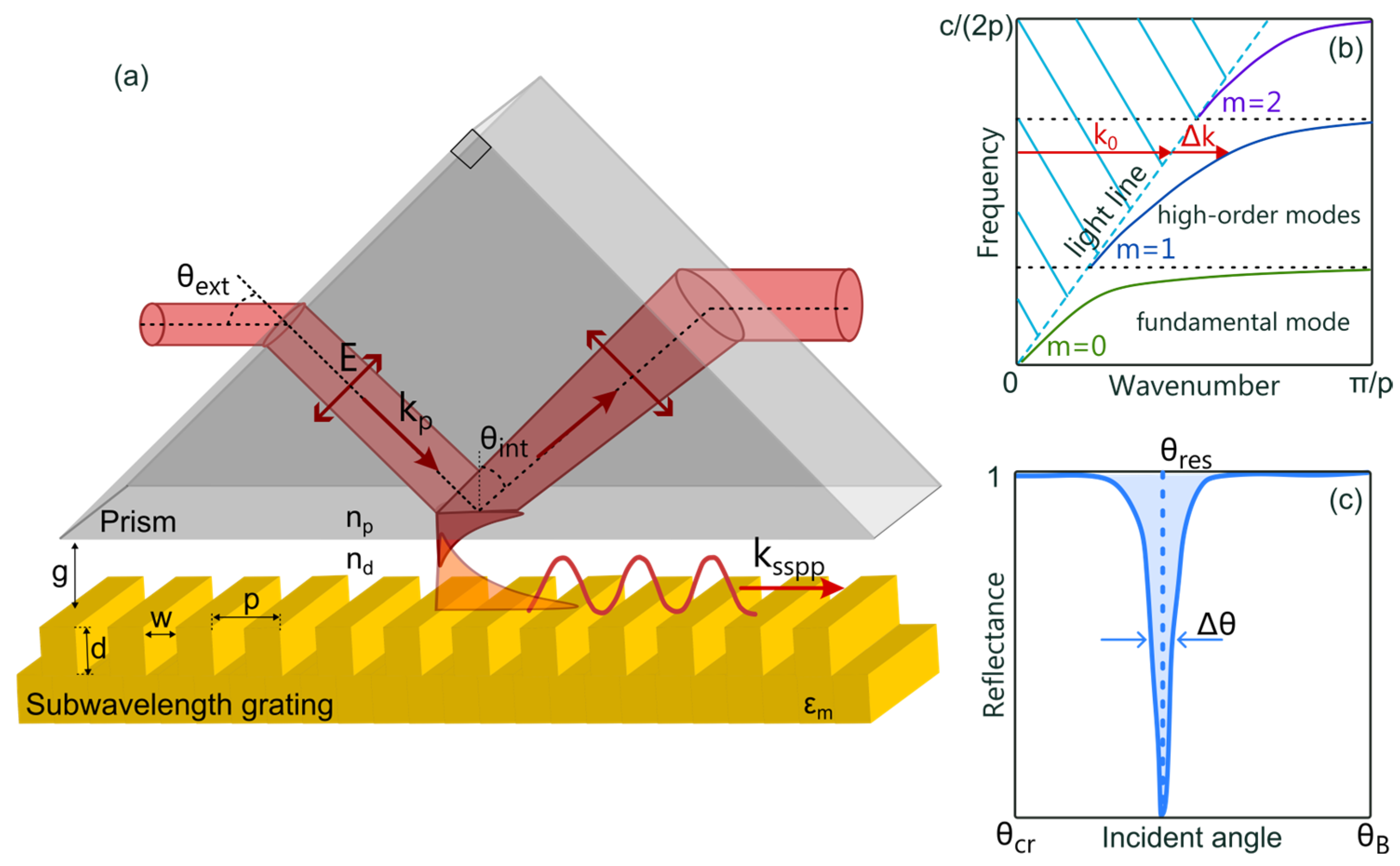
2. Theoretical Description
- Internal damping (), associated with absorption in the metallic grating and proportional to the imaginary part of the effective dielectric constant.
- Radiation damping (), arising from the emission of SSPPs into the prism, which depends on the gap between the prism and the grating.
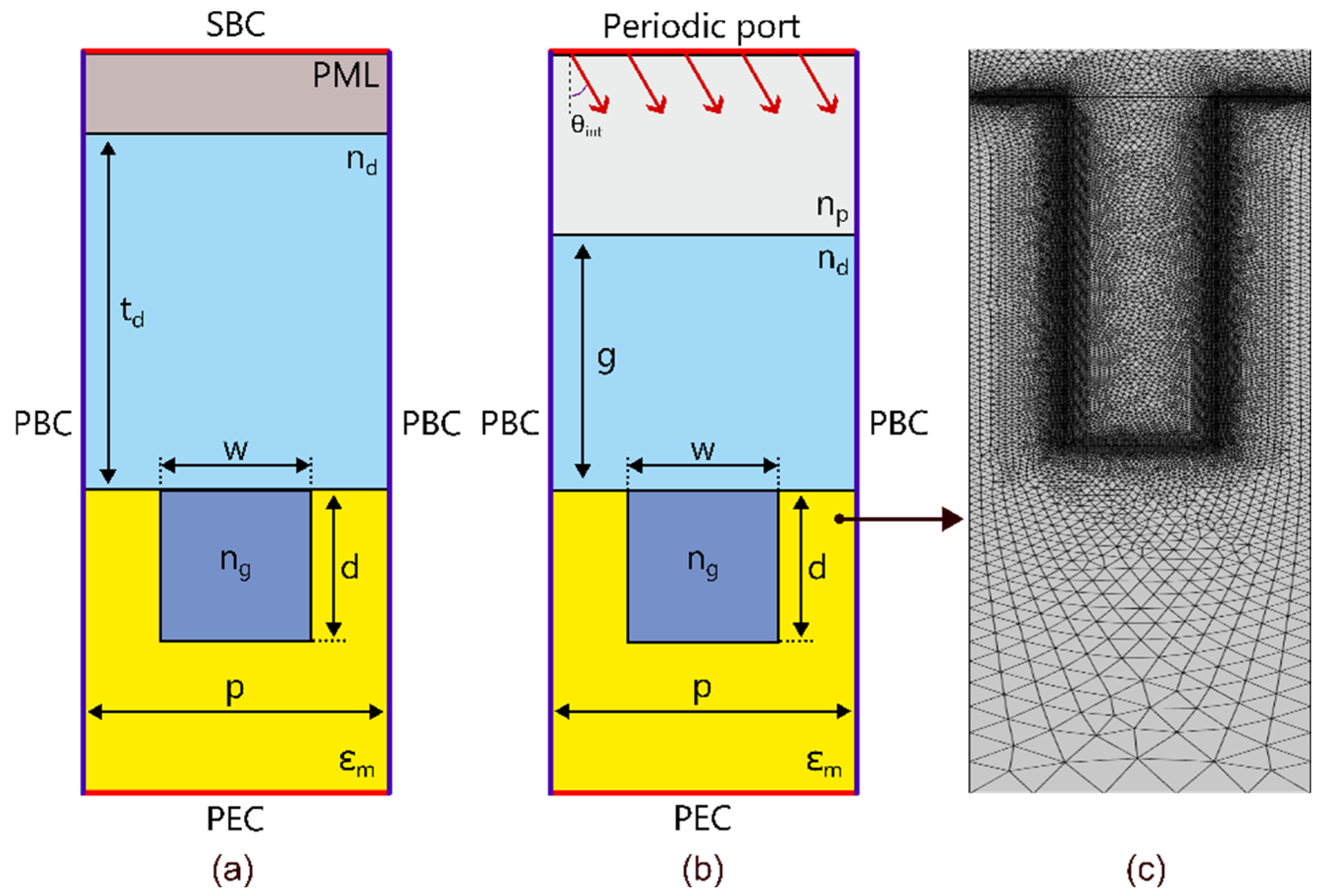
3. Numerical Simulation
4. Fabrication Process
5. Experimental Scheme
6. Simulation Results
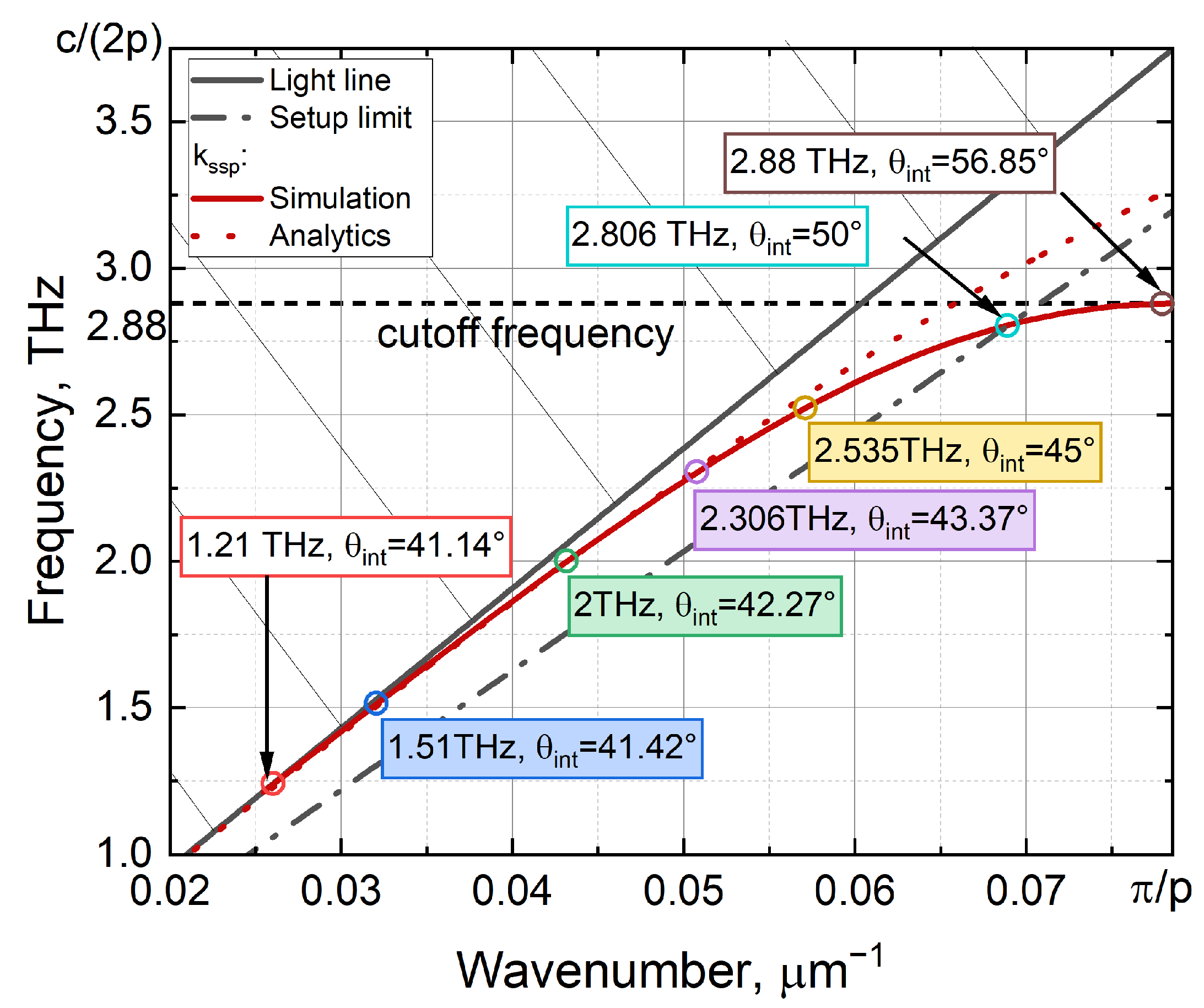
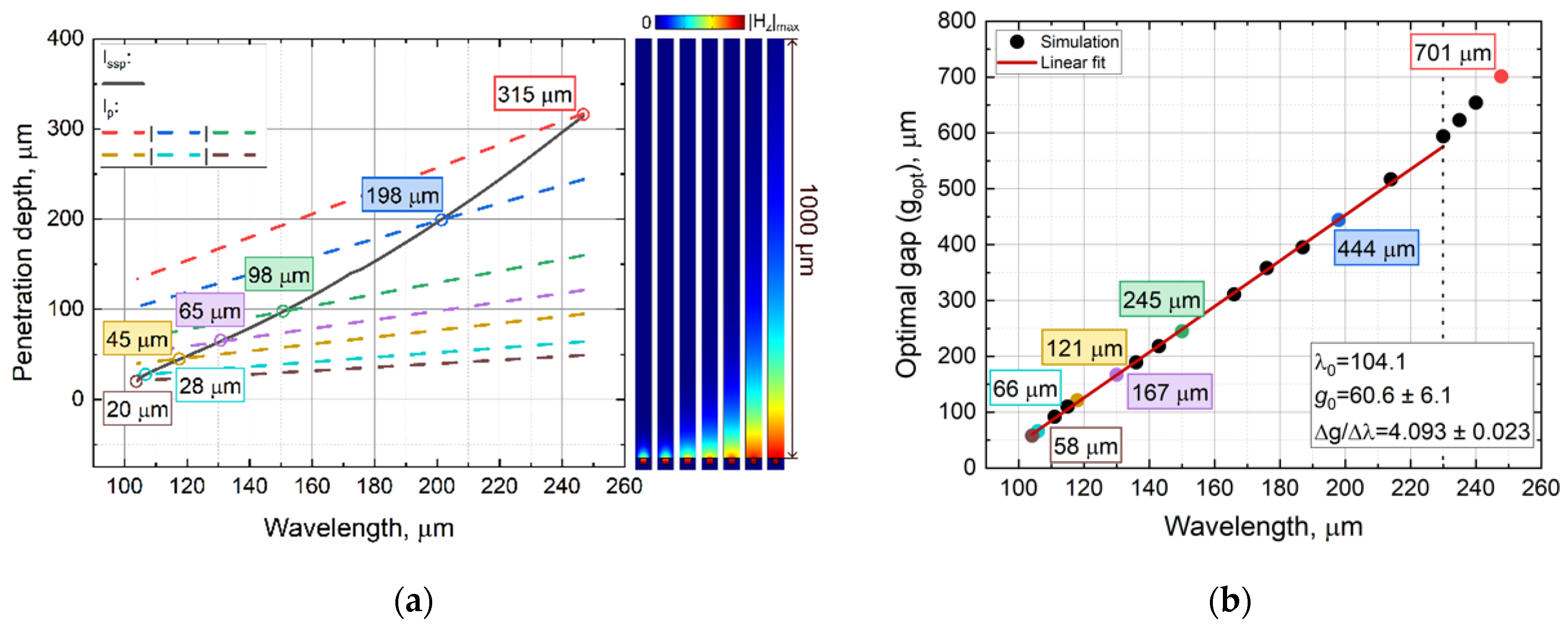
6.1. Dispersion Curve
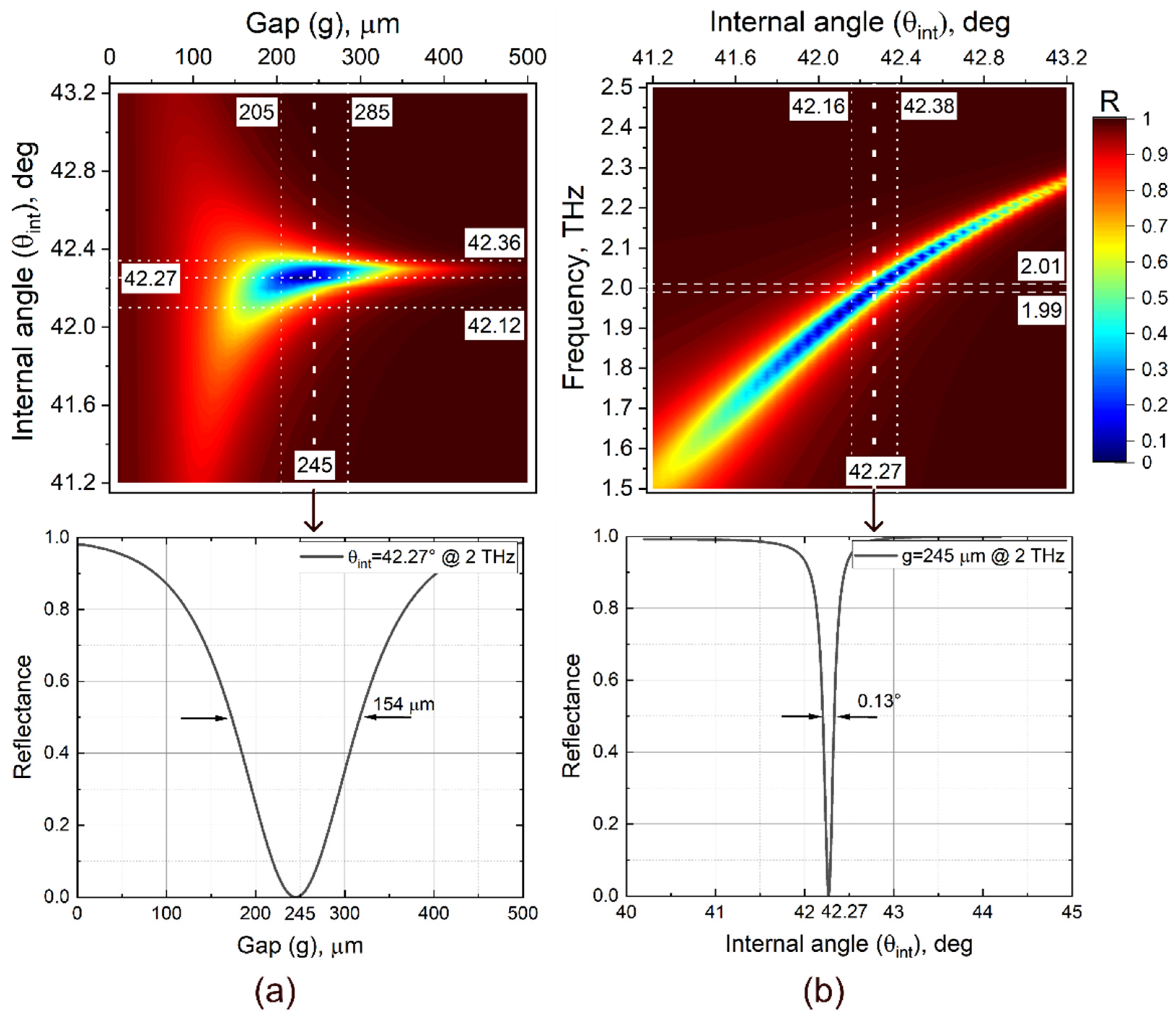
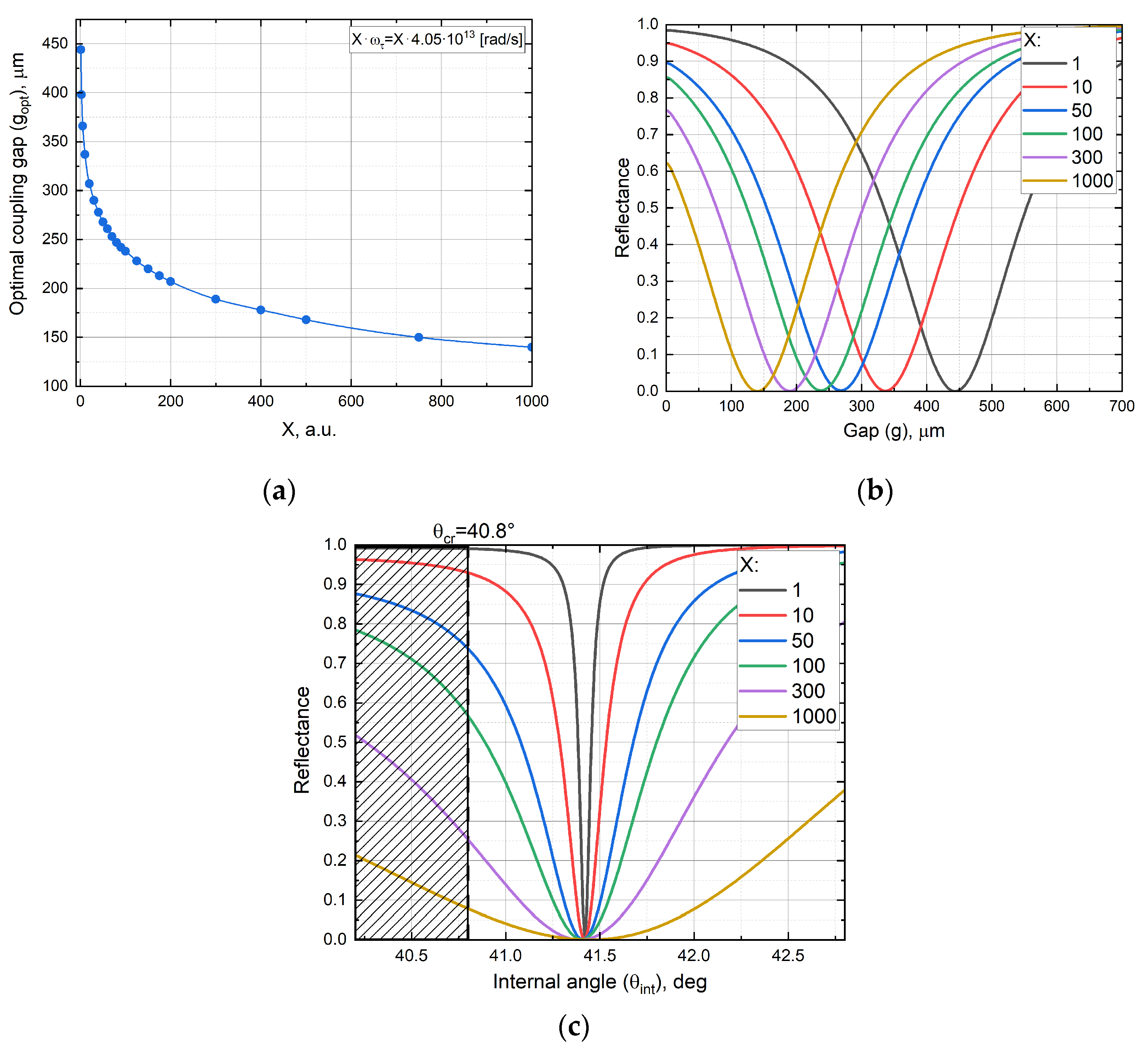
6.2. Gap and Frequency Variations
6.3. Field Confinement and Optimal Gap
6.4. Losses and Optimal Gap
7. Experimental Results
7.1. Measurement Procedure
- The beam signal normalised to the reference one was averaged over the detector matrix to yield the integral response of the grating.
- The obtained angular spectra at various spectral frequencies were then normalised to the attenuated total reflection angular spectrum without the grating in the vicinity of the prism to account for the interaction of the incident beam with the prism under different conditions.
- To obtain the reflectance, we divided the entire angular and gap spectrum by its maximum value reached at large air gaps and angles far from the resonance, correspondingly.
- The measured intensity errors were about ±5%, which corresponded to the NovoFEL average power instability.
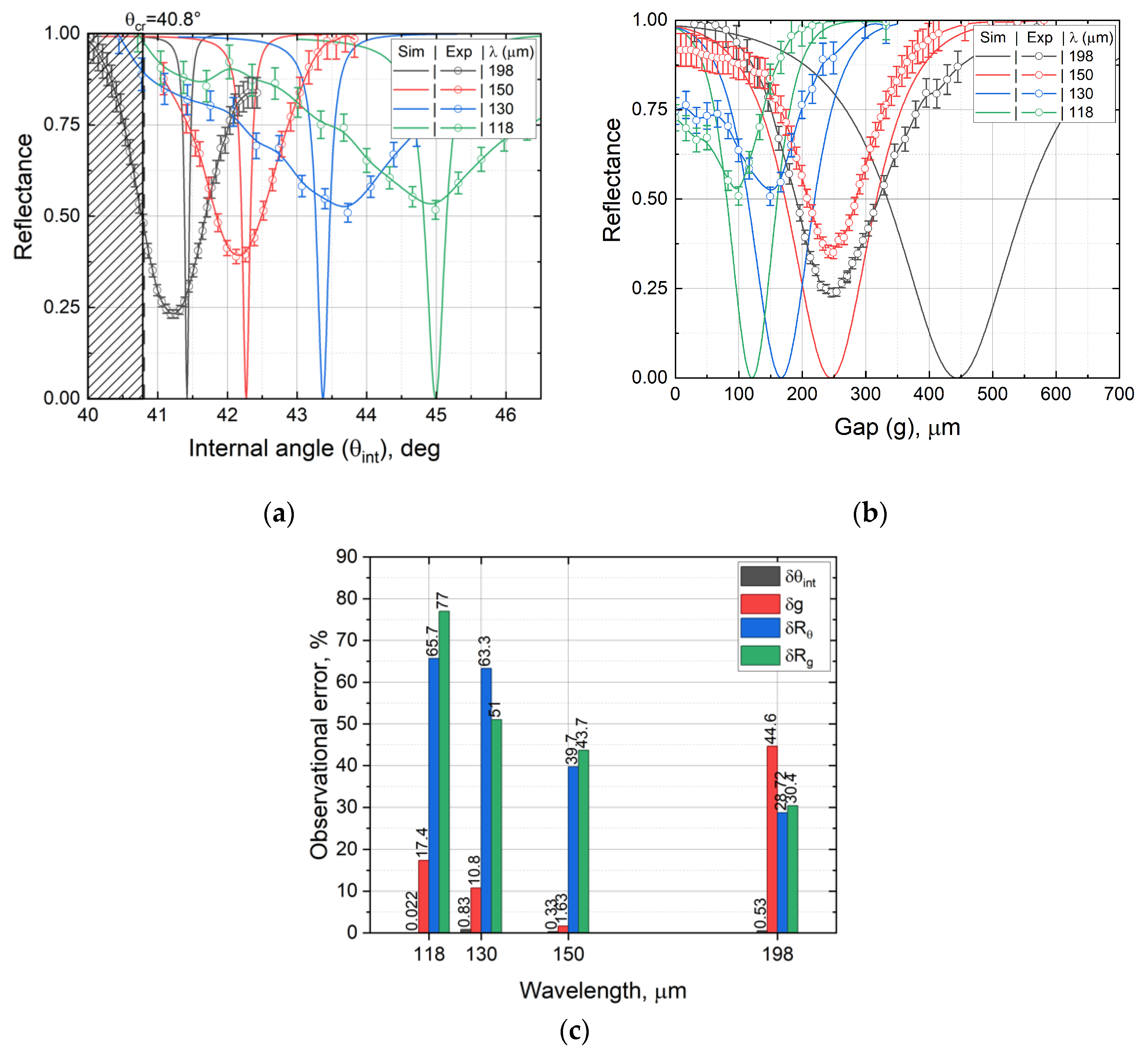
7.2. Angular and Gap Spectra
7.3. Optimal Incident Angle and Gap Distance
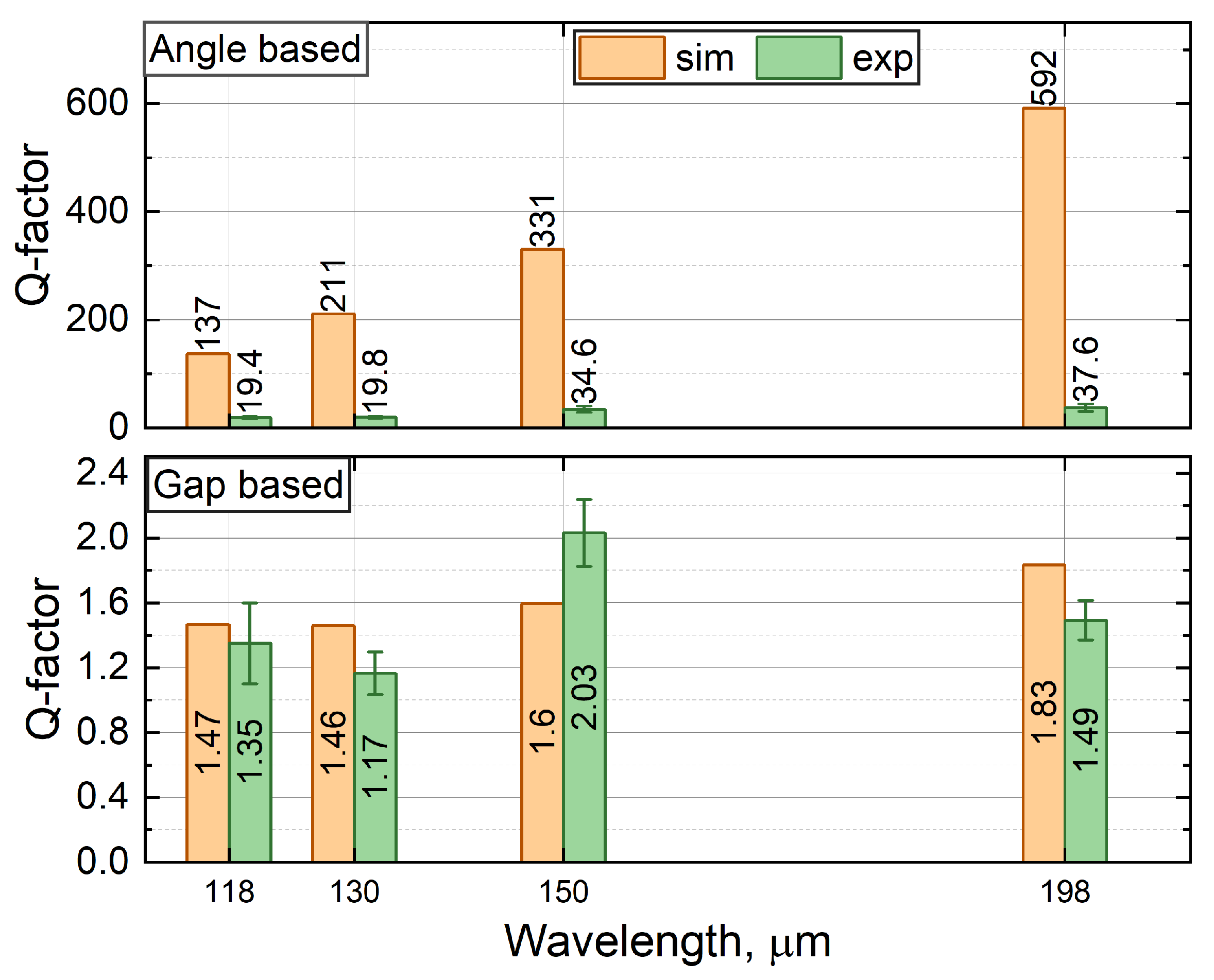
7.4. Quality Factor
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SSPP | spoof surface plasmon polariton |
| SPP | surface plasmon polaritons |
| THz | terahertz |
| ATR | attenuated total reflection |
| NovoFEL | Novosibirsk free electron laser |
References
- Zayats, A.V.; Smolyaninov, I.I.; Maradudin, A.A. Nano-Optics of Surface Plasmon Polaritons. Phys. Rep. 2005, 408, 131–314. [Google Scholar] [CrossRef]
- Shalabney, A.; Abdulhalim, I. Sensitivity-enhancement Methods for Surface Plasmon Sensors. Laser Photonics Rev. 2011, 5, 571–606. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007; ISBN 978-0-387-33150-8. [Google Scholar]
- Knyazev, B.A.; Kuzmin, A.V. Surface electromagnetic waves: From visible range to microwaves. Vestn. NGU Ser. Fiz. 2007, 2, 108–122. [Google Scholar] [CrossRef]
- Kukotenko, V.D.; Gerasimov, V.V.; Khasanov, I.S.; Lemzyakov, A.G.; Ivanov, A.I.; Antonova, I.V. Experimental Study of Terahertz Surface Wave Field on Metallic and Composite Graphene Films. In Proceedings of the 2024 IEEE 25th International Conference of Young Professionals in Electron Devices and Materials (EDM), Altai, Russian, 28 June–2 July 2024; pp. 1070–1073. [Google Scholar] [CrossRef]
- Gerasimov, V.V.; Knyazev, B.A.; Lemzyakov, A.G.; Nikitin, A.K.; Zhizhin, G.N. Growth of Terahertz Surface Plasmon Propagation Length Due to Thin-Layer Dielectric Coating. J. Opt. Soc. Am. B 2016, 33, 2196. [Google Scholar] [CrossRef]
- Gerasimov, V.V.; Nikitin, A.K.; Lemzyakov, A.G.; Azarov, I.A.; Kotelnikov, I.A. Obtaining the Effective Dielectric Permittivity of a Conducting Surface in the Terahertz Range via the Characteristics of Surface Plasmon Polaritons. Appl. Sci. 2023, 13, 7898. [Google Scholar] [CrossRef]
- Isaac, T.H.; Barnes, W.L.; Hendry, E. Determining the Terahertz Optical Properties of Subwavelength Films Using Semiconductor Surface Plasmons. Appl. Phys. Lett. 2008, 93, 241115. [Google Scholar] [CrossRef]
- Gerasimov, V.V.; Khasanov, I.S.; Kukotenko, V.D.; Lemzyakov, A.G.; Ivanov, A.I.; Antonova, I.V.; Cherevko, A.G. Terahertz Surface Plasmon Refractometry of Composite Graphene Nanoparticle Films. IEEE Trans. THZ Sci. Technol. 2025, 15, 61–68. [Google Scholar] [CrossRef]
- Rivas, J.G.; Kuttge, M.; Bolivar, P.H.; Kurz, H.; Sánchez-Gil, J.A. Propagation of Surface Plasmon Polaritons on Semiconductor Gratings. Phys. Rev. Lett. 2004, 93, 256804. [Google Scholar] [CrossRef]
- Gong, M.; Jeon, T.-I.; Grischkowsky, D. THz Surface Wave Collapse on Coated Metal Surfaces. Opt. Express 2009, 17, 17088. [Google Scholar] [CrossRef]
- Garcia-Vidal, F.J.; Fernández-Domínguez, A.I.; Martin-Moreno, L.; Zhang, H.C.; Tang, W.; Peng, R.; Cui, T.J. Spoof Surface Plasmon Photonics. Rev. Mod. Phys. 2022, 94, 025004. [Google Scholar] [CrossRef]
- Gao, Z.; Wu, L.; Gao, F.; Luo, Y.; Zhang, B. Spoof Plasmonics: From Metamaterial Concept to Topological Description. Adv. Mater. 2018, 30, 1706683. [Google Scholar] [CrossRef]
- Ng, B.; Wu, J.; Hanham, S.M.; Fernández-Domínguez, A.I.; Klein, N.; Liew, Y.F.; Breese, M.B.H.; Hong, M.; Maier, S.A. Spoof Plasmon Surfaces: A Novel Platform for THz Sensing. Adv. Opt. Mater. 2013, 1, 543–548. [Google Scholar] [CrossRef]
- Ng, B.; Hanham, S.M.; Wu, J.; Fernández-Domínguez, A.I.; Klein, N.; Liew, Y.F.; Breese, M.B.H.; Hong, M.; Maier, S.A. Broadband Terahertz Sensing on Spoof Plasmon Surfaces. ACS Photonics 2014, 1, 1059–1067. [Google Scholar] [CrossRef]
- Yao, H.; Zhong, S. High-Mode Spoof SPP of Periodic Metal Grooves for Ultra-Sensitive Terahertz Sensing. Opt. Express 2014, 22, 25149. [Google Scholar] [CrossRef] [PubMed]
- Yao, H.; Zhong, S.; Tu, W. Performance Analysis of Higher Mode Spoof Surface Plasmon Polariton for Terahertz Sensing. J. Appl. Phys. 2015, 117, 133104. [Google Scholar] [CrossRef]
- Zhang, Y.; Hong, Z.; Han, Z. Spoof Plasmon Resonance with 1D Periodic Grooves for Terahertz Refractive Index Sensing. Opt. Commun. 2015, 340, 102–106. [Google Scholar] [CrossRef]
- Chen, L.; Yin, H.; Chen, L.; Zhu, Y. Ultra-Sensitive Fluid Fill Height Sensing Based on Spoof Surface Plasmon Polaritons. J. Electromagn. Waves Appl. 2018, 32, 471–482. [Google Scholar] [CrossRef]
- Zhao, R.; Lu, G.; Yin, H.; Liang, J.; Zeng, D.; Xiao, H. Terahertz Sensor Study Based on Spoof Surface Plasmon Polaritons. Int. J. Antennas Propag. 2020, 2020, 2504626. [Google Scholar] [CrossRef]
- Chen, X.; Xiao, H.; Lu, G.; Zhao, R. Refractive Index Sensing Based on Terahertz Spoof Surface Plasmon Polariton Structure. J. Phys. Conf. Ser. 2020, 1617, 012008. [Google Scholar] [CrossRef]
- Yao, H.; Zhang, W.; Liu, W.; Mei, H. Resolved Terahertz Spectroscopy of Tiny Molecules Employing Tunable Spoof Plasmons in an Otto Prism Configuration. J. Opt. 2022, 24, 045301. [Google Scholar] [CrossRef]
- Huang, Y.; Zhong, S.; Shi, T.; Shen, Y.-C.; Cui, D. HR-Si Prism Coupled Tightly Confined Spoof Surface Plasmon Polaritons Mode for Terahertz Sensing. Opt. Express 2019, 27, 34067. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhong, S.; Shi, T.; Shen, Y.; Cui, D. Terahertz Plasmonic Phase-Jump Manipulator for Liquid Sensing. Nanophotonics 2020, 9, 3011–3021. [Google Scholar] [CrossRef]
- Huang, Y.; Singh, R.; Xie, L.; Ying, Y. Attenuated Total Reflection for Terahertz Modulation, Sensing, Spectroscopy and Imaging Applications: A Review. Appl. Sci. 2020, 10, 4688. [Google Scholar] [CrossRef]
- Kameshkov, O.E.; Gerasimov, V.V. Excitation of Terahertz Plasmonic Resonance on a Subwavelength Metallic Grating in an Attenuated Total Reflection Scheme Using a Monochromatic Radiation Source. J. Surf. Investig. 2023, 17, 1463–1471. [Google Scholar] [CrossRef]
- Garcia-Vidal, F.J.; Martín-Moreno, L.; Pendry, J.B. Surfaces with Holes in Them: New Plasmonic Metamaterials. J. Opt. A Pure Appl. Opt. 2005, 7, S97–S101. [Google Scholar] [CrossRef]
- Shen, L.; Chen, X.; Yang, T.-J. Terahertz Surface Plasmon Polaritons on Periodically Corrugated Metal Surfaces. Opt. Express 2008, 16, 3326. [Google Scholar] [CrossRef] [PubMed]
- Rusina, A.; Durach, M.; Stockman, M.I. Theory of Spoof Plasmons in Real Metals. Appl. Phys. A 2010, 100, 375–378. [Google Scholar] [CrossRef]
- Erementchouk, M.; Joy, S.R.; Mazumder, P. Electrodynamics of Spoof Plasmons in Periodically Corrugated Waveguides. Proc. R. Soc. A 2016, 472, 20160616. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Shen, L.; Zhang, X.; Ran, L.-X. High-order modes of spoof surface plasmon polaritons on periodically corrugated metal surfaces. PIER M 2009, 8, 91–102. [Google Scholar] [CrossRef]
- Bulgakova, V.V.; Gerasimov, V.V.; Goldenberg, B.G.; Lemzyakov, A.G.; Malkin, A.M. Study of Terahertz Spoof Surface Plasmons on Subwavelength Gratings with Dielectric Substance in Grooves. Procedia Eng. 2017, 201, 14–23. [Google Scholar] [CrossRef]
- Khasanov, I.S.; Gerasimov, V.V.; Kameshkov, O.E.; Nikitin, A.K.; Kassandrov, V.V. Observation of Surface Plasmon Resonance in Monochromatic Terahertz Radiation on Indium Antimonide. J. Surf. Investig. 2023, 17, 1052–1059. [Google Scholar] [CrossRef]
- Dominique, B.; Otto, A. Excitations of Surface Plasmon Polaritons by Attenuated Total Reflection, Revisited. Riv. Nuovo C. 2013, 36, 173–209. [Google Scholar] [CrossRef]
- Otto, A. Excitation of Nonradiative Surface Plasma Waves in Silver by the Method of Frustrated Total Reflection. Z. Phys. 1968, 216, 398–410. [Google Scholar] [CrossRef]
- Mason, D.R.; Menabde, S.G.; Park, N. Unusual Otto Excitation Dynamics and Enhanced Coupling of Light to TE Plasmons in Graphene. Opt. Express 2014, 22, 847. [Google Scholar] [CrossRef]
- Yeatman, E.M. Resolution and Sensitivity in Surface Plasmon Microscopy and Sensing. Biosens. Bioelectron. 1996, 11, 635–649. [Google Scholar] [CrossRef]
- RF Module User’s Guide, version 6.0, COMSOL, Inc. Available online: https://doc.comsol.com/6.0/doc/com.comsol.help.rf/RFModuleUsersGuide.pdf (accessed on 13 June 2025).
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical Properties of Fourteen Metals in the Infrared and Far Infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl. Opt. 1985, 24, 4493. [Google Scholar] [CrossRef]
- Reznikova, E.; Mohr, J.; Boerner, M.; Nazmov, V.; Jakobs, P.-J. Soft X-ray Lithography of High Aspect Ratio SU8 Submicron Structures. Microsyst. Technol. 2008, 14, 1683–1688. [Google Scholar] [CrossRef]
- Goldenberg, B.G.; Lemzyakov, A.G.; Zelinsky, A.G.; Nazmov, V.P.; Pindyurin, V.F. Multibeam X-ray Lithography to Form Deep Regular Microstructures. J. Synch. Investig. 2016, 10, 92–95. [Google Scholar] [CrossRef]
- Siberian Center for Synchrotron and Terahertz Radiation on the Basis of the Novosibirsk Free Electron Laser at Budker Institute of Nuclear Physics SB RAS. Available online: https://ssrc.biouml.org (accessed on 24 March 2025).
- Goldenberg, B.G.; Lemzyakov, A.G.; Nazmov, V.P.; Pindyurin, V.F. Multifunctional X-ray Lithography Station at VEPP-3. Phys. Procedia 2016, 84, 205–212. [Google Scholar] [CrossRef]
- Shevchenko, O.A.; Vinokurov, N.A.; Arbuzov, V.S.; Chernov, K.N.; Davidyuk, I.V.; Deichuly, O.I.; Dementyev, E.N.; Dovzhenko, B.A.; Getmanov, Y.V.; Gorbachev, Y.I.; et al. The Novosibirsk Free-Electron Laser Facility. Bull. Russ. Acad. Sci. Phys. 2019, 83, 228–231. [Google Scholar] [CrossRef]
- Tydex. Available online: https://www.tydexoptics.com (accessed on 24 March 2024).
- Kubarev, V.V.; Kulipanov, G.N.; Kolobanov, E.I.; Matveenko, A.N.; Medvedev, L.E.; Ovchar, V.K.; Salikova, T.V.; Scheglov, M.A.; Serednyakov, S.S.; Vinokurov, N.A. Modulation Instability, Three Mode Regimes and Harmonic Generation at the Novosibirsk Terahertz Free Electron Laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 603, 25–27. [Google Scholar] [CrossRef]
- Gerasimov, V.V.; Kameshkov, O.E.; Nikitin, A.K.; Khasanov, I.S.; Lemzyakov, A.G.; Antonova, I.V.; Ivanov, A.I.; Lien, N.T.H.; Nghia, N.T.; Anh, L.T.; et al. First Experimental Demonstration of the Wide-Field Amplitude Surface Plasmon Resonance Microscopy in the Terahertz Range. Photonics 2023, 10, 723. [Google Scholar] [CrossRef]
- Gerasimov, V.V.; Nikitin, A.K.; Vanda, V.S.; Lemzyakov, A.G.; Azarov, I.A. Dispersion of attenuation of surface plasmon polaritons on metal in the terahertz range. J. Infrared Millim. Terahz. Waves 2025, 46, 32. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Zong, G.; Hu, W.; Lu, Y. Liquid Crystal Based Tunable Terahertz Metadevices. J. Mater. 2025, 11, 100888. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Yan, D.; Fan, F.; Chen, K.; Zhong, K.; Wang, Y.; Tian, Z.; Xu, D. A Review: Active Tunable Terahertz Metamaterials. Adv. Photonics Res. 2024, 5, 2300351. [Google Scholar] [CrossRef]
- Tumashov, M.A.; Baena, J.D.; Del Risco, J.P.; Lazorskiy, P.A.; Glybovski, S.B.; Kuznetsov, S.A. Angle-Dependent Metasurface for Nonspectroscopic THz Sensing of Submicrometer Films. IEEE Sens. J. 2023, 23, 27262–27272. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, X.; Zhou, J.; Zhang, H.; Lin, J.-Y.; Chen, W.; Zhu, L.-G.; Meng, K.; Liu, Q.H.; Zhu, J. Enhancing Trace Terahertz Fingerprint Sensing by the Lossy Silicon Metagrating with a Gold Mirror. IEEE Trans. Microw. Theory Tech. 2024, 72, 2368–2377. [Google Scholar] [CrossRef]
- Zhu, W.M.; Liu, A.Q.; Zhang, X.M.; Tsai, D.P.; Bourouina, T.; Teng, J.H.; Zhang, X.H.; Guo, H.C.; Tanoto, H.; Mei, T.; et al. Switchable Magnetic Metamaterials Using Micromachining Processes. Adv. Mater. 2011, 23, 1792–1796. [Google Scholar] [CrossRef]
- Pitchappa, P.; Manjappa, M.; Krishnamoorthy, H.N.S.; Chang, Y.; Lee, C.; Singh, R. Bidirectional Reconfiguration and Thermal Tuning of Microcantilever Metamaterial Device Operating from 77 K to 400 K. Appl. Phys. Lett. 2017, 111, 261101. [Google Scholar] [CrossRef]
- Wang, L.; Ge, S.; Hu, W.; Nakajima, M.; Lu, Y. Graphene-Assisted High-Efficiency Liquid Crystal Tunable Terahertz Metamaterial Absorber. Opt. Express 2017, 25, 23873. [Google Scholar] [CrossRef]
- Lewis, R.A. A Review of Terahertz Sources. J. Phys. D Appl. Phys. 2014, 47, 374001. [Google Scholar] [CrossRef]


| Simulation | Experiment | ||||
|---|---|---|---|---|---|
| Wavelength, μm | Frequency, THz | Gap, μm | Angle, deg | Gap, μm | Angle, deg |
| 198 ± 0.51 | 1.51 ± 0.008 | 444 ± 0.5 | 41.42 ± 0.005 | 245.8 ± 5 | 41.2 ± 0.1 |
| 150 ± 0.85 | 2 ± 0.01 | 245 ± 0.5 | 42.27 ± 0.005 | 249 ± 5 | 42.13 ± 0.1 |
| 130 ± 0.67 | 2.306 ± 0.012 | 167 ± 0.5 | 43.37 ± 0.005 | 149 ± 5 | 43.73 ± 0.1 |
| 118 ± 0.34 | 2.535 ± 0.013 | 121 ± 0.5 | 44.99 ± 0.005 | 100 ± 5 | 44.98 ± 0.1 |
| Approach | Spectral Tuning Range, THz | Tunable Range, GHz | Reference |
|---|---|---|---|
| Angle-dependent metasurface | 0.139–0.1498 | 10.8 | [51] |
| Angle-dependent metagrating | 0.5–0.55 | 50 | [52] |
| MEMS, thermal tuning | 0.32–0. 43 | 110 | [53] |
| MEMS, mechanical tuning | 2.12–2.28 | 160 | [54] |
| Liquid crystal, electrical tuning | 0.75–1 | 250 | [55] |
| Metal grating with angular dispersion | 1.51–2.54 | 1030 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kameshkov, O.; Gerasimov, V.; Goldenberg, B.; Nazmov, V. Spectral Tuning and Angular–Gap Interrogation of Terahertz Spoof Surface Plasmon Resonances Excited on Rectangular Subwavelength Grating Using Attenuated Total Reflection in Otto Configuration. Photonics 2025, 12, 651. https://doi.org/10.3390/photonics12070651
Kameshkov O, Gerasimov V, Goldenberg B, Nazmov V. Spectral Tuning and Angular–Gap Interrogation of Terahertz Spoof Surface Plasmon Resonances Excited on Rectangular Subwavelength Grating Using Attenuated Total Reflection in Otto Configuration. Photonics. 2025; 12(7):651. https://doi.org/10.3390/photonics12070651
Chicago/Turabian StyleKameshkov, Oleg, Vasily Gerasimov, Boris Goldenberg, and Vladimir Nazmov. 2025. "Spectral Tuning and Angular–Gap Interrogation of Terahertz Spoof Surface Plasmon Resonances Excited on Rectangular Subwavelength Grating Using Attenuated Total Reflection in Otto Configuration" Photonics 12, no. 7: 651. https://doi.org/10.3390/photonics12070651
APA StyleKameshkov, O., Gerasimov, V., Goldenberg, B., & Nazmov, V. (2025). Spectral Tuning and Angular–Gap Interrogation of Terahertz Spoof Surface Plasmon Resonances Excited on Rectangular Subwavelength Grating Using Attenuated Total Reflection in Otto Configuration. Photonics, 12(7), 651. https://doi.org/10.3390/photonics12070651





