Experimental Validation of Designs for Permeable Diffractive Lenses Based on Photon Sieves for the Sensing of Running Fluids
Abstract
1. Introduction
2. Materials and Methods
2.1. Types of Focusing Photon Sieves
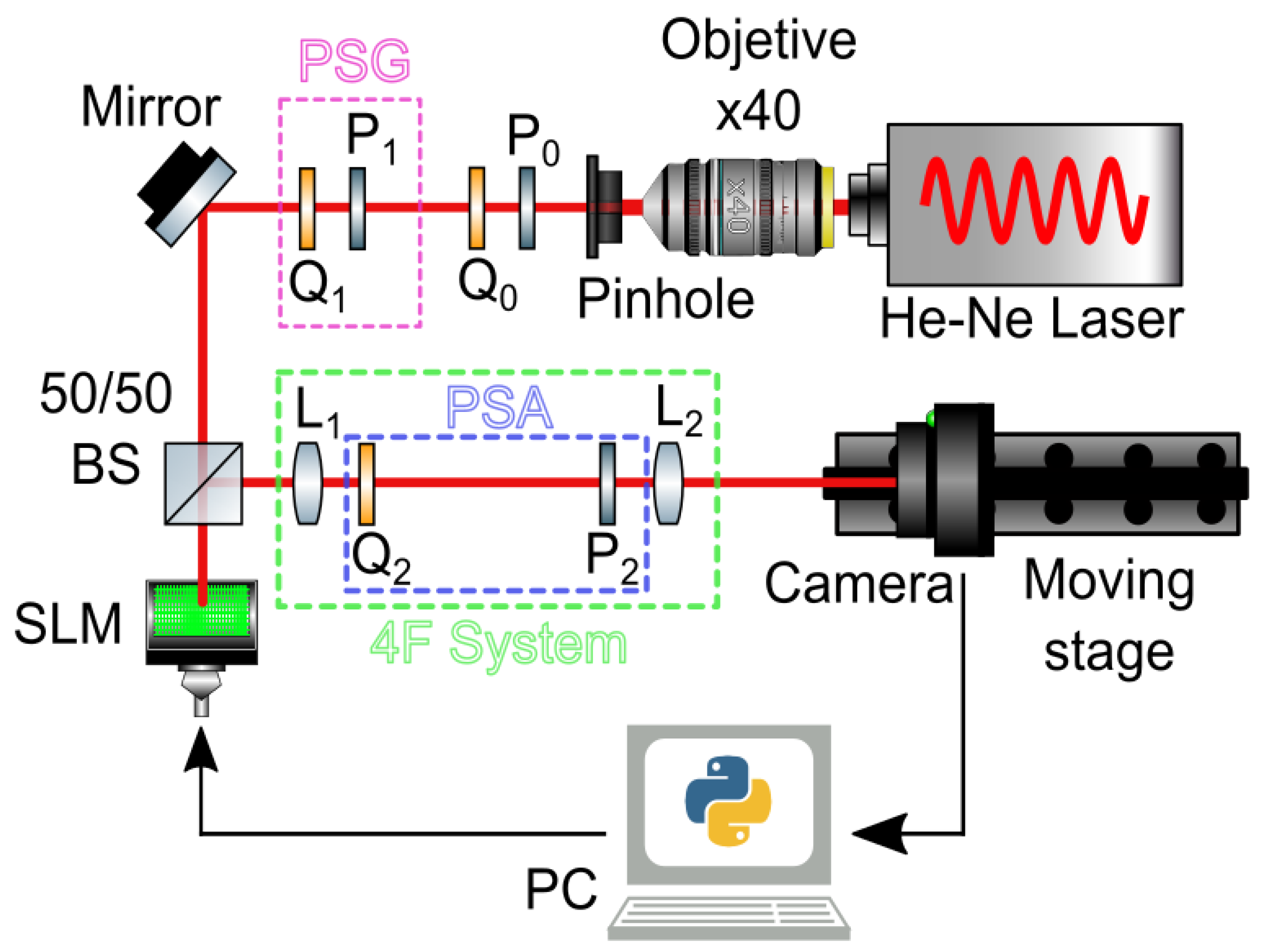
2.2. Experimental Setup
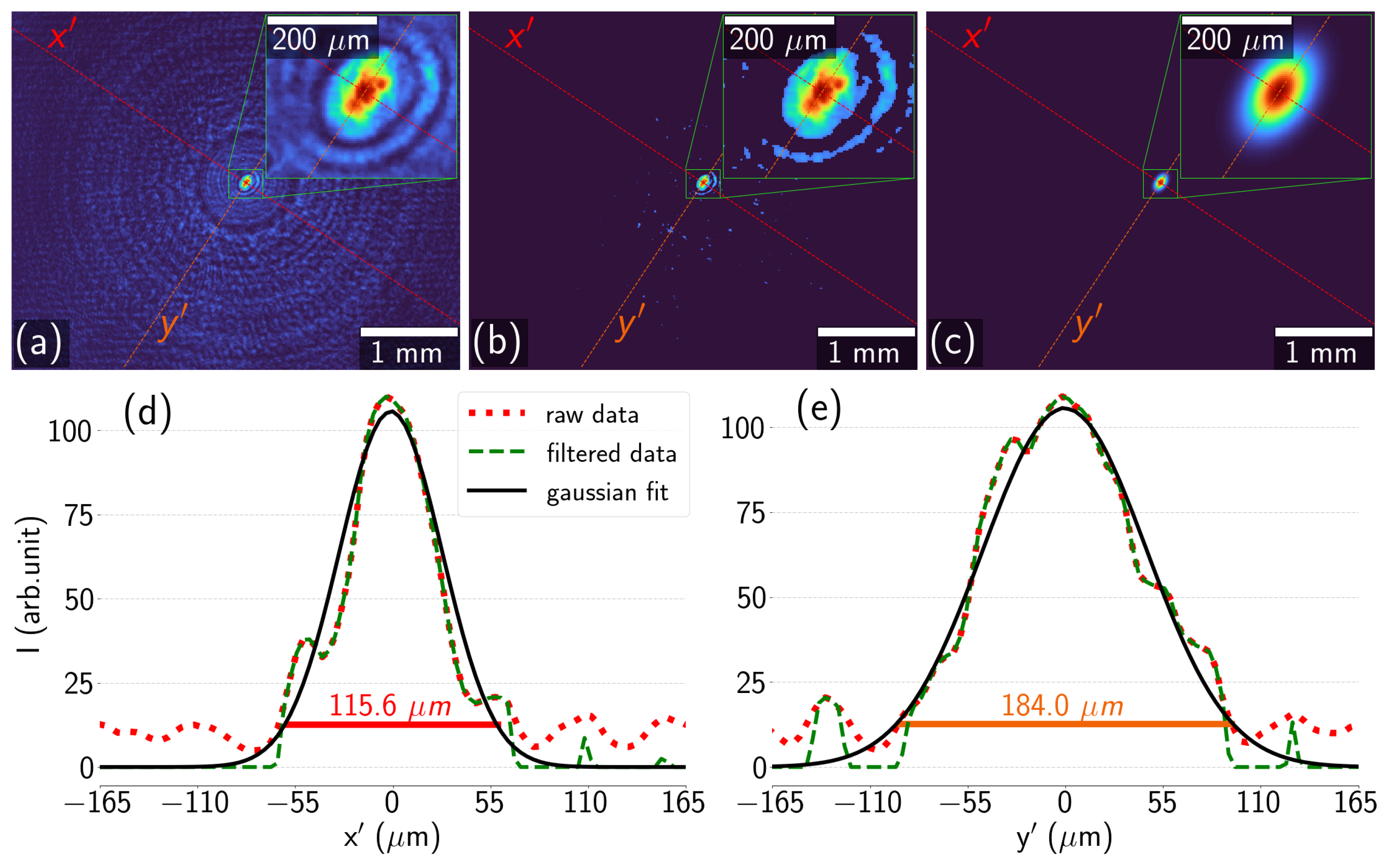
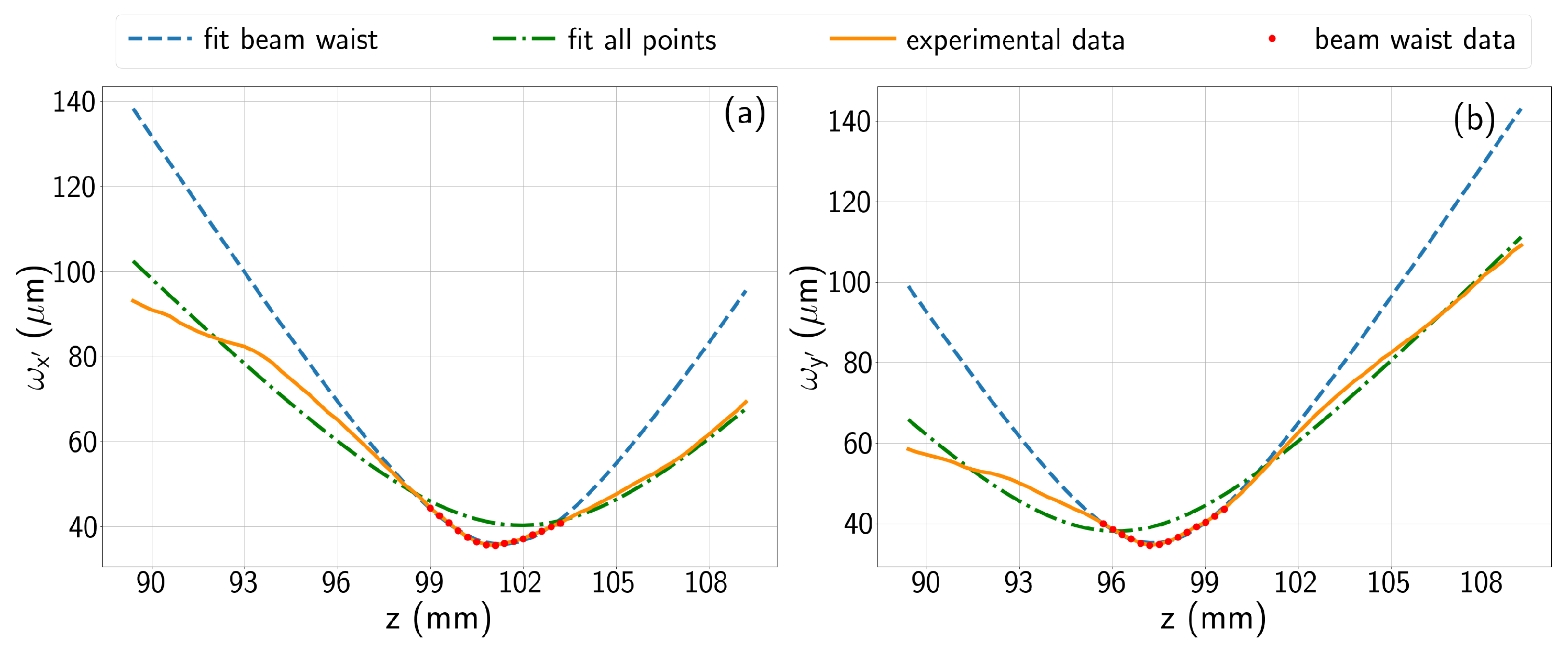
2.3. Parameterization of the Focal Region and Mask
3. Results and Discussion
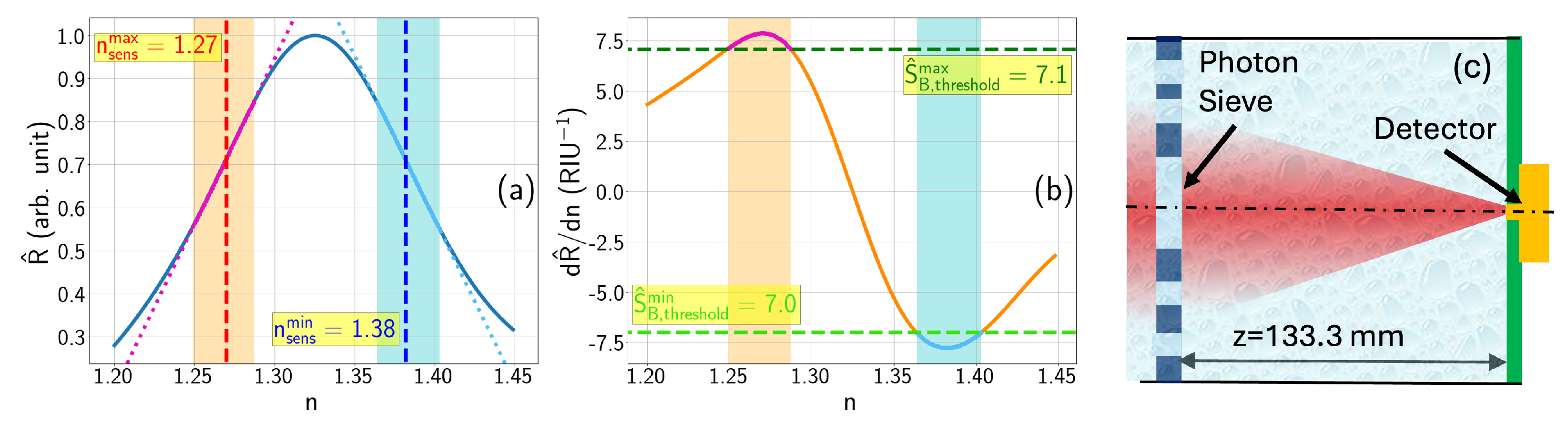
Refractometric Sensing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOE | Diffractive Optical Element |
| DOF | Depth of Focus |
| FWHM | Full Width at Half Maximum |
| FZP | Fresnel Zone Plate |
| GMF | Geometrical Merit Function |
| HbH | Hole-by-Hole |
| HDMI | High-Definition Multimedia Interface |
| HiR | Hole-in-Ring |
| PS | Photon Sieve |
| PSA | Polarization State Analyzer |
| PSG | Polarization State Generator |
| RbR | Ring-by-Ring |
| RIU | Refractive Index Unit |
| SLM | Spatial Light Modulator |
| WMF | Weighted Merit Function |
References
- Khonina, S.N.; Kazanskiy, N.L.; Skidanov, R.V.; Butt, M.A. Advancements and Applications of Diffractive Optical Elements in Contemporary Optics: A Comprehensive Overview. Adv. Mater. Technol. 2024, 10, 2401028. [Google Scholar] [CrossRef]
- Kim, H.J.; Aguillard, J.; Julian, M.; Bartram, S.; Macdonnell, D. Photon Sieve Design and Fabrication for Imaging Characteristics Using UAV Flight; NASA/TM; 2019-220252; National Aeronautics and Space Administration, Langley Research Center: Hampton, VA, USA, 2019.
- Sabatyan, A.; Mirzaie, S. Efficiency-enhanced photon sieve using Gaussian/overlapping distribution of pinholes. Appl. Opt. 2011, 50, 1517–1522. [Google Scholar] [CrossRef]
- Sabatyan, A.; Hoseini, S.A. Diffractive performance of a photon-sieve-based axilens. Appl. Opt. 2014, 53, 7331–7336. [Google Scholar] [CrossRef]
- Davis, A.; Kühnlenz, F. Optical Design using Fresnel Lenses. Opt. Photonik 2007, 2, 52–55. [Google Scholar] [CrossRef]
- Vila-Comamala, J.; Borrisé, X.; Pérez-Murano, F.; Campos, J.; Ferrer, S. Nanofabrication of Fresnel zone plate lenses for X-ray optics. Microelectron. Eng. 2006, 83, 1355–1359. [Google Scholar] [CrossRef]
- Michette, A.G. Diffractive Optics II Zone Plates; Springer US: Greer, SC, USA, 1986; pp. 165–215. [Google Scholar] [CrossRef]
- Baez, A.V. Fresnel Zone Plate for Optical Image Formation Using Extreme Ultraviolet and Soft X Radiation. J. Opt. Soc. Am. 1961, 51, 405–412. [Google Scholar] [CrossRef]
- Soria-Garcia, A.; del Hoyo, J.; Sanchez-Brea, L.M.; Pastor-Villarrubia, V.; Gonzalez-Fernandez, V.; Elshorbagy, M.H.; Alda, J. Vector diffractive optical element as a full-Stokes analyzer. Opt. Laser Technol. 2023, 163, 109400. [Google Scholar] [CrossRef]
- Yamada, K.; Watanabe, W.; Li, Y.; Itoh, K.; Nishii, J. Multilevel phase-type diffractive lenses in silica glass induced by filamentationof femtosecond laser pulses. Opt. Lett. 2004, 29, 1846–1848. [Google Scholar] [CrossRef]
- Moreno, V.; Román, J.F.; Salgueiro, J.R. High efficiency diffractive lenses: Deduction of kinoform profile. Am. J. Phys. 1997, 65, 556–562. [Google Scholar] [CrossRef]
- Andersen, G. Membrane photon sieve telescopes. Appl. Opt. 2010, 49, 6391–6394. [Google Scholar] [CrossRef]
- Andersen, G.; Tullson, D. Photon sieve telescope. In Proceedings of the Space Telescopes and Instrumentation I: Optical, Infrared, and Millimeter, Orlando, FL, USA, 24–31 May 2006; Mather, J.C., MacEwen, H.A., de Graauw, M.W.M., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2006; Volume 6265, p. 626523. [Google Scholar] [CrossRef]
- Lambrou, T.P.; Anastasiou, C.C.; Panayiotou, C.G.; Polycarpou, M.M. A low-cost sensor network for real-time monitoring and contamination detection in drinking water distribution systems. IEEE Sens. J. 2014, 14, 2765–2772. [Google Scholar] [CrossRef]
- Bernasconi, G.; Del Giudice, S.; Giunta, G.; Dionigi, F. Advanced pipeline vibroacoustic monitoring. In Proceedings of the Pressure Vessels and Piping Conference, Paris, France, 14–18 July 2013; American Society of Mechanical Engineers: New York City, NY, USA, 2013; Volume 55690, p. V005T10A008. [Google Scholar]
- Oktem, F.S.; Kamalabadi, F.; Davila, J.M. High-resolution computational spectral imaging with photon sieves. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 5122–5126. [Google Scholar] [CrossRef]
- Cao, Q.; Jahns, J. Focusing analysis of the pinhole photon sieve: Individual far-field model. J. Opt. Soc. Am. A 2002, 19, 2387–2393. [Google Scholar] [CrossRef]
- Snigirev, A.; Kohn, V.; Snigireva, I.; Lengeler, B. A compound refractive lens for focusing high-energy X-rays. Nature 1996, 384, 49–51. [Google Scholar] [CrossRef]
- Machado, F.; Zagrajek, P.; Monsoriu, J.A.; Furlan, W.D. Terahertz Sieves. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 140–143. [Google Scholar] [CrossRef]
- Cheng, C.; Cao, Q.; Bai, L.; Li, C.; Zhu, J.; Chen, W.; Mao, Y. High-efficiency square-hole single-mode waveguide photon sieves for THz waves. Appl. Opt. 2023, 62, 2403–2409. [Google Scholar] [CrossRef]
- Rijfkogel, L.S.; Ghanbarian, B.; Hu, Q.; Liu, H.H. Clarifying pore diameter, pore width, and their relationship through pressure measurements: A critical study. Mar. Pet. Geol. 2019, 107, 142–148. [Google Scholar] [CrossRef]
- Sanchez-Brea, L.M.; Soria-Garcia, A.; Andres-Porras, J.; Pastor-Villarrubia, V.; Elshorbagy, M.H.; del Hoyo Muñoz, J.; Torcal-Milla, F.J.; Alda, J. Diffractio: An open-source library for diffraction and interference calculations. In Proceedings of the Optics and Photonics for Advanced Dimensional Metrology III, Strasbourg, France, 7–11 April 2024; de Groot, P.J., Guzman, F., Picart, P., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2024; Volume 12997, p. 129971B. [Google Scholar] [CrossRef]
- Soria-Garcia, A.; Sanchez-Brea, L.M.; del Hoyo, J.; Torcal-Milla, F.J.; Gomez-Pedrero, J.A. Fourier series diffractive lens with extended depth of focus. Opt. Laser Technol. 2023, 164, 109491. [Google Scholar] [CrossRef]
- Garcia-Lozano, G.; Mercant, G.; Fernandez-Rodriguez, M.; Torquemada, M.C.; Gonzalez, L.M.; Belenguer, T.; Cuadrado, A.; Sanchez-Brea, L.M.; Alda, J.; Elshorbagy, M. Experimental Analysis of the Spectral Reflectivity of Metallic Blazed Diffraction Gratings in the THz Range for Space Instrumentation. IEEE Trans. Terahertz Sci. Technol. 2025, 15, 8–16. [Google Scholar] [CrossRef]
- Kang, E.K.; Lee, Y.W.; Ravindran, S.; Lee, J.K.; Choi, H.J.; Ju, G.W.; Min, J.W.; Song, Y.M.; Sohn, I.B.; Lee, Y.T. 4 channel × 10 Gb/s bidirectional optical subassembly using silicon optical bench with precise passive optical alignment. Opt. Express 2016, 24, 10777–10785. [Google Scholar] [CrossRef]
- Chen, S.T.; Luo, T.S. Fabrication of micro-hole arrays using precision filled wax metal deposition. J. Mater. Process. Technol. 2010, 210, 504–509. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, L.; Zhao, Y.; Ke, M.; Li, B.; Chen, L.; Cai, S. A perforated microhole-based microfluidic device for improving sprouting angiogenesis in vitro. Biomicrofluidics 2017, 11, 054111. [Google Scholar] [CrossRef]
- Jia, P.; Zhou, S.; Cai, X.; Guo, Q.; Niu, H.; Ning, W.; Sun, Y.; Zhang, D. High-fidelity synthesis of microhole templates with low-surface-energy-enabled self-releasing photolithography. RSC Adv. 2024, 14, 12125–12130. [Google Scholar] [CrossRef]
- Pastor-Villarrubia, V.; Soria-Garcia, A.; Andres-Porras, J.; del Hoyo, J.; Elshorbagy, M.H.; Sanchez-Brea, L.M.; Alda, J. Optimum design of permeable diffractive lenses based on photon sieves. Optik 2024, 330, 172342. [Google Scholar] [CrossRef]
- Pastor-Villarrubia, V.; Soria-Garcia, A.; del Hoyo, J.; Sanchez-Brea, L.M.; Alda, J. Permeable diffractive optical elements for real-time sensing of running fluids. In Proceedings of the Optical Sensors, Prague, Czech Republic, 24–26 April 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12572, pp. 170–177. [Google Scholar]
- Joignant, A.N.; Xi, Y.; Muddiman, D.C. Impact of wavelength and spot size on laser depth of focus: Considerations for mass spectrometry imaging of non-flat samples. J. Mass Spectrom. 2023, 58, e4914. [Google Scholar] [CrossRef]
- Siegman, A.E. Defining, measuring, and optimizing laser beam quality. In Proceedings of the Laser Resonators and Coherent Optics: Modeling, Technology, and Applications, Los Angeles, CA, USA, 18–20 January 1993; Bhowmik, A., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 1993; Volume 1868, pp. 2–12. [Google Scholar] [CrossRef]
- Rabiner, L.; Schafer, R.; Rader, C. The chirp z-transform algorithm. IEEE Trans. Audio Electroacoust. 1969, 17, 86–92. [Google Scholar] [CrossRef]
- Bluestein, L. A linear filtering approach to the computation of discrete Fourier transform. IEEE Trans. Audio Electroacoust. 1970, 18, 451–455. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Z.; Wang, X.; Ji, S.; Zhang, C.; Li, J.; Zhu, W.; Wu, D.; Chu, J. Efficient full-path optical calculation of scalar and vector diffraction using the Bluestein method. Light. Sci. Appl. 2020, 9, 119. [Google Scholar] [CrossRef]
- Huang, D.W.; Ma, Y.F.; Sung, M.J.; Huang, C.P. Approach the angular sensitivity limit in surface plasmon resonance sensors with low index prism and large resonant angle. Opt. Eng. 2010, 49, 054403. [Google Scholar] [CrossRef]
- Elshorbagy, M.H.; Cuadrado, A.; Romero, B.; Alda, J. Enabling selective absorption in perovskite solar cells for refractometric sensing of gases. Sci. Rep. 2020, 10, 7761. [Google Scholar] [CrossRef]
- Elshorbagy, M.H.; Esteban, O.; Cuadrado, A.; Alda, J. Optoelectronic refractometric sensing device for gases based on dielectric bow-ties and amorphous silicon solar cells. Sci. Rep. 2022, 12, 18355. [Google Scholar] [CrossRef]
- Khodaie, A.; Heidarzadeh, H.; Harzand, F.V. Development of an advanced multimode refractive index plasmonic optical sensor utilizing split ring resonators for brain cancer cell detection. Sci. Rep. 2025, 15, 433. [Google Scholar] [CrossRef] [PubMed]
- Bouandas, H.; Kumar, R.; Benhaliliba, M.; Singh, S.; Garia, L. Plasmonic sensor design: Cu-SiO2-Ni-black phosphorus for enhanced surface plasmon resonance in visible regime. Microchim. Acta 2025, 192, 114. [Google Scholar] [CrossRef] [PubMed]
- Bouandas, H.; Slimani, Y.; Daher, M.G.; Djemli, A.; Fatm, M.; Aldossari, S.A.; Mika, S. Design of an Advanced Sensor Based on Surface Plasmon Resonance with Ultra-High Sensitivity. Plasmonics 2025. [Google Scholar] [CrossRef]
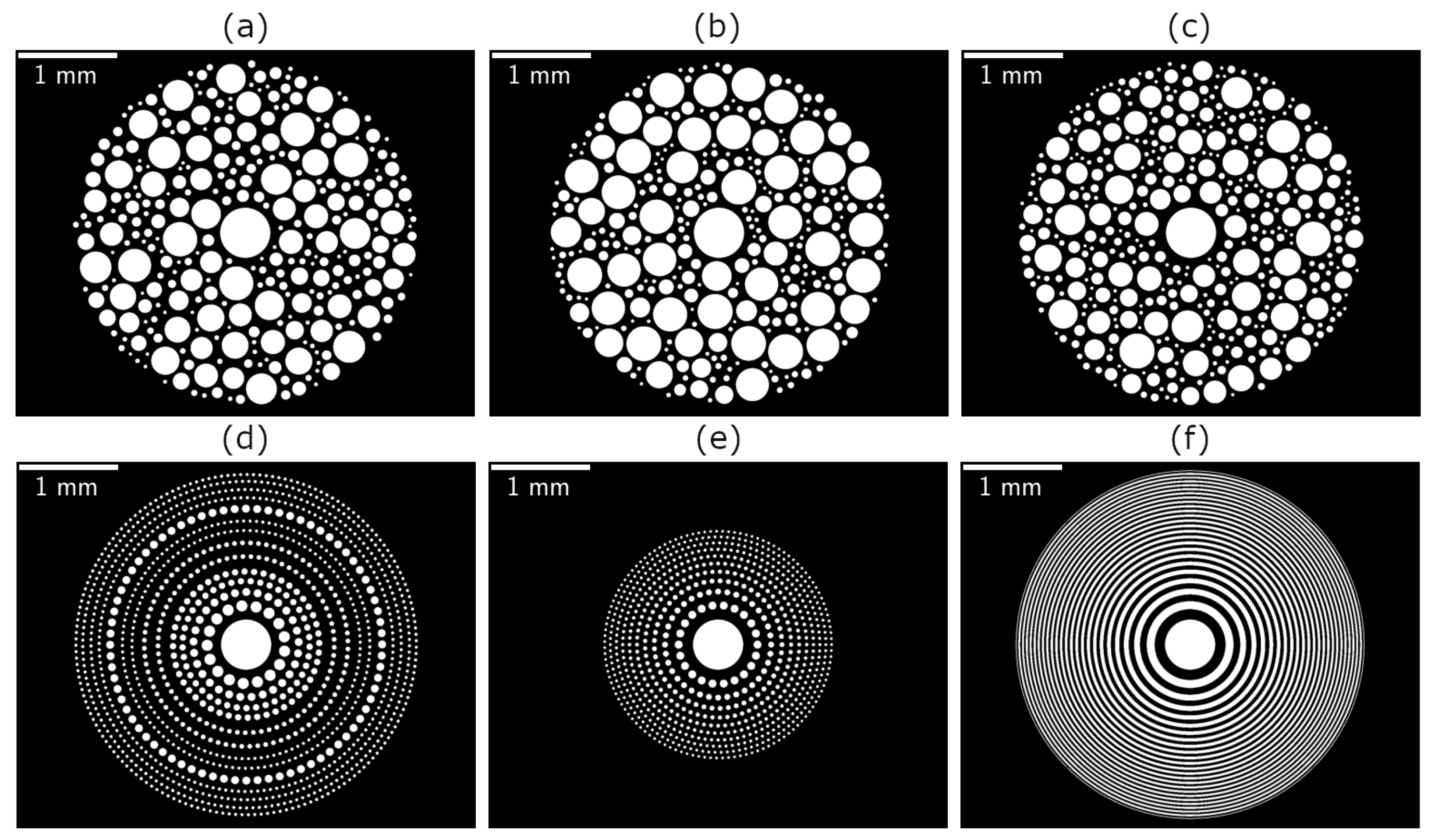


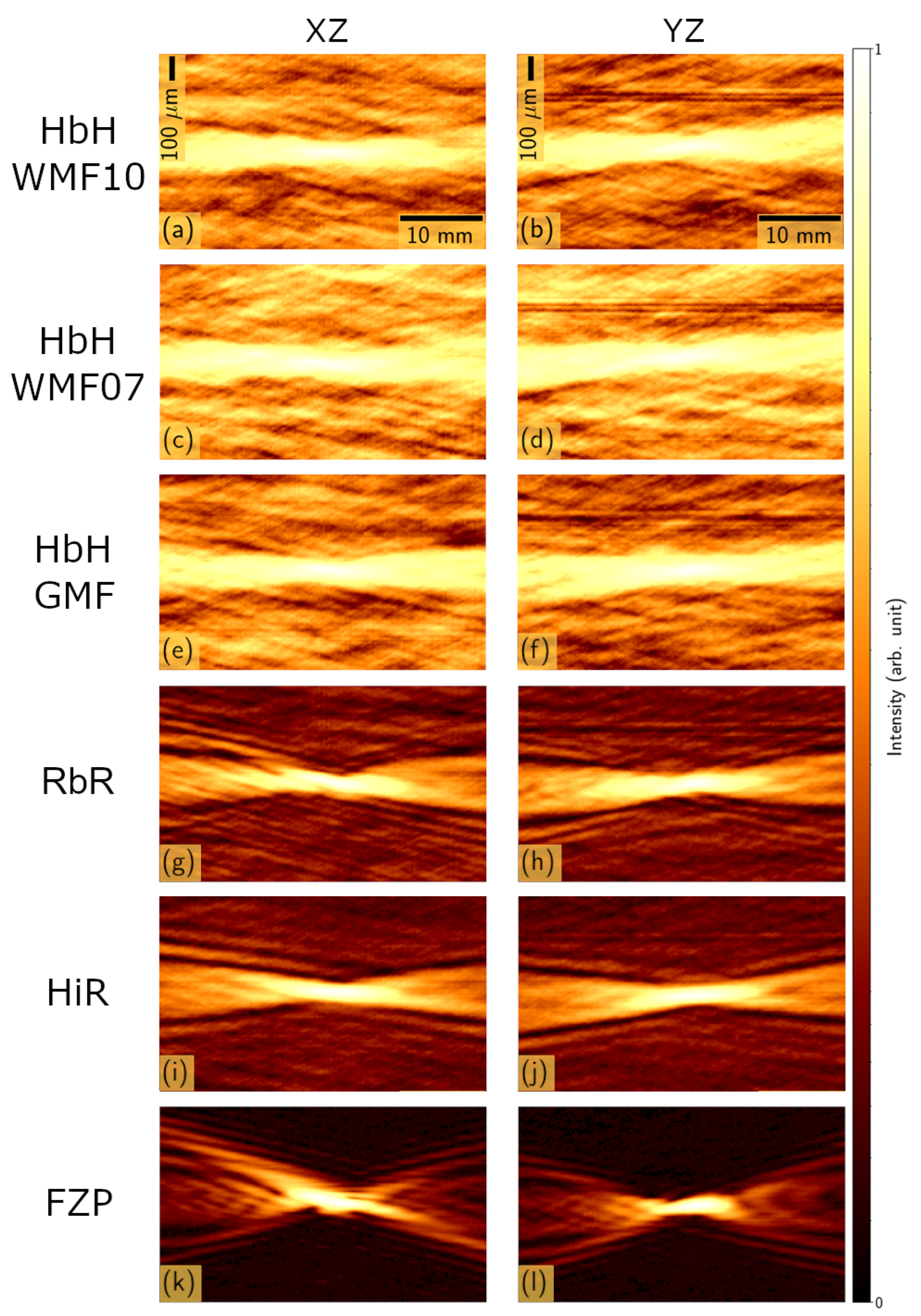
| HbH WMF 1.0 | HbH WMF 0.7 | HbH GMF | RbR | HiR | FZP |
|---|---|---|---|---|---|
| DOF [mm] | |||||
| 10.9 ± 0.4 | 10.6 ± 0.4 | 11.8 ± 0.4 | 9.0 ± 0.4 | 8.9 ± 0.4 | 5.3 ± 0.4 |
| [μm] | |||||
| 9.80 ± 0.05 | 60.96 ± 0.09 | 48.88 ± 0.03 | 33.5 ± 0.2 | 32.91 ± 0.04 | 24.25 ± 0.03 |
| [μm] | |||||
| 52.05 ± 0.05 | 53.50 ± 0.07 | 59.86 ± 0.03 | 33.5 ± 0.2 | 32.91 ± 0.04 | 24.25 ± 0.03 |
| [mm] | |||||
| 0.16 ± 0.02 | 0.02 ± 0.04 | 0.38 ± 0.02 | 0.00 ± 0.03 | 0.00 ± 0.02 | 0.00 ± 0.01 |
| 136 ± 2 | 192.6 ± 0.2 | −204.1 ± 0.1 | −0.09 ± 0.03 | −0.07 ± 0.03 | −0.00 ± 0.01 |
| 1.79 ± 0.01 | 1.87 ± 0.03 | 1.63 ± 0.01 | 1.27 ± 0.01 | 1.32 ± 0.02 | 1.09 ± 0.03 |
| 1.49 ± 0.02 | 1.72 ± 0.02 | 1.86 ± 0.02 | 1.28 ± 0.01 | 1.32 ± 0.02 | 1.09 ± 0.03 |
| [%] | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pastor-Villarrubia, V.; Soria-Garcia, A.; Andres-Porras, J.; del Hoyo, J.; Elshorbagy, M.H.; Sanchez-Brea, L.M.; Alda, J. Experimental Validation of Designs for Permeable Diffractive Lenses Based on Photon Sieves for the Sensing of Running Fluids. Photonics 2025, 12, 486. https://doi.org/10.3390/photonics12050486
Pastor-Villarrubia V, Soria-Garcia A, Andres-Porras J, del Hoyo J, Elshorbagy MH, Sanchez-Brea LM, Alda J. Experimental Validation of Designs for Permeable Diffractive Lenses Based on Photon Sieves for the Sensing of Running Fluids. Photonics. 2025; 12(5):486. https://doi.org/10.3390/photonics12050486
Chicago/Turabian StylePastor-Villarrubia, Veronica, Angela Soria-Garcia, Joaquin Andres-Porras, Jesus del Hoyo, Mahmoud H. Elshorbagy, Luis Miguel Sanchez-Brea, and Javier Alda. 2025. "Experimental Validation of Designs for Permeable Diffractive Lenses Based on Photon Sieves for the Sensing of Running Fluids" Photonics 12, no. 5: 486. https://doi.org/10.3390/photonics12050486
APA StylePastor-Villarrubia, V., Soria-Garcia, A., Andres-Porras, J., del Hoyo, J., Elshorbagy, M. H., Sanchez-Brea, L. M., & Alda, J. (2025). Experimental Validation of Designs for Permeable Diffractive Lenses Based on Photon Sieves for the Sensing of Running Fluids. Photonics, 12(5), 486. https://doi.org/10.3390/photonics12050486







