Abstract
In optical fiber communication, recent advances in multiple-input and multiple-output (MIMO) systems using space-division multiplexing have helped achieve higher spectral efficiency and data rates. Propagating higher-order modulation formats over MIMO systems further strengthens the capacity of the transmission link. In the optical-MIMO system, the dispersion impairments originating from a km long multi-mode fiber (MMF) are mitigated using the proposed joint-transceiver equalization technique. A numerical convex optimization algorithm is used to compute and optimize the pre- and post-equalization (PPE) coefficients jointly restricted by cost and power budgets. The potential of the proposed joint-PPE technique is tested on an MMF link, which is severely degraded by dispersion compared to a single-mode fiber channel. From the experimental results, the average optical received power gain necessary to reach bit-error rate is improved by nearly dB using the joint-PPE compared to the post-equalization only based on the minimum mean-squared error principle. When the efficiency of the conventional zero-forcing (ZF) principle-based PPE and the joint-PPE is compared, the joint-PPE scheme outperforms the ZF-PPE by approximately dB. The enhancement in the transmission quality is observed with experimentally measured eye diagrams using the joint-PPE scheme. Under the analyzed scenarios, computer simulation also confirms the hypothesis, which establishes the effectiveness of the proposed joint-transceiver equalization over the conventional ZF-PPE scheme. Moreover, the simulated performance benefits of the joint-PPE are evaluated using the singular value decomposition (SVD) technique. Improvement of ≈3.86 dB in the average optical received power gain required to reach bit-error rate is witnessed with the PAM-4 format. Overall, the joint-transceiver equalization technique is proven to be beneficial in optical MIMO systems.
1. Introduction
In recent years, phenomenal growth in the demand for bandwidth has been witnessed due to the progress in cloud computing, high-definition video streaming, and the internet of things. The surge in the increasing data requirements has inspired the expansion of telecommunication networks by developing better modulation and coding techniques. Optical networks have provided support to match the high-bandwidth requirements from short-haul to the long-haul transmission links.
Single-mode fibers (SMFs) are preferred for long-distance optical systems due to their low dispersion properties and low signal attenuation. Despite the availability of degrees of freedom such as time, wavelength, or polarization, the capacity of an SMF is rapidly reaching Shannon’s limit [1,2,3]. Furthermore, the small core diameter of an SMF causes sub-micron alignment tolerances. Multi-mode fibers (MMFs) consist of a larger core ( μm or μm) and hence have higher alignment margins. Due to the larger core diameter, the MMF core can support multiple parallel data channels using up to 100 transverse spatial mode groups [4,5,6]. The orthogonality between different mode groups is only preserved for a short distance. In an intensity modulation/direct detection (IM/DD) system for short-reach optical links, an MMF is preferred over an SMF due to higher spectral efficiency, cost-effectiveness and simple implementation. However, MMFs adversely affect the available bandwidth distance product as a result of intermodal dispersion and mode-dependent losses such as mode scrambling [6,7,8].
The technique for creating multiple parallel data channels using the transverse spatial extent of an MMF is known as space-division multiplexing (SDM) [9]. Offset light-launching conditions excite two or more parallel data streams in the SDM technique. The considerable enhancement in the data rates and the mitigation of mode scrambling are handled by incorporating the multiple-input and multiple-output (MIMO) signal-processing technique [6,7]. Moreover, the spectral efficiency of the transmission link is boosted using the higher-order modulation (HOM) formats, where the constellation size is more than two. In particular, in an IM/DD system, the pulse-amplitude modulation (PAM) formats are preferred over subcarrier modulation (SCM) [10], carrier-less amplitude modulation (CAP) [11], or discrete multitone (DMT) [12,13] in terms of simple implementation and better sensitivity regarding the received optical power. However, an MMF channel is severely impaired by intermodal dispersion compared to an SMF link [8]. Dispersion compensation mechanisms include physical components, such as dispersion-shifted fibers or fiber Bragg gratings, and digital mitigation using equalization.
In an IM/DD system, when a trade-off between complexity and cost-effectiveness is considered, digital dispersion compensation mechanisms, especially linear MIMO equalizers, are preferred. On the other hand, the performance of non-linear MIMO equalizers surpasses most optimal linear MIMO equalizers based on the minimum mean-squared error (MMSE) principle [13,14,15,16,17]. However, a linear MMSE-based equalizer is selected because of comprehensive implementation, simple realization and analytical traceability [3,18]. Additionally, a further boost in the system performance is evident in the presence of a transceiver equalization compared to the equalization applied either at the transmitter or the receiver [14,15,19]. According to the literature, the zero-forcing (ZF) principle is commonly adapted for the design of the pre-equalizer. Moreover, a separate equalization principle is utilized to calculate the post-equalization coefficients [16,17,20,21]. Additionally, the performance evaluation of these pre- and post-equalization (PPE) schemes is validated either on the single-input and single-output (SISO) system model or over an SMF fiber [16,17,21,22]. Although the PPE schemes are reported in [14,15,19,23], the experimental comparison with conventional PPE schemes using a longer MMF and higher data rate needs to be investigated. Moreover, addressing the lower convergence rate to achieve the optimal design of PPE coefficients is crucial [19,23]. This research gap limits the feasible use of a pre-equalizer on the transmitter side due to high complexity. In MIMO signal processing, the singular value decomposition (SVD) technique is well established, and it has been proven to be advantageous as the MIMO channel is transformed into several parallel transmission layers [24,25,26,27]. The advantages of an SDM-based MIMO model deploying an MMF channel with HOM formats have not been characterized in depth. Therefore, this work focuses on low-cost SDM-based IM/DD systems for short-distance transmission.
Against this background, the novelty of this work is the enhancement of the transmission quality and the bit-error rate (BER) performance using the proposed transceiver–joint equalization scheme over an optical MIMO system with an MMF transmission link. This novel joint-PPE scheme mitigates the impairments originating from a km long MMF channel. The performance benefits of the joint-PPE scheme are yielded by optimally designing both of the PPE coefficients simultaneously using a numerical optimization solver. The performance analysis of the transceiver–joint equalization is also conducted with a SVD-based MIMO system incorporating the HOM format. The analytical model-based simulations and the experimental setup verify the benefits of the provided joint-PPE scheme. Additionally, the supremacy of the joint-PPE scheme is established over the conventional ZF-PPE and MMSE-based post-equalization only (PE-only).
Hereinafter, this paper is organized as follows: Section 1 describes the system model in the electrical domain. An analytical description of the provided system model and the quality criteria are also included in this section. Furthermore, the optimization and design of the joint-PPE scheme are presented in the Section 3, and the solver using the interior-point algorithm is explained in detail. In the Section 4, the simulation and experimental results are discussed and compared with other equalization techniques. Finally, the conclusion is outlined in the Section 5. The literature with a similar overlap in this area is reported in the Section 6.
2. System Model
The proposed transceiver–joint equalization technique in a MIMO system is analyzed using an electrical system model with , where and represent number of transmitters and receivers, respectively. In Figure 1, a MIMO transmission model with is segregated into three parts, namely the transmitter, the channel, and the receiver. The symbols utilized in the system model are described in Table 1. The MIMO transmitter consists of a serial-to-parallel (S/P) converter and a pre-equalizer. Using the S/P converter, encoded serial binary data are transformed into parallel data streams, where represents the total number of MIMO inputs. The parallel symbol streams , with and are mapped on to -ary PAM constellation. The bit-to-symbol mapping is conducted using Gray coding as it improves the system performance. The transmit symbol space of , where , consists of symbols in accordance to the chosen -ary PAM constellation. It is worth noting that the symbols in are independent and identically distributed. The amplitude of the symbols is defined as
.
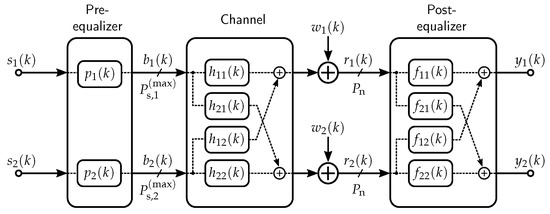
Figure 1.
MIMO system model description with a frequency-selective channel incorporated with the PPE scheme.

Table 1.
List of symbols and their respective description.
In (1), is the maximum transmit power at the -th MIMO input. The constellation diagram is modeled to provide the maximum power to the last symbol irrespective of the selected PAM format. Consequently, the parallel symbol streams are pre-equalized using the pre-equalizer at the -th input. Therefore, is converted into pre-equalized multi-level signals . The total number of distinct pre-equalized signal levels at the -th input is defined as , where represents the number of pre-equalizer filter taps. The resulting pre-equalized signal complies with the power constraint, which is given as
where is a conversion factor for converting an electrical signal into an optical signal. Although implementing the pre-equalization, a constant peak-to-average power ratio is also maintained in (2).
Subsequently, the multi-level pre-equalized signal is propagated through the MIMO channel, which is an MMF link. The transmitted signal is deteriorated with the inter-symbol interference (ISI) and the inter-channel interference (ICI) originating from the MMF channel , where and the number of MIMO outputs is denoted by . The temporal pulse broadening and chirping occur due to the frequency-selective behavior of the MMF channel . Moreover, the indirect components of the channel , when , are responsible for the crosstalk between the MIMO layers. An MMF channel supports several guided modes and provides easier light-launching conditions into the fiber due to the larger core diameter. Hence, the parallel data streams are generated by offset light-launching conditions to achieve a higher spectral efficiency. This technique is known as SDM using an MMF [6]. In the given system model, the first layer is created by launching the light into the center of the MMF core. Similarly, the second MIMO layer is formed by a μm offset launching condition into the fiber core, as shown in Figure 2. When traveling through the MMF channel, the transmitted signal is degraded due to ISI and ICI, originating from the channel. Afterwards, the IM/DD noise impairments further degrade the transmitted signal [26]. At the MIMO receiver, the post-processing of the received signal with is conducted using a post-equalizer . The residual interferences are mitigated with the help of an MMSE-based post-equalizer. When designing the post-equalizer, the MMSE principle is preferred over the ZF principle as the optimized coefficients of an MMSE equalizer contribute less to noise amplification.
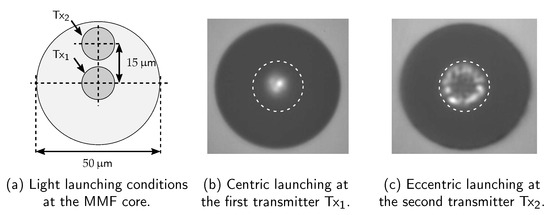
Figure 2.
In (a), the transmitter’s configuration for launching the light into an MMF core is depicted. Measured mean power distribution with (b) centric (offset: μm) and (c) eccentric (offset: μm) light-launching conditions into an MMF core, which is represented by the white dashed circle.
2.1. Analytical Description of the System Model
A frequency-selective channel-based MIMO system with , as shown in Figure 1, is analytically represented as
From (3), the pre-equalized transmitted signal is represented as with dimensions. The channel matrix describes the block-oriented system model, and is defined as
where is the SISO channel matrix, which characterizes the influence of the channel over the pre-equalized transmitted signal . The noise vector pertains to the noise in an IM/DD system. Finally, the received signal is represented as with dimensions. The transmitted signal is decomposed as
where is the pre-equalizer with a size of , and represents the input vector of . For a limited increase in the complexity, the pre-equalizer is considered to be a diagonal matrix. Ultimately, the post-equalization is executed to mitigate the residual interference. The final expression of the given system model with PPE is formulated as
with denoting the post-equalizer with dimensions. In (6), the first term implies that the channel influence can be mitigated with the aid of PPE. Similarly, the noise amplification due to post-equalization is evident in (6). The system performance is adversely degraded due to noise enhancement from post-equalization. Hence, a well-designed pre-equalizer will be capable of compensating for the channel along with negligible noise amplification. When a trade-off between complexity and cost-effectiveness is considered, a pre-equalizer with a few taps is preferred in conjunction to a post-equalizer.
The quantification of the noise amplification due to the post-equalization filter taps is expressed with the noise weighting factor (NWF) and is given as
where is the number of post-equalization taps and represents the post-equalizer taps for -th input and -th output. From (7), it is evident that the amplitude of the post-equalization taps is responsible for the noise amplification.
2.2. Quality Criteria
The BER is considered to be the key indicator to evaluate the performance of an MMF channel. The transmission quality of the -th MIMO input is defined as
where represents the half-vertical eye-opening of the -th input and the noise power after the post-equalization is defined with . From (7) and (8), the relationship between and is given by
In (10), the noise amplification factor is inversely proportional to the transmission quality. Typically, for an SDM-based MIMO system, the BER performance of the -th input is
with erfc(·) denoting the complimentary error function, the constellation size and the transmission quality at the -th input is represented by and , respectively.
In (11), when an error is encountered during the transmission, it is assumed that the error will only be limited to its neighboring symbol, i.e., only a one-bit error due to the use of Gray coding. However, more-than-one-bit errors can occur at low received power due to the high noise variance. Second, the noise variance of each symbol is considered to be identical in (11). In contrast, the noise variances are different in the shot noise dominant region. Hence, the area integration method is adapted to accurately estimate the BER incorporating probability density function (PDF). The symbol-specific BER is calculated as
where represents the Hamming distance between the symbols and at -th input. The PDF of the received symbol is described as and is the decision region. The overall BER is defined as
In summary, the system performance will be degraded due to the noise amplification originating from the extensive utilization of the post-equalizer. Theoretically, this deterioration in the system performance is shown in (12). From an analytical perspective, it is worth investigating, in order to practically estimate the usefulness of shifting the post-equalizer taps to the transmitter side with the given system model. The challenges of designing the optimal PPE filter and evaluating the system performance are addressed in the following sections.
3. Design and Optimization of Pre- and Post-Equalization
According to the literature, a few-tap pre-equalizer is preferred to compensate for the channel influence without any noise enhancement [16,17,20,22]. The zero-forcing design of a pre-equalizer is chosen predominantly due to the simple implementation. Moreover, the post-equalizer filter taps are separately calculated. By contrast, in the proposed transceiver–joint equalization, the pre-equalizer and the post-equalizer are calculated and jointly optimized to yield performance benefits. The pre-equalizer is characterized as a finite impulse response (FIR) filter, and the role of pre-equalizer taps is shown as
where is the length of the pre-equalizer at the -th MIMO layer. The structure of a linear FIR pre-equalizer present on each MIMO layer is shown in Figure 3. The main goal is to design and optimize the PPE filter taps to enhance the system performance while maintaining power and cost budgets.
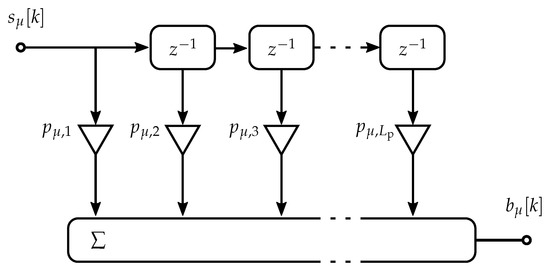
Figure 3.
The structure of a linear FIR pre-equalizer filter, where the delay by one symbol is denoted by .
In this work, a numerical convex optimization is applied to calculate and optimize the PPE coefficients. The primal–dual interior-point constrained algorithm is tailored with respect to the analytical solution of the given system model [28]. Hence, the objective function subjected to the constraints is stated as follows
The objective function is defined to minimize the NWF on each MIMO layer in accordance with the channel state information. The values of and will converge to their optimal value with each iteration. In (16), the first constraint determines the complete removal of the ISI and ICI with the PPE filter. Additionally, the second constraint assures that the symbol with the highest amplitude is limited to the maximum transmit power of the laser source. In (16), the optimization problem is called the primal problem. In order to solve this problem, the duality optimization is utilized, where the constraints are incorporated with the objective function. The modified objective function of the optimization statement is
where and represent the scalar slopes of the penalty function. The purpose of the penalty function is to penalize the objective function when the constraints are not followed. Furthermore, the objective function is rewarded when the constraints are obeyed. The objective function (17) is termed as the primal problem, which is converted into the duality problem, as the min and max operators are in the function simultaneously. Thus, the dual problem can be written as
The objective function in (18) can be easily solved with the Lagrangian solver. Hence, in order to find the optimal coefficients of the proposed joint-PPE scheme, the following condition should be satisfied
To hold the strong duality between the primal and dual problems, there should be zero difference between the primal optimal solution and the dual optimal solution. The strong duality is executed using the Karush–Kuhn–Tucker (KKT) optimality conditions, which are given as
For solving such a problem, the KKT conditions are modified, where a variable named t is introduced. This variable t is a positive number to control the degree of perturbation towards the optimal solution. The constraints, mentioned in (20), are adapted with where n is the total number of constraints, and mentioned as
The characteristics of are that the zero-duality gap is achieved between the primal and the dual problems when , . By combining (19), (20) and (21), the final optimization problem is defined as
Using the Newton solver, (22) is solved by choosing larger values for , which results in discovering the analytical center of the feasible region. Afterwards, the value of decreases to locate the optimal solution of the given statement.
Ultimately, the jointly designed PPE filter taps are optimized to remove the interferences, given minimal increment in the NWF. From joint-PPE, the post-equalizer will contribute to nominal noise amplification. Therefore, the hypothesis states that the joint-PPE is expected to yield better performance than ZF-based PPE and MMSE-based PE-only.
4. System Model Using SVD
When considering the SVD technique applied to a frequency-selective MIMO channel, the resulting discrete-time block-oriented system is illustrated in Figure 4. The joint-PPE and ZF-PPE schemes are analyzed over the SVD-based MIMO system. The advantage of utilizing SVD is that the channel is converted into a diagonal matrix. It implies that the crosstalk components, when , will be completely mitigated. The modified frequency-selective channel is defined as
where contains the positive square roots of the eigenvalues of matrix with and denotes the unitary matrix of dimensions. The matrix of dimension represents the conjugate transpose (Hermitian operation H) of the unitary matrix . The resulting numerical matrix after SVD is the real-valued diagonal matrix , which has the following form
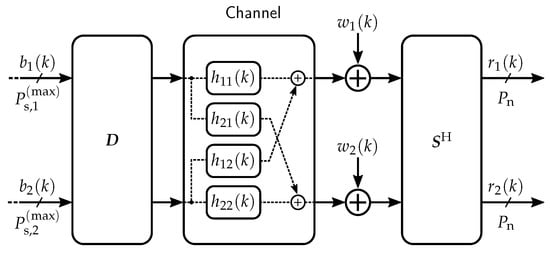
Figure 4.
Optical MIMO channel utilizing the SVD technique.
The overall transmission of the system using SVD is described as
The implication of incorporating SVD is distinct eye-openings, which is formulated as
with denoting the half-vertical transmit amplitude at -the MIMO input and is the positive root of the eigenvalue of . The quality of transmission is calculated as
The advantage of incorporating SVD in the system model is transforming the channel into non-interfering and independent transmission layers with unequal gains. Please note that neither the noise power nor the transmit power are enhanced. The resulting orthogonal system model of the -th layer based on SVD is shown in Figure 5.
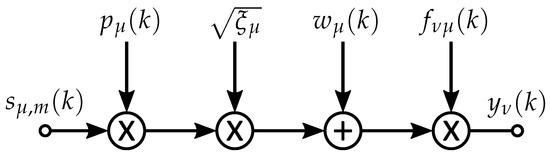
Figure 5.
Simplified layer-specific MIMO system model with joint-PPE scheme.
5. Results
In this section, the performance of the proposed joint-PPE scheme is assessed using the given system model with a 1.4 km MMF channel. Moreover, the performance comparison is demonstrated between the ZF-based PPE and the proposed joint-PPE using Monte Carlo simulations and the experimental setup.
5.1. Simulation Results
The discrete-time Monte Carlo simulations are incorporated with a MIMO system using a km long MMF channel. The simulations are implemented using three sequential steps. In the first step, the MMSE-based PE-only is applied to the provided system model while considering the pre-equalizer as a Dirac delta function. Additionally, the channel state information is computed from the received data using the pilot-based least-square algorithm. The second step involves the design and optimization of the PPE coefficients with the help of the given constrained numerical optimization. In the last step, the optimal joint-PPE coefficients are integrated in the system model, and the BER performance is calculated. Finally, the performance of the joint-PPE, the ZF-PPE and the PE-MMSE (also known as PE-only) are compared. Please note that the ZF-PPE incorporates a ZF-based pre-equalizer with an MMSE-based post-equalizer [29,30].
The primary features of an IM/DD system are simple implementation and cost-effectiveness. Therefore, limiting the complexity of the transmitter is a factor, which should be considered while evaluating the system performance. In order to determine the optimal number of pre-equalizer filter taps, the relationship of the NWF with the pre-equalizer taps is calculated. The results are illustrated in Figure 6, where the optimized pre-equalizer coefficients achieve a significant reduction in the NWF on both the MIMO layers as compared to the PE-MMSE NWF of 7 on the first layer and 58.48 on the second layer. The extent of NWF decrement is directly related to the improvements in the system performance. Clearly, the optimally designed pre-equalizer using the joint-PPE scheme surpasses the ZF-PPE scheme. Hence, the joint-PPE is expected to yield better BER performance. It is noteworthy that the maximum reduction in the NWF is observed with the joint-PPE using at the first layer. However, the ZF-PPE scheme on the first MIMO layer has attained the maximum reduction in the NWF with . Similarly, the maximum reduction in the NWF on the second MIMO layer is observed at and with the joint-PPE and the ZF-PPE schemes, respectively. On the basis of the reduction of the NWF and minimal transmitter’s complexity, a pre-equalizer with at most four-taps on each layer is chosen for further performance analysis. Evidently, the joint-PPE requires a considerably smaller number of pre-equalizer taps. Thus, the prerequisites of the IM/DD systems are followed by a few pre-equalizer taps in conjunction with a post-equalizer.
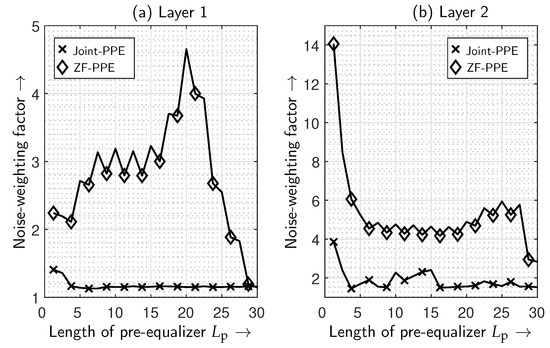
Figure 6.
Noise weighting factor with increasing number of pre-equalization coefficients, where a layer-wise comparison between the proposed joint-PPE scheme and the ZF-based PPE is exhibited.
Prior to the system performance evaluation, the measured channel impulse response of a 1.4 km MMF is illustrated in Figure 7. The measured channel state information is obtained using an SDM-based optical MIMO experimental setup with offset launching conditions into an MMF. Afterwards, the estimated channel contains dispersion impairments and mode-dependent losses in accordance with the excited mode groups. This channel information is incorporated in the computer simulation to imitate the SDM technique. From Figure 7, it is clear that both MIMO layers are adversely affected due to crosstalk , when . Additionally, a significant amount of ISI is also observed due to differential mode group delays.
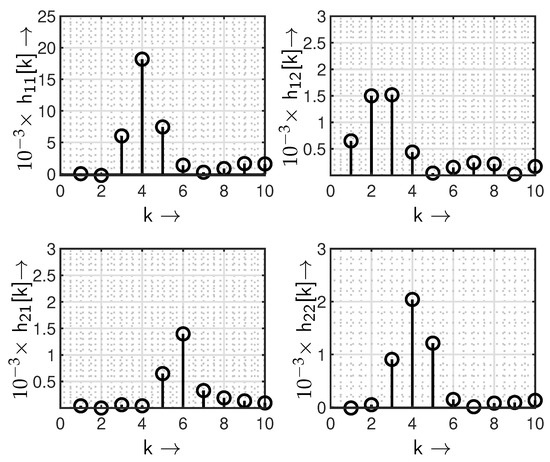
Figure 7.
Measured channel impulse response of a 1.4 km long MMF with respect to the symbol rate per MIMO layer at an operating wavelength of 1550 .
The proposed joint-transceiver equalization system performance is compared with the conventional ZF-PPE and PE-MMSE. The BER performances using PAM-2 and PAM-4 transmissions are demonstrated in Figure 8 and Figure 9. The enhancements in the average received power compared to the PE-MMSE are presented in Table 2 at a BER of . The BER results prove that the joint-PPE outperforms the ZF-PPE and PE-MMSE. Additionally, the BER performance of the joint-PPE can be advanced using the SVD-based joint-PPE. Under the first PAM-2 transmission scenario, a gain SVD-PPE of ≈3.52 dB is observed in comparison to PE-MMSE. Similarly, the performance improvement of ≈2.54 dB is marked while solely using the joint-PPE. The joint-PPE scheme achieves an identical BER performance with only half of the optimized pre-equalizer taps compared to the ZF-PPE. It is evident by the overlapping BER performances of the joint-PPE with and ZF-PPE with . Considering the PAM-4 transmission on both MIMO inputs under the second scenario, a slight improvement is noted in comparison to the first scenario. The joint-PPE in conjunction with SVD yields the best system performance, surpassing PE-MMSE by ≈3.86 dB. The joint-PPE single-handedly achieves a gain of ≈2.73 dB compared to PE-MMSE. An improvement in of ≈1.13 dB indicates that the proposed joint-PPE enhances the system performance to a higher extent than the conventionally deployed ZF-PPE.
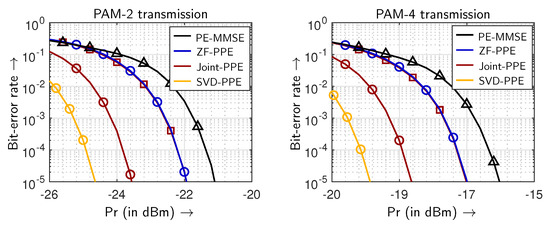
Figure 8.
BER dependent on simulated received power for PAM-2 and PAM-4 transmissions. The BER values associated with and are represented with the square and the circle markers, respectively.
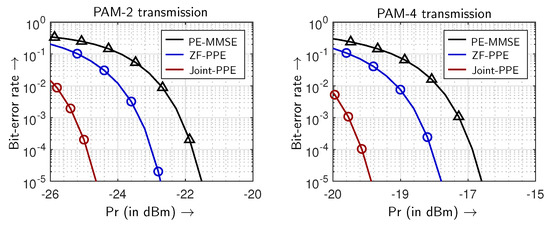
Figure 9.
BER dependent on simulated received power for PAM-2 and PAM-4 transmissions for SVD-based optical MIMO system.

Table 2.
Overall simulated gains of the optical MIMO system at BER using a 1.4 km long MMF channel at GHz.
In summary, the simulated BER performances and the gains testify to the advantages of using the jointly designed and optimized PPE filter with PAM-2 and PAM-4 formats. Moreover, the hypothesis is established with the analytical proof that, by shifting the post-equalization taps to the transmitter side, the system performance is boosted due to the limited amplification of the noise.
5.2. Experimental Results
A optical MIMO experimental setup is developed, which is shown in Figure 10 and Figure 11. Similar to the provided system model, this measurement setup is also divided into three parts: MIMO transmitter, MMF channel and MIMO receiver.
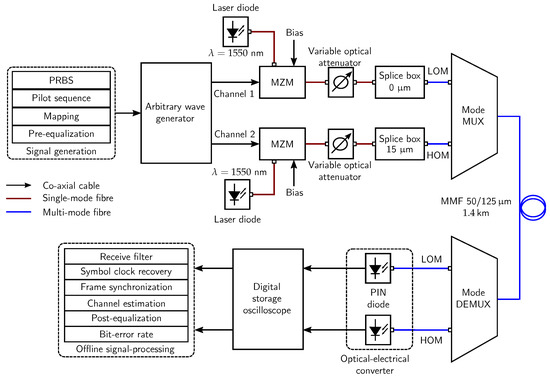
Figure 10.
Experimental setup for the joint-PPE scheme using an optical MIMO system with a 1.4 km long MMF channel.

Figure 11.
Experimental setup of optical MIMO system for performance evaluation of the proposed joint-transceiver scheme.
Starting from the transmitter side, a S/P converter is applied to convert a serial data stream into two pseudo-random binary sequences (PRBSs). Afterward, these sequences are mapped on the Gray coded symbols in accordance with the chosen PAM-2 or PAM-4 modulation formats. Additionally, the pilot symbols are also appended to the data symbols for the purpose of channel estimation. By using the above-mentioned optimization statement, the optimal pre-equalizer coefficients are computed using channel information. Consequently, multi-level signals are enabled by applying pre-equalization to the input data streams. In case no channel state information is available, the pre-equalizer acts as a Dirac delta function, and the results for the PE-only are obtained. The signal-generation process is concluded by generating the electrical signals from the input symbols using an arbitrary waveform generator (AWG). The channels of the AWG are operated on the symbol rate of GBaud per MIMO layer. The electrical signals are converted into the optical signals using chirp-free external Mach-Zehnder modulators (MZMs). A lithium-niobate (LiNbO3) substrate is used in the optical circuit of the MZM. The bias of the MZM is manually adjusted, and the quadrature points are stabilized using a temperature controller. The carrier laser sources work on the operating wavelength nm. Using variable optical attenuators (VOAs), the overall BER performance is calculated over a distinct range of the average received optical power (). Thereafter, the MMF splice boxes are utilized for the excitation of the selective mode groups by launching the light with a certain offset. In this provided experimental setup, the SDM scheme is enabled by utilizing centric and eccentric launching conditions into a 1.4 km long MMF with the offsets of μm and μm, respectively. The offset light-launching conditions are demonstrated in Figure 2 and Figure 10. Centric launching of the light into the MMF results in the excitation of the fundamental mode group or lower-order mode (LOM) group. Similarly, the high-order mode (HOM) groups are excited with the μm offset launching condition. The last part of the transmitter includes an optical fusion coupler, which is useful in multiplexing the mode groups. In this setup, custom-made fusion couplers are utilized with a slight asymmetric power split ratio as these are well suited for mode multiplexing (MUX) applications [31,32]. The function of a mode MUX is to combine the LOM groups with HOM groups using an x-shaped structure. The LOM groups travel from the center of the fiber core. Thus, these groups are more likely to travel in a transverse direction. However, the HOM groups couple with LOM groups because of their wider electric field distribution. The mode MUX and mode demultiplexer (DMUX) have 45% power-splitting ratio with ≈3 dB insertion loss.
The optical signal, containing the LOM groups and HOM groups, is propagated through the OM4 MMF channel with a length of km. The transmitted signal suffers from degradation due to ISI and ICI due to a greater amount of interference present in an MMF compared to an SMF. The measured channel impulse response is demonstrated in Figure 7. The channel state information is obtained by estimating the influence on the appended pilot symbols in the data streams. A least-square pilot estimator algorithm is developed to measure the channel. The significant amount of interference is evident from Figure 7. The challenge of recovering the transmitted data is dealt with by the MIMO receiver.
After propagating through the MMF channel, the degraded signal is received by the PIN photo-detector on each layer. These diodes act as optical-to-electrical converters. An inherent increment in capacitance is observed due to the presence of a large detection area. Consequently, the sensitivity of the receiver suffers from this property. An internal trans-impedance amplifier is present, which amplifies the received electrical signals. A digital storage oscilloscope (DSO) is utilized to capture the electrical signals using a resolution of 40 GSa/s at a bandwidth of 13.6 GHz. The stored signals undergo an offline signal-processing chain with one sample per symbol. The first step includes receive filtering, where a rectangular filter similar to the transmit filter response is applied. Afterward, the symbol clock is recovered from the down-sampled filter signal. The next step involves the estimation of the frequency-selective channel. Most importantly, a post-equalizer is used to mitigate all the interference due to the channel. In the end, hard decision decoding is employed to retrieve the original data and subsequently, the performance is evaluated in terms of the BER performance. To obtain reliable and repetitive results, 74 frames are calculated on each MIMO layer for every instance, which adds up to five million bits approximately. The symbol clock recovery is conducted using an open loop timing recovery method for estimating the exact sampling time. Additionally, the beginning of the data frame is computed using the fine-timing acquisition algorithm. In this acquisition process, the cross-correlation between a segment of the received signal and the pilot sequence provides an aid to determine the exact starting of the data frame. Moreover, the forward error correcting decoding is not deployed at the receiver.
Using the experimental setup of a MIMO system with a km long MMF channel, the average optical received power dependent on the overall BER system is illustrated in Figure 12 and in Table 3. The performance comparison is conducted between the PE-MMSE, the ZF-PPE and the joint-PPE schemes. Moreover, the results are also obtained for two different scenarios, which includes the use of PAM-2 and PAM-4 formats. From the BER performances shown in Figure 12, the proposed joint-PPE clearly outperforms the ZF-PPE and the PE-MMSE schemes. When PAM-2 is utilized on both MIMO layers, the joint-PPE scheme achieves the maximum gain of ≈2.58 dB. Moreover, an improvement of ≈1.74 dB in gain is observed by the joint-PPE compared to the ZF-PPE. Similarly, the highest performance improvements of ≈2.68 dB are indicated by the joint-PPE using the PAM-4 format. The gain ≈1.73 dB of the joint-PPE over the conventional ZF-PPE scheme proves the effectiveness of the proposed joint-PPE. The transmission qualities of all three equalization schemes are demonstrated in Figure 13 and Figure 14. The wider eye-opening of the PPE schemes compared to the PE-only verifies that the transmission quality is boosted using a few-tap pre-equalizer. When the transmission qualities of the ZF-PPE and the joint-PPE are measured, better eye-opening is exhibited by the joint-PPE scheme.
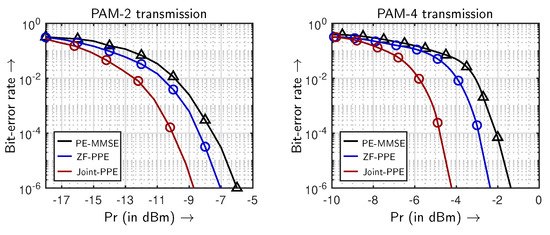
Figure 12.
Overall BER performance comparison between the PE-MMSE, ZF-PPE and Joint-PPE with PAM-2 and PAM-4 formats, where four-tap pre-equalizers are utilized in both PPE schemes.

Table 3.
Measured average optical received power gain of the optical MIMO system at BER using a 1.4 km long MMF channel at GHz.
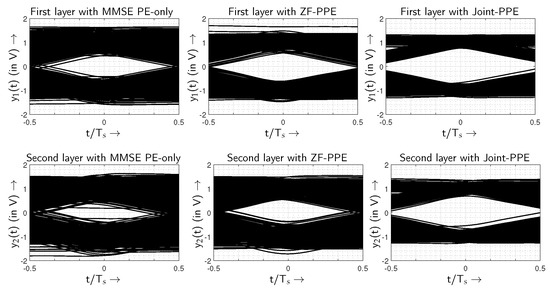
Figure 13.
Eye diagrams of the joint-PPE, ZF-PPE and MMSE PE-only using PAM-2 transmission.
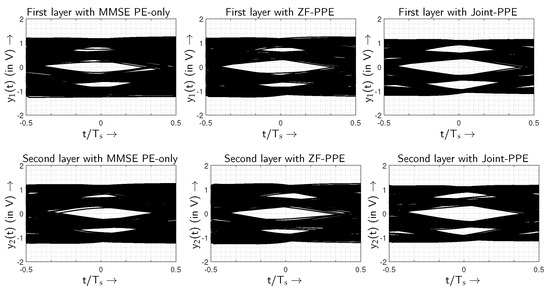
Figure 14.
Eye diagrams of the joint-PPE, ZF-PPE and MMSE PE-only using PAM-4 transmission.
6. Discussion
In this work, the effectiveness of the proposed transceiver–joint equalization filter is evaluated and compared with the conventional PPE and the PE-only schemes. The performance evaluation is conducted using the HOM formats over a SDM-based optical MIMO system with a km MMF transmission link. The average optical received power required to reach a BER of using the PAM-4 formats is improved by ≈2.68 dB with just a four-tap optimally designed pre-equalizer with post-equalization. Similarly, an enhancement of ≈2.58 dB in the gain is achieved by the joint-PPE using PAM-2 format. Despite using a longer MMF channel with twice the bit-rate compared to [19], the improvement of ≈0.65 dB and ≈0.84 dB in the gains at BER is still accomplished. Additionally, with the improved numerical optimization of the PPE taps, an enhancement of nearly two folds in the required Pr gain at BER is attained using PAM-2 constellation compared to [23]. In contrary to the existing joint PPE schemes, the efficiency of the proposed transceiver–joint equalization is verified on a critical dispersion-impaired channel with the MIMO configuration. Further research should focus on the channel robustness in a dynamic environment.
7. Conclusions
In conclusion of this work, the performance of a short-reach optical MIMO system with PAM-2 and PAM-4 constellations is demonstrated. This work aims to compute the effectiveness of the jointly computed pre- and post-equalizer within the power and cost constraints. The experimental results from this study reveal that the system performance is improved by ≈2.5 dB while utilizing the proposed joint-PPE with PAM-2 and PAM-4 over PE-only. Additionally, when a performance evaluation between the conventional PPE scheme and the joint-PPE is conducted, a significant (≈1.5 times) improvement is observed with a constant number of PPE coefficients in both PPE schemes. These results support the hypothesis that the optimally designed PPE coefficients can improve the BER performance of an MMF-based optical system. The findings have implications for increasing the spectral efficiency of critical dispersion-impaired transmission links, and emphasize the need for cost-effectiveness and simple implementation. Future research should focus on optimizing the PPE coefficients with channel robustness. Additionally, the potential of PPE schemes with an MMF link should be explored in the area of quantum communication utilizing quantum key distribution mechanisms [33,34,35]. In summary, this work adds valuable insight into the optimization and utilization of the joint-PPE with the HOM formats in an optical MIMO system consisting of an MMF link.
Author Contributions
Conceptualization, J.S. and A.A.; methodology, J.S. and A.A.; software, J.S.; validation, A.A.; formal analysis, J.S.; investigation, J.S.; resources, J.S. and A.A.; data curation, J.S.; writing—original draft preparation, J.S.; writing—review and editing, A.A.; visualization, J.S.; supervision, A.A.; project administration, A.A.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bai, N.; Ip, E.; Huang, Y.K.; Mateo, E.; Yaman, F.; Li, M.J.; Bickham, S.; Ten, S.; Liñares, J.; Montero, C.; et al. Mode-division multiplexed transmission with inline few-mode fiber amplifier. Opt. Express 2012, 20, 2668. [Google Scholar] [CrossRef] [PubMed]
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, J.; Zhao, M.; Pang, F.; Zhang, Q.; Ye, N. IM/DD mode division multiplexing transmission enabled by machine learning-based linear and nonlinear MIMO equalization. Opt. Commun. 2021, 488, 126832. [Google Scholar] [CrossRef]
- Chen, H.; van Uden, R.; Okonkwo, C.; Koonen, T. Compact spatial multiplexers for mode division multiplexing. Opt. Express 2014, 22, 31582. [Google Scholar] [CrossRef]
- Sillard, P.; Molin, D.; Bigot-Astruc, M.; Jongh, K.D.; Achten, F.; Velazquez-Benitez, A.M.; Amezcua-Correa, R.; Okonkwo, C.M. Low-Differential-Mode-Group-Delay 9-LP-Mode Fiber. J. Light. Technol. 2016, 34, 425–430. [Google Scholar] [CrossRef]
- Pauwels, J.; der Sande, G.V.; Verschaffelt, G. Space division multiplexing in standard multi-mode optical fibers based on speckle pattern classification. Sci. Rep. 2019, 9, 17597. [Google Scholar] [CrossRef]
- Lei, Y.; Xu, K.; Li, J.; Meng, Z.; Wu, R.; Wan, Z.; Fan, Y.; Zhang, W.; Yin, F.; Dai, Y. Feasibility of Space-Division-Multiplexed Transmission of IEEE 802.11 n/ac-Compliant Wireless MIMO Signals over OM3 Multimode Fiber. J. Light. Technol. 2018, 36, 2076–2082. [Google Scholar] [CrossRef]
- Agrawal, G.P. Fiber-Optic Communication Systems; WILEY: Hoboken, NJ, USA, 2021. [Google Scholar]
- Velázquez-Benítez, A.M.; Antonio-López, J.E.; Alvarado-Zacarías, J.C.; Fontaine, N.K.; Ryf, R.; Chen, H.; Hernández-Cordero, J.; Sillard, P.; Okonkwo, C.; Leon-Saval, S.G.; et al. Scaling photonic lanterns for space-division multiplexing. Sci. Rep. 2018, 8, 8897. [Google Scholar] [CrossRef]
- Szczerba, K.; Westbergh, P.; Karout, J.; Gustavsson, J.S.; Haglund, Å.; Karlsson, M.; Andrekson, P.A.; Agrell, E.; Larsson, A. 4-PAM for High-Speed Short-Range Optical Communications. J. Opt. Commun. Netw. 2012, 4, 885. [Google Scholar] [CrossRef]
- Olmedo, M.I.; Zuo, T.; Jensen, J.B.; Zhong, Q.; Xu, X.; Popov, S.; Monroy, I.T. Multiband Carrierless Amplitude Phase Modulation for High Capacity Optical Data Links. J. Light. Technol. 2014, 32, 798–804. [Google Scholar] [CrossRef]
- Wei, J.; Stojanovic, N.; Zhang, L.; Calabrò, S.; Rahman, T.; Xie, C.; Charlet, G. Experimental comparison of modulation formats for 200 G/λ IMDD data centre networks. In Proceedings of the 45th European Conference on Optical Communication (ECOC 2019), Dublin, Ireland, 22–26 September 2019; Institution of Engineering and Technology: Hertfordshire, UK, 2019. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, J.; Stojanovic, N.; Prodaniuc, C.; Xie, C. Beyond 200-Gb/s DMT Transmission over 2-km SMF Based on A Low-Cost Architecture with Single-Wavelength, Single-DAC/ADC and Single-PD. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018. [Google Scholar] [CrossRef]
- Rajbhandari, S.; Chun, H.; Faulkner, G.; Haas, H.; Xie, E.; McKendry, J.J.D.; Herrnsdorf, J.; Gu, E.; Dawson, M.D.; OBrien, D. Neural Network-Based Joint Spatial and Temporal Equalization for MIMO-VLC System. IEEE Photonics Technol. Lett. 2019, 31, 821–824. [Google Scholar] [CrossRef]
- Zhai, Z.; Jiang, H.; Fu, M.; Liu, L.; Yi, L.; Hu, W.; Zhuge, Q. An Interpretable Mapping From a Communication System to a Neural Network for Optimal Transceiver-Joint Equalization. J. Light. Technol. 2021, 39, 5449–5458. [Google Scholar] [CrossRef]
- Guo, M.; Qiao, Y.; Tang, X.; Liu, S.; Sun, Z.; Cui, H.; Xu, X.; Rusch, L.A. 112-Gb/s PAM4 with Joint Pre- and Post-Equalization for Data Center Interconnects. In Proceedings of the Asia Communications and Photonics Conference (ACPC) 2019, Chengdu, China, 2–5 November 2019; Optica Publishing Group: Washington, DC, USA, 2019; p. T2G.2. [Google Scholar]
- Zou, D.; Chen, Y.; Li, F.; Li, Z.; Sun, Y.; Ding, L.; Li, J.; Yi, X.; Li, L.; Li, Z. Comparison of Bit-Loading DMT and Pre-Equalized DFT-Spread DMT for 2-km Optical Interconnect System. J. Light. Technol. 2019, 37, 2194–2200. [Google Scholar] [CrossRef]
- Iijima, Y.; Yuminaka, Y. Double-Rate Equalization Using Tomlinson-Harashima Precoding for Multi-valued Data Transmission. In Proceedings of the 2016 IEEE 46th International Symposium on Multiple-Valued Logic (ISMVL), Sapporo, Japan, 18–20 May 2016. [Google Scholar] [CrossRef]
- Singh, J.; Ahrens, A.; Lochmann, S. Joint Pre- and Post-Equalization with Higher-Order Modulation Formats in SDM-Based Optical MIMO Systems. Photonics 2022, 9, 876. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, J.; Chien, H.C. Single-carrier 400G based on 84-GBaud PDM-8QAM transmission over 2,125 km SSMF enhanced by pre-equalization, LUT and DBP. In Proceedings of the 2017 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 19–23 March 2017; pp. 1–3. [Google Scholar]
- Tang, X.; Qiao, Y.; kung Chang, G. Experimental Demonstration of C-band 112-Gb/s PAM4 over 20-km SSMF with Joint Pre- and Post-equalization. In Proceedings of the Optical Fiber Communication Conference (OFC) 2020, San Diego, CA, USA, 8–12 March 2020; Optica Publishing Group: Washington, DC, USA, 2020. [Google Scholar] [CrossRef]
- Tang, X.; Qiao, Y.; Chen, Y.W.; Lu, Y.; Chang, G.K. Digital Pre- and Post-Equalization for C-Band 112-Gb/s PAM4 Short-Reach Transport Systems. J. Light. Technol. 2020, 38, 4683–4690. [Google Scholar] [CrossRef]
- Singh, J.; Gotten, M.; Ahrens, A.; Lochmann, S. Joint Pre- and Post-Equalization in Optical MIMO Systems using Multi-Level Signaling. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022. [Google Scholar] [CrossRef]
- Fazea, Y.; Amphawan, A.; Al-Gumaei, Y.; Al-Samman, A.M.; Al-Rahmi, W.M. Modes power equalization based-singular value decomposition in mode division multiplexing systems for multi-hungry bandwidth applications. Opt. Fiber Technol. 2021, 61, 102389. [Google Scholar] [CrossRef]
- Pankow, J.; Aust, S.; Lochmann, S.; Ahrens, A. Modulation-mode assignment in SVD-assisted optical MIMO multimode fiber links. In Proceedings of the 15th International Conference on Optical Network Design and Modeling—ONDM 2011, Bologna, Italy, 8–10 February 2011; pp. 1–6. [Google Scholar]
- Ahrens, A.; Kuhn, V. Modulation-mode and power assignment for MIMO-BICM schemes. In Proceedings of the 2008 International ITG Workshop on Smart Antennas, Darmstadt, Germany, 26–27 February 2008. [Google Scholar] [CrossRef]
- Ahrens, A.; Lange, C. Modulation-mode and power assignment in SVD-equalized MIMO systems. Facta Univ.-Ser. Electron. Energetics 2008, 21, 167–181. [Google Scholar] [CrossRef]
- Stephen Boyd, L.V. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Jiang, Y.; Varanasi, M.K.; Li, J. Performance Analysis of ZF and MMSE Equalizers for MIMO Systems: An In-Depth Study of the High SNR Regime. IEEE Trans. Inf. Theory 2011, 57, 2008–2026. [Google Scholar] [CrossRef]
- Proakis, J.G.; Salehi, M. Digital Communications; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Sandmann, A.; Ahrens, A.; Lochmann, S. Experimental Description of Multimode MIMO Channels utilizing Optical Couplers. In Proceedings of the Photonic Networks, 15. ITG Symposium, Leipzig, Germany, 5–6 May 2014; pp. 1–6. [Google Scholar]
- Ahrens, A.; Lochmann, S. Optical couplers in multimode MIMO transmission systems measurement results and performance analysis. In Proceedings of the 2013 International Conference on Optical Communication Systems (OPTICS), Reykjavik, Iceland, 29–31 July 2013; pp. 1–6. [Google Scholar]
- Xie, Y.M.; Lu, Y.S.; Weng, C.X.; Cao, X.Y.; Jia, Z.Y.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.L.; Chen, Z.B. Breaking the Rate-Loss Bound of Quantum Key Distribution with Asynchronous Two-Photon Interference. PRX Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Lucamarini, M.; Yuan, Z.L.; Dynes, J.F.; Shields, A.J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 2018, 557, 400–403. [Google Scholar] [CrossRef]
- Gu, J.; Cao, X.Y.; Fu, Y.; He, Z.W.; Yin, Z.J.; Yin, H.L.; Chen, Z.B. Experimental measurement-device-independent type quantum key distribution with flawed and correlated sources. Sci. Bull. 2022, 67, 2167–2175. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).