A Polarized Structured Light Method for the 3D Measurement of High-Reflective Surfaces
Abstract
:1. Introduction
2. Related Work
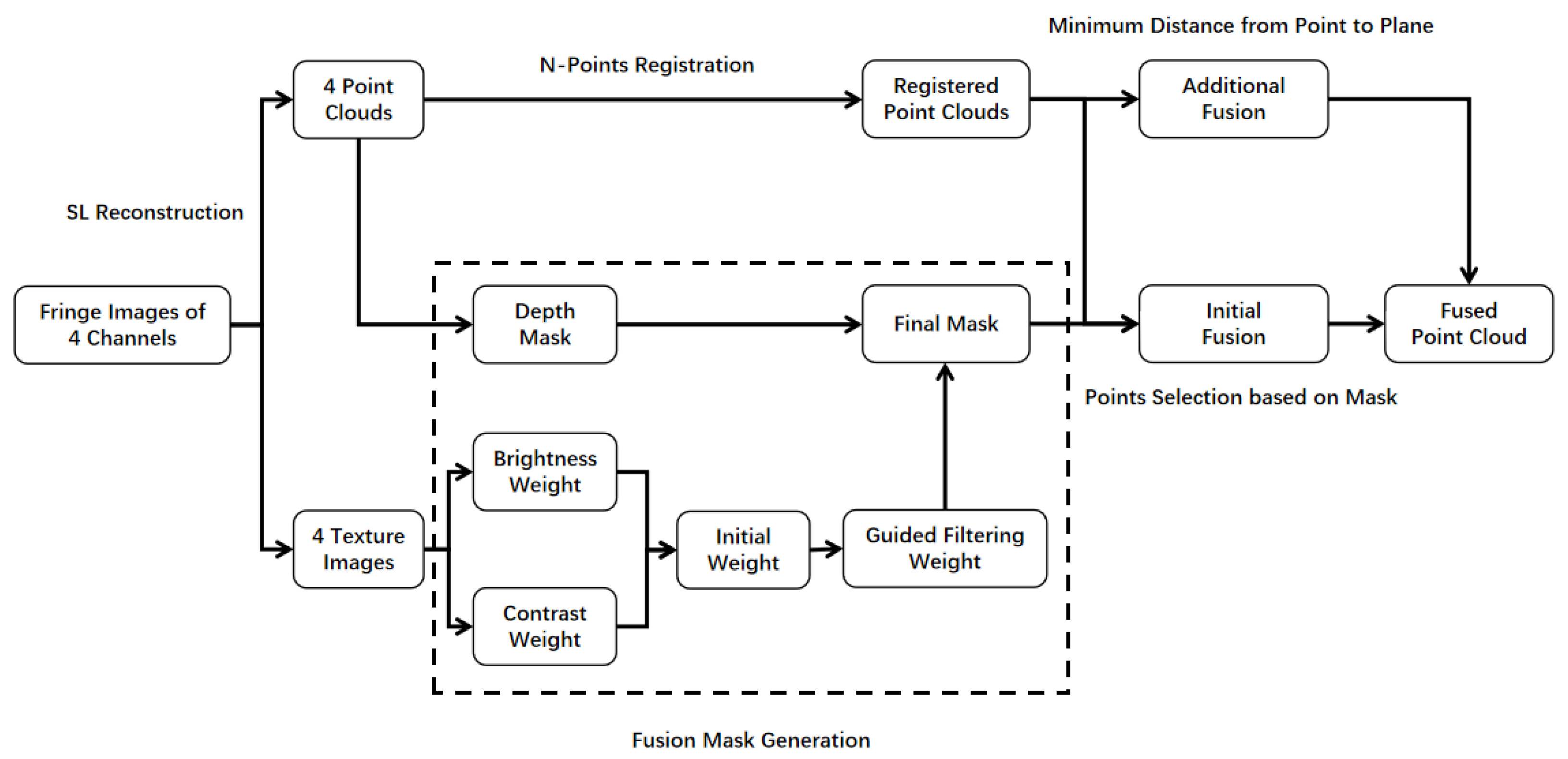
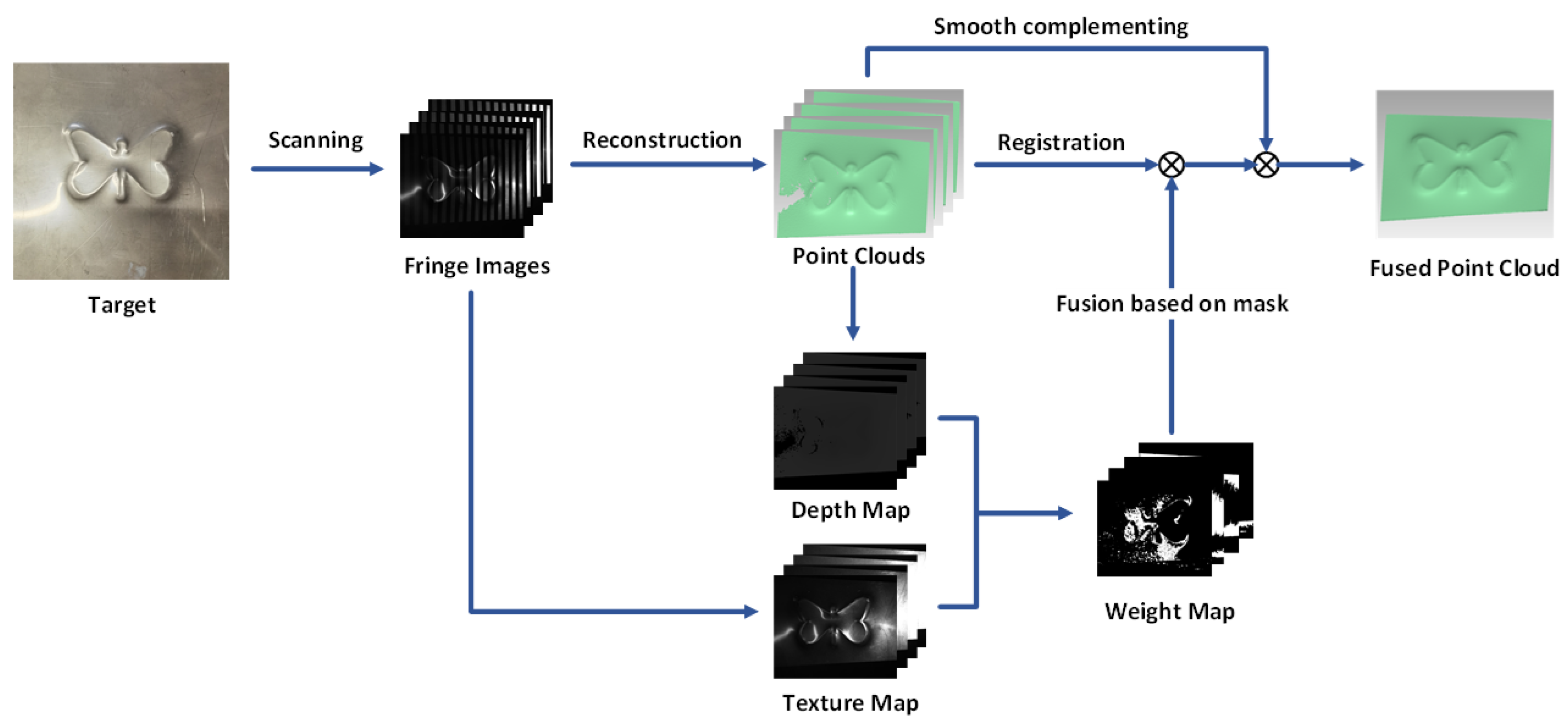
3. Methodology
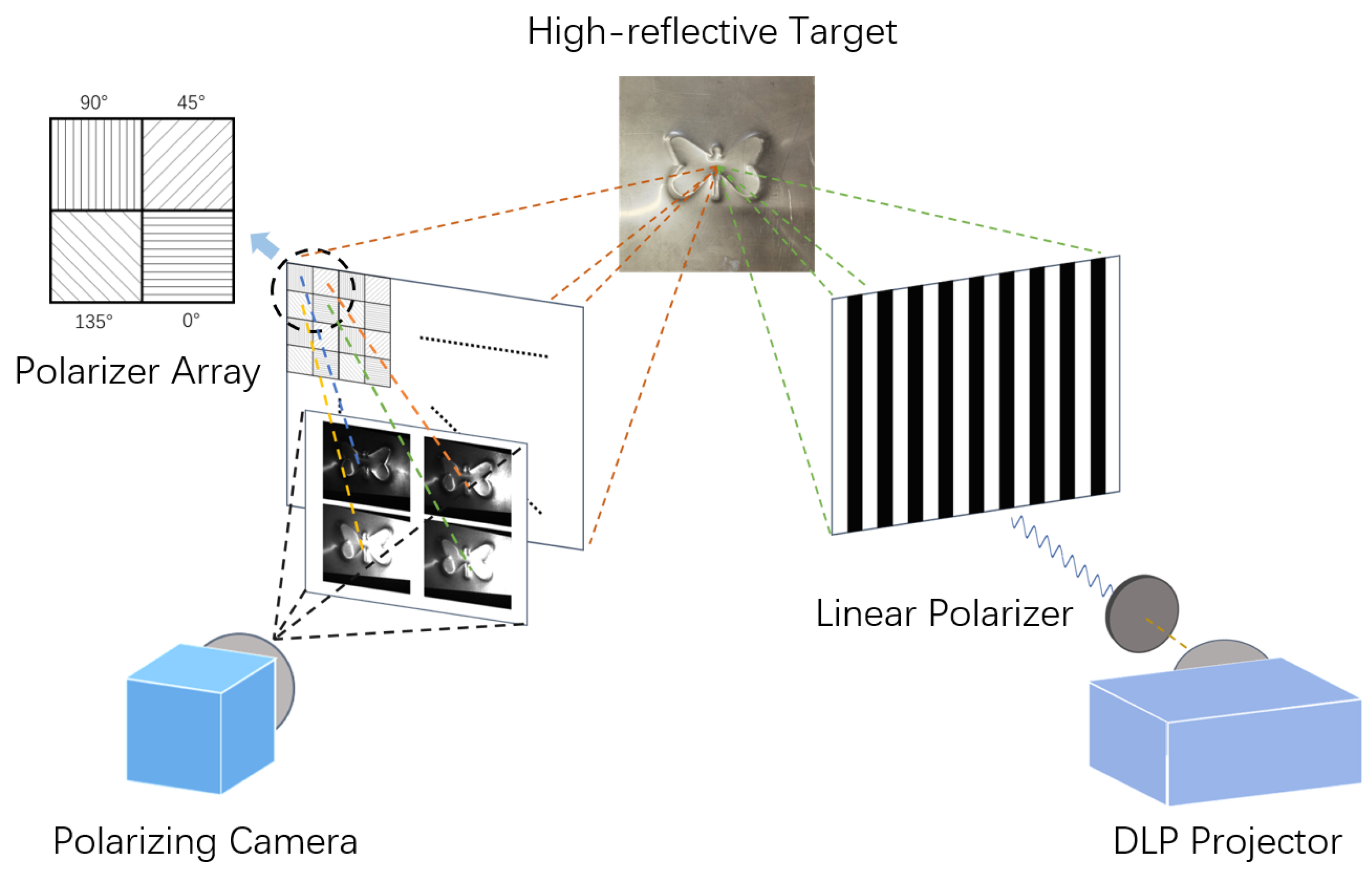
3.1. Binary Coding Polarized SL System
3.2. Point Cloud Registration
- (1)
- Use the system to scan a calibration plate and output four point clouds according to pixel array. The missing positions were recorded with identifiers;
- (2)
- Traversing according to pixel array, only the pixels with 4 effective points are retained, and 4 point clouds are stored, respectively;
- (3)
- Point clouds of the other three polarization channels are registered with the first polarization channel, respectively.
3.3. Point Cloud Fusion
4. Experimental Results
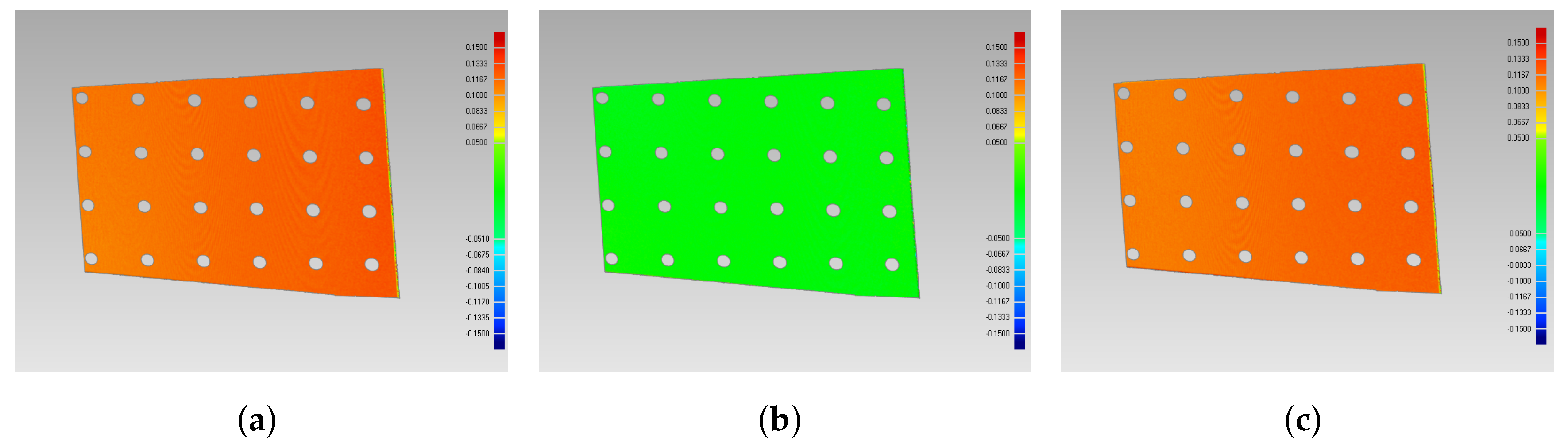
4.1. Analysis of Point Cloud Registration
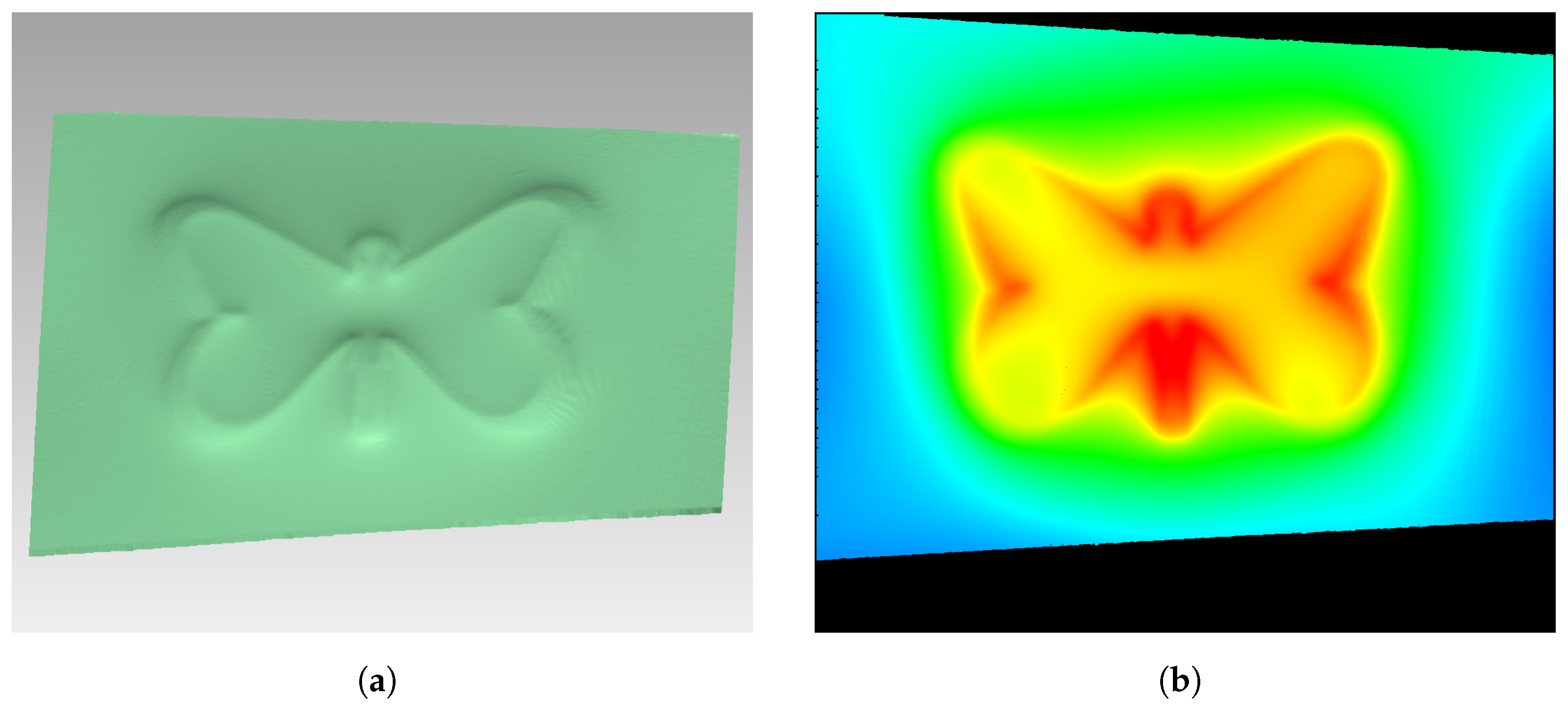
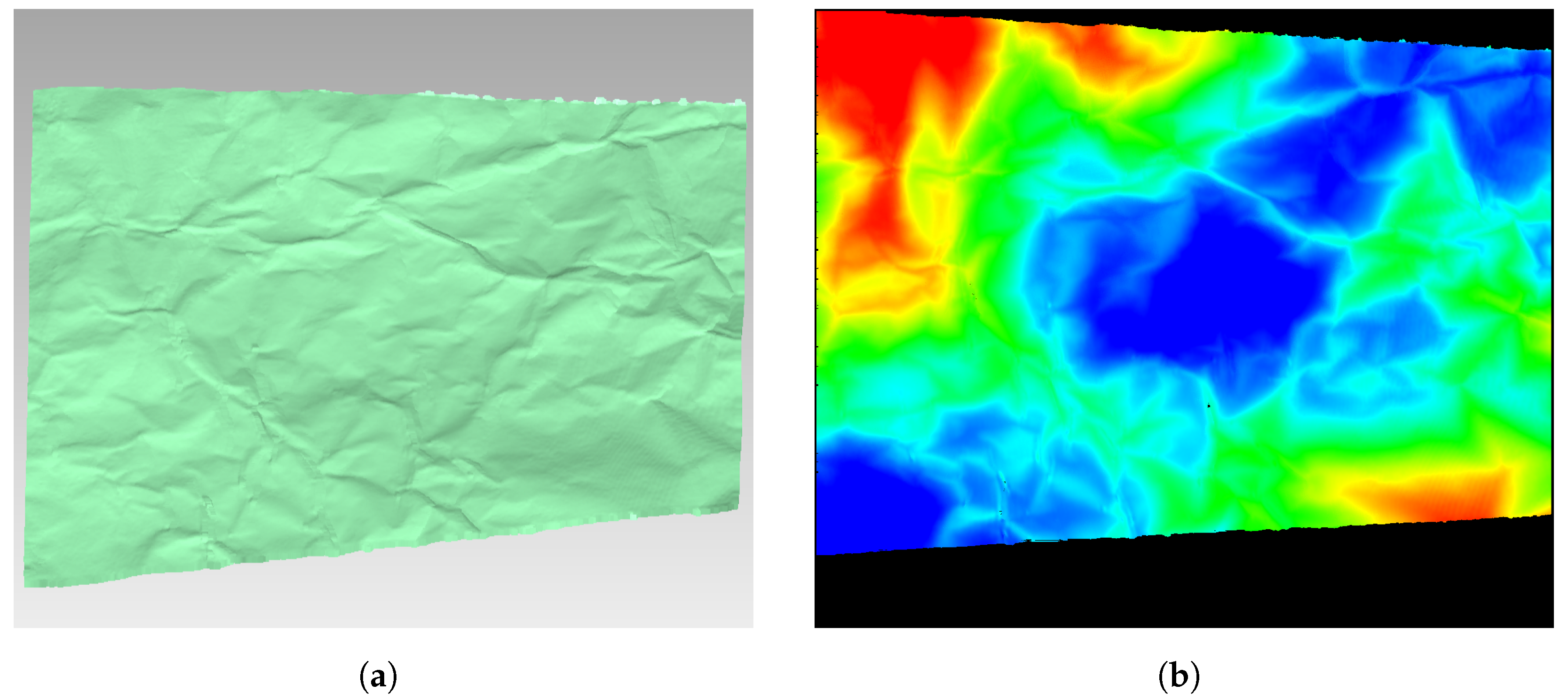
4.2. Point Cloud Fusion
5. Discussion
- (1)
- The polarized SL method proposed in this paper reconstructs four channels of point clouds simultaneously for point cloud fusion by projecting 18 binary-encoded stripe patterns at a time. The method does not require manual adjustment of hardware devices or multiple acquisitions of the target, which has the advantage of speed; it uses polarization technology to suppress high light and directly generates four point clouds for fusion, but fusion, which can achieve complete reconstruction, based on more robust binary-encoded stripe reconstruction with high precision [23] and high-precision registration by calibration plate, it can obtain high-precision fused point clouds. Therefore, this method is capable of fast, complete and high-precision reconstruction of highly reflective surfaces.
- (2)
- The polarized SL method we proposed also has some problems. Firstly, the polarization camera is used to split the four channels to obtain the images, so the resolution of the fringe patterns is decreased, and the number of point clouds is also decreased. Secondly, only the first channel of the polarization camera is used for calibration in this paper, so the phenomenon of pixel deviation is generated. This phenomenon is solved by using high-precision point cloud registration in this paper. In addition, polarization methods rely on spatial multiplexity and sacrifice SNR due to pixelated polarizers, resulting in lower total signal strength at a fixed acquisition time [24]. Using a circular polarizer might alleviate the problem of light intensity reduction.
- (3)
- Next, we will investigate the principles of pixel shifting and continue to improve the speed and robustness of our polarized SL method, applied to dynamic scanning. Additionally, we will reproduce other phase-shift coding methods for highly reflective surfaces and compare them with ours.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ye, Y.; Chang, H.; Song, Z.; Zhao, J. Accurate infrared structured light sensing system for dynamic 3D acquisition. Appl. Opt. 2020, 59, E80–E88. [Google Scholar] [CrossRef]
- Wan, M.; Kong, L.; Peng, X. Single-Shot Three-Dimensional Measurement by Fringe Analysis Network. Photonics 2023, 10, 417. [Google Scholar] [CrossRef]
- Zhang, S. Recent progresses on real-time 3D shape measurement using digital fringe projection techniques. Opt. Lasers Eng. 2010, 48, 149–158. [Google Scholar] [CrossRef]
- Cao, W.; Wang, R.; Ye, Y.; Shi, C.; Song, Z. CSIE: Coded strip-patterns image enhancer embedded in structured light-based methods. Opt. Lasers Eng. 2023, 166, 107561. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridgeshire, UK, 2003. [Google Scholar]
- Gu, F.; Cao, H.; Xie, P.; Song, Z. Accurate Depth Recovery Method Based on the Fusion of Time-of-Flight and Dot-Coded Structured Light. Photonics 2022, 9, 333. [Google Scholar] [CrossRef]
- Sansoni, G.; Carocci, M.; Rodella, R. Calibration and performance evaluation of a 3-D imaging sensor based on the projection of structured light. IEEE Trans. Instrum. Meas. 2000, 49, 628–636. [Google Scholar] [CrossRef]
- Lin, H.; Han, Z. Automatic optimal projected light intensity control for digital fringe projection technique. Opt. Commun. 2021, 484, 126574. [Google Scholar] [CrossRef]
- Song, Z.; Jiang, H.; Lin, H.; Tang, S. A high dynamic range structured light means for the 3D measurement of specular surface. Opt. Lasers Eng. 2017, 95, 8–16. [Google Scholar] [CrossRef]
- Li, B.; Xu, Z.; Gao, F.; Cao, Y.; Dong, Q. 3d reconstruction of high reflective welding surface based on binocular structured light stereo vision. Machines 2022, 10, 159. [Google Scholar] [CrossRef]
- Cao, J.; Li, C.; Li, C.; Zhang, X.; Tu, D. High-reflectivity surface measurement in structured-light technique by using a transparent screen. Measurement 2022, 196, 111273. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiao, D.; Xia, C.; Yang, D.; Fang, S. A method for high dynamic range 3D color modeling of objects through a color camera. Mach. Vis. Appl. 2023, 34, 6. [Google Scholar] [CrossRef]
- Porras-Aguilar, R.; Falaggis, K. Absolute phase recovery in structured light illumination systems: Sinusoidal vs. intensity discrete patterns. Opt. Lasers Eng. 2016, 84, 111–119. [Google Scholar] [CrossRef]
- Gühring, J. Dense 3D surface acquisition by structured light using off-the-shelf components. SPIE Proc. 2000, 4309, 220–231. [Google Scholar]
- Wolff, L.B. Using polarization to separate reflection components. In Proceedings of the 1989 IEEE Computer Society Conference on Computer Vision and Pattern Recognitiony, San Diego, CA, USA, 4–8 June 1989; pp. 363–364. [Google Scholar]
- Salahieh, B.; Chen, Z.; Rodriguez, J.J.; Liang, R. Multi-polarization fringe projection imaging for high dynamic range objects. Opt. Express 2014, 22, 10064–10071. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wang, X.; Liang, R. Snapshot phase shift fringe projection 3D surface measurement. Opt. Express 2015, 23, 667–673. [Google Scholar] [CrossRef]
- Zhu, Z.; Xiang, P.; Zhang, F. Polarization-based method of highlight removal of high-reflectivity surface. Optik 2020, 221, 165345. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhu, T.; Sun, X.; Zhang, F. 3D reconstruction method based on the optimal projection intensity of a polarization system. Appl. Opt. 2022, 61, 10290–10298. [Google Scholar] [CrossRef] [PubMed]
- Mertens, T.; Kautz, J.; Van Reeth, F. Exposure fusion. In Proceedings of the 15th Pacific Conference on Computer Graphics and Applications (PG’07), Maui, HI, USA, 29 October–2 November 2007; pp. 382–390. [Google Scholar]
- Li, S.; Kang, X.; Hu, J. Image fusion with guided filtering. IEEE Trans. Image Process. 2013, 22, 2864–2875. [Google Scholar]
- Han, X.F.; Jin, J.S.; Wang, M.J.; Jiang, W.; Gao, L.; Xiao, L. A review of algorithms for filtering the 3D point cloud. Signal Process. Image Commun. 2017, 57, 103–112. [Google Scholar] [CrossRef]
- Song, Z.; Chung, R.; Zhang, X.T. An accurate and robust strip-edge-based structured light means for shiny surface micromeasurement in 3-D. IEEE Trans. Ind. Electron. 2012, 60, 1023–1032. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, L.; Zuo, C.; Tao, T.; Chen, Q.; Gu, G. High dynamic range 3d measurements with fringe projection profilometry: A review. Meas. Sci. Technol. 2018, 29, 122001. [Google Scholar] [CrossRef]


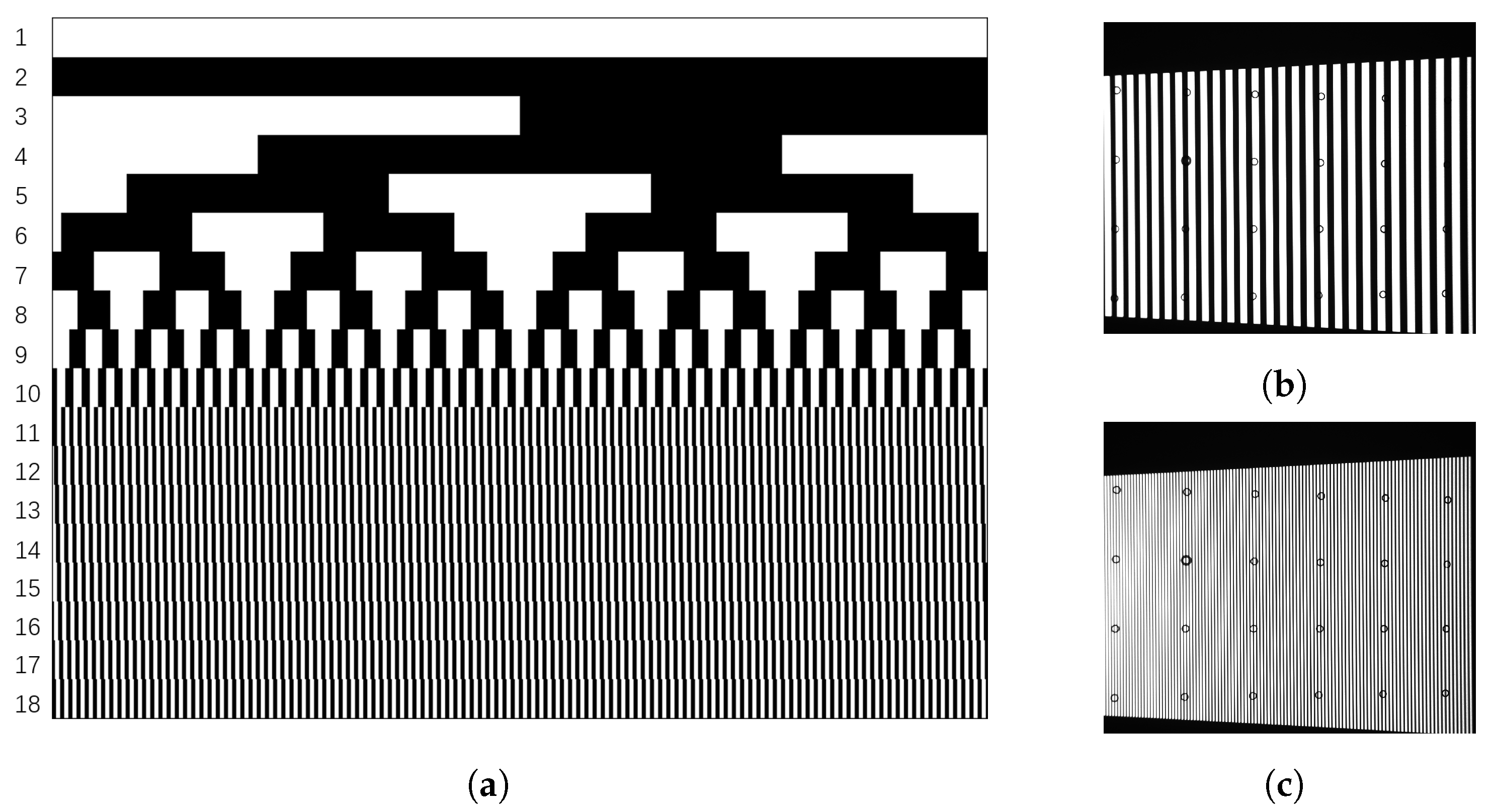






| Transmittance | ||||
|---|---|---|---|---|
(Pixels) | (Pixels) | ||||||
|---|---|---|---|---|---|---|---|
| Camera | 2305.5486 2305.1569 | 609.9492 536.1492 | |||||
| Projector | 2230.4738 2230.5685 | 500.0181 305.3961 | |||||
| R | T (mm) | ||||||
| Channel | R | T (mm) | ||||
|---|---|---|---|---|---|---|
| Channel | Distance (mm) | |||
|---|---|---|---|---|
| Min | Max | Mean | std. | |
| 2 → 1 | ||||
| 3 → 1 | ||||
| 4 → 1 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Ye, Y.; Gu, F.; Zhang, J.; Zhao, J.; Song, Z. A Polarized Structured Light Method for the 3D Measurement of High-Reflective Surfaces. Photonics 2023, 10, 695. https://doi.org/10.3390/photonics10060695
Liang J, Ye Y, Gu F, Zhang J, Zhao J, Song Z. A Polarized Structured Light Method for the 3D Measurement of High-Reflective Surfaces. Photonics. 2023; 10(6):695. https://doi.org/10.3390/photonics10060695
Chicago/Turabian StyleLiang, Jixin, Yuping Ye, Feifei Gu, Jiankai Zhang, Juan Zhao, and Zhan Song. 2023. "A Polarized Structured Light Method for the 3D Measurement of High-Reflective Surfaces" Photonics 10, no. 6: 695. https://doi.org/10.3390/photonics10060695
APA StyleLiang, J., Ye, Y., Gu, F., Zhang, J., Zhao, J., & Song, Z. (2023). A Polarized Structured Light Method for the 3D Measurement of High-Reflective Surfaces. Photonics, 10(6), 695. https://doi.org/10.3390/photonics10060695






