Dual-Parameter Sensor for Temperature and Strain Measurement Based on Antiresonance Effect and Few-Mode Fiber
Abstract
1. Introduction
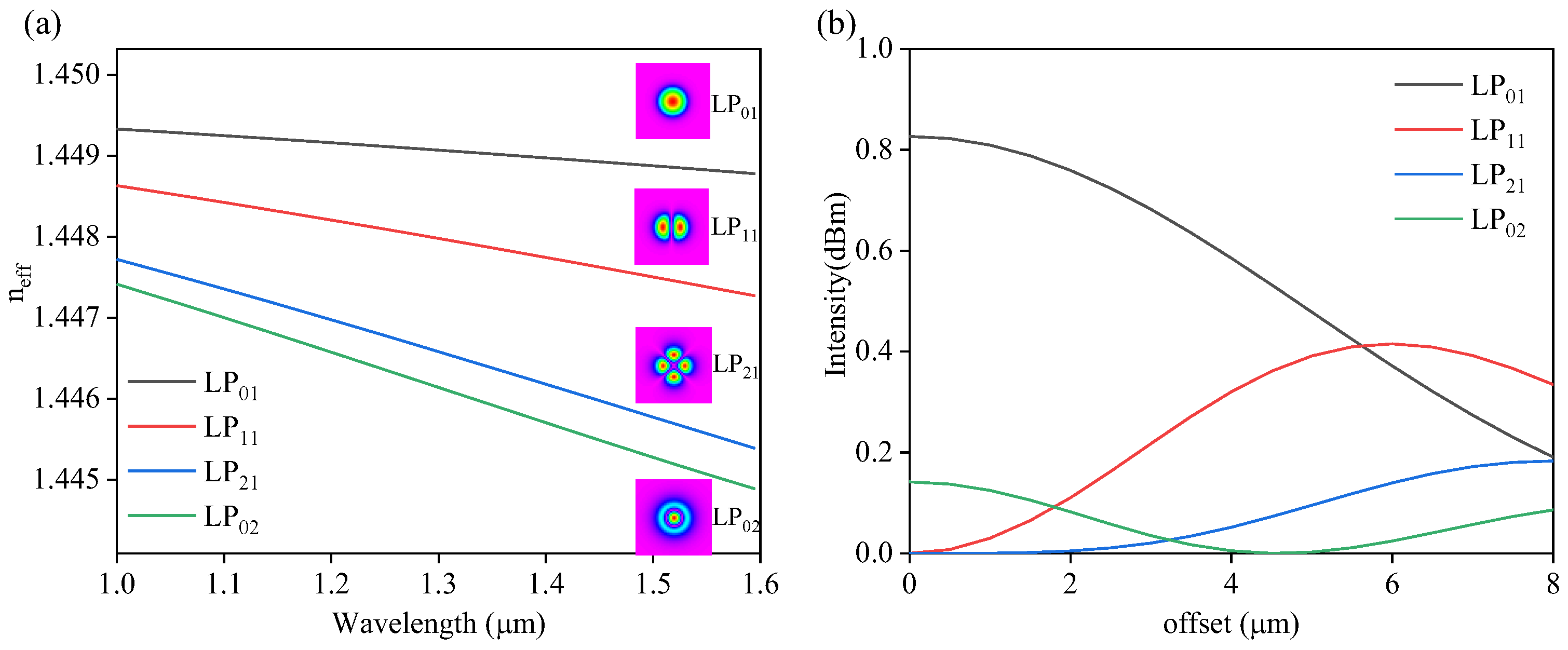
2. Principle
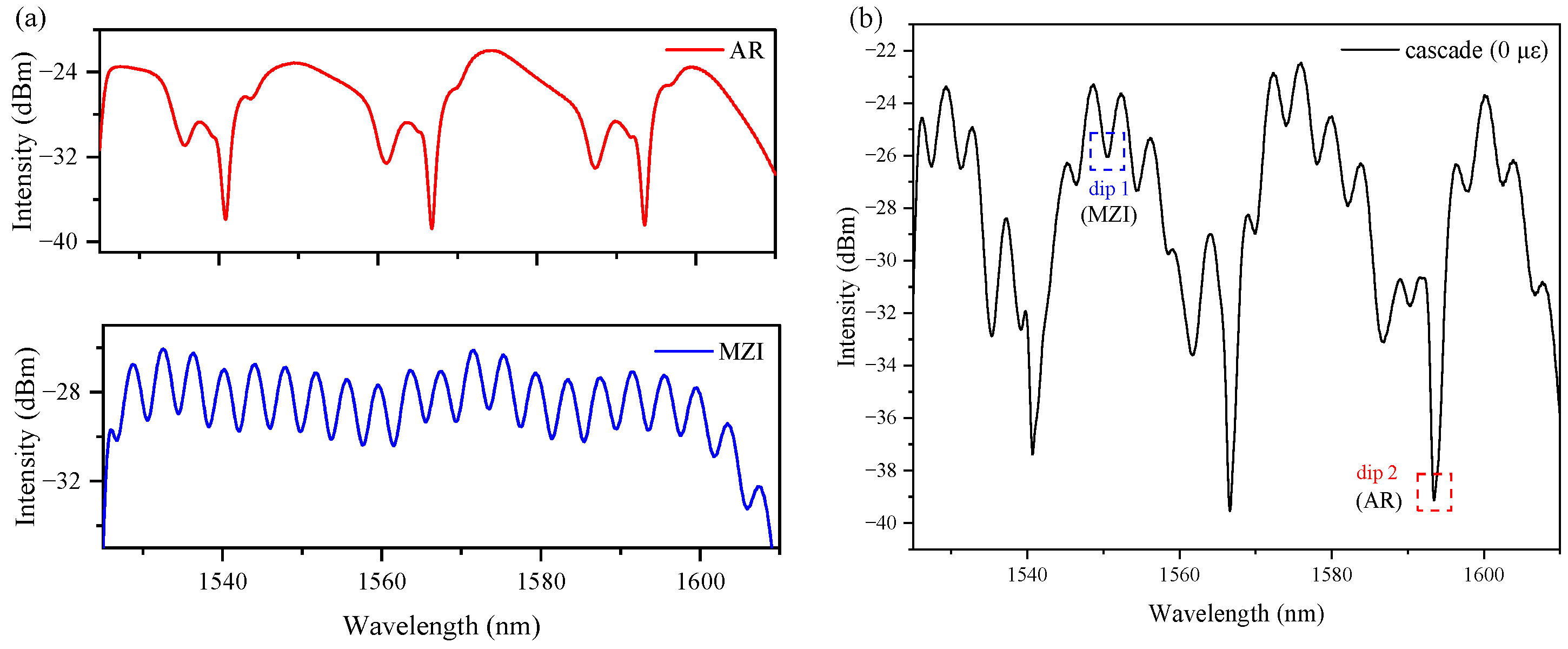
2.1. Principle of MZI
2.2. Principle of the AR Effect
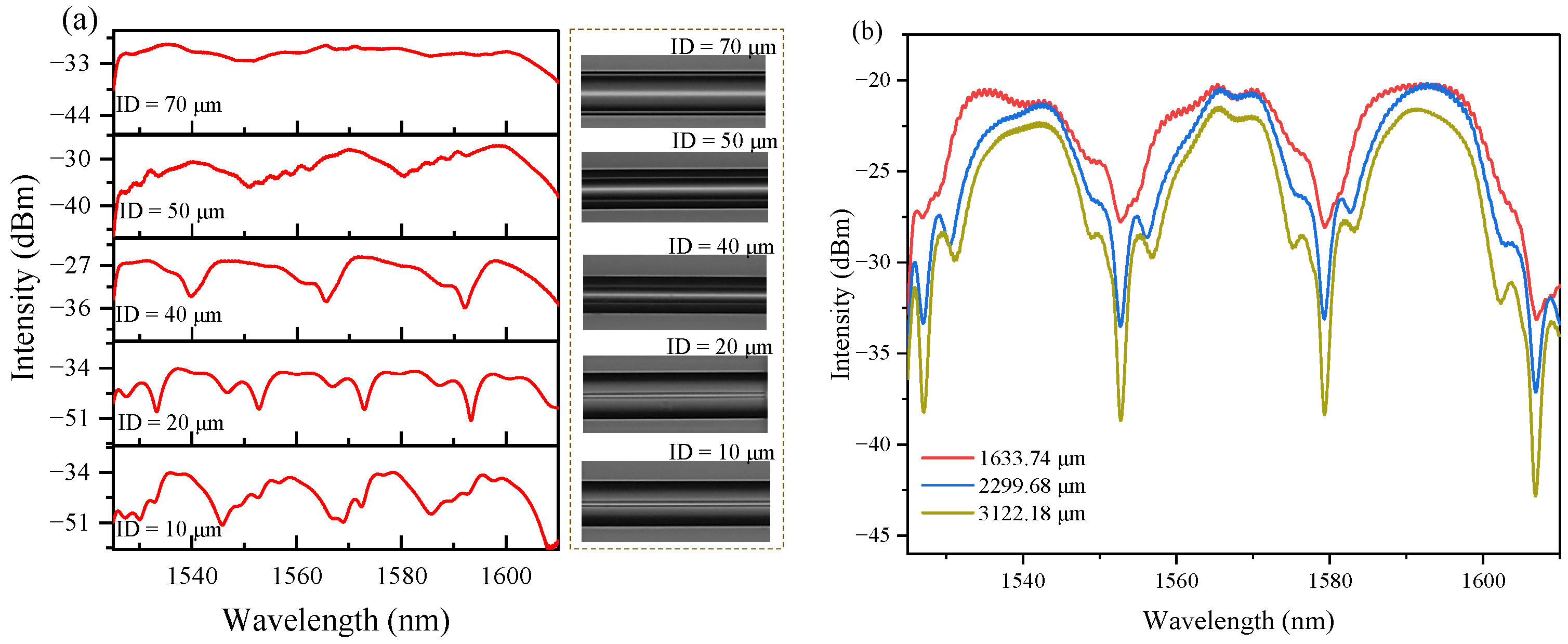
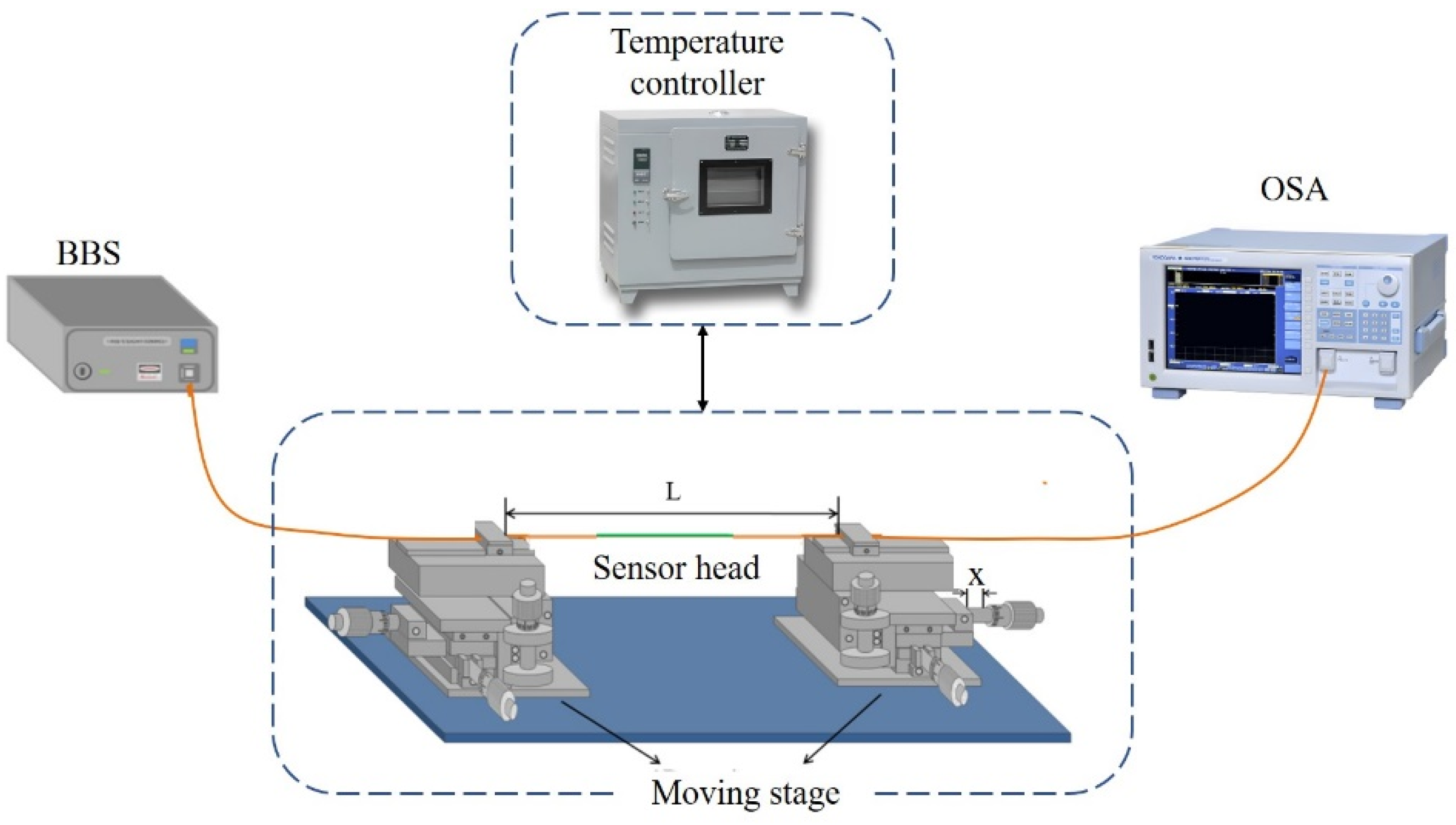
3. Design and Fabrication
4. Experiments and Results
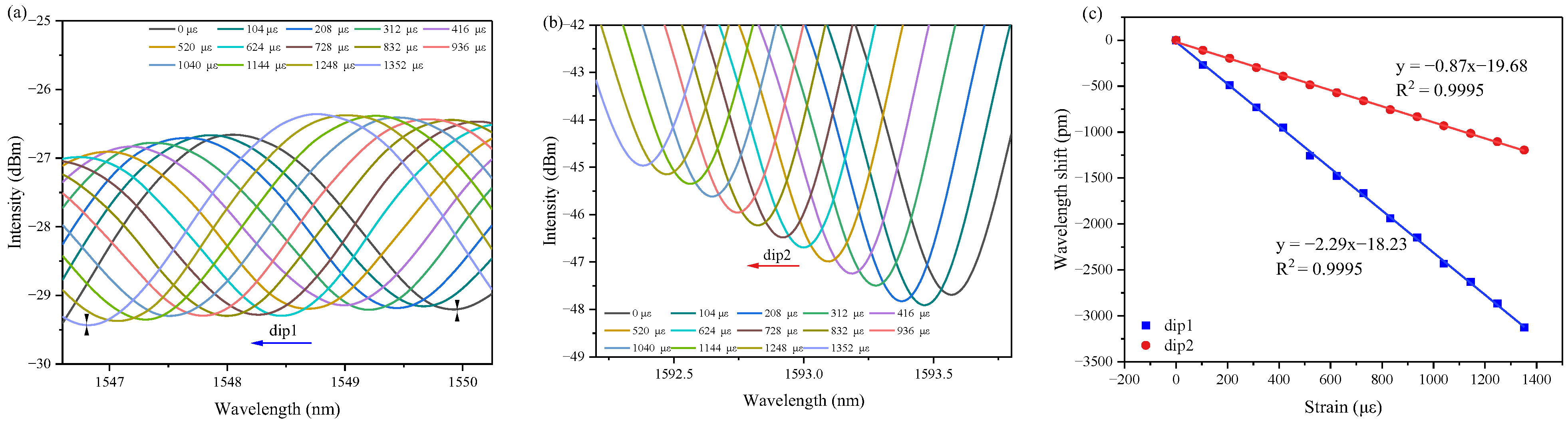
4.1. Strain Response Characteristics
4.2. Temperature Response Characteristics
5. Discussion
5.1. Temperature–Strain Dual-Parameter Demodulation
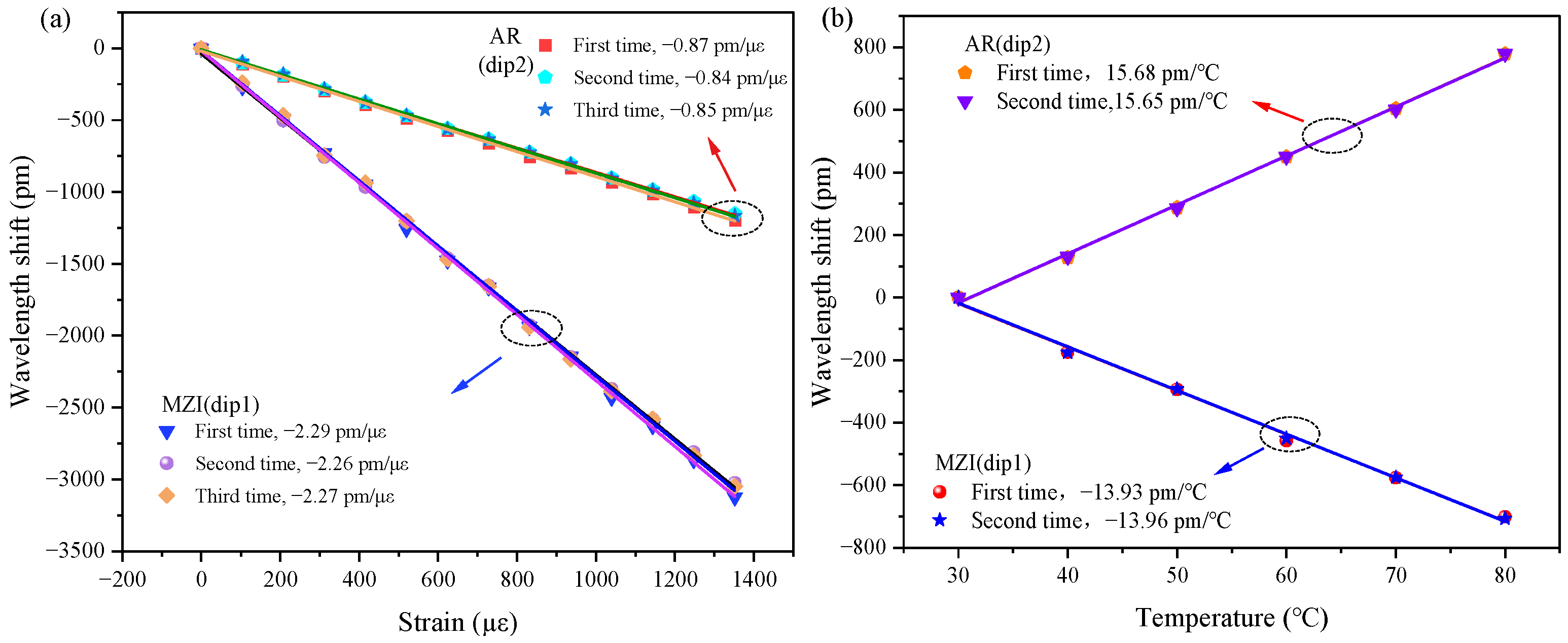
5.2. Repeatability Measurement
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Li, W.; Wu, Q.; Ling, F.; Tian, K.; Shen, C.; Wei, F.; Farrell, G.; Semenova, Y.; Wang, P. Strain-, Curvature- and Twist-Independent Temperature Sensor Based on a Small Air Core Hollow Core Fiber Structure. Opt. Express 2021, 29, 26353. [Google Scholar] [CrossRef]
- Gao, R.; Jiang, Y.; Zhao, Y. Magnetic Field Sensor Based on Anti-Resonant Reflecting Guidance in the Magnetic Gel-Coated Hollow Core Fiber. Opt. Lett. 2014, 39, 6293. [Google Scholar] [CrossRef]
- Mao, L.; Lu, P.; Lao, Z.; Liu, D.; Zhang, J. Highly Sensitive Curvature Sensor Based on Single-Mode Fiber Using Core-Offset Splicing. Opt. Laser Technol. 2014, 57, 39–43. [Google Scholar] [CrossRef]
- Fan, H.; Chen, L.; Bao, X. Temperature-Insensitive Strain Sensor Based on Microsphere-Embedded Core-Offset Fiber with High Sensitivity. J. Light. Technol. 2021, 39, 2547–2551. [Google Scholar] [CrossRef]
- Fu, G.; Li, Y.; Fu, X.; Jin, W.; Bi, W. Temperature Insensitive Curvature Sensor Based on Cascading Photonic Crystal Fiber. Opt. Fiber Technol. 2018, 41, 64–68. [Google Scholar] [CrossRef]
- Gu, B.; Yuan, W.; He, S.; Bang, O. Temperature Compensated Strain Sensor Based on Cascaded Sagnac Interferometers and All-Solid Birefringent Hybrid Photonic Crystal Fibers. IEEE Sens. J. 2012, 12, 1641–1646. [Google Scholar] [CrossRef]
- Yang, X.; Liu, C.; Yang, J.; Sun, D.; Ran, L. Fiber-Optic Axial-Strain Sensor with Sensitivity Enhancement and Temperature Compensation. Photonics 2022, 9, 709. [Google Scholar] [CrossRef]
- Feng, W.; Yang, X.; Yu, J.; Yue, Z. Strain and Temperature Sensor Based on Fiber Bragg Grating Cascaded Bi-Tapered Four-Core Fiber Mach–Zehnder Interferometer. J. Phys. D Appl. Phys. 2020, 53, 465104. [Google Scholar] [CrossRef]
- Xiong, L.; Zhang, D.; Li, L.; Guo, Y. EFPI-FBG Hybrid Sensor for Simultaneous Measurement of High Temperature and Large Strain. Chin. Opt. Lett. 2014, 12, 120605. [Google Scholar] [CrossRef]
- Jin, W.; Xu, Y.; Jiang, Y.; Wu, Y.; Yao, S.; Xiao, S.; Qi, Y.; Ren, W.; Jian, S. Strain and Temperature Characteristics of the LP11 Mode Based on a Few-Mode Fiber Bragg Grating and Core-Offset Splicing. Laser Phys. 2018, 28, 025103. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Y.; Zhang, W.; Li, Z.; Kong, L.; Yu, L.; Ge, J.; Yan, T. Ultra-High Sensitivity and Temperature-Compensated Fabry–Perot Strain Sensor Based on Tapered FBG. Opt. Laser Technol. 2020, 124, 105997. [Google Scholar] [CrossRef]
- Liu, Q.; Ran, Z.L.; Rao, Y.J.; Luo, S.C.; Yang, H.Q.; Huang, Y. Highly Integrated FP/FBG Sensor for Simultaneous Measurement of High Temperature and Strain. IEEE Photon. Technol. Lett. 2014, 26, 1715–1717. [Google Scholar] [CrossRef]
- Ascorbe, J.; Coelho, L.; Santos, J.L.; Frazão, O.; Corres, J.M. Temperature Compensated Strain Sensor Based on Long-Period Gratings and Microspheres. IEEE Photon. Technol. Lett. 2018, 30, 67–70. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, M.; Peng, Y. Tapered Hollow-Core Fiber Air-Microbubble Fabry-Perot Interferometer for High Sensitivity Strain Measurement. Adv. Mater. Interfaces 2018, 5, 1800886. [Google Scholar] [CrossRef]
- Yan, S.-C.; Zhao, Y.; Chen, M.-Q.; Liu, Q. Optical Fiber Strain Sensor with Double S-Tapers. Instrum. Sci. Technol. 2021, 49, 313–326. [Google Scholar] [CrossRef]
- Zhang, H.; Kang, J.; Zhang, M.; Liu, C.; Yang, J. Intensity-Modulated Fiber-Optic Strain Sensor Using Multimode Fiber and Microfiber Joint-Assisted Micro-Cavity Interferometer. IEEE Sens. J. 2021, 21, 22728–22734. [Google Scholar] [CrossRef]
- Hu, Y.; Lin, Q.; Yan, F.; Xiao, L.; Ni, L.; Liang, W.; Chen, L.; Liu, G.; Chen, Y.; Luo, Y.; et al. Simultaneous Measurement of the Refractive Index and Temperature Based on a Hybrid Fiber Interferometer. IEEE Sens. J. 2020, 20, 13411–13417. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, W.; Shao, L.-Y.; Pan, W.; Yan, L. Strain and Temperature Discrimination by Using Temperature-Independent FPI and FBG. Sens. Actuators A Phys. 2018, 272, 134–138. [Google Scholar] [CrossRef]
- Wang, S.; Niu, P.; Liu, S.; Wu, S.; Jin, R.-B.; Lu, P.; Yang, Y. Curvature and Temperature Sensor Based on Anti-Resonant Effect Combined with Multimode Interference. IEEE Photon. Technol. Lett. 2021, 33, 127–130. [Google Scholar] [CrossRef]
- Liu, S.; Yang, T.; Zhang, L.; Tian, M.; Dong, Y. An Intensity Demodulated Refractive Index Sensor Based on a Hollow-Core Anti-Resonant Fiber. J. Phys. D Appl. Phys. 2022, 55, 155107. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, H.; Liu, Y.; Wang, Y.; Fan, X.; Bai, G.; Zhang, M.; Du, H. A Self-Verification Temperature Sensor Based on Surface Plasmon Resonance in a Hollow Core Negative Curvature Fiber. J. Phys. D Appl. Phys. 2022, 55, 225208. [Google Scholar] [CrossRef]
- Ni, W.; Lu, P.; Zhang, J.; Yang, C.; Fu, X.; Sun, Y.; Liao, H.; Liu, D. Single Hole Twin Eccentric Core Fiber Sensor Based on Anti-Resonant Effect Combined with Inline Mach-Zehnder Interferometer. Opt. Express 2017, 25, 12372. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Ji, Y.; Cui, L.; Sun, W.; Yang, J.; Li, H. Humidity-Insensitive Temperature Sensor Based on a Quartz Capillary Anti-Resonant Reflection Optical Waveguide. Opt. Express 2017, 25, 18929. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.B.; Wang, D.N.; Xu, B.; Wang, Z.K. Optical Fiber Tip Interferometer Gas Pressure Sensor Based on Anti-Resonant Reflecting Guidance Mechanism. Opt. Fiber Technol. 2018, 42, 11–17. [Google Scholar] [CrossRef]
- Liu, S.; Tian, J.; Liu, N.; Xia, J.; Lu, P. Temperature Insensitive Liquid Level Sensor Based on Antiresonant Reflecting Guidance in Silica Tube. J. Light. Technol. 2016, 34, 5239–5243. [Google Scholar] [CrossRef]
- Gui, Y.; Shu, Q.; Lu, P.; Peng, J.; Zhang, J.; Liu, D. Optical Fiber Sensor for Curvature and Temperature Measurement Based on Anti-Resonant Effect Cascaded with Multimode Interference. Sensors 2022, 22, 8457. [Google Scholar] [CrossRef]
- Zuo, G.; Li, W.; Yang, Z.; Li, S.; Qi, R.; Huang, Y.; Xia, L. Double Phase Matching in MZI with Antiresonant Effect for Optical Fiber Sensor Application. J. Light. Technol. 2021, 39, 660–666. [Google Scholar] [CrossRef]
- Nan, T.; Liu, B.; Wu, Y.; Mao, Y.; Wang, J.; Zhao, L.; Sun, T.; Wang, J.; Han, Y. Three-Parameter Measurement Optical Fiber Sensor Based on a Hybrid Structure. Appl. Opt. 2020, 59, 8190. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, M.; Jing, L.; Tong, Z.; Li, P.; Dong, M.; Tian, X.; Yan, G. Research on In-Line MZI Optical Fiber Salinity Sensor Based on Few-Mode Fiber with Core-Offset Structure. Measurement 2022, 202, 111857. [Google Scholar] [CrossRef]
- Gao, X.; Ning, T.; Zheng, J.; Li, J.; Pei, L.; Zhang, C.; Liu, L.; He, X. Simultaneous Measurement of Refractive Index, Strain, and Temperature Based on a Mach–Zehnder Interferometer with Hybrid Structure Optical Fiber. Appl. Opt. 2019, 58, 8187. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, Y.; Hu, X.; Wang, X.; Lin, Z. Wavelength Modulated Anti-Resonant Fiber-Optic Microfluidic Device Based on SMF-HCTF-SMF Structure. J. Light. Technol. 2023, 41, 374–380. [Google Scholar] [CrossRef]
- He, C.; Zhou, C.; Zhou, Q.; Xie, S.; Xiao, M.; Tian, J.; Yao, Y. Simultaneous Measurement of Strain and Temperature Using Fabry–Pérot Interferometry and Antiresonant Mechanism in a Hollow-Core Fiber. Chin. Opt. Lett. 2021, 19, 041201. [Google Scholar] [CrossRef]
- Wang, J.; Liu, B.; Wu, Y.; Mao, Y.; Zhao, L.; Sun, T.; Nan, T.; Han, Y. Dual Parameter In-Line Fiber Mach-Zehnder Interferometer Based on Few-Mode Fiber. Microw. Opt. Technol. Lett. 2021, 63, 980–986. [Google Scholar] [CrossRef]
- Li, A.; Wang, Y.; Fang, J.; Li, M.-J.; Kim, B.Y.; Shieh, W. Few-Mode Fiber Multi-Parameter Sensor with Distributed Temperature and Strain Discrimination. Opt. Lett. 2015, 40, 1488. [Google Scholar] [CrossRef]
- Dong, L.; Gang, T.; Bian, C.; Tong, R.; Wang, J.; Hu, M. A High Sensitivity Optical Fiber Strain Sensor Based on Hollow Core Tapering. Opt. Fiber Technol. 2020, 56, 102179. [Google Scholar] [CrossRef]
- Hou, M.; He, J.; Xu, X.; Li, Z.; Zhang, Z.; Guo, K.; Ju, S.; Wang, Y. Antiresonant Reflecting Guidance and Mach-Zender Interference in Cascaded Hollow-Core Fibers for Multi-Parameter Sensing. Sensors 2018, 18, 4140. [Google Scholar] [CrossRef] [PubMed]
- Zhou, A.; Qin, B.; Zhu, Z.; Zhang, Y.; Liu, Z.; Yang, J.; Yuan, L. Hybrid Structured Fiber-Optic Fabry–Perot Interferometer for Simultaneous Measurement of Strain and Temperature. Opt. Lett. 2014, 39, 5267–5270. [Google Scholar] [CrossRef]




| Parameters | Condition (T = 25 °C, ε = 520 µε) |
|---|---|
| −0.65 | |
| −1.0 | |
| Determined data by Equation (14) | |
| Measured and | |
| Configuration | Simultaneous | Strain Sensitivity (pm/µε) | Temperature Sensitivity (pm/°C) |
|---|---|---|---|
| FBG and MZI [8] | Yes | −1.83 | 46.93 |
| (0–1000 µε) | (2.2–80 °C) | ||
| FMF and FBG [10] | Yes | 0.8778 | 9.92 |
| (0–1000 µε) | (10–70 °C) | ||
| LPG and a microsphere [13] | Yes | 0.86 | 0.79 |
| (0–1500 µε) | (30–80 °C) | ||
| tapered HCF air-microbubble FPI [14] | No | 8.62 | - |
| (0–3200 µε) | |||
| double S-tapers [15] | No | 6.63 | - |
| (0–800 µε) | |||
| micro-cavity MZI [16] | Yes | 0.02 dB/µε | 0.003 dB/°C |
| (0–300 µε) | (23–28 °C) | ||
| FPI and ARROW [31] | Yes | 2 | 21.11 |
| (0–1000 µε) | (30–70 °C) | ||
| tapered MZI [35] | Yes | 2.7 | 1.6 |
| (0–2100 µε) | (20–80 °C) | ||
| ARROW and MZI [36] | Yes | −0.8 | 28.5 |
| (0–1000 µε) | (0–300 °C) | ||
| Hollow annular core fiber [37] | Yes | 1.1 | 13 |
| (0–1500 µε) | (50–500 °C) | ||
| FMF and ARROW (this work) | Yes | −2.29 | 15.68 |
| (0–1352 µε) | (30–80 °C) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, S.; Yang, P.; Wang, Z.; Zhang, Y.; Bao, W.; Peng, B. Dual-Parameter Sensor for Temperature and Strain Measurement Based on Antiresonance Effect and Few-Mode Fiber. Photonics 2023, 10, 642. https://doi.org/10.3390/photonics10060642
Jiang S, Yang P, Wang Z, Zhang Y, Bao W, Peng B. Dual-Parameter Sensor for Temperature and Strain Measurement Based on Antiresonance Effect and Few-Mode Fiber. Photonics. 2023; 10(6):642. https://doi.org/10.3390/photonics10060642
Chicago/Turabian StyleJiang, Shaocui, Peng Yang, Zenghui Wang, Yujuan Zhang, Wangge Bao, and Baojin Peng. 2023. "Dual-Parameter Sensor for Temperature and Strain Measurement Based on Antiresonance Effect and Few-Mode Fiber" Photonics 10, no. 6: 642. https://doi.org/10.3390/photonics10060642
APA StyleJiang, S., Yang, P., Wang, Z., Zhang, Y., Bao, W., & Peng, B. (2023). Dual-Parameter Sensor for Temperature and Strain Measurement Based on Antiresonance Effect and Few-Mode Fiber. Photonics, 10(6), 642. https://doi.org/10.3390/photonics10060642




