Abstract
A nanoscale plasmonic temperature sensor via a metal-insulator-metal (MIM) structure is proposed in this paper, and the waveguide structure is composed of a coin-like resonator. The finite element method (FEM) is used to study the structure’s transmission characteristics and electromagnetic field distributions. The calculated maximum temperature sensitivity is about 0.38 nm/°C, and the figure of (FOM) merit can be as high as 30,158, higher than most of the published MIM structure research. Compared to the structure without a square resonator, the FOM is enhanced by about 479%. We believe the proposed sensor can be a promising platform for future sensing applications such as filters, absorbers, and splitters.
1. Introduction
Surface plasmon polaritons (SPPS) are transverse electromagnetic (TM) waves propagating along the metal-dielectric surface and decay exponentially away from the meta-dielectric interface. Spps have unique properties that make them suitable for research in areas such as photonic integrated circuits [1,2], filters [3,4,5], splitters [6,7], modulators [8], switchers [9], and plasmonic sensors [10,11,12]. One structure that stands out is the metal-insulator-metal (MIM) structure, which has solid optical confinement and a long propagation distance. Compared to other sensors, such as Bragg grating with a dielectric solution or hybrid ones [13,14], whose sensitivity usually reaches about 500 nm/RIU, the MIM structure has a more prominent and straightforward structure. However, maintaining relatively high sensitivities with a high figure of merit (FOM) is difficult in the MIM structure. Therefore, there is a need for novel MIM structures with high sensitivity and high quality. For example, Zhang et al. [15] proposed a refractive index sensor based on a MIM waveguide coupled with dual rectangular cavities, which achieved a sensitivity of 596 nm/RIU. Li [16] reported a cascaded optical device with double cavities with a 701 nm/RIU sensitivity. However, the sensitivities and FOM of these proposed structures still need to be higher [17,18,19] compared to what can be achieved with improved MIM structures. In summary, apps offer a promising avenue for exploring novel photonic devices. Improving the sensitivity and FOM of MIM structures will lead to better performance in various applications, including plasmonic sensors.
Optical signals possess properties such as transmission flexibility, anti-interference abilities, and high sensitivity, which make them excellent carriers for detecting changes in the background. MIM structures [20,21] are preferred because they have a compact structure of only a nano-meter scale and can easily be integrated into optoelectronic chips [22,23,24]. For example, a temperature sensor based on the MIM structure can transfer ambient temperature signals to the optical transmission spectrum [25,26]. Analyzing the correlation between temperature and optical spectral lines enables the successful design of a high-resolution optical sensor.
In this article, we present a temperature sensor that resembles a coin in shape and has high resolution and a high figure of merit (FOM). The sensor is based on a MIM structure and includes a square resonator embedded with a ring resonator. Additionally, two vertical rectangular channels are utilized to connect the two resonators. The waveguide features two silver walls that induce a broad mode and couple it to resonance modes in the resonator. For optimization of the structural parameter, we employed the finite element method (FEM, COMSOL 5.6). Our calculations demonstrate that this structure has superior sensitivity of 0.38 nm/°C and a high FOM of 30,158.4, higher than most proposed MIM sensors. Our proposed structure has a significant advantage over other MIM optical sensors and may inspire other broadband passers, filters, absorbers, and switchers that incorporate a similar structural design.
2. Schematic and Theoretical Analysis
Figure 1a displays a two-dimensional schematic of the proposed structure. The grey and white portions indicate silver and dielectric materials. A material under sensing (MUS) that responds to the surroundings can replace the dielectric region. Silver has been chosen due to its minimal loss in the near-infrared spectrum. The ring resonator’s inner radius measures 300 nm while its width is 50 nm, with the stubs measuring 10 nm in thickness and 20 nm in distance apart. The waveguide width is also fixed at 50 nm, ensuring only the fundamental transverse magnetic mode (TM0) exists [27]. Table 1 provides further details on the proposed structure.
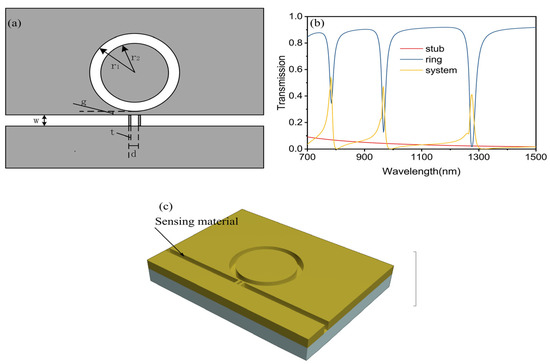
Figure 1.
(a) Schematic of the proposed MIM optical sensor. (b) Transmittance spectrum when the dielectric n = 1.36. The red, blue, and yellow lines represent the transmittance spectrum of the stub, the ring resonator, and the system, respectively. (c) The 3D schematic of the proposed structure.

Table 1.
Parameters of the proposed nanosensor.
Regarding the material parameter, the dielectric’s relative permittivity is set as . For silver, the Drude model [11,28] can be utilized to characterize it in the NIR region. The Drude model is expressed as follows:
Here, represents the angular frequency of incident light while is the plasma frequency. Additionally, is the damping frequency, and is the relative permittivity at infinite frequency. The detail of the parameter is presented in Table 2.

Table 2.
Drude model for silver.
The dispersion equation [29,30] of the TM0 mode in the MIM structure can be represented by
where are the propagated mode in dielectric and silver, respectively, is the propagation constant, is the wavevector in vacuum.
According to standing wave theory, the resonant wavelength is proportional to the effective refractive index and the length of the resonator, which can be represented as
where and represented the mode integer and the phase shift due to reflection from the resonator, respectively. is the effective length of the cavity and is the real part of the effective refractive index.
3. Results and Discussion
3.1. Ring Resonator with High Sensitivity
In Figure 1b, three fano resonances originate from the interface of resonance modes in waveguide and ring resonator of different orders. The detail of the broad continuous mode in the waveguide and the narrow linewidth mode in the ring resonator are plotted in Figure 1b. The study investigates the relationship between structural parameters and the peak of different orders’ modes in transmission patterns, such as the stub distance d in the waveguide, the radius r of the ring resonator, and the coupling distance g. Figure 2 demonstrates that decreasing the coupling distance g and the stub distance d heightens the significance of the peak of these fano modes while the center of these modes remains stable. This is because the coupling process loses less energy, strengthening the coupling amplitude between the two modes. Another observation is that the location of the maximum transmission of different fano resonances experiences a red shift when the radius of the ring resonator is larger. This may be explained by the standing wave theory when the length of the resonator corresponds to a longer resonance wavelength.
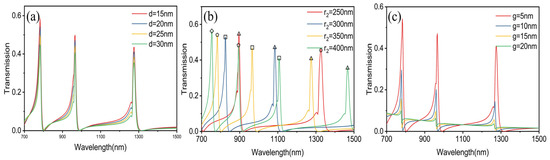
Figure 2.
(a) Transmittance spectrum for stub distance from d = 15 nm to d = 30 nm. (b) Transmittance spectrum for ring resonator radius from r2 = 250 nm to r2 = 400 nm. The red, yellow, blue, and green lines represent radii from 250nm to 400nm at intervals of 50nm, and the dots of the circle, triangle, diamond, and pentagonal represent the second, third, fourth, and fifth order annular cavity mode field resonance wavelengths, respectively. (c) Transmittance spectrum for coupling distance from g = 5 nm to g = 20 nm.
The plasmonic sensor based on the MIM structure is suitable for sensing due to its compactness, immunity to an electromagnetic interface, wide sensing range, and high sensitivity. For example, ethanol has a melting point of −114.3 °C and a boiling point of 78.4 °C, which covers the most possible temperature on earth, making it a suitable dielectric for sensing. The refractive index of ethanol can be expressed as [28]
where T0 is room temperature (20 °C), and T is the ambient temperature. Figure 3a illustrates the transmittance profile from T = −60 °C to T = 60 °C with a step of 40 °C. Sensitivity is defined as , where is the change is resonance wavelength and represent the temperature change. In addition, FOM is defined as , where represent the transmission rate change and T’ representing the transmission rate in the spectrum [31]. The results show that the location of the peak increases linearly with temperature increase, and our sensor has a sensitivity of 0.365 nm/°C and a FOM of 5208.5. Additionally, Figure 3d–i. Display the magnetic field distribution of different orders at the peaks and valleys of Fano resonance.
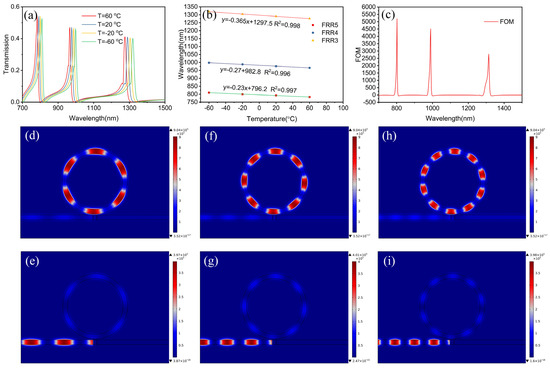
Figure 3.
(a) Transmission spectrum of the proposed temperature nanosensor, when the MUS area is filled with ethanol and ambient temperature T, is from −60 °C to 60 °C at 40 °C intervals. (b) The linear relationship fit for temperature versus resonance wavelength of FR3, FR4, and FR5. (c) The FOM of the proposed nanosensor. (d) FR3, λpeak = 1290 nm. (e) FR3, λvalley = 1330 nm. (f) FR4, λpeak = 976 nm. (g) FR4, λvalley = 1002 nm. (h) FR5, λpeak = 792 nm. (i) FR5, λvalley = 812 nm.
3.2. Coin-like Resonator
Studies have indicated that adding grooves and baffles in a cavity can enhance sensitivity. However, the FOM for such high-sensitivity MIM structures is typically around 10. Because the multiple Fano resonances originate from different mechanisms, they can be turned semi-independently by changing the cavity’s parameters around the ring resonator. Structure with high sensitivity and high FOM has potential in sensing, slow light, and other nonlinear devices in highly integrated devices. Here, we propose a resonator resembling a coin, which has been successful in increasing sensitivity to 0.38 nm/°C as well as its FOM to over 30,158. Figure 4a illustrates the schematic, from which we can observe that two additional fano modes are generated due to the square resonator and the rectangle channel connecting two resonators. This relationship is further supported by the linear relationship between the square resonator length and the fano peak wavelength shown in Figure 4b,c. As the temperature decrease, peaks of different order modes also exhibit a redshift, as seen in Figure 4d. The FOM of this coin-like resonator is plotted in Figure 4d. Compared to the ring resonator MIM structure, our sensor has an increased sensitivity of approximately 5% and a FOM increase of about 479%. Results from Table 3 comparing the sensitivity and FOM of our sensor with those published in the relevant literature demonstrate its significant advantages over other sensors.
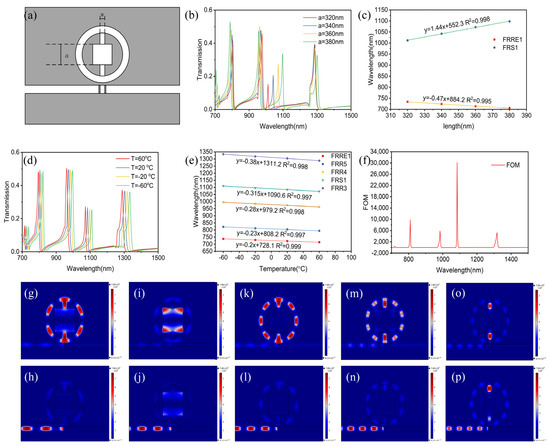
Figure 4.
(a) Schematic of the coin-like resonator based on MIM structure. (b) Transmission spectrum for square resonator length a from 320 nm to 380 nm. (c) The linear relationship fit for resonator length versus resonance wavelength of FRRE1 and FRS1. (d) Transmission spectrum of the coin-like nanosensor when the temperature T is from −60 °C to 60 °C at 40 °C intervals. (e) The linear relationship fit for temperature versus resonance wavelength of FR3, FRS1, FR4, FR5, and FRRE1. (f) The FOM of the proposed coin-like sensor. (g) FR3, λpeak = 1288 nm. (h) FR3, λvalley = 1320 nm. (i) FRS1, λpeak = 1072 nm. (j) FRS1, λvalley = 1084 nm. (k) FR4, λpeak = 962 nm. (l) FR4, λvalley = 986 nm. (m) FR5, λpeak = 794 nm. (n) FR5, λvalley = 810 nm. (o) FRRE1, λpeak = 714 nm. (p) FRRE1, λvalley = 718 nm.

Table 3.
Comparison of sensitivity with the recent literature.
4. Conclusions
In this manuscript, we have presented a high-sensitivity sensor in the shape of a coin, utilizing the MIM structure. The coin-like resonant cavity and waveguide obtain Fano resonances by interacting with the narrowband discrete and broad-band contiguous states. By analyzing the device’s geometrical parameters, we could tune the transmittance peaks and resonance modes. Our findings demonstrate that the coin-like cavity achieved a sensitivity of 0.38 nm/°C and a figure of merit (FOM) of 30,158. Compared to the cavity without a square resonator, the sensitivity increased marginally while the FOM increased to over 479%. The quality can be further enhanced when combined with other structures, such as photonic crystals, reaching as high as 109 [36,37]. We believe the proposed structure can be applied to the on-chip plasmonic nano-sensor and may inspire other future integrated optical systems on chips.
Author Contributions
Conceptualization and funding acquisition, N.L. Investigation and writing, C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The Fundamental Research Funds for the Central Universities (No. 2022RC23).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data are available from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Truong, C.D.; Van, T.N.; Trinh, M.T.; Manh, H.C.; Tan, H.N.; Hoai, B.D. Triple-wavelength filter based on the nanoplasmonic metal-insulator-metal waveguides. Opt. Quantum Electron. 2021, 53, 223. [Google Scholar] [CrossRef]
- Khonina, S.; Kazanskiy, N.; Butt, M.; Ka´zmierczak, A.; Piramidowicz, R. Plasmonic sensor based on metal-insulator-metal waveguide square ring cavity filled with functional material for the detection of CO2 gas. Opt. Express 2021, 29, 16584–16594. [Google Scholar] [CrossRef]
- Pooretemad, S.; Malekijavan, A.; Aslinezhad, M. Ultrawideband bandstop filter based on Fano resonance and rectangular resonators. Appl. Opt. 2021, 60, 4266–4272. [Google Scholar] [CrossRef]
- Karimi, Y.; Kaatuzian, H.; Tooghi, A.; Danaie, M. All-optical plasmonic switches based on Fano resonance in an X-shaped resonator coupled to parallel stubs for telecommunication applications. Optik 2021, 243, 167424. [Google Scholar] [CrossRef]
- Heenkenda, R.; Hirakawa, K.; Sarangan, A. Tunable optical filter using phase change materials for smart IR night vision applications. Opt. Express 2021, 29, 33795–33803. [Google Scholar] [CrossRef]
- Wahsheh, R.A.; Lu, Z.; Abushagur, M.A. Nanoplasmonic couplers and splitters. Opt. Express 2009, 17, 19033–19040. [Google Scholar] [CrossRef] [PubMed]
- Faghani, A.A.; Yaghoubi, E.; Yaghoubi, E. Triple-channel glasses-shape nanoplasmonic demultiplexer based on multi nanodisk resonators in MIM waveguide. Optik 2021, 237, 166697. [Google Scholar] [CrossRef]
- Haffner, C.; Heni, W.; Fedoryshyn, Y.; Niegemann, J.; Melikyan, A.; Elder, D.L.; Baeuerle, B.; Salamin, Y.; Josten, A.; Koch, U.; et al. All-plasmonic Mach–Zehnder modulator enabling optical high-speed communication at the microscale. Nat. Photonics 2015, 9, 525–528. [Google Scholar] [CrossRef]
- Karimi, Y.; Kaatuzian, H. Low-Power Fano Resonance-Based MIM Plasmonic Switch Using Kerr-Type Nonlinear Material. In Proceedings of the 2021 29th Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 18–20 May 2021; pp. 32–35. [Google Scholar]
- Li, J.; Chen, J.; Liu, X.; Tian, H.; Wang, J.; Cui, J.; Rohimah, S. Optical sensing based on multimode Fano resonances in metal-insulator-metal waveguide systems with X-shaped resonant cavities. Appl. Opt. 2021, 60, 5312–5319. [Google Scholar] [CrossRef] [PubMed]
- Hassan, M.F.; Sagor, R.H.; Tathfif, I.; Rashid, K.S.; Radoan, M. An optimized dielectric-metal-dielectric refractive index nanosensor. IEEE Sens. J. 2020, 21, 1461–1469. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Y. Tunable ultra-narrow band band-stop filter based on metal–insulator–metal plasmonic waveguide with square resonator. Opt. Commun. 2021, 501, 127395. [Google Scholar] [CrossRef]
- Hessler, S.; Knopf, S.; Rommel, M.; Girschikofsky, M.; Schmauss, B.; Hellmann, R. Advancing the sensitivity of integrated epoxy-based Bragg grating refractometry by high-index nanolayers. Opt. Lett. 2020, 45, 5510–5513. [Google Scholar] [CrossRef] [PubMed]
- Saha, N.; Brunetti, G.; Kumar, A.; Armenise, M.N.; Ciminelli, C. Highly sensitive refractive index sensor based on polymer bragg grating: A case study on extracellular vesicles detection. Biosensors 2022, 12, 415. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.H.; Wang, L.L.; Li, H.J.; Zhai, X.; Xia, S.X. Two kinds of double Fano resonances induced by an asymmetric MIM waveguide structure. J. Opt. 2016, 18, 065001. [Google Scholar] [CrossRef]
- Li, X.; Wang, D.; Wang, S.; Yuan, L.; Lei, J.; Li, X. Enhanced plasmonic-induced absorption using a cascade scheme and its application as refractive-index sensor. Photonic Sens. 2020, 10, 162–170. [Google Scholar] [CrossRef]
- Rashid, K.S.; Tathfif, I.; Yaseer, A.A.; Hassan, M.F.; Sagor, R.H. Cog-shaped refractive index sensor embedded with gold nanorods for temperature sensing of multiple analytes. Opt. Express 2021, 29, 37541–37554. [Google Scholar] [CrossRef]
- Rakhshani, M.R. Refractive index sensor based on dual side-coupled rectangular resonators and nanorods array for medical applications. Opt. Quantum Electron. 2021, 53, 232. [Google Scholar] [CrossRef]
- Shen, S.; She, S.; Wang, Z.; Tan, Q.; Xiong, J.; Zhang, W. MIM waveguide structure consisting of two triangle stubs, side-coupled with an eight-like resonant cavity. Opt. Commun. 2021, 495, 127087. [Google Scholar] [CrossRef]
- Su, C.; Zhu, J. Novel SPR sensor based on MIM-based waveguide and an asymmetric cross-shaped resonator. Plasmonics 2021, 16, 769–775. [Google Scholar] [CrossRef]
- Rakhshani, M.R.; Mansouri-Birjandi, M.A. High-sensitivity plasmonic sensor based on metal–insulator–metal waveguide and hexagonal-ring cavity. IEEE Sens. J. 2016, 16, 3041–3046. [Google Scholar] [CrossRef]
- Fitrakis, E.P.; Kamalakis, T.; Sphicopoulos, T. Slow light in insulator–metal–insulator plasmonic waveguides. JOSA B 2011, 28, 2159–2164. [Google Scholar] [CrossRef]
- Dionne, J.A.; Verhagen, E.; Polman, A.; Atwater, H.A. Are negative index materials achievable with surface plasmon waveguides? A case study of three plasmonic geometries. Opt. Express 2008, 16, 19001–19017. [Google Scholar] [CrossRef]
- Ghasemi, M.R.; Bayati, M.S. Proposal for metal–insulator–metal plasmonic power splitter and demultiplexer suitable for implementation in optical switches. IET Optoelectron. 2021, 15, 200–206. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. A compact design of a modified Bragg grating filter based on a metal-insulator-metal waveguide for filtering and temperature sensing applications. Optik 2022, 251, 168466. [Google Scholar] [CrossRef]
- Tathfif, I.; Yaseer, A.A.; Rashid, K.S.; Sagor, R.H. Metal-insulator-metal waveguide-based optical pressure sensor embedded with arrays of silver nanorods. Opt. Express 2021, 29, 32365–32376. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.; Verma, A.; Prajapati, Y.K. Theoretical study of hazardous carbon-di-oxide gas sensing using MIM structure-based SPR sensing scheme. IET Optoelectron. 2021, 15, 167–177. [Google Scholar] [CrossRef]
- Zhou, P.; Liang, K.; Wang, Y.; Sun, Q.A.; Guo, J.; Jin, L.; Yu, L. Research on A High-Sensitivity Temperature Sensor with Multi-Indicator Based on Nano-Cylinder-Loaded Ring Resonator. Photonics 2023, 10, 69. [Google Scholar] [CrossRef]
- Fan, H.; Fan, H.; Fan, H. Multiple Fano resonance refractive index sensor based on a plasmonic metal-insulator-metal based Taiji resonator. JOSA B 2022, 39, 32–39. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Liu, X.; Rohimah, S.; Tian, H.; Qi, D. Fano resonance in a MIM waveguide with double symmetric rectangular stubs and its sensing characteristics. Opt. Commun. 2021, 482, 126563. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Zhang, Y.; Yu, L. Independently formed multiple Fano resonances for ultra-high sensitivity plasmonic nanosensor. Plasmonics 2018, 13, 107–113. [Google Scholar] [CrossRef]
- Khani, S.; Hayati, M. Optical sensing in single-mode filters base on surface plasmon H-shaped cavities. Opt. Commun. 2022, 505, 127534. [Google Scholar] [CrossRef]
- Guo, Z.; Wen, K.; Qin, Y.; Fang, Y.; Li, Z.; Chen, L. A plasmonic refractive-index sensor based multiple Fano resonance multiplexing in slot-cavity resonant system. Photonic Sens. 2022, 12, 175–184. [Google Scholar] [CrossRef]
- Hassan, M.F.; Hasan, M.M.; Radoan, M.; Sagor, R.H. Design and performance analysis of an ultra-compact nano-plasmonic refractive index sensor. In Proceedings of the 2020 8th International Electrical Engineering Congress (iEECON), Chiang Mai, Thailand, 4–6 March 2020; pp. 1–5. [Google Scholar]
- Shahamat, Y.; Ghaffarinejad, A.; Vahedi, M. Plasmon induced transparency and refractive index sensing in two nanocavities and double nanodisk resonators. Optik 2020, 202, 163618. [Google Scholar] [CrossRef]
- Brunetti, G.; Olio, F.D.; Conteduca, D.; Armenise, M.N.; Ciminelli, C. Comprehensive mathematical modelling of ultra-high Q grating-assisted ring resonators. J. Opt. 2020, 22, 035802. [Google Scholar] [CrossRef]
- Liu, K.; Jin, N.; Cheng, H.; Chauhan, N.; Puckett, M.W.; Nelson, K.D.; Behunin, R.O.; Rakich, P.T.; Blumenthal, D.J. Ultralow 0.034 dB/m loss wafer-scale integrated photonics realizing 720 million Q and 380 μW threshold Brillouin lasing. Opt. Lett. 2022, 47, 1855–1858. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).