Valley-Selective Polarization in Twisted Bilayer Graphene Controlled by a Counter-Rotating Bicircular Laser Field
Abstract
1. Introduction
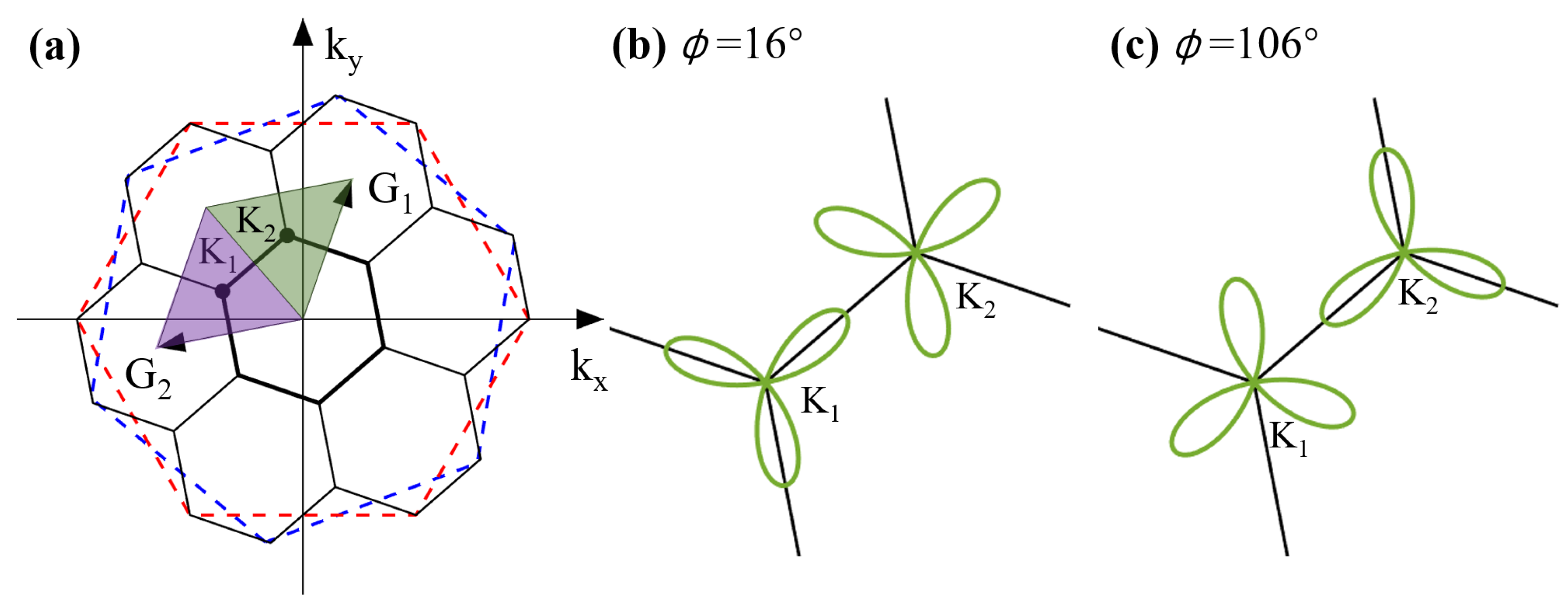
2. Theoretical Method
3. Results and Discussion
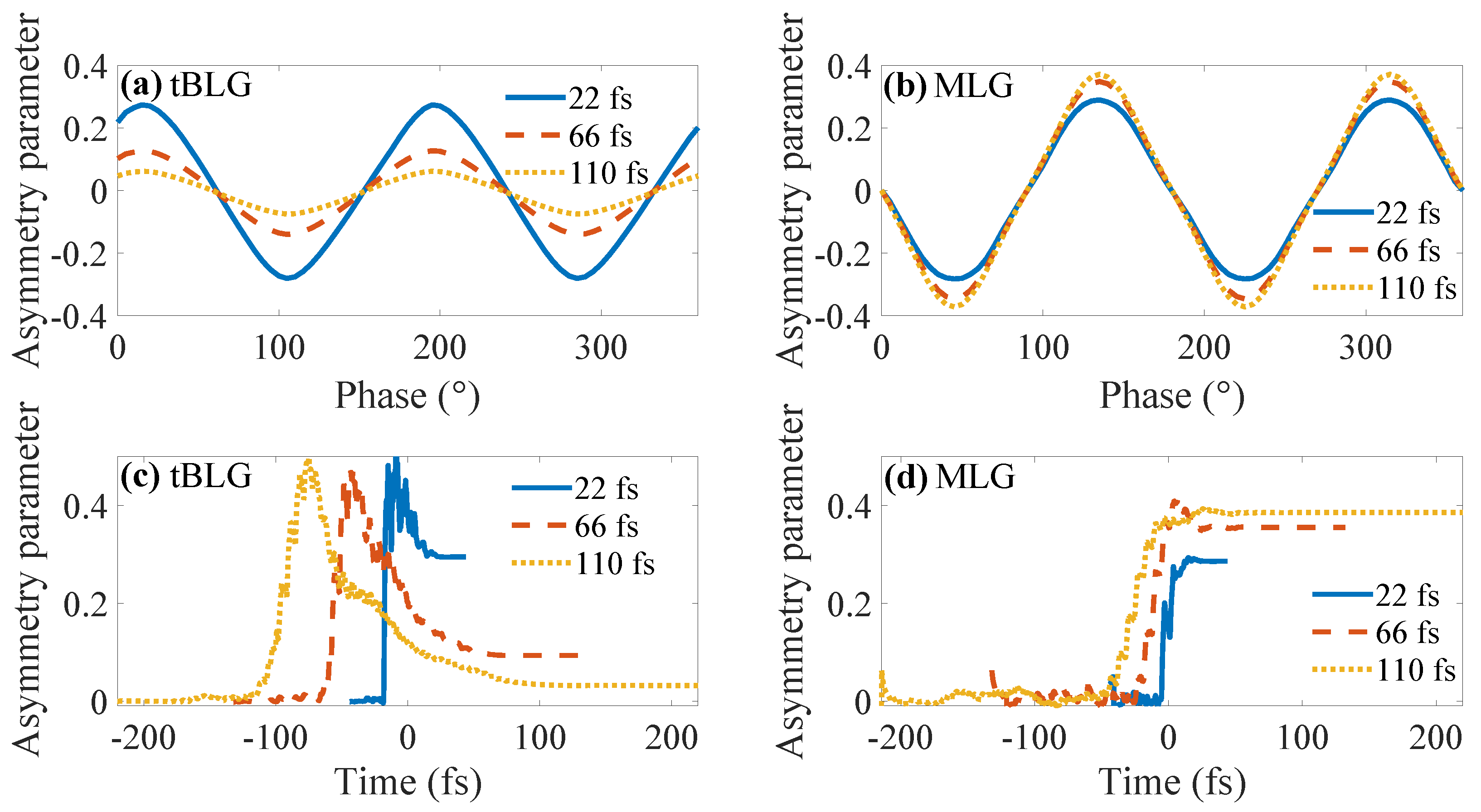
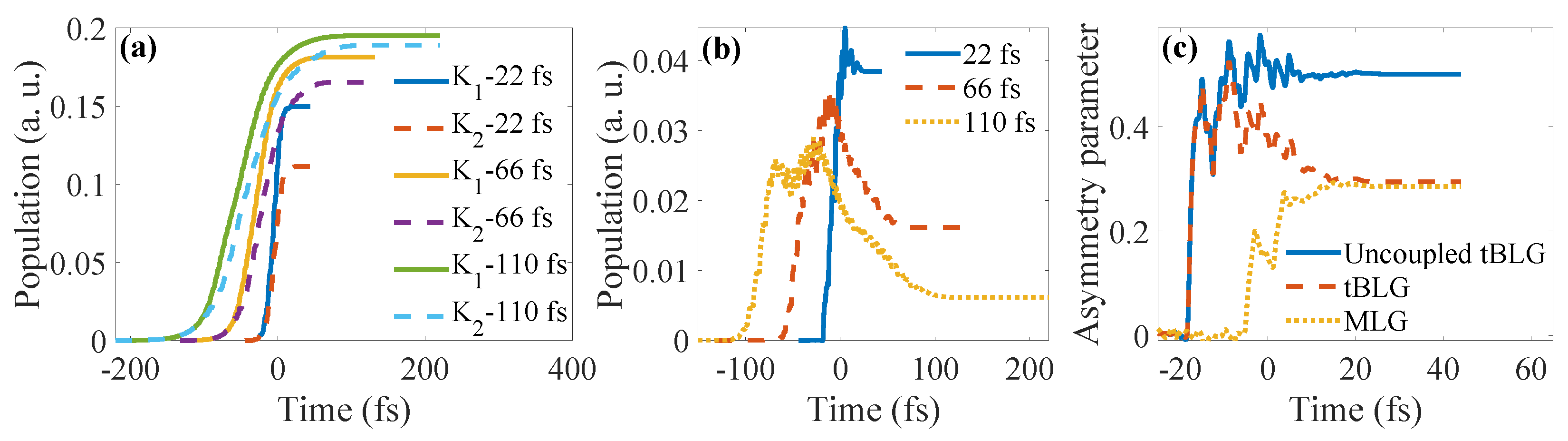
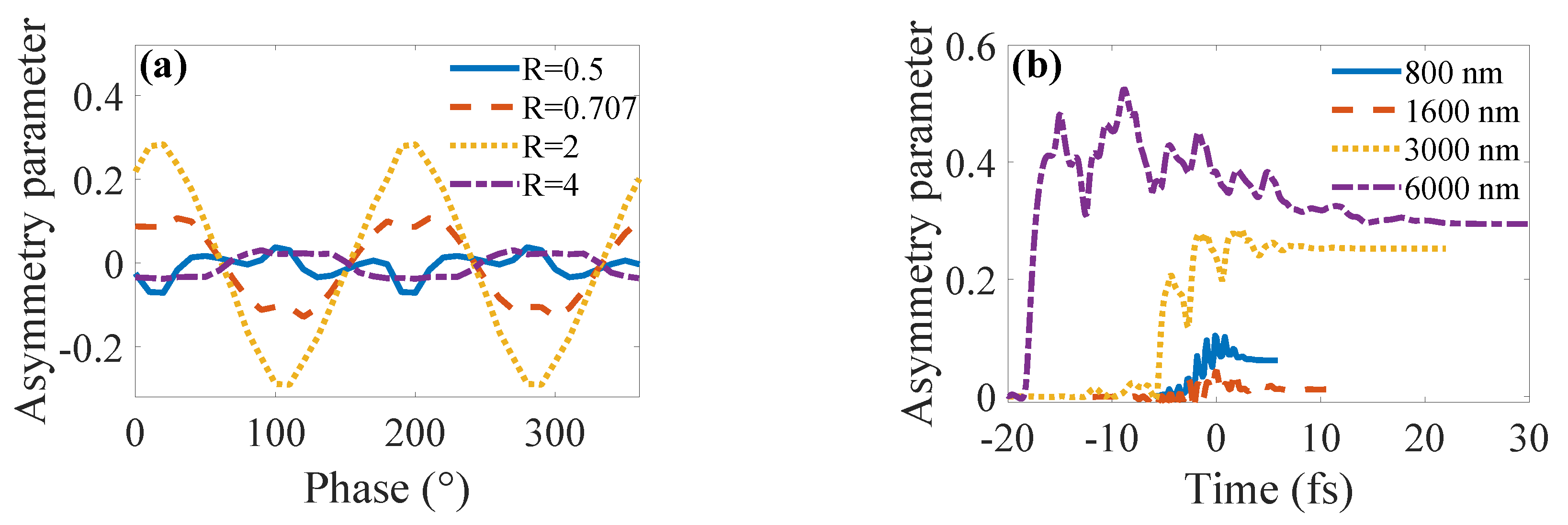
3.1. Valley-Asymmetry Parameter in tBLG and MLG
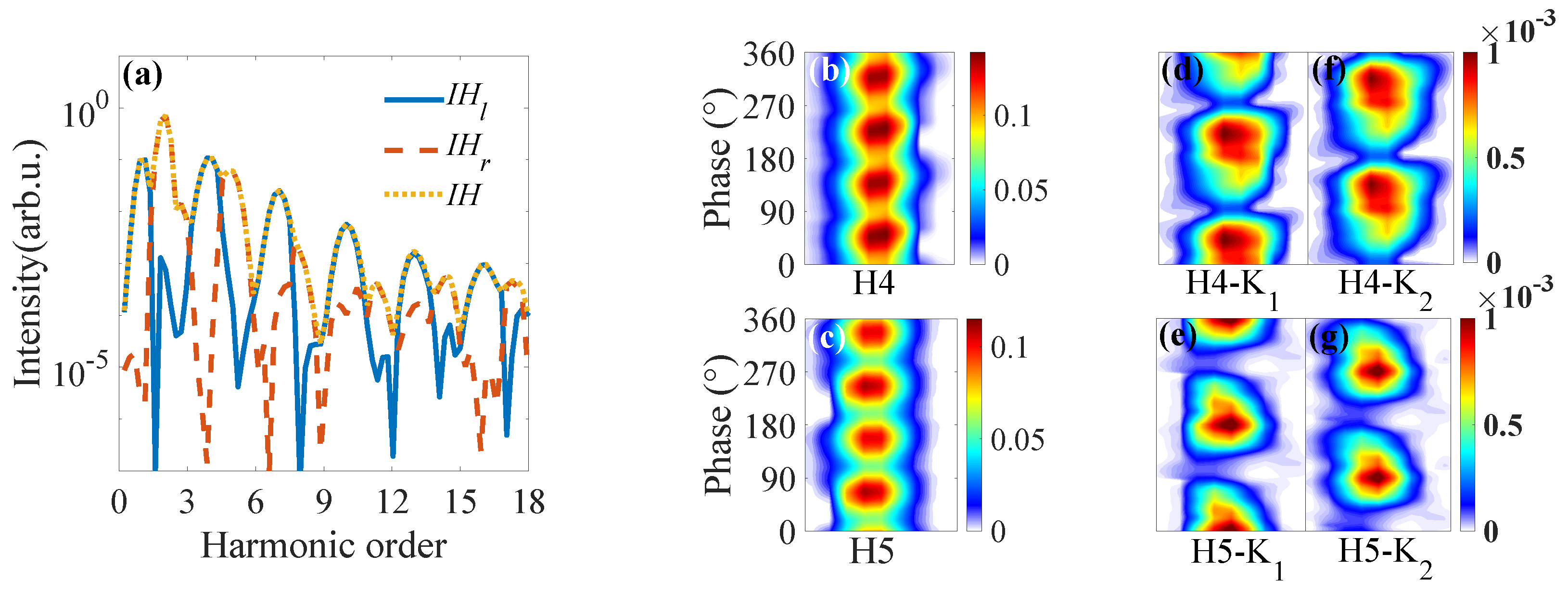
3.2. HHG Analysis and Valley Pseudospin Measurement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lazenka, V.; Lorenz, M.; Modarresi, H.; Bisht, M.; Rüffer, R.; Bonholzer, M.; Grundmann, M.; Van Bael, M.J.; Vantomme, A.; Temst, K. Magnetic spin structure and magnetoelectric coupling in BiFeO3-BaTiO3 multilayer. Appl. Phys. Lett. 2015, 106, 082904. [Google Scholar] [CrossRef]
- Fan, Y.; Finley, J.; Han, J.; Holtz, M.E.; Quarterman, P.; Zhang, P.; Safi, T.S.; Hou, J.T.; Grutter, A.J.; Liu, L. Resonant Spin Transmission Mediated by Magnons in a Magnetic Insulator Multilayer Structure. Adv. Mater. 2021, 33, 2008555. [Google Scholar] [CrossRef] [PubMed]
- Hirohata, A.; Yamada, K.; Nakatani, Y.; Prejbeanu, I.L.; Diény, B.; Pirro, P.; Hillebrands, B. Review on spintronics: Principles and device applications. J. Magn. Magn. Mater. 2020, 509, 166711. [Google Scholar] [CrossRef]
- Mrudul, M.S.; Jiménez-Galán, Á.; Ivanov, M.; Dixit, G. Light-induced valleytronics in pristine graphene. Optica 2021, 8, 422–427. [Google Scholar] [CrossRef]
- Chen, F.; Lv, Q.; Xia, Y.; Mao, S.; Fu, L.; Zhao, S. Two-dimensional bilayer MoS2 flakes with variable size of the upper layer grown by chemical vapor deposition. Micro Nanostruct. 2022, 169, 207358. [Google Scholar] [CrossRef]
- Selhorst, R.; Yu, Z.; Moore, D.; Jiang, J.; Susner, M.A.; Glavin, N.R.; Pachter, R.; Terrones, M.; Maruyama, B.; Rao, R. Precision Modification of Monolayer Transition Metal Dichalcogenides via Environmental E-Beam Patterning. ACS Nano 2023, 17, 2958–2967. [Google Scholar] [CrossRef]
- Tchoumakov, S.; Bujnowski, B.; Noky, J.; Gooth, J.; Grushin, A.G.; Cayssol, J. Conservation of chirality at a junction between two Weyl semimetals. Phys. Rev. B 2021, 104, 125308. [Google Scholar] [CrossRef]
- Huang, Z.M.; Zhou, J.; Shen, S.Q. Topological responses from chiral anomaly in multi-Weyl semimetals. Phys. Rev. B 2017, 96, 085201. [Google Scholar] [CrossRef]
- Wu, M.M.; Sun, Y.; Li, J.; Zhao, H.; Pan, H. Valley-dependent electron scattering in Weyl semimetals. Solid State Commun. 2021, 334–335, 114387. [Google Scholar] [CrossRef]
- Schaibley, J.R.; Yu, H.; Clark, G.; Rivera, P.; Ross, J.S.; Seyler, K.L.; Yao, W.; Xu, X. Valleytronics in 2D materials. Nat. Rev. Mater. 2016, 1, 16055. [Google Scholar] [CrossRef]
- He, Y.L.; Guo, J.; Gao, F.Y.; Liu, X.S. Dynamical symmetry and valley-selective circularly polarized high-harmonic generation in monolayer molybdenum disulfide. Phys. Rev. B 2022, 105, 024305. [Google Scholar] [CrossRef]
- Nakagahara, K.; Wakabayashi, K. Enhanced valley polarization of graphene on h-BN under circularly polarized light irradiation. Phys. Rev. B 2022, 106, 075403. [Google Scholar] [CrossRef]
- Hung, C.M.; Dang, D.T.X.; Chanda, A.; Detellem, D.; Alzahrani, N.; Kapuruge, N.; Pham, Y.T.H.; Liu, M.; Zhou, D.; Gutierrez, H.R.; et al. Enhanced Magnetism and Anomalous Hall Transport through Two-Dimensional Tungsten Disulfide Interfaces. Nanomaterials 2023, 13, 771. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Fang, Y.; Jin, G. Valley-polarized and supercollimated electronic transport in an 8-Pmmn borophene superlattice. New J. Phys. 2023, 25, 013020. [Google Scholar] [CrossRef]
- Norden, T.; Zhao, C.; Zhang, P.; Sabirianov, R.; Petrou, A.; Zeng, H. Giant valley splitting in monolayer WS2 by magnetic proximity effect. Nat. Commun. 2019, 10, 4163. [Google Scholar] [CrossRef]
- Rosati, R.; Wagner, K.; Brem, S.; Perea-Causin, R.; Wietek, E.; Zipfel, J.; Ziegler, J.D.; Selig, M.; Taniguchi, T.; Watanabe, K.; et al. Temporal Evolution of Low-Temperature Phonon Sidebands in Transition Metal Dichalcogenides. ACS Photonics 2020, 7, 2756–2764. [Google Scholar] [CrossRef]
- Ye, J.; Yan, T.; Niu, B.; Li, Y.; Zhang, X. Nonlinear dynamics of trions under strong optical excitation in monolayer MoSe2. Sci. Rep. 2018, 8, 2389. [Google Scholar] [CrossRef]
- Yuan, H.; Wang, X.; Lian, B.; Zhang, H.; Fang, X.; Shen, B.; Xu, G.; Xu, Y.; Zhang, S.C.; Hwang, H.Y.; et al. Generation and electric control of spin-valley-coupled circular photogalvanic current in WSe2. Nat. Nanotechnol. 2014, 9, 851–857. [Google Scholar] [CrossRef]
- Mak, K.F.; He, K.; Shan, J.; Heinz, T.F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol. 2012, 7, 494–498. [Google Scholar] [CrossRef]
- Vitale, S.A.; Nezich, D.; Varghese, J.O.; Kim, P.; Gedik, N.; Jarillo-Herrero, P.; Xiao, D.; Rothschild, M. Valleytronics: Opportunities, Challenges, and Paths Forward. Small 2018, 14, 1801483. [Google Scholar] [CrossRef]
- Hashmi, A.; Yamada, S.; Yamada, A.; Yabana, K.; Otobe, T. Valley polarization control in WSe2 monolayer by a single-cycle laser pulse. Phys. Rev. B 2022, 105, 115403. [Google Scholar] [CrossRef]
- Langer, F.; Schmid, C.P.; Schlauderer, S.; Gmitra, M.; Fabian, J.; Nagler, P.; Schueller, C.; Korn, T.; Hawkins, P.G.; Steiner, J.T.; et al. Lightwave valleytronics in a monolayer of tungsten diselenide. Nature 2018, 557, 76–80. [Google Scholar] [CrossRef]
- Jimenez-Galan, A.; Silva, R.E.F.; Smirnova, O.; Ivanov, M. Sub-cycle valleytronics: Control of valley polarization using few-cycle linearly polarized pulses. Optica 2021, 8, 277–280. [Google Scholar] [CrossRef]
- Motlagh, S.A.O.; Wu, J.S.; Apalkov, V.; Stockman, I.M. Femtosecond valley polarization and topological resonances in transition metal dichalcogenides. Phys. Rev. B 2018, 98, 081406. [Google Scholar] [CrossRef]
- Motlagh, S.A.O.; Nematollahi, F.; Apalkov, V.; Stockman, I.M. Topological resonance and single-optical-cycle valley polarization in gapped graphene. Phys. Rev. B 2019, 100, 115431. [Google Scholar] [CrossRef]
- Mrudul, M.S.; Dixit, G. Controlling valley-polarisation in graphene via tailored light pulses. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 224001. [Google Scholar] [CrossRef]
- Rana, N.; Dixit, G. All-Optical Ultrafast Valley Switching in Two-Dimensional Materials. Phys. Rev. Appl. 2023, 19, 034056. [Google Scholar] [CrossRef]
- Heide, C.; Boolakee, T.; Higuchi, T.; Weber, H.B.; Hommelhoff, P. Interaction of carrier envelope phase-stable laser pulses with graphene: The transition from the weak-field to the strong-field regime. New J. Phys. 2019, 21, 045003. [Google Scholar] [CrossRef]
- Stoudenmire, E.M.; Schwab, D.J. Supervised Learning with Quantum-Inspired Tensor Networks. arXiv 2017, arXiv:stat.ML/1605.05775. [Google Scholar]
- Flouris, K.; Mendoza Jimenez, M.; Debus, J.D.; Herrmann, H.J. Confining massless Dirac particles in two-dimensional curved space. Phys. Rev. B 2018, 98, 155419. [Google Scholar] [CrossRef]
- Kristinsson, K.; Kibis, O.V.; Morina, S.; Shelykh, I.A. Control of electronic transport in graphene by electromagnetic dressing. Sci. Rep. 2016, 6, 20082. [Google Scholar] [CrossRef] [PubMed]
- Tseluikin, V.; Dzhumieva, A.; Tikhonov, D.; Yakovlev, A.; Strilets, A.; Tribis, A.; Lopukhova, M. Pulsed Electrodeposition and Properties of Nickel-Based Composite Coatings Modified with Graphene Oxide. Coatings 2022, 12, 656. [Google Scholar] [CrossRef]
- Li, X.; Shen, Q.; Zhang, Y.; Wang, L.; Nie, C. Wear behavior of electrodeposited nickel/graphene composite coating. Diam. Relat. Mater. 2021, 119, 108589. [Google Scholar] [CrossRef]
- Sboychakov, A.O.; Rakhmanov, A.L.; Rozhkov, A.V.; Nori, F. Electronic spectrum of twisted bilayer graphene. Phys. Rev. B 2015, 92, 075402. [Google Scholar] [CrossRef]
- Lee, S.Y.; Duong, D.L.; Vu, Q.A.; Jin, Y.; Kim, P.; Lee, Y.H. Chemically Modulated Band Gap in Bilayer Graphene Memory Transistors with High On/Off Ratio. ACS Nano 2015, 9, 9034–9042. [Google Scholar] [CrossRef]
- Li, S.Y.; Zhang, Y.; Ren, Y.N.; Liu, J.; Dai, X.; He, L. Experimental evidence for orbital magnetic moments generated by moire-scale current loops in twisted bilayer graphene. Phys. Rev. B 2020, 102, 121406. [Google Scholar] [CrossRef]
- Silva, R.E.F.; Martin, F.; Ivanov, M. High harmonic generation in crystals using maximally localized Wannier functions. Phys. Rev. B 2019, 100, 195201. [Google Scholar] [CrossRef]
- Rozhkov, A.V.; Sboychakov, A.O.; Rakhmanov, A.L.; Nori, F. Electronic properties of graphene-based bilayer systems. Phys. Rep. 2016, 648, 1–104. [Google Scholar] [CrossRef]
- Mele, E.J. Interlayer coupling in rotationally faulted multilayer graphenes. J. Phys. D 2012, 45, 154004. [Google Scholar] [CrossRef]
- Lopes dos Santos, J.M.B.; Peres, N.M.R.; Castro Neto, A.H. Graphene Bilayer with a Twist: Electronic Structure. Phys. Rev. Lett. 2007, 99, 256802. [Google Scholar] [CrossRef]
- Lopes dos Santos, J.M.B.; Peres, N.M.R.; Castro Neto, A.H. Continuum model of the twisted graphene bilayer. Phys. Rev. B 2012, 86, 155449. [Google Scholar] [CrossRef]
- Du, M.; Liu, C.; Zeng, Z.; Li, R. High-order harmonic generation from twisted bilayer graphene driven by a midinfrared laser field. Phys. Rev. A 2021, 104, 033113. [Google Scholar] [CrossRef]
- Moon, P.; Koshino, M. Optical absorption in twisted bilayer graphene. Phys. Rev. B 2013, 87, 205404. [Google Scholar] [CrossRef]
- Neufeld, O.; Podolsky, D.; Cohen, O. Floquet group theory and its application to selection rules in harmonic generation. Nat. Commun. 2019, 10, 405. [Google Scholar] [CrossRef] [PubMed]

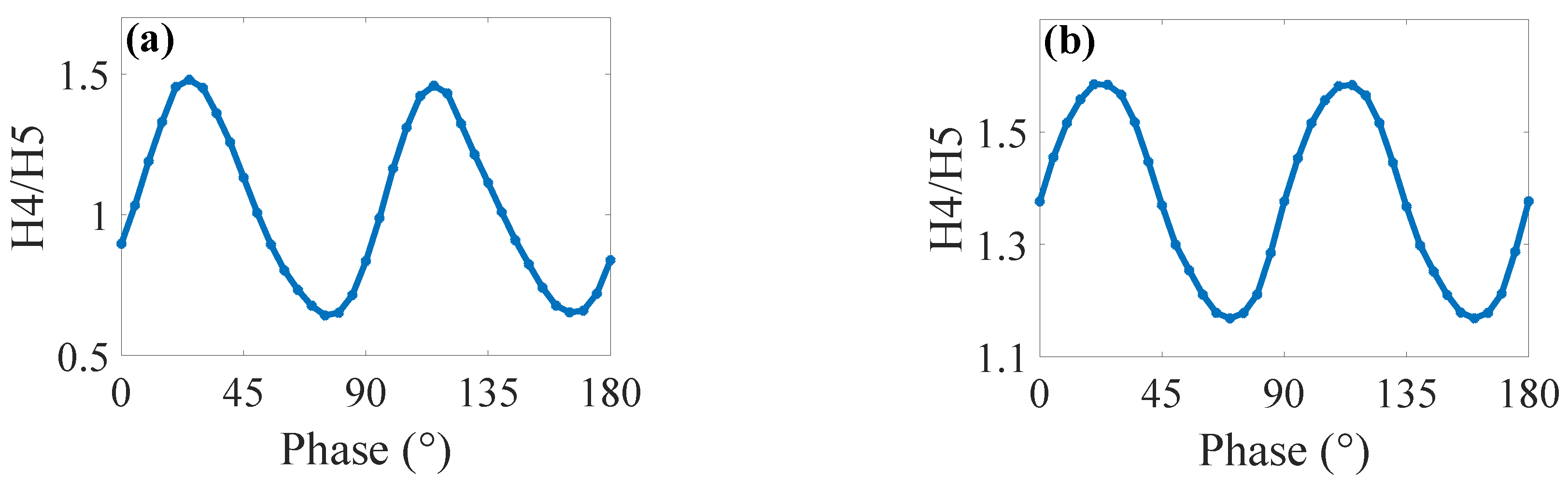
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Liu, C.; Li, R. Valley-Selective Polarization in Twisted Bilayer Graphene Controlled by a Counter-Rotating Bicircular Laser Field. Photonics 2023, 10, 516. https://doi.org/10.3390/photonics10050516
Chen J, Liu C, Li R. Valley-Selective Polarization in Twisted Bilayer Graphene Controlled by a Counter-Rotating Bicircular Laser Field. Photonics. 2023; 10(5):516. https://doi.org/10.3390/photonics10050516
Chicago/Turabian StyleChen, Jiayin, Candong Liu, and Ruxin Li. 2023. "Valley-Selective Polarization in Twisted Bilayer Graphene Controlled by a Counter-Rotating Bicircular Laser Field" Photonics 10, no. 5: 516. https://doi.org/10.3390/photonics10050516
APA StyleChen, J., Liu, C., & Li, R. (2023). Valley-Selective Polarization in Twisted Bilayer Graphene Controlled by a Counter-Rotating Bicircular Laser Field. Photonics, 10(5), 516. https://doi.org/10.3390/photonics10050516




