Flexible Terahertz Metamaterials Absorber based on VO2
Abstract
1. Introduction
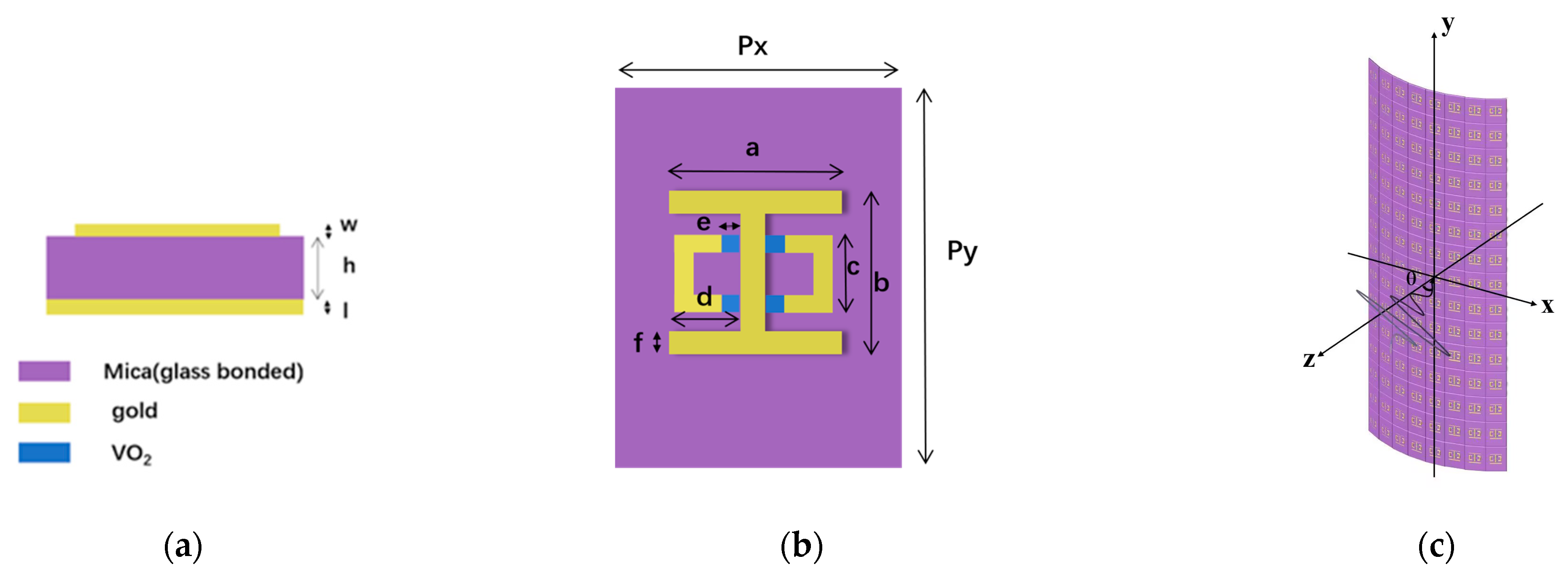
2. Materials and Methods
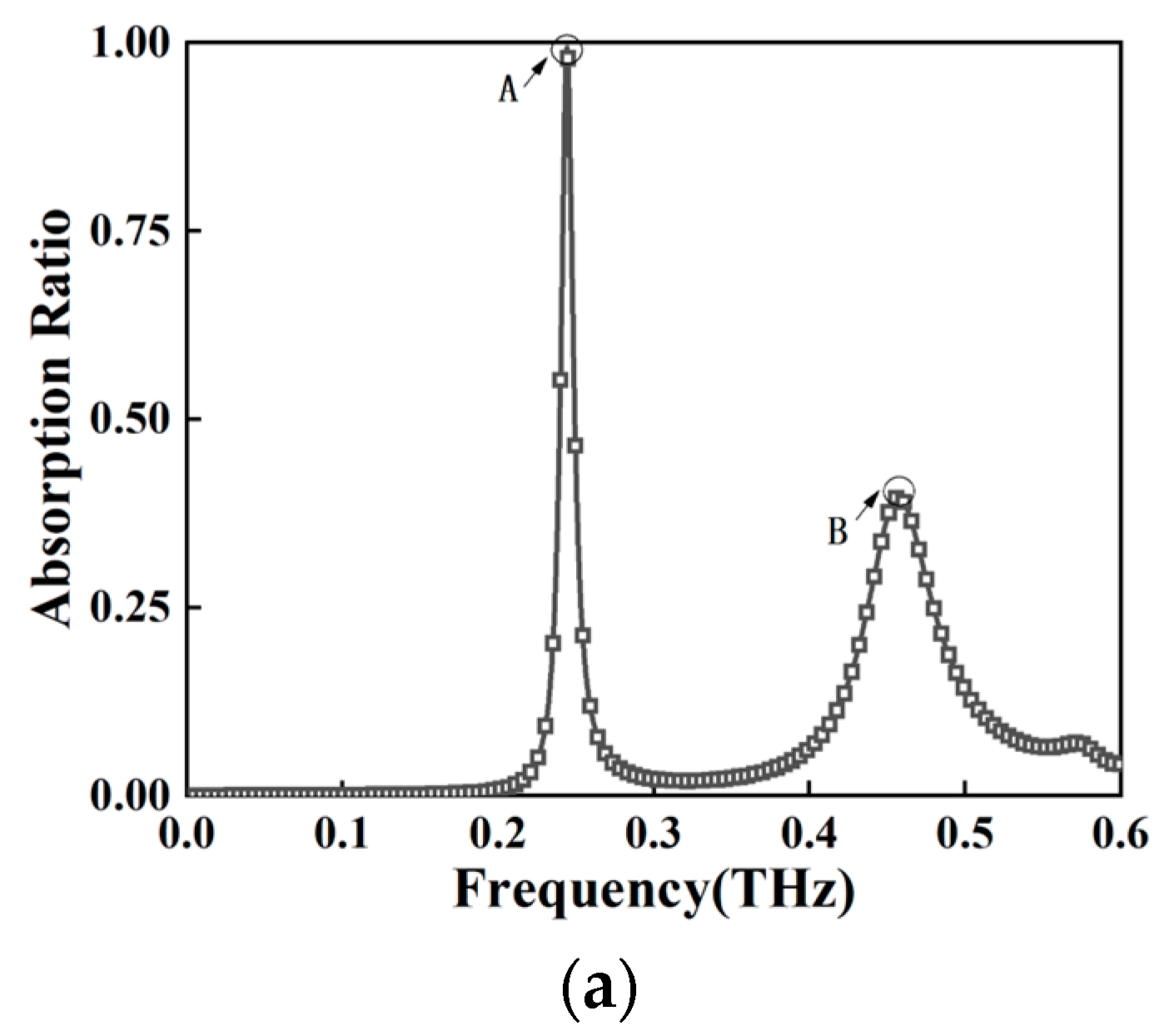
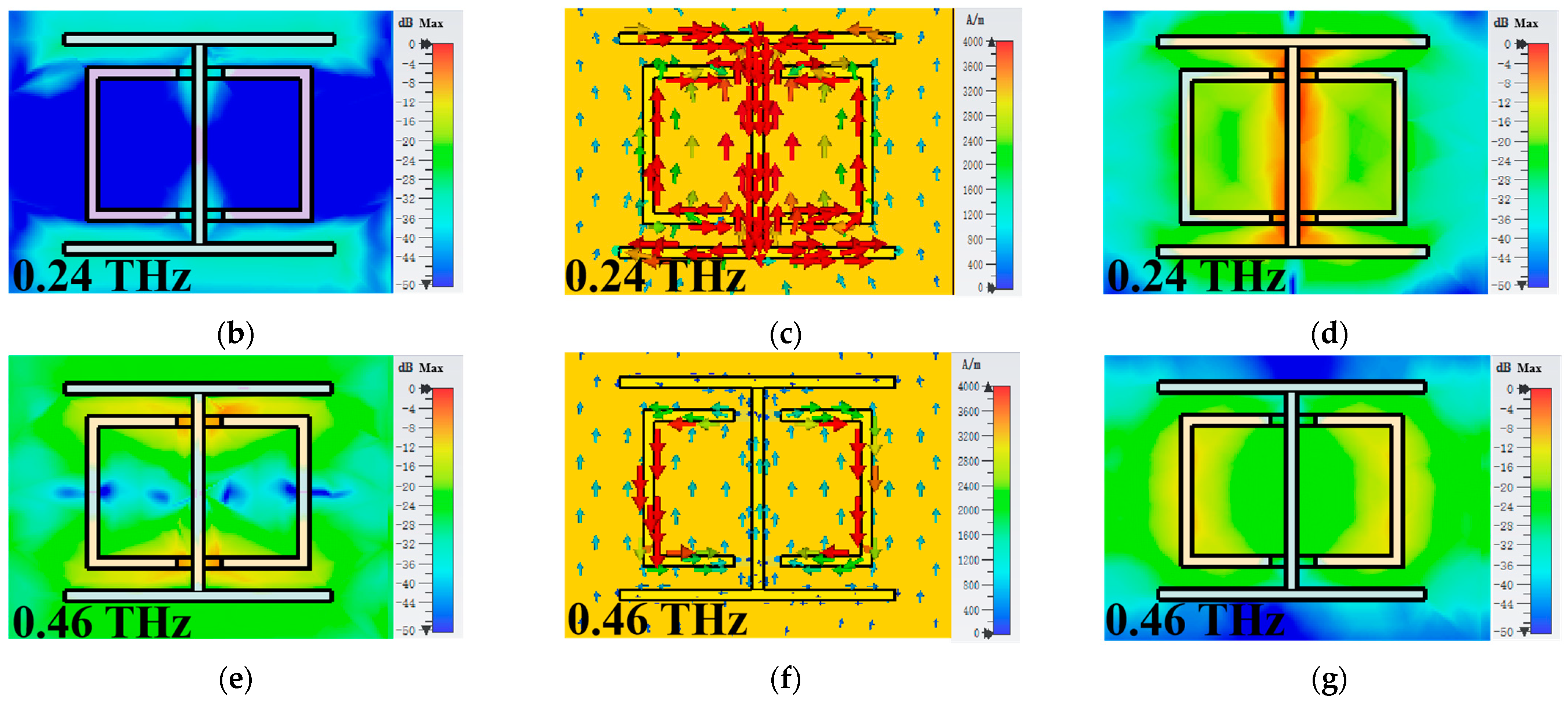
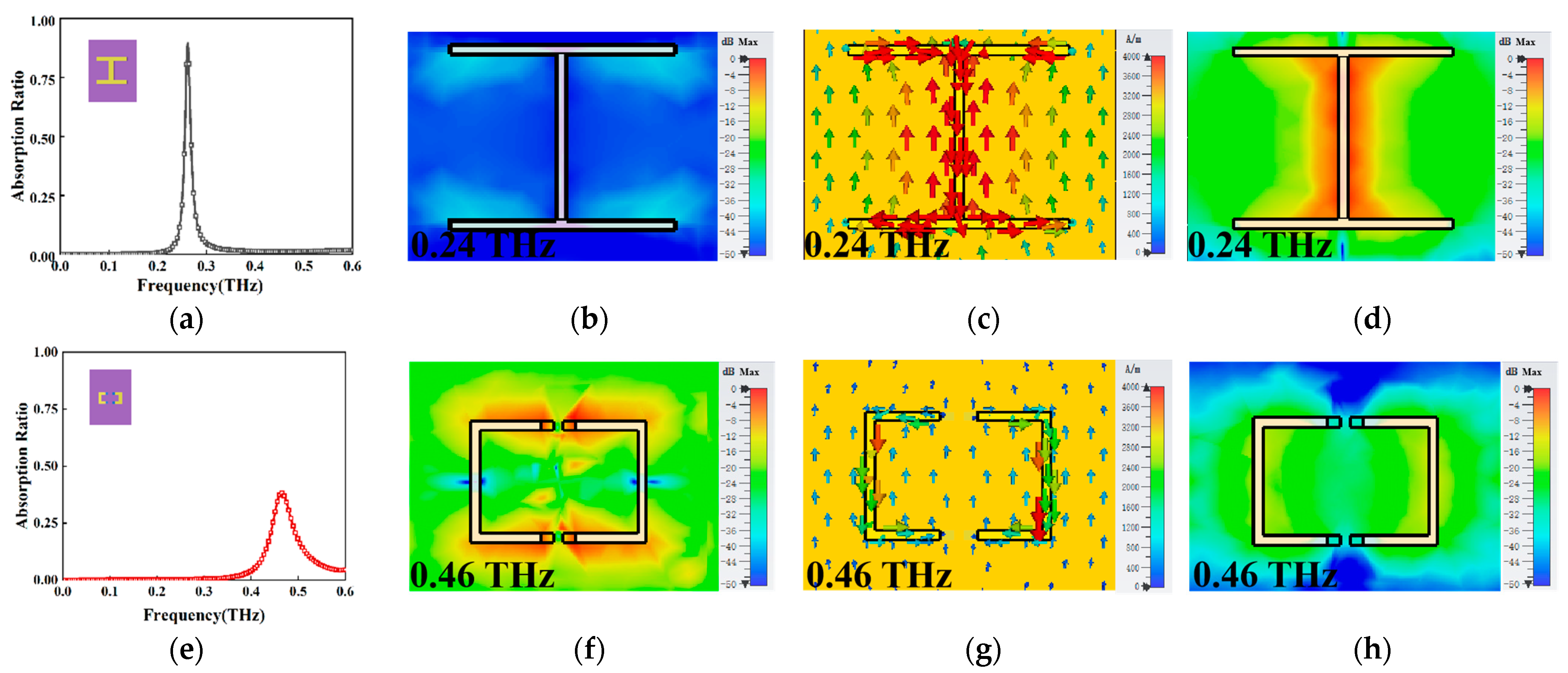
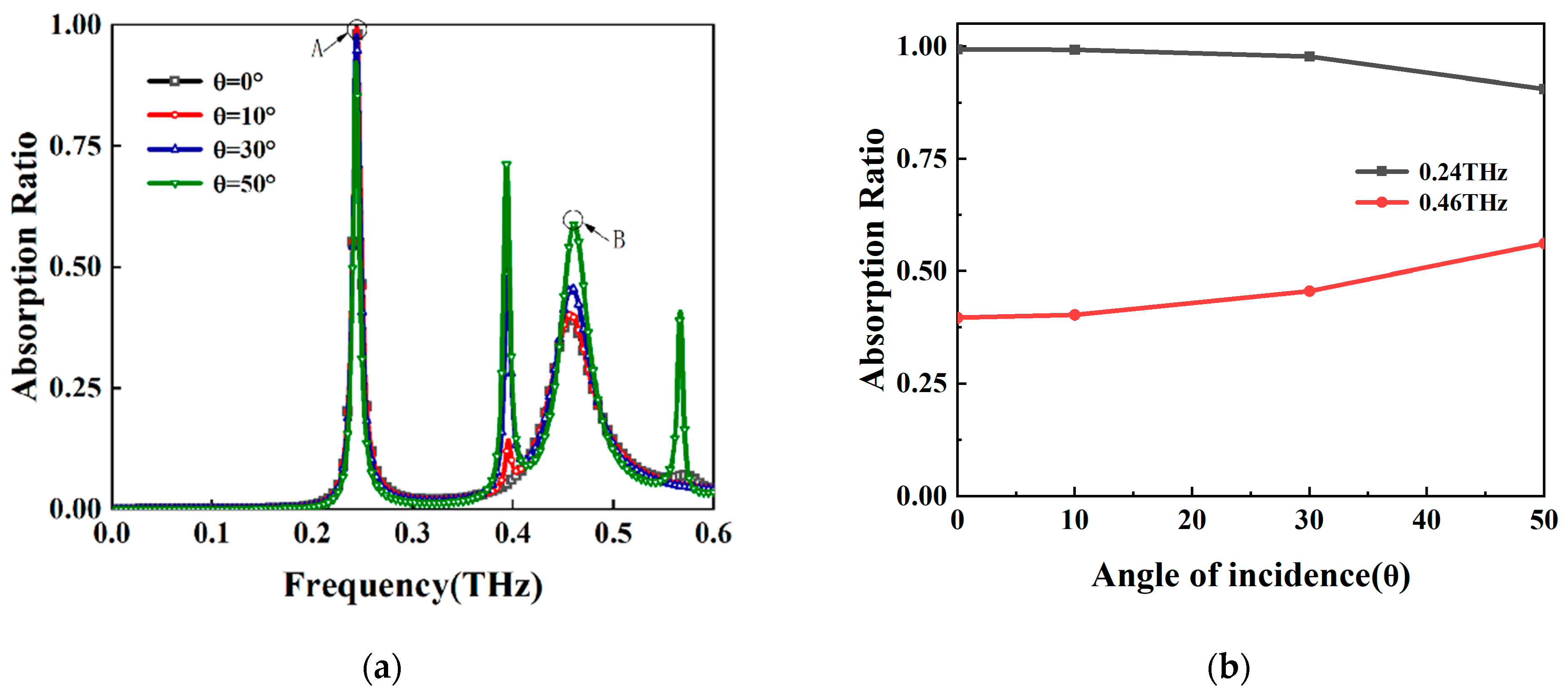
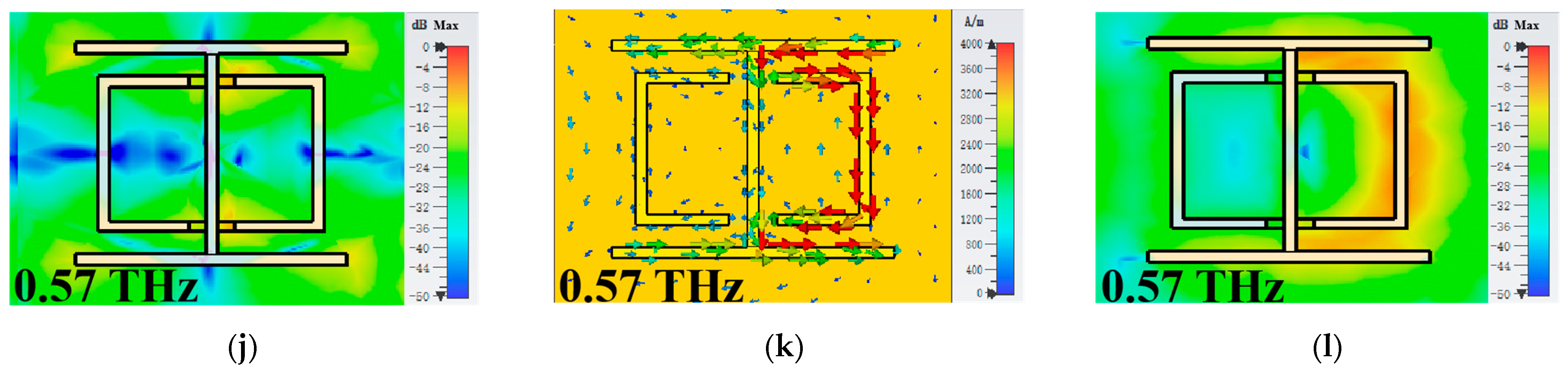
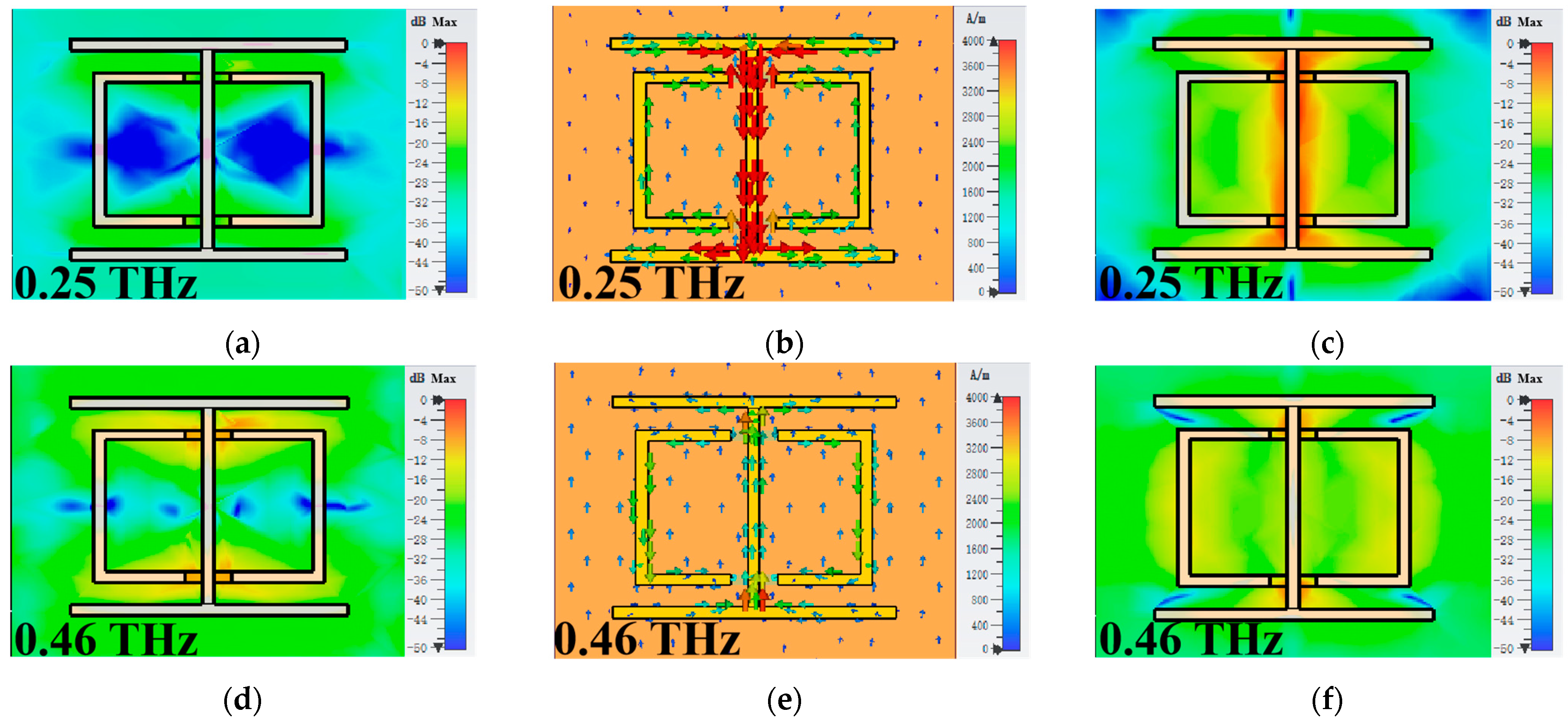
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hillger, P.; Grzyb, J.; Jain, R.; Pfeiffer, U. Terahertz imaging and sensing applications with silicon-based technologies. IEEE Trans. Terahertz Sci. Technol. 2018, 9, 1–19. [Google Scholar] [CrossRef]
- Glück, A.; Rothbart, N.; Schmalz, K. Hübers, H. SiGe BiCMOS Heterodyne receiver frontend for remote sensing with small satellites. IEEE Trans. Terahertz Sci. Technol. 2022, 12, 603–610. [Google Scholar] [CrossRef]
- Zhong, S. Progress in terahertz nondestructive testing: A review. Front. Mech. Eng. 2019, 14, 273–281. [Google Scholar] [CrossRef]
- Schalch, J.S.; Chi, Y.; He, Y.; Tang, Y.; Zhao, X.; Zhang, X.; Wen, Q.; Averittl, R.D. Broadband electrically tunable VO2-metamaterial terahertz switch with suppressed reflection. Microw. Opt. Technol. Lett. 2020, 62, 2782–2790. [Google Scholar] [CrossRef]
- Zhai, Z.H.; Zhu, H.F.; Shi, Q.; Chen, S.C.; Li, J.; Li, Z.R.; Schneider, H.; Zhu, L.G. Enhanced photo responses of an optically driven VO2-based terahertz wave modulator near percolation threshold. Appl. Phys. Lett. 2018, 113, 231104. [Google Scholar] [CrossRef]
- Ferraro, A.; Zografopoulos, D.C.; Caputo, R.; Beccherelli, R. Angle-resolved and polarization-dependent investigation of cross-shaped frequency-selective surface terahertz filters. Appl. Phys. Lett. 2017, 110, 141107. [Google Scholar] [CrossRef]
- Wu, C.; Fang, Y.; Luo, L.; Guo, K.; Guo, Z. A dynamically tunable and wide-angle terahertz absorber based on graphene-dielectric grating. Mod. Phys. Lett. B 2020, 34, 2050292. [Google Scholar] [CrossRef]
- Zubair, A.; Tsentalovich, D.E.; Young, C.C.; Heimbeck, M.S.; Everitt, H.O.; Pasquali, M.; Kono, J. Carbon nanotube fiber terahertz polarizer. Appl. Phys. Lett. 2016, 108, 141107. [Google Scholar] [CrossRef]
- Jiang, S.; Liu, X.; Liu, J.; Ye, D.; Duan, Y.; Li, K.; Yin, Z.; Huang, Y. Flexible metamaterial electronics. Adv. Mater. 2022, 34, 2200070. [Google Scholar] [CrossRef]
- Hengbo, X. Design, simulation and measurement of a single-band high-transmittance all-dielectric metamaterial filter. Opt. Mater. 2022, 125, 112145. [Google Scholar] [CrossRef]
- Liu, S.; Yin, X.; Zhao, H. The tunable single-/narrow-band terahertz metamaterial absorber through photoconductivity. Results Phys. 2022, 39, 105741. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, H.; Zhang, L.; Zhao, Y.; Xie, W. Temperature insensitive ultra-broadband THz metamaterial absorber based on metal square ring resonators. Results Phys. 2021, 22, 103915. [Google Scholar] [CrossRef]
- Liang, Y.; Lin, H.; Lin, S.; Wu, J.; Li, W.; Meng, F.; Yang, Y.; Huang, X.; Jia, B.; Kivshar, Y. Hybrid anisotropic plasmonic metasurfaces with multiple resonances of focused light beams. Nano Lett. 2021, 21, 8917–8923. [Google Scholar] [CrossRef]
- Stewart, J.W.; Nebabu, T.; Mikkelsen, M.H. Control of Nanoscale Heat Generation with Lithography-Free Metasurface Absorbers. Nano Lett. 2022, 22, 5151–5157. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, Q.; Guo, L.; Su, C.; Wang, M.; Xia, F.; Sun, J.; Li, K.; Feng, H.; Yun, M. Dual-controlled tunable dual-band and ultra-broadband coherent perfect absorber in the THz range. Opt. Express 2022, 30, 30832–30844. [Google Scholar] [CrossRef]
- Yao, G.; Ling, F.; Yue, J.; Luo, C.; Ji, J.; Yao, J. Dual-band tunable perfect metamaterial absorber in the THz range. Opt. Express 2016, 24, 1518–1527. [Google Scholar] [CrossRef]
- Meng, H.; Shang, X.; Xue, X.; Tang, K.; Xia, S.; Zhai, X.; Liu, Z.; Chen, J.; J, H.; Wang, L. Bidirectional and dynamically tunable THz absorber with Dirac semimetal. Opt. Express 2019, 27, 31062–31074. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, P.; Zhou, Z.; Chen, X.; Yi, Z.; Zhu, J.; Zhang, T.; Jile, H. Study on temperature adjustable terahertz metamaterial absorber based on vanadium dioxide. IEEE Access. 2020, 8, 85154–85161. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Z.H.; Li, L.; Fan, Y.X.; Tao, Z.Y. Vanadium dioxide-assisted broadband tunable terahertz metamaterial absorber. Sci. Rep. 2019, 9, 5751. [Google Scholar] [CrossRef]
- Mou, N.; Tang, B.; Li, J.; Dong, H.; Zhang, L. Switchable ultra-broadband terahertz wave absorption with VO2-based metasurface. Sci. Rep. 2022, 12, 1–8. [Google Scholar] [CrossRef]
- Thompson, Z.J.; Stickel, A.; Jeong, Y.G.; Han, S.; Son, B.H.; Paul, M.J.; Lee, B.; Mousavian, A.; Seo, G.; Kim, H.T.; et al. Terahertz-triggered phase transition and hysteresis narrowing in a nanoantenna patterned vanadium dioxide film. Nano Lett. 2015, 15, 5893–5898. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, D.; Oda, S.; Kawano, Y. A flexible and wearable terahertz scanner. Nat. Photonics 2016, 10, 809–813. [Google Scholar] [CrossRef]
- Cai, T.; Zheng, B.; Lou, J.; Cai, T.; Zheng, B.; Lou, J.; Shen, L.; Yang, Y.; Tang, S.; Li, E.; et al. Experimental Realization of a Superdispersion-Enabled Ultrabroadband Terahertz Cloak. Adv. Mater. 2022, 34, 2205053. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Cui, Y.; Tentzeris, M.M. Tile-based massively scalable MIMO and phased arrays for 5G/B5G-enabled smart skins and reconfigurable intelligent surfaces. Sci. Rep. 2022, 12, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Lv, Z.; Mohan, M.P.; Cui, Z.; Liu, Z.; Jiang, Y.; Li, J.; Wang, C.; Pan, S.; Karim, M.F.; et al. Pangolin-Inspired Stretchable, Microwave-Invisible Metascale. Adv. Mater. 2021, 33, 2102131. [Google Scholar] [CrossRef]
- Bilal, O.R.; Costanza, V.; Israr, A.; Palermo, A.; Celli, P.; Lau, F.; Daraio, C. A Flexible Spiraling-Metasurface as a Versatile Haptic Interface. AMT 2020, 5, 2000181. [Google Scholar] [CrossRef]
- Xiao, D.; Chen, W.; Sun, L.; Zhu, M.; Ng, Z.K.; Teo, E.H.T.; Zhang, J.; Hu, F. A Flexible and Ultra-Wideband Terahertz Wave Absorber Based on Pyramid-Shaped Carbon Nanotube Array via Femtosecond-Laser Microprocessing and Two-Step Transfer Technique. Adv. Mater. Interfaces 2022, 9, 2102414. [Google Scholar] [CrossRef]
- Yu, X.; Gao, X.; Qiao, W.; Wen, L.; Yang, W. Broadband tunable polarization converter realized by graphene-based metamaterial. IEEE Photon. Technol. Lett. 2016, 28, 2399–2402. [Google Scholar] [CrossRef]
- Chen, X.; Fan, W. Ultra-flexible polarization-insensitive multiband terahertz metamaterial absorber. Appl. Opt. 2015, 54, 2376–2382. [Google Scholar] [CrossRef]
- Yang, P.; Qin, J.; Xu, J.; Tian-Cheng, H. Ultrathin flexible transmission metamaterial absorber. Acta Phys. Sin. 2019, 68, 087802. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef]
- Huang, W.; Yin, S.; Zhang, W.; Wang, K.; Zhang, Y.; Han, J. Robust and broadband integrated terahertz coupler conducted with adiabatic following. New J. Phys. 2019, 21, 113004. [Google Scholar] [CrossRef]
- Huang, W.; Qu, X.; Yin, S.; Zubair, M.; Yuan, M.; Zhang, W.; Han, J. Quantum engineering enables broadband and robust terahertz surface plasmon-polaritons coupler. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 1–7. [Google Scholar] [CrossRef]
- Huang, W.; Qu, X.; Yin, S.; Zubair, M.; Guo, C.; Xiong, X.; Zhang, W. Long-distance adiabatic wireless energy transfer via multiple coils coupling. Results Phys. 2020, 19, 103478. [Google Scholar] [CrossRef]
- Niu, L.; Xu, Q.; Zhang, X.; Zhang, Z.; Li, S.; Chen, X.; Xu, Y.; Ma, J.; Kang, M.; Han, J.; et al. Coupling plasmonic system for efficient wavefront control. ACS Appl. Mater. Interfaces 2021, 13, 5844–5852. [Google Scholar] [CrossRef]
- Liu, H.; Lu, J.; Wang, X.R. Metamaterials based on the phase transition of VO2. Nanotechnology 2017, 29, 024002. [Google Scholar] [CrossRef]
- Ahadi, S.; Neshat, M.; Moravvej-Farshi, M.K. Binary THz modulator based on silicon Schottky-metasurface. Sci. Rep. 2022, 12, 18871. [Google Scholar] [CrossRef]
- Gong, D.; Mei, J.; Li, N.; Shi, Y. Tunable metamaterial absorber based on VO2-graphene. Mater. Res. Express 2022, 9, 115803. [Google Scholar] [CrossRef]
- Wang, X.; Wu, G.; Wang, Y.; Liu, J. Terahertz Broadband Adjustable Absorber Based on VO2 Multiple Ring Structure. Appl. Sci. 2022, 13, 252. [Google Scholar] [CrossRef]
- Han, X.; Zhang, Z.; Qu, X. A novel miniaturized tri-band metamaterial THz absorber with angular and polarization stability. Optik 2021, 228, 166086. [Google Scholar] [CrossRef]
- Zhou, R.; Jiang, T.; Peng, Z.; Li, Z.; Zhang, M.; Wang, S.; Li, L.; Liang, H.; Ruan, S.; Su, H. Tunable broadband terahertz absorber based on graphene metamaterials and VO2. Opt. Mater. 2021, 114, 110915. [Google Scholar] [CrossRef]
- Qi, Y.; Zhang, Y.; Liu, C.; Zhang, T.; Zhang, B.; Wang, L.; Deng, X.; Wang, X.; Yu, Y. A tunable terahertz metamaterial absorber composed of hourglass-shaped graphene arrays. Nanomaterials 2020, 10, 533. [Google Scholar] [CrossRef] [PubMed]





| Ref. | Material | Frequency (THz) | Absorption | Layer | Thickness (μm) | Flexible |
|---|---|---|---|---|---|---|
| [19] | polyimide, copper | 0.72, 1.4, 2.3 | 89%, 98%, 85% | three-layer | 16.2 | yes |
| [29] | VO2 | 1.96 | Nearly 100% | three-layer | 26 | no |
| [38] | VO2, graphene | 0.75–1.15; 2.5–4.5 | 94%, 90% | five-layer | 49.6 | no |
| [39] | VO2 | 93.01–7.27 | 90% | three-layer | 7.4 | no |
| [40] | Silicon, polyimide, copper | 0.33, 0.62, 0.82 | 98%, 96%, 98% | four-layer | 69 | no |
| [41] | VO2, graphene | 1.2 | 99.3% | three-layer | 30.7 | no |
| [42] | Si, SiO2, Au, graphene | - | 41.7% | three-layer | 0.94 | no |
| Our paper | VO2, mica, gold | 0.24, 0.46 | 99.7%, 99.3% | three-layer | 42.3 | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Leng, J.; Li, J.; Li, J.; Li, B.; Yang, M.; Wang, X.; Shi, Q. Flexible Terahertz Metamaterials Absorber based on VO2. Photonics 2023, 10, 621. https://doi.org/10.3390/photonics10060621
Jiang Z, Leng J, Li J, Li J, Li B, Yang M, Wang X, Shi Q. Flexible Terahertz Metamaterials Absorber based on VO2. Photonics. 2023; 10(6):621. https://doi.org/10.3390/photonics10060621
Chicago/Turabian StyleJiang, Zhaoxia, Jin Leng, Jin Li, Jianfei Li, Boyang Li, Mao Yang, Xiaolian Wang, and Qiwu Shi. 2023. "Flexible Terahertz Metamaterials Absorber based on VO2" Photonics 10, no. 6: 621. https://doi.org/10.3390/photonics10060621
APA StyleJiang, Z., Leng, J., Li, J., Li, J., Li, B., Yang, M., Wang, X., & Shi, Q. (2023). Flexible Terahertz Metamaterials Absorber based on VO2. Photonics, 10(6), 621. https://doi.org/10.3390/photonics10060621






