Abstract
The propagation characteristics of Airy beams in an inhomogeneous medium with periodic potential are studied theoretically and numerically. The Gross–Pitaevskii equation was solved with periodic potential using the separating variables method, and a breathing soliton solution and the breathing period were obtained. Further, the propagation properties of an Airy beam, and the interaction between two Airy beams while considering the medium parameters and beam parameters were numerically simulated in detail. First, we discuss the influence of the initial medium parameters (modulation intensity P and modulation frequency ω) on the propagation characteristics. Then, we investigate the effect of the initial beam parameters (initial chirp C and position x0) on the propagation characteristics. Lastly, the interaction of two Airy beams with opposite spatial positions for different phase φ, amplitude A, and initial interval x0 is analyzed. The breathing period and central position of the breathing solitons could be controlled by changing the initial medium parameters. By varying the initial beam parameters, the deflection direction and size, and the maximal intensity of the breathing solitons were manipulated. The breathing solitons of different bound states were formed by changing the phase φ, amplitude A, and initial interval x0 of two Airy beams. The results provide a theoretical basis for the propagation and manipulation of Airy beams.
1. Introduction
The realization of self-bending and even self-revolving light has always been the dream and pursuit of scientists. About 40 years ago, the pioneering work of Berry and Balazs [1] proposed the dispersion-free Airy wave. Because of the similarity between the Schrödinger equation in quantum mechanics and the paraxial equation in optics, this concept has been extended to the field of optics. Airy beams are nondiffractive, self-bending, and self-accelerating, that is, the field profile along the propagation direction is unchanged and can achieve self-acceleration deflection without the refractive index gradient and self-heal of the main lobe in the presence of obstacles [2,3,4,5]. The propagation properties of Airy waves in nonlinear media [6,7,8,9,10], and the interaction between Airy waves and other waves [11] could have many interesting and important applications, such as vacuum electron accelerators [12], light bullets [13,14], optical particle manipulation [15,16,17], and optical routing [18]. These application prospects render Airy beams a very popular, exciting, and groundbreaking hot topic.
Periodic potential is one of the most fundamental concepts in physics. Periodic structures are widely found in nonlinear physical systems [19], such as Bose–Einstein condensates [20], fluid mechanics [21], and optics [22]. This type of complex physical system, which has been widely investigated, has periodic modulation effects on waves that propagate through it. For example, applying an electrostatic field to the periodic lattice of electrons causes them to periodically oscillate in the spatial and frequency domains, that is, the Bloch oscillation effect. The optical analogies of electron Bloch oscillation effects were also demonstrated in many systems, such as waveguide modulators [23], photonic spectral lattices [24], fiber loops [25], and plasmas [26]. The periodic potential intermittently regulates the waveform and spectrum of the initial input beam, resulting in periodic changes in the energy and width of the beam, and the generation of breathing solitons [27,28]. When these effects are combined with an Airy beam’s propagation properties, the Airy beam obtains unique propagation properties that further enrich the shape of the signal for optical communication.
Due to the effect of periodic potential in inhomogeneous media, the central position and intensity of the beam periodically change to form breathing solitons. In the formation, propagation, and manipulation of breathing solitons when various forms of beams propagate in periodic potentials, numerous scientific issues remain to be resolved.
As an effective method for manipulating the propagation of light beams, linear [29] and parabolic [30] potentials change the propagation trajectory of light beams. There is little research on the generation and manipulation of the breathing solitons of self-bending and self-bent Airy beams in an optical lattice with periodic nonlinear potential. Airy beams also generate breathing properties in an inhomogeneous medium with periodic potential, and their self-accelerating and self-bending properties enrich the morphology of the breathing beam. This paper studies the propagation characteristics and interactions of Airy beams in periodic potential, and seeks ways to manipulate their breathing period and morphology.
2. Theoretical Model
In paraxial approximation, the nonlinear Schrödinger equation can be used to describe the propagation of a laser beam in an inhomogeneous medium with periodic potential. The normalized form for the nonlinear (2+1)D Schrödinger equation is as follows [19]:
In Equation (1), ψ(x, y, z) is the light field, x and y are the dimensionless transverse space position, z is the dimensionless longitudinal propagation distance, V(x, y) is the potential coefficient, and g is the general nonlinear coefficient. When the general nonlinear refractive index is greater than 0, the beam is self-focusing, and when the general nonlinear refractive index is less than 0, the beam is self-defocusing. Equation (1) is also known as the Gross–Pitaevskii equation (GPE). Researchers have studied the analytical solution of the generalized (2+1)-dimensional particle equation. However, its stable soliton solution is only present in an inhomogeneous medium with periodic potential and a fixed modulation frequency, and the exact derivation of the period of the breathing solitons is unknown. The periodically varying potential field studied in this paper satisfies the following [19]:
where ω is the repetition frequency of the periodic potential. The most common periodic potential, V(x, y), can be expressed as follows:
Due to the periodic structure of the lattice, the periodic potential model is widely used in the study of various crystal materials and devices. In Formula (3), P is the modulation strength of the periodic potential, and η is the anisotropy factor. Thus, the normalized form of the (2+1) GPE is as follows:
The exact solution of nonlinear Schrodinger Equation (4) with a periodic potential remains a great challenge. In this paper, we find a breathing soliton solution for Equation (4), and demonstrate the relationship between the period of the breathing solitons and the characteristic inhomogeneous medium parameters. The results play an important role in guiding the propagation of Airy beams. Equation (4) can be solved by using the separation of the variables. Assuming that the solution of optical waves propagated in an inhomogeneous medium with periodic potential had the form of , Equation (4) could be converted into the following form:
where µ is the chemical potential and the normalized period of the inhomogeneous medium. The two parts of Equation (5) were assumed to be zero. Then,
When g = 1, we have the class of the periodic soliton solution of Equation (6):
where a is an arbitrary constant from −1 to 1. From Equation (9), we can interpret the period of the wave function in the mode of propagation into the following form:
The 1D GPE can be expressed as follows [31]:
The most common periodic potential V(x) can be expressed as follows:
Using the same method of separation of variables, could can obtain a class of the periodic soliton solutions of (1+1)D GPE:
Therefore, the special periodic solutions of Equation (12) with g = 1 were obtained:
Through Analytical Equation (15), we could interpret the period of the wave function in the mode of propagation into the following form:
The above theoretical analysis shows that the periodic soliton solutions existed in an inhomogeneous medium with periodic potential. The law described in Formula (15) is applicable to the evolution of beams of other shapes in an inhomogeneous medium with periodic potential. When the shape of the incident beam is different, the shape of the breathing solitons is different, but the breathing law is similar. Therefore, some evolution rules of the beam were obtained from Formula (15). Therefore, we predicted that the period would decrease with P and ω. The prediction results were consistent with the numerical simulation results.
Next, we discuss the propagation properties of a single Airy beam and two Airy beams with opposite spatial positions in an inhomogeneous medium with periodic potential. When studying the propagation characteristics of a single beam, the field distribution of the initial Airy beam can be written as follows:
where x0 is the translational distance of the beam’s transverse position; and a0 is the decay factor associated with an infinite Airy mode that has a positive value, so that the infinite Airy tail could be contained; C is the quadratic chirp factors of the Airy beam; Ai(x) is an Airy function, whose expression is as follows:
In order to study the interaction of Airy beams, a more complex incident beam should be constructed. The Airy beam was composed of two parallel Airy beams at opposite acceleration directions. Consequently, we assumed that the incident beam consisted of two spatially opposed Airy beams with a constant phase difference and distinct amplitudes:
where A1 and A2 are the relative amplitudes of the two Airy beams; φ is the phase factor controlling the phase shift between the two Airy beams: when φ = 0, the two Airy beams were in-phase; when φ = π, they were out-of-phase.
3. Analysis of Numerical Calculation Results
The electric field distribution was equivalent in the x and y directions of Equations (1)–(4); thus, the propagation properties of Airy beams were similar in the x and y directions. To reduce the computational complexity, we only considered the (1+1)D GPE in the numerical simulation.
It is generally difficult to solve the nonlinear Schrödinger equation with analytical methods, and only various approximate numerical methods can be used. The split-step Fourier method is a widely used numerical method in the problem of light wave transmission in nonlinear media. Its basic idea is to separate the diffractive and nonlinear effects to simulate their interaction. First, the transmission length is divided into many small and equal intervals called step lengths. When the beam propagates in the first ½ step, it is only affected by the diffraction effect. After the operation is completed, the calculation of the latter ½ step is performed. Only the influence of nonlinear effect is considered in the latter ½ step. This calculative process is repeated until the final transmission distance is calculated. Then, various storage data from the beginning are output to the final position, including on strength, width, frequency, and peak position.
In this paper, the propagation characteristics of an Airy beam in an inhomogeneous medium with periodic potential are studied. When Airy beams with different initial parameters propagate in an inhomogeneous medium with varying initial parameters, different types of breathing characteristics are evidently formed. We discuss the characteristic parameters of a periodic potential inhomogeneous medium (modulation frequency P and modulation strength ω) (Figure 1 and Figure 2), and the influence of the characteristic parameters of Airy beams (chirp C and initial position x) (Figure 3 and Figure 4) on the propagation characteristics of a single Airy beam. In order to further investigate the interaction between two Airy beams at opposite spatial positions in an inhomogeneous medium with periodic potential, the propagation characteristics of Airy beams with different phases φ (Figure 5), amplitudes A (Figure 6) and positions x0 (Figure 7) are discussed.
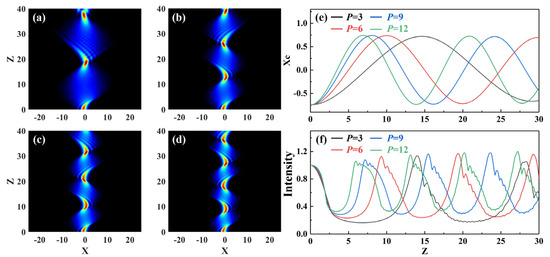
Figure 1.
Spatial propagation characteristics of Airy beams in optical lattices with four different modulation intensities when a0 = 0.3 and ω = 0.1: (a) P = 3, (b) P = 6, (c) P = 9 and (d) P = 12; (e) central position evolution of Airy beams; (f) maximal intensity evolution of Airy beams: P = 3 (black line), P = 6 (red line), P = 9 (blue line) and P = 12 (green line).
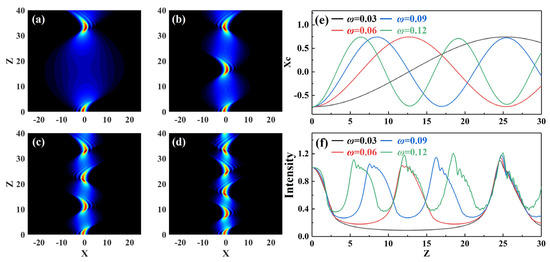
Figure 2.
Spatial propagation characteristics of Airy beams in optical lattices with four different modulation frequency levels when a0 = 0.3 and P = 3: (a) ω = 0.03, (b) ω = 0.06, (c) ω = 0.09 and (d) ω = 0.12; (e) central position evolution of Airy beams; (f) maximal intensity evolution of Airy beams: ω = 0.03 (black line), ω = 0.06 (red line), ω = 0.09 (blue line) and ω = 0.12 (green line).
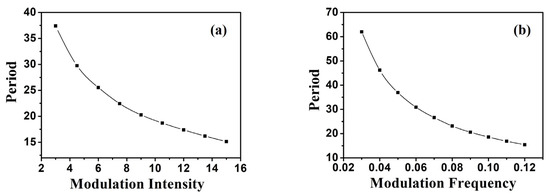
Figure 3.
Figure 3. Influence of different modulation (a) intensities and (b) modulation frequencies on the period of Airy breathing soliton in an inhomogeneous medium with periodic potential when a0 = 0.3.
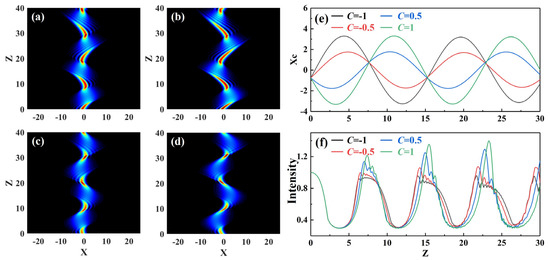
Figure 4.
Spatial propagation characteristics of Airy beams with four different chirps when a0 = 0.3, P = 3 and ω = 0.03: (a) C = −1, (b) C = −0.5, (c) C = 0.5 and (d) C = 1; (e) central position evolution of the Airy beams; (f) maximal intensity evolution of the Airy beams: C = −1 (black line), C = −0.5 (red line), C = 0.5 (blue line) and C = 1 (green line).
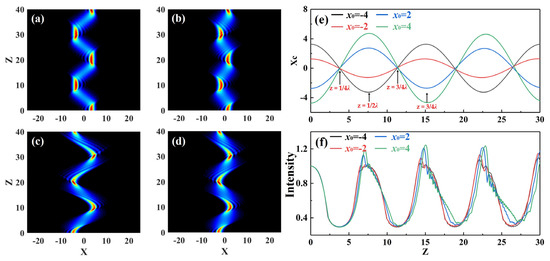
Figure 5.
Spatial propagation characteristics of Airy beams with four different initial transverse positions when a0 = 0.3, P = 3 and ω = 0.03: (a) x0 = −4, (b) x0 = −2, (c) x0 = 4 and (d) x0 = 2; (e) central position evolution of the Airy beams; (f) maximal intensity evolution of the Airy beams: x0 = −4 (black line), x0 = −2 (red line), x0 = 4 (green line) and x0 = 2 (blue line).
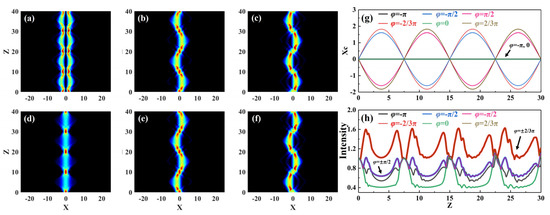
Figure 6.
Interactions of two incident (a–c) in-phase and (d–f) out-of-phase Airy beams with different phases when a0 = 0.3, P = 3 and ω = 0.03: (a) φ = −π; (b) φ = −π/2; (c) φ = −2π/3; (d) φ = 0; (e) φ = π/2; (f) φ = 2π/3; (g) central position evolution of the Airy beams; (h) maximal intensity evolution of the Airy beams.
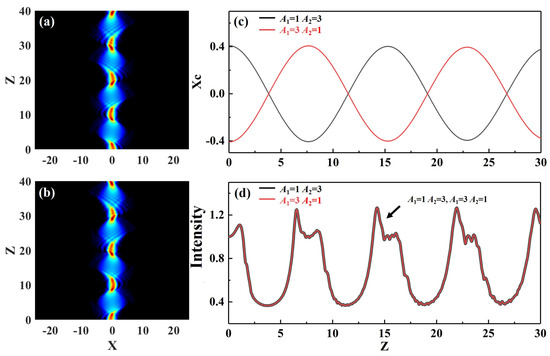
Figure 7.
Interaction of two in-phase incident Airy beams at different amplitudes when a0 = 0.3, P = 3 and ω = 0.03: (a) A1 = 1, A2 = 3, (b) A1 = 3, A2 = 1. (c) central position evolution of the Airy beams; (d) maximal intensity evolution of the Airy beams.
3.1. Propagation Characteristics of a Single Airy Beam in an Inhomogeneous Medium with Periodic Potential
Figure 1 shows the propagation diagram of an Airy beam in an inhomogeneous medium with different modulation strength levels when truncation coefficient a0 = 0.3 and modulation frequency ω = 0.1. Figure 1a–d show the propagation characteristics of the Airy beam’s intensity, and Figure 1e,f demonstrate the changes in the center of mass and intensity of the Airy beam, respectively. Asymmetric spatial solitons could be formed when the broadening caused by diffraction and the compression caused by the modulation effect of the inhomogeneous medium with periodic potential reached a balance. The incident Airy beam in the inhomogeneous medium was localized in the transverse position, and its diffraction phenomena during propagation were reduced to some extent by the nonlinear effect, which formed the breathing features of a periodic S-type oscillation. In the initial propagation phase of the Airy beam, diffraction plays a dominant role, and the beam is widened. However, as the propagation distance increases, the nonlinear effect dominates. Due to the high nonlinear effect at the center of the lattice, the Airy beam gathers up to the center and is compressed in the process. When its peak reaches a certain value, the Airy beam is reflected in the opposite direction because of the potential well of the lattice that it encounters. The beam is then spread and reflected again. Thus, periodic breathing behavior with sigmoid oscillations occurs. When modulation intensity P increases, the nonlinear effect of the corresponding central region also increases, and the inhomogeneous medium has more power to bind the Airy beams. As a result, the breathing period of the Airy beam becomes shorter during propagation (Figure 1e,f). The above analysis shows that the breathing period of Airy space solitons can be controlled by varying the inhomogeneous medium’s modulation intensity. The numerical simulation results of the effect of modulation intensity P on the breathing period of Airy space solitons in an inhomogeneous medium with periodic potential are basically consistent with the theoretical analysis of Equation (16).
The modulation frequency ω of the inhomogeneous medium is an important parameter affecting breathing speed. Simulations were performed to investigate the effect of the modulation frequency on the breathing solitons created by the Airy beam. Figure 2 shows the propagation of an Airy beam in an inhomogeneous medium with different modulation frequencies when truncation coefficient a0 = 0.3 and modulation intensity P = 10. Figure 2a–d show the propagation characteristics of the intensity of an Airy beam. Figure 2e,f show the changes in the center of mass and intensity of the Airy beam, respectively. When propagating into an inhomogeneous medium, an Airy beam could be bound to the inhomogeneous medium for stable propagation, and form breathing optical solitons with periodic sigmoid oscillations (Figure 2a–d). The breathing solitons show local characteristics in the spatial distribution direction, and periodic breathing characteristics in the propagation direction. As modulation frequency ω increases, for the same longitudinal propagation distance (Z = 100), the pulsation period gradually decreases, and the frequency gradually increases (Figure 1e,f). Modulation frequency ω can slightly change the maximal intensity of the breathing solitons (Figure 2f). Breathing solitons conserve energy throughout the propagation. The above analysis shows that the breathing period of Airy spatial solitons can be controlled by changing the lattice modulation frequency. The numerical simulation results of the breathing period of the Airy spatial solitons were basically consistent with the theoretical analysis in Formula (16).
The period of the Airy beam propagating in inhomogeneous medium with periodic potential was calculated. The relationship between the two characteristic parameters of the medium and the period of the Airy breathing soliton show that the period of the Airy breathing soliton monotonously decreased with the increase in modulation intensity (Figure 3a) and modulation frequency (Figure 3b); the rate of the decrease in the breathing period was rapidly reduced. The above analysis shows that the period of Airy breathing solitons could be controlled by changing the characteristic parameters of inhomogeneous media. The statistical numerical simulation results of the Airy breathing soliton period were basically consistent with the theoretical analysis in Formula (16).
Initial chirp C is an important characteristic parameter of Airy beams, and a numerical simulation study was conducted to explore its effects on breathing soliton production by Airy beams. Figure 4 shows the propagation diagram of Airy beam with different initial chirps in an inhomogeneous medium when truncation coefficient a0 = 0.3, modulation intensity P = 10, and modulation frequency ω = 0.1. Figure 4a–d show the propagation characteristics of the intensity of an Airy beam, and Figure 4e,f show the changes in the center of center of mass and intensity of an Airy beam, respectively. The results show that, as the initial chirp C increased, the propagation dynamics of the Airy beam also changed with vibration. As chirp parameter C increased, both the maximal central position (Figure 4e) and the maximal oscillation amplitude of the Airy beam (Figure 4f) increased. However, in the propagation process, the propagation characteristic frequency remained unchanged, while the multipeak structure became inconspicuous. When the absolute values of the chirp parameters were equal, the corresponding maximal oscillation amplitude was the same, but the Airy beam was deflected in the opposite direction, while its shape and motion state were the same (Figure 4e). Meanwhile, the energy of the breathing solitons was conserved throughout the propagation. The above analysis shows that the direction, magnitude, and maximal intensity of the spatial soliton deflection could be controlled by changing initial chirp C of the Airy beam.
By choosing an appropriate initial transverse position x0 of the Airy beam in inhomogeneous media, the direction of the binding force on the beam caused by the nonlinear force of the periodic potential can be changed. To investigate the effects of initial transverse position x0 on the generation of breathing solitons with an Airy beam, numerical simulations were conducted. Figure 5 shows the propagation of an Airy beam with different initial positions in an inhomogeneous medium when truncation coefficient a0 = 0.3, modulation intensity P = 10, and modulation frequency ω = 0.1. When x0 < 0, the Airy beam was deflected in a negative direction from its lateral negative in the first half period, but in a positive direction from its lateral position in the second half period (Figure 5a,b). The deflection direction of the Airy beam was the opposite of the deflection direction when x0 < 0 (Figure 5c,d). Even if the transverse position of an incident Airy beam does not overlap with the nonlinear potential, Airy beams could periodically reproduce their initial envelope shape during propagation in order to attain properties such as being diffraction-free over long distances. The Airy beam had a side lobe to the left of the main lobe during its initial propagation. However, when the propagation distance was the ¼λ ≤ z ≤ ¾λ cycle, the side lobe was located on the right-hand side of the main lobe. Moreover, when the propagation distance was the ¾λ ≤ z ≤ λ period, the side lobe was again on the left-hand side of the main lobe due to the periodic potential Airy beam leading to two reversions of the intensity distribution. The above analysis implies that the deflection direction and size, and the maximal intensity of the spatial solitons can be controlled by changing the initial position x of Airy beams.
3.2. Propagation Characteristics of Two Airy Beams with Opposite Spatial Positions in an Inhomogeneous Medium with Periodic Potential
Figure 6 shows the interaction diagram of positive/negative Airy beams with different values of initial phase φ when truncation coefficient a0 = 0.3, initial amplitude A1 = A2 = 1, modulation intensity P = 10, modulation frequency ω = 0.1, and initial interval B = 1. When φ = 0, the Airy beams propagated in the same phase, resulting in a mutually attractive force. Because B = 1, the positions of the main lobes of the two Airy beams basically coincided, and the attraction of the interaction between two Airy beams was the strongest. Therefore, almost all of the energy of the two Airy beams converged at the central position, where the breather was formed (Figure 6d). When φ = π, the Airy beams propagated in the reverse phase, and the interacting force was repulsive. In the propagation, when the repulsive force was balanced with the binding force of the periodic potential well, the energy was evenly distributed on both sides, forming the double soliton phenomenon of periodic breathing (Figure 6a). When the initial phase took on other values, the energy of the Airy beams underwent an S-shaped lateral deviation, resulting in its energy being alternately distributed on both sides of the center of the transverse position within the same period (Figure 6b,c,e,f). When −π < φ < 0, the Airy beams first deflected to the right-hand side of the transverse position and then periodically propagated in an S-shaped trajectory (Figure 6b,c). When 0 < φ < π, the propagation situation was exactly the opposite to that when −π < φ < 0 (Figure 6e,f). The larger the φ was, the larger the central position deflection (Figure 6g) and maximal intensity (Figure 6h) of Airy beams are.
Figure 7 shows the interaction diagram of two Airy beams with opposite spatial positions with truncation coefficient a = 0.3, modulation intensity P = 10, modulation frequency ω = 0.1, initial interval B = 1, initial phase φ = 0, and initial amplitude A1 ≠ A2. When A1 ≠ A2, the interaction of the Airy beams is affected, and the stronger beam amplitude dominates the interaction, as can be seen in Figure 7a,b, resulting in changes in the propagation characteristics of the interaction. When A1 > A2, the central position of an Airy beam first deflected to the left and then to the right when it encountered the potential well of the lattice. When A1 < A2, the deflection direction was opposite to that when A1 > A2 (Figure 7c). The propagation characteristics of the amplitude of Airy beams were consistent when A1 = 1 and A2 = 3 and when A1 = 1 and A2 = 3.
Figure 8 shows the interaction diagram of two Airy beams with opposite spatial positions with different values of initial interval x0 when truncation coefficient a0 = 0.3, initial amplitude A1 = A2 = 1, modulation intensity P = 10, modulation frequency ω = 0.1, initial phase φ = 0, and two in-phase Airy beams attracted each other (Figure 8a1–e1), and two antiphase Airy beams repelled each other (Figure 8a2–e2). First, the interaction between two Airy beams at the same direction and different intervals was studied. When x0 = 3, due to the mutual attraction, the energy of the main lobe of the Airy beams converged near the central position to form breathers. The attraction between the side lobes was weak, and the energy that it radiated outwards was also bounced back after meeting the potential well to form symmetric tails on both sides (Figure 8c1). As the interval between tnhe main lobes gradually decrease, the energy of some side lobes also converged to the central position, and the number of the breathing solitons gradually decreased (Figure 8a1,b1). When x0 = 0, the space between the main lobes was small, and the energy of the two Airy beams was concentrated near the central position to form breathers (Figure 8a1). With the increase in x0, the space between the main lobes gradually increased, and the number of produced breathing solitons increased due to the interaction between the Airy beams (Figure 8c1,d1). Second, the interaction between two reverse-incident Airy beams at different intervals was studied. When x0 = 3, the energy of the Airy beams transmitted in the opposite direction converged to form two breathing solitons near the central position due to the repulsive force. Meanwhile, the energy of the main lobes of the two beams was symmetrically distributed on both sides (Figure 8c2). Significantly, the reverse-incident Airy beams displayed multiple breathing solitons at all values of initial interval x0.
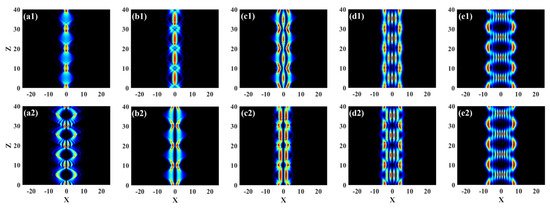
Figure 8.
Iinteraction between two incident (a1–e1) in-phase and (a2–e2) out-of-phase Airy beams at different intervals when a0 = 0.3, P = 3 and ω = 0.03: (a1,a2) x0 = 0; (b1,b2) x0 = 2; (c1,c2) x0 = 3; (d1,d2) x0 = 5; (e1,e2) x0 = 8.
4. Conclusions
In this paper, the propagation characteristics of Airy beams in an inhomogeneous medium with periodic potential, and the interaction between two Airy beams with opposite spatial positions were studied. By reasonably selecting the initial parameters of the inhomogeneous medium and the Airy beams, the latter could exhibit the transmission characteristics of varying periods, intensities, and deflection directions and sizes, whereas the two Airy beams with opposite spatial positions exhibited multiple breathing solitons with periodic changes. First, when a single Airy beam propagated in an inhomogeneous medium, the beam exhibited localized properties in the spatial distribution direction, and periodic breathing properties in the propagation direction. When the initial parameters of an inhomogeneous medium were altered, the breathing period of the Airy breathing solitons decreased as modulation intensity P and frequency ω increased. The deflection direction and size, and maximal intensity of the Airy breathing solitons changed with the initial chirp C and position x0 of Airy beam when its initial parameters were altered. Then, the propagation characteristics of two Airy beams with different phase φ, amplitude A, and position x0 in inhomogeneous media were investigated. Multiple bundles of breathing solitons with different bound states could be formed, which enriched the morphology of Airy breathing solitons to perfect the soliton theory. In a word, these research results serve as a guide for the investigation of laser propagation characteristics in complex physical systems.
Author Contributions
Data curation, C.G.; methodology, B.W. and Y.D.; software, J.W., Y.F. and D.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Hunan Province, grant numbers 2022JJ50276 and 2021JJ30075, the Scientific Research Fund of Hunan Provincial Education Department, grant numbers 21A0499, 20B107, and 20A095, and the Yiyang Science and Technology Plan Project, grant number 2021133.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berry, M.V.; Balazs, N.L. Nonspreading wave packets. Am. J. Phys. 1979, 47, 264–267. [Google Scholar] [CrossRef]
- Broky, J.; Siviloglou, G.A.; Dogariu, A.; Christodoulides, D.N. Self-healing properties of optical airy beams. Opt. Express 2008, 16, 12880–12891. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Zhang, P.; Lou, C.; Huang, S.; Xu, J.; Chen, Z. Optimal control of the ballistic motion of airy beams. Opt. Lett. 2010, 35, 2260–2262. [Google Scholar] [CrossRef]
- Gu, Y.; Gbur, G. Scintillation of airy beam arrays in atmospheric turbulence. Opt. Lett. 2010, 35, 3456–3458. [Google Scholar] [CrossRef]
- Chu, X. Evolution of an airy beam in turbulence. Opt. Lett. 2011, 36, 2701–2703. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Peng, Y.; Li, D.; Zhang, L.; Zhuang, J.; Zhao, F.; Chen, X.; Yang, X.; Deng, D. Propagation properties of spatiotemporal chirped Airy Gaussian vortex wave packets in a quadratic index medium. Opt. Express 2017, 25, 13527–13538. [Google Scholar] [CrossRef]
- Chen, C.; Peng, X.; Chen, B.; Peng, Y.; Zhou, M.; Yang, X.; Deng, D. Propagation of an Airy–Gaussian vortex beam in linear and nonlinear media. J. Opt. 2016, 18, 055505. [Google Scholar] [CrossRef]
- Deng, F.; Deng, D.M. Nonparaxial propagation of an Airy-Gaussian beam in uniaxial crystal orthogonal to the optical axis. Opt. Commun. 2016, 380, 280–286. [Google Scholar] [CrossRef]
- Zhu, W.; Guan, J.; Deng, F.; Deng, D.; Huang, J. The propagation properties of the first-order and the second-order Airy vortex beams through strongly nonlocal nonlinear medium. Opt. Commun. 2016, 380, 434–441. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, K.; Liang, J.; Lai, Z.; Yang, X.; Deng, D. Nonparaxial propagation of the chirped Airy vortex beams in uniaxial crystal orthogonal to the optical axis. Opt. Express 2018, 26, 1290–1304. [Google Scholar] [CrossRef]
- Peng, Y.; Peng, X.; Chen, B.; Zhou, M.; Chen, C.; Deng, D. Interaction of Airy–Gaussian beams in Kerr media. Opt. Commun. 2016, 359, 116–122. [Google Scholar] [CrossRef]
- Li, J.X.; Fan, X.L.; Zang, W.P.; Tian, J.G. Vacuum electron acceleration driven by two crossed airy beams. Opt. Lett. 2011, 36, 648–650. [Google Scholar] [CrossRef] [PubMed]
- Chong, A.; Renninger, W.H.; Christodoulides, D.N.; Wise, F.W. Airy-bessel wave packets as versatile linear light bullets. Nat. Photonics 2010, 4, 103–106. [Google Scholar] [CrossRef]
- Panagiotopoulos, P.; Papazoglou, D.G.; Couairon, A.; Tzortzakis, S. Sharply autofocused ring-airy beams transforming into non-linear intense light bullets. Nat. Commun. 2013, 4, 2622. [Google Scholar] [CrossRef]
- Zhang, P.; Prakash, J.; Zhang, Z.; Mills, M.S.; Efremidis, N.K.; Christodoulides, D.N.; Chen, Z. Trapping and guiding microparticles with morphing autofocusing airy beams. Opt. Lett. 2011, 36, 2883–2885. [Google Scholar] [CrossRef]
- Baumgartl, J.; Mazilu, M.; Dholakia, K. Optically mediated partical clearing using airy wavepackets. Nat. Photonics 2008, 2, 675–678. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, B.F.; Chen, H.; Ding, J.; Wang, H.T. Optical trapping with focused airy beams. Appl. Opt. 2011, 50, 43–49. [Google Scholar] [CrossRef]
- Rose, P.; Diebel, F.; Boguslawski, M.; Denz, C. Airy beam induced optical routing. Appl. Phys. Lett. 2013, 102, 101101. [Google Scholar] [CrossRef]
- Liu, C.F.; Zhu, A.J. Matter-wave exact periodic solutions in optical lattices with periodic potential. AIP Conf. Proc. 2013, 1558, 1947–1950. [Google Scholar]
- Trombettoni, A.; Smerzi, A. Discrete solitons and breathers with dilute Bose-Einstein condensates. Phys. Rev. Lett. 2001, 86, 2353–2356. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.P.; Akhmediev, N. Rogue wave observation in a water wave tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities breathers and rogue waves in optics. Nat. Photonics 2014, 8, 755–764. [Google Scholar] [CrossRef]
- Qin, C.; Yuan, L.; Wang, B.; Fan, S.; Lu, P. Effective electric-field for a photon in a synthetic frequency lattice created in a waveguide modulator. Phys. Rev. A 2018, 97, 063838. [Google Scholar] [CrossRef]
- Li, W.; Qin, C.; Han, T.; Chen, H.; Wang, B.; Lu, P. Bloch oscillations in photonic spectral lattices through phase-mismatched four-wave mixing. Opt. Lett. 2019, 44, 5430–5433. [Google Scholar] [CrossRef]
- Chen, H.; Yang, N.; Qin, C.; Li, W.; Wang, B.; Han, T.; Zhang, C.; Liu, W.; Wang, K.; Long, H.; et al. Real-time observation of frequency Bloch oscillations with fiber loop modulation. Light Sci. Appl. 2021, 10, 48. [Google Scholar] [CrossRef]
- Block, A.; Etrich, C.; Limboeck, T.; Bleckmann, F.; Soergel, E.; Rockstuhl, C.; Linden, S. Bloch oscillations in plasmonic waveguide arrays. Nat. Commun. 2014, 5, 3843. [Google Scholar] [CrossRef]
- Kratzer, P.; Neugebauer, J. The basics of electronic structure theory for periodic systems. Front. Chem. 2019, 7, 106. [Google Scholar] [CrossRef]
- Dong, S.H.; Dong, S.; Dong, Q.; Sun, G.H.; Femmam, S. Exact Solutions of the Razavy Cosine Type Potential. Adv. High Energy Phys. 2018, 2018, 5824271. [Google Scholar] [CrossRef]
- Huang, X.W.; Deng, Z.X.; Fu, X.Q. Dynamics of finite energy Airy beams modeled by the fractional Schrödinger equation with a linear potential. J. Opt. Soc. Am. B 2017, 35, 976–982. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.; Liu, Z.; Zhang, J.; Cai, W.; Gao, Y.; Fan, D. Controlling cosine-Gaussian beams in linear media with quadratic external potential. Opt. Express 2021, 29, 5128–5140. [Google Scholar] [CrossRef]
- Wen, B.; Deng, Y.; Wei, J.; Chen, D.; Leng, X. Evolution of Cos–Gaussian Beams in the Periodic Potential Optical Lattice. Crystals 2022, 12, 1097. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).