Numerical Method for the Design of Compact Adiabatic Devices with Multiple Parameter Variations
Abstract
1. Introduction
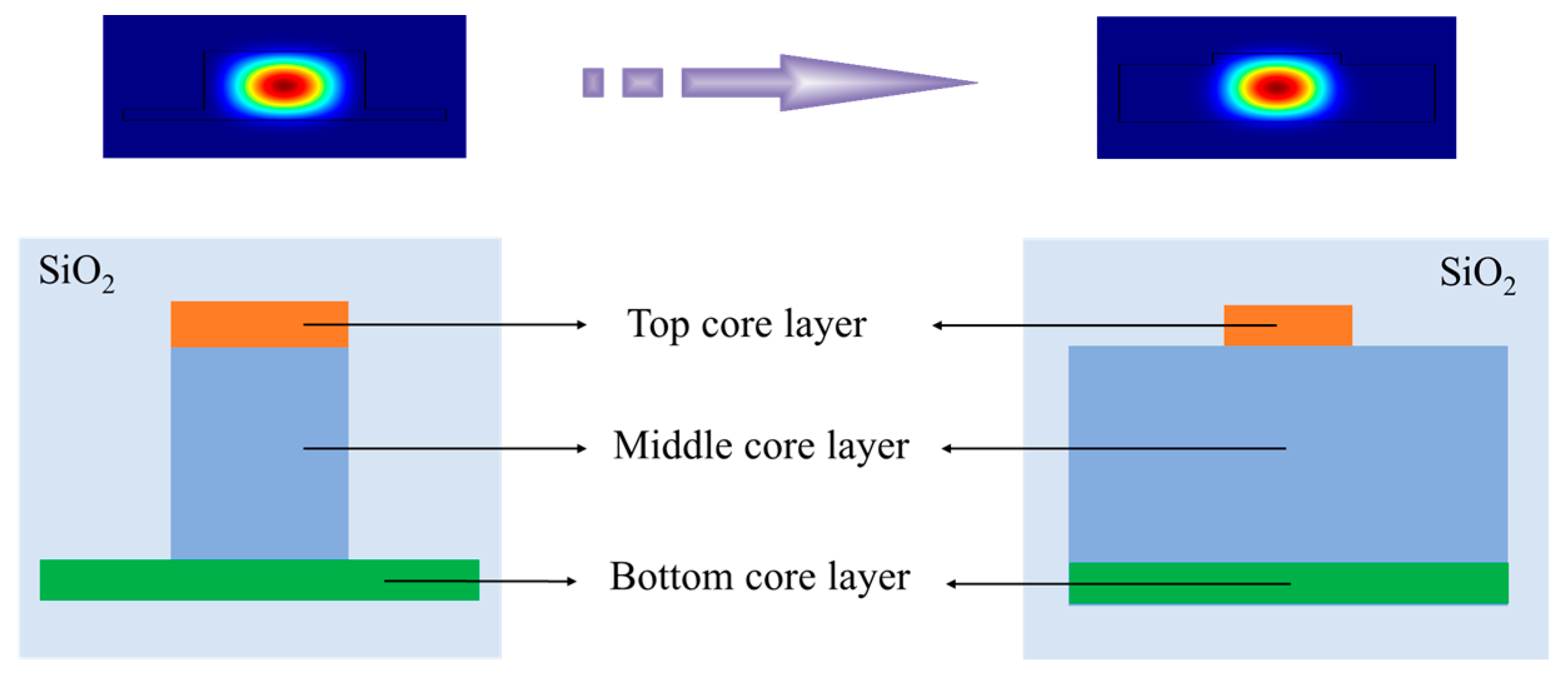
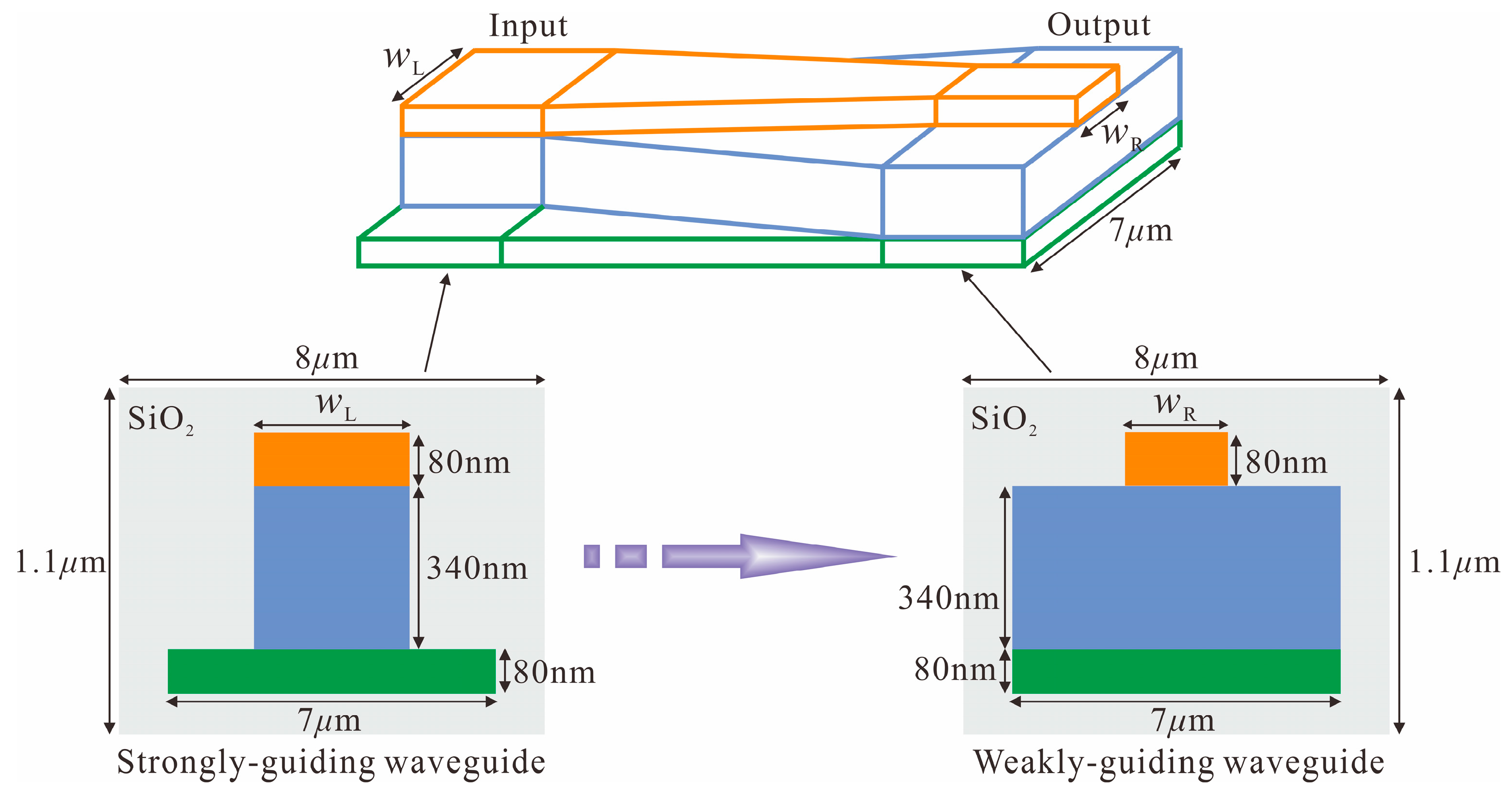
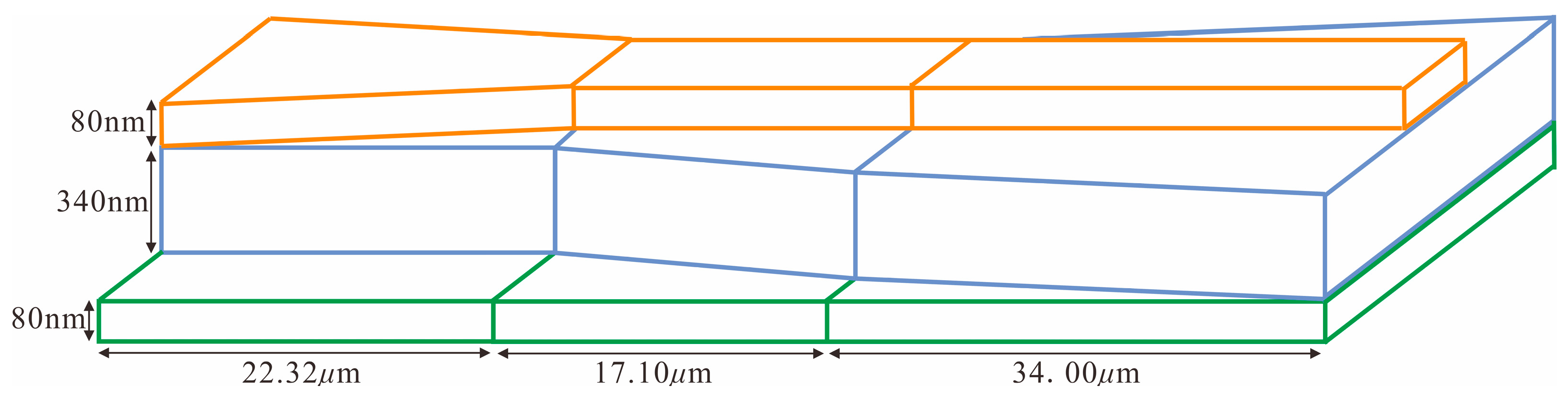
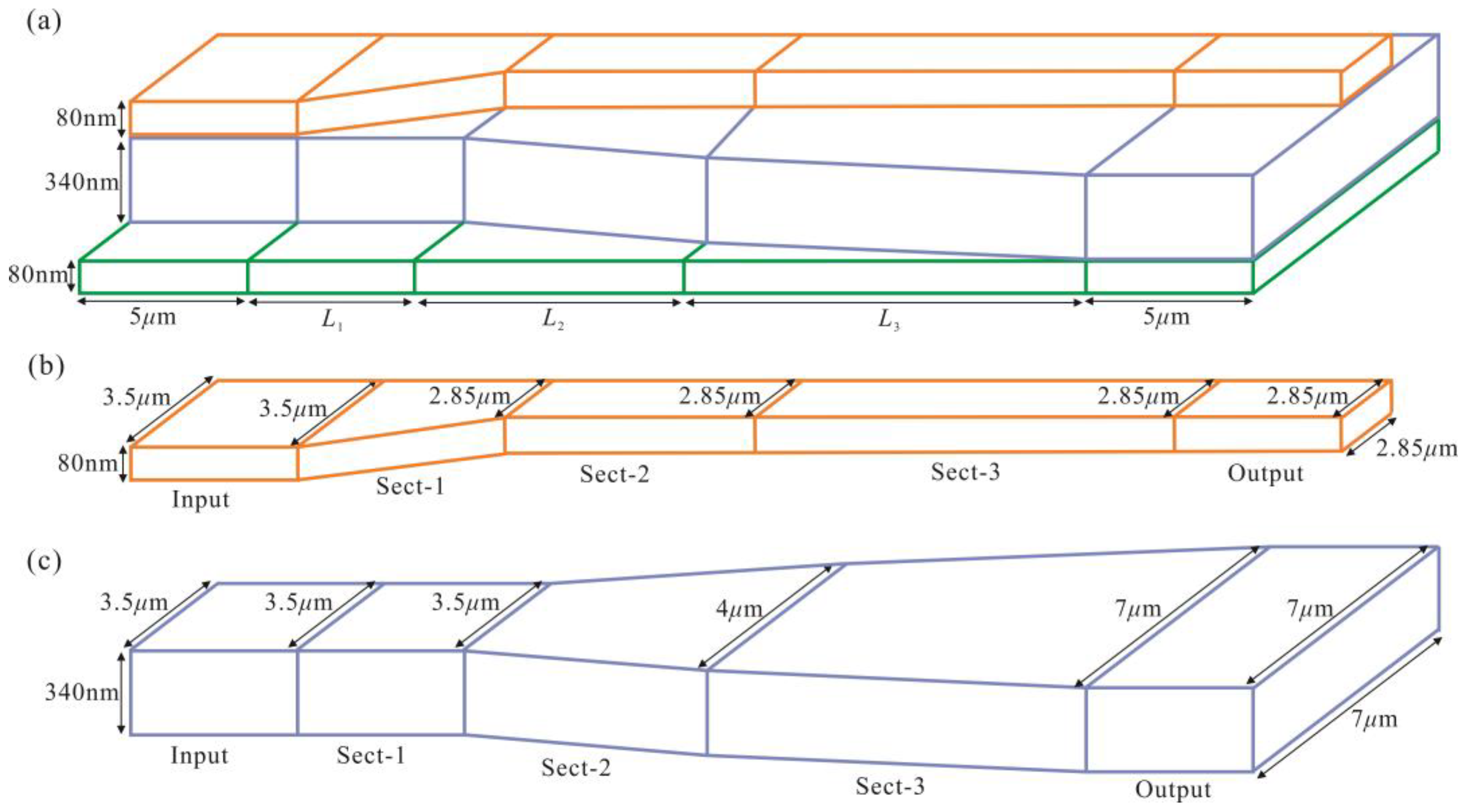
2. Structure and Analysis
3. Description of the NAMSP Method for the Adiabatic Device
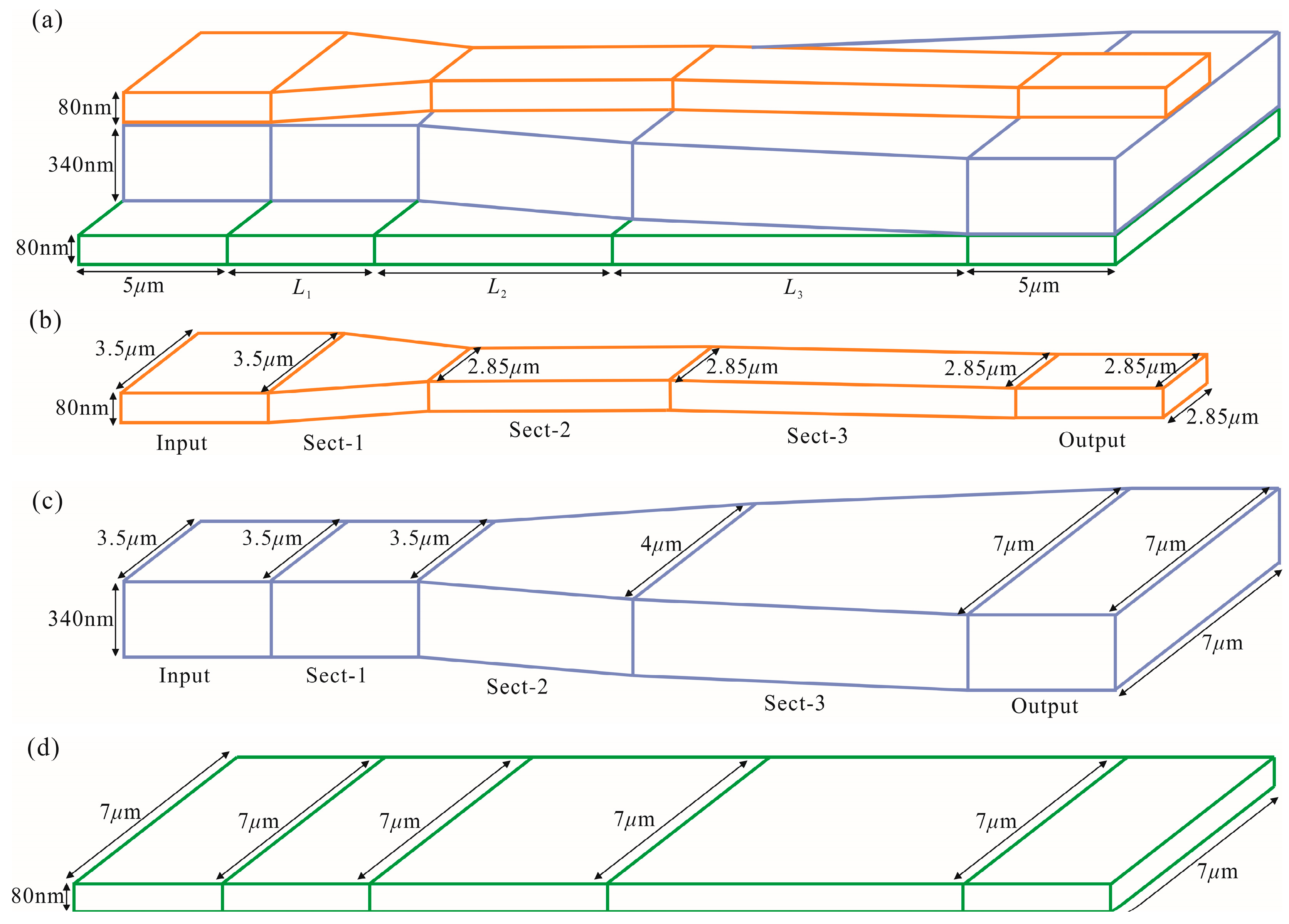
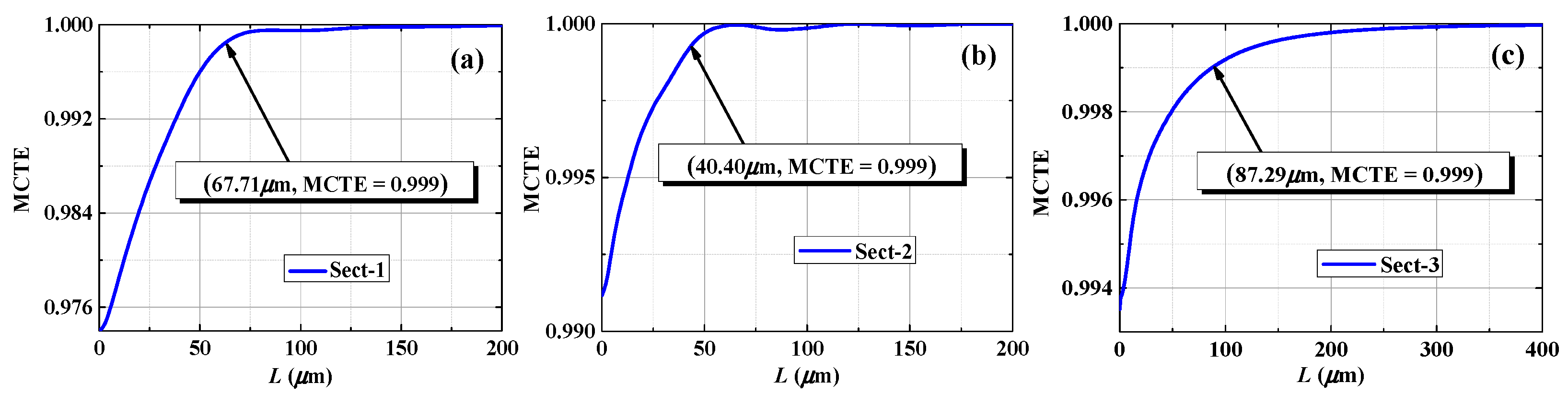
3.1. The NAMSP Method
3.2. Operating Bandwidth of Adiabatic Devices Designed by NAMSP
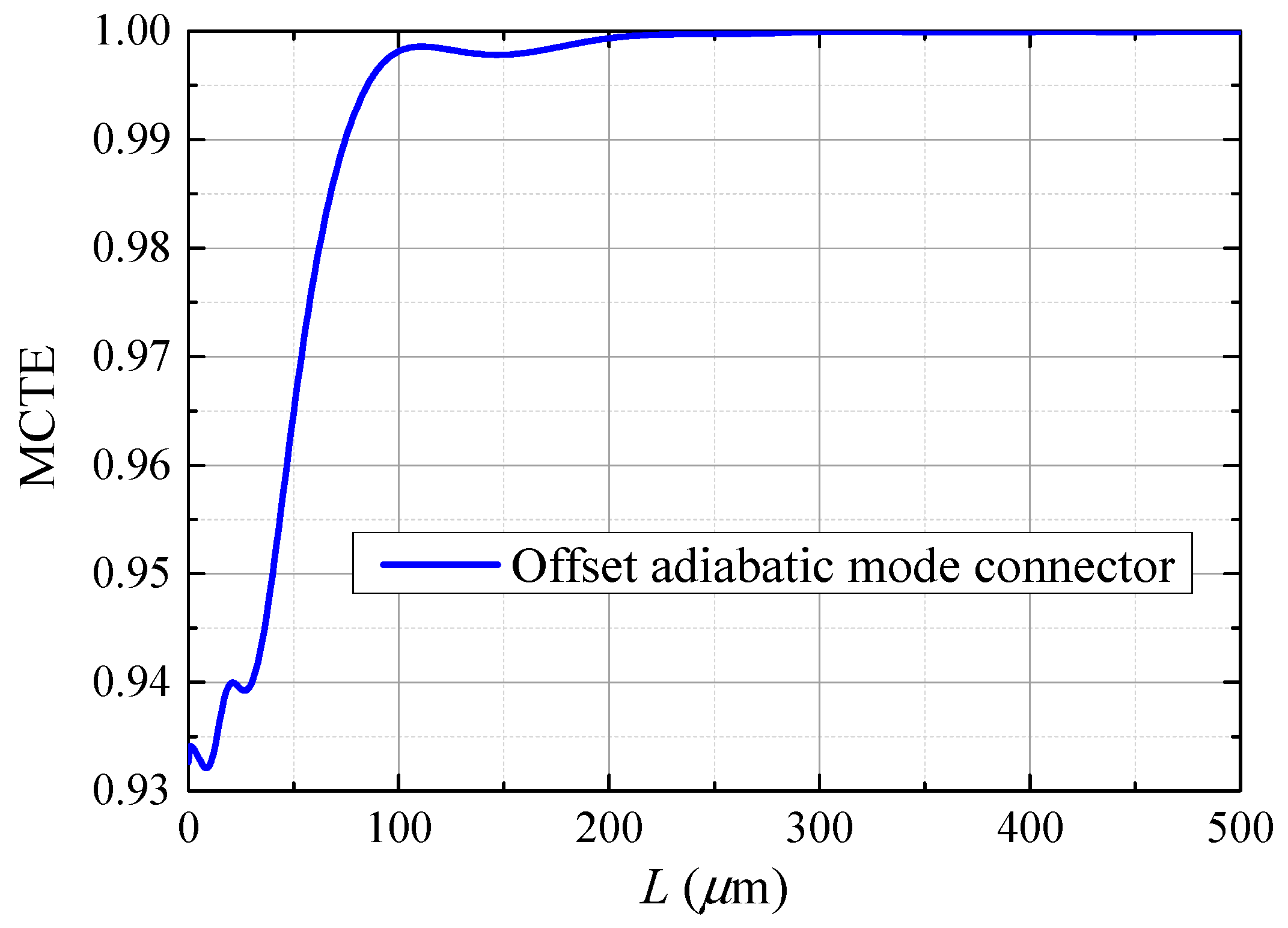
3.3. Offset Adiabatic Device Designed by NAMSP
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tsuchizawa, T.; Yamada, K.; Fukuda, H.; Watanabe, T.; Takahashi, J.; Takahashi, M.; Shoji, T.; Tamechika, E.; Itabashi, S.; Morita, H. Microphotonics devices based on silicon microfabrication technology. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 232–240. [Google Scholar]
- Manolatou, C.; Johnson, S.G.; Fan, S.; Villeneuve, P.R.; Haus, H.A.; Joannopoulos, J.D. High density integrated optics. J. Light. Technol. 1999, 17, 1682–1692. [Google Scholar] [CrossRef]
- Li, C.; Zhou, L.; Poon, A.W. Silicon microring carrier-injection-based modulators/switches with tunable extinction ratios and OR-logic switching by using waveguide cross-coupling. Opt. Express 2007, 15, 5069–5076. [Google Scholar] [CrossRef] [PubMed]
- Rong, H.; Jones, R.; Liu, A.; Cohen, O.; Hak, D.; Fang, A.; Paniccia, M. A continuous-wave Raman silicon laser. Nature 2005, 433, 725–728. [Google Scholar] [CrossRef] [PubMed]
- Barrios, C.A.; Almeida, V.R.; Panepucci, R.; Lipson, M. Electrooptic modulation of silicon-on-insulator submicrometer-size waveguide devices. J. Light. Technol. 2003, 21, 2332–2339. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, H.-W.; Jain, S.; Peters, J.D.; Westergren, U.; Bowers, J.E. 50 Gb/s hybrid silicon traveling wave electro absorption modulator. Opt. Express 2011, 19, 5811–5816. [Google Scholar] [CrossRef] [PubMed]
- Dai, D.; Bowers, J.E. Novel concept for ultracompact polarization splitter-rotator based on silicon nanowires. Opt. Express 2011, 19, 10940–10949. [Google Scholar] [CrossRef] [PubMed]
- Dai, D.; Tang, Y.B.; Bowers, J.E. Mode conversion in tapered submicron silicon ridge optical waveguides. Opt. Express 2012, 20, 13425–13439. [Google Scholar] [CrossRef] [PubMed]
- Schmid, J.H.; Lamontagne, B.; Cheben, P.; Delage, A.; Janz, S.; Densmore, A.; Lapointe, J.; Post, E.; Waldron, P.; Xu, D.X. Mode converters for coupling to high aspect ratio silicon-on-insulator channel waveguides. IEEE Photonics Technol. Lett. 2007, 19, 855–857. [Google Scholar] [CrossRef]
- Aalto, T.; Solehmainen, K.; Harjanne, M.; Kapulainen, M.; Heimala, P. Low-loss converters between optical silicon waveguides of different sizes and types. IEEE Photonics Technol. Lett. 2006, 18, 709–711. [Google Scholar] [CrossRef]
- Dai, D.; He, J.; He, S. Elimination of multimode effects in a silicon-on-insulator etched diffraction grating demultiplexer with lateral tapered air slots. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 439–443. [Google Scholar]
- Liang, T.L.; Tu, Y.; Chen, X.; Huang, Y.; Bai, Q.; Zhao, Y.; Zhang, J.; Yuan, Y.; Li, J.; Yi, F.; et al. A Fully Numerical Method for Designing Efficient Adiabatic Mode Evolution Structures (Adiabatic Taper, Coupler, Splitter, Mode Converter) Applicable to Complex Geometries. J. Lightw. Technol. 2021, 39, 5531–5547. [Google Scholar] [CrossRef]
- Liang, T.L.; Cheng, X.; Yu, M.; Zhang, L.; Shi, J.; Shao, W. Numerical method for designing ultrashort and efficient adiabatic mode converters. J. Opt. Soc. Am. B 2022, 39, 2637–2642. [Google Scholar] [CrossRef]
- Lumerical Solutions. FDTD Solutions. 2018. Available online: https://www.lumerical.com (accessed on 13 September 2020).
- Lumerical Solutions. Mode Solutions. 2018. Available online: https://www.lumerical.com (accessed on 22 September 2020).
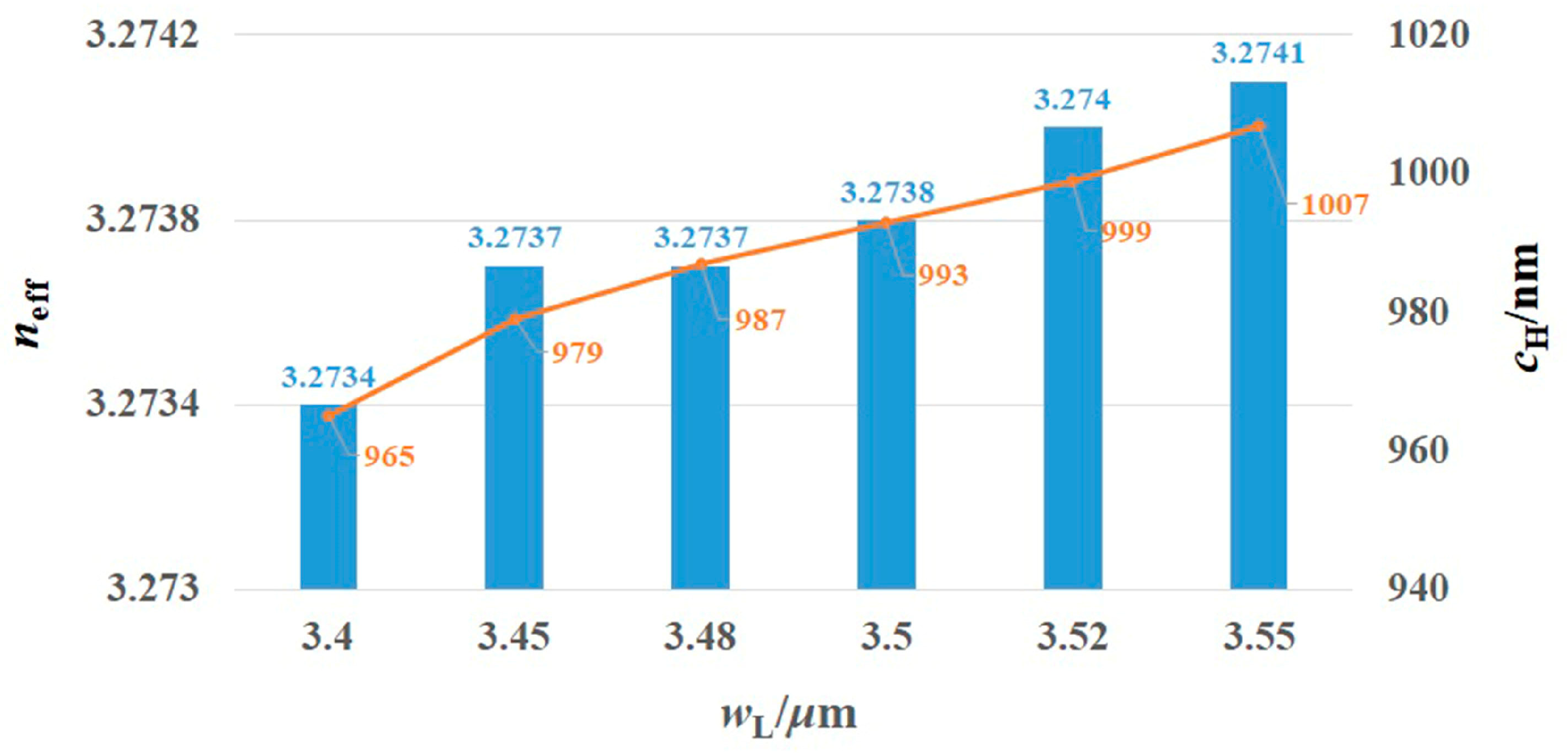



| Type | wL/μm | neff | cH/nm | cV/nm |
|---|---|---|---|---|
| Weakly guiding waveguide | 2.85 | 3.2738 | 996 | 192 |
| Strongly guiding waveguide | 3.40 | 3.2734 | 965 | 192 |
| 3.45 | 3.2737 | 979 | 192 | |
| 3.48 | 3.2737 | 987 | 192 | |
| 3.50 | 3.2738 | 993 | 192 | |
| 3.52 | 3.2740 | 999 | 192 | |
| 3.55 | 3.2741 | 1007 | 192 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, T.-L.; Cheng, X.; Yu, M.; Zhang, L.; Shi, J.; Wu, G.; Rong, W.; Shao, W. Numerical Method for the Design of Compact Adiabatic Devices with Multiple Parameter Variations. Photonics 2023, 10, 517. https://doi.org/10.3390/photonics10050517
Liang T-L, Cheng X, Yu M, Zhang L, Shi J, Wu G, Rong W, Shao W. Numerical Method for the Design of Compact Adiabatic Devices with Multiple Parameter Variations. Photonics. 2023; 10(5):517. https://doi.org/10.3390/photonics10050517
Chicago/Turabian StyleLiang, Tu-Lu, Xi Cheng, Mei Yu, Lingyan Zhang, Jin Shi, Gangxiong Wu, Weiwei Rong, and Wei Shao. 2023. "Numerical Method for the Design of Compact Adiabatic Devices with Multiple Parameter Variations" Photonics 10, no. 5: 517. https://doi.org/10.3390/photonics10050517
APA StyleLiang, T.-L., Cheng, X., Yu, M., Zhang, L., Shi, J., Wu, G., Rong, W., & Shao, W. (2023). Numerical Method for the Design of Compact Adiabatic Devices with Multiple Parameter Variations. Photonics, 10(5), 517. https://doi.org/10.3390/photonics10050517





