An Experimental Study of Multiphoton Ionization in Fused Silica at IR and Visible Wavelengths
Abstract
1. Introduction
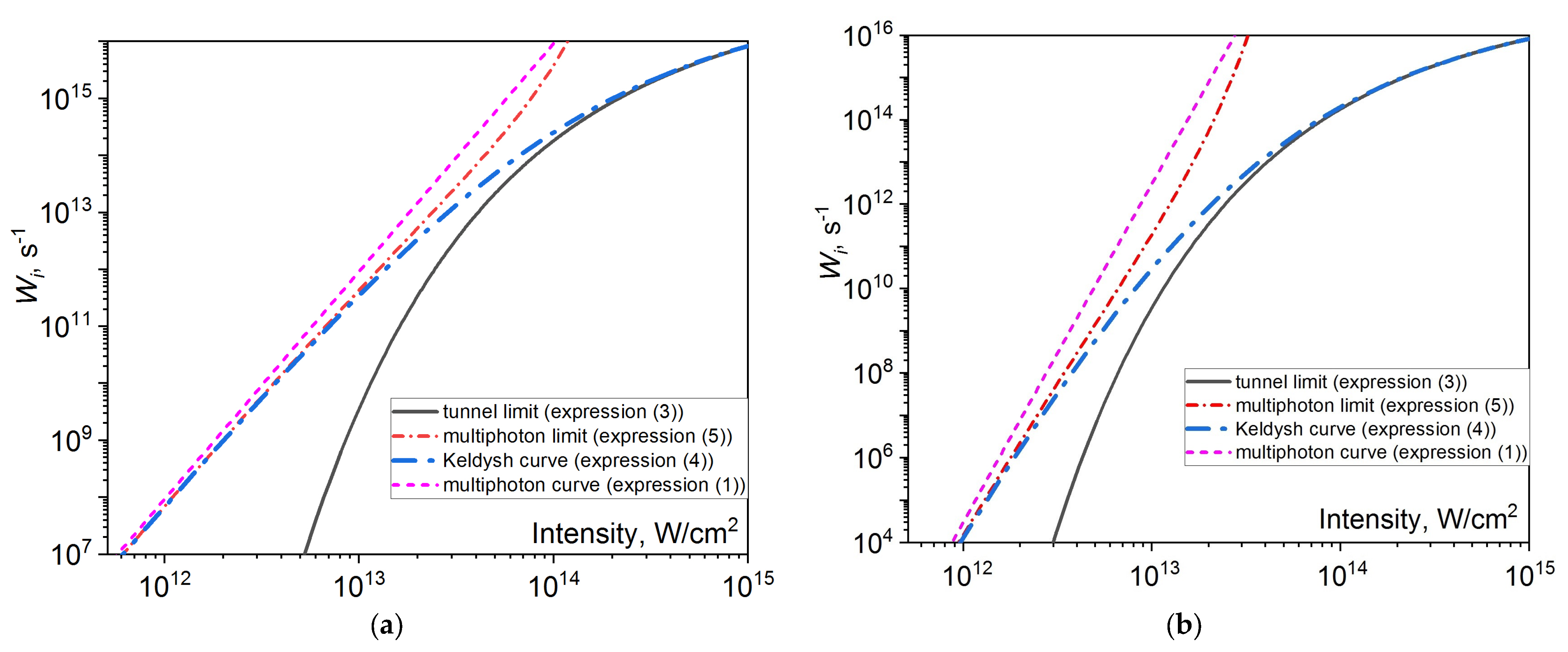
2. Keldysh Theory of Photoionization Applied to Dielectric Materials
3. Experiment
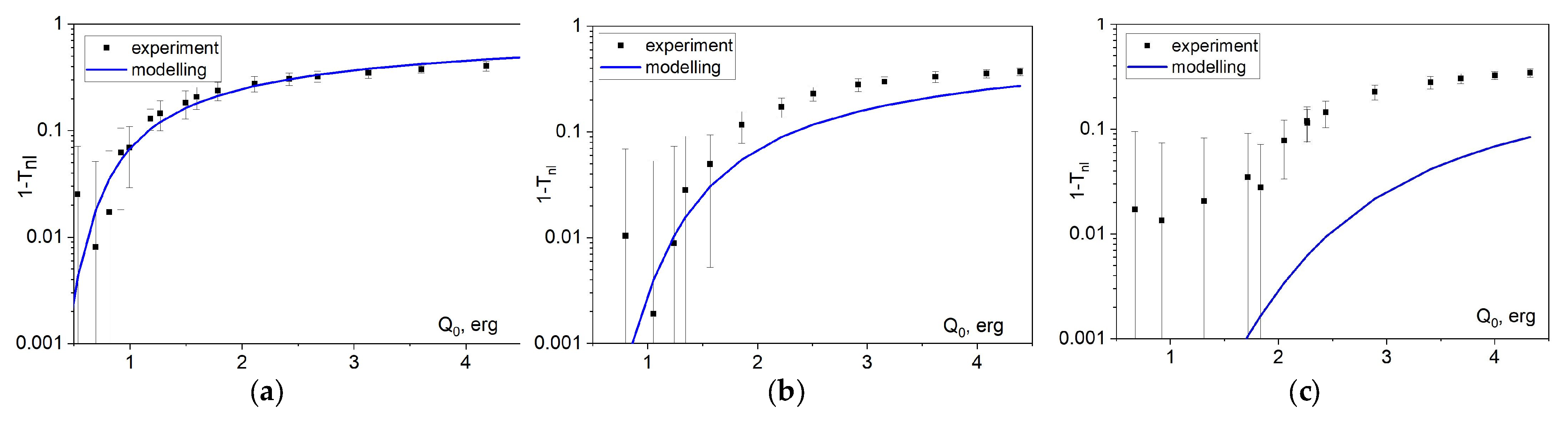
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Jiang, Q.; Long, M.; Han, R.; Cao, K.; Zhang, S.; Feng, D.; Jia, T.; Sun, Z.; Qiu, J.; et al. Femtosecond laser-induced periodic structures: Mechanisms, techniques, and applications. Opto-Electron. Sci. 2022, 1, 220005. [Google Scholar] [CrossRef]
- Shimotsuma, Y.; Sakakura, M.; Kazansky, P.G.; Beresna, M.; Qiu, J.; Miura, K.; Hirao, K. Ultrafast Manipulation of Self-Assembled Form Birefringence in Glass. Adv. Mater. 2010, 22, 4039–4043. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Liu, X.; Qiu, J. Single femtosecond laser beam induced nanogratings in transparent media—Mechanisms and applications. J. Mater. 2019, 5, 1–14. [Google Scholar] [CrossRef]
- Murata, A. Control of Periodic Nanostructure Embedded in SiO2 Glass under Femtosecond Double-Pulse Irradiation. J. Laser Micro/Nanoeng. 2016, 11, 95–99. [Google Scholar] [CrossRef]
- Andreeva, Y.; Suvorov, A.; Grigoryev, E.; Khmelenin, D.; Zhukov, M.; Makin, V.; Sinev, D. Laser Fabrication of Highly Ordered Nanocomposite Subwavelength Gratings. Nanomaterials 2022, 12, 2811. [Google Scholar] [CrossRef] [PubMed]
- Temnov, V.; Sokolowski-Tinten, K.; Zhou, P.; El-Khamhawy, A.; Von Der Linde, D. Multiphoton Ionization in Dielectrics: Comparison of Circular and Linear Polarization. Phys. Rev. Lett. 2006, 97, 237403. [Google Scholar] [CrossRef]
- Joglekar, A.P.; Liu, H.-H.; Meyhöfer, E.; Mourou, G.; Hunt, A.J. Optics at critical intensity: Applications to nanomorphing. Proc. Natl. Acad. Sci. USA 2004, 101, 5856–5861. [Google Scholar] [CrossRef]
- Stuart, B.C.; Feit, M.D.; Herman, S.; Rubenchik, A.M.; Shore, B.W.; Perry, M.D. Nanosecond-to-femtosecond laser-induced breakdown in dielectrics. Phys. Rev. B 1996, 53, 1749. [Google Scholar] [CrossRef]
- Bulgakova, N.; Stoian, R.; Rosenfeld, A.; Hertel, I.V.; Campbell, E. Electronic transport and consequences for material removal in ultrafast pulsed laser ablation of materials. Phys. Rev. B 2004, 69, 054102. [Google Scholar] [CrossRef]
- Voronov, G.S.; Delone, N.B. Many-photon Ionization of the Xenon Atom by Ruby Laser Radiation. JETP 1966, 23, 54. [Google Scholar]
- Delone, N.B. Multiphoton ionization of atoms. Sov. Phys. Usp. 1975, 18, 169–189. [Google Scholar] [CrossRef]
- Keldysh, L.V. Ionization in the Field of a Strong Electromagnetic Wave. JETP 1964, 20, 1307–1314. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics—Non-Relativistic Theory, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 1981. [Google Scholar]
- Perelomov, A.M.; Popov, V.S.; Terent’ev, M.B. Ionization of Atoms in an Alternating Electric Field. JETP 1966, 23, 924–934. [Google Scholar]
- Popov, V.S. Tunnel and multiphoton ionization of atoms and ions in a strong laser field (Keldysh theory). Physics-Uspekhi 2004, 47, 855–885. [Google Scholar] [CrossRef]
- Chimier, B.; Utéza, O.; Sanner, N.; Sentis, M.; Itina, T.; Lassonde, P.; Légaré, F.; Vidal, F.; Kieffer, J.C. Damage and ablation thresholds of fused-silica in femtosecond regime. Phys. Rev. B 2011, 84, 094104. [Google Scholar] [CrossRef]
- Schaffer, C.B.; Brodeur, A.; Mazur, E. Laser-induced breakdown and damage in bulk transparent materials induced by tightly focused femtosecond laser pulses. Meas. Sci. Technol. 2001, 12, 1784–1794. [Google Scholar] [CrossRef]
- Gruzdev, V. Fundamental mechanisms of laser damage of dielectric crystals by ultrashort pulse: Ionization dynamics for the Keldysh model. Opt. Eng. 2014, 53, 122515. [Google Scholar] [CrossRef]
- Mao, S.; Quéré, F.; Guizard, S.; Mao, X.; Russo, R.; Petite, G.; Martin, P. Dynamics of femtosecond laser interactions with dielectrics. Appl. Phys. A 2004, 79, 1695–1709. [Google Scholar] [CrossRef]
- Eaton, S.M.; Cerullo, G.; Osellame, R. Fundamentals of Femtosecond Laser Modification of Bulk Dielectrics. In Femtosecond Laser Micromachining; Osellame, R., Cerullo, G., Ramponi, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 3–18. [Google Scholar] [CrossRef]
- Grojo, D.; Gertsvolf, M.; Lei, S.; Barillot, T.; Rayner, D.M.; Corkum, P.B. Exciton-seeded multiphoton ionization in bulk SiO2. Phys. Rev. B 2010, 81, 212301. [Google Scholar] [CrossRef]
- Krasin, G.K.; Gulina, Y.S.; Kuzmin, E.V.; Martovitskii, V.P.; Kudryashov, S.I. Polarization-Sensitive Nonlinear Optical Interaction of Ultrashort Laser Pulses with HPHT Diamond. Photonics 2023, 10, 106. [Google Scholar] [CrossRef]
- Dostovalov, A.V.; Wolf, A.A.; Mezentsev, V.K.; Okhrimchuk, A.G.; Babin, S.A. Quantitative characterization of energy absorption in femtosecond laser micro-modification of fused silica. Opt. Express 2015, 23, 32541–32547. [Google Scholar] [CrossRef] [PubMed]
- Slattery, S.A.; Nikogosyan, D.N. Two-photon absorption at 211 nm in fused silica, crystalline quartz and some alkali halides. Opt. Commun. 2003, 228, 127–131. [Google Scholar] [CrossRef]
- Gulina, Y.S. Measurement of two-photon absorption coefficient of 1030 nm ultrashort laser pulses on natural diamond color centers. Opt. Spectrosc. 2022, 130, 422–425. [Google Scholar] [CrossRef]
- Raizer, Y.P. Laser-Induced Discharge Phenomena; Consultants Bureau: New York, NY, USA, 1977. [Google Scholar]
- Grudtsyn, Y.V.; Koribut, A.V.; Rogashevskii, A.A.; Gerasimova, Y.A.; Trofimov, V.A.; Yalovoi, V.I.; Semjonov, S.L. Multiphoton and plasma absorption measurements in CaF2 and UV fused silica at 473 nm. Laser Phys. Lett. 2021, 18, 035401. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogatskaya, A.; Gulina, Y.; Smirnov, N.; Gritsenko, I.; Kudryashov, S.; Popov, A. An Experimental Study of Multiphoton Ionization in Fused Silica at IR and Visible Wavelengths. Photonics 2023, 10, 515. https://doi.org/10.3390/photonics10050515
Bogatskaya A, Gulina Y, Smirnov N, Gritsenko I, Kudryashov S, Popov A. An Experimental Study of Multiphoton Ionization in Fused Silica at IR and Visible Wavelengths. Photonics. 2023; 10(5):515. https://doi.org/10.3390/photonics10050515
Chicago/Turabian StyleBogatskaya, Anna, Yulia Gulina, Nikita Smirnov, Ilia Gritsenko, Sergey Kudryashov, and Alexander Popov. 2023. "An Experimental Study of Multiphoton Ionization in Fused Silica at IR and Visible Wavelengths" Photonics 10, no. 5: 515. https://doi.org/10.3390/photonics10050515
APA StyleBogatskaya, A., Gulina, Y., Smirnov, N., Gritsenko, I., Kudryashov, S., & Popov, A. (2023). An Experimental Study of Multiphoton Ionization in Fused Silica at IR and Visible Wavelengths. Photonics, 10(5), 515. https://doi.org/10.3390/photonics10050515




