The Optical Inverse Problem in Quantitative Photoacoustic Tomography: A Review
Abstract
1. Introduction
2. Theoretical Fundamentals
2.1. Generation of Initial Pressure Rise
2.2. Photoacoustic Tomography-Based Concentration Measurement
2.3. Spectral Coloring
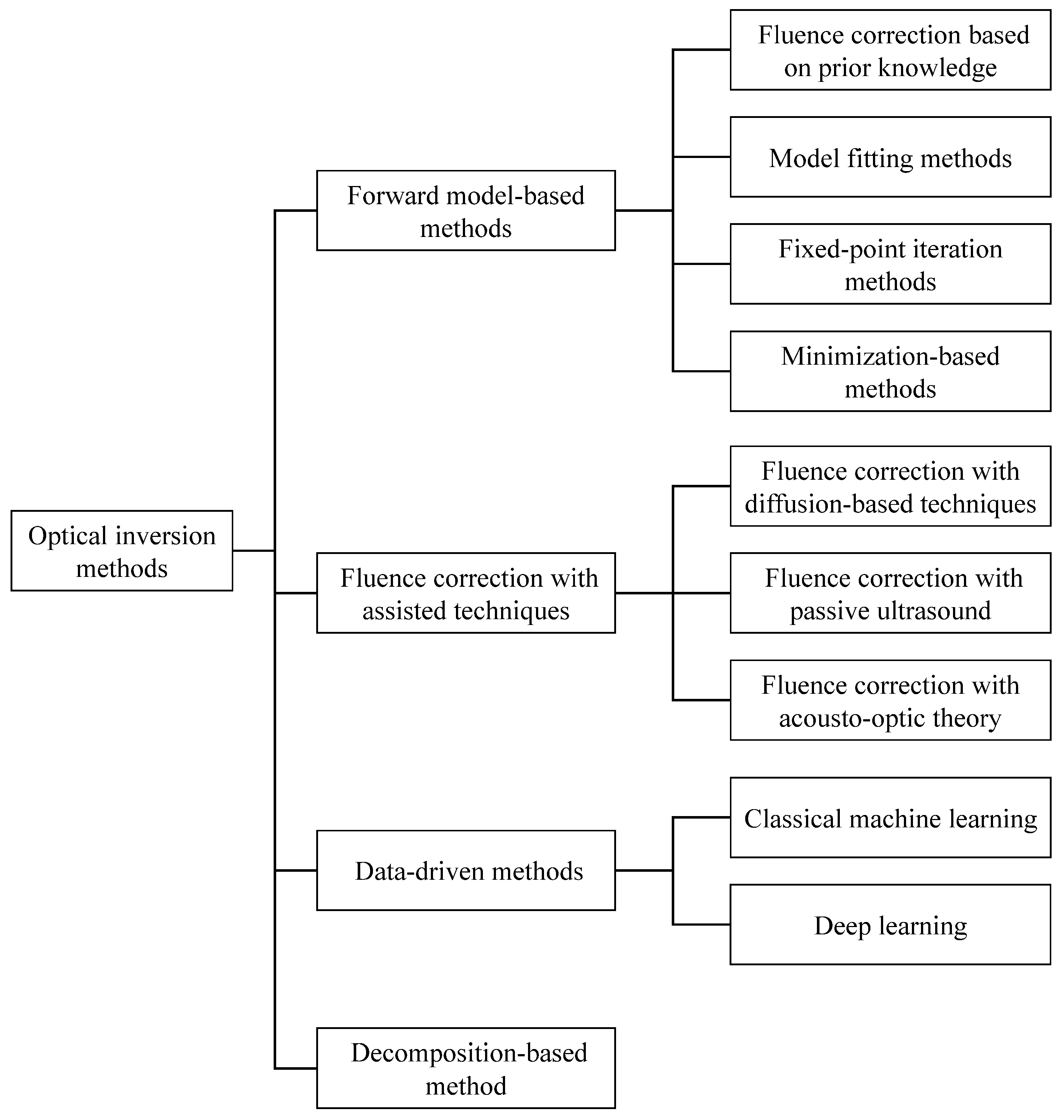
3. Methods for the Optical Inverse Problem
3.1. Forward Model-Based Methods
3.1.1. Fluence Correction Based on Prior Knowledge
3.1.2. Model Fitting Methods
3.1.3. Fixed-Point Iteration Methods
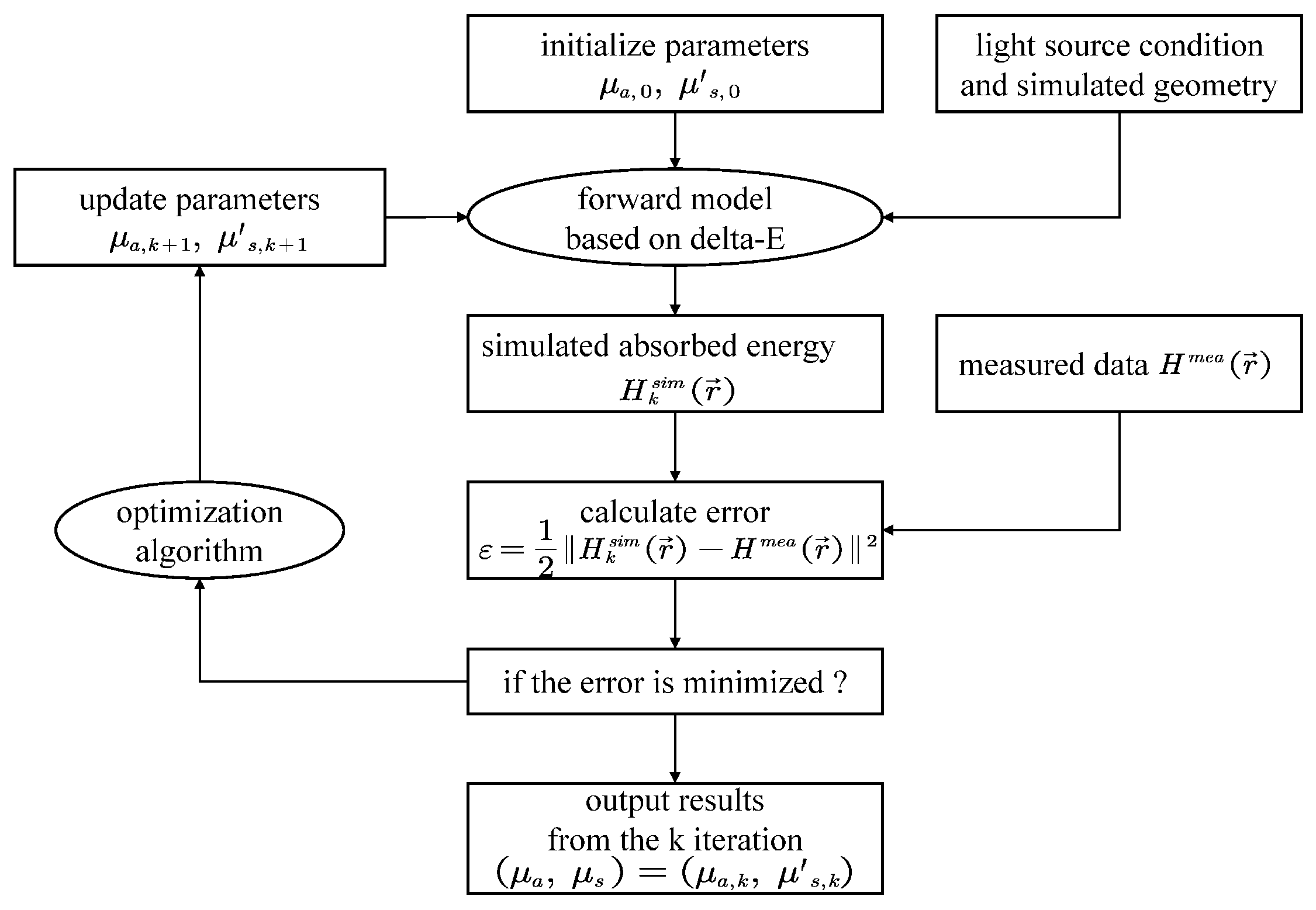
3.1.4. Minimization-Based Methods
3.2. Fluence Correction with Assisted Techniques
3.2.1. Fluence Correction with Diffusion-Based Techniques
3.2.2. Fluence Correction with Acousto-Optic Theory
3.2.3. Fluence Correction with Passive Ultrasound
3.3. Data-Driven Methods
3.3.1. Methods Based on U-Net
3.3.2. Dataset Acquisition
3.4. Decomposition-Based Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Liu, C.; Wang, L. Functional Photoacoustic Microscopy of Hemodynamics: A Review. Biomed. Eng. Lett. 2022, 12, 97–124. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Zhao, L.; Yang, F.; Wang, M.; Su, N.; Zhao, C.; Gui, Y.; Wei, Y.; Zhang, R.; Li, J.; et al. Quantitative Analysis of Breast Tumours Aided by Three-Dimensional Photoacoustic/Ultrasound Functional Imaging. Sci. Rep. 2020, 10, 8047. [Google Scholar] [CrossRef] [PubMed]
- Ganzleben, I.; Klett, D.; Hartz, W.; Götzfried, L.; Vitali, F.; Neurath, M.F.; Waldner, M.J. Multispectral Optoacoustic Tomography for the Non-Invasive Identification of Patients with Severe Anemia In Vivo. Photoacoustics 2022, 28, 100414. [Google Scholar] [CrossRef] [PubMed]
- Arabul, M.; Rutten, M.; Bruneval, P.; van Sambeek, M.; van de Vosse, F.; Lopata, R. Unmixing Multi-Spectral Photoacoustic Sources in Human Carotid Plaques Using Non-Negative Independent Component Analysis. Photoacoustics 2019, 15, 100140. [Google Scholar] [CrossRef] [PubMed]
- Regensburger, A.P.; Fonteyne, L.M.; Jüngert, J.; Wagner, A.L.; Gerhalter, T.; Nagel, A.M.; Heiss, R.; Flenkenthaler, F.; Qurashi, M.; Neurath, M.F.; et al. Detection of Collagens by Multispectral Optoacoustic Tomography as an Imaging Biomarker for Duchenne Muscular Dystrophy. Nat. Med. 2019, 25, 1905–1915. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Blutke, A.; Feuchtinger, A.; Klemm, U.; Zachariah Tom, R.; Hofmann, S.M.; Stiel, A.C.; Ntziachristos, V. Functional Multispectral Optoacoustic Tomography Imaging of Hepatic Steatosis Development in Mice. EMBO Mol. Med. 2021, 13, e13490. [Google Scholar] [CrossRef] [PubMed]
- Attia, A.B.E.; Moothanchery, M.; Li, X.; Yew, Y.W.; Thng, S.T.G.; Dinish, U.; Olivo, M. Microvascular Imaging and Monitoring of Hemodynamic Changes in the Skin during Arterial-Venous Occlusion Using Multispectral Raster-Scanning Optoacoustic Mesoscopy. Photoacoustics 2021, 22, 100268. [Google Scholar] [CrossRef]
- Ashkenazi, S. Photoacoustic Lifetime Imaging of Dissolved Oxygen Using Methylene Blue. J. Biomed. Opt. 2010, 15, 040501. [Google Scholar] [CrossRef]
- Dantuma, M.; Kruitwagen, S.; Ortega-Julia, J.; Pompe van Meerdervoort, R.P.; Manohar, S. Tunable Blood Oxygenation in the Vascular Anatomy of a Semi-Anthropomorphic Photoacoustic Breast Phantom. J. Biomed. Opt. 2021, 26, 036003. [Google Scholar] [CrossRef]
- Li, M.-L.; Oh, J.-T.; Xie, X.; Ku, G.; Wang, W.; Li, C.; Lungu, G.; Stoica, G.; Wang, L.V. Simultaneous Molecular and Hypoxia Imaging of Brain Tumors In Vivo Using Spectroscopic Photoacoustic Tomography. Proc. IEEE 2008, 96, 481–489. [Google Scholar] [CrossRef]
- Wang, L.V.; Wu, H.i. Biomedical Optics: Principles and Imaging; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Wang, L.V. Multiscale Photoacoustic Microscopy and Computed Tomography. Nat. Photonics 2009, 3, 503–509. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V.; Hu, S. Photoacoustic Tomography: In Vivo Imaging from Organelles to Organs. Science 2012, 335, 1458–1462. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Wang, L.V. Photoacoustic Imaging in Biomedicine. Rev. Sci. Instruments 2006, 77, 041101. [Google Scholar] [CrossRef]
- Le, T.D.; Kwon, S.Y.; Lee, C. Segmentation and Quantitative Analysis of Photoacoustic Imaging: A Review. Photonics 2022, 9, 176. [Google Scholar] [CrossRef]
- Li, M.; Tang, Y.; Yao, J. Photoacoustic Tomography of Blood Oxygenation: A Mini Review. Photoacoustics 2018, 10, 65–73. [Google Scholar] [CrossRef]
- Taruttis, A.; Ntziachristos, V. Advances in Real-Time Multispectral Optoacoustic Imaging and Its Applications. Nat. Photonics 2015, 9, 219–227. [Google Scholar] [CrossRef]
- An, L.; Cox, B.T. Estimating Relative Chromophore Concentrations from Multiwavelength Photoacoustic Images Using Independent Component Analysis. J. Biomed. Opt. 2018, 23, 076007. [Google Scholar] [CrossRef]
- Gröhl, J.; Kirchner, T.; Adler, T.J.; Hacker, L.; Holzwarth, N.; Hernández-Aguilera, A.; Herrera, M.A.; Santos, E.; Bohndiek, S.E.; Maier-Hein, L. Learned Spectral Decoloring Enables Photoacoustic Oximetry. Sci. Rep. 2021, 11, 6565. [Google Scholar] [CrossRef]
- Hochuli, R.; An, L.; Beard, P.C.; Cox, B.T. Estimating Blood Oxygenation from Photoacoustic Images: Can a Simple Linear Spectroscopic Inversion Ever Work? J. Biomed. Opt. 2019, 24, 121914. [Google Scholar] [CrossRef]
- Laufer, J.; Delpy, D.; Elwell, C.; Beard, P. Quantitative Spatially Resolved Measurement of Tissue Chromophore Concentrations Using Photoacoustic Spectroscopy: Application to the Measurement of Blood Oxygenation and Haemoglobin Concentration. Phys. Med. Biol. 2007, 52, 141–168. [Google Scholar] [CrossRef]
- Cox, B.T.; Laufer, J.G.; Beard, P.C.; Arridge, S.R. Quantitative Spectroscopic Photoacoustic Imaging: A Review. J. Biomed. Opt. 2012, 17, 061202. [Google Scholar] [CrossRef] [PubMed]
- Laufer, J.; Elwell, C.; Delpy, D.; Beard, P. In Vitro Measurements of Absolute Blood Oxygen Saturation Using Pulsed Near-Infrared Photoacoustic Spectroscopy: Accuracy and Resolution. Phys. Med. Biol. 2005, 50, 4409–4428. [Google Scholar] [CrossRef] [PubMed]
- Ding, T.; Ren, K.; Vallélian, S. A One-Step Reconstruction Algorithm for Quantitative Photoacoustic Imaging. Inverse Probl. 2015, 31, 095005. [Google Scholar] [CrossRef]
- Javaherian, A.; Holman, S. Direct Quantitative Photoacoustic Tomography for Realistic Acoustic Media. Inverse Probl. 2019, 35, 084004. [Google Scholar] [CrossRef]
- Tarvainen, T.; Pulkkinen, A.; Cox, B.T.; Kaipio, J.P.; Arridge, S.R. Bayesian Image Reconstruction in Quantitative Photoacoustic Tomography. IEEE Trans. Med. Imaging 2013, 32, 2287–2298. [Google Scholar] [CrossRef] [PubMed]
- Rosenthal, A.; Ntziachristos, V.; Razansky, D. Acoustic Inversion in Optoacoustic Tomography: A Review. Curr. Med. Imaging Rev. 2014, 9, 318–336. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Yao, J.; Wang, L.V. Tutorial on Photoacoustic Tomography. J. Biomed. Opt. 2016, 21, 061007. [Google Scholar] [CrossRef]
- Wang, L.V. Tutorial on Photoacoustic Microscopy and Computed Tomography. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 171–179. [Google Scholar] [CrossRef]
- Bendinger, A.L.; Glowa, C.; Peter, J.; Karger, C.P. Photoacoustic Imaging to Assess Pixel-Based sO2 Distributions in Experimental Prostate Tumors. J. Biomed. Opt. 2018, 23, 036009. [Google Scholar] [CrossRef]
- Comenge, J.; Fragueiro, O.; Sharkey, J.; Taylor, A.; Held, M.; Burton, N.C.; Park, B.K.; Wilm, B.; Murray, P.; Brust, M.; et al. Preventing Plasmon Coupling between Gold Nanorods Improves the Sensitivity of Photoacoustic Detection of Labeled Stem Cells In Vivo. ACS Nano 2016, 10, 7106–7116. [Google Scholar] [CrossRef]
- Joseph, J.; Tomaszewski, M.R.; Quiros-Gonzalez, I.; Weber, J.; Brunker, J.; Bohndiek, S.E. Evaluation of Precision in Optoacoustic Tomography for Preclinical Imaging in Living Subjects. J. Nucl. Med. 2017, 58, 807–814. [Google Scholar] [CrossRef] [PubMed]
- Lavaud, J.; Henry, M.; Coll, J.L.; Josserand, V. Exploration of Melanoma Metastases in Mice Brains Using Endogenous Contrast Photoacoustic Imaging. Int. J. Pharm. 2017, 532, 704–709. [Google Scholar] [CrossRef] [PubMed]
- Tzoumas, S.; Ntziachristos, V. Spectral Unmixing Techniques for Optoacoustic Imaging of Tissue Pathophysiology. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2017, 375, 20170262. [Google Scholar] [CrossRef] [PubMed]
- Maslov, K.; Zhang, H.F.; Wang, L.V. Effects of Wavelength-Dependent Fluence Attenuation on the Noninvasive Photoacoustic Imaging of Hemoglobin Oxygen Saturation in Subcutaneous Vasculature In Vivo. Inverse Probl. 2007, 23, S113–S122. [Google Scholar] [CrossRef]
- Cox, B.T.; Laufer, J.G.; Beard, P.C. The Challenges for Quantitative Photoacoustic Imaging. In Proceedings of the SPIE BiOS: Biomedical Optics, San Jose, CA, USA, 24–29 January 2009; Oraevsky, A.A., Wang, L.V., Eds.; SPIE: Bellingham, WA, USA, 2009; p. 717713. [Google Scholar] [CrossRef]
- Tarvainen, T.; Vauhkonen, M.; Kolehmainen, V.; Kaipio, J.P. Finite Element Model for the Coupled Radiative Transfer Equation and Diffusion Approximation. Int. J. Numer. Methods Eng. 2006, 65, 383–405. [Google Scholar] [CrossRef]
- Chai, C.; Chen, Y.; Li, P.; Luo, Q. Improved Steady-State Diffusion Approximation with an Anisotropic Point Source and the δ–Eddington Phase Function. Appl. Opt. 2007, 46, 4843. [Google Scholar] [CrossRef]
- Hayakawa, C.K.; Hill, B.Y.; You, J.S.; Bevilacqua, F.; Spanier, J.; Venugopalan, V. Use of the δ-P_1 Approximation for Recovery of Optical Absorption, Scattering, and Asymmetry Coefficients in Turbid Media. Appl. Opt. 2004, 43, 4677. [Google Scholar] [CrossRef]
- Fang, Q.; Boas, D.A. Monte Carlo Simulation of Photon Migration in 3D Turbid Media Accelerated by Graphics Processing Units. Opt. Express 2009, 17, 20178. [Google Scholar] [CrossRef]
- Brochu, F.M.; Brunker, J.; Joseph, J.; Tomaszewski, M.R.; Morscher, S.; Bohndiek, S.E. Towards Quantitative Evaluation of Tissue Absorption Coefficients Using Light Fluence Correction in Optoacoustic Tomography. IEEE Trans. Med. Imaging 2017, 36, 322–331. [Google Scholar] [CrossRef]
- Gehrung, M.; Bohndiek, S.E.; Brunker, J. Development of a Blood Oxygenation Phantom for Photoacoustic Tomography Combined with Online pO2 Detection and Flow Spectrometry. J. Biomed. Opt. 2019, 24, 121908. [Google Scholar] [CrossRef]
- Vogt, W.C.; Zhou, X.; Andriani, R.; Wear, K.A.; Pfefer, T.J.; Garra, B.S. Photoacoustic Oximetry Imaging Performance Evaluation Using Dynamic Blood Flow Phantoms with Tunable Oxygen Saturation. Biomed. Opt. Express 2019, 10, 449. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Akhlaghi, N.; Wear, K.A.; Garra, B.S.; Pfefer, T.J.; Vogt, W.C. Evaluation of Fluence Correction Algorithms in Multispectral Photoacoustic Imaging. Photoacoustics 2020, 19, 100181. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Zhang, S.; Wu, J.; Li, X.; Zhuang, Z.; Feng, Q.; Chen, W.; Qi, L. Automatic 3-D Segmentation and Volumetric Light Fluence Correction for Photoacoustic Tomography Based on Optimal 3-D Graph Search. Med. Image Anal. 2022, 75, 102275. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; Li, C. Noninvasively Measuring Oxygen Saturation of Human Finger-Joint Vessels by Multi-Transducer Functional Photoacoustic Tomography. J. Biomed. Opt. 2016, 21, 061009. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Yang, M.; Jiang, Y.; Li, C. Optical Fluence Compensation for Handheld Photoacoustic Probe: An In Vivo Human Study Case. J. Innov. Opt. Health Sci. 2017, 10, 1740002. [Google Scholar] [CrossRef]
- Tang, Y.; Yao, J. 3D Monte Carlo Simulation of Light Distribution in Mouse Brain in Quantitative Photoacoustic Computed Tomography. Quant. Imaging Med. Surg. 2020, 11, 1046–1059. [Google Scholar] [CrossRef]
- Han, T.; Yang, M.; Yang, F.; Zhao, L.; Jiang, Y.; Li, C. A Three-Dimensional Modeling Method for Quantitative Photoacoustic Breast Imaging with Handheld Probe. Photoacoustics 2021, 21, 100222. [Google Scholar] [CrossRef]
- Pattyn, A.; Mumm, Z.; Alijabbari, N.; Duric, N.; Anastasio, M.A.; Mehrmohammadi, M. Model-Based Optical and Acoustical Compensation for Photoacoustic Tomography of Heterogeneous Mediums. Photoacoustics 2021, 23, 100275. [Google Scholar] [CrossRef]
- Mandal, S.; Dean-Ben, X.L.; Razansky, D. Visual Quality Enhancement in Optoacoustic Tomography Using Active Contour Segmentation Priors. IEEE Trans. Med. Imaging 2016, 35, 2209–2217. [Google Scholar] [CrossRef]
- Held, K.G.; Jaeger, M.; Rička, J.; Frenz, M.; Akarçay, H.G. Multiple Irradiation Sensing of the Optical Effective Attenuation Coefficient for Spectral Correction in Handheld OA Imaging. Photoacoustics 2016, 4, 70–80. [Google Scholar] [CrossRef]
- Perekatova, V.V.; Subochev, P.V.; Kirillin, M.Y.; Sergeeva, E.A.; Kurakina, D.A.; Orlova, A.G.; Postnikova, A.S.; Turchin, I.V. Quantitative Techniques for Extraction of Blood Oxygenation from Multispectral Optoacoustic Measurements. Laser Phys. Lett. 2019, 16, 116201. [Google Scholar] [CrossRef]
- Cox, B.T.; Arridge, S.R.; Köstli, K.P.; Beard, P.C. Two-Dimensional Quantitative Photoacoustic Image Reconstruction of Absorption Distributions in Scattering Media by Use of a Simple Iterative Method. Appl. Opt. 2006, 45, 1866. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Jiang, H.; Yuan, Z. Two Schemes for Quantitative Photoacoustic Tomography Based on Monte Carlo Simulation: Quantitative Photoacoustic Tomography Based on Monte Carlo Simulation. Med. Phys. 2016, 43, 3987–3997. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Liu, J.; Liang, Z.; Ge, J.; Feng, Y.; Chen, W.; Qi, L. Pixel-Wise Reconstruction of Tissue Absorption Coefficients in Photoacoustic Tomography Using a Non-Segmentation Iterative Method. Photoacoustics 2022, 28, 100390. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Qi, L.; Li, X.; Liang, Z.; Sun, X.; Liu, J.; Lu, L.; Feng, Y.; Chen, W. MRI Information-Based Correction and Restoration of Photoacoustic Tomography. IEEE Trans. Med. Imaging 2022, 41, 2543–2555. [Google Scholar] [CrossRef]
- Wu, Y.; Kang, J.; Lesniak, W.G.; Pomper, M.G.; Boctor, E.M. Iterative Fluence Compensation and Spectral Unmixing for Spectroscopic Photoacoustic Imaging. In Proceedings of the 2021 IEEE International Ultrasonics Symposium (IUS), Xi’an, China, 11–16 September 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Cox, B.T.; Arridge, S.R.; Beard, P.C. Gradient-Based Quantitative Photoacoustic Image Reconstruction for Molecular Imaging. In Proceedings of the Biomedical Optics (BiOS), San Jose, CA, USA, 20–21 January 2007; Oraevsky, A.A., Wang, L.V., Eds.; SPIE: Bellingham, WA, USA, 2007; p. 64371. [Google Scholar] [CrossRef]
- Gao, H.; Feng, J.; Song, L. Limited-View Multi-Source Quantitative Photoacoustic Tomography. Inverse Probl. 2015, 31, 065004. [Google Scholar] [CrossRef]
- Saratoon, T.; Tarvainen, T.; Cox, B.T.; Arridge, S.R. A Gradient-Based Method for Quantitative Photoacoustic Tomography Using the Radiative Transfer Equation. Inverse Probl. 2013, 29, 075006. [Google Scholar] [CrossRef]
- Saratoon, T.; Tarvainen, T.; Arridge, S.R.; Cox, B.T. 3D Quantitative Photoacoustic Tomography Using the δ-Eddington Approximation. In Proceedings of the SPIE BiOS, San Francisco, CA, USA, 2–3 February 2013; Oraevsky, A.A., Wang, L.V., Eds.; SPIE: Bellingham, WA, USA, 2013; p. 85810. [Google Scholar] [CrossRef]
- Al-Baali, M.; Spedicato, E.; Maggioni, F. Broyden’s quasi-Newton methods for a nonlinear system of equations and unconstrained optimization: A review and open problems. Optim. Methods Softw. 2014, 29, 937–954. [Google Scholar] [CrossRef]
- Pulkkinen, A.; Cox, B.T.; Arridge, S.R.; Kaipio, J.P.; Tarvainen, T. A Bayesian Approach to Spectral Quantitative Photoacoustic Tomography. Inverse Probl. 2014, 30, 065012. [Google Scholar] [CrossRef]
- Tarvainen, T.; Cox, B.T.; Kaipio, J.P.; Arridge, S.R. Reconstructing Absorption and Scattering Distributions in Quantitative Photoacoustic Tomography. Inverse Probl. 2012, 28, 084009. [Google Scholar] [CrossRef]
- Song, N.; Deumié, C.; Da Silva, A. Considering sources and detectors distributions for quantitative photoacoustic tomography. Biomed. Opt. Express 2014, 5, 3960–3974. [Google Scholar] [CrossRef] [PubMed]
- Schweiger, M.; Arridge, S.R.; Nissilä, I. Gauss–Newton Method for Image Reconstruction in Diffuse Optical Tomography. Phys. Med. Biol. 2005, 50, 2365–2386. [Google Scholar] [CrossRef] [PubMed]
- Hochuli, R.; Powell, S.; Arridge, S.; Cox, B. Quantitative Photoacoustic Tomography Using Forward and Adjoint Monte Carlo Models of Radiance. J. Biomed. Opt. 2016, 21, 126004. [Google Scholar] [CrossRef] [PubMed]
- Buchmann, J.; Kaplan, B.A.; Powell, S.; Prohaska, S.; Laufer, J. Three-Dimensional Quantitative Photoacoustic Tomography Using an Adjoint Radiance Monte Carlo Model and Gradient Descent. J. Biomed. Opt. 2019, 24, 066001. [Google Scholar] [CrossRef] [PubMed]
- Capart, A.; Wojak, J.; Allais, R.; Ghiss, M.; Boiron, O.; Da Silva, A. Quantitative Photoacoustic Reconstruction of the Optical Properties of Intervertebral Discs Using a Gradient Descent Scheme. Photonics 2022, 9, 116. [Google Scholar] [CrossRef]
- Macdonald, C.M.; Arridge, S.; Powell, S. Efficient Inversion Strategies for Estimating Optical Properties with Monte Carlo Radiative Transport Models. J. Biomed. Opt. 2020, 25, 085002. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Yingsa, H.; Meichen, S.; Qi, M. Quantitative Photoacoustic Tomography with Light Fluence Compensation Based on Radiance Monte Carlo Model. Phys. Med. Biol. 2023, 68, 065009. [Google Scholar] [CrossRef]
- Leino, A.A.; Lunttila, T.; Mozumder, M.; Pulkkinen, A.; Tarvainen, T. Perturbation Monte Carlo Method for Quantitative Photoacoustic Tomography. IEEE Trans. Med. Imaging 2020, 39, 2985–2995. [Google Scholar] [CrossRef]
- Hayakawa, C.K.; Spanier, J.; Bevilacqua, F.; Dunn, A.K.; You, J.S.; Tromberg, B.J.; Venugopalan, V. Perturbation Monte Carlo Methods to Solve Inverse Photon Migration Problems in Heterogeneous Tissues. Opt. Lett. 2001, 26, 1335. [Google Scholar] [CrossRef]
- De Cezaro, A.; Travessini De Cezaro, F.; Sejje Suarez, J. Regularization Approaches for Quantitative Photoacoustic Tomography Using the Radiative Transfer Equation. J. Math. Anal. Appl. 2015, 429, 415–438. [Google Scholar] [CrossRef]
- Arridge, S.; Beard, P.; Betcke, M.; Cox, B.; Huynh, N.; Lucka, F.; Ogunlade, O.; Zhang, E. Accelerated High-Resolution Photoacoustic Tomography via Compressed Sensing. Phys. Med. Biol. 2016, 61, 8908–8940. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Han, B.; Han, W.; Bi, B.; Li, L. Mixed Total Variation and L 1 Regularization Method for Optical Tomography Based on Radiative Transfer Equation. Comput. Math. Methods Med. 2017, 2017, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Biton, S.; Arbel, N.; Drozdov, G.; Gilboa, G.; Rosenthal, A. Optoacoustic Model-Based Inversion Using Anisotropic Adaptive Total-Variation Regularization. Photoacoustics 2019, 16, 100142. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, C.; Wang, Y. A Photoacoustic Imaging Reconstruction Method Based on Directional Total Variation with Adaptive Directivity. Biomed. Eng. Online 2017, 16, 64. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Lai, R.; Kuo, C.C.J. Latent Fingerprint Detection and Segmentation with a Directional Total Variation Model. In Proceedings of the 2012 19th IEEE International Conference on Image Processing, Orlando, FL, USA, 30 September–3 October 2012; pp. 1145–1148. [Google Scholar] [CrossRef]
- Harrison, T.; Shao, P.; Zemp, R.J. A Least-Squares Fixed-Point Iterative Algorithm for Multiple Illumination Photoacoustic Tomography. Biomed. Opt. Express 2013, 4, 2224. [Google Scholar] [CrossRef] [PubMed]
- Jeng, G.S.; Li, M.L.; Kim, M.; Yoon, S.J.; Pitre, J.J.; Li, D.S.; Pelivanov, I.; O’Donnell, M. Real-Time Interleaved Spectroscopic Photoacoustic and Ultrasound (PAUS) Scanning with Simultaneous Fluence Compensation and Motion Correction. Nat. Commun. 2021, 12, 716. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Jeng, G.S.; O’Donnell, M.; Pelivanov, I. Correction of Wavelength-Dependent Laser Fluence in Swept-Beam Spectroscopic Photoacoustic Imaging with a Hand-Held Probe. Photoacoustics 2020, 19, 100192. [Google Scholar] [CrossRef]
- Shao, P.; Harrison, T.J.; Zemp, R.J. Consecutively Reconstructing Absorption and Scattering Distributions in Turbid Media with Multiple-Illumination Photoacoustic Tomography. J. Biomed. Opt. 2014, 19, 126009. [Google Scholar] [CrossRef]
- Shao, P.; Cox, B.; Zemp, R.J. Estimating Optical Absorption, Scattering, and Grueneisen Distributions with Multiple-Illumination Photoacoustic Tomography. Appl. Opt. 2011, 50, 3145. [Google Scholar] [CrossRef]
- Zemp, R.J. Quantitative Photoacoustic Tomography with Multiple Optical Sources. Appl. Opt. 2010, 49, 3566. [Google Scholar] [CrossRef]
- Buchmann, J.; Kaplan, B.; Powell, S.; Prohaska, S.; Laufer, J. Quantitative PA Tomography of High Resolution 3-D Images: Experimental Validation in a Tissue Phantom. Photoacoustics 2020, 17, 100157. [Google Scholar] [CrossRef] [PubMed]
- Laufer, J.; Cox, B.; Zhang, E.; Beard, P. Quantitative Determination of Chromophore Concentrations from 2D Photoacoustic Images Using a Nonlinear Model-Based Inversion Scheme. Appl. Opt. 2010, 49, 1219. [Google Scholar] [CrossRef] [PubMed]
- Naser, M.A.; Sampaio, D.R.T.; Munoz, N.M.; Wood, C.A.; Mitcham, T.M.; Stefan, W.; Sokolov, K.V.; Pavan, T.Z.; Avritscher, R.; Bouchard, R.R. Improved Photoacoustic-Based Oxygen Saturation Estimation with SNR-Regularized Local Fluence Correction. IEEE Trans. Med. Imaging 2019, 38, 561–571. [Google Scholar] [CrossRef] [PubMed]
- Nykänen, O.; Pulkkinen, A.; Tarvainen, T. Quantitative Photoacoustic Tomography Augmented with Surface Light Measurements. Biomed. Opt. Express 2017, 8, 4380. [Google Scholar] [CrossRef]
- Poudel, J.; Lou, Y.; Anastasio, M.A. A Survey of Computational Frameworks for Solving the Acoustic Inverse Problem in Three-Dimensional Photoacoustic Computed Tomography. Phys. Med. Biol. 2019, 64, 14TR01. [Google Scholar] [CrossRef]
- Wang, K.; Su, R.; Oraevsky, A.A.; Anastasio, M.A. Investigation of Iterative Image Reconstruction in Three-Dimensional Optoacoustic Tomography. Phys. Med. Biol. 2012, 57, 5399–5423. [Google Scholar] [CrossRef]
- Yuan, Z.; Jiang, H. A Calibration-Free, One-Step Method for Quantitative Photoacoustic Tomography: Quantitative Photoacoustic Tomography. Med. Phys. 2012, 39, 6895–6899. [Google Scholar] [CrossRef]
- Zuo, H.; Cui, M.; Wang, X.; Ma, C. Spectral Crosstalk in Photoacoustic Computed Tomography. Photoacoustics 2022, 26, 100356. [Google Scholar] [CrossRef]
- Hänninen, N.; Pulkkinen, A.; Leino, A.; Tarvainen, T. Application of Diffusion Approximation in Quantitative Photoacoustic Tomography in the Presence of Low-Scattering Regions. J. Quant. Spectrosc. Radiat. Transf. 2020, 250, 107065. [Google Scholar] [CrossRef]
- Tick, J.; Pulkkinen, A.; Lucka, F.; Ellwood, R.; Cox, B.T.; Kaipio, J.P.; Arridge, S.R.; Tarvainen, T. Three Dimensional Photoacoustic Tomography in Bayesian Framework. J. Acoust. Soc. Am. 2018, 144, 2061–2071. [Google Scholar] [CrossRef]
- Tick, J.; Pulkkinen, A.; Tarvainen, T. Image Reconstruction with Uncertainty Quantification in Photoacoustic Tomography. J. Acoust. Soc. Am. 2016, 139, 1951–1961. [Google Scholar] [CrossRef] [PubMed]
- Pandey, P.K.; Gottam, O.; Naik, N.; Pradhan, A. Comparative Study of One-Step and Two-Step Quantitative Fluorescence Photoacoustic Tomography. Appl. Opt. 2019, 58, 3116. [Google Scholar] [CrossRef] [PubMed]
- Pulkkinen, A.; Cox, B.T.; Arridge, S.R.; Goh, H.; Kaipio, J.P.; Tarvainen, T. Direct Estimation of Optical Parameters From Photoacoustic Time Series in Quantitative Photoacoustic Tomography. IEEE Trans. Med. Imaging 2016, 35, 2497–2508. [Google Scholar] [CrossRef] [PubMed]
- Venugopal, M.; van Es, P.; Manohar, S.; Roy, D.; Vasu, R.M. Quantitative Photoacoustic Tomography by Stochastic Search: Direct Recovery of the Optical Absorption Field. Opt. Lett. 2016, 41, 4202. [Google Scholar] [CrossRef] [PubMed]
- Yin, L.; Wang, Q.; Zhang, Q.; Jiang, H. Tomographic Imaging of Absolute Optical Absorption Coefficient in Turbid Media Using Combined Photoacoustic and Diffusing Light Measurements. Opt. Lett. 2007, 32, 2556. [Google Scholar] [CrossRef] [PubMed]
- Bauer, A.Q.; Nothdurft, R.E.; Erpelding, T.N.; Wang, L.V.; Culver, J.P. Quantitative photoacoustic imaging: Correcting for heterogeneous light fluence distributions using diffuse optical tomography. J. Biomed. Opt. 2011, 16, 096016. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, L.; Ahnen, L.; Akarçay, H.G.; Majos, S.S.; Jaeger, M.; Held, K.G.; Wolf, M.; Frenz, M. Spectral Correction for Handheld Optoacoustic Imaging by Means of Near-Infrared Optical Tomography in Reflection Mode. J. Biophotonics 2019, 12, e201800112. [Google Scholar] [CrossRef]
- Mahmoodkalayeh, S.; Zarei, M.; Ansari, M.A.; Kratkiewicz, K.; Ranjbaran, M.; Manwar, R.; Avanaki, K. Improving Vascular Imaging with Co-Planar Mutually Guided Photoacoustic and Diffuse Optical Tomography: A Simulation Study. Biomed. Opt. Express 2020, 11, 4333. [Google Scholar] [CrossRef]
- Daoudi, K.; Hussain, A.; Hondebrink, E.; Steenbergen, W. Correcting photoacoustic signals for fluence variations using acousto-optic modulation. Opt. Express 2012, 20, 14117–14129. [Google Scholar] [CrossRef]
- Hussain, A.; Petersen, W.; Staley, J.; Hondebrink, E.; Steenbergen, W. Quantitative Blood Oxygen Saturation Imaging Using Combined Photoacoustics and Acousto-Optics. Opt. Lett. 2016, 41, 1720. [Google Scholar] [CrossRef]
- Hussain, A.; Daoudi, K.; Hondebrink, E.; Steenbergen, W. Mapping Optical Fluence Variations in Highly Scattering Media by Measuring Ultrasonically Modulated Backscattered Light. J. Biomed. Opt. 2014, 19, 066002. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V. Mechanisms of Ultrasonic Modulation of Multiply Scattered Coherent Light: An Analytic Model. Phys. Rev. Lett. 2001, 87, 043903. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ku, G.; Wang, L.V. Ultrasound-Modulated Optical Tomography of Biological Tissue by Use of Contrast of Laser Speckles. Appl. Opt. 2002, 41, 6030. [Google Scholar] [CrossRef] [PubMed]
- Hussain, A.; Hondebrink, E.; Staley, J.; Steenbergen, W. Photoacoustic and Acousto-Optic Tomography for Quantitative and Functional Imaging. Optica 2018, 5, 1579. [Google Scholar] [CrossRef]
- Jin, H.; Zhang, R.; Liu, S.; Zheng, Z.; Zheng, Y. A Single Sensor Dual-Modality Photoacoustic Fusion Imaging for Compensation of Light Fluence Variation. IEEE Trans. Biomed. Eng. 2019, 66, 1810–1813. [Google Scholar] [CrossRef]
- Jin, H.; Zhang, R.; Liu, S.; Zheng, Y. Passive Ultrasound Aided Acoustic Resolution Photoacoustic Microscopy Imaging for Layered Heterogeneous Media. Appl. Phys. Lett. 2018, 113, 241901. [Google Scholar] [CrossRef]
- Kirchner, T.; Gröhl, J.; Maier-Hein, L. Context Encoding Enables Machine Learning-Based Quantitative Photoacoustics. J. Biomed. Opt. 2018, 23, 056008. [Google Scholar] [CrossRef]
- Gröhl, J.; Schellenberg, M.; Dreher, K.; Maier-Hein, L. Deep Learning for Biomedical Photoacoustic Imaging: A Review. Photoacoustics 2021, 22, 100241. [Google Scholar] [CrossRef]
- Hsu, K.T.; Guan, S.; Chitnis, P.V. Comparing deep learning frameworks for photoacoustic tomography image reconstruction. Photoacoustics 2021, 23, 100271. [Google Scholar] [CrossRef]
- Yang, C.; Lan, H.; Gao, F.; Gao, F. Review of deep learning for photoacoustic imaging. Photoacoustics 2021, 21, 100215. [Google Scholar] [CrossRef]
- Cai, C.; Deng, K.; Ma, C.; Luo, J. End-to-End Deep Neural Network for Optical Inversion in Quantitative Photoacoustic Imaging. Opt. Lett. 2018, 43, 2752. [Google Scholar] [CrossRef] [PubMed]
- Bench, C.; Hauptmann, A.; Cox, B. Toward Accurate Quantitative Photoacoustic Imaging: Learning Vascular Blood Oxygen Saturation in Three Dimensions. J. Biomed. Opt. 2020, 25, 085003. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar] [CrossRef]
- Madasamy, A.; Gujrati, V.; Ntziachristos, V.; Prakash, J. Deep Learning Methods Hold Promise for Light Fluence Compensation in Three-Dimensional Optoacoustic Imaging. J. Biomed. Opt. 2022, 27, 106004. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Gao, F. EDA-Net: Dense aggregation of deep and shallow information achieves quantitative photoacoustic blood oxygenation imaging deep in human breast. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2019: 22nd International Conference, Shenzhen, China, 13–17 October 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 246–254. [Google Scholar] [CrossRef]
- Yang, C.; Lan, H.; Zhong, H.; Gao, F. Quantitative Photoacoustic Blood Oxygenation Imaging Using Deep Residual And Recurrent Neural Network. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 741–744. [Google Scholar] [CrossRef]
- Luke, G.P.; Hoffer-Hawlik, K.; Van Namen, A.C.; Shang, R. O-Net: A convolutional neural network for quantitative photoacoustic image segmentation and oximetry. arXiv 2019, arXiv:1911.01935. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Wang, C.; Chen, T.; Lu, T.; Li, S.; Sun, B.; Sun, B.; Sun, B.; Gao, F.; et al. Deep Learning-Based Quantitative Optoacoustic Tomography of Deep Tissues in the Absence of Labeled Experimental Data. Optica 2022, 9, 32–41. [Google Scholar] [CrossRef]
- Chen, T.; Lu, T.; Song, S.; Miao, S.; Gao, F.; Li, J. A Deep Learning Method Based on U-Net for Quantitative Photoacoustic Imaging. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing 2020, San Francisco, CA, USA, 2–5 February 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11240, pp. 216–223. [Google Scholar] [CrossRef]
- Zou, Y.; Amidi, E.; Luo, H.; Zhu, Q. Ultrasound-Enhanced Unet Model for Quantitative Photoacoustic Tomography of Ovarian Lesions. Photoacoustics 2022, 28, 100420. [Google Scholar] [CrossRef] [PubMed]
- Lan, H.; Jiang, D.; Yang, C.; Gao, F.; Gao, F. Y-Net: Hybrid deep learning image reconstruction for photoacoustic tomography in vivo. Photoacoustics 2020, 20, 100197. [Google Scholar] [CrossRef]
- Schellenberg, M.; Gröhl, J.; Dreher, K.K.; Nölke, J.H.; Holzwarth, N.; Tizabi, M.D.; Seitel, A.; Maier-Hein, L. Photoacoustic Image Synthesis with Generative Adversarial Networks. Photoacoustics 2022, 28, 100402. [Google Scholar] [CrossRef]
- Lyu, T.; Yang, C.; Gao, F.; Gao, F. 3D Photoacoustic Simulation of Human Skin Vascular for Quantitative Image Analysis. In Proceedings of the 2021 IEEE International Ultrasonics Symposium (IUS), Xi’an, China, 11–16 September 2021; pp. 1–3. [Google Scholar] [CrossRef]
- Lyu, T.; Zhang, J.; Gao, Z.; Yang, C.; Gao, F.; Gao, F. Photoacoustic digital brain: Numerical modelling and image reconstruction via deep learning. arXiv 2021, arXiv:2109.09127. [Google Scholar] [CrossRef]
- Rosenthal, A.; Razansky, D.; Ntziachristos, V. Quantitative Optoacoustic Signal Extraction Using Sparse Signal Representation. IEEE Trans. Med Imaging 2009, 28, 1997–2006. [Google Scholar] [CrossRef]
- Tzoumas, S.; Nunes, A.; Olefir, I.; Stangl, S.; Symvoulidis, P.; Glasl, S.; Bayer, C.; Multhoff, G.; Ntziachristos, V. Eigenspectra Optoacoustic Tomography Achieves Quantitative Blood Oxygenation Imaging Deep in Tissues. Nat. Commun. 2016, 7, 12121. [Google Scholar] [CrossRef] [PubMed]
- Olefir, I.; Tzoumas, S.; Yang, H.; Ntziachristos, V. A Bayesian Approach to Eigenspectra Optoacoustic Tomography. IEEE Trans. Med. Imaging 2018, 37, 2070–2079. [Google Scholar] [CrossRef] [PubMed]
- Olefir, I.; Tzoumas, S.; Restivo, C.; Mohajerani, P.; Xing, L.; Ntziachristos, V. Deep Learning-Based Spectral Unmixing for Optoacoustic Imaging of Tissue Oxygen Saturation. IEEE Trans. Med. Imaging 2020, 39, 3643–3654. [Google Scholar] [CrossRef] [PubMed]
- Leino, A.A.; Pulkkinen, A.; Tarvainen, T. ValoMC: A Monte Carlo software and MATLAB toolbox for simulating light transport in biological tissue. Osa Contin. 2019, 2, 957–972. [Google Scholar] [CrossRef]
- Yan, S.; Fang, Q. Hybrid mesh and voxel based Monte Carlo algorithm for accurate and efficient photon transport modeling in complex bio-tissues. Biomed. Opt. Express 2020, 11, 6262–6270. [Google Scholar] [CrossRef]
- Shen, K.; Liu, S.; Feng, T.; Yuan, J.; Zhu, B.; Tian, C. Negativity artifacts in back-projection based photoacoustic tomography. J. Phys. D Appl. Phys. 2020, 54, 074001. [Google Scholar] [CrossRef]


| Category | Number of Forward Modeling | Advantages | Major Limitations |
|---|---|---|---|
| Fluence correction methods [9,41,42,43,44,45,46,47,48,49,50,51] | Single | Easy implementation; little computational load. | Extremely high dependence on predefined tissue properties, both geometrical and optical. |
| Model fitting methods [23,52,53] | Multiple | Certain applicability to unknown simple media; good computational efficiency. | Low accuracy due to the unrealistic optical homogeneity assumption. |
| Fixed-point iteration methods [54,55,56,57,58] | Iterative | High accuracy; high capability for unknown absorption distributions. | Requiring specified scattering distributions. |
| Minimization-based methods [59] | Iterative | Highest accuracy; high capability for all unknown optical property distributions. | Computationally intensive and time- consuming. |
| Category | Key Processes | Advantages | Limitations |
|---|---|---|---|
| Forward modeling-based methods | Utilizing a forward model to generate simulated counterparts of related variables. | Abundant choices of available frameworks with distinct features; a logically simple understanding due to the high conformity to the underlying physical process. | High dependence on the performance of the used light propagation model; a strict requirement of adequate knowledge of the experimental configurations. |
| Fluence correction via other techniques | Resorting to other techniques to measure the fluence map and correcting its impact. | Avoiding inherent complexity and limitations in the PA field. | Inherent drawbacks from the used assisted techniques; incorporating additional devices and procedures; compromising the system’s compactness. |
| Deep learning methods | Training deep neural networks to produce desired distributions in an end-to-end manner. | Significantly less dependence on prior knowledge of the object tissue and related physics; high computational efficiency in the implementation phase. | The extensive demand for training data labeled with true values and the lack of reliable in vivo measurement techniques; low generality of trained networks to system configurations and target scenario. |
| Decomposition-based methods | Decomposing related variables into a linear combination of a set of prescribed basis functions. | Producing acceptable results at a relatively less computational cost. | Very limited applicable cases due to the use of strong assumptions and the incomplete collection of basis functions. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Tao, W.; Zhao, H. The Optical Inverse Problem in Quantitative Photoacoustic Tomography: A Review. Photonics 2023, 10, 487. https://doi.org/10.3390/photonics10050487
Wang Z, Tao W, Zhao H. The Optical Inverse Problem in Quantitative Photoacoustic Tomography: A Review. Photonics. 2023; 10(5):487. https://doi.org/10.3390/photonics10050487
Chicago/Turabian StyleWang, Zeqi, Wei Tao, and Hui Zhao. 2023. "The Optical Inverse Problem in Quantitative Photoacoustic Tomography: A Review" Photonics 10, no. 5: 487. https://doi.org/10.3390/photonics10050487
APA StyleWang, Z., Tao, W., & Zhao, H. (2023). The Optical Inverse Problem in Quantitative Photoacoustic Tomography: A Review. Photonics, 10(5), 487. https://doi.org/10.3390/photonics10050487




