Creation of a Periodic Domain Structure in MgOLN by Femtosecond Laser Irradiation

Abstract

The systematic imaging of the damaged tracks and domain patterns created in the MgOLN plates by one-step fs-laser irradiation at different depths was carried out. It is shown that the domains in the bulk have a spindle-like shape and start to grow in the Z− direction from the track ends. The domain shape changes from a spindle-like one with charged walls to a hexagonal prism with neutral walls after the domain reaches the polar surface. The length of the domains located in the bulk increases linearly with the pulse energy. The hexagonal domain shape at the surface is typical for the crystals of the lithium niobate family. The obtained effects have been considered in terms of the kinetic approach. After irradiation, the domains appear in the vicinity of the track ends with maximum electric field strength and grow under the action of a spatially nonuniform pyroelectric field. The key role of the pyroelectric field is confirmed by the creation of new domains at the surface without correlation with the position of the focusing point located at the vicinity of the surface. The 3D domain pattern was produced, which represented four layers of the regular matrices consisting of elongated domains about 100 μm in length.

1. Introduction

Quasi-phase matching (QPM) that employs a spatial modulation of the second-order nonlinear coefficient χ⁽²⁾ is an important technique in nonlinear optics [1,2]. The QPM can be realized through periodic domain inversion and χ⁽²⁾ erasing in ferroelectric bulk crystals or optical waveguides [3]. The creation of stable periodical domain structures in ferroelectric crystals (domain engineering) has been successfully applied for optical and photonic applications based on the realization of QPM, such as second-harmonic generation (SHG) [2,4] and optical parametric oscillation (OPO) [5,6]. Ferroelectric crystals of the lithium niobate LiNbO₃ family are the most popular materials for domain engineering due to their simple domain structure with 180-degree domain walls only, high temperature of the phase transition (above 1100 °C), and high second-order nonlinear permittivity coefficient [4,7]. The special attention to MgO-doped lithium niobate crystals (MgOLN) is caused by a sufficiently higher value of the optical damage threshold [8,9].

Along with the most popular methods of periodical poling by application of spatially nonuniform electric field using lithographically produced electrodes, the all-optical poling methods of domain patterning were developed [10,11]. The main advantage of these methods is that there is no need to produce electrodes and apply an external electric field. Moreover, it is necessary to point out that the electric field poling cannot be used in the cases of thin films or ferroelectrics deposited onto nonconductive substrates such as ion-sliced lithium niobate films on isolator substrate [12,13,14].

A new branch of all-optical methods using irradiation by tightly focused ultrashort pulses of near-infrared lasers (NIR fs-laser) has appeared recently [15,16]. This method is now considered as an effective and flexible instrument for local polarization reversal and the creation of stable periodical domain patterns [15,16]. It is important to emphasize that this technique is the only one that allows realizing domain formation in the crystal bulk, thus creating the 3D domain patterns [17,18,19,20]; moreover, it allows erasing the already written domains locally [21]. The method can be applied to any ferroelectric that is transparent in the near-infrared spectral range.

The pulse energy regime is necessary for the following reasons. Lithium niobate is transparent in the infrared spectral range. Thus, only the high-intensity light would heat the crystal in the focal area as a result of the multi-photon absorption [15]. The fundamental wavelength of the used femtosecond laser (about 1 μm) is too long for band-to-band two-photon absorption in lithium niobate with a band gap of about 4 eV. Thus, the absorption process could involve higher-order photon absorption as well as defects or impurity states within the gap [22]. The realized tight light focusing on the crystal bulk leads to a high-temperature gradient and, consequently, a high local value of the electric field. The domain creation is obtained in the submicron size region, where the local field exceeds the coercive threshold value.

The first creation of periodical domain patterns in lithium niobate by NIR fs-laser with 800 nm wavelength and pulse frequency 76 MHz was achieved by a one-step method with motion of the laser spot along the polar axis at 10 µm/s speed from the Z− polar surface to the bulk [15]. Owing to the high transparency of a lithium niobate crystal in the infrared spectral range, it produced stable inverted domains extending from the surface up to 60 μm inside the crystal. The two-dimensional domain patterns were demonstrated with a distance between the centers of neighboring isolated domains down to 1.5 µm, thus allowing the production of fine two-dimensional structures. The authors also successfully applied the Cerenkov-type second harmonic generation for monitoring the created domain pattern in the crystal bulk [15]. They also expect to achieve an even higher resolution of domain patterning by using spatial beam shaping and tighter focusing with oil-immersed objectives [15].

Later, the same method was applied for the creation of the periodical domain structure in a Ti-diffused channel waveguide in congruent lithium niobate [23]. The produced 10 mm long periodic domain pattern in the waveguide contained more than 3500 periods and demonstrated its performance as an efficient QPM frequency convertor. The realized second harmonic generation efficiency of 17.45% was up to 440 times larger than that achieved in the pure waveguide channel without a domain pattern. The obtained results indicate that the infrared laser poling is a powerful method for the all-optical fabrication of periodic ferroelectric domains.

The domain switching was attributed to the action of thermoelectric and pyroelectric fields, which occurred because of the multiphoton absorption of the NIR irradiation. The domain inversion was obtained in the regions where the value of the electric field exceeded the threshold [15,23].

The same method was applied to create 3D multilayer domain structures in ferroelectric Ca_0.28Ba_0.72Nb₂O₆ with a period down to 5 μm. The created hexagonal domain patterns were used to demonstrate nonlinear diffraction based on second harmonic generation [19]. The local switching of the spontaneous polarization in the bulk of the single-domain crystal was done by a tightly focused short-pulse infrared beam. Domain patterns constituting 2D and 3D nonlinear photonic crystals were subsequently used in the second harmonic generation experiment via the nonlinear Raman–Nath diffraction. The stability of the laser-created domains under illumination by a strong, loosely focused infrared beam for a period of 3 months was demonstrated. It was shown that the created structure was completely erased as a result of thermal annealing above Curie temperature. This fact definitely proved that the fabricated quadratic nonlinearity patterns were ferroelectric domains and not structural modifications of the crystal. The authors claim that the obtained results open up possibilities to fabricate complex multi-dimensional QPM domain structures inside single-domain ferroelectrics, allowing their integration with other ferroelectrics-based devices such as phase modulators and switches [19].

A one-step method without laser spot motion during 0.5 s irradiation (wavelength 800 nm, pulse frequency 76 MHz) was applied to create periodical 3D domain structures in various ferroelectric crystals, such as Sr_0.61Ba_0.39Nb₂O₆ [17], 0.62Pb(Mg_1/3Nb_2/3)O₃-0.38PbTiO₃ [18,24], and Ba_0.77Ca_0.23TiO₃ [20]. The created domains were arranged into several structures with cubic symmetry used for SHG measurements [17]. The formation of two types of ferroelectric domains was demonstrated [18]. Domains of the first type had a narrow, elongated shape—the “primary” domain. The second type of domain—the “secondary” domain—was observed at higher irradiation energy compared to the first type. “Secondary” domains had a hollow cylinder shape changing with depth. Both domain types coexisted after the high-energy irradiation.

The creation and erasing of the domain patterns in the bulk of nonpolar cut MgOLN were demonstrated by the motion of the laser spot with a wavelength of 800 nm and pulse frequency of 80 MHz [21]. The laser spot created the polar components of the thermoelectric field, oriented in two opposite directions. Using the appropriate direction of spot motion allows using the spot either as a pencil or as an eraser. The erasing allows for the reduction of the width of the written stripe domains from 400 to 100 nm. The 2D matrices created at the first stage consisting of stripe domains were transformed into 3D structures by partial erasing [21]. The authors claim that the non-reciprocity of the proposed laser-writing technique also provides a critical tool to re-write lithium niobate domain structures. Moreover, high-resolution reconfigurable manipulation of lithium niobate domains can significantly enhance the ability to control non-linear optical interactions for high-efficiency frequency conversion and narrow-linewidth quantum entanglement generation [21].

A two-step periodical poling method representing the creation of locally modified elongated volumes (tracks) and their growth by further uniform heating and cooling cycle was realized in MgOLN crystal. The tracks oriented along the polar axis were created by NIR fs-laser irradiation with 800 and 1030 nm wavelengths and 1 kHz pulse frequency [25,26]. The laser spot was moved from any polar surface to the bulk or vice versa with 80 µm/s speed. The tracks acted as the seeds for domain growth under the action of the pyroelectric field [25,26]. The domains appeared below the tracks and grew over the whole sample depth, thus forming a 2D periodical domain structure. A threshold temperature was identified and determined. It was shown that in the optimal temperature range between 220 °C and 300 °C the isolated domains can be organized in a 2D rectangular lattice with periods of 15 μm × 6.3 μm. Such a nonlinear photonic lattice was used for simultaneous quasi-phase-matched second harmonic generation of 1030 nm and 1200 nm, respectively. Smaller lattice periods and lower temperatures resulted in the defective lattice. The pronounced backswitching of the created domains was obtained in the center of the lattices for temperatures above 300 °C. The average diameter of the central domains, about 2.4 μm, is almost independent of temperature and lattice periods. The authors pointed out the limitation of the duty cycles of the created domain patterns and suggested using a biased electric field in addition to the pyroelectric field to obtain higher conversion efficiencies [26].

Another two-step method, named ‘laser marking’, represented the creation of modified areas at the Z+ polar surface by 1026 nm NIR fs-laser with 1 MHz pulse frequency and subsequent heating by local irradiation, which led to the formation of domains with lengths up to 100 µm [27]. The obtained results were attributed to a thermoelectric field arising from a temperature gradient caused by local heating.

The two-step periodical poling with track creation by local fs-laser irradiation in the crystal depth without spot motion and subsequent uniform heating/cooling cycle was realized by us in MgOLN crystal [28]. Sets of 5000 pulses with energy above 2.5 µJ were used for the track creation in the bulk. For pulse energy above 4 µJ, the domains grew from the tracks to the Z− surface. The following heating/cooling treatment allowed the creation of 2D patterns consisting of domains, which grew over the whole sample depth.

The 3D modulation offers exclusive access to reciprocal lattice vectors in the third dimension and, therefore, enables phase matching of nonlinear processes along an arbitrary direction [20]. Thus, 3D nonlinear photonic crystals represent ideal systems for the realization of a variety of second-order nonlinear interactions and effects. From a practical point of view, these crystals enable the realization of new classes of photonic devices, including true χ⁽²⁾ volume holography [29], 3D nonlinear photonic integrated circuits, and 3D domain-wall-based photovoltaic devices and non-volatile memory [30].

The realization of 3D χ⁽²⁾ modulation is beyond the reach of traditional fabrication techniques. The most popular approach of electric field poling of ferroelectrics cannot modulate χ⁽²⁾ along the depth of the medium. As the external poling field must be applied via patterned electrodes, the domain-switching process in this method always begins with nucleation (the inception of new domains) on the surface.

In this work, we have studied the domain growth from the tracks created in the bulk of MgOLN crystal by fs-laser irradiation of different polar surfaces with spot positions at different depths. The domain growth along the Z− crystal direction only and linear dependence of the domain length on pulse energy have been revealed. The obtained results have been attributed to the local electric field arising at the end of the tracks, which creates the domain nuclei. The subsequent domain growth has been explained by the action of the pyroelectric field.

2. Materials and Methods

A uniaxial ferroelectric crystal of lithium niobate doped with 5% MgO was chosen for the study. The samples represented 1-mm thick single-domain plates cut perpendicular to the polar axis and polished to optical quality (Jiangxi Unicrystal Technology, Nanchang, China).

A femtosecond regenerative amplifier (TETA-10, Avesta Project, Moscow, Russia) based on a Yb-crystal solid-state laser (NIR fs-laser) was used for local irradiation of the samples. The parameters of the used NIR fs-laser irradiation: wavelength 1030 nm, frequency 100 kHz, pulse duration 240 fs, and energy per pulse ranged from 2 to 10.7 µJ. Samples were mounted on a 3D-motorized table (horizontal motorized table XY5050 combined with vertical translation KA050-Z, Zolix Instruments, Beijing, China).

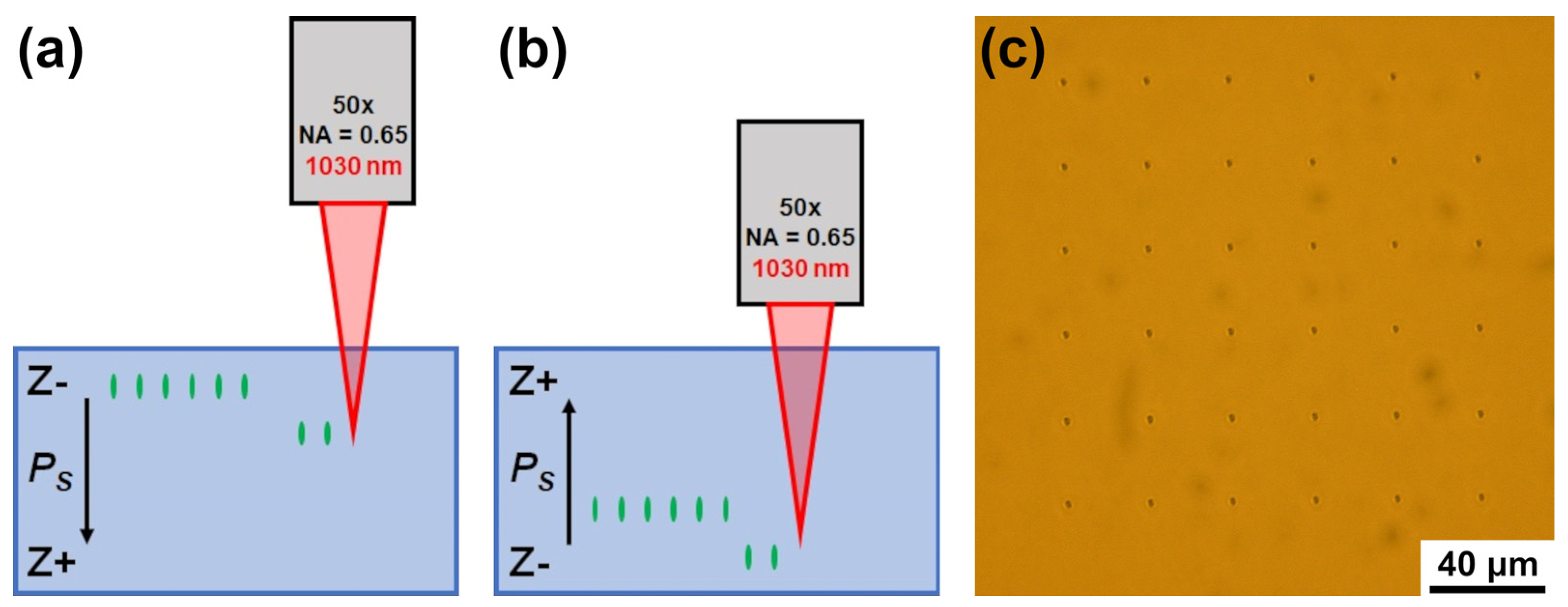
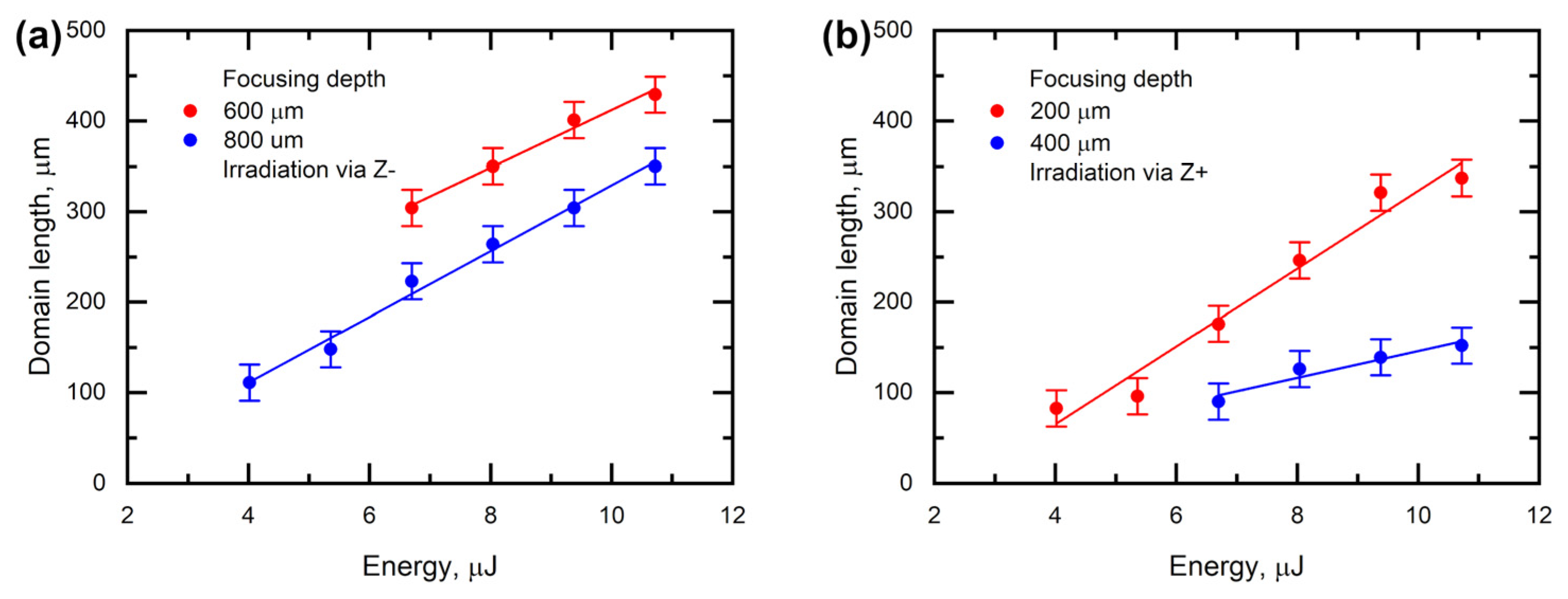
Laser irradiation was focused on the bulk of the sample at a depth from 200 to 800 µm from the surface by the objective with antireflective coating (50×, NA = 0.65). The focusing depth was determined considering the refractive index of MgOLN for 1030 nm wavelength. The irradiation points arranged in matrices of 6 × 6 with a 30 µm period were exposed at the fixed depth without laser spot motion. Every point was exposed with 5000 laser pulses. The delay between subsequent exposures was 1 s. The domain structures created by irradiation via Z+ and Z− polar surfaces were compared (Figure 1a,b).

Several experimental methods have been used for imaging of the tracks and domains. The tracks were imaged by the optical microscope (Olympus BX-61, Olympus, Tokyo, Japan) in transmission mode.

It is known that domain walls in nonlinear-optical ferroelectrics generate conical radiation at a double frequency under the laser exposing so-called Cherenkov-type second harmonic generation [31]. A confocal microscope combined with a laser source allows domain imaging in the bulk by Cherenkov-type Confocal Second Harmonic Generation Microscopy (CSHGM) [31,32]. We imaged the domain structures and tracks in the bulk using a self-made setup based on Ntegra Spectra, NT-MDT, Russia. Scanning of the samples in XY-cross-section with filtering of the light with SHG wavelength allows obtaining the sets of 2D images at different depths. They were reconstructed into 3D images of tracks and domains.

The domain structures arising on the polar surfaces were imaged with high-spatial resolution using the scanning probe microscope Aura (NT-MDT, Russia) in the Piezo-response Force Microscopy (PFM) mode. The PFM technique is based on measurements of local piezoelectric response phase and amplitude, which can be transformed into the contrast of domains and domain walls, respectively [33,34]. NSC14 probes with titanium-platinum conductive coating and 30 nm curvature radius (MikroMash, Sofia, Bulgaria) were used in the PFM experiments. The probe curvature radius determined the PFM spatial resolution.

3. Results and Discussion

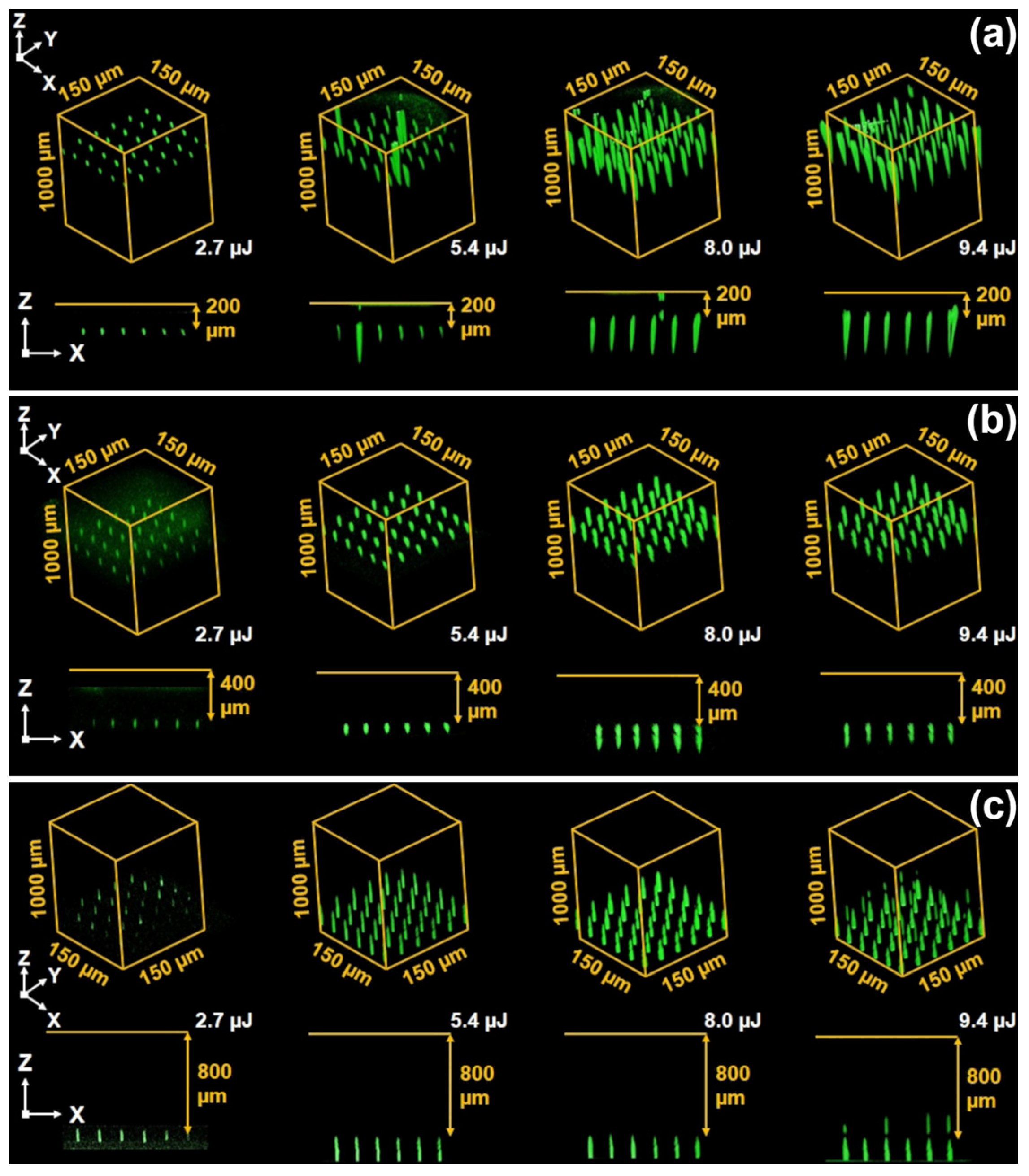
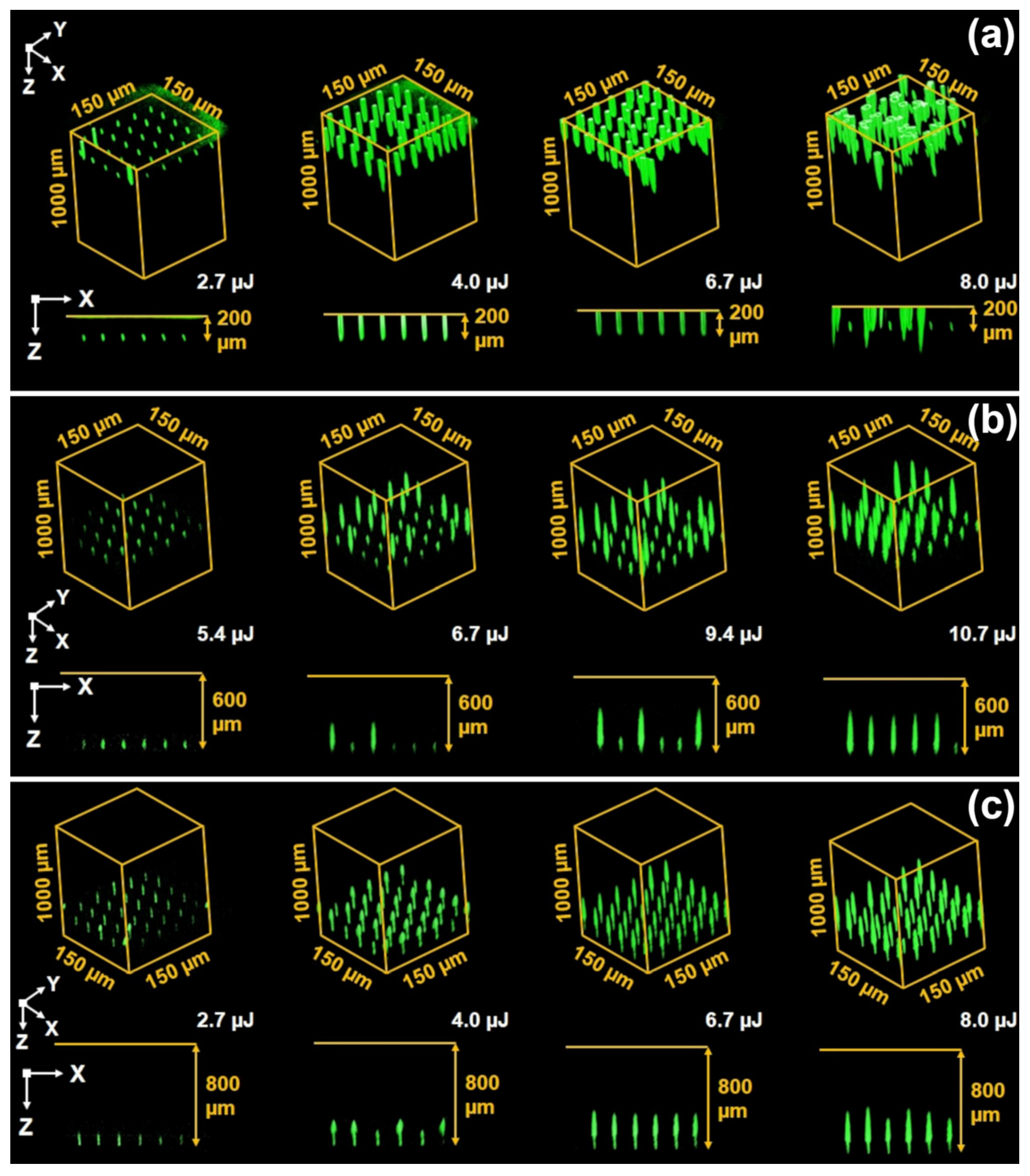
The systematic study of MgOLN single domain plates treated by NIR fs-laser irradiation at different depths via Z+ (Figure 2) and Z− (Figure 3) polar surfaces, respectively, allows obtaining 3D CSHGM images of arising domains.

The elongated tracks and localized narrow domains appeared in the bulk for pulse energy ranging from 2 to 10.7 µJ (Figure 2 and Figure 3) [35]. The optical contrast of the tracks is evidence of the volumes with modified refractive index and the diminished value of spontaneous polarization (Figure 1c). The domains started to grow from the tracks for pulse energy above 4 µJ for 200 μm focusing depth (Figure 2 and Figure 3). The threshold energy needed for domain growth increased with the depth of the focusing point. The appearance of domains was always accompanied by the appearance of damage in the crystal bulk. Thus, the domain formation without damage was not detected in the used range of irradiation parameters.

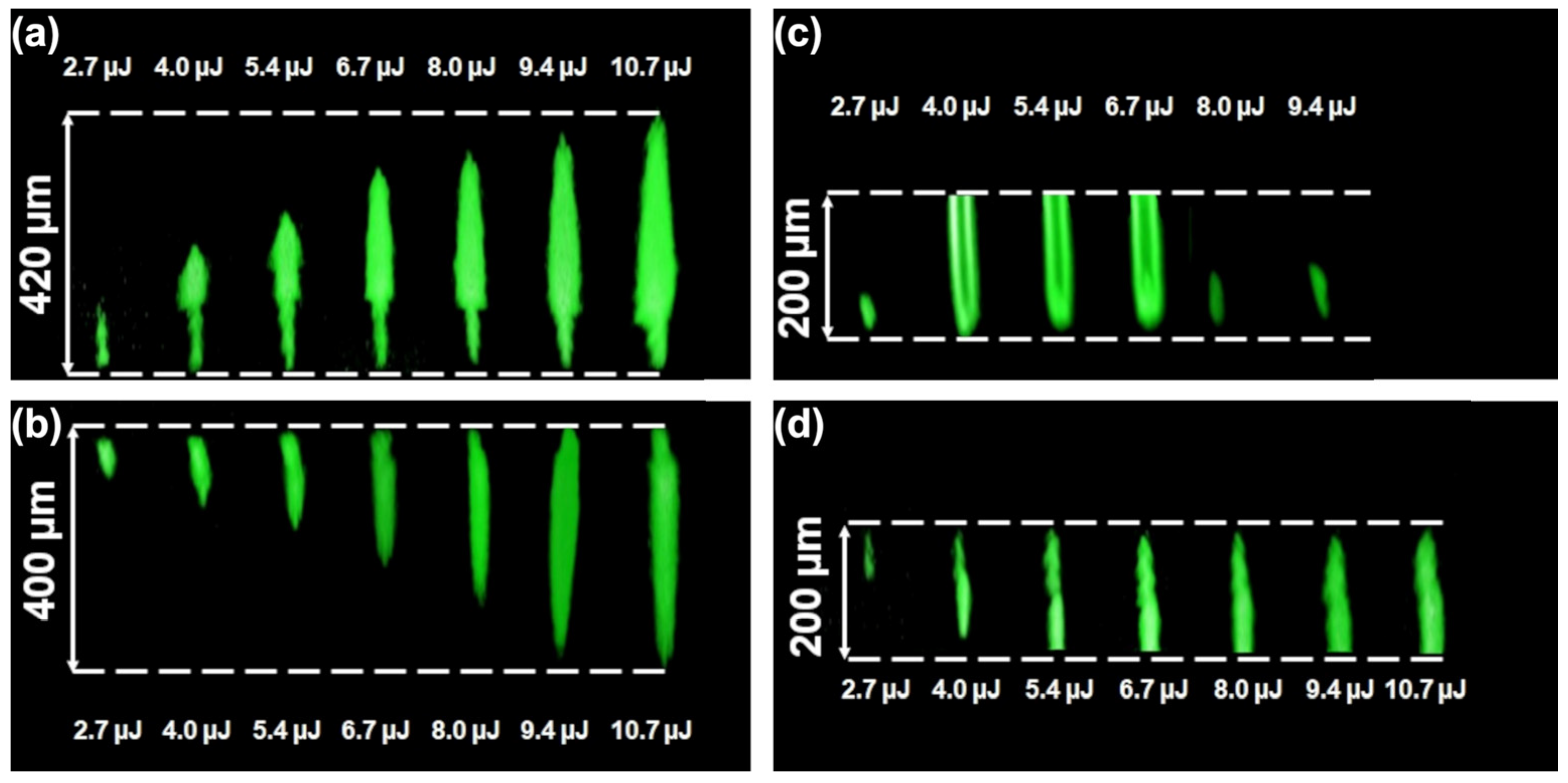
The CSHGM imaging allowed for characterizing the shape of the domains and their position in relation to the tracks. The domains in the bulk had a spindle-like shape (Figure 4a,b). It was revealed that the domains started to grow from the ends of the tracks in the Z− direction only (Figure 4a). The resolution of the CSHGM method does not allow distinguishing domain wall position and, accordingly, the exact domain sizes, but it allows estimating the domain shape and approximate length. It was shown that the domain shape changed from a conical one with charged walls to a hexagonal prism with neutral walls just after the domain reached the polar surface (Figure 4c,d).

In the case of irradiation via both polar surfaces, the length of the domains located far from the polar surfaces increased linearly with the pulse energy (Figure 5), whereas the randomly localized conical domains started to grow from the polar surface in the Z+ direction for energy above 4 µJ and the focusing point localized in the vicinity of the polar surface (Figure 3a). The positions of these domains did not correlate with the focusing points.

High-resolution PFM images of the domains arising at the polar surface allowed the revealing of their hexagonal shape, typical for isolated domains growing under the action of an electric field in the crystals of the lithium niobate family [4] (Figure 6a). The hexagonal domain shape was attributed to the determined generation of the steps at the polygon vertices and the anisotropic motion of the charged kinks [4]. The domain appearance is a clear demonstration of the role of the pyroelectric field arising at the surface as a result of laser irradiation. The forward domain growth in the polar direction is a result of kink motion in the field produced by the neighboring charged kinks. Thus, the heating of the polar surface leads to the formation of the domains with the shape of a hexagonal pyramid (Figure 3a) [4].

The obtained effects can be considered in terms of the kinetic approach based on the analogy of domain and crystal growth [9]. Domain shape evolution is considered a result of the generation of 1D, 2D, and 3D nuclei. The growth of the 3D nucleus represents the generation of elementary steps on the domain wall (2D nuclei) and subsequent kink motion (1D nuclei).

The domain formation requires the local application of the electric field with the polar component above the threshold value for domain nucleation E_th.n. The driving force of the domain growth represents the excess of the local value of the polar component of the electric field E_loc.z over the threshold values for step generation E_th.s. The velocity of domain wall motion is proportional to the local field excess:

v(r,t) = µ ΔE(r,t) = µ(E_loc.z(r,t) − E_th.s),

(1)

where µ is domain wall mobility.

After irradiation by the NIR fs-laser, the domains appeared in the vicinity of the tracks. The domain growth is obtained under the action of E_loc.z consisting of two inputs: (i) the polar component of the pyroelectric field arising in the vicinity of the track during cooling after irradiation E_pyr.z and (ii) the polar component of the field produced by the charged kinks E_k.z [10]:

E_loc.z(r,t) = E_pyr.z(r,t) + E_k.z(r,t).

(2)

The elongated tracks represent modified crystal areas with diminished value of spontaneous polarization, which leads to the formation of bound charges at the track boundary. The bound charge density depends on the local orientation of the track boundary and increases with its tilt from the polar direction. Thus, the maximal charge density is localized at the track ends, which leads to local electric field maxima.

In such a case, the domain appears at the field maxima at the proper end of the track and grows in a polar direction. Such forward domain growth can be considered in analogy with the studied detail of local switching at the nonpolar cuts of lithium niobate crystals under the application of the field by the biased tip of the scanning probe microscope [36]. In this case, the base of the conical domain is located near the point of field application. The domain base grows by step generation under the action of the applied field (Equation (1)). The domain forward growth in the polar direction is due to kink motion in the field produced by neighboring charged kinks (Equation (2)).

In the case of irradiation by NIR fs-laser, the base of the formed spindle-like domain grows due to the step generation induced by the high value of the pyroelectric field in the vicinity of the track end, whereas the domain elongation is caused by the propagation of the charged kinks in the field produced by the neighboring kinks [36].

The domain shape changes from a spindle-like one with a charged domain wall to a hexagonal pyramid with neutral domain walls just after the kink reaches the polar surface. Different charge signs of kinks and antikinks facilitate their approaching and annihilation, which leads to a decrease in the domain wall tilt and the formation of almost neutral domain walls with minimal kink concentrations. The domains have the shape of a hexagonal prism, which is typical for the uniaxial ferroelectrics of C₃ symmetry (Figure 6a–c) [10]. Moreover, the additional pyramidal shape domains appear at the surface and grow toward the bulk (Figure 3a).

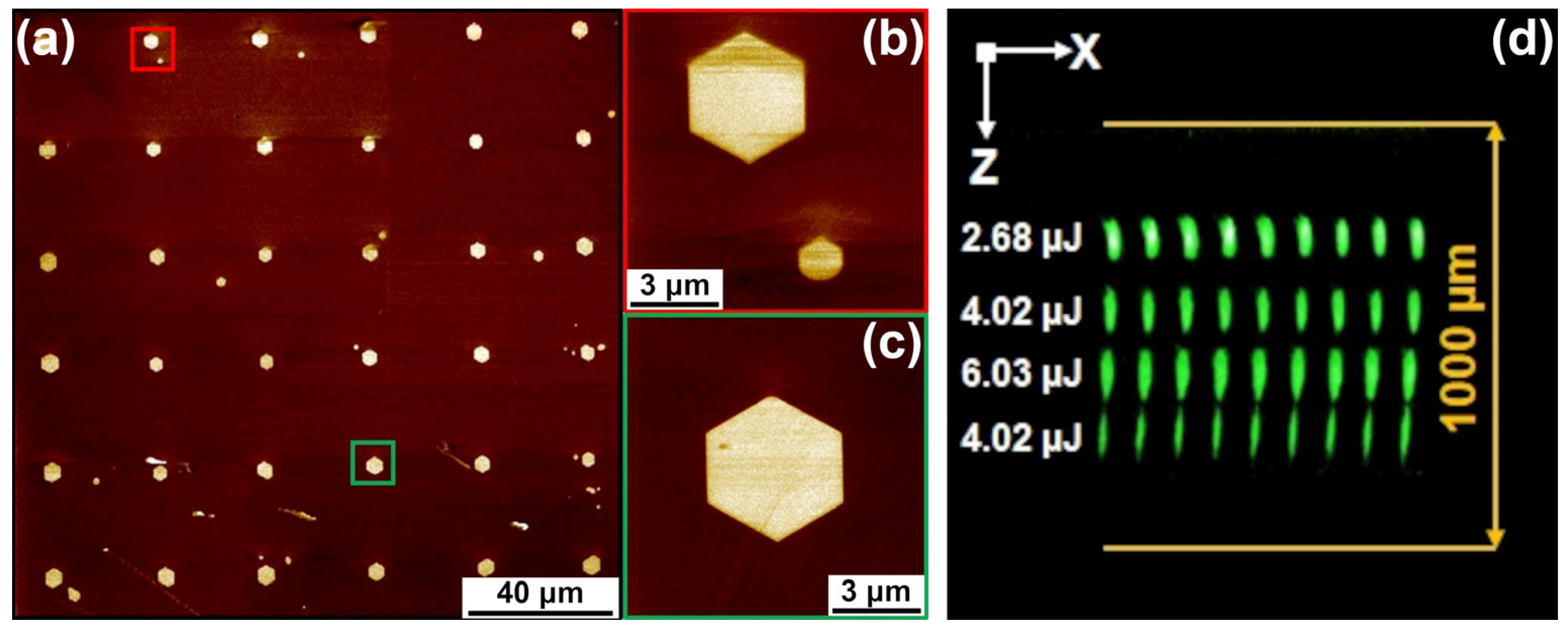
A change in the focusing depth allowed the creation of the 3D domain pattern consisting of the four regular matrices of elongated domains with a length of about 100 μm (Figure 6d). NIR-fs irradiation was propagated through the Z− surface. The matrices were created with a shift of 200 μm along the polar axis from bottom to top. The pulse energy was adjusted for each layer.

The interaction between domains with head-to-head and tail-to-tail domain walls mainly depends on the writing space period in the 3D domain pattern. The desire to reduce the period encounters the effect of pyroelectric fields of the irradiating region on already recorded neighboring domains. This effect during local heating and subsequent cooling will determine the minimum period between domains. As for the length of the domains, it is determined by the diameter of the region where E_pyr.z > E_th.n. Further growth of the domain beyond the irradiated region occurs, as noted above, in the field of charged domain walls. Electrostatic interaction between the charged walls of neighboring domains leads to retardation of the counter motion of approaching domains [4].

4. Conclusions

The systematic imaging of the damaged tracks and domain patterns arising in the MgOLN single-domain plates as a result of one-step NIR fs-laser irradiation at different depths via Z+ and Z− polar surfaces was carried out. It was shown that the spindle-like domains started to grow in the Z− direction from the track ends. The domain shape changed from a spindle-like one with charged walls to a hexagonal prism with neutral walls after the domain reached the polar surface. In the case of irradiation via both polar surfaces, the length of the domains located far from the Z− surface increased linearly with the pulse energy. High-resolution PFM images of the domains at the polar surface allowed the revealing of the hexagonal shape typical for isolated domains growing in the crystals of the LN family under the application of an electric field.

The experimental study of the domain creation by NIR fs-laser irradiation in the crystal bulk allowed us to suggest the model of domain growth in the vicinity of the tracks produced by irradiation under the action of the pyroelectric field. The explanation was done in terms of a kinetic approach based on an analogy between the growth of crystals and ferroelectric domains. The key role of the pyroelectric field was pointed out. The domains grow under the action of a spatially nonuniform electric field consisting of two inputs: (i) the pyroelectric field arising in the vicinity of the track during cooling after irradiation and (ii) the field produced by the charged kinks. In such a case, the domain appears at the field maxima at the proper end of the track and grows in a polar direction. Such forward domain growth was considered in analogy with studied in detail local switching at the nonpolar cuts of LN crystals under field application by the biased tip of the scanning probe microscope. For the focusing point located at the vicinity of the surface, the pyroelectric field is strong enough for the creation of new domains at the surface without any correlation with the position of the focusing point. A change in the depth of the focusing point allowed the creation of the 3D domain pattern consisting of the four regular matrices of elongated domains with a length of about 100 μm.

Summing up all mentioned above: (i) the position of the damaged track can be controlled by the depth of the focusing point, (ii) the track end acts as the nucleation point for domain growth in the pyroelectric field arising during sample cooling, (iii) the domains grow in Z− direction only, (iv) the domain length increases linearly with the irradiation energy.