A Diamond Terahertz Large Aperture Photoconductive Antenna Biased by a Longitudinal Field

Abstract

The novel design of a terahertz large aperture photoconductive antenna (LAPCA) is reported. It features a longitudinal orientation of the bias electric field within the photoconductive substrate, and has the advantage of a small interelectrode gap, resulting in a higher field for the same applied voltage. The proposed LAPCA configuration has been tested with a nitrogen-doped (∼10 ppm) synthetic monocrystalline diamond, which is a promising material for high-intensity and high-power terahertz sources. Two antennas with different high-voltage electrode realizations were assembled, pumped by a 400 nm femtosecond laser, and tested for THz emitter function. The experimental data are found to be in good correlation with the numerical simulation results. The performance of antennas with the conventional transverse E-field configuration and the novel longitudinal configuration is compared and discussed.

1. Introduction

Terahertz (THz) electromagnetic radiation has been at the forefront of photonics for the last thirty years. This is due to the continuous development of spectroscopically resolved imaging in life sciences, materials analysis, security applications, communications, etc., which increasingly exploit the possibilities of the terahertz region [1,2,3,4,5,6,7]. Today, the creation of robust sources of broadband, high power, and intense THz radiation is still topical, and serious efforts are focused on this problem.

For this purpose, various mechanisms of THz radiation emission can be used, but two are the most popular and technologically simple: nonlinear conversion of optical beams in electro-optical crystals (optical rectification) [8] and optical pumping of transversely biased semiconductors [9]. The THz sources associated with the latter mechanism are called photoconductive antennas (PCAs) [10,11]. In short, the electromagnetic pulse generated by a PCA arises as a result of a fast rise of the photocurrent in the biased semiconductor substrate, which in turn is generated by a photoplasma excited by femtosecond optical pumping [12,13]. The search for promising semiconductors suitable for commercial pump lasers and the development of different configurations of PCAs are the tasks of great interest for THz photonics [14,15,16,17,18].

There are obvious ways to increase the amplitude of the single THz pulse and the average power of the THz pulse sequence. They consist, respectively, of increasing the bias voltage applied to the PCA and in increasing the repetition rate of the optical pumping of the PCA. Arguably, diamond is the most promising material for high-power THz emitters, as it is suitable for both methods of power enhancement. First, compared to the numerous semiconductors used for THz emission, diamond has the highest dielectric strength: its electrical breakdown threshold is 10 MV/cm [19]. Second, the thermal conductivity of diamond is even higher than that of copper, enabling efficient heat dissipation and utilization of extra high pump and emission powers. (The thermal diffusivity of copper is about 1.1 cm${}^2$/s, while for diamond it exceeds 10 cm${}^2$/s). Besides these main points, diamond is highly transparent in the THz region [20], and has a high electron mobility ∼4500 cm${}^2$ V${}^{-1}$ s${}^{-1}$ at room temperature [21]. Synthetic diamonds produced by either chemical vapor deposition (CVD) or high-pressure, high-temperature (HPHT) growth are now available and relatively inexpensive.

On the other hand, as an optically pumped emitter, diamond has a significant drawback. It is a wide bandgap semiconductor (5.46 eV) and requires ultraviolet light for one-photon excitation of the electronic subsystem. For this reason, the first diamond PCA was triggered by 248 nm pulses from a femtosecond excimer laser [14]. However, this success did not continue. Fast UV lasers are rather complex systems and cannot be used today to build robust THz sources. This obstacle has recently been overcome with the use of nitrogen-doped diamonds [22]. The doping introduces optical defects into the crystals and results in the appearance of ∼2.2 eV electron transitions from the defect levels to the conduction bands [23]. Thus, doped diamond PCAs have been adapted to operate with the second harmonic of commercial Ti:sapphire lasers and have demonstrated an emitted energy of 0.2–0.3 nJ at a bias field of 25 kV/cm [24].

The THz emission level of diamond PCA is rather modest compared to, for example, GaAs PCA, which has been reported to emit ∼800 nJ per pulse [25]. The difference is in the size of the emitting area—a multiple increase in yield is achieved by a multiple increase in PCA aperture. The first designed antennas generated the photocurrent pulses in the quite narrow single photoconductive gap [26]. So-called large aperture photoconductive antennas (LAPCAs) consist of thousands of such gaps and reach sizes of tens of square centimeters. The fabrication of such structures is a complex technological problem, which appears even more difficult in view of the necessity to mask half of these gaps to prevent destructive interference of THz radiation in the far-field zone [14]. An additional requirement is to bury the conductive wires to eliminate surface current leakage. Recently, the first prototype of diamond PCA with buried high-voltage electrodes drawn by direct laser writing technique has been realized and investigated [27].

This work is devoted to the alternative approach, which allows to create a high bias field in the photoexcited semiconductor slab over the large aperture. The key peculiarity is the orientation of the applied field. A conventional configuration of the PCA implies that the applied field is transverse to the incoming optical beam and to the normal of the sample surface (Figure 1a). In the proposed configuration, three conditions should be met. First, the electric field is longitudinal with respect to the substrate normal (Figure 1b). Since the substrate can be thin enough (∼300 $\mathsf{\mu }$m and less), the high electric field can be obtained with relatively modest applied voltage. Second, the optical beam should be tilted to obtain a bias field component that is perpendicular to the photoconductivity pulse passing through the semiconducting substrate. Therefore, only part of the electric field is used in this design, but this lack is easily overwhelmed by an increase in field due to the reduction of the gap. It should be noted that the generation of electromagnetic pulses by obliquely incident X-rays has been observed as early as 1976 [28]. And third, and most complex, the LAPCA electrodes must be transparent to both optical and THz radiation.

In this work, we have assembled and tested two configurations of LAPCA based on nitrogen-doped diamond with different types of high-voltage electrodes: indium tin oxide (ITO) film electrodes and grid electrodes fabricated directly on the diamond surfaces by laser-stimulated surface graphitization.

2. Materials and Methods

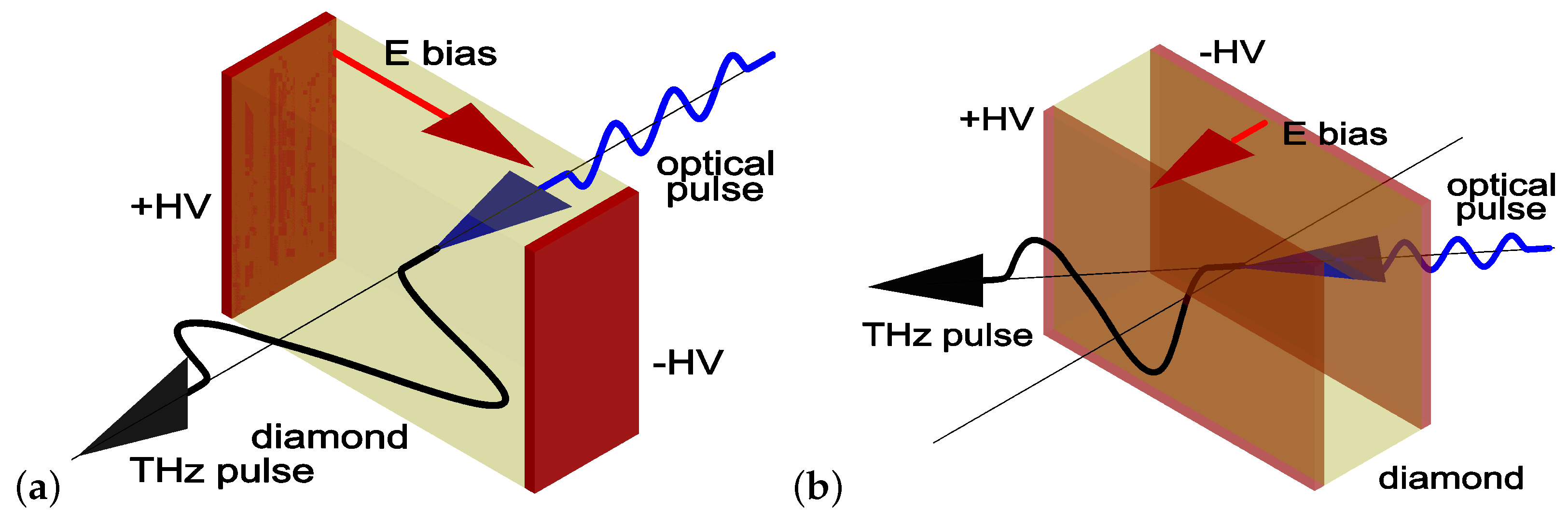
2.1. Assembling LAPCAs

The same monocrystalline diamond plate (5.2 × 2.6 × 0.5 mm) grown by an HPHT process was used to sequentially test the configuration of LAPCA with transversal E-field and two configurations of LAPCAs with longitudinal E-field. The pristine crystal was laser-cut and the faces of the largest plate were mechanically polished to optical quality. The conventional configuration of the assembled antenna consisted of this diamond substrate with graphite electrodes written by a laser on the diamond side and glued to the printed circuit board (PCB) by a conductive paste. (The description of the graphite electrode fabrication is given below). The substrate was placed on the gap cut through the PCB, which was only slightly narrower than the substrate to maximize the aperture of the LAPCA (Figure 2a). The opposite diamond edges were in ohmic contact with the copper pads—electrodes supplied with a constant bias voltage ($V_b$). In all LAPCAs tested, the maximum applied $V_b$ magnitude was limited by the development of surface electrical breakdown, which occurred at an E-field strength of about 10 kV/cm.

The first longitudinal-field LAPCA configuration was a sandwich of two transparent plastic films with a conductive ITO coating pressed onto both sides of the diamond substrate (Figure 2b). The sandwich was encapsulated in the 3D-printed thermoplastic polyester package, which holds it together with conductive terminals for attaching the HV wires (Figure 2c). This LAPCA assembly has no ohmic contact between the diamond and the HV circuit. To avoid static surface charge build-up in the antenna, it was driven by a pulse voltage (up to 3 kV). The HV pulses had a duration of ∼10 ns and were synchronized with the 1 kHz optical pumping.

The second longitudinal-field LAPCA had an essentially different type of HV electrodes. After testing the two LAPCAs described above, the conductive grids shown schematically in Figure 2d were drawn on both sides of the diamond substrate by direct laser writing. Laser graphitization of diamond is a well-known technique that allows the fabrication of graphite-like surface structures with micrometer-scale spatial resolution [29,30]. The 10 $\mathsf{\mu }$m wide wires were spaced 100 $\mathsf{\mu }$m apart and connected to the common bus. Each of two grid electrodes had its own bus of 100 $\mathsf{\mu }$m width. The high voltage biased copper strips were bonded to the graphite buses with a conductive paste (Figure 2e). Like the first longitudinal-field LAPCA, this antenna was mounted in a 3D-printed plastic housing with a rapidly expanding funnel for oblique optical pumping and THz emission (Figure 2f).

The nanosecond excimer KrF laser (wavelength of 248 nm) was used to produce graphite-like grid structures. The obtained wires are expected to have a thickness of ∼200 nm [31] and an ohmic resistance of ∼1 kOm [32]. In contrast to ITO, the graphite is a good absorber and the grid electrodes shaded about 10% of the pump beam. However, these losses were completely compensated by the presence of an ohmic contact between the HV electrodes and the emitting substrate, which guaranteed that the field inside the substrate will correspond to the applied voltage. In addition, the graphite-like electrodes were found to be quite robust compared to the ITO ones, as we will show below.

The known drawback of grid electrodes is that the field is not uniform in the vicinity of the conductors. Calculation of the static electric field showed that its spatial modulation took place within the subsurface layer of about ∼40 $\mathsf{\mu }$m thickness (Figure 2g). The generation of THz radiation within this subsurface layer is rather weak, so the diamond crystal was chosen to allow the pump beam to penetrate much deeper into the substrate, through the 40 $\mathsf{\mu }$m layer to the high E-field region. At 400 nm wavelength, the absorption depth ($1/e$ level) of the selected crystal was ≈220 $\mathsf{\mu }$m, which was expected to be sufficient for effective pumping of the designed LAPCA.

2.2. Testing LAPCAs

The simplified experimental scheme is depicted in Figure 3. The femtosecond Ti:sapphire laser system (Spectra Physics) emitting 1 mJ pulses of ∼120 fs duration at 800 nm wavelength with 1 kHz repetition rate was used to pump the diamond LAPCAs. Second, harmonic radiation with a maximum pulse energy of ≈100 $\mathsf{\mu }$J was obtained with a BBO crystal ($\beta$-barium borate, I-type, 10 × 10 × 0.2 mm). The energy of the second harmonic pulse was varied by rotating a half-wave plate with a Glan polarizer.

The THz radiation emitted by LAPCA was focused by a polytetrafluoroethylene spherical lens (50 mm diameter, 6 cm focal length). The collected THz power modulated at 10 Hz was measured with a Golay cell (Tydex GC-1P, aperture 6 mm, illumination sensitivity 5 × 10${}^3$ V/W). The detailed experimental scheme can be found in [24].

The waveform of the emitted THz pulses was measured with an electro-optical sampling technique using a ZnTe crystal (<110> cut, 3 × 3 × 0.5 mm), a quarter-wave plate, a Wollaston prism, and balanced photodetectors. The THz beam from the diamond antenna was focused into the ZnTe crystal by the same lens as above. The probe laser beam was introduced into the THz beam path by a THz transparent pellicle beam splitter placed between the lens and the crystal. The time delay between the THz pulse and the laser probe pulse was controlled by a mechanical translation stage with a mounted retroreflector placed in the probe beam path.

2.3. Numerical Simulation of LAPCA Operation

Terahertz wave generation was studied numerically in COMSOL Multiphysics to gain insight into the operation of the longitudinal-field LAPCA emitter. A simulation of the electromagnetic field dynamics was performed in the Electromagnetic Waves, Transient package. The diamond antenna was modeled as a 2D slab (5 × 0.5 mm) with a permittivity of 2.4${}^2$ biased by the static electric field, the strength of which was varied from 10${}^2$ V/cm to 10${}^4$ V/cm.

Optical pumping was introduced as an electrical conductivity ($\sigma$) wave propagating over the slab at the group velocity of light in diamond. The front rise time of the conductivity wave was 120 fs, corresponding to the duration of the fs pulses used in the experiments. The fall time was assumed to be infinite. The $\sigma$ amplitude was varied in the range from 1 to 3 × 10${}^3$ S·cm${}^{-1}$. The conductivity wavefront was tilted with respect to the slab surface. The angle of incidence ($\alpha$) was varied from 0${}^{\circ }$ to 80${}^{\circ }$. The normalized electric field was probed at a point 1 mm behind the back of the antenna. The electromagnetic permittivity dispersion was omitted.

To obtain the theoretical spectrum of the emitted THz pulse, the electric field was recorded at a point 1 cm from the center of the antenna. The probe point was located on the axis originating from the PCA center and directed along the THz beam propagation. The fast Fourier transform was used to calculate the $E_{THz}\left(f\right)$ dependence (f is the THz wave frequency). Its square, $E_{THz}^2\left(f\right)$, gave the power spectrum presented below.

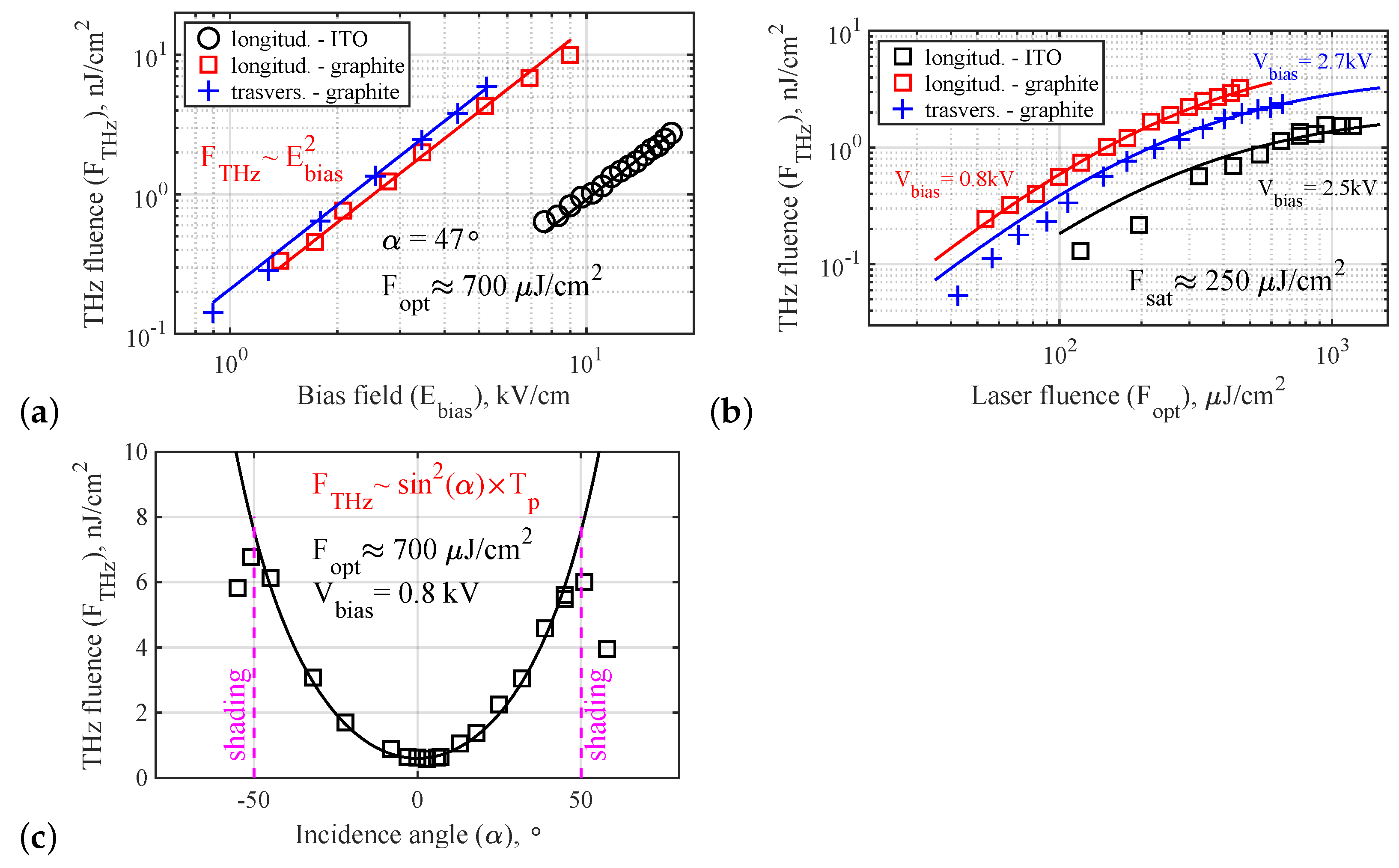
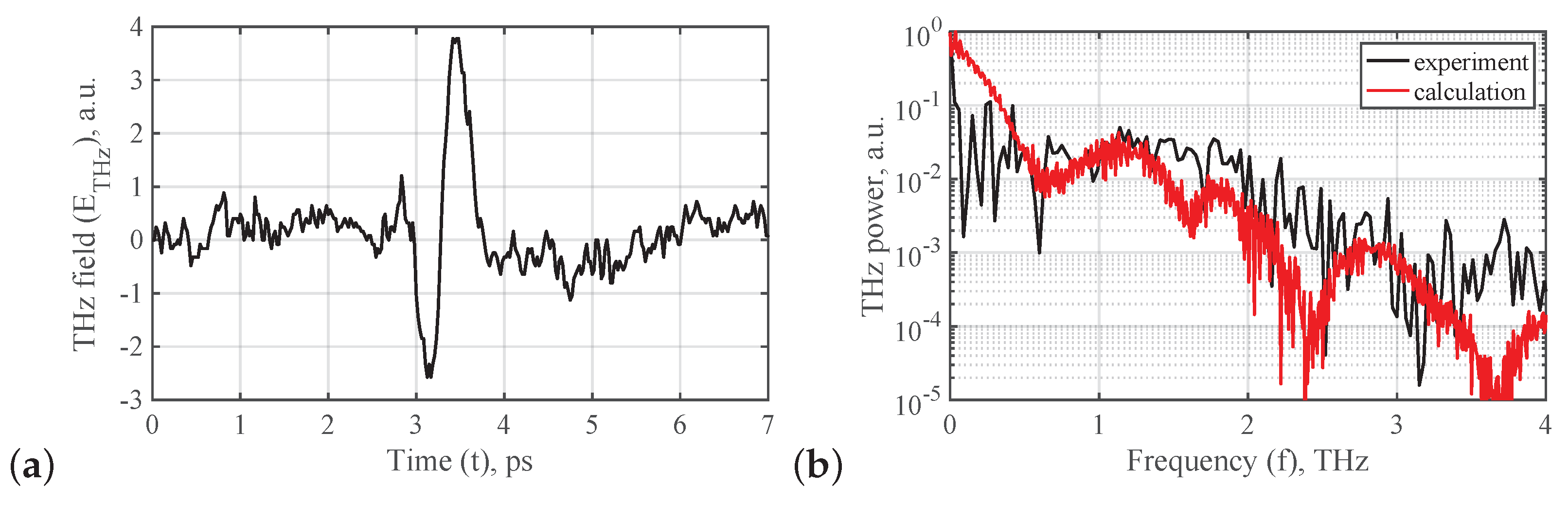
3. Results and Discussion

3.1. Analytical Description of the Transversal Field LAPCA Output

The phenomenological model used for transversal-field LAPCAs is based on the idea of a surface current driven by the static E-field and triggered by the short optical pulse generating the free carriers [33,34]. In accordance with Maxwell’s equations, the photocurrent pulse forms the broadband electromagnetic wave emitted into free space. The detailed first-principles consideration, which includes the effect of the moving plasma pulse through the bulk of the antenna slab, revealed more subtle effects such as the generation of twin terahertz pulses and the enhancement of the terahertz emission under velocity matching conditions [35]. However, the surface current approach describes the THz output of transversal-field LAPCA very well when the plasma screening can be neglected [36].

This model gives the fluence of the emitted terahertz wave as

$$F_{THz}=\frac{{\tau }_{THz}{E}^2}{2Z_0}{\left(\frac{F_{opt}}{F_{opt}+F_{sat}}\right)}^2$$

(1)

where ${\tau }_{THz}$ is the THz pulse duration, E is the applied transverse field, $Z_0\approx 376.73$ Ohm is the free space impedance, $F_{opt}$ is the pump fluence, and $F_{sat}$ is the saturation fluence.

The E-field of the THz wave is expected to be proportional to the bias field, and according to Equation (1) the growth of the bias field results in the quadratic increase in the THz output. Also according to Equation (1), the THz output grows as the square of the pump fluence and then saturates incrementally as $F_{opt}$ increases. The saturation fluence $F_{sat}$ characterizes the performance of the PCA. Essentially, $F_{sat}$ indicates how small an optical fluence can be that still provides effective carrier generation in terms of THz emission. It is expressed as [36]:

$$F_{sat}^a=\frac{h\nu (1+n)}{e\mu Z_0(1-R)}$$

(2)

where $h\nu$ is the photon energy, n is the substrate (diamond) refractive index, e is the electron charge, $\mathsf{\mu }$ is the carrier mobility, R is the air-semiconductor interface reflection. The superscript “a” indicates that Equation (2) explicitly suggests the total absorption of the pump radiation.

3.2. Computation of LAPCA with Longitudinal Bias Field

As mentioned above, the THz generation in longitudinal-field LAPCA is assumed to result from the bulk photocurrent driven by the component of the E-field orthogonal to the optical pump beam. To validate this assumption, the results of the numerical calculation given below were approximated by Equation (1) at $E=E_{bias}\times sin\left(\beta \right)=E_{bias}\times sin\left(\alpha \right)/n$ ($E_{bias}$ is the longitudinal bias field, $\alpha$ is the incident angle, $\beta$ is the refracted angle).

The calculations of the THz generation in a longitudinally biased ideal diamond LAPCA are shown in Figure 4. Parts (a–c) illustrate the dynamics of the THz electromagnetic wave arising at $E_{bias}=1$ kV/cm and a 45${}^{\circ }$ angle of incidence. The 2D maps show the THz pulse before and after it is torn off the diamond slab. As expected, the THz beam appears to be parallel to the optical beam both in the substrate and in the surrounding space in which they move. The back wave predicted in [35] is seen. It is also clear how the E-field is depleted as the conductivity wave propagates through the emitter slab. The calculated waveform of the THz field seems to show a two peak structure with a delay of ∼1 ps and a long weak tail containing the low frequency part of the THz spectrum (Figure 4c). Thus, the numerical simulation confirms the principle possibility of longitudinal biasing for large photoconductive antennas.

The last parts of Figure 4 show the magnitude of the THz field taken at the probe point as a function of the bias field, the amplitude of the conductivity wave, and the angle of incidence. In general, the dependencies are in good agreement with Equation (1). First, the THz field increases linearly with the static E-field, at least in the range realized in the experiments—below the surface electrical breakdown of diamond (Figure 4d). Second, the dependence of the THz amplitude on the conductivity amplitude follows a rational function of the form $E_{THz}\sim \sigma /(\sigma +const)$ (Figure 4e). The discrepancy occurs at high conductivity (i.e., high laser fluence) and is likely to be caused by the screening effect of the photoplasma. And third, an excellent agreement was found for the incident angle dependence when the partial reflection of the p-polarized THz wave at the diamond-vacuum interface is taken into account. The transmission coefficient in this case is described by the Fresnel equations: $t_p=2n·cos\left(\beta \right)/(cos\left(\beta \right)+n·cos\left(\alpha \right))$. The resulting E-field in the emitted pulse is proportional to the $E_{THz}\sim sin\left(\alpha \right)\times t_p$, as can be seen from the data in Figure 4f. Thus, the calculation suggests that, to a first approximation, the THz output of the longitudinal-field LAPCA can be described in the frame of a simple model of the surface photocurrent pulse.

3.3. Main Characteristics of Longitudinal Bias Field LAPCAs

Analogous dependencies were measured in the experiments for all assembled LAPCAs. The THz output as a function of the applied E-field is shown in Figure 5a. The measured power was recalculated into emitted fluence to allow correct comparison of the LAPCAs, which are quite different in aperture.

The antenna with ITO electrodes was found to be much less effective than the two antennas with graphite electrodes. The reason is the rather fast degradation of the ITO films induced by the repetitive HV pulses. The conductive layers were destroyed within several seconds and their resistance increased from ∼1 kOhm to a level comparable to the resistance of diamond. Obviously, the $F_{THz}\left(E_{bias}\right)$ curve for the ITO emitter is strongly shifted to the high bias region—the real $E_{bias}$ magnitude was significantly lower. The both LAPCAs equipped with graphite electrodes showed close output levels, the linear relationship between the static field and the THz field, and close coefficients of transformation from the static field to the THz field (Figure 5a). The maximum yield of THz radiation from the longitudinal configuration of a diamond LAPCA was about ≈0.62 nJ, while the emission level for the transverse configuration was somewhat higher, reaching ≈0.76 nJ.

The laser fluence dependence of the THz power was also found to obey Equation (1), especially in the case of longitudinal field LAPCA with graphite grid electrodes (Figure 5b). It is instructive to note that regardless of the different bias fields, the saturation fluence values of the LAPCAs involved are quite close to each other ($F_{sat}\approx 250$$\mathsf{\mu }$J/cm${}^2$). This is because $F_{sat}$ is a property of the substrate, not of the antenna design, and is defined only by the sample absorption at the laser wavelength. Since the substrate crystal was the same, the data described suggest that the longitudinal field design provides the THz output in strict accordance with the applied bias and pump level, satisfying (1). Note that from the data in Figure 5b, the optical-to-THz conversion efficiency was estimated to be at the level of ≈0.0008% for the longitudinal configuration of LAPCA and ≈0.0004% for the transverse one.

For the emitter with graphite grids, the THz output was measured as a function of the angle of incidence of the pump beam (Figure 5c). As can be seen, the data are ideally fitted by the curve:

$$F_{THz}\sim si{n}^2\left(\alpha \right)\times T_p\left(\alpha \right)$$

(3)

where $T_p$ is the Fresnel coefficient for the transmitted power of the p-polarized wave. Since the first interface (vacuum–diamond) is traversed by visible light and the second (diamond–vacuum) by THz electromagnetic wave, two different transmission coefficients should be used. For simplicity, the optical dispersion of the medium was omitted and the $T_p$ formula was used for the diamond slab. Despite this simplification, only two deviations of the experimental data from the Formula (3) were observed. The first is the non-monotonic character of the $F_{THz}\left(\alpha \right)$ dependence. The local symmetrical maxima appeared at incident angles of ≈$\pm {50}^{\circ }$ (Figure 5c). The reason is purely technical: the plastic enclosure shaded the radiation at such large angles. The second anomaly is a non-zero THz signal measured at normal incidence, the reason for which is still unclear. We tentatively assume that the not completely symmetrical design of the grid electrodes (the buses are asymmetrical) resulted in a small transverse component of the bias field, which in turn causes the LAPCA to generate THz pulses even at $\alpha =0^{\circ }$.

The THz pulse waveform acquired by electro-optical sampling and the corresponding spectrum calculated by Fourier transform of the waveform are presented in Figure 6. They show the typical behavior of THz photoconductive antennas. The main electrical pulse lasts ∼1 ps and is followed by a long tail of relatively low amplitude. The spectrum shows a low frequency maximum (about 1 THz) with a high frequency shoulder that propagates up to ∼3 THz. Note that several low frequency components are quite strong and even higher than the main maximum.

On the whole, the calculated spectrum is in good agreement with the experiment (Figure 6b). It consists of ∼1 THz wide bands whose heights decrease with frequency growth. The main band is centered around $f=1$ THz. The calculated spectrum also showed the strong long wavelength shoulder. The presence of these frequencies in the emitted radiation is questionable. The measured spectrum shows rather weak radiation in this spectral range, but it cannot be said with certainty that this shoulder is really absent, because the sensitivity of the detectors in this range is quite low.

4. Conclusions

In conclusion, this work reports the realization of a large aperture terahertz diamond photoconductive antennas with a longitudinally oriented bias field. The novel design allows the interelectrode gap to be reduced compared to the conventional transverse-field design, and remarkably enhances the field at the same applied voltage. It was shown that the THz output of the longitudinal-field LAPCAs can be well described by the well-known simple model of the photocurrent driven by the E-field, the value of which is adjusted for oblique incidence. The static-to-THz field conversion efficiencies of the longitudinal-field emitter with the graphite laser-written grid electrodes and the conventional transverse-field emitter were shown to be quite close. The saturation fluence of the assembled LAPCAs was found to be independent of the electrode design. The summarized parameters characterizing photoconductive antennas with the conventional transverse E-field configuration and the novel longitudinal configuration are given in

Table 1. Comparison of different configurations of diamond LAPCAs.

	Transverse E-Field	Longitudinal E-Field
Clear biased aperture, A	5.2 × 2.4 mm	3.6 × 2.0 mm
Incidence angle	0${}^{\circ }$	45–50${}^{\circ }$
HV electrodes	Edge graphitized surface	Grid graphitized surface
Saturation fluence, F${}_{sat}$	245 $\mathsf{\mu }$J/cm${}^2$	255 $\mathsf{\mu }$J/cm${}^2$
Maximum THz yield	0.76 nJ	0.62 nJ
Optical-to-THz conversion	0.0004%	0.0008%

. These results open the way to the construction of new large-aperture, high-energy, high-power diamond-based THz antennas pumped by portable ultrafast lasers. Future work should aim at encapsulating the graphite electrodes in the diamond bulk. This will allow to eliminate the surface discharge current and to explore the operation of such LAPCAs with a bias field that is maximum for the diamond.