Periodical Ultra-Modulation of Broadened Laser Spectra in Dielectrics at Variable Ultrashort Laser Pulsewidths: Ultrafast Plasma, Plasmonic and Nanoscale Structural Effects
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Effect of Nitrogen Impurity
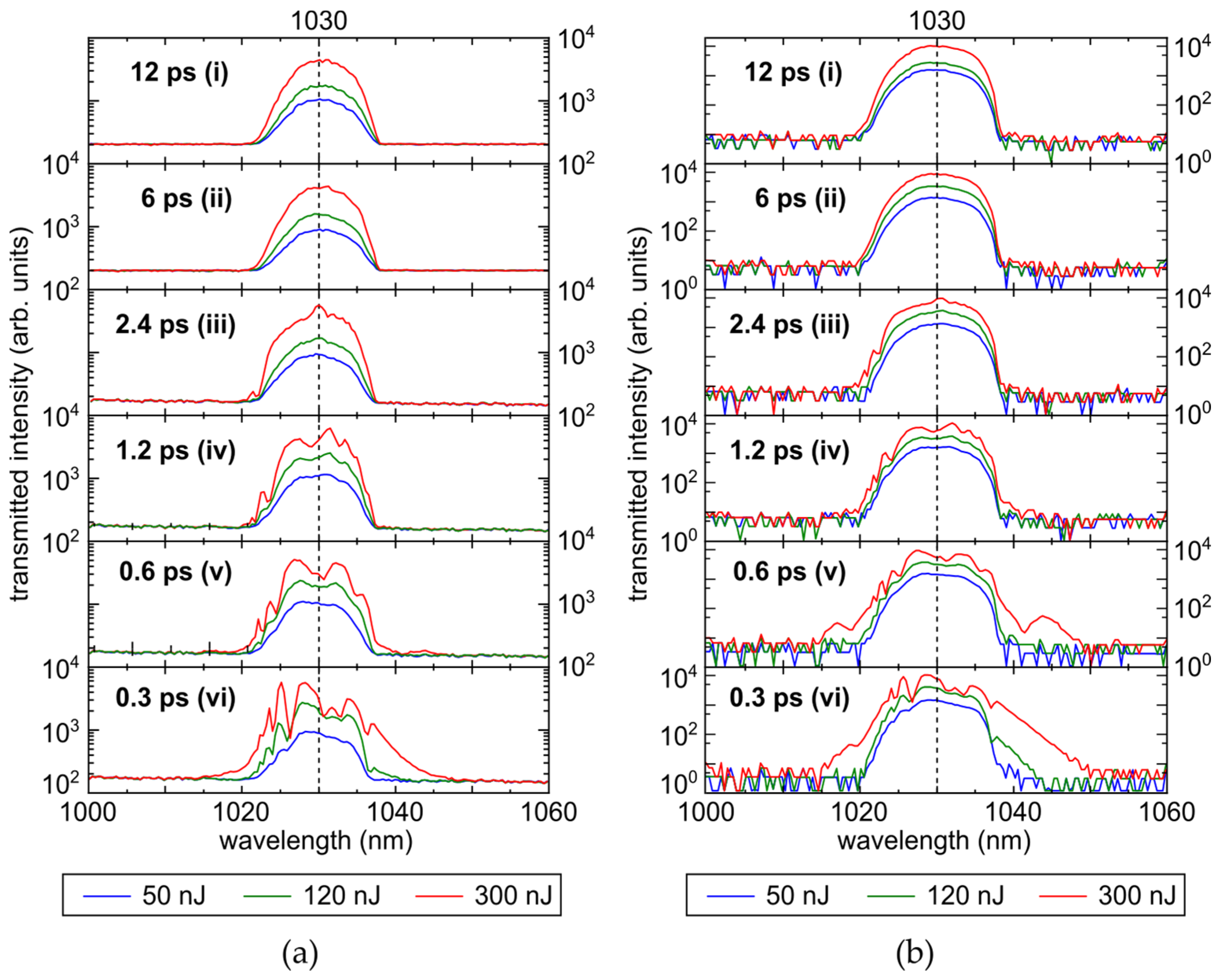
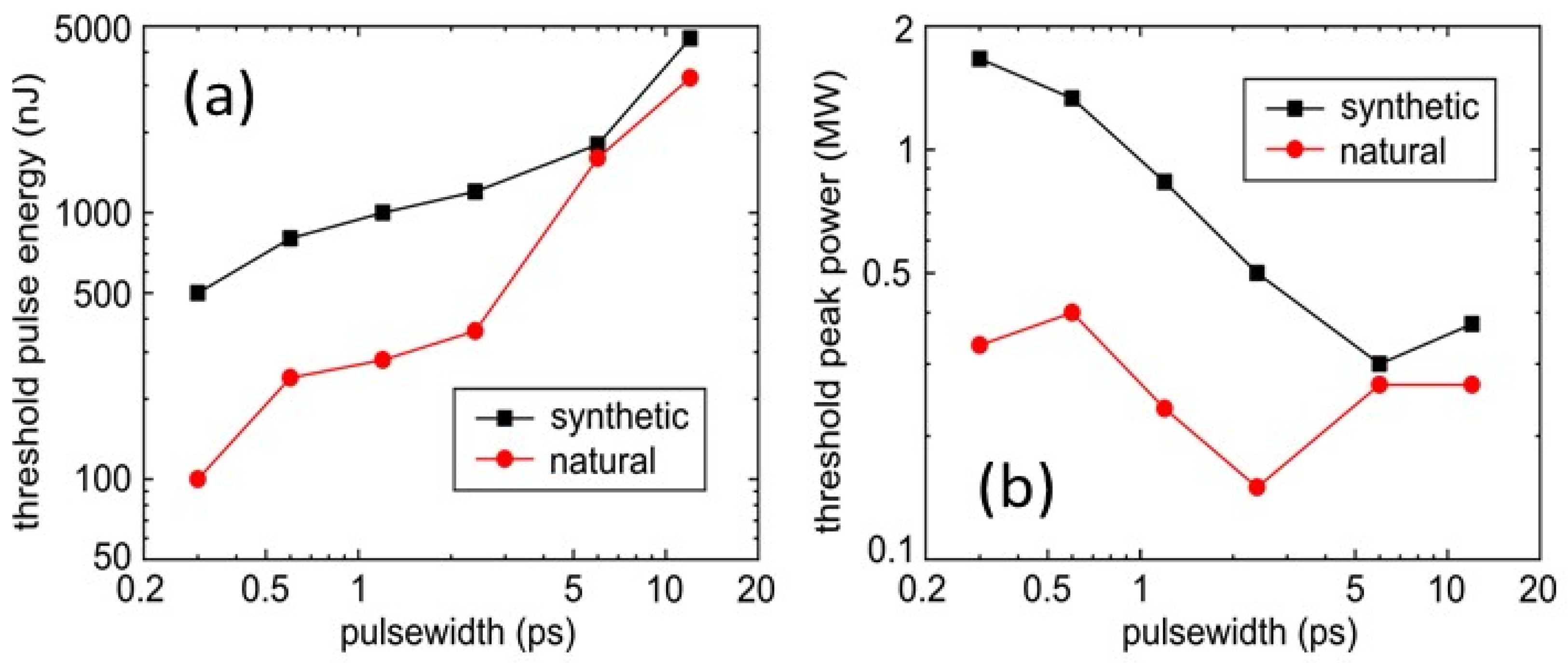
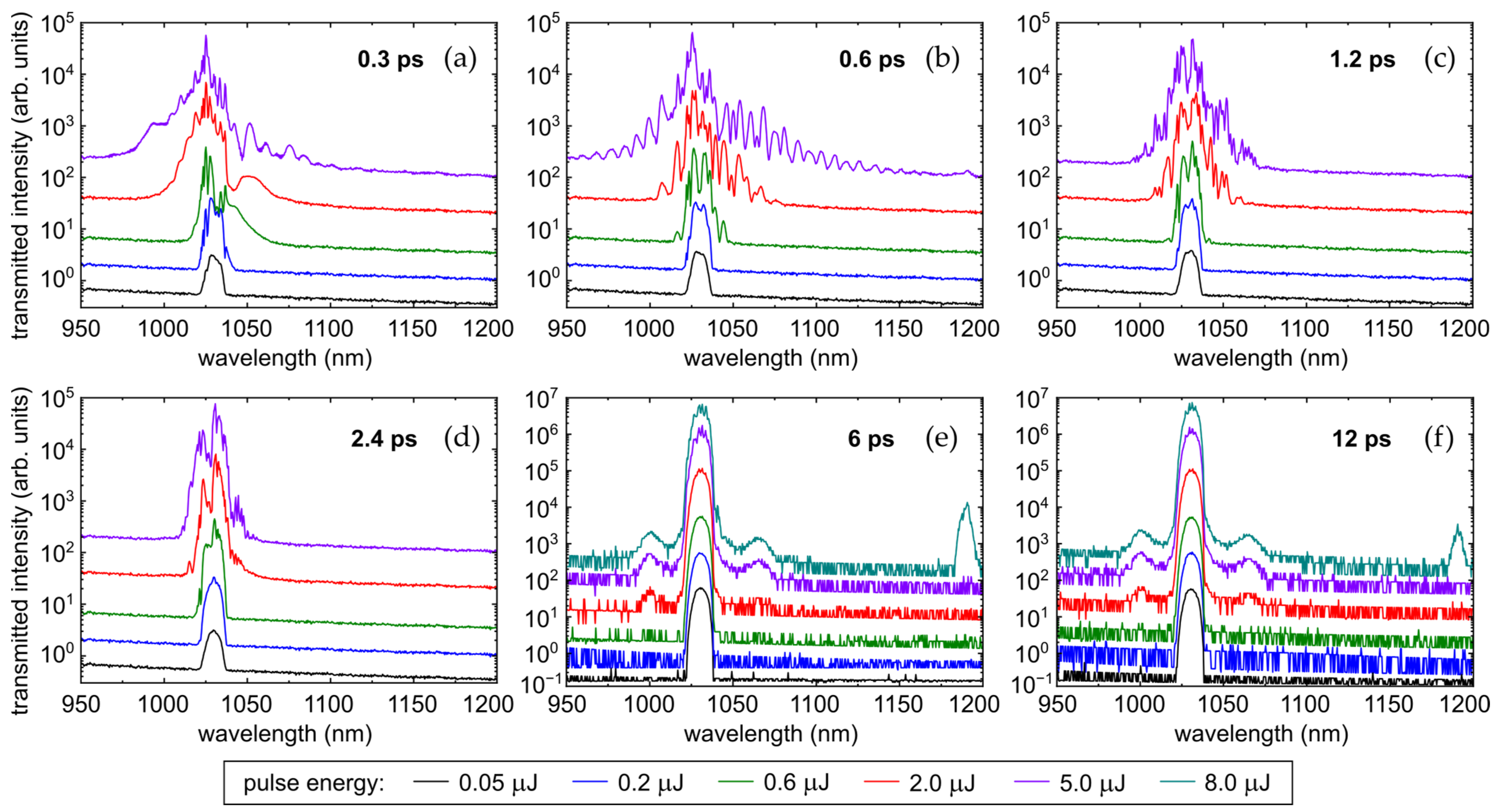
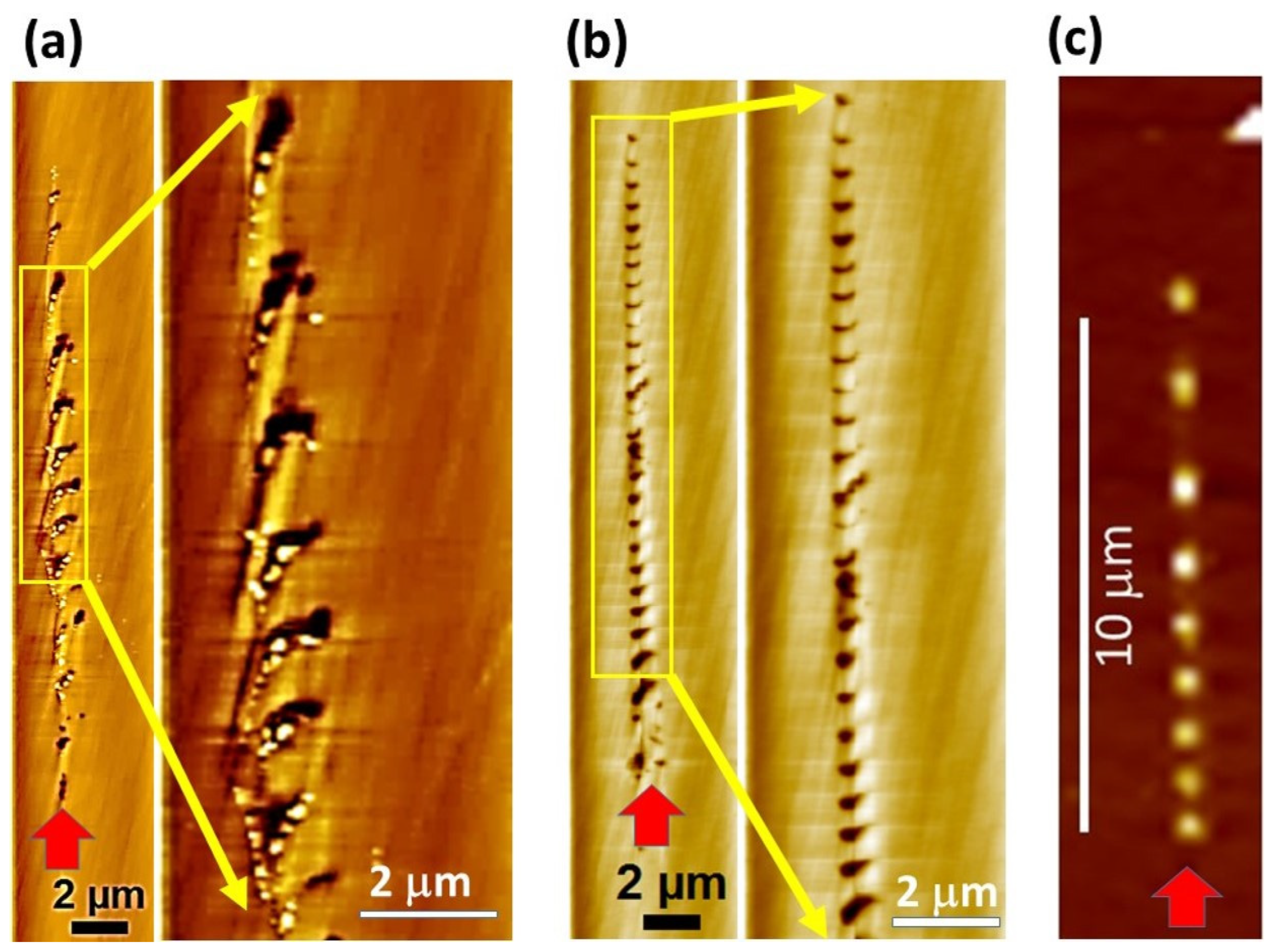
3.2. Effect of Pulsewidth
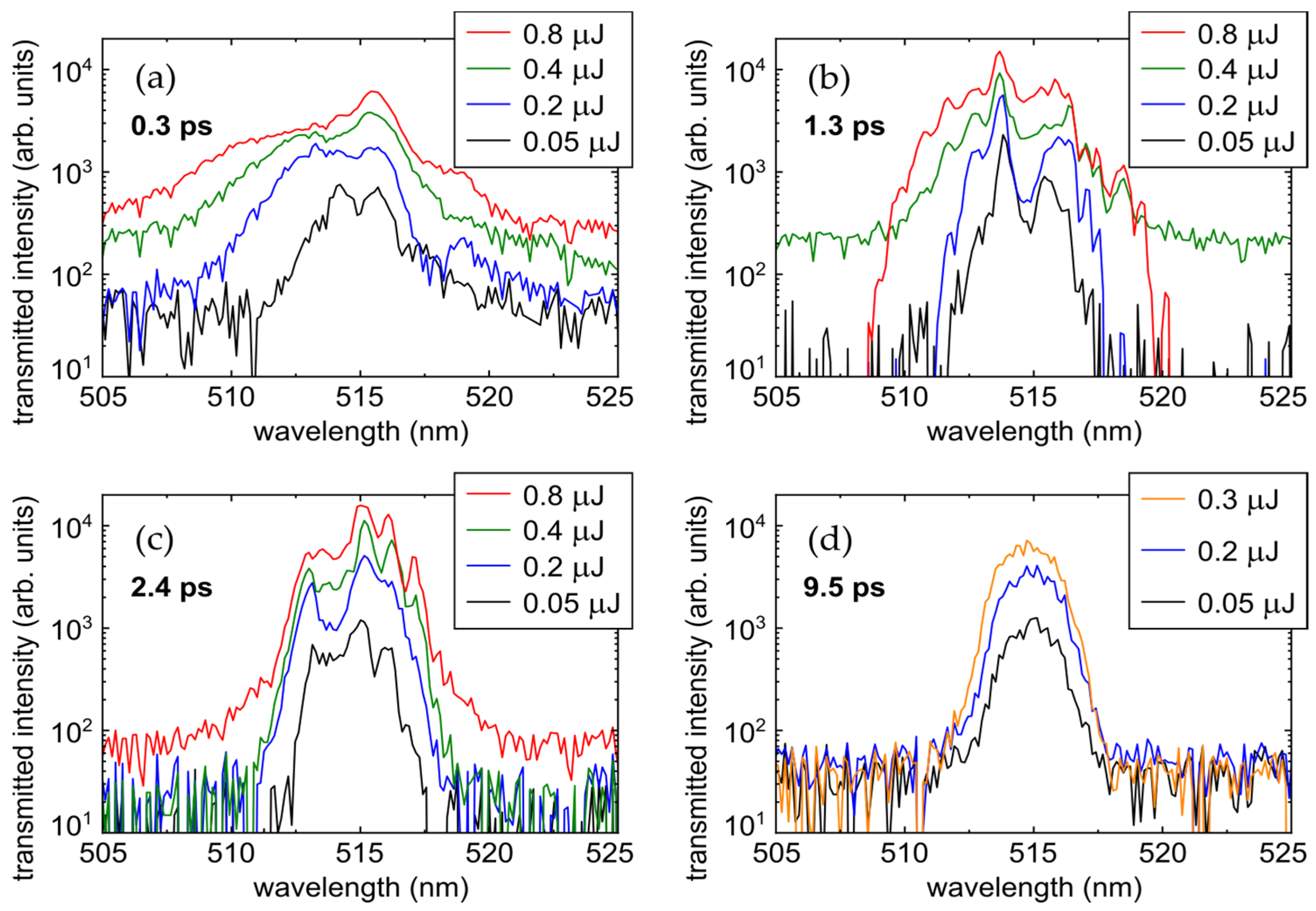
3.3. Effect of Pulse Energy
3.4. Effect of Wavelength
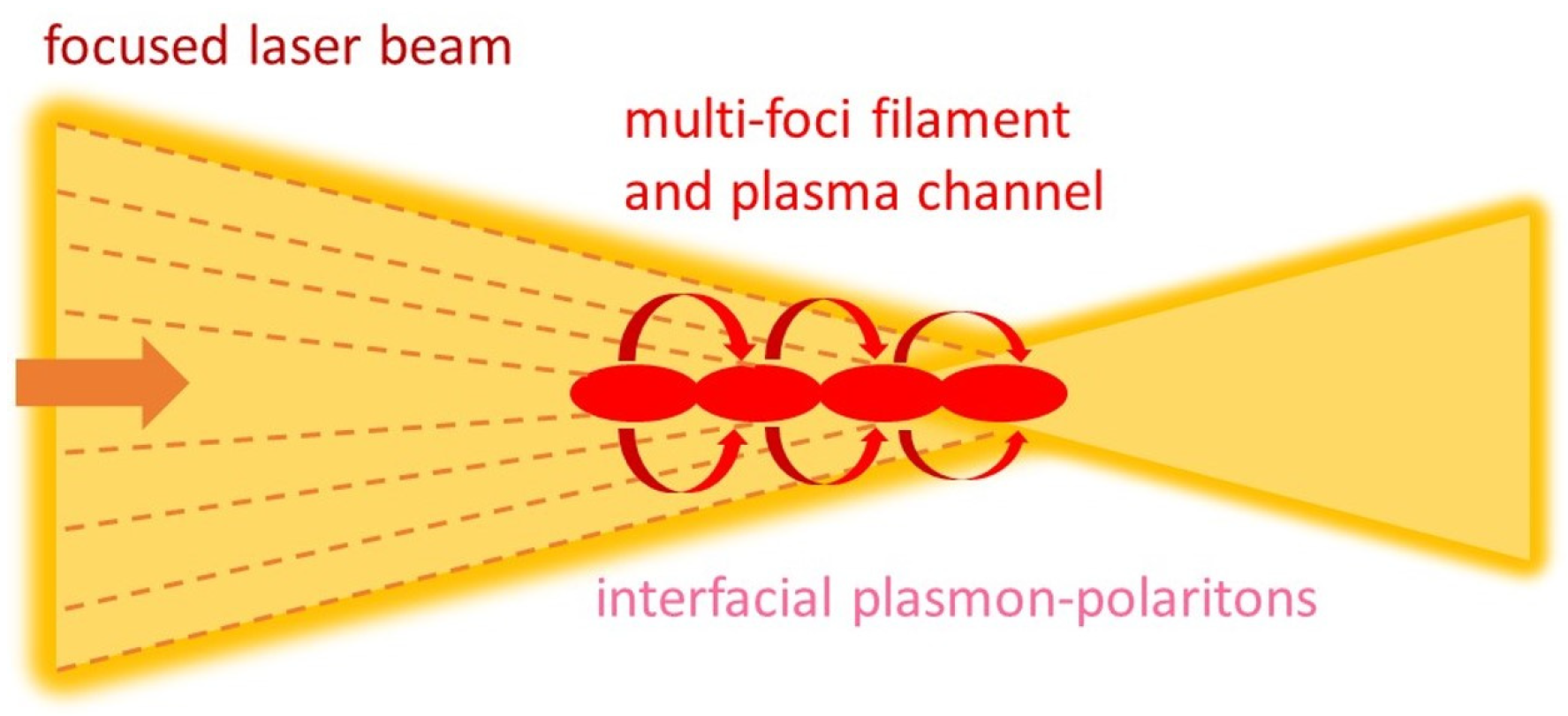
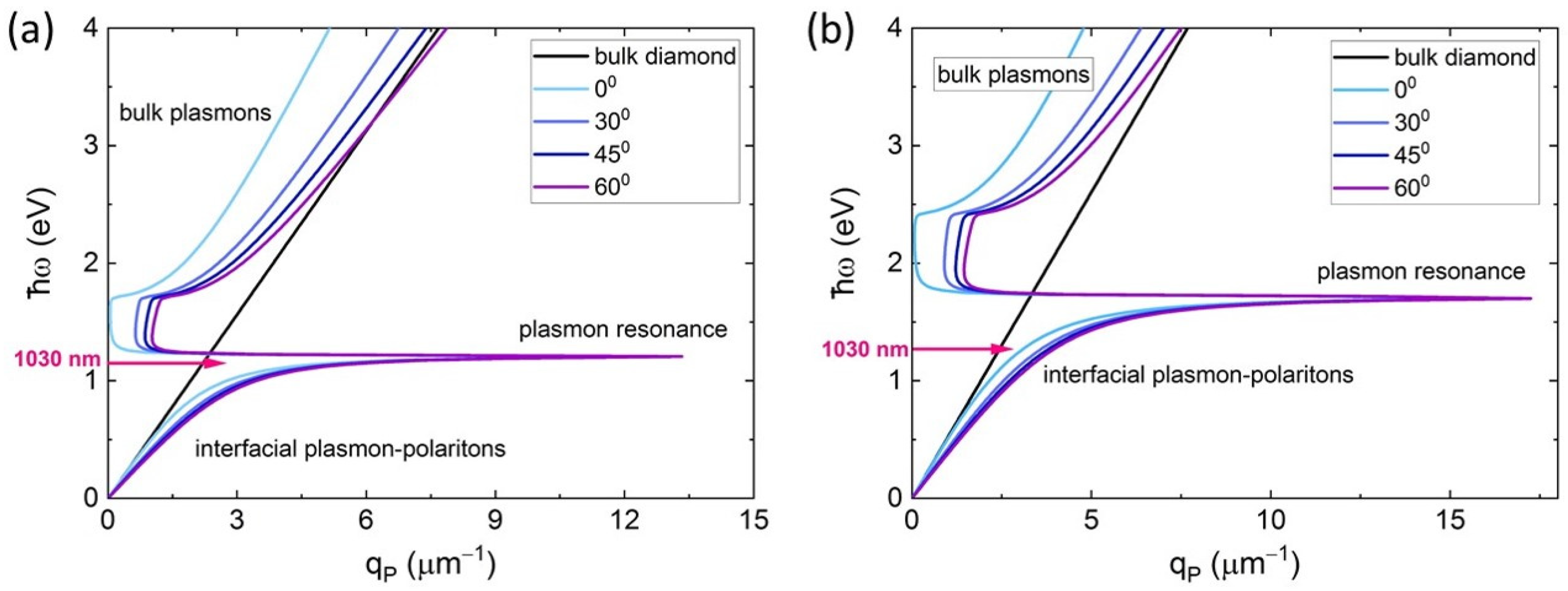
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sugioka, K.; Cheng, Y. Ultrafast Lasers-Reliable Tools for Advanced Materials Processing. Light Sci. Appl. 2014, 3, 149. [Google Scholar] [CrossRef]
- Sotillo, B.; Bharadwaj, V.; Hadden, J.P.; Sakakura, M.; Chiappini, A.; Fernandez, T.T.; Longhi, S.; Jedrkiewicz, O.; Shimotsuma, Y.; Criante, L.; et al. Diamond photonics platform enabled by femtosecond laser writing. Sci. Rep. 2016, 6, 35566. [Google Scholar] [CrossRef] [PubMed]
- Couairon, A.; Sudrie, L.; Franco, M.; Prade, B.; Mysyrowicz, A. Filamentation and damage in fused silica induced by tightly focused femtosecond laser pulses. Phys. Rev. B 2005, 71, 125435. [Google Scholar] [CrossRef]
- Klimov, V. Nanoplasmonics; CRC Press: Singapore, 2014. [Google Scholar]
- Kudryashov, S.; Rupasov, A.; Kosobokov, M.; Akhmatkhanov, A.; Krasin, G.; Danilov, P.; Lisjikh, B.; Abramov, A.; Greshnyakov, E.; Kuzmin, E.; et al. Hierarchical Multi-Scale Coupled Periodical Photonic and Plasmonic Nanopatterns Inscribed by Femtosecond Laser Pulses in Lithium Niobate. Nanomaterials 2022, 12, 4303. [Google Scholar] [CrossRef] [PubMed]
- Mouskeftaras, A.; Rode, A.V.; Clady, R.; Sentis, M.; Utéza, O.; Grojo, D. Self-limited underdense microplasmas in bulk silicon induced by ultrashort laser pulses. Appl. Phys. Lett. 2014, 105, 191103. [Google Scholar] [CrossRef]
- Papazoglou, D.G.; Abdollahpour, D.; Tzortzakis, S. Ultrafast electron and material dynamics following femtosecond filamentation induced excitation of transparent solids. Appl. Phys. A 2014, 114, 161–168. [Google Scholar] [CrossRef]
- Jürgens, P.; Vrakking, M.J.J.; Husakou, A.; Stoian, R.; Mermillod-Blondin, A. Plasma formation and relaxation dynamics in fused silica driven by femtosecond short-wavelength infrared laser pulses. Appl. Phys. Lett. 2019, 115, 191903. [Google Scholar] [CrossRef]
- Geints, Y.E.; Zemlyanov, A.A.; Ionin, A.A.; Kudryashov, S.I.; Seleznev, L.V.; Sinitsyn, D.V.; Sunchugasheva, E.S. Peculiarities of filamentation of sharply focused ultrashort laser pulses in air. J. Exp. Theor. Phys. 2010, 111, 724–730. [Google Scholar] [CrossRef]
- Song, J.; Wang, X.; Hu, X.; Dai, Y.; Qiu, J.; Cheng, Y.; Xu, Z. Formation mechanism of self-organized voids in dielectrics induced by tightly focused femtosecond laser pulses. Appl. Phys. Lett. 2008, 92, 092904. [Google Scholar] [CrossRef]
- Li, X.; Xu, J.; Lin, Z.; Qi, J.; Wang, P.; Chu, W.; Fang, Z.; Wang, Z.; Chai, Z.; Cheng, Y. Polarization-insensitive space-selective etching in fused silica induced by picosecond laser irradiation. Appl. Surf. Sci. 2019, 485, 188–193. [Google Scholar] [CrossRef]
- Xu, S.; Fan, H.; Li, Z.-Z.; Hua, J.-G.; Yu, Y.-H.; Wang, L.; Chen, Q.-D.; Sun, H.-B. Ultrafast laser-inscribed nanogratings in sapphire for geometric phase elements. Opt. Lett. 2021, 46, 536–539. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Liu, X.; Qiu, J. Single femtosecond laser beam induced nanogratings in transparent media—Mechanisms and applications. J. Mater. 2019, 5, 1–14. [Google Scholar] [CrossRef]
- Kudryashov, S.; Rupasov, A.; Zakoldaev, R.; Smaev, M.; Kuchmizhak, A.; Zolot’ko, A.; Kosobokov, M.; Akhmatkhanov, A.; Shur, V. Nanohydrodynamic Local Compaction and Nanoplasmonic Form-Birefringence Inscription by Ultrashort Laser Pulses in Nanoporous Fused Silica. Nanomaterials 2022, 12, 3613. [Google Scholar] [CrossRef] [PubMed]
- Shimotsuma, Y.; Kazansky, P.G.; Qiu, J.; Hirao, K. Self-organized nanogratings in glass irradiated by ultrashort light pulses. Phys. Rev. Lett. 2003, 91, 247405. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.; Hnatovsky, C.; Simova, E. Applications of femtosecond laser induced self-organized planar nanocracks inside fused silica glass. Laser Photonics Rev. 2008, 2, 26–46. [Google Scholar] [CrossRef]
- Kudryashov, S.I.; Danilov, P.A.; Rupasov, A.E.; Smayev, M.P.; Kirichenko, A.N.; Smirnov, N.A.; Ionin, A.A.; Zolot’ko, A.S.; Zakoldaev, R.A. Birefringent microstructures in bulk fluorite produced by ultrafast pulsewidth-dependent laser inscription. Appl. Surf. Sci. 2021, 568, 150877. [Google Scholar] [CrossRef]
- Couairon, A.; Mysyrowicz, A. Femtosecond filamentation in transparent media. Phys. Rep. 2007, 441, 47–189. [Google Scholar] [CrossRef]
- Kudryashov, S.; Danilov, P.; Chen, J. Intrapulse correlated dynamics of self-phase modulation and spontaneous Raman scattering in synthetic diamond excited and probed by positively chirped ultrashort laser pulses. Photonics 2023, 10, 626. [Google Scholar] [CrossRef]
- Kudryashov, S.; Krasin, G.; Rupasov, A.; Danilov, P.; Kosobokov, M.; Akhmatkhanov, A.; Lisjikh, B.; Turygin, A.; Greshnyakov, E.; Kovalev, M.; et al. Ferroelectric nanodomain engineering in bulk lithium niobate crystals in ultrashort-pulse laser nanopatterning regime. Nanomaterials 2022, 12, 4147. [Google Scholar] [CrossRef]
- Krasin, G.K.; Gulina, Y.S.; Kuzmin, E.V.; Martovitskii, V.P.; Kudryashov, S.I. Polarization-Sensitive Nonlinear Optical Interaction of Ultrashort Laser Pulses with HPHT Diamond. Photonics 2023, 10, 106. [Google Scholar] [CrossRef]
- Zaitsev, A.M. Optical Properties of Diamond: A Data Handbook; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kudryashov, S.I.; Danilov, P.A.; Kuzmin, E.V.; Gulina, Y.S.; Rupasov, A.E.; Krasin, G.K.; Zubarev, I.G.; Levchenko, A.O.; Kovalev, M.S.; Pakholchuk, P.P.; et al. Pulse-width-dependent critical power for self-focusing of ultrashort laser pulses in bulk dielectrics. Opt. Lett. 2022, 47, 3487–3490. [Google Scholar] [CrossRef] [PubMed]
- Ishioka, K.; Hase, M.; Kitajima, M.; Petek, H. Coherent optical phonons in diamond. Appl. Phys. Lett. 2006, 89, 231916. [Google Scholar] [CrossRef]
- Zukerstein, M.; Kozák, M.; Trojánek, F.; Malý, P. Experimental observation of anharmonic effects in coherent phonon dynamics in diamond. Diam. Relat. Mater. 2018, 90, 202–206. [Google Scholar] [CrossRef]
- Liu, S.; Hammud, A.; Hamada, I.; Wolf, M.; Müller, M.; Kumagai, T. Nanoscale coherent phonon spectroscopy. Sci. Adv. 2022, 8, eabq5682. [Google Scholar] [CrossRef] [PubMed]
- Klemens, P.G. Anharmonic decay of optical phonon in diamond. Phys. Rev. B 1975, 11, 3206. [Google Scholar] [CrossRef]
- Kudryashov, S.; Danilov, P.; Smirnov, N.; Krasin, G.; Khmelnitskii, R.; Kovalchuk, O.; Kriulina, G.; Martovitskiy, V.; Lednev, V.; Sdvizhenskii, P.; et al. “Stealth Scripts”: Ultrashort Pulse Laser Luminescent Microscale Encoding of Bulk Diamonds via Ultrafast Multi-Scale Atomistic Structural Transformations. Nanomaterials 2023, 13, 192. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.R. The Principles of Nonlinear Optics; Wiley-Interscience: New York, NY, USA, 1984. [Google Scholar]
- Grudtsyn, Y.V.; Zubarev, I.G.; Koribut, A.V.; Kuchik, I.E.; Mamaev, S.B.; Mikheev, L.D.; Semjonov, S.L.; Stepanov, S.G.; Trofimov, V.A.; Yalovoi, V.I. Self-Phase modulation in a thin fused silica plate upon interaction with a converging beam of down-chirped femtosecond radiation. Quantum Electron. 2015, 45, 415–420. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, L.; Wang, L.; Fang, C. Cascaded four-wave mixing for broadband tunable laser sideband generation. Opt. Lett. 2013, 38, 1772–1774. [Google Scholar] [CrossRef]
- Bencivenga, F.; Cucini, R.; Capotondi, F.; Battistoni, A.; Mincigrucci, R.; Giangrisostomi, E.; Gessini, A.; Manfredda, M.; Nikolov, I.P.; Masciovecchio, C.; et al. Four-wave mixing experiments with extreme ultraviolet transient gratings. Nature 2015, 520, 205–208. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Orlando, FL, USA, 1998. [Google Scholar]
- Bell, R.J.; Alexander, R.W., Jr.; Parks, W.F.; Kovener, G. Surface excitations in absorbing media. Opt. Commun. 1973, 8, 147–150. [Google Scholar] [CrossRef]
- He, L.; Yi, Y.; Zhang, J.; Xu, X.; Tang, B.; Li, G.; Zeng, L.; Chen, J.; Sun, T.; Yi, Z. A four-narrowband terahertz tunable absorber with perfect absorption and high sensitivity. Mater. Res. Bull. 2024, 170, 112572. [Google Scholar] [CrossRef]
- Yuan, X.; Xu, Q.; Lang, Y.; Jiang, X.; Xu, Y.; Chen, X.; Han, J.; Zhang, X.; Han, J.; Zhang, W. Tailoring spatiotemporal dynamics of plasmonic vortices. Opto-Electron. Adv. 2023, 6, 220133. [Google Scholar] [CrossRef]
- Guo, X.; Ma, Y.; Wang, Y.; Tong, L. Nanowire plasmonic waveguides, circuits and devices. Laser Photonics Rev. 2013, 7, 855–881. [Google Scholar] [CrossRef]
- Kudryashov, S.I.; Nastulyavichus, A.A.; Saraeva, I.N.; Rudenko, A.A.; Zayarny, D.A.; Ionin, A.A. Deeply sub-wavelength laser nanopatterning of Si surface in dielectric fluids: Manipulation by surface plasmon resonance. Appl. Surf. Sci. 2020, 519, 146204. [Google Scholar] [CrossRef]
- Bak, J.; Suazo Betancourt, J.L.; Rekhy, A.; Abbasszadehrad, A.; Miles, R.B.; Limbach, C.M.; Walker, M.L. High resolution spatially extended 1D laser scattering diagnostics using volume Bragg grating notch filters. Rev. Sci. Instrum. 2023, 94, 023003. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudryashov, S.; Danilov, P.; Gorevoy, A.; Kovalov, V.; Kosobokov, M.; Akhmatkhanov, A.; Lisjikh, B.; Turygin, A.; Greshnyakov, E.; Shur, V. Periodical Ultra-Modulation of Broadened Laser Spectra in Dielectrics at Variable Ultrashort Laser Pulsewidths: Ultrafast Plasma, Plasmonic and Nanoscale Structural Effects. Photonics 2023, 10, 1316. https://doi.org/10.3390/photonics10121316
Kudryashov S, Danilov P, Gorevoy A, Kovalov V, Kosobokov M, Akhmatkhanov A, Lisjikh B, Turygin A, Greshnyakov E, Shur V. Periodical Ultra-Modulation of Broadened Laser Spectra in Dielectrics at Variable Ultrashort Laser Pulsewidths: Ultrafast Plasma, Plasmonic and Nanoscale Structural Effects. Photonics. 2023; 10(12):1316. https://doi.org/10.3390/photonics10121316
Chicago/Turabian StyleKudryashov, Sergey, Pavel Danilov, Alexey Gorevoy, Volodymyr Kovalov, Mikhail Kosobokov, Andrey Akhmatkhanov, Boris Lisjikh, Anton Turygin, Evgeny Greshnyakov, and Vladimir Shur. 2023. "Periodical Ultra-Modulation of Broadened Laser Spectra in Dielectrics at Variable Ultrashort Laser Pulsewidths: Ultrafast Plasma, Plasmonic and Nanoscale Structural Effects" Photonics 10, no. 12: 1316. https://doi.org/10.3390/photonics10121316
APA StyleKudryashov, S., Danilov, P., Gorevoy, A., Kovalov, V., Kosobokov, M., Akhmatkhanov, A., Lisjikh, B., Turygin, A., Greshnyakov, E., & Shur, V. (2023). Periodical Ultra-Modulation of Broadened Laser Spectra in Dielectrics at Variable Ultrashort Laser Pulsewidths: Ultrafast Plasma, Plasmonic and Nanoscale Structural Effects. Photonics, 10(12), 1316. https://doi.org/10.3390/photonics10121316







