Model-Based Real Time Operation of the Freeze-Drying Process
Abstract
1. Introduction
- It shows how the identification problem (i.e., characterization of product and equipment) can be simplified by solving a (decoupled) sequence of parameter identification problems, this is, by considering food matrix and freeze-drying chamber as two separate subsystems, which are described by physics-based operational models developed to satisfy identifiability.
- It provides a robust, digital tool that supports decision-making in real time for complex food structuring processes (such freeze-drying). This has potential for significant reductions in cost and processing times, waste generation (e.g., reducing batch rejection) and energy demand (e.g., off-line and in-line strategies can be used to minimize energy use during processing) [10,28].
2. Lyophilization Plant and Mathematical Model
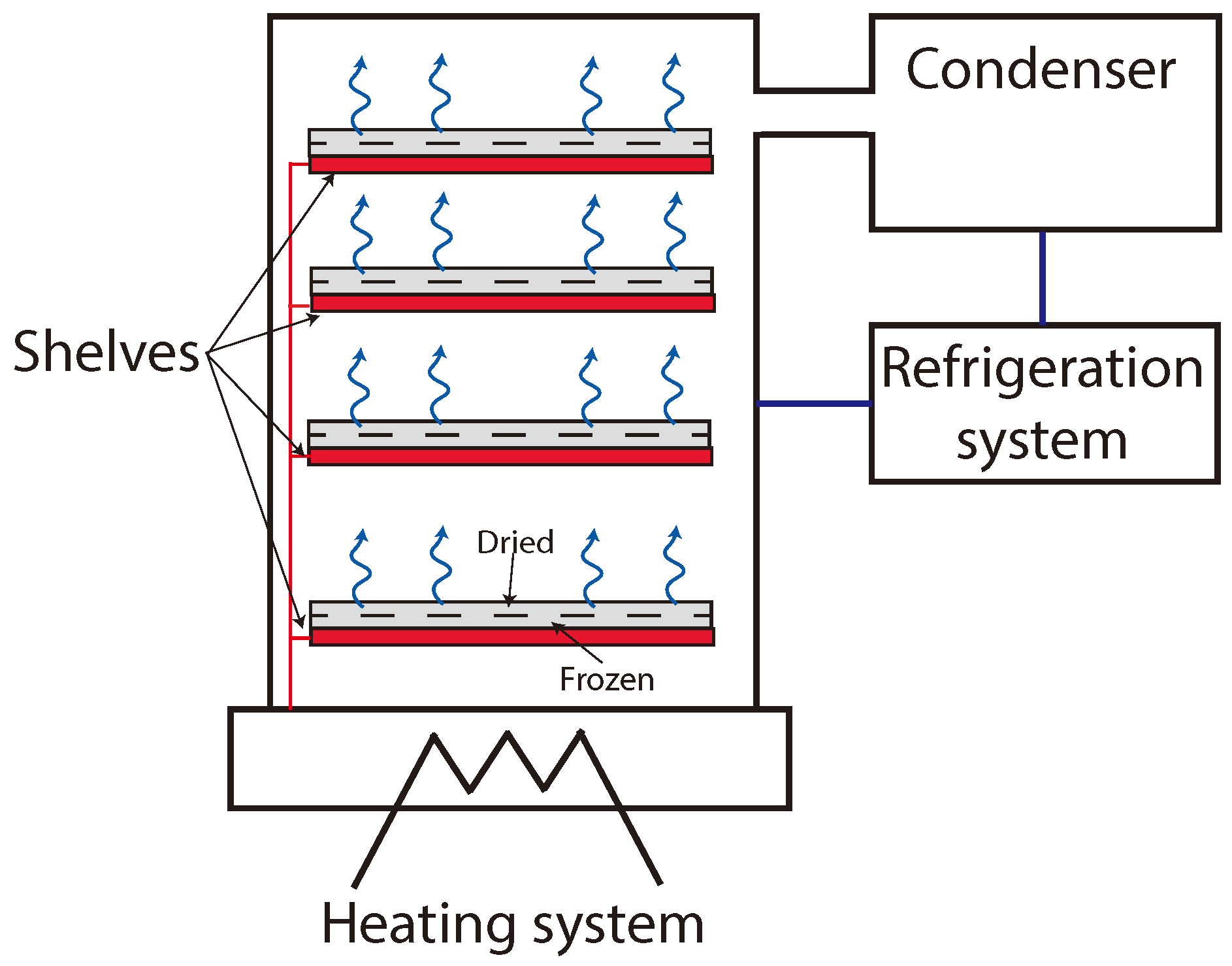
2.1. Lyophilization Pilot Plant and Experimental Setup Description
2.2. A Physical Model for the Freeze-Drying Process
- Freezing. The product is frozen in controlled conditions to avoid possible damage, by crystal growth, to the food or biological material. Our model does not include this stage. The product temperature is assumed to be uniform at the end of the freezing stage, and it is used as the initial temperature for the primary drying.
- Primary drying. In this stage, ice is removed from the product by sublimation. Pressure conditions are kept below the triple point and the product is heated from the bottom. An excessive temperature increase in this stage will cause product to collapse so it must be kept below a given value, see Section 2.2.4 for details.
- Secondary drying. The aim is to remove water bound to the solid matrix by desorption. This stage allows for reaching low moisture contents. The food product is more stable during secondary drying so its temperature may be increased to accelerate the process.
- The frozen region has uniform heat and mass transfer properties.
- The interface between the frozen and dried layers (sublimation front) is continuous and has infinitesimal thickness.
- Vapor and ice are at equilibrium at the interface.
- The matrix pore structure is permeable to the vapor flux and it is not deformable.
2.2.1. The Primary Drying
2.2.2. The Secondary Drying
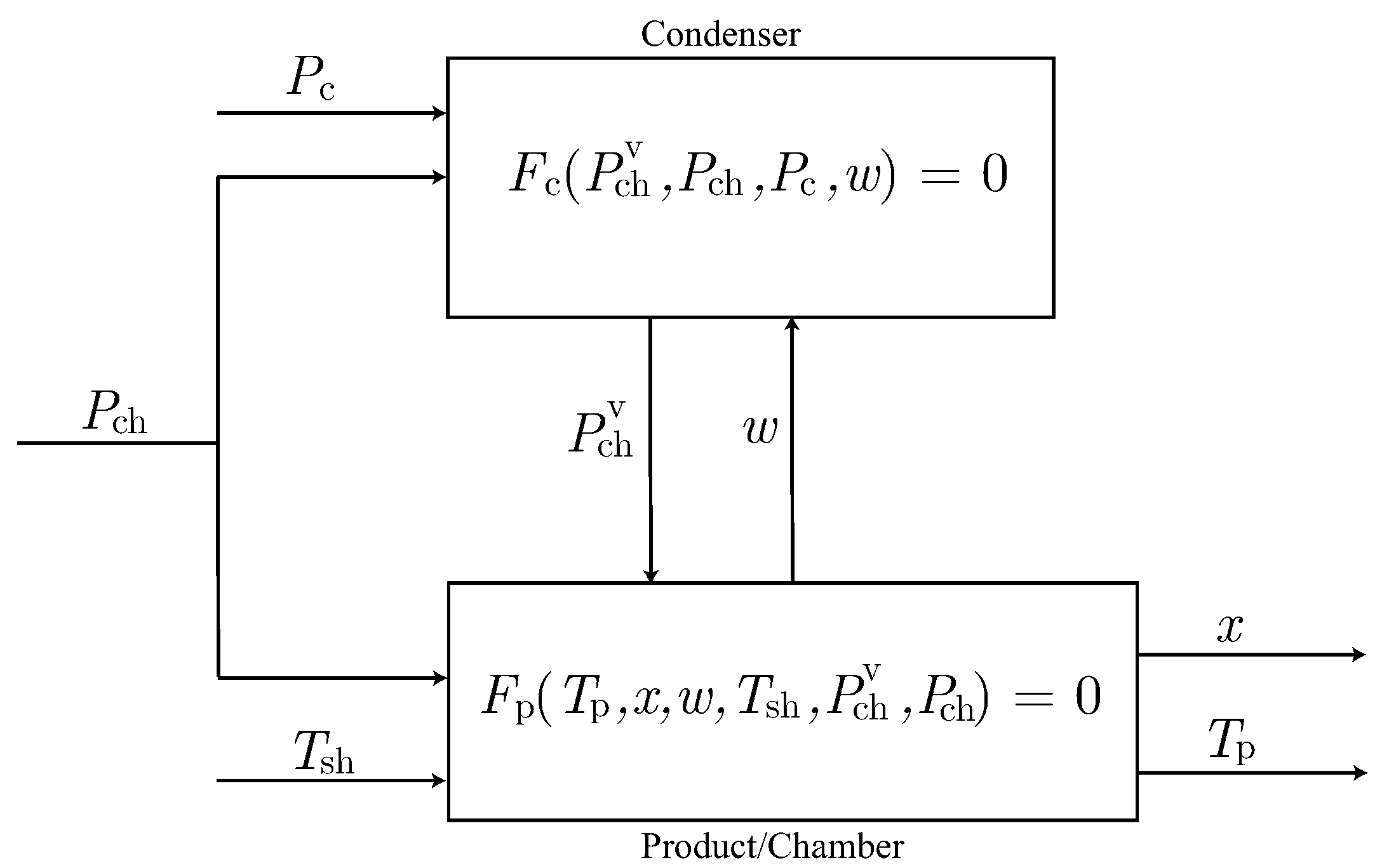
2.2.3. The Condenser Model
2.2.4. The Desorption Model
3. Strategies for Model Parameter Identification
- A set of model parameters to be estimated. Usually, these are parameters that are difficult to measure or cannot be found in the literature.
- Experimental measurements to compare against model results. Measured variables are usually state variables (e.g., temperature, concentration, pressure) or combinations of state variables. The quantities to be measured are known as the observables. Changes on the unknown model parameters should have an effect on the observables, otherwise such parameters cannot be estimated.
- A measure of the distance between model predictions and experimental data (cost function).
- An optimization algorithm to find the parameter values that minimize the cost function.
- Estimation of the unknown parameters involved in the product model, using the indirect measurements of instead of the condenser model. On the one hand, this reduces the number of parameters to be estimated together since the unknown condenser parameter is not taken into account. On the other hand, possible modeling errors on the condenser model are avoided.
- Estimation of the unknown parameters involved in the condenser model. As it is sketched in Figure 2, this estimation requires the product model and the parameters estimated in the previous step to compute the front velocity. Note that, if a procedure to measure w, such as an on-line sensor of front velocity, were available, product model could be disregarded in this step.
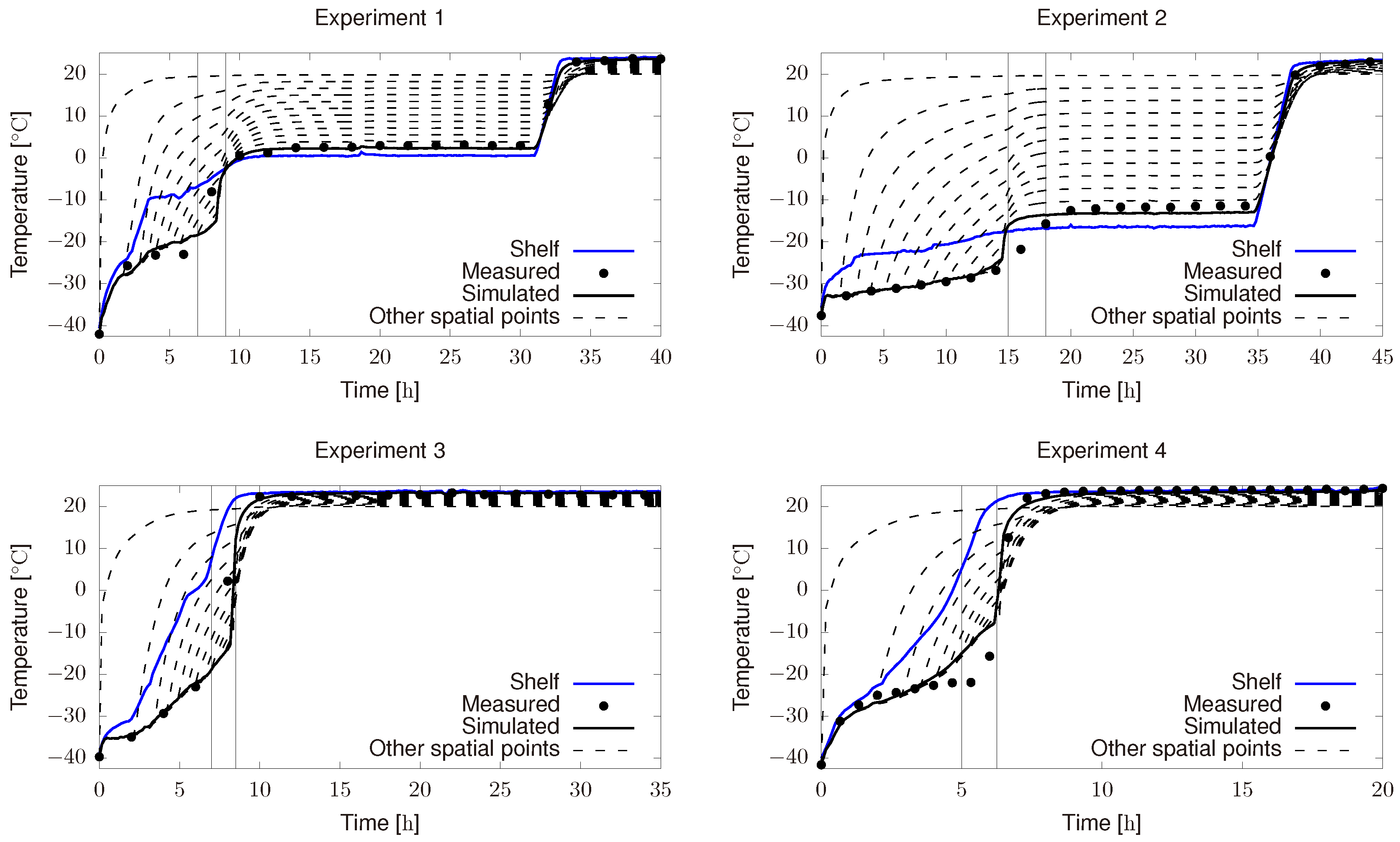
- Product freezing using −50 as a set point (cooling rate of 0,6 ).
- Primary drying varying from freezing temperature to −10, 0 or 20 depending on the experiment.
- Secondary drying using 25 as the set point.
- Total chamber pressure was kept at 20 or 60 depending on the experiment.
3.1. Parameter Estimation in the Product/Chamber Subsystem
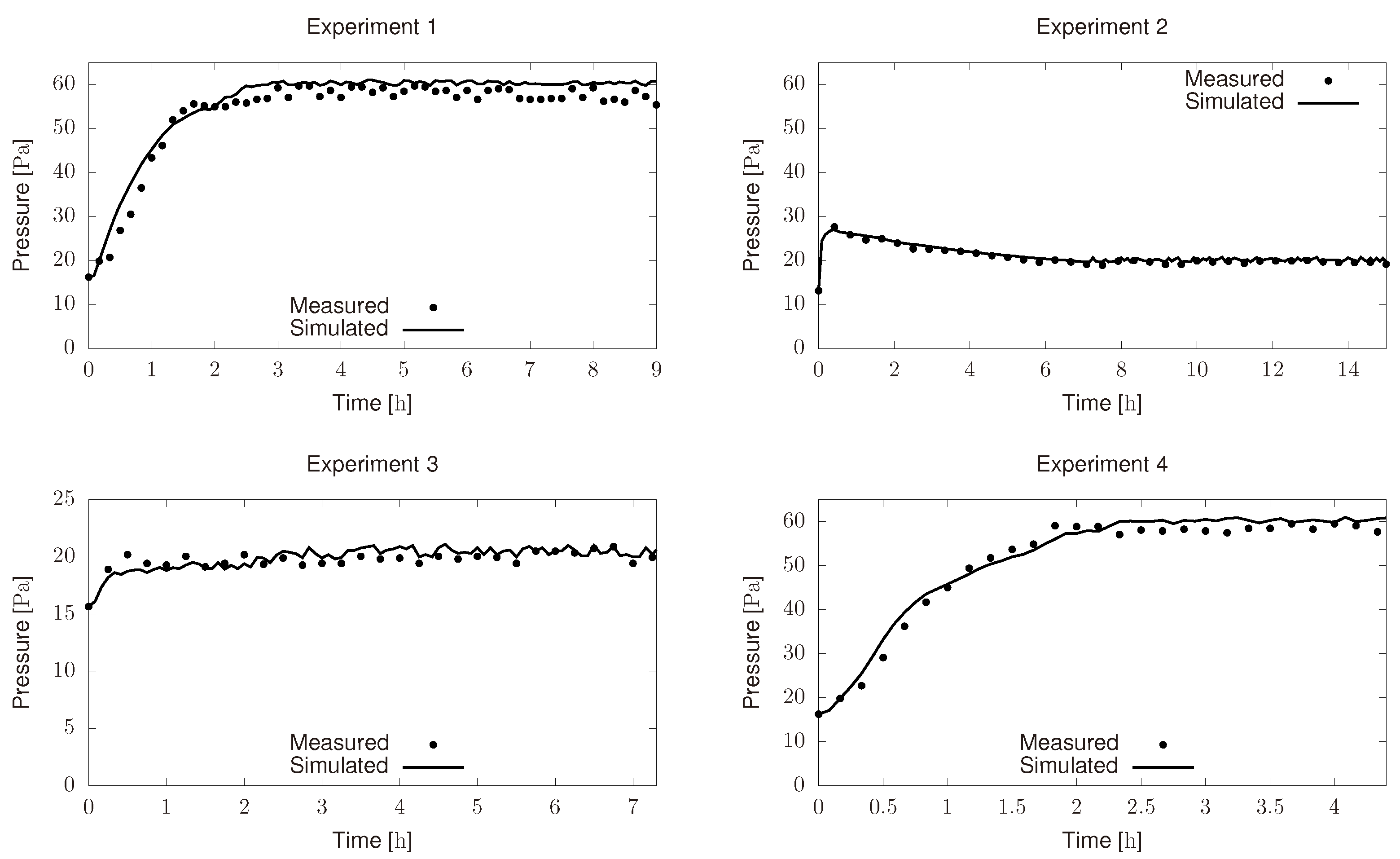
3.2. Parameter Estimation for the Condenser Model
4. Real time Optimization of the Freeze-Drying Process
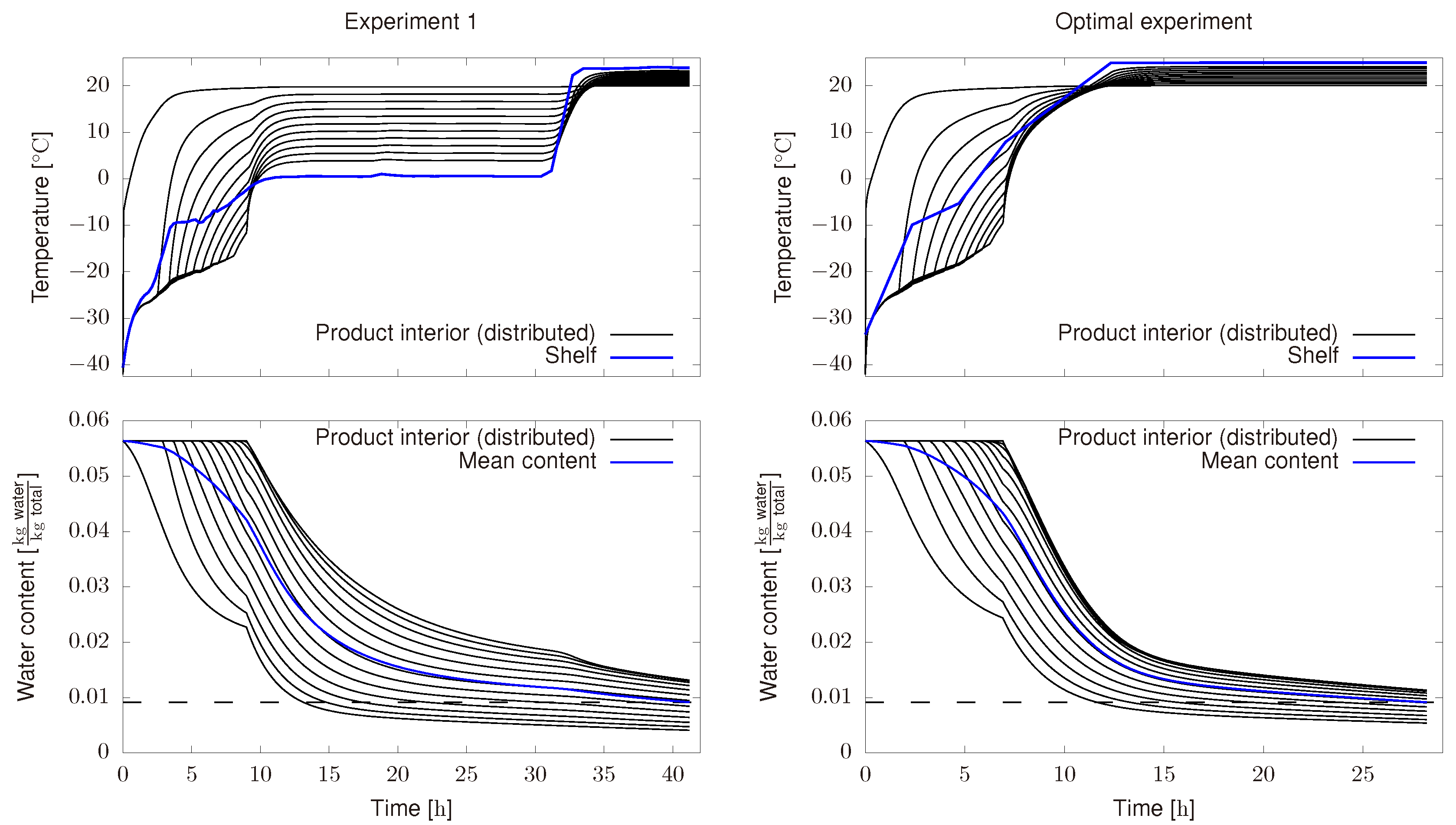
4.1. Off-Line Dynamic Optimization
4.2. Real Time Optimization
- An optimal profile for the shelf temperature is computed as in previous section.
- Such profile is sent to the freeze-drying plant as the set point for the PI control.
- As the process is running, measurements of relevant variables are being recorded. In this case, we measure, shelf temperature, chamber temperature, Pirani pressure and product temperature.
- After a given period of time, 1 in this case, measured information is introduced in the model. Then, a new optimal profile is computed by solving the optimization problem defined in Equation (24) and taking into account the new available information.
- Steps 2–4 are repeated till the end of the process.
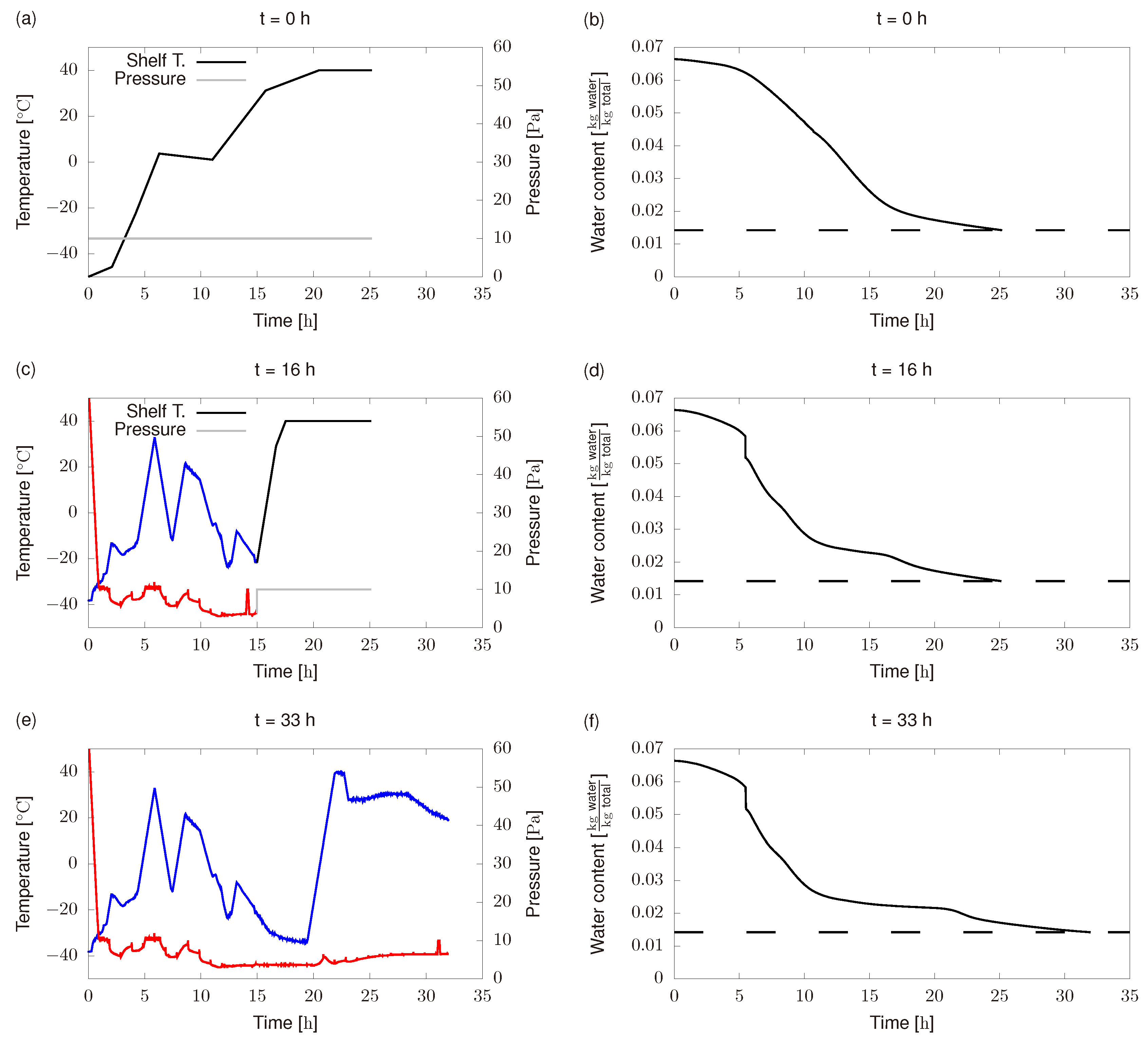
- Product freezing temperature differs from the expected one, i.e., from the one used in Figure 6a,c. This was because the refrigerant group was not able to reach −50 .
- Initial chamber pressure was around 60 and it was supposed to be 10 . Besides, chamber pressure controller did not perform as expected and most of the time it remains below the set point (10 ).
- Shelf temperature controller is not able to exactly follow the optimal profiles.
- We do not use available plant measurements and force the system to follow the off-line profile previously computed (dashed black line in Figure 7a).
- Unknown disturbances cause lower product temperatures than the predicted ones in the off-line scheme. In this case, final product water content might be larger than the targeted one, i.e., product quality would be lower than required. The RTO scheme can either increase process time or increase shelf temperature to reach the required quality.
- Unknown disturbances cause higher product temperatures than the predicted ones in the off-line scheme. In this case, safety constraints might be not fulfilled which can cause product collapse. The RTO scheme can reduce shelf temperature to avoid product collapse.
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Landau Transform
References
- Andrieu, J.; Vessot, S. A review on experimental determination and optimization of physical quality factors during pharmaceuticals freeze-drying cycles. Dry. Technol. 2018, 36, 129–145. [Google Scholar] [CrossRef]
- Harguindeguy, M.; Fissore, D. On the effects of freeze-drying processes on the nutritional properties of foodstuff: A review. Dry. Technol. 2019. [Google Scholar] [CrossRef]
- Trelea, I.C.; Passot, S.; Fonseca, F.; Marin, M. An interactive tool for the optimization of freeze-drying cycles based on quality criteria. Dry. Technol. 2007, 25, 741–751. [Google Scholar] [CrossRef]
- Ratti, C. Freeze-Drying Process Design. In Handbook of Food Process Design; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; Chapter 22; pp. 621–647. [Google Scholar] [CrossRef]
- Malik, N.; Gouseti, O.; Bakalis, S. Effect of freezing on microstructure and reconstitution of freeze-dried high solid hydrocolloid-based systems. Food Hydrocoll. 2018, 83, 473–484. [Google Scholar] [CrossRef]
- Lopez-Quiroga, E.; Prosapio, V.; Fryer, P.J.; Norton, I.T.; Bakalis, S. Model discrimination for drying and rehydration kinetics of freeze-dried tomatoes. J. Food Process Eng. 2019, e13192. [Google Scholar] [CrossRef]
- Wang, R.; Gouseti, O.; Lopez-Quiroga, E.; Fryer, P.J.; Bakalis, S. Water Crystallization in Highly Concentrated Carbohydrate-Based Systems. Cryst. Growth Des. 2019, 19, 2081–2088. [Google Scholar] [CrossRef]
- Pisano, R.; Arsiccio, A.; Nakagawa, K.; Barresi, A. Tuning, measurement and prediction of the impact of freezing on product morphology: A step toward improved design of freeze-drying cycles. Dry. Technol. 2019, 37, 579–599. [Google Scholar] [CrossRef]
- Prosapio, V.; Norton, I.; De Marco, I. Optimization of freeze-drying using a Life Cycle Assessment approach: Strawberries’ case study. J. Clean. Prod. 2017, 168, 1171–1179. [Google Scholar] [CrossRef]
- Ladha-Sabur, A.; Bakalis, S.; Fryer, P.; Lopez-Quiroga, E. Mapping energy consumption in food manufacturing. Trends Food Sci. Technol. 2019, 86, 270–280. [Google Scholar] [CrossRef]
- Vilas, C.; Balsa-Canto, E.; García, M.S.G.; Banga, J.R.; Alonso, A.A. Dynamic optimization of distributed biological systems using robust and efficient numerical techniques. BMC Syst. Biol. 2012, 6, 79. [Google Scholar] [CrossRef]
- Balsa-Canto, E.; Alonso, A.; Arias-Méndez, A.; García, M.; López-Núñez, A.; Mosquera-Fernández, M.; Vázquez, C.; Vilas, C. Modeling and optimization techniques with applications in food processes, bio-processes and bio-systems. SEMA SIMAI Springer Ser. 2016, 9, 187–216. [Google Scholar] [CrossRef]
- Datta, A. Toward computer-aided food engineering: Mechanistic frameworks for evolution of product, quality and safety during processing. J. Food Eng. 2016, 176, 9–27. [Google Scholar] [CrossRef]
- Fissore, D.; Pisano, R.; Barresi, A.A. A model-based framework to optimize pharmaceuticals freeze drying. Dry. Technol. 2012, 30, 946–958. [Google Scholar] [CrossRef]
- Pisano, R.; Fissore, D.; Barresi, A.A. In-line and off-line optimization of freeze-drying cycles for pharmaceutical products. Dry. Technol. 2013, 31, 905–919. [Google Scholar] [CrossRef][Green Version]
- Bosca, S.; Barresi, A.A.; Fissore, D. Fast freeze-drying cycle design and optimization using a PAT based on the measurement of product temperature. Eur. J. Pharm. Biopharm. 2013, 85, 253–262. [Google Scholar] [CrossRef]
- Bosca, S.; Barresi, A.A.; Fissore, D. On the use of model-based tools to optimize in-line a pharmaceuticals freeze-drying process. Dry. Technol. 2016, 34, 1831–1842. [Google Scholar] [CrossRef]
- Fissore, D. Model-Based PAT for Quality Management in Pharmaceuticals Freeze-Drying: State of the Art. Front. Bioeng. Biotechnol. 2017, 5, 5. [Google Scholar] [CrossRef][Green Version]
- Shivkumar, G.; Kazarin, P.; Strongrich, A.; Alexeenko, A. LyoPRONTO: An Open-Source Lyophilization Process Optimization Tool. AAPS PharmSciTech 2019, 20. [Google Scholar] [CrossRef]
- Nakagawa, K.; Ochiai, T. A mathematical model of multi-dimensional freeze-drying for food products. J. Food Eng. 2015, 161, 55–67. [Google Scholar] [CrossRef]
- Warning, A.; Arquiza, J.; Datta, A. A multiphase porous medium transport model with distributed sublimation front to simulate vacuum freeze drying. Food Bioprod. Process. 2015, 94, 637–648. [Google Scholar] [CrossRef]
- Aydin, E.; Yucel, O.; Sadikoglu, H. Modelling and simulation of a moving interface problem: Freeze drying of black tea extract. Heat Mass Transf./Waerme- Stoffuebertragung 2017, 53, 2143–2154. [Google Scholar] [CrossRef]
- Tarafdar, A.; Shahi, N. Application and comparison of genetic and mathematical optimizers for freeze-drying of mushrooms. J. Food Sci. Technol. 2018, 55, 2945–2954. [Google Scholar] [CrossRef] [PubMed]
- Antelo, L.T.; Passot, S.; Fonseca, F.; Trelea, I.C.; Alonso, A.A. Toward Optimal Operation Conditions of Freeze-Drying Processes via a Multilevel Approach. Dry. Technol. 2012, 30, 1432–1448. [Google Scholar] [CrossRef]
- Fissore, D.; Pisano, R.; Barresi, A.A. Applying quality-by-design to develop a coffee freeze-drying process. J. Food Eng. 2014, 123, 179–187. [Google Scholar] [CrossRef]
- Lopez-Quiroga, E.; Antelo, L.T.; Alonso, A.A. Time-scale modeling and optimal control of freeze-drying. J. Food Eng. 2012, 111, 655–666. [Google Scholar] [CrossRef]
- Jennings, T.A. Lyophilization: Introduction and Basic Principles; Interpharm/CRC: Boca Raton, FL, USA, 1999. [Google Scholar]
- Saguy, I.S. Challenges and opportunities in food engineering: Modeling, virtualization, open innovation and social responsibility. J. Food Eng. 2016, 176, 2–8. [Google Scholar] [CrossRef]
- Passot, S.; Cenard, S.; Douania, I.; Trelea, I.C.; Fonseca, F. Critical water activity and amorphous state for optimal preservation of lyophilized lactic acid bacteria. Food Chem. 2012, 132, 1699–1705. [Google Scholar] [CrossRef]
- Song, C.; Nam, J.H.; Kim, C.J. A finite volume analysis of vacuum freeze-drying processes of skim milk solution in trays and vials. Dry. Technol. 2002, 20, 283–305. [Google Scholar] [CrossRef]
- Litchfield, R.J.; Liapis, A.I. An adsorption-sublimation model for a freeze-dryer. Chem. Eng. Sci. 1979, 34, 1085–1090. [Google Scholar] [CrossRef]
- Mascarenhas, W.J.; Akay, H.U.; Pikal, M.J. A computational model for finite element analysis of the freeze-drying process. Comput. Methods Appl. Mech. Eng. 1997, 148, 105–124. [Google Scholar] [CrossRef]
- Pikal, M.J. Transport Processes in Pharmaceutical Systems. Drugs and The Pharmaceutical Sciences. In Heat and Mass Transfer in Low Pressure Gases: Applications to Freeze Drying; Marcel Dekker: New York, NY, USA, 2000; Volume 102, Chapter 16; pp. 611–686. [Google Scholar]
- Landau, H.G. Heat conduction in a melting solid. Q. Appl. Math. 1950, 8, 81–94. [Google Scholar] [CrossRef]
- Illingworth, T.C.; Golosnoy, I.O. Numerical solutions of diffusion–controlled moving boundary problems which conserve solute. J. Comput. Phys. 2005, 209, 207–225. [Google Scholar] [CrossRef]
- Trelea, I.C.; Fonseca, F.; Passot, S.; Flick, D. A Binary Gas Transport Model Improves the Prediction of Mass Transfer in Freeze Drying. Dry. Technol. 2015, 33, 1849–1858. [Google Scholar] [CrossRef]
- Nam, J.H.; Song, C.S. Numerical simulation of conjugate heat and mass transfer during multi-dimensional freeze drying of slab-shaped food products. Int. J. Heat Mass Transf. 2007, 50, 4891–4900. [Google Scholar] [CrossRef]
- Millman, M.J.; Liapis, A.I.; Marchello, J.M. Guidelines for the desirable operation of batch freeze dryers during removal of free water. J. Food Technol. 1984, 19, 725–738. [Google Scholar] [CrossRef]
- Boss, E.A.; Filho, R.M.; de Toledo, E.C.V. Freeze-drying process: Real-time model and optimization. Chem. Eng. Process. 2004, 43, 1475–1485. [Google Scholar] [CrossRef]
- Pikal, M.J.; Shah, S.; Roy, M.L.; Putman, R. The secondary drying stage of freeze drying: Drying kinetics as a function of temperature and chamber pressure. Int. J. Pharm. 1990, 60, 203–217. [Google Scholar] [CrossRef]
- Pisano, R.; Fissore, D.; Barresi, A.A. Quality by Design in the Secondary Drying Step of a Freeze-Drying Process. Dry. Technol. 2012, 30, 1307–1316. [Google Scholar] [CrossRef]
- Trelea, I.C.; Fonseca, F.; Passot, S. Dynamic modeling of the secondary drying stage of freeze drying reveals distinct desorption kinetics for bound water. Dry. Technol. 2016, 34, 335–345. [Google Scholar] [CrossRef]
- Pikal, M.J.; Shah, S. The collapse temperature in freeze drying: Dependence on measurement methodology and rate of water removal from the glassy phase. Int. J. Pharm. 1990, 62, 165–186. [Google Scholar] [CrossRef]
- Wilhelm, L.R. Numerical calculation of psychrometric properties in SI units. Trans. ASAE 1976, 19, 318–325. [Google Scholar] [CrossRef]
- Egea, J.A.; Vazquez, E.; Banga, J.R.; Marti, R. Improved scatter search for the global optimization of computationally expensive dynamic models. J. Glob. Opt. 2009, 43, 175–190. [Google Scholar] [CrossRef]
- Balsa-Canto, E.; Banga, J.R. AMIGO, a toolbox for advanced model identification in systems biology using global optimization. Bioinformatics 2011, 27, 2311–2313. [Google Scholar] [CrossRef] [PubMed]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; PTR Prentice Hall: Prentice-Hall, NJ, USA, 1999. [Google Scholar]
- Vassiliadis, V.S.; Sargent, R.W.H.; Pantelides, C.C. Solution of a Class of Multistage Dynamic Optimization Problems .2. Problems with Path Constraints. Ind. Eng. Chem. Res. 1994, 33, 2123–2133. [Google Scholar] [CrossRef]
- Vassiliadis, V.S.; Sargent, R.W.H.; Pantelides, C.C. Solution of a Class of Multistage Dynamic Optimization Problems. 1. Problems Without Path Constraints. Ind. Eng. Chem. Res. 1994, 33, 2111–2122. [Google Scholar] [CrossRef]
- Balsa-Canto, E.; Banga, J.R.; Alonso, A.A.; Vassiliadis, V. Dynamic optimization of distributed parameter systems using second-order directional derivatives. Ind. Eng. Chem. Res. 2004, 43, 6756–6765. [Google Scholar] [CrossRef]
- Banga, J.R.; Seider, W.D. Global optimization of chemical processes using stochastic algorithms. State of the Art in Global Optimization—Computational Methods and Applications. In Nonconvex Optimization and Its Applications; Floudas, C.A., Pardalos, P.M., Eds.; Kluwer Academic Publ.: Dordrecht, The Netherlands, 1996; Volume 7, pp. 563–583. [Google Scholar]
- Akterian, S.G. On-line control strategy for compensating for arbitrary deviations in heating-medium temperature during batch thermal sterilization processes. J. Food Eng. 1999, 39, 1–7. [Google Scholar] [CrossRef]
- Simpson, R.; Figeroa, I.; Teixeira, A. Simple, practical, and efficient on-line correction of process deviations in batch retort through simulation. Food Control 2007, 18, 458–465. [Google Scholar] [CrossRef]
- Alonso, A.A.; Arias-Méndez, A.; Balsa-Canto, E.; García, M.R.; Molina, J.I.; Vilas, C.; Villafín, M. Real time optimization for quality control of batch thermal sterilization of prepackaged foods. Food Control 2013, 32, 392–403. [Google Scholar] [CrossRef][Green Version]
- Marchetti, A.G.; François, G.; Faulwasser, T.; Bonvin, D. Modifier Adaptation for Real-Time Optimization-Methods and Applications. Processes 2016, 4, 55. [Google Scholar] [CrossRef]

| Parameter | Value | Units | Description |
|---|---|---|---|
| 200.31 | Dried region density | ||
| 1001.6 | Frozen region density | ||
| 1254 | Dried region heat capacity | ||
| 1818.8 | Frozen region heat capacity | ||
| t.b.e. | Dried region heat conductivity | ||
| 2.4 | Frozen region heat conductivity | ||
| 5.6704 × 10−8 | Stefan–Boltzmann constant | ||
| 0.78 | - | Thermal emissivity at the product top | |
| 0.99 | - | Geometrical correction factor | |
| 1.6548 × 10−4 | Constant in the Clapeyron equation | ||
| 2791.2 × 10−3 | Sublimation heat | ||
| R | 8314 | Ideal gas constant | |
| 5.75 × 10−3 | Food product height | ||
| 0.242 | Food product length | ||
| 0.307 | Food product width | ||
| 18 | Water molecular mass | ||
| 3.3 | Heat transfer coefficient constant | ||
| t.b.e. | Heat transfer coefficient constant | ||
| 34.4 | Heat transfer coefficient constant | ||
| 430.0 | Mass transfer coefficient constant in Darcy’s equation | ||
| t.b.e. | Mass transfer coefficient constant in Darcy’s equation | ||
| t.b.e. | Mass transfer coefficient constant in | ||
| chamber/condenser flux | |||
| 293.15 | Chamber temperature | ||
| 0.202 | Chamber volume | ||
| 2.689 × 104 | Compartment A reference time constant | ||
| 6.493 × 105 | Compartment B reference time constant | ||
| 4.271 × 104 | Activation energy in desorption model | ||
| 273.15 | Reference temperature in desorption model | ||
| 0.669 | - | Compartment A ratio between equilibrium water content | |
| 0.331 | - | Compartment B ratio between equilibrium water content | |
| 0.0434 | -water -total | Constant of the GAB equation | |
| 7.4789 | - | Constant of the GAB equation | |
| 0.9827 | - | Constant of the GAB equation | |
| 8.2 | - | Constant of the glass transition temperature | |
| −135 | °C | Constant of the glass transition temperature | |
| 75.58 | °C | Constant of the glass transition temperature | |
| 1.6 | - | Ratio of molecular heat conductivities of vapor | |
| and nitrogen |
| Parameter | Excluded Experiment | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1.96 | 1.86 | 1.93 | 1.82 | 2.03 | |
| 8.60 × 107 | 7.86 × 107 | 6.52 × 107 | 9.41 × 107 | 9.51 × 107 | |
| 2.45 × 10−4 | 4.13 × 10−4 | 2.41 × 10−4 | 2.85 × 10−4 | 2.85 × 10−4 | |
| 2.15 | 1.64 | 2.11 | 2.10 | 2.00 | |
| 1.62 | 3.10 | 2.01 | 2.49 | 2.54 | |
| Parameter | Excluded Experiment | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 2.31 × 103 | 2.17 × 103 | 2.31 × 103 | 2.37 × 103 | 2.37 × 103 | |
| 1.6 | 1.7 | 2.2 | 2.0 | 1.8 | |
| 2.8 | 2.1 | 0.6 | 0.6 | 2.3 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilas, C.; A. Alonso, A.; Balsa-Canto, E.; López-Quiroga, E.; Trelea, I.C. Model-Based Real Time Operation of the Freeze-Drying Process. Processes 2020, 8, 325. https://doi.org/10.3390/pr8030325
Vilas C, A. Alonso A, Balsa-Canto E, López-Quiroga E, Trelea IC. Model-Based Real Time Operation of the Freeze-Drying Process. Processes. 2020; 8(3):325. https://doi.org/10.3390/pr8030325
Chicago/Turabian StyleVilas, Carlos, Antonio A. Alonso, Eva Balsa-Canto, Estefanía López-Quiroga, and Ioan Cristian Trelea. 2020. "Model-Based Real Time Operation of the Freeze-Drying Process" Processes 8, no. 3: 325. https://doi.org/10.3390/pr8030325
APA StyleVilas, C., A. Alonso, A., Balsa-Canto, E., López-Quiroga, E., & Trelea, I. C. (2020). Model-Based Real Time Operation of the Freeze-Drying Process. Processes, 8(3), 325. https://doi.org/10.3390/pr8030325






