The different process schemes previously described will be analysed and compared in this section. The processes employing a membrane reactor, which have been detailed in this work, will be firstly detailed. Subsequently, a techno-economic comparison between the selected process schemes will be carried out, focusing on the differences that the different reactor configurations imply on the rest of the plant.
4.1. Membrane Reactor OCM Process Scheme
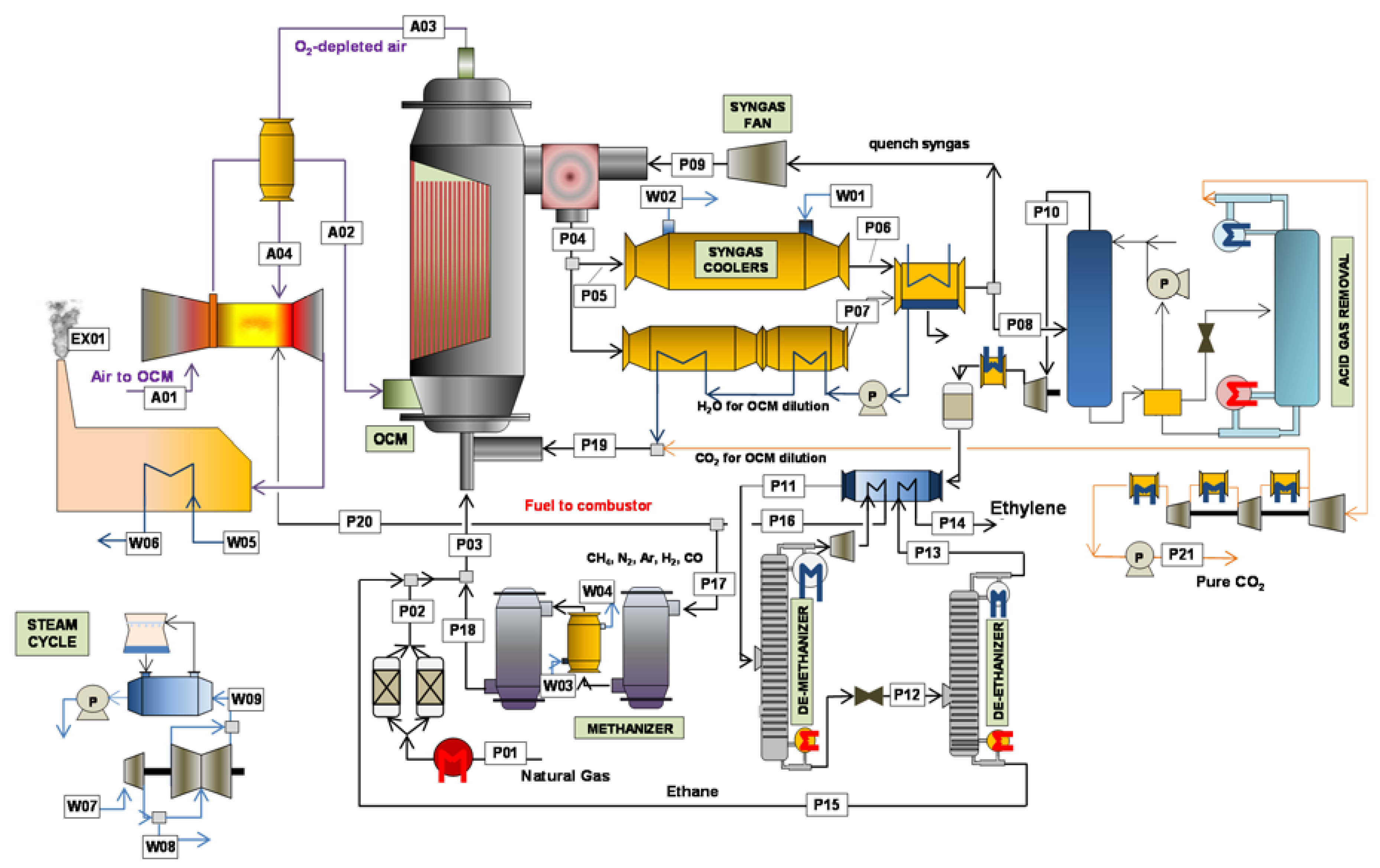
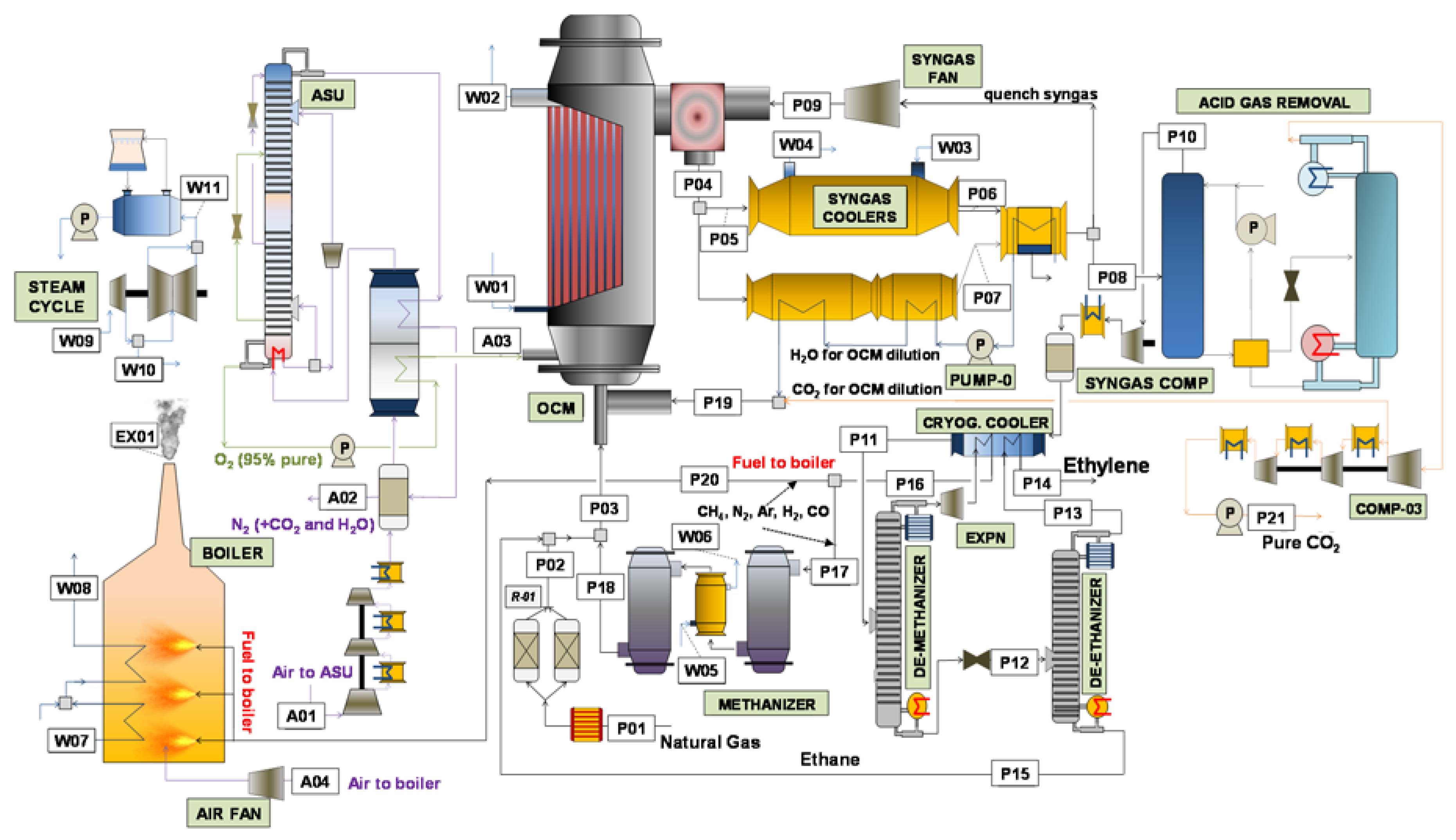
As previously explained, two different configurations (employing a dense and a porous membrane reactor) have been considered to study the feasibility of the membrane reactor. The integration of membranes is expected to increase the C
2 reactor yield because of the even distribution of the oxygen along all the reactor length, hence favoring the desired reactions over the undesired ones. In this work, first a complete sensitivity analysis has been carried out on a reactor level, where the reaction temperature and the CH
4/O
2 ratio has been varied. Since the economic evaluation calculator is embedded in the Aspen software, though this sensitivity also the economic indicators could be obtained. To study both configurations in detail,
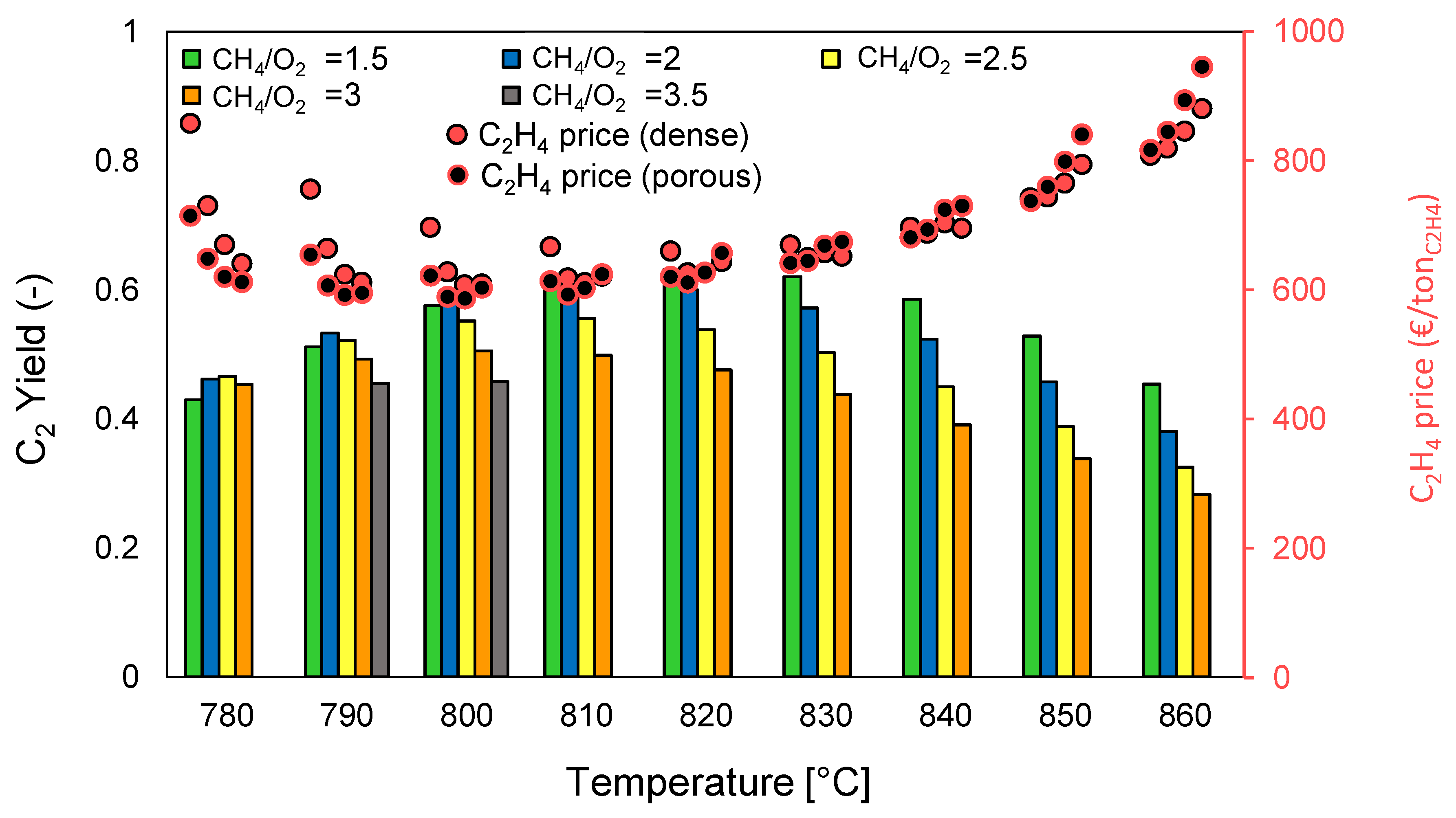
Figure 3 is presented. Since both dense and porous membranes distribute the oxygen homogeneously along the reactor length (see assumptions in
Section 3.1), no reactor performance differences are found between these configurations and therefore the C
2 yield reported in
Figure 3 is valid for both the dense and the porous membrane reactor cases. However, the ethylene price obtained for each case studied differ between the porous and the dense configuration.
It can be observed in the graph that the reactor yield achieved with the OCM membrane reactor configurations (both porous and dense), ranges from approximately 30% to above 60%, and it clearly overcomes the maximum reactor yield obtained with the conventional packed bed reactor (around 14% in the case in which the lowest ethylene price was obtained) [
6,
12]. This increase in the reactor performance is translated into a steep decrease in the ethylene price calculated from the process plant. When reaching higher yields, like in this case, the process becomes more efficient, reducing the energy requirement for the refrigeration in the separation train and decreasing the amount of natural gas required to reach the selected C
2H
4 production (1 MTPY) because of the higher conversion and selectivity reached in the reactor towards the desired products.
The maximum C
2 reactor yield is found to be 63.1% (84.8% CH
4 conversion with 74.5% C
2 selectivity), achieved at 820 °C and with a CH
4/O
2 ratio of 1.5. The temperature at which this maximum is found maximizes the C
2 selectivity, as it is known to be in the range of “optimal operating conditions” while the big amounts of oxygen fed (low CH
4/O
2 ratio) maximize the conversion of CH
4. However, the highest reactor yield does not imply a minimization in the ethylene price, that is, the optimal operating conditions in terms of minimization of the C
2H
4 price are not found at the maximum C
2 reactor yield. This conclusion was also withdrawn in the OCM conventional packed bed reactor case [
12], meaning that the final ethylene price is not just a function of the C
2 reactor performance, but also to all the equipment associated to the process plant and the utilities required.
The lowest ethylene price for the case of the MIEC membranes reactor is found to be 625 €/ton
C2H4 at 800 °C and a CH
4/O
2 ratio of 2.5 while for the porous membranes case is 595 €/ton
C2H4 (again at 800 °C and CH
4/O
2 ratio of 2.5). As shown in
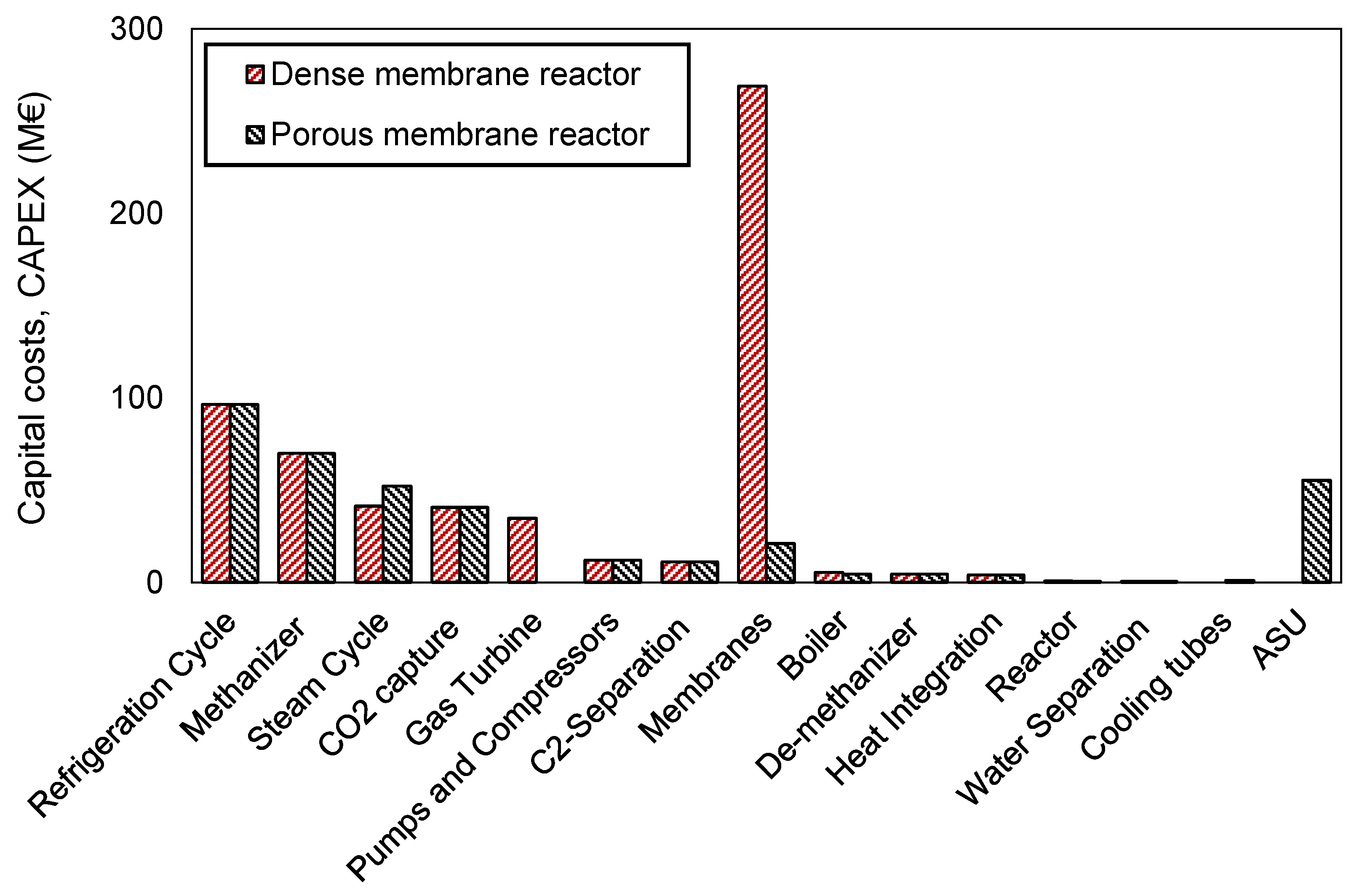
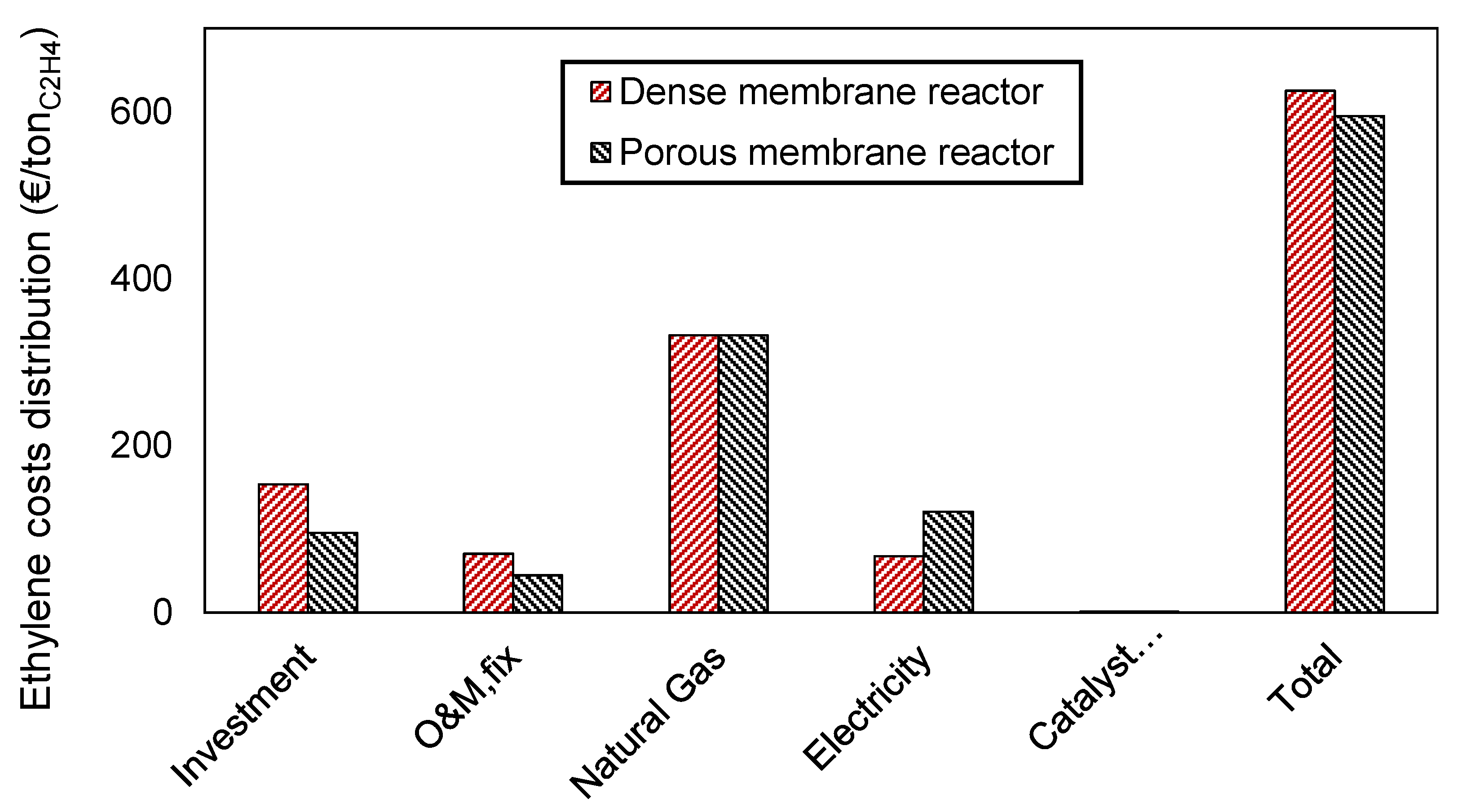
Figure 3, the ethylene price is generally 30–70 € more expensive when employing dense membranes compared to the porous membranes configuration. In order to identify the differences between the two plants, the CAPEX and OPEX of the optimal cases are here presented. In terms of CAPEX, the disaggregated unit costs are shown in
Figure 4.
The total plant cost (BEC) of the two plants is 367 M€ for the porous configuration and 590 M€ for the dense configuration. It is clearly seen that the biggest difference between both configurations relates to the membrane cost. Dense membranes are considered to be supported, namely a porous support in which a dense layer of a material selective to oxygen is coated. Because of that, they will always be more expensive than the porous membranes (respectively 1000 €/m2 and 700 €/m2 in this work). However, this price difference cannot explain the large difference in the total cost of the membranes. This remarkable difference is associated to the flux of oxygen that dense and porous membranes can offer. The oxygen flux of porous membranes is roughly one order of magnitude higher than the dense ones, this being translated in a reduction of the membrane area required to feed the desired amount of oxygen into the reactor (the membrane area required for the optimal porous membranes case is 6010 m2 while for the dense case is 53,812 m2). Considering that BSCF membranes are employed for these calculations and that these membranes are known to have high oxygen fluxes (among oxygen-selective membranes), the differences shown here could be even increased when employing the flux of a CO2-tolerant dense membrane.
Therefore, the repercussion of the membrane cost part in the total CAPEX cost is major in the case of the dense membranes, accounting for almost 50% of the total CAPEX, while it decreases to 6% when porous membranes are employed.
The second important variation between both configurations is the need of the air separation unit (ASU) to feed pure oxygen into the reactor in the case of the porous membranes’ reactor. This unit accounts in this specific case for roughly 15% of the total plant cost (≈55 M€), although in some conditions it can be up to 30% of all the CAPEX. The need of an ASU does not just impact the investments, but also the utilities, as electricity needs to be supplied to this unit in order to operate at cryogenic conditions.
Differently, the cost caused by the integration of cooling tubes in the porous membrane reactor is negligible when compared to the total CAPEX cost. Through these tubes, heat is recovered by producing high pressure steam, which is subsequently used in the steam cycle, posing a benefit in the net electricity generation compared to the dense membrane case. This argumentation is supported by the fact that the cost of the steam cycle in the porous membrane case is larger, meaning that larger steam turbine and heat rejection units are required.
On the other hand, in the dense membranes case technology, the heat removed from the reactor is taken by the depleted air at the outlet of the MIEC membranes. This high temperature high-pressure air burns part of the recycle stream, increasing the temperature and accelerating the gas velocity to drive the gas turbine, where electricity is produced. Opposite to the porous case, the heat management strategy for the dense membranes case is translated into the gas turbine cost, and a surplus of electricity generated.
The disaggregated ethylene cost, containing OPEX (electricity, natural gas, and catalyst replacement) and CAPEX (investment and O&M), is shown in
Figure 5.
In both membrane reactors, the cost of the raw material emerges as the main contributor to the final ethylene cost. It should be mentioned here that this fact is strongly influenced by the selection of the location of the plant (Europe), which subsequently determines the price and composition of natural gas. As typically happens for chemical plants, and as presented in our previous work on conventional OCM packed bed case [
12], the OPEX cost weights more than the CAPEX (showed in the graph as “investment”, referring to the cost of all the units shown in
Figure 4, and “O&M
fix”). The higher yearly fixed costs are related to a higher cost of maintenance for the dense membranes and, overall, it can be said that the cost of the dense membranes is the main contributor to the higher price with the dense configuration.
4.1.1. Sensitivity on Membrane Costs
To analyse in detail how the cost of the membranes affects the overall ethylene price calculated in each of the selected configurations, a sensitivity analysis has been carried out.
As can be seen in
Figure 6, the cost of the membranes in both configurations has been varied in a wide range to investigate its effect in the final ethylene price. This sensitivity is essential because of the lack of data regarding this parameter when considering industrial applications, since none of the membranes simulated here have been produced at industrial scale for the specific OCM process in such large quantity.
The fact that the trend line in the dense membranes case is much steeper than the porous one indicates that this configuration is more impacted by the membranes price. As explained before, this mostly relates to the larger membrane area required for this configuration. Differently, the porous configuration remains (almost) unaffected by the increment in the membrane price, since the increase in price considered for this sensitivity is not sufficient to significantly influence the relatively low membrane area required. Subsequently, it can be said that the porous membranes case is independent from the membrane’s price (in the price range analysed), this factor being especially relevant because of the uncertainty of their industrial scale price.
Going to the specific values, it is noticeable that both dense and porous membranes are competitive in most of the cases analysed compared with the conventional naphtha steam cracking, resulting in an ethylene price lower than 1000 €/tonC2H4. The different tendency of both configurations is also remarkable: the lower the price of the membranes, the more competitive the dense membranes case will be in comparison with the porous membranes one. Actually, if the fabrication of dense membranes does not overcome 1000 €/m2, this technology can already compete with the porous membranes one while if the price is set below 500 €/m2 starts to be even more convenient because the investment cost will drop significantly while no relevant effects are detected in the porous configuration where the ASU affects significantly the overall costing.
As previously mentioned, the lack of industrial scale dense membranes gives uncertainty to their predicted cost, which has been used to run all the simulations in this work. That is the main reason why it is essential to highlight that the characteristics of the employed membranes in a hypothetic OCM reactor can strongly modify the economics of the process. For instance, the performance of dense membranes is currently limited by the relatively low O2 flux achieved with this type of membranes. If the oxygen flux considered in this work is doubled because of the employment of a different membrane, the membrane area required in the process would be halved and also the cost associated to these membranes. A proper selection of the membrane characteristics can make the oxygen flux through the membrane to vary in even more than one order of magnitude, thus affecting the total membrane area and the total cost of the membranes. In particular, the type of membrane (supported or self-supported), membrane material (fluorite, perovskite), membrane thickness, membranes lifetime (currently set to 5 years), or recyclability to a certain extent are examples of parameters that need to be addressed for a proper membrane reactor design, given their effect in the final total plant cost. A trade-off between high oxygen flux, low cost, and membrane stability and durability under OCM conditions (both chemical and mechanical) should be made to find the most suitable membrane for this specific application.
4.1.2. Analysis of Electricity Production/Consumption
Besides the difference in investment and fixed costs, the rest of OPEX variables seems to be very similar when comparing porous and dense membranes configurations, although some differences caused by the modifications in the plant scheme can be analysed. Even if the net electricity demand is very similar for both configurations, there is a different distribution of the energy demand throughout the plant as presented in
Table 6.
The steam cycle in the porous membrane configuration produces almost twice the electricity than in the dense membranes case. This is mainly related to the different strategy used to remove the heat produced by the OCM reaction. In the porous membranes process scheme, the cooling tubes placed inside the OCM reactor allow the generation of an additional amount of HP steam, thus increasing the power produced in the steam cycle. On the contrary, the heat of reaction is taken by the depleted air in the dense membranes process case. This hot stream is used to burn part of the recirculated gases, hence producing electricity in a gas turbine. Therefore, the electricity production/consumption distribution clearly evidences the different approaches taken for the heat management inside the reactor in both configurations. The second relevant difference relates, as aforementioned, to the air separation unit. It can be seen in the table that the air separation unit does not only affect the CAPEX, but also has a non-negligible influence to the electricity balance of the process, being responsible for around 30% of the total electricity that needs to be imported in the porous membranes case (43 MW out of 163 MW).
4.2. Comparison of Different Reactor Configurations
One of the main assumptions taken to perform the economic evaluation detailed in
Section 4.1 relates to the kinetics selected to run the OCM reactor [
5]. This OCM kinetics was initially developed and validated for specific packed bed lab-scale reactor conditions, and its validation when integrating membranes was not carried out. Nevertheless, the high C
2 reactor yields (up to 60%) achieved in this work with the membrane reactor are in agreement with other modelling OCM membrane reactor works [
6]. However, these yields have never been validated with experiments. As a matter of fact, the discrepancies in results between modelling and experimental works are significant and should be somehow considered. Therefore, and in order to make a more reliable evaluation, two extra scenarios have been considered here. The reactor performance obtained with the membrane reactors has been reduced by decreasing the reaction rate of the desired primary reaction (oxidative production of ethane from methane) such that a more reasonable C
2 yield, from an experimental point of view, is achieved. The system has been adjusted in a way that, as a result, a C
2 yield of around 30% is obtained, which is in line with the best OCM experimental publications when employing a membrane reactor [
22]. Following the approach of this work, this modification has been applied to the dense and the porous membrane reactor cases. The techno-economic evaluation of the previously mentioned membrane based processes and the experimental state-of-the-art membrane reactor configurations (indicated as low yield) have been also compared with the conventional OCM packed bed process [
12] and to the naphtha steam cracking [
11] in order to have a broader framework of the ethylene production market.
A summary of all the selected configurations together with the main operating parameters of each of them are listed in
Table 7.
4.2.1. Ethylene Price
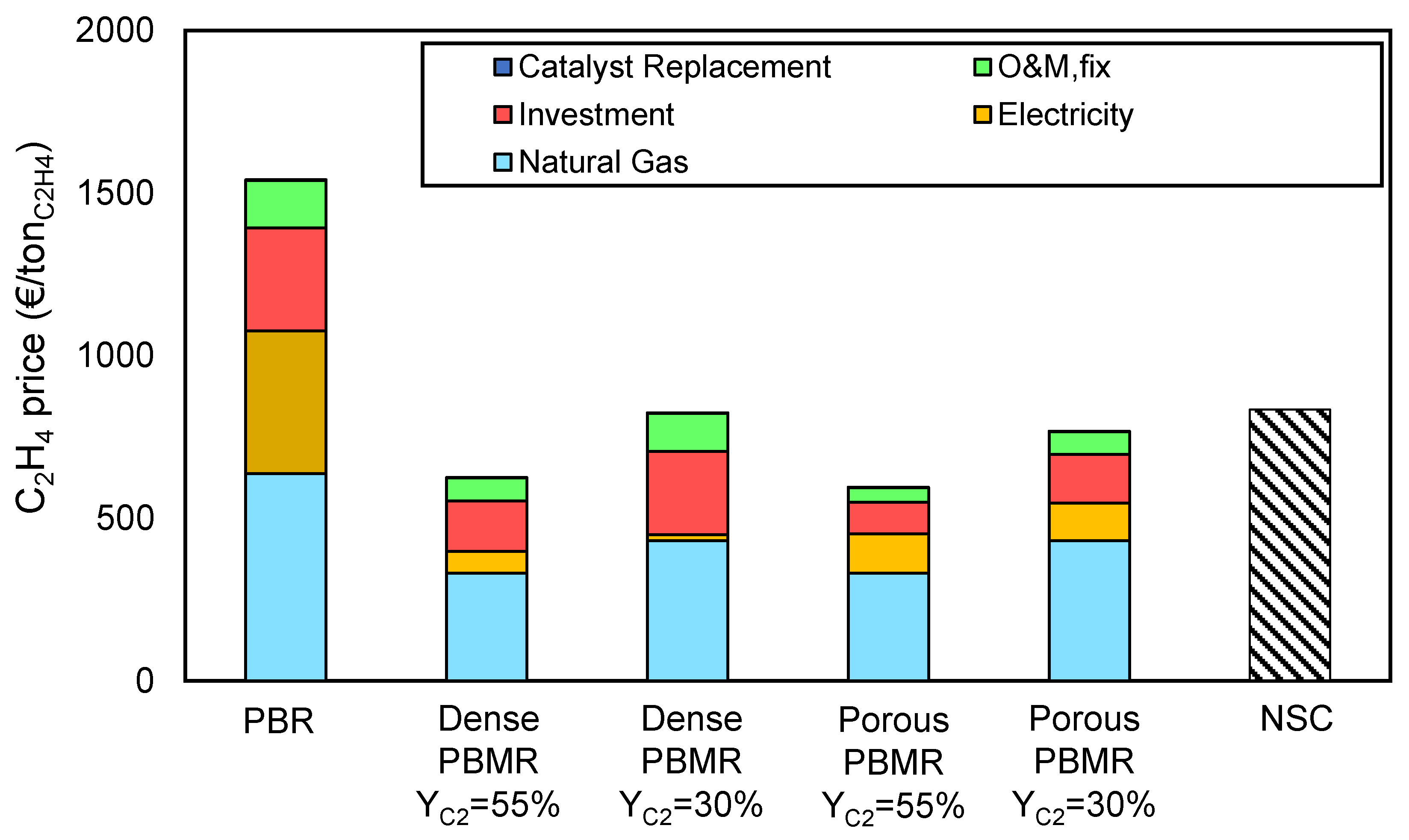
The first index chosen to evaluate all these configurations is the final ethylene price that comes out from the process, disaggregated into the main cost contributors. The results of this comparison can be seen in
Figure 7.
Among the different OCM technologies, the maturity of the packed bed is the main advantage of the conventional packed bed configuration. However, it seems clear that a breakthrough in the technology is required to industrially compete with conventional ethylene production technologies, represented in this graph by the naphtha steam cracking. One of the most promising options to reach this necessary breakthrough is the integration of membranes in the reactor. It has already been widely explained that this reactor modification would increase the C
2 reactor yield, increasing the profitability of the process. The first consequence of this performance improvement relates to the decrease in the cost related to the raw material, natural gas. The more optimized methane conversion occurring in the OCM reactor decreases the total feed inlet requirement, thus reducing the costs associated with the overall cost of purchasing raw material. Secondly, electricity demand and investment are strongly reduced when employing a membrane reactor. The higher yields in all the membrane reactor cases makes all the separation train cheaper. For instance, the stream comprising the incondensable gases remained after the C
2 separation, which actually contains some of the undesired products formed in the OCM reaction (stream P16 in
Figure 1 and
Figure 2) is reduced from 20.6 in the conventional OCM packed bed reactor to 3.9 kmol/s when the membrane reactor is employed. This is reflected in the investment cost, since the size of all the units downstream the reactor could be lowered, also including a lower electricity demand due to the lower amount of energy required to carry out the component separations in the various distillation columns utilized during the process (in particular the de-methanizer and de-ethanizer, which are very energy-consuming because of the utilization of cryogenic temperatures).
The ethylene price in the cases in which the C
2 reactor yield has been decreased are still comparable to the price calculated by Spallina et al. [
11] for the conventional naphtha steam cracking. This means that if the membrane reactor experiments, in which the 30% C
2 yield has been overcome [
32,
33,
34], can be extrapolated at industrial conditions without any loss in performance, the OCM technology could be located within the range of industrial viability for ethylene production. However, this step is not as straight-forward as it could seem, since most of these experimental works are carried out at very specific conditions. Commonly, in the experiments at lab scale the extent of reaction is controlled by diluting the feed with an inert (usually N
2) and by using low flow feeds (in the range of mL) in small reactors. With these actions, the reaction temperature can be easily kept in the optimal OCM range, where selectivity towards the desired products is maximized. Instead, these shortcuts cannot be applied when attempting the industrial application of the process, since they will significantly hinder its efficiency. As a result, the upscaling of the OCM membrane reactor process can be complex and it has not been yet experimentally tested.
When confronting the dense-porous cases, it turns out that the ethylene price obtained from the porous configurations (for both reduced and non-reduced C
2 reactor yield) is just slightly lower. In terms of technology maturity, MIEC membranes are still very far from commercialization and most of the research has been devoted to pure O
2 production or solid oxide fuel cells in which the presence of an electric field improves the oxygen transfer rate [
35]. If the fact that the maturity of porous membranes is much larger than the one of dense (MIEC) membranes is taken into account, porous membranes like the ones simulated in this work are commercially available while MIEC dense membranes are certainly not produced at industrial scale yet (it is very doubtful that in a relatively short timeframe the number of membranes required to run the OCM dense membrane reactor plant can be produced), it comes out that the feasibility of the porous membrane reactor configuration clearly overcomes the one of the dense membranes case. In addition, possible extra issues of dense membranes that have not been tested yet, like long term stability of membranes and sealing, possible interaction with the catalyst, etc., can direct the decision more towards the implementation of the porous membranes case, where many more aspects are simplified.
4.2.2. CO2 Emissions
Another relevant parameter to study in detail, especially considering all the political-environmental aspects that are currently being discussed in the society, is the environmental impact and the carbon footprint of the process. Because of that, the CO
2 emissions derived from all the aforementioned processes have been evaluated and are shown in
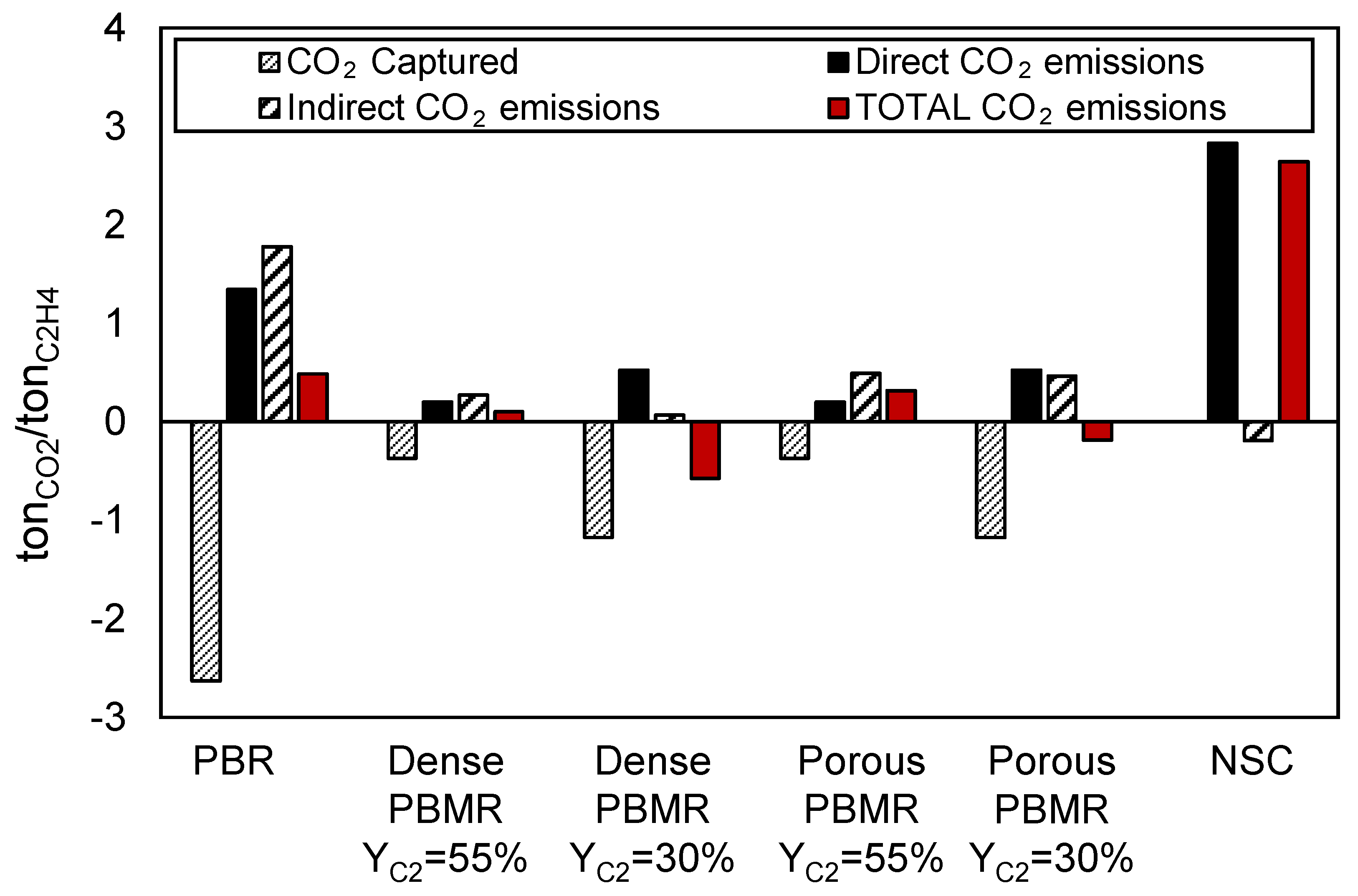
Figure 8.
Differently to the conventional NSC, where the need of a fuel to supply heat to the reaction cracking reaction directly impacts the CO2 emissions, the OCM technology requires a CO2 separation unit in the plant which is able to deliver a stream of pure CO2 which can be sent for long storage or used as carbon feedstock without being emitted to the atmosphere. This comes from the fact that CO2 is produced itself in the process (as a by-product of the OCM reaction), being consequently necessary its removal from the outlet reactor stream in order to be able to obtain pure ethylene. That is also the reason why the CO2 capture rate in the conventional OCM case, that is, packed bed reactor (PBR), is much larger than in all the other cases because of the more C2 unselective reactions taking place in such configuration.
In the case of NSC, CO2 is not produced in the cracking process itself, but as off-gas from the combustion of light alkanes derived from the cracking technology to provide heat and/or electricity to the process. As a result, no CO2 is captured in the NSC process and all the positive CO2 emissions are considered to be direct and are originated by the combustion of these hydrocarbons. The negative value shown in the indirect CO2 emissions relies on the fact that, when combusting these hydrocarbons, the heat produced is recovered by high pressure steam to power a steam cycle, resulting in a large production of electricity, larger than that required in the plant, and thus having a surplus that can be exported. Therefore, the negative emissions refer to the CO2 that is saved when exporting electricity.
When comparing the different OCM configurations, it can be observed that direct CO2 emissions, related to the CO2 emitted within the process (in the particular of OCM in the boilers used to supply energy for the plant), are much higher in the PBR configuration than in all the other cases. The large unconverted methane stream of this particular configuration, which partially goes to the burner to produce electricity, is the main cause of this big contribution. Since the reaction is more selective towards the desired products, this term gets strongly reduced when integrating membranes in the reactor.
Similarly, the indirect CO2 emissions, which account for the import/export of electricity and/or heat, are also much larger in the PBR respect to all the other OCM cases. These emissions come from the need of electricity import because of the very energy intensive separation train required to separate the big amounts of undesired products formed in the OCM reactor from ethylene. In the case of integrated renewable plant to account for the electricity demand, the indirect CO2 emissions could be removed, significantly reducing the footprint of the process. In the medium-long term scenario this is likely to happen, although several technical and policy-related aspects are still open to guarantee that the quantity of electricity required will be available for more than 8000 h per years.
Overall, the total CO2 emissions (accounting for direct, indirect, and captured) are much lower for the OCM cases that for the NSC. In particular, total CO2 emissions in the OCM dense membranes configuration case are reduced by 96% and in the OCM porous membranes configuration by 88% when compared to the NSC. This factor is especially relevant if taxes are applied to CO2 emissions, as is likely to happen in the near future. The conventional packed bed is still CO2 positive because of the requirement of importing electricity, while the cases of which membranes are integrated are roughly CO2 neutral. In addition, these cases have the potential to become CO2 emissions-negative if the electricity that they demand comes from a renewable source, hence removing the indirect CO2 emissions contribution.