Do Bioreactor Designs with More Efficient Oxygen Supply to Ovarian Cortical Tissue Fragments Enhance Follicle Viability and Growth In Vitro?
Abstract
:1. Introduction
2. Materials and Methods
2.1. Bioreactor Designs
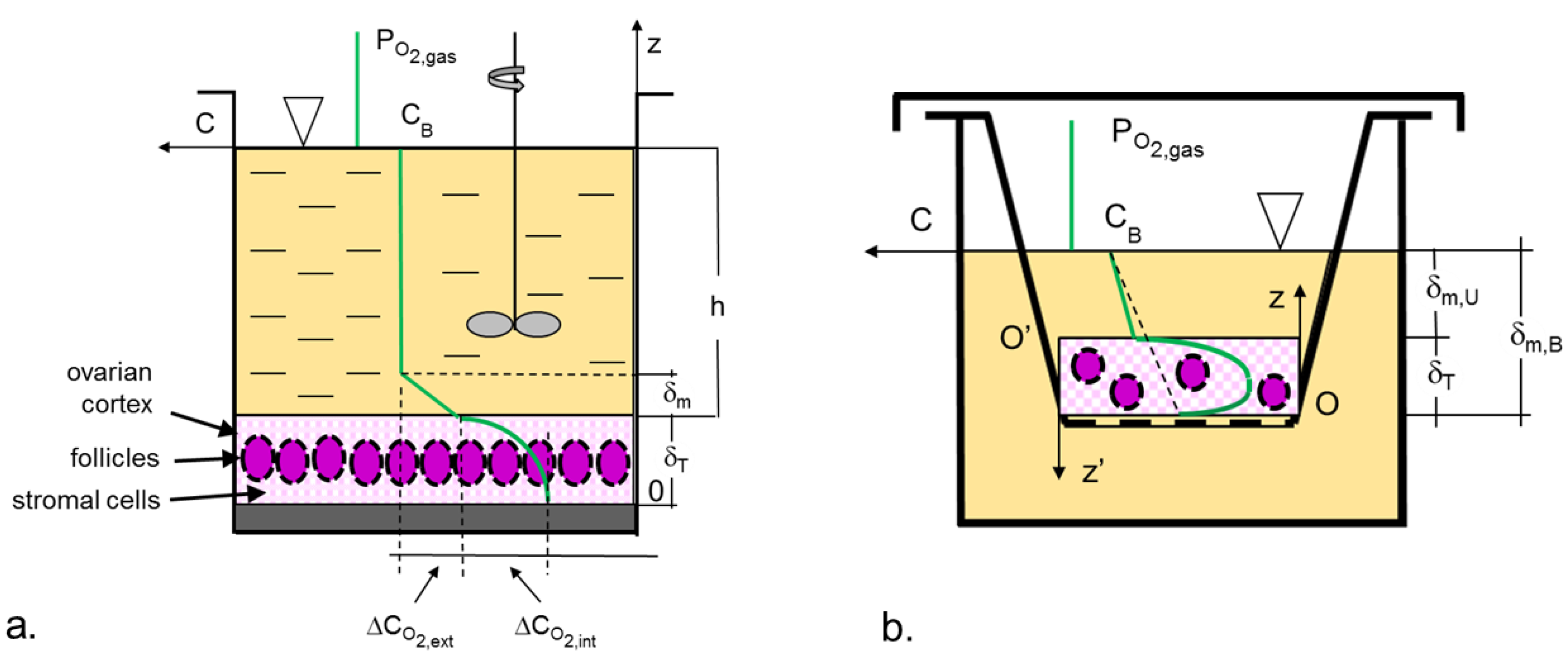
2.2. Models of Oxygen Transport
2.3. Estimation of the Oxygen Transport Coefficient, kL
2.3.1. Static Bioreactors
2.3.2. Mixed Bioreactors
3. Results and Discussion
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Donnez, J.; Dolmans, M.M. Fertility preservation in women. N. Engl. J. Med. 2018, 378, 399–401. [Google Scholar]
- Donnez, J.; Silber, S.; Andersen, C.Y.; Demeestere, I.; Piver, P.; Meirow, D. Children born after autotransplantation of cryopreserved ovarian tissue. A review of 13 live births. Ann. Med. 2011, 43, 437–450. [Google Scholar] [CrossRef] [PubMed]
- Dolmans, M.M.; Luyckx, V.; Donnez, J.; Andersen, C.Y.; Greve, T. Risk of transferring malignant cells with transplanted frozen-thawed ovarian tissue. Fert. Steril. 2013, 99, 1514–1522. [Google Scholar] [CrossRef] [PubMed]
- Abir, R.; Aviram, A.; Feinmesser, M.; Stein, J.; Yaniv, I.; Parnes, D. Ovarian minimal residual disease in chronic myeloid leukaemia. Reprod Biomed. Online 2014, 28, 255–260. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abir, R.; Nitke, S.; Ben-Haroush, A.; Fisch, B. In vitro maturation of human primordial ovarian follicles: Clinical significance, progress in mammals, and methods for growth evaluation. Histol. Histopathol. 2006, 21, 887–898. [Google Scholar]
- Carroll, J.; Gosden, R.G. Transplantation of frozen-thawed mouse primordial follicles. Hum. Reprod. 1993, 8, 1163–1167. [Google Scholar] [CrossRef] [PubMed]
- Kniazeva, E.; Hardy, A.N.; Boukaidi, S.A.; Woodruff, T.K.; Jeruss, J.S.; Shea, L.D. Primordial follicle transplantation within designer biomaterial grafts produce live births in a mouse infertility model. Sci. Rep. 2015. [Google Scholar] [CrossRef]
- Telfer, E.E.; McLaughlin, M.; Ding, T.; Thong, K.J. A two-step serum-free culture system supports development of human oocytes from primordial follicles in the presence of activin. Hum. Reprod. 2008, 23, 1151–1158. [Google Scholar] [CrossRef] [Green Version]
- McLaughlin, M.; Albertini, D.F.; Wallace, W.H.B.; Anderson, R.A.; Telfer, E.E. Metaphase II oocytes from human unilaminar follicles grown in a multi-step culture system. Mol. Hum. Reprod. 2018, 24, 135–142. [Google Scholar] [CrossRef] [Green Version]
- Hornick, J.E.; Duncan, F.E.; Shea, L.D.; Woodruff, K. Isolated primate primordial follicles require a rigid physical environment to survive and grow in vitro. Hum. Reprod. 2012, 27, 1801–1810. [Google Scholar] [CrossRef] [Green Version]
- Sudhakaran, S.; Gualtieri, R.; Barbato, V.; Fiorentino, I.; Braun, S.; Merolla, A.; Talevi, R. Isolated ovarian follicle culture: A promising strategy for fertility preservation. Curr. Trends. Clin. Embriol. 2015, 2, 177–185. [Google Scholar]
- Telfer, E.E. Future developments: In vitro growth (IVG) of human ovarian follicles. Acta Obs. Gynecol. Scand. 2019, 98, 653–658. [Google Scholar] [CrossRef] [PubMed]
- Smitz, J.; Dolmans, M.M.; Donnez, J.; Fortune, J.E.; Hovatta, O.; Jewgenow, K.; Picton, H.M.; Plancha, C.; Shea, L.D.; Stouffer, R.L.; et al. Current achievements and future research directions in ovarian tissue culture, in vitro follicle development and transplantation: Implications for fertility preservation. Hum. Reprod. Update 2010, 16, 395–414. [Google Scholar] [CrossRef] [PubMed]
- Catapano, G.; Gualtieri, R.; Talevi, R. Transport analysis of bioreactors for the in vitro culture of ovarian tissue. Curr. Trends. Clin. Embryol. 2016, 3, 54–65. [Google Scholar] [CrossRef]
- Hovatta, O.; Silye, R.; Abir, R.; Krausz, T.; Winston, R.M.L. Extracellular matrix improves survival of both stored and fresh human primordial and primary ovarian follicles in long-term culture. Hum. Reprod. 1997, 12, 1032–1036. [Google Scholar] [CrossRef]
- Wright, C.S.; Hovatta, O.; Margara, R.; Trew, G.; Winston, R.M.L.; Franks, S.; Hardy, K. Effects of follicle-stimulating hormone and serum substitution on the in-vitro growth of human ovarian follicles. Hum. Reprod. 1999, 14, 1555–1562. [Google Scholar] [CrossRef]
- Isachenko, V.; Montag, M.; Isachenko, E.; van der Ven, K.; Dorn, C.; Roesing, B.; Braun, F.; Sadek, F.; van der Ven, H. Effective method for in-vitro culture of cryopreserved human ovarian tissue. Reprod. Biomed. Online 2006, 13, 228–234. [Google Scholar] [CrossRef]
- Liebenthron, J.; Koester, M.; Drengner, C.; Reinsberg, J.; van der Ven, H.; Montag, M. The impact of culture conditions on early follicle recruitment and growth from human ovarian cortex biopsies in vitro. Fert. Steril. 2013, 100, 483–491. [Google Scholar] [CrossRef]
- Talevi, R.; Sudhakaran, S.; Barbato, V.; Merolla, A.; Braun, S.; Di Nardo, M.; Costanzo, V.; Ferraro, R.; Iannantuoni, N.; Catapano, G.; et al. Is oxygen availability a limiting factor for in vitro folliculogenesis? PLoS ONE 2018, 13. [Google Scholar] [CrossRef]
- Fraser, I.S.; Baird, D.T.; Cockburn, F. Ovarian venous blood PO2, PCO2 and pH in women. J. Reprod. Fert. 1973, 33, 11–17. [Google Scholar] [CrossRef]
- Cargill, W.; Hickam, J.B. The oxygen consumption of the normal and the diseased human kidney. J. Clin. Investig. 1949, 28, 526–532. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Saidel, G.M.; Cabrera, M.E. Multi-Scale computational model of fuel homeostasis during exercise: Effect of hormonal control. Ann. Biomed. Eng. 2006, 35, 69–90. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Betzendahl, I.; Cortvrindt, R.; Smitz, J.; Eichenlaub-Ritter, U. Effects of low O2 and ageing on spindles and chromosomes in mouse oocytes from pre-antral follicle culture. Hum. Reprod. 2001, 16, 737–748. [Google Scholar] [CrossRef] [PubMed]
- Gigli, I.; Cushman, R.A.; Wahl, C.M.; Fortune, J.E. Evidence for a role for anti-Mullerian hormone in the suppression of follicle activation in mouse ovaries and bovine ovarian cortex grafted beneath the chick chorioallantoic membrane. Mol. Reprod. Dev. 2005, 71, 480–488. [Google Scholar] [CrossRef] [PubMed]
- Kirkegaard, K.; Hindkjaer, J.J.; Ingersley, H.J. Effect of oxygen concentration on human embryo development evaluated by time-lapse monitoring. Fert. Steril. 2013, 99, 738–744. [Google Scholar] [CrossRef] [PubMed]
- Jorssen, E.P.; Langbeen, A.; Fransen, E.; Martinez, E.L.; Leroy, J.L.; Bols, P.E. Monitoring preantral follicle survival and growth in bovine ovarian biopsies by repeated use of neutral red and cultured in vitro under low and high oxygen tension. Theriogenology 2014, 82, 387–395. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Lawson, M.S.; Yeoman, R.R.; Pau, K.Y.; Barrett, S.L.; Zelinski, M.B.; Stouffer, R.L. Secondary follicle growth and oocyte maturation during encapsulated three-dimensional culture in rhesus monkeys: Effects of gonadotrophins, oxygen and fetuin. Hum. Reprod. 2011, 26, 1061–1072. [Google Scholar] [CrossRef] [PubMed]
- Gook, D.A.; Edgar, D.H.; Lewis, K.; Sheedy, J.R.; Gardner, D.K. Impact of oxygen concentration on adult murine pre-antral follicle development in vitro and the corresponding metabolic profile. Mol. Hum. Reprod. 2013. [Google Scholar] [CrossRef] [PubMed]
- Connolly, J.M.; Kane, M.T.; Quinlan, L.R.; Dockery, P.; Hynes, A.C. Hypoxia limits mouse follicle growth in vitro. Reprod. Fertil. Dev. 2015. [Google Scholar] [CrossRef]
- Zeilmaker, G.H.; Verhamme, C.M. Observations on rat oocyte maturation in vitro: Morphology and energy requirements. Biol. Reprod. 1974, 11, 145–152. [Google Scholar] [CrossRef]
- Van Blerkom, J. Epigenetic influences on oocyte developmental competence: Perifollicular vascularity and intrafollicular oxygen. J. Assist. Reprod. Genet. 1998, 15, 226–234. [Google Scholar] [CrossRef] [PubMed]
- Morimoto, Y.; Oku, Y.; Sonoda, M.; Haruki, A.; Ito, K.; Hashimoto, S.; Fukuda, A. High oxygen atmosphere improves human follicle development in organ cultures of ovarian cortical tissues in vitro. Hum. Reprod. 2007, 22, 3170–3177. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hovatta, O.; Wright, C.; Krausz, T.; Hardy, K.; Winston, R.M.L. Human primordial, primary and secondary ovarian follicles in long-term culture: Effect of partial isolation. Hum. Reprod. 1999, 14, 2519–2524. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; J. Wiley & Sons: New York, NY, USA, 2002; pp. 303–305, 543–581. [Google Scholar]
- Dardik, A.; Chen, L.; Frattini, J.; Asada, H.; Aziz, F.; Kudo, F.A.; Sumpio, B.E. Differential effects of orbital and laminar shear stress on endothelial cells. J. Vasc. Surg. 2005, 41, 869–880. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Understanding Effects of Viscosity in the BioFlux System. Available online: https://support.fluxionbio.com/hc/en-us/articles/203649638-Viscosity-Understanding-effects-of-viscosity-in-the-BioFlux-system (accessed on 29 May 2019).
- Available online: https://www.thermofisher.com/order/catalog/product/140620 (accessed on 16 October 2018).
- Doig, S.D.; Pickering, S.C.R.; Lye, G.J.; Baganz, F. Modelling surface aeration rates in shaken microtitre plates using dimensionless groups. Chem. Eng. Sci. 2005, 60, 2741–2750. [Google Scholar] [CrossRef]
- Kloeckner, W.; Buechs, J. Advances in shaking technologies. Trends Biotechnol. 2012, 30, 307–313. [Google Scholar] [CrossRef] [PubMed]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems, 3rd ed.; Cambridge Univ Press: Cambridge, UK, 1984; p. 254. [Google Scholar]
- Gosden, R.G.; Byatt-Smith, J.G. Oxygen concentration gradient across the ovarian follicular epithelium: Model, predictions and implications. Hum. Reprod. 1986, 1, 65–68. [Google Scholar] [CrossRef] [PubMed]
- Clark, A.R.; Stokes, Y.M.; Lane, M.; Thompson, J.G. Mathematical modelling of oxygen concentration in bovine and murine cumulus-oocyte complexes. Reproduction 2006, 131, 999–1006. [Google Scholar] [CrossRef]
- Redding, G.P.; Bronlund, J.E.; Hart, A.L. Mathematical modelling of oxygen transport-limited follicle growth. Reproduction 2007, 133, 1095–1106. [Google Scholar] [CrossRef] [Green Version]
- Clark, A.R.; Stokes, Y.M. Follicle Structure influences the availability of oxygen to the oocyte in antral follicles. Comput. Math. Methods Med. 2011. [Google Scholar] [CrossRef]
- Schmidt, K.L.T.; Byskov, A.G.; Nyboe Anderson, A.; Mueller, J.; Yding Anderson, C. Density and distribution of primordial follicles in single pieces of cortex from 21 patients and in individual pieces of cortex from three entire human ovaries. Hum. Reprod. 2003, 18, 1158–1164. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 4th ed.; Prentice Hall: Westford, MA, USA, 2006; pp. 813–867. [Google Scholar]
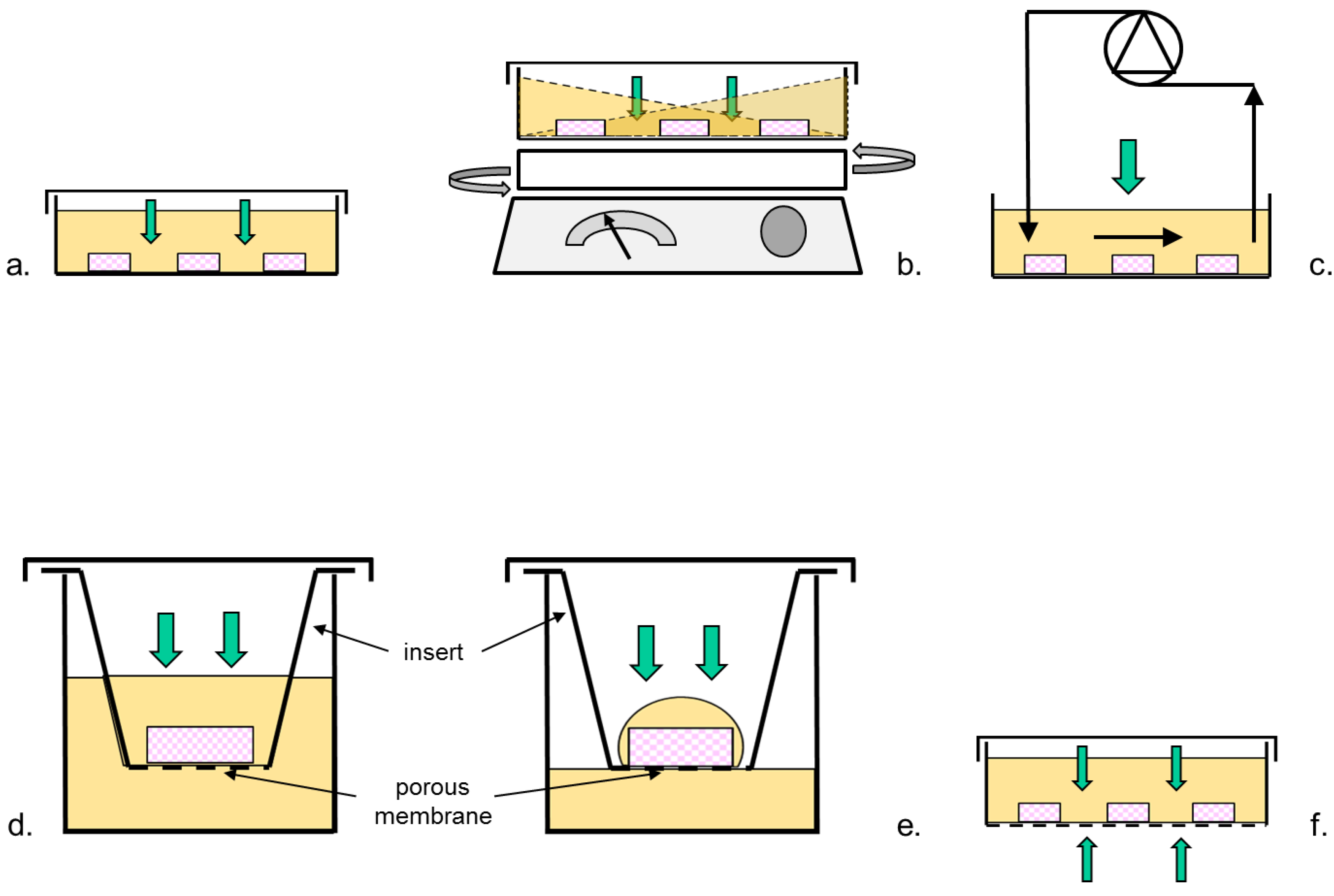
| Authors | Medium Used | Growth-Affecting Supplements | Culture System | Support Coating | Culture Mode | No Strips Per Well | Medium Volume | Medium Change | pO2 | Tissue | Assessment Follicles State | Reference | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data on Fresh Tissue Y/N | Culture Time Days | Viability | Stage | Grade | Hormones | ||||||||||||
| Hovatta et al., 1997 | -MEM, Earle’s | FSH, IHS, Ins, LH, Pyr | Inserts in well in 24 well plate | none, MatrigelTM | static, double medium layer | 1–3 | NA | 2nd day | air | Fresh & thawed | Y | up to 21 | Morph | Y | N | N | [15] |
| Wright et al., 1999 | -MEM, | FSH, HSA, ITS-G BrG, cMP | Inserts in well in 24 well plate | MatrigelTM | static, double medium layer | NA | 100 uL + 400 uL | 150 uL @ 2nd day | air | Fresh | Y | up to 14 | Morph | Y | N | N | [16] |
| Isachenko et al., 2006 | Iskove’s modified Dulbecco’s | EGF, FCS, FSH, ITS, | 200 mL dishes | none | static vs. mixed on orbital shaker | 20 | 30 mL | NO | air | Fresh & thawed | N | up to 21 | Morph | Y | N | N | [17] |
| Liebenthron et al., 2013 | McCoy’s 5a + HEPES | AA, BSA, Glu, ITS | 6 well plate | none | static vs. medium recirculation | NA | 4.5 mL | NO | air | Fresh | Y | up to 6 | Morph calcein AM | Y | N | Y | [18] |
| Talevi et al., 2018 | -MEM | AA, Am, BSA, Glu, ITS, PS | 50 mm dishes | none | static, conventional vs. permeable bottom | 10 | 5 mL | half every other day | air | Fresh | Y | up to 9 | Morph dead/live | Y | Y | N | [19] |
| Bioreactor # | Bioreactor Type | Fragment Side of O2 Supply | δT m | δm m | kL m/s | Thiele Number ϕ | Biot Bim | Oxygen Availability | Anoxic Core | Reference | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CT,m/CB % | CT,avg/CB % | wac/δT % | |||||||||
| 1 | Static CD | Upper | 1.00 × 10−3 | 8.18 × 10−4 | 4.28 × 10−6 | 6.0 | 1.53 | 3.07 | 3.07 × 10−3 | 95.85 | [17] |
| 2 | CD on orbital shaker | Upper | 1.00 × 10−3 | NA | 1.13 × 10−4 | 6.0 | 40.37 | 81.14 | 3.15 × 10−1 | 78.68 | [17] |
| 3 | Static CD | Upper | 1.00 × 10−3 | 3.69 × 10−3 | 9.49 × 10−7 | 6.0 | 0.34 | 0.16 | 1.60 × 10−4 | 99.05 | [18] |
| 4 | CD w/ periodic medium flow | Upper | 1.00 × 10−3 | NA | 9.94 × 10−7 | 6.0 | 0.36 | 0.18 | 1.76 × 10−4 | 99.01 | [18] |
| 5 | Culture on insert in well | Upper | 2.00 × 10−3 | 2.26 × 10−3 | 1.55 × 10−6 | 12.0 | 1.10 | 0.42 | 5.44 × 10−4 | 98.82 | [16] |
| Lower | 4.26 × 10−3 | 8.21 × 10−7 | 0.59 | 0.12 | |||||||
| 6 | Culture on insert in well | Upper | 2.00 × 10−3 | 5.00 × 10−4 | 7.00 × 10−6 | 12.0 | 5.00 | 7.49 | 1.69 × 10−5 | 95.61 | [16] |
| Lower | 2.33 × 10−6 | 1.67 | 0.95 | ||||||||
| 7 | Culture on insert in well | Upper | 3.00 × 10−4 | 1.33 × 10−3 | 2.63 × 10−6 | 1.8 | 0.28 | 1.20 | 1.53 × 10−3 | 84.25 | [15] |
| Lower | 1.63 × 10−3 | 2.15 × 10−6 | 0.23 | 0.81 | |||||||
| 8 | Static CD | Upper | 5.00 × 10−4 | 1.40 × 10−3 | 2.50 × 10−6 | 2.5 | 0.7 | 3.6 | 5.30 × 10−2 | 89.3 | [19] |
| 9 | Static PD | Lower | 5.00 × 10−4 | 1.40 × 10−3 | 2.50 × 10−6 | 2.5 | 0.7 | 3.6 | 1.25 | 32.6 | [19] |
| NA | 100 | ||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Catapano, G.; Fragomeni, G.; Falvo D’Urso Labate, G.; De Napoli, L.; Barbato, V.; Di Nardo, M.; Costanzo, V.; Capriglione, T.; Gualtieri, R.; Talevi, R. Do Bioreactor Designs with More Efficient Oxygen Supply to Ovarian Cortical Tissue Fragments Enhance Follicle Viability and Growth In Vitro? Processes 2019, 7, 450. https://doi.org/10.3390/pr7070450
Catapano G, Fragomeni G, Falvo D’Urso Labate G, De Napoli L, Barbato V, Di Nardo M, Costanzo V, Capriglione T, Gualtieri R, Talevi R. Do Bioreactor Designs with More Efficient Oxygen Supply to Ovarian Cortical Tissue Fragments Enhance Follicle Viability and Growth In Vitro? Processes. 2019; 7(7):450. https://doi.org/10.3390/pr7070450
Chicago/Turabian StyleCatapano, Gerardo, Gionata Fragomeni, Giuseppe Falvo D’Urso Labate, Luigi De Napoli, Vincenza Barbato, Maddalena Di Nardo, Valentina Costanzo, Teresa Capriglione, Roberto Gualtieri, and Riccardo Talevi. 2019. "Do Bioreactor Designs with More Efficient Oxygen Supply to Ovarian Cortical Tissue Fragments Enhance Follicle Viability and Growth In Vitro?" Processes 7, no. 7: 450. https://doi.org/10.3390/pr7070450





