Discrete-Time Kalman Filter Design for Linear Infinite-Dimensional Systems
Abstract
:1. Introduction
2. Mathematical Preliminaries
2.1. Model Description
2.2. Model Discretization
2.3. Stochastic Discrete Model
3. Discrete-Time Kalman Filter Design
4. Single-Phase Pipeline Hydraulic Model
4.1. Model Description
4.2. Model Linearization
4.3. In-Domain Control Problem
4.4. Model Discretization
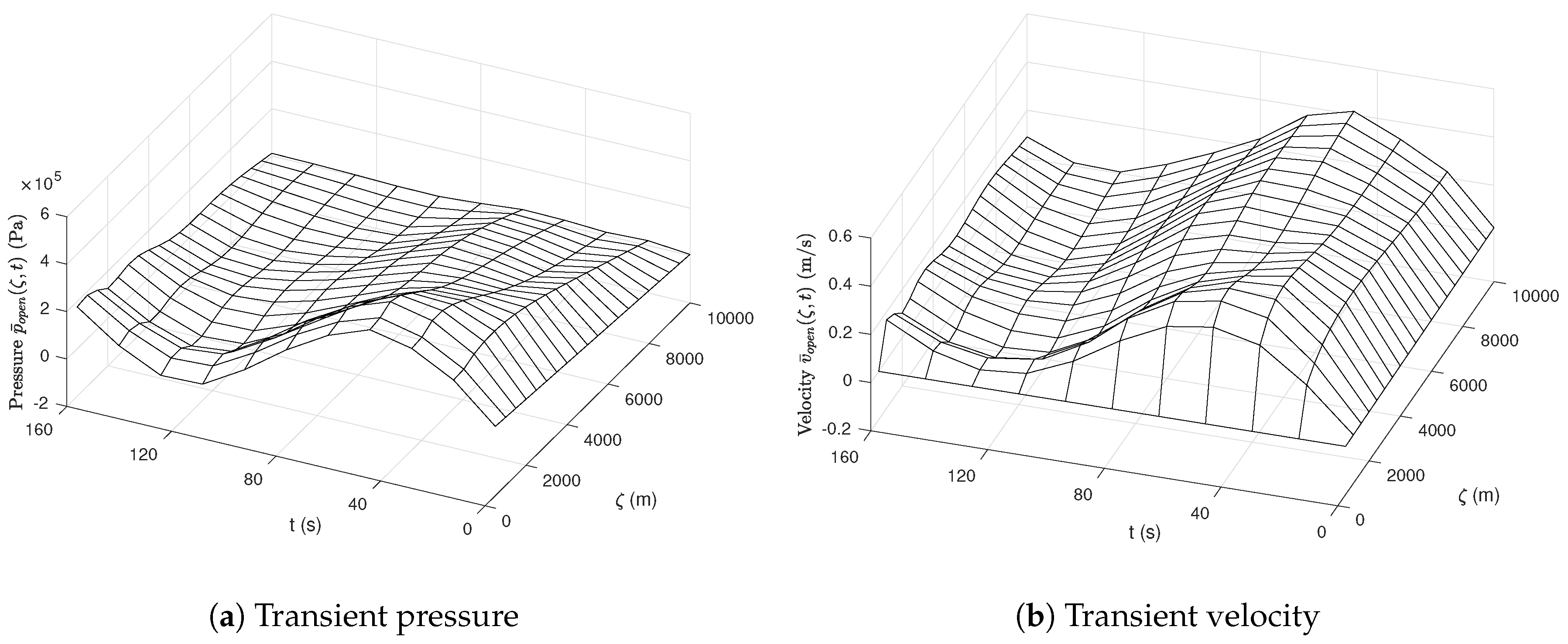
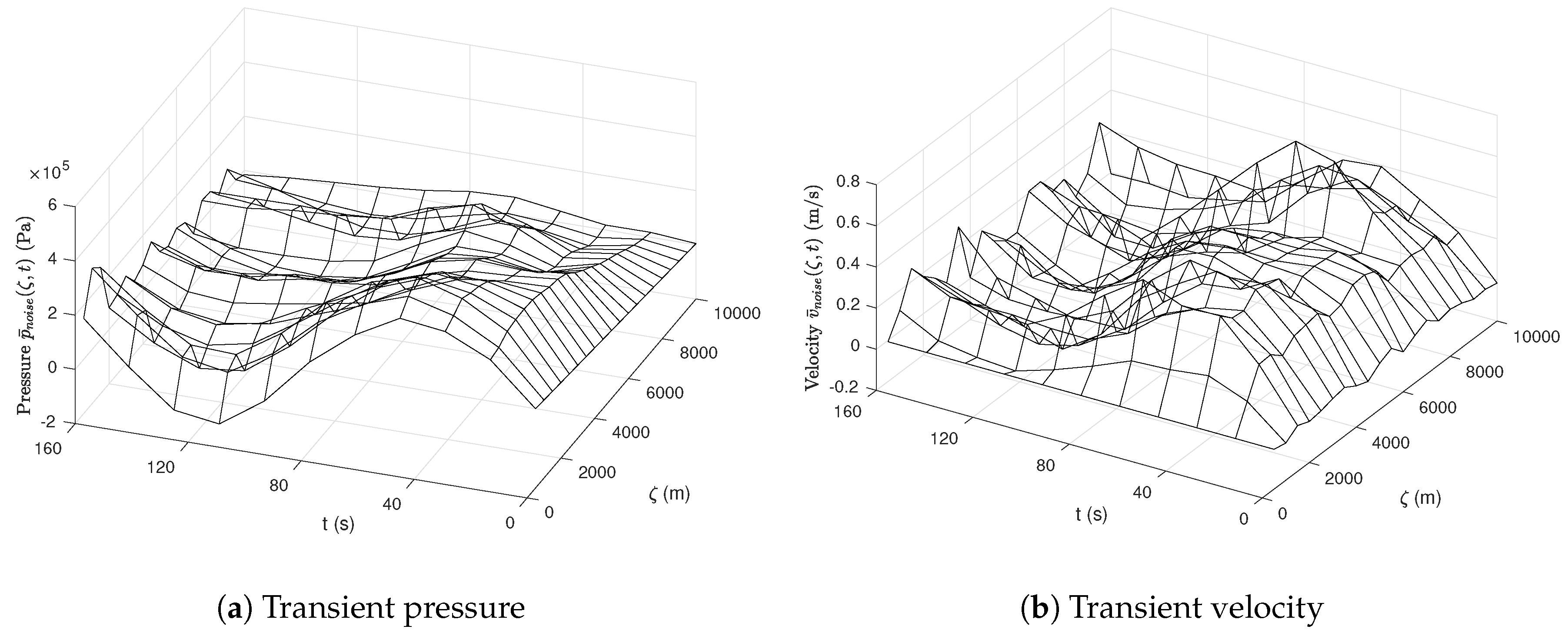
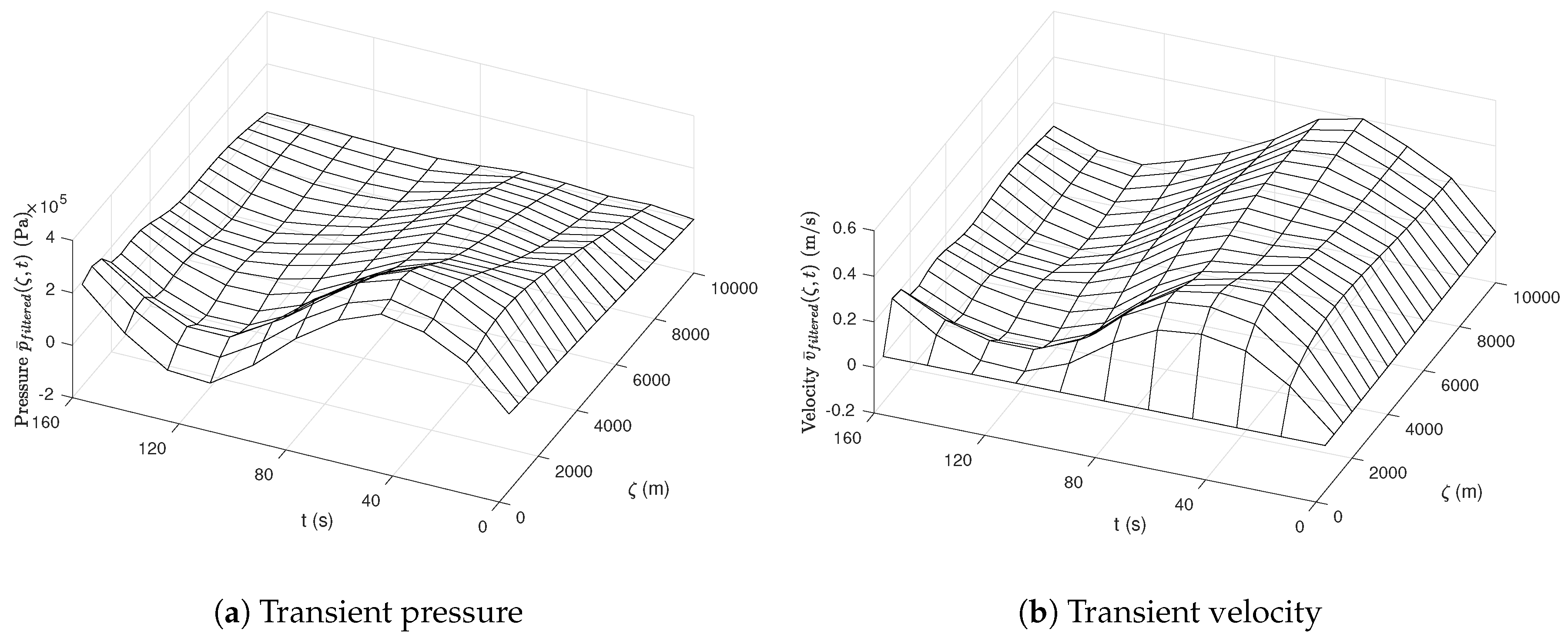
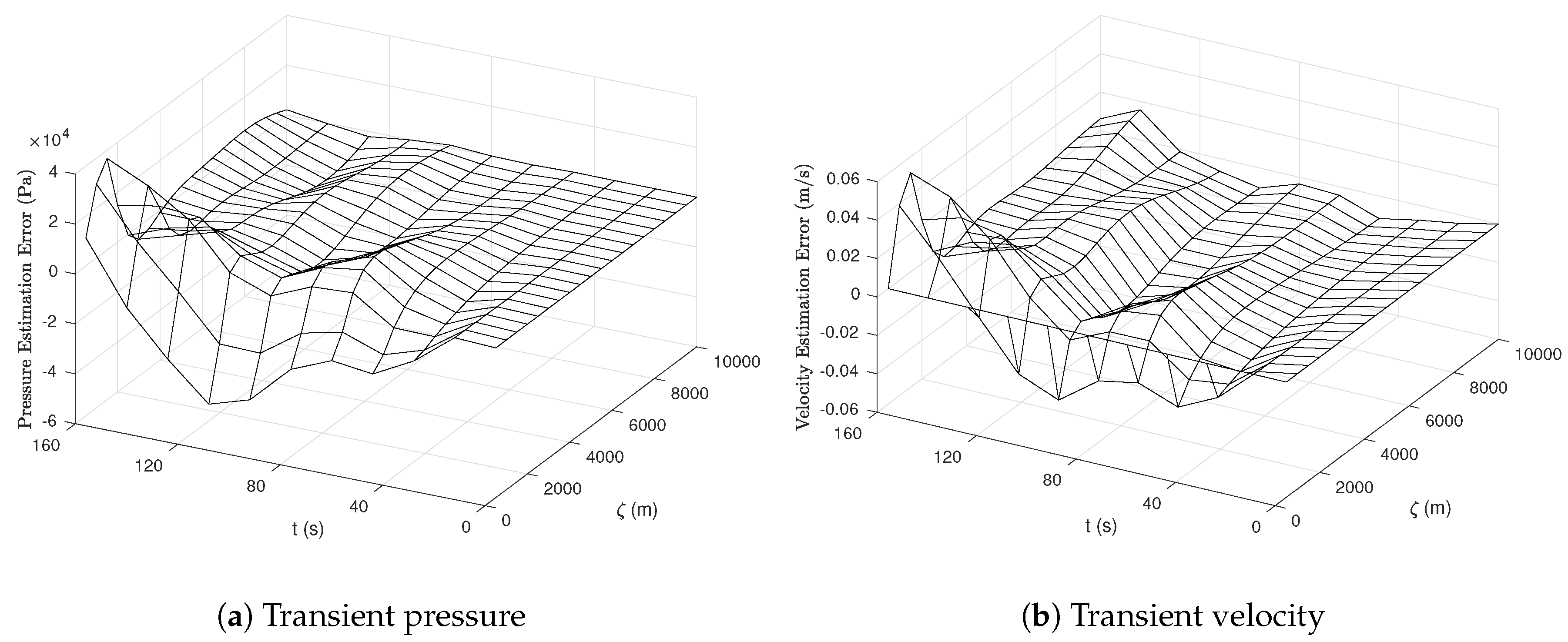
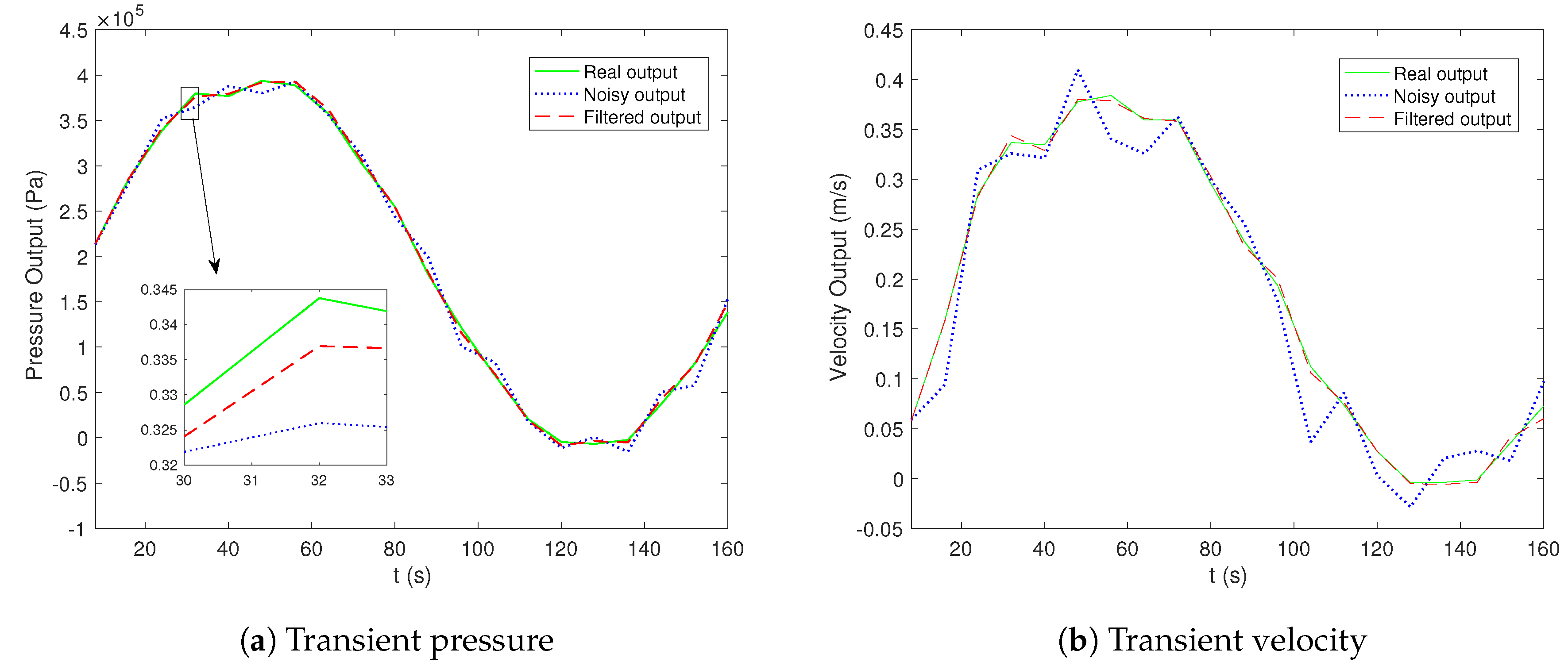
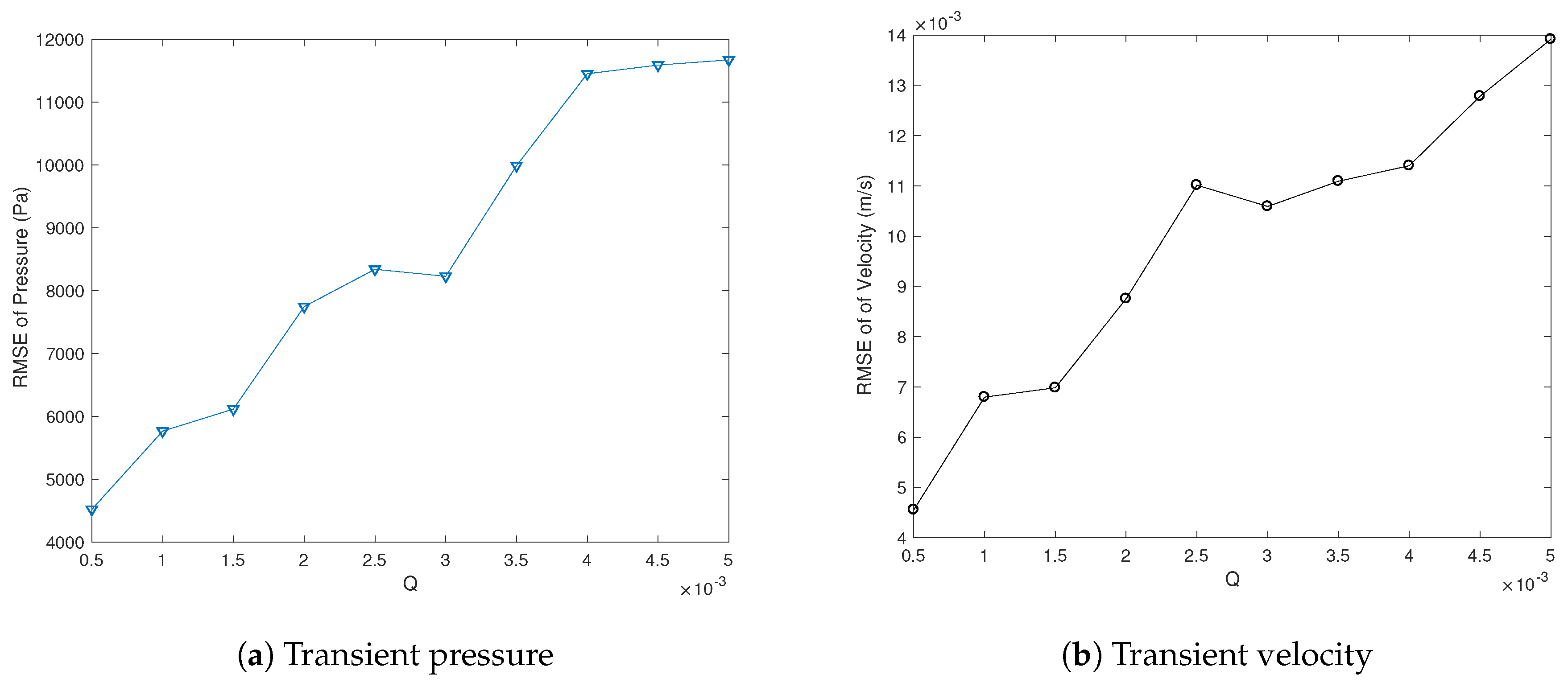
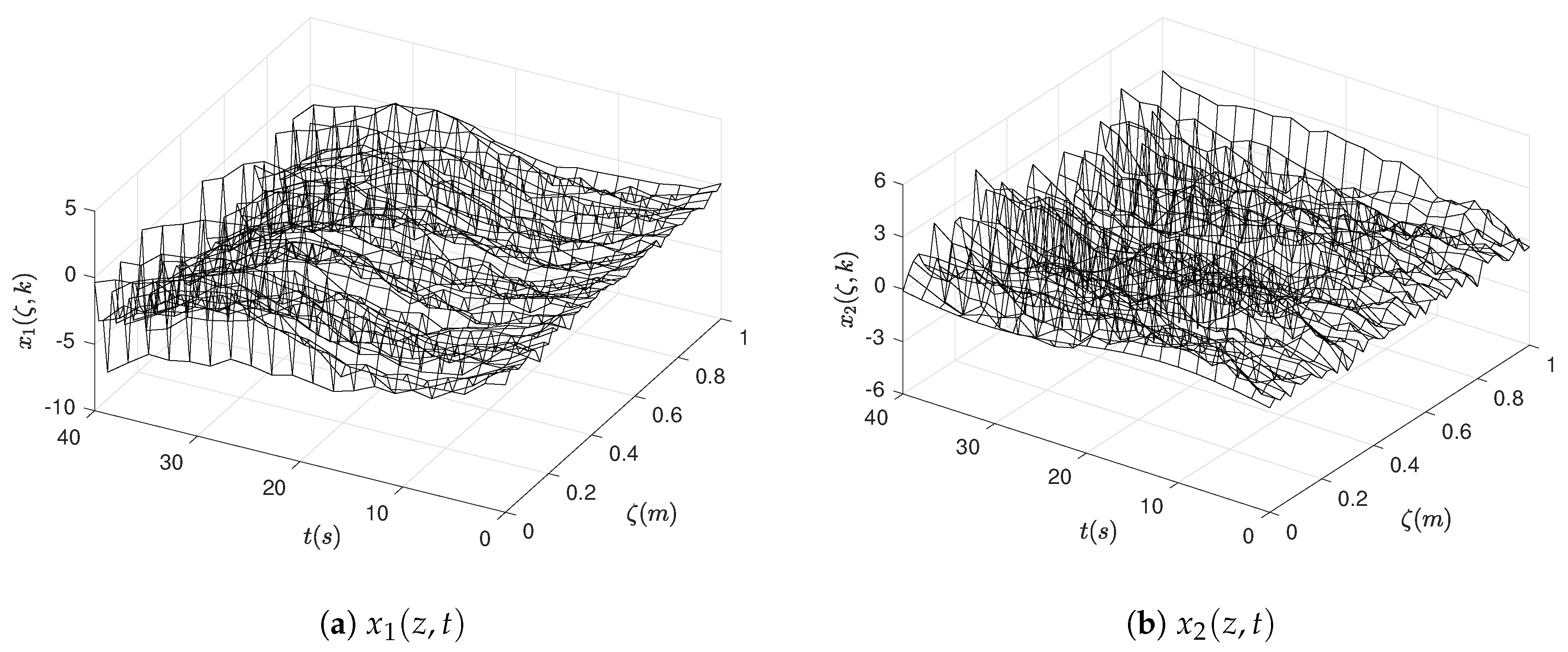
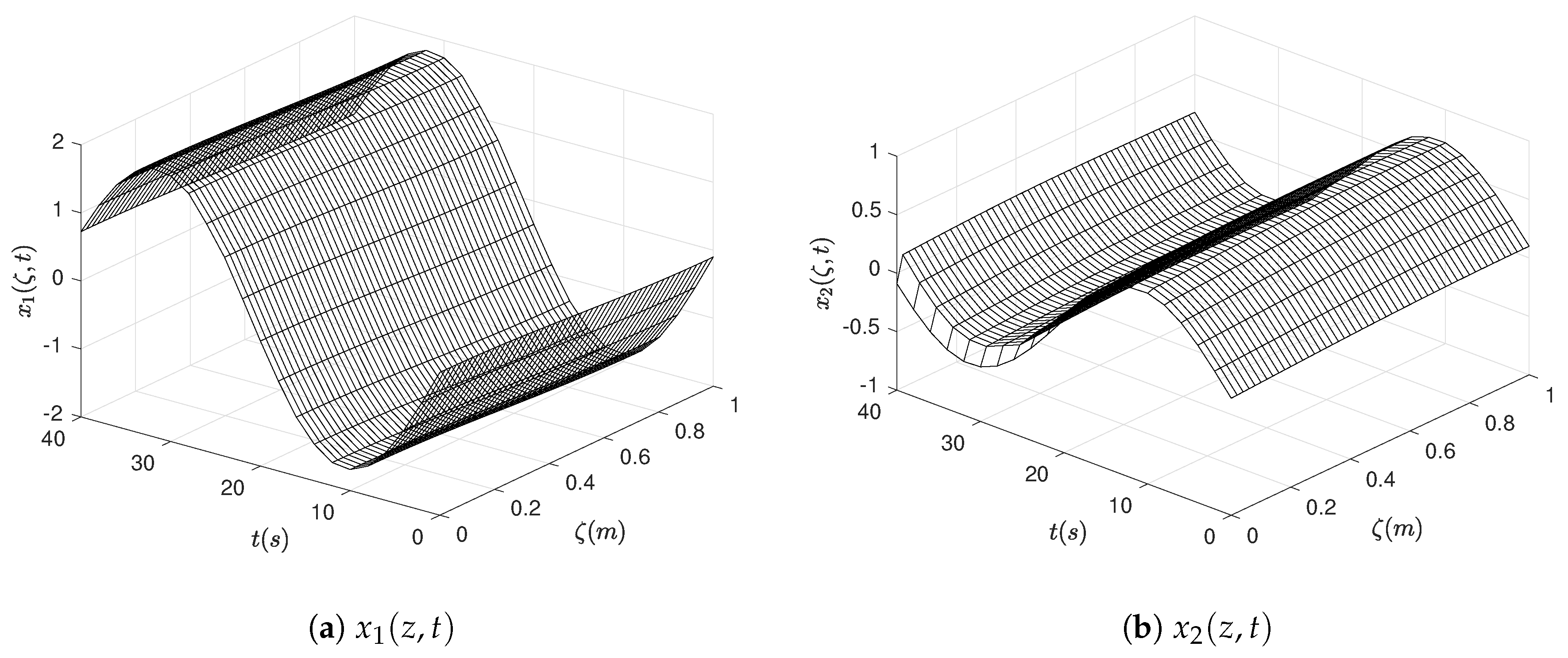
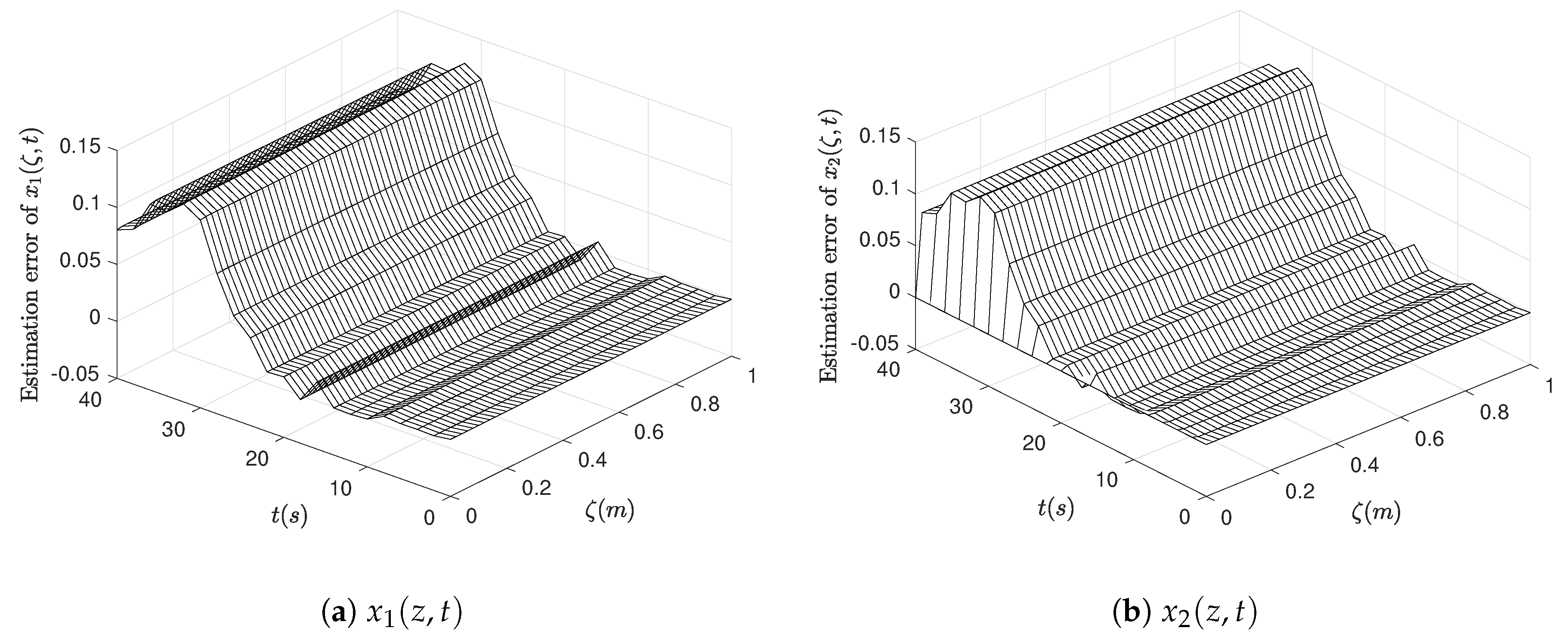
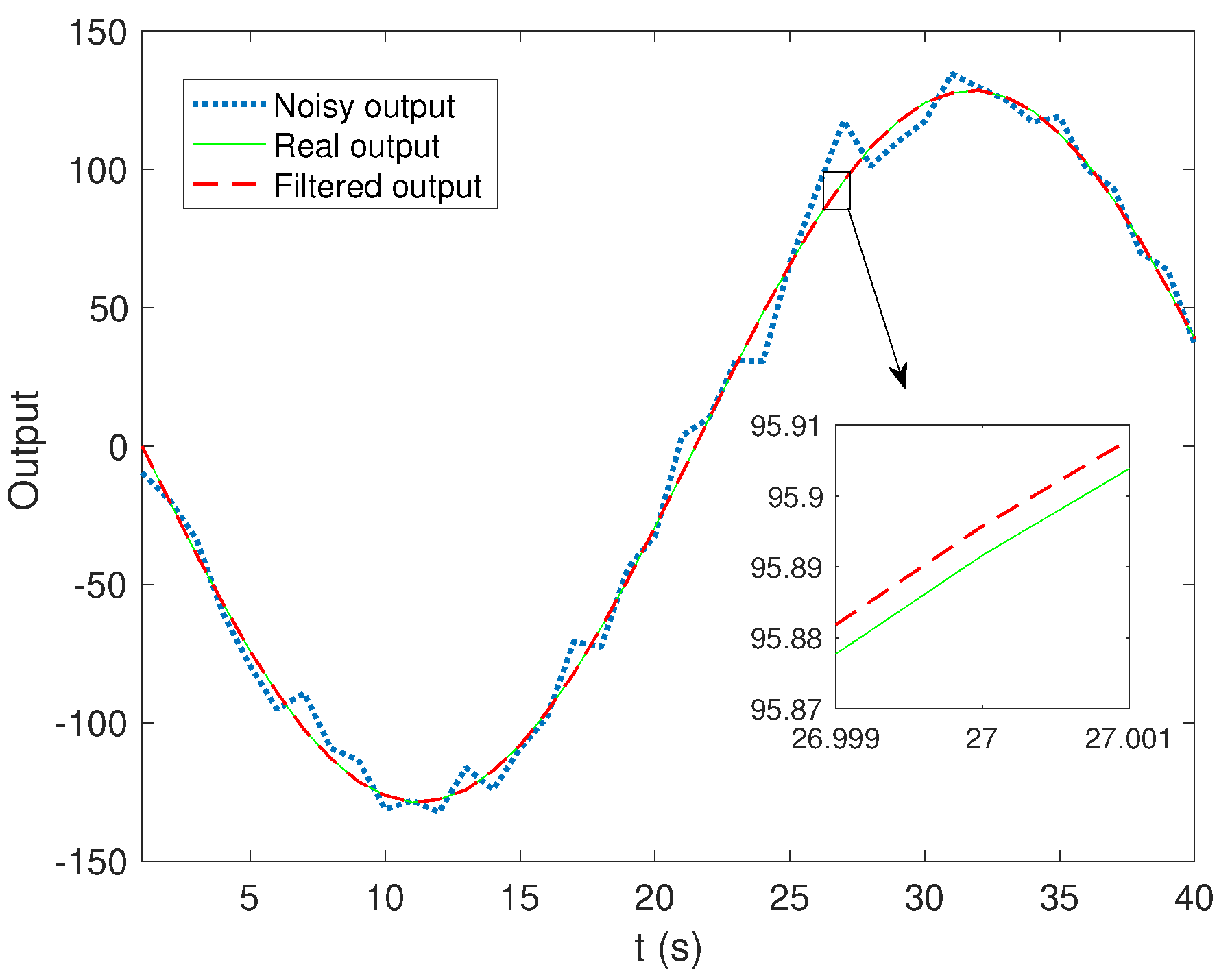
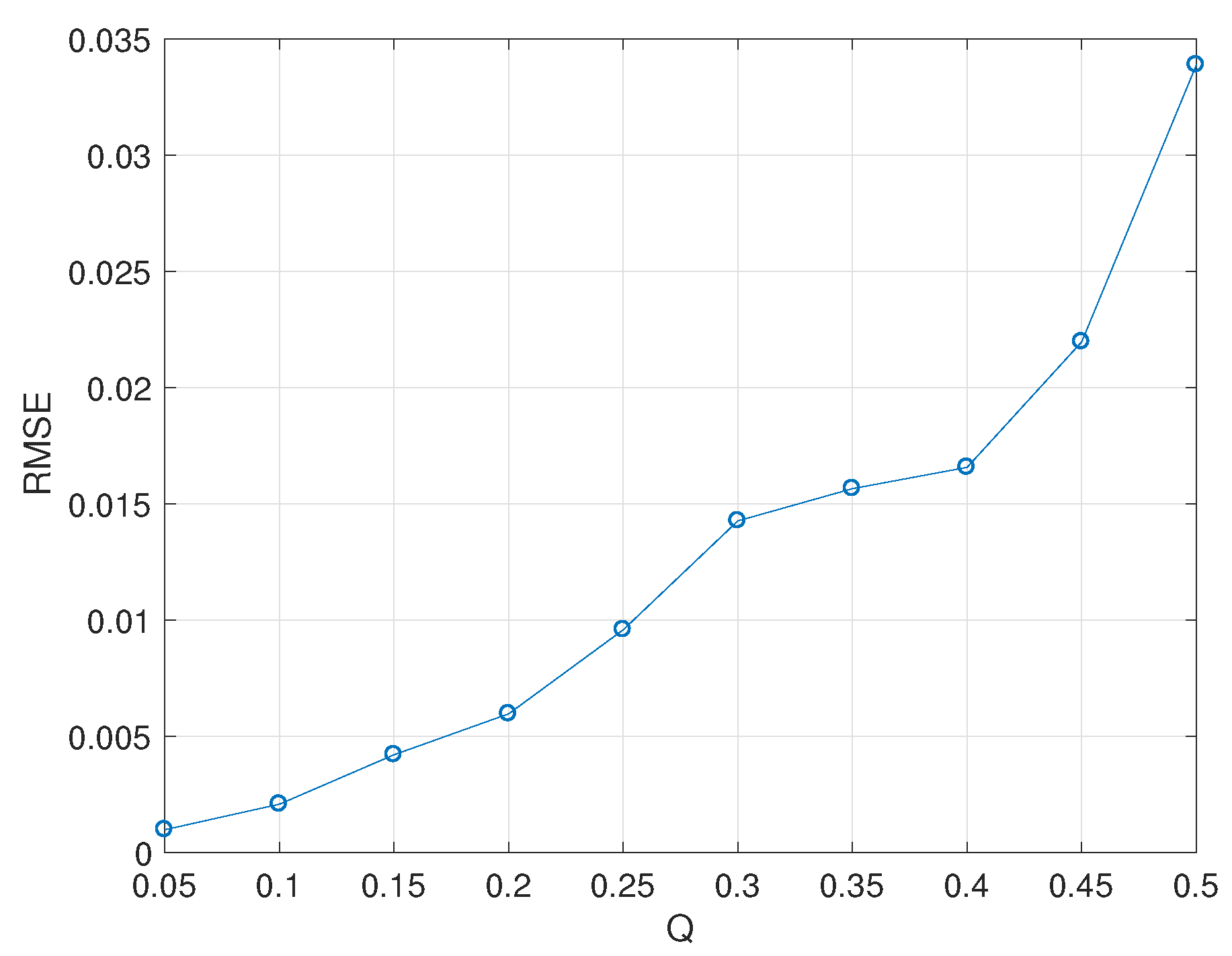
4.5. Simulation Results of the Water Hammer Equation
5. Wave System
5.1. Model Description
5.2. Model Discretization
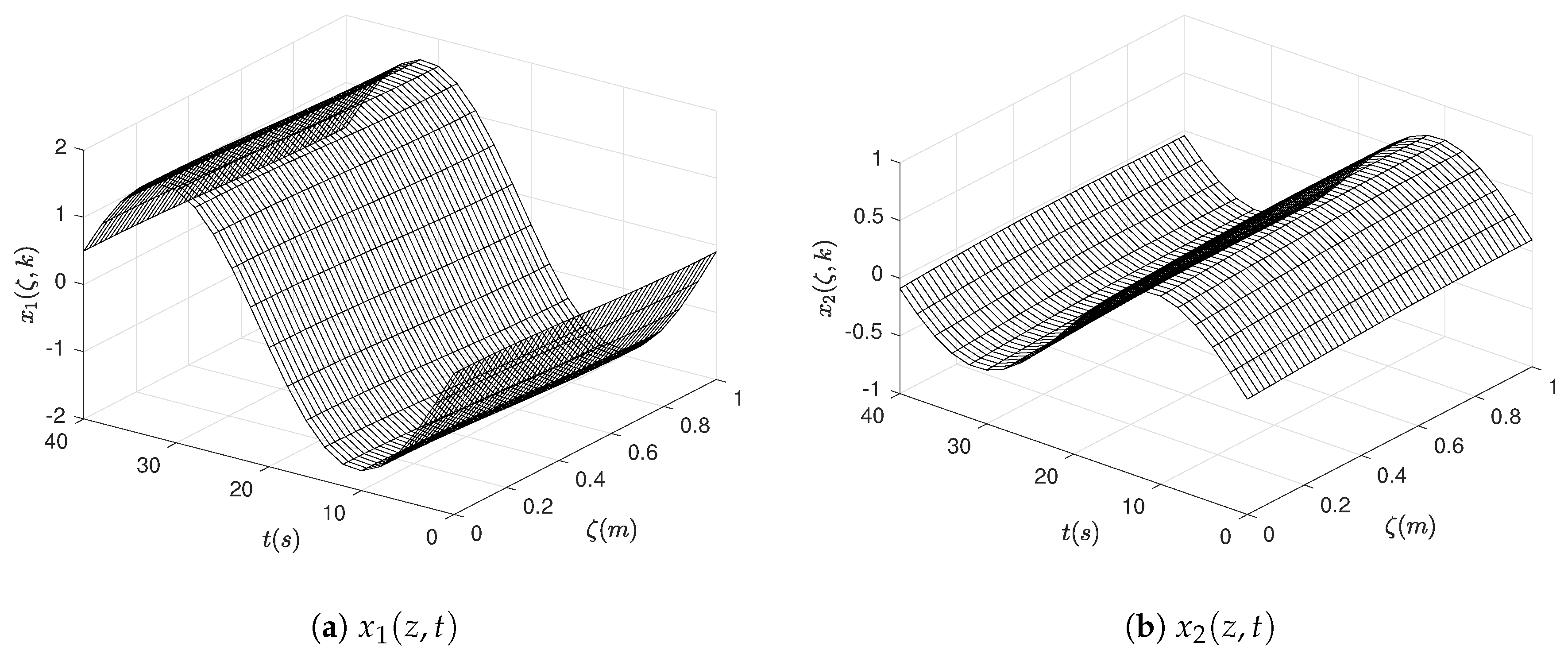
5.3. Simulation Results for the Wave Equation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Curtain, R.F.; Zwart, H. An Introduction to Infinite-Dimensional Linear Systems Theory; Springer-Verlag: New York, NY, USA, 1995. [Google Scholar]
- Ray, W.H. Advanced Process Control; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Tucsnak, M.; Weiss, G. Observation and Control for Operator Semigroups; Springer Science & Business Media: Basel, Switzerland, 2009. [Google Scholar]
- Yu, T.K.; Seinfeld, J.H. Observability and optimal measurement location in linear distributed parameter systems. Int. J. Control 1973, 18, 785–799. [Google Scholar] [CrossRef]
- Temam, R. Infinite-Dimensional Dynamical Systems in Mechanics and Physics; Springer Science & Business Media: New York, NY, USA, 2012; Volume 68. [Google Scholar]
- Wu, R.B.; Tarn, T.J.; Li, C.W. Smooth controllability of infinite-dimensional quantum-mechanical systems. Phys. Rev. A 2006, 73, 012719. [Google Scholar] [CrossRef] [Green Version]
- Bastin, G.; Dochain, D. On-Line Estimation and Adaptive Control of Bioreactors; Elsevier Science Pub. B. V.: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Dochain, D.; Babary, J.P.; Tali-Manaar, M.N. Modeling and Adaptive Control of Nonlinear Distributed Parameter Bioreactors via Orthogonal Collocation. Automatica 1992, 68, 873–883. [Google Scholar] [CrossRef]
- Renard, P.; Dochain, D.; Bastin, G.; Naveau, H.; Nyns, E.J. Adaptive Control of Anaerobic Digestion Processes: A Pilot-scale Application. Biotechnol. Bioeng. 1988, 31, 287–294. [Google Scholar] [CrossRef] [PubMed]
- Werner, J. Distributed-Parameter-Control of Human Body-Temperature. IFAC Proc. Vol. 1975, 8, 328–334. [Google Scholar] [CrossRef]
- Nagaiah, C.; Kunisch, K.; Plank, G. Numerical solution for optimal control of the reaction-diffusion equations in cardiac electrophysiology. Comput. Optim. Appl. 2011, 49, 149–178. [Google Scholar] [CrossRef]
- Chakrabarty, S.P.; Hanson, F.B. Optimal control of drug delivery to brain tumors for a distributed parameters model. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 973–978. [Google Scholar]
- Schenk, O.; Manguoglu, M.; Sameh, A.; Christen, M.; Sathe, M. Parallel scalable PDE-constrained optimization: Antenna identification in hyperthermia cancer treatment planning. Comput. Sci.-Res. Dev. 2009, 23, 177–183. [Google Scholar] [CrossRef]
- Ray, W.H. Some recent applications of distributed parameter systems theory: A survey. Automatica 1978, 14, 281–287. [Google Scholar] [CrossRef]
- Luo, Z.H.; Guo, B.Z.; Morgül, Ö. Stability and Stabilization of Infinite Dimensional Systems with Applications; Springer Science & Business Media: London, UK, 2012. [Google Scholar]
- Tzafestas, S.G. Distributed Parameter Control Systems: Theory and Application; Elsevier: Amsterdam, The Netherlands, 2013; Volume 6. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. Trans. ASME J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 1995. [Google Scholar]
- Luenberger, D.G. Observing the state of a linear system. IEEE Trans. Mil. Electron. 1964, 8, 74–80. [Google Scholar] [CrossRef]
- Luenberger, D. Observers for multivariable systems. IEEE Trans. Autom. Control 1966, 11, 190–197. [Google Scholar] [CrossRef]
- Luenberger, D. An introduction to observers. IEEE Trans. Autom. Control 1971, 16, 596–602. [Google Scholar] [CrossRef]
- Dochain, D. State and parameter estimation in chemical and biochemical processes: A tutorial. J. Process Control 2003, 13, 801–818. [Google Scholar] [CrossRef]
- Dochain, D. State estimation in chemical and biochemical processes with uncertain kinetics. Ind. Eng. Chem. Res. 2002, 41, 4777. [Google Scholar]
- Bastin, G. On-Line Estimation and Adaptive Control of Bioreactors; Elsevier: Amsterdam, The Netherlands, 2013; Volume 1. [Google Scholar]
- Ali, J.M.; Hoang, N.H.; Hussain, M.A.; Dochain, D. Review and classification of recent observers applied in chemical process systems. Comput. Chem. Eng. 2015, 76, 27–41. [Google Scholar] [Green Version]
- Christofides, P.D. Control of nonlinear distributed process systems: Recent developments and challenges. AIChE J. 2001, 47, 514–518. [Google Scholar] [CrossRef]
- Dubljevic, S.; Mhaskar, P.; El-Farra, N.H.; Christofides, P.D. Predictive control of transport-reaction processes. Comput. Chem. Eng. 2005, 29, 2335–2345. [Google Scholar] [CrossRef]
- Christofides, P.D. Nonlinear and Robust Control of PDE Systems: Methods and Applications to Transport-Reaction Processes; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Christofides, P.D.; Scattolini, R.; de la Pena, D.M.; Liu, J. Distributed model predictive control: A tutorial review and future research directions. Comput. Chem. Eng. 2013, 51, 21–41. [Google Scholar] [CrossRef]
- Lao, L.; Ellis, M.; Christofides, P.D. Economic model predictive control of parabolic PDE systems: Addressing state estimation and computational efficiency. J. Process Control 2014, 24, 448–462. [Google Scholar] [CrossRef]
- Zeitz, M. Observability canonical (phase-variable) form for non-linear time-variable systems. Int. J. Syst. Sci. 1984, 15, 949–958. [Google Scholar] [CrossRef]
- Zeitz, M. The extended Luenberger observer for nonlinear systems. Syst. Control Lett. 1987, 9, 149–156. [Google Scholar] [CrossRef]
- Mangold, M.; Lauschke, G.; Schaffner, J.; Zeitz, M.; Gilles, E.D. State and parameter estimation for adsorption columns by nonlinear distributed parameter state observers. J. Process Control 1994, 4, 163–172. [Google Scholar] [CrossRef]
- Zeitz, M. Nonlinear observers for chemical reactors. In Fortschrittberichte der VDI-Zeitschriften; VDI-Verlag: Duesseldorf, Germany, 1977. [Google Scholar]
- Bitzer, M.; Zeitz, M. Design of a nonlinear distributed parameter observer for a pressure swing adsorption plant. J. Process Control 2002, 12, 533–543. [Google Scholar] [CrossRef]
- Bück, A.; Peglow, M.; Tsotsas, E.; Mangold, M.; Kienle, A. Model-based measurement of particle size distributions in layering granulation processes. AIChE J. 2011, 57, 929–941. [Google Scholar] [CrossRef]
- Bakir, T.; Othman, S.; Fevotte, G.; Hammouri, H. Non linear observer for the reconstruction of crystal size distributions in polymorphic crystallization processes. IFAC Proc. Vol. 2006, 39, 667–672. [Google Scholar] [CrossRef]
- Pourkargar, D.B.; Armaou, A. Dynamic shaping of transport–reaction processes with a combined sliding mode controller and Luenberger-type dynamic observer design. Chem. Eng. Sci. 2015, 138, 673–684. [Google Scholar] [CrossRef]
- Krstic, M.; Kanellakopoulos, I.; Petar, V. Nonlinear Adaptive Control Design; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Di Meglio, F.; Vazquez, R.; Krstic, M. Stabilization of a system of n + 1 coupled first-order hyperbolic linear PDEs with a single boundary input. IEEE Trans. Autom. Control 2013, 58, 3097–3111. [Google Scholar] [CrossRef]
- Krstic, M.; Fontaine, D.; Kokotovic, P.V.; Paduano, J.D. Useful nonlinearities and global stabilization of bifurcations in a model of jet engine surge and stall. IEEE Trans. Autom. Control 1998, 43, 1739–1745. [Google Scholar] [CrossRef]
- Aamo, O.M.; Krstic, M. Flow Control by Feedback: Stabilization and Mixing; Springer Science & Business Media: London, UK, 2013. [Google Scholar]
- Smyshlyaev, A.; Guo, B.Z.; Krstic, M. Arbitrary decay rate for Euler-Bernoulli beam by backstepping boundary feedback. IEEE Trans. Autom. Control 2009, 54, 1134–1140. [Google Scholar] [CrossRef]
- Meditch, J. On state estimation for distributed parameter systems. J. Frankl. Inst. 1970, 290, 49–59. [Google Scholar] [CrossRef]
- VandeWouwer, A.; Zeitz, M. State Estimation in Distributed Parameter Systems. In Encyclopedia of Life Support Systems (EOLSS): Control Systems, Robotics and Automation; EOLSS Publishers: London, UK, 2003. [Google Scholar]
- Hidayat, Z.; Babuska, R.; De Schutter, B.; Nunez, A. Observers for linear distributed-parameter systems: A survey. In Proceedings of the 2011 IEEE International Symposium on Robotic and Sensors Environments (ROSE), Montreal, QC, Canada, 17–18 September 2011; pp. 166–171. [Google Scholar]
- Yang, Y.; Dubljevic, S. Linear matrix inequalities (LMIs) observer and controller design synthesis for parabolic PDE. Eur. J. Control 2014, 20, 227–236. [Google Scholar] [CrossRef]
- Xu, X.; Huang, B.; Dubljevic, S. Optimal continuous-time state estimation for linear finite and infinite-dimensional chemical process systems with state constraints. J. Process Control 2015, 35, 127–142. [Google Scholar] [CrossRef]
- Kreuzinger, T.; Bitzer, M.; Marquardt, W. State estimation of a stratified storage tank. Control Eng. Pract. 2008, 16, 308–320. [Google Scholar] [CrossRef]
- John, T.; Guay, M.; Hariharan, N.; Naranayan, S. POD-based observer for estimation in Navier–Stokes flow. Comput. Chem. Eng. 2010, 34, 965–975. [Google Scholar] [CrossRef]
- Lehmann, O.; Luchtenburg, M.; Noack, B.R.; King, R.; Morzynski, M.; Tadmor, G. Wake stabilization using POD Galerkin models with interpolated modes. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 500–505. [Google Scholar]
- Van Waterschoot, T.; Leus, G. Distributed estimation of static fields in wireless sensor networks using the finite element method. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 2853–2856. [Google Scholar]
- Mechhoud, S.; Witrant, E.; Dugard, L.; Moreau, D. Estimation of heat source term and thermal diffusion in tokamak plasmas using a Kalman filtering method in the early lumping approach. IEEE Trans. Control Syst. Technol. 2014, 23, 449–463. [Google Scholar] [CrossRef]
- Smyshlyaev, A.; Krstic, M. Backstepping observers for a class of parabolic PDEs. Syst. Control Lett. 2005, 54, 613–625. [Google Scholar] [CrossRef]
- Jadachowski, L.; Meurer, T.; Kugi, A. Backstepping observers for linear PDEs on higher-dimensional spatial domains. Automatica 2015, 51, 85–97. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Georges, D.; Besançon, G. State and parameter estimation in 1-D hyperbolic PDEs based on an adjoint method. Automatica 2016, 67, 185–191. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Xu, Q.; Ni, D.; Dubljevic, S. Observer and filter design for linear transport-reaction systems. Eur. J. Control 2019. [Google Scholar] [CrossRef]
- Puust, R.; Kapelan, Z.; Savic, D.; Koppel, T. A review of methods for leakage management in pipe networks. Urban Water J. 2010, 7, 25–45. [Google Scholar] [CrossRef]
- Streeter, V.L.; Wylie, E.B.; Bedford, K.W. Fluid Mechanics. WCB; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Ferrante, M.; Brunone, B.; Meniconi, S. Wavelets for the analysis of transient pressure signals for leak detection. J. Hydraul. Eng. 2007, 133, 1274–1282. [Google Scholar] [CrossRef]
- Wang, S.; Carroll, J.J. Leak detection for gas and liquid pipelines by transient modelling. In Proceedings of the International Oil & Gas Conference and Exhibition in China, Beijing, China, 5–7 December 2006; pp. 1–9. [Google Scholar]
- Colombo, A.F.; Lee, P.; Karney, B.W. A selective literature review of transient-based leak detection methods. J. Hydro-Environ. Res. 2009, 2, 212–227. [Google Scholar] [CrossRef]
- Vítkovskỳ, J.P.; Simpson, A.R.; Lambert, M.F. Leak detection and calibration using transients and genetic algorithms. J. Water Resour. Plan. Manag. 2000, 126, 262–265. [Google Scholar] [CrossRef]
- Krstic, M. Adaptive control of an anti-stable wave PDE. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 1505–1510. [Google Scholar]
- Zhou, H.C.; Guo, B.Z.; Wu, Z.H. Output feedback stabilisation for a cascaded wave PDE-ODE system subject to boundary control matched disturbance. Int. J. Control 2016, 89, 2396–2405. [Google Scholar] [CrossRef]
- Feng, H.; Guo, B.Z. A new active disturbance rejection control to output feedback stabilization for a one-dimensional anti-stable wave equation with disturbance. IEEE Trans. Autom. Control 2016, 62, 3774–3787. [Google Scholar] [CrossRef]
- Rigatos, G.G. A Kalman Filtering approach of improved precision for fault diagnosis in distributed parameter systems. arXiv 2013, arXiv:1310.3358. [Google Scholar]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations; Springer Series in Computational Mathematics; Springer: Berlin, Germany, 2002; Volume 31. [Google Scholar]
- Havu, V.; Malinen, J. The Cayley transform as a time discretization scheme. Numer. Funct. Anal. Optim. 2007, 28, 825–851. [Google Scholar] [CrossRef]
- Staffans, O. Well-Posed Linear Systems; Cambridge University Press: Cambridge, UK, 2005; Volume 103. [Google Scholar]
- Malinen, J.; Staffans, O.; Weiss, G. When is a linear system conservative? Q. Appl. Math. 2006, 64, 61–91. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Dubljevic, S. Linear model predictive control for transport-reaction processes. AIChE J. 2017, 63, 2644–2659. [Google Scholar] [CrossRef]
- Havu, V.; Malinen, J. Laplace and Cayley transforms—An approximation point of view. In Proceedings of the 44th IEEE Conference on Decision and Control, 2005 and 2005 European Control Conference, CDC-ECC’05, Seville, Spain, 15 December 2005; pp. 5971–5976. [Google Scholar]
- Malinen, J. Tustin’s method for final state approximation of conservative dynamical systems. IFAC Proc. Vol. 2011, 44, 4564–4569. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H∞, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Xie, J.; Xu, X.; Dubljevic, S. Long range pipeline leak detection and localization using discrete observer and support vector machine. AIChE J. 2019, 65, e16532. [Google Scholar] [CrossRef]
- Blažič, S.; Matko, D.; Geiger, G. Simple model of a multi-batch driven pipeline. Math. Comput. Simul. 2004, 64, 617–630. [Google Scholar] [CrossRef] [Green Version]
- Colebrook, C.F.; Blench, T.; Chatley, H.; Essex, E.; Finniecome, J.; Lacey, G.; Williamson, J.; Macdonald, G. Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 12, 393–422. [Google Scholar] [CrossRef]
- Dubljevic, S.; Humaloja, J.P. Model Predictive Control for Regular Linear Systems. arXiv 2018, arXiv:1808.10021. [Google Scholar]

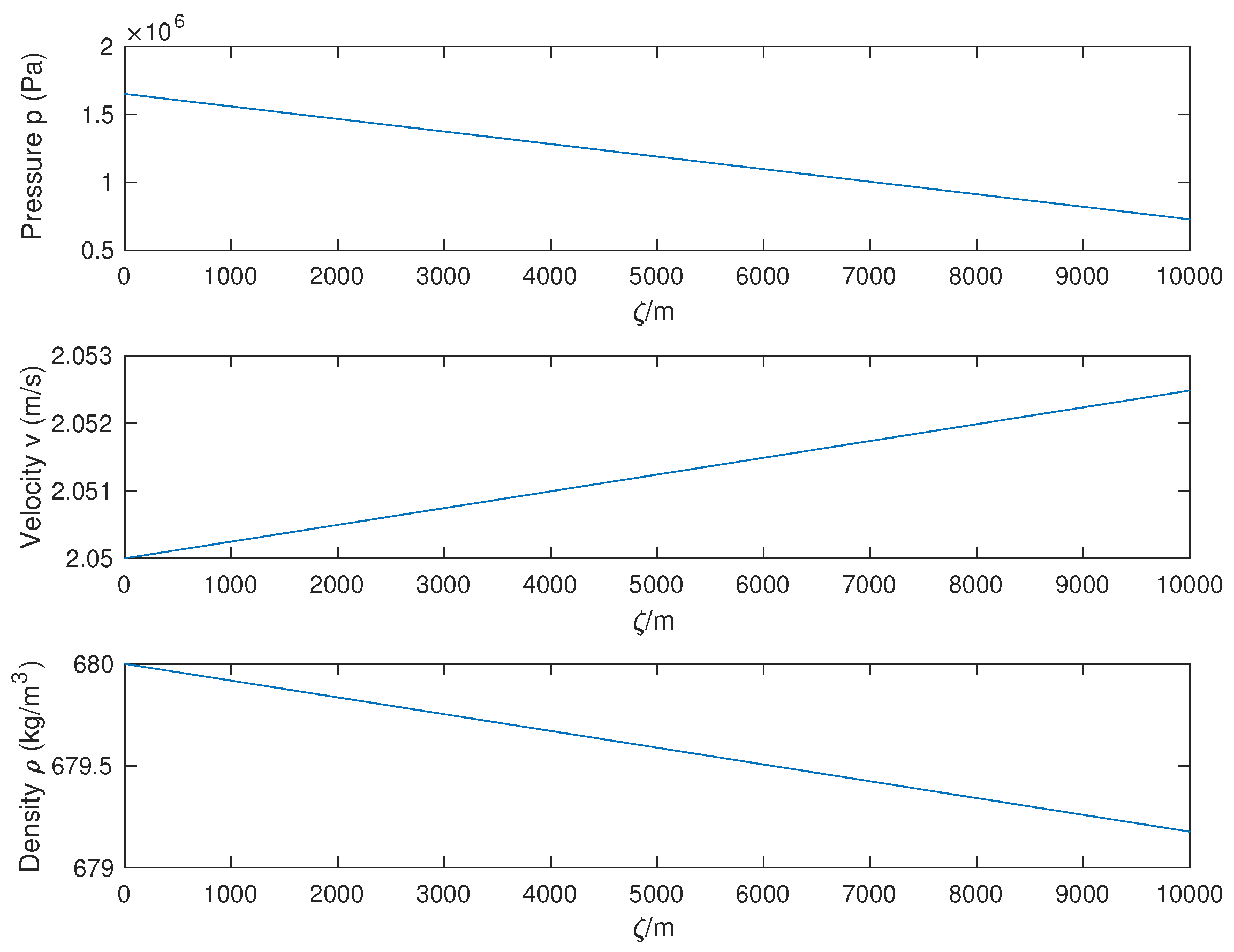
| Term | Notation | Numerical Value |
|---|---|---|
| Pipeline Length | 10,000 m | |
| Speed of Sound | a | 1059 m/s |
| Friction Coefficient | 0.0158 | |
| Gravity Acceleration | g | m/s |
| Pipe Diameter | D | m |
| Inclination Angle | −0.00256 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Dubljevic, S. Discrete-Time Kalman Filter Design for Linear Infinite-Dimensional Systems. Processes 2019, 7, 451. https://doi.org/10.3390/pr7070451
Xie J, Dubljevic S. Discrete-Time Kalman Filter Design for Linear Infinite-Dimensional Systems. Processes. 2019; 7(7):451. https://doi.org/10.3390/pr7070451
Chicago/Turabian StyleXie, Junyao, and Stevan Dubljevic. 2019. "Discrete-Time Kalman Filter Design for Linear Infinite-Dimensional Systems" Processes 7, no. 7: 451. https://doi.org/10.3390/pr7070451
APA StyleXie, J., & Dubljevic, S. (2019). Discrete-Time Kalman Filter Design for Linear Infinite-Dimensional Systems. Processes, 7(7), 451. https://doi.org/10.3390/pr7070451






