Measurement of the Effective Refractive Index of Suspensions Containing 5 µm Diameter Spherical Polystyrene Microparticles by Surface Plasmon Resonance and Scattering
Abstract
1. Introduction
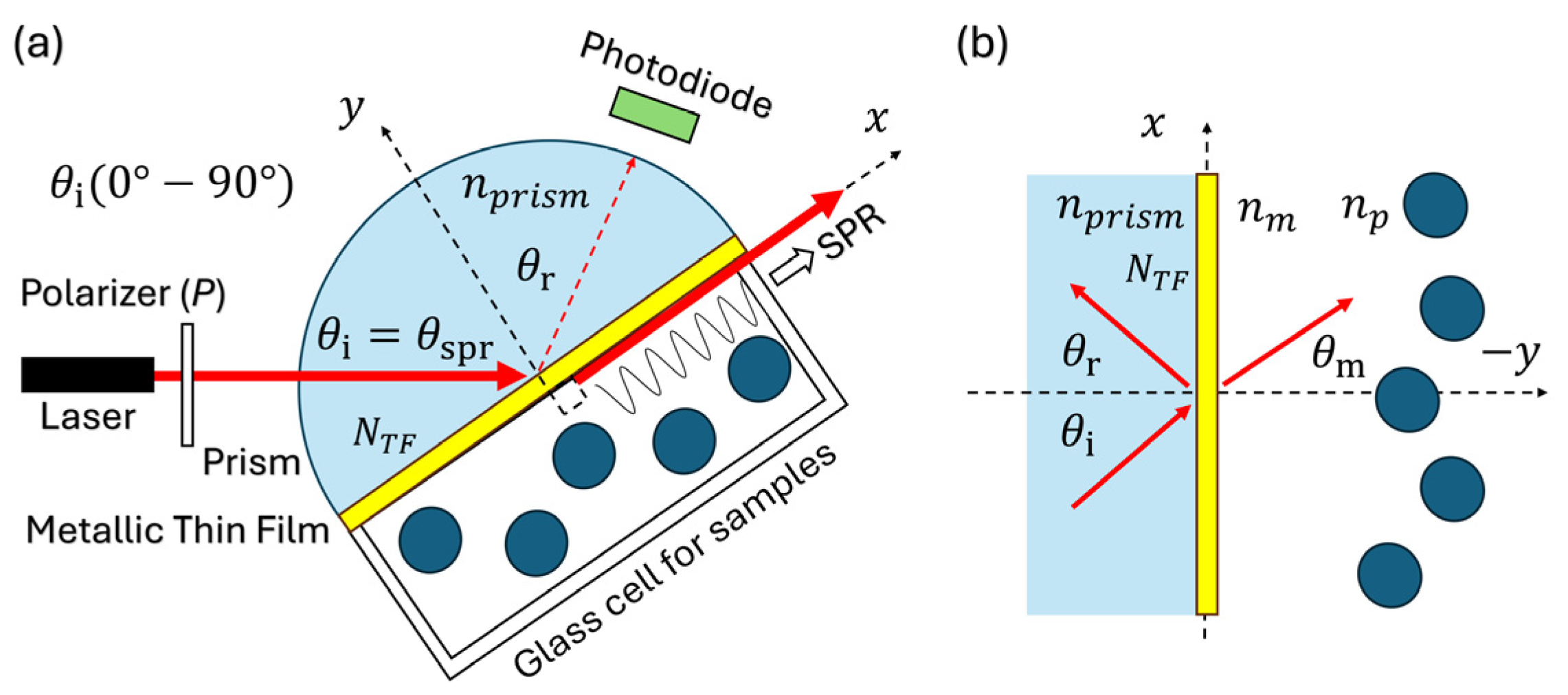
2. Theory
3. System and Methodology
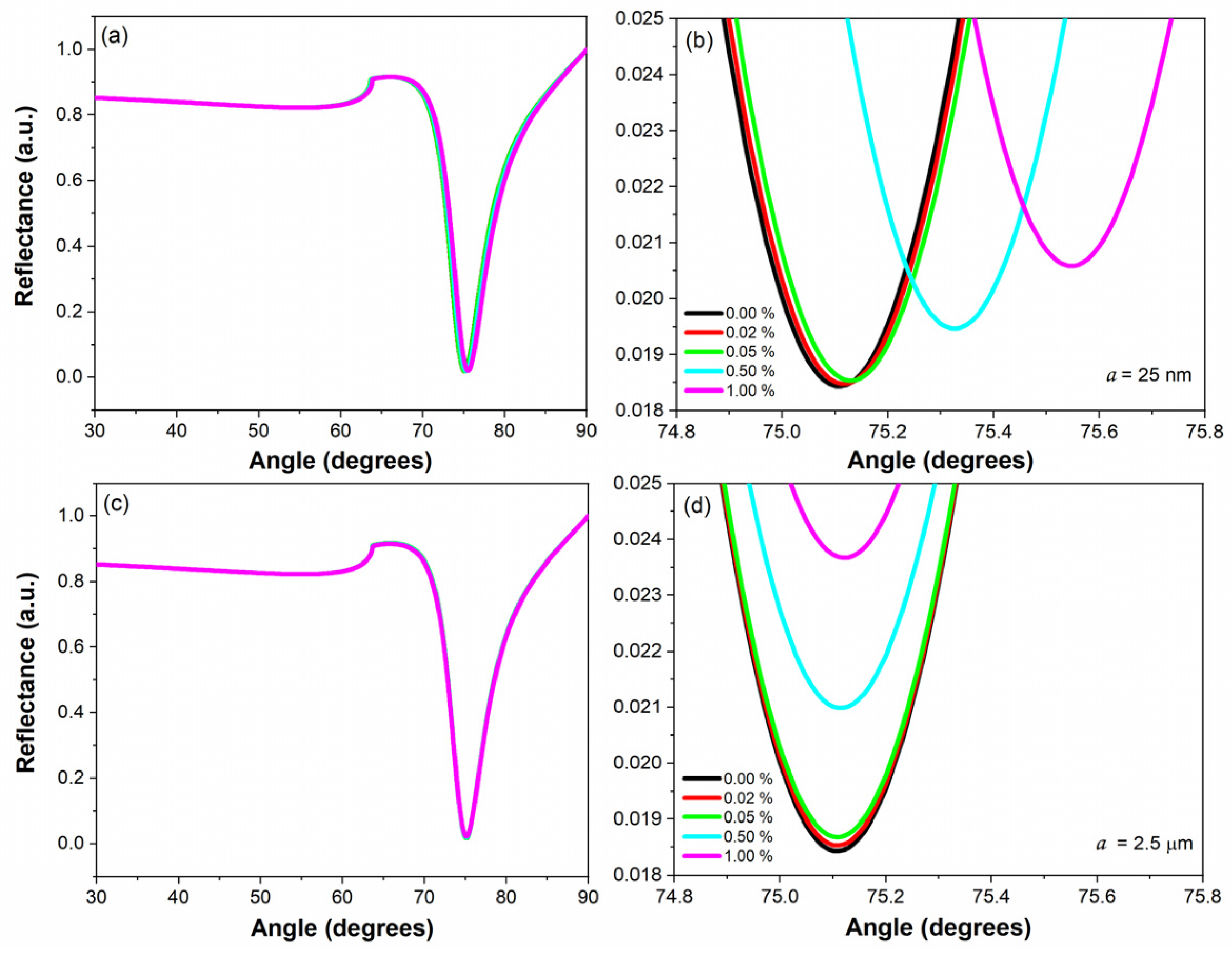
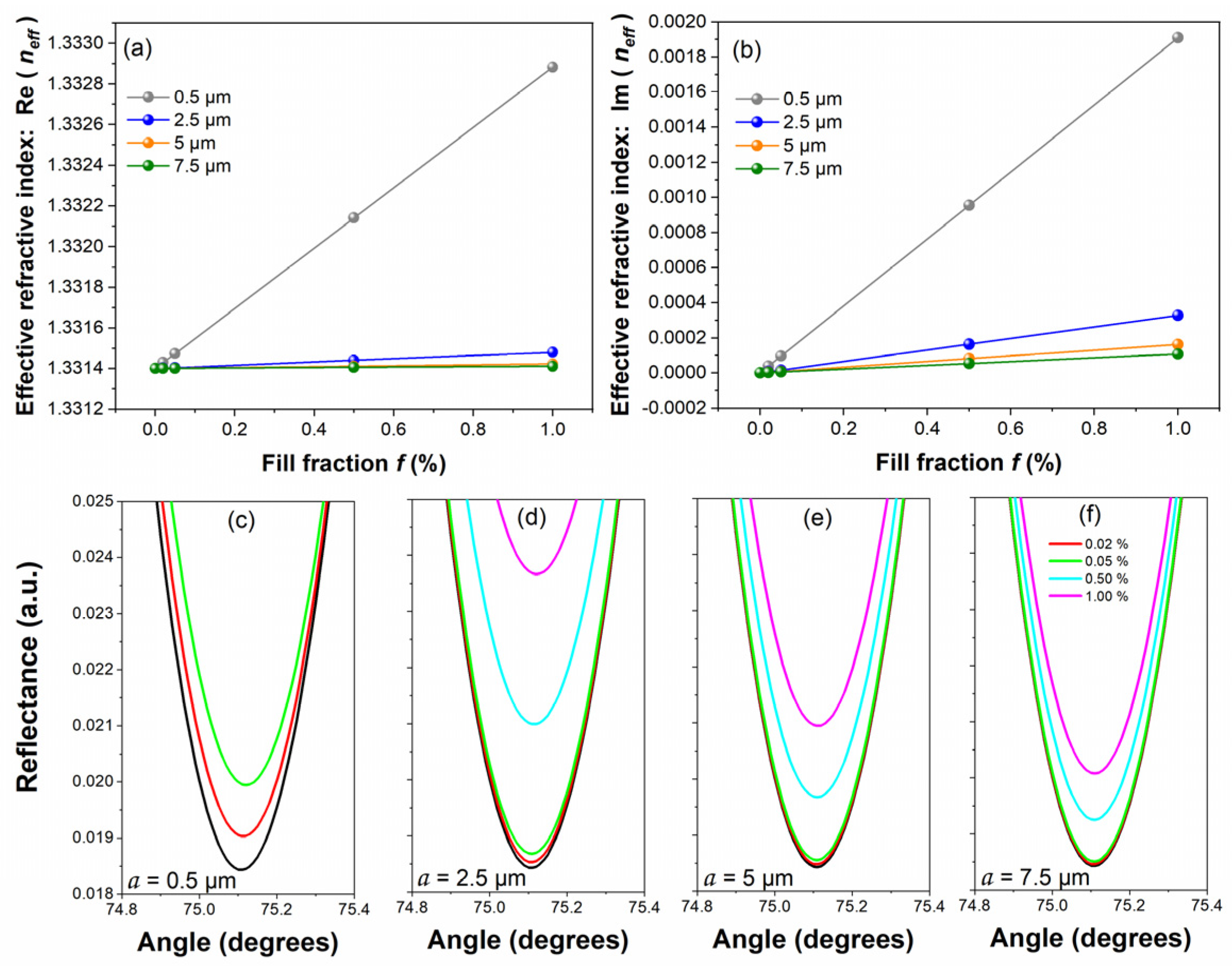
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Frias, J.P.G.L.; Nash, R. Microplastics: Finding a consensus on the definition. Mar. Pollut. Bull. 2019, 138, 145–147. [Google Scholar] [CrossRef] [PubMed]
- Gigault, J.; Ter Halle, A.; Baudrimont, M.; Pascal, P.Y.; Gauffre, F.; Phi, T.L.; El Hadri, H.; Grassl, B.; Reynaud, S. Current opinion: What is a nanoplastic? Environ. Pollut. 2018, 235, 1030–1034. [Google Scholar] [CrossRef] [PubMed]
- Tuoriniemi, J.; Moreira, B.; Safina, G. Determining number concentrations and diameters of polystyrene particles by measuring the effective refractive index of colloids using surface plasmon resonance. Langmuir 2016, 32, 10632–10640. [Google Scholar] [CrossRef] [PubMed]
- Márquez-Islas, R.; Sánchez-Pérez, C.; García-Valenzuela, A. Determination of refractive index, size, and concentration of nonabsorbing colloidal nanoparticles from measurements of the complex effective refractive index. Opt. Lett. 2014, 39, 559–562. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.C.; Olsen, Y.; Mitchell, R.P.; Davis, A.; Rowland, S.J.; John, A.W.G.; McGonigle, D.; Russell, A.E. Lost at sea: Where is all the plastic? Science 2004, 304, 838. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.C.; Courtene-Jones, W.; Boucher, J.; Pahl, S.; Raubenheimer, K.; Koelmans, A.A. Twenty years of microplastic pollution research—What have we learned? Science 2024, 386, eadl2746. [Google Scholar] [CrossRef] [PubMed]
- Adediran, G.A.; Cox, R.; Jürgens, M.D.; Morel, E.; Cross, R.; Carter, H.; Pereira, M.G.; Read, D.S.; Johnson, A.C. Fate and behaviour of Microplastics (>25µm) within the water distribution network, from water treatment works to service reservoirs and customer taps. Water Res. 2024, 255, 121508. [Google Scholar] [CrossRef] [PubMed]
- Ya, H.; Jiang, B.; Xing, Y.; Zhang, T.; Lv, M.; Wang, X. Recent advances on ecological effects of microplastics on soil environment. Sci. Total Environ. 2021, 798, 149338. [Google Scholar] [CrossRef] [PubMed]
- Issac, M.N.; Kandasubramanian, B. Effect of microplastics in water and aquatic systems. Environ. Sci. Pollut. Res. 2021, 28, 19544–19562. [Google Scholar] [CrossRef] [PubMed]
- Vo, H.C.; Pham, M.H. Ecotoxicological effects of microplastics on aquatic organisms: A review. Environ. Sci. Pollut. Res. 2021, 28, 44716–44725. [Google Scholar] [CrossRef] [PubMed]
- Leonard, S.V.L.; Liddle, C.R.; Atherall, C.A.; Chapman, E.; Watkins, M.; Calaminus, S.D.J.; Rotchell, J.M. Microplastics in human blood: Polymer types, concentrations and characterisation using μFTIR. Environ. Int. 2024, 188, 108751. [Google Scholar] [CrossRef] [PubMed]
- Kwon, J.H.; Kim, J.W.; Pham, T.D.; Tarafdar, A.; Hong, S.; Chun, S.H.; Lee, S.H.; Kang, D.Y.; Kim, J.Y.; Kim, S.B.; et al. Microplastics in food: A review on analytical methods and challenges. Int. J. Environ. Res. Public Health 2020, 17, 6710. [Google Scholar] [CrossRef] [PubMed]
- Sapkale, D.; Kurkute, P.; Mistry, A.; Pandit, S.V. Polyethylene Microplastics Affected Survival Rate, Food Intake and Altered Oxidative Stress Parameters in Freshwater Snail Indoplanorbis exustus. Bull. Environ. Contam. Toxicol. 2023, 111, 67. [Google Scholar] [CrossRef] [PubMed]
- Berber, A.A. Genotoxic evaluation of polystyrene microplastic. Sak. Univ. J. Sci. 2019, 23, 358–367. [Google Scholar] [CrossRef]
- Primpke, S.; Wirth, M.; Lorenz, C.; Gerdts, G. Reference database design for the automated analysis of microplastic samples based on Fourier transform infrared (FTIR) spectroscopy. Anal. Bioanal. Chem. 2018, 410, 5131–5141. [Google Scholar] [CrossRef] [PubMed]
- Ragusa, A.; Notarstefano, V.; Svelato, A.; Belloni, A.; Gioacchini, G.; Blondeel, C.; Zucchelli, E.; De Luca, C.; D’avino, S.; Gulotta, A.; et al. Raman microspectroscopy detection and characterisation of microplastics in human breastmilk. Polymers 2022, 14, 2700. [Google Scholar] [CrossRef] [PubMed]
- Rivera-Rivera, D.M.; Quintanilla-Villanueva, G.E.; Luna-Moreno, D.; Sánchez-Álvarez, A.; Rodríguez-Delgado, J.M.; Cedillo-González, E.I.; Kaushik, G.; Villarreal-Chiu, J.F.; Rodríguez-Delgado, M.M. Exploring Innovative Approaches for the Analysis of Micro- and Nanoplastics: Breakthroughs in (Bio)Sensing Techniques. Biosensors 2025, 15, 44. [Google Scholar] [CrossRef] [PubMed]
- Sierra, I.; Chialanza, M.R.; Faccio, R.; Carrizo, D.; Fornaro, L.; Pérez-Parada, A. Identification of microplastics in wastewater samples by means of polarized light optical microscopy. Environ. Sci. Pollut. Res. 2020, 27, 7409–7419. [Google Scholar] [CrossRef] [PubMed]
- Miserli, K.; Lykos, C.; Kalampounias, A.G.; Konstantinou, I. Screening of microplastics in aquaculture systems (fish, mussel, and water samples) by FTIR, scanning electron microscopy–energy dispersive spectroscopy and micro-raman spectroscopies. Appl. Sci. 2023, 13, 9705. [Google Scholar] [CrossRef]
- Ompala, C.; Renault, J.P.; Taché, O.; Cournède, É.; Devineau, S.; Chivas-Joly, C. Stability and dispersibility of microplastics in experimental exposure medium and their dimensional characterization by SMLS, SAXS, Raman microscopy, and SEM. J. Hazard. Mater. 2024, 469, 134083. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Kim, M.J.; Kim, C.S.; Cheon, S.J.; Choi, K.I.; Kim, J.; Jung, J.; Yoon, J.K.; Lee, S.H.; Jeong, D.H. Detection of microplastic traces in four different types of municipal wastewater treatment plants through FT-IR and TED-GC-MS. Environ. Pollut. 2023, 333, 122017. [Google Scholar] [CrossRef] [PubMed]
- Santos, L.H.M.L.M.; Insa, S.; Arxé, M.; Buttiglieri, G.; Rodríguez-Mozaz, S.; Barceló, D. Analysis of microplastics in the environment: Identification and quantification of trace levels of common types of plastic polymers using pyrolysis-GC/MS. MethodsX 2023, 10, 102143. [Google Scholar] [CrossRef] [PubMed]
- Luna-Moreno, D.; Sánchez-Espinosa, Y.M.; Ponce de León, Y.R.; Arias, E.N.; Garnica-Campos, G. Virtual instrumentation in LabVIEW for multiple optical characterizations on the same opto-mechanical system. Opt.-Int. J. Light Electron Opt. 2015, 126, 1923–1929. [Google Scholar] [CrossRef]
- Pines, D.; Bohm, D. A collective description of electron interactions: II. Collective vs individual particle aspects of the interactions. Phys. Rev. 1952, 85, 338. [Google Scholar] [CrossRef]
- Otto, A. Excitation of nonradiative surface plasma waves in silver by the method of frustrated total reflection. Z. Für Phys. A Hadron. Nucl. 1968, 216, 398–410. [Google Scholar] [CrossRef]
- Kretschmann, E. Die bestimmung optischer konstanten von metallen durch anregung von oberflächenplasmaschwingungen. Z. Fur Phys. 1971, 241, 313–324. [Google Scholar] [CrossRef]
- Liedberg, B.; Nylander, C.; Lunström, I. Surface plasmon resonance for gas detection and biosensing. Sens. Actuators 1983, 4, 299–304. [Google Scholar] [CrossRef]
- Huang, Y.H.; Ho, H.P.; Kong, S.K.; Kabashin, A.V. Phase-sensitive surface plasmon resonance biosensors: Methodology, instrumentation and applications. Ann. Phys. 2012, 524, 637–662. [Google Scholar] [CrossRef]
- Salamon, Z.; Macleod, H.A.; Tollin, G. Coupled plasmon-waveguide resonators: A new spectroscopic tool for probing proteolipid film structure and properties. Biophys. J. 1997, 73, 2791–2797. [Google Scholar] [CrossRef] [PubMed]
- Homola, J.; Vaisocherová, H.; Dostálek, J.; Piliarik, M. Multi-analyte surface plasmon resonance biosensing. Methods 2005, 37, 26–36. [Google Scholar] [CrossRef] [PubMed]
- Karabchevsky, A.; Krasnykov, O.; Abdulhalim, I.; Hadad, B.; Goldner, A.; Auslender, M.; Hava, S. Metal grating on a substrate nanostructure for sensor applications. Photonics Nanostruct. 2009, 7, 170–175. [Google Scholar] [CrossRef]
- Shalabney, A.; Khare, C.; Rauschenbach, B.; Abdulhalim, I. Sensitivity of surface plasmon resonance sensors based on metallic columnar thin films in the spectral and angular interrogations. Sens. Actuators B Chem. 2011, 159, 201–212. [Google Scholar] [CrossRef]
- Szunerits, S.; Shalabney, A.; Boukherroub, R.; Abdulhalim, I. Dielectric coated plasmonic interfaces: Their interest for sensitive sensing of analyte-ligand interactions. Rev. Anal. Chem. 2012, 31, 15–28. [Google Scholar] [CrossRef]
- Yang, D.; Liu, X.; Ma, J.; Cui, B.; Wang, Y.; Xu, J.; Zhang, Y.; Ding, H.; Wang, D.; Liu, Q.; et al. Probing Single-Cell Adhesion Kinetics and Nanomechanical Force with Surface Plasmon Resonance Imaging. ACS Nano 2025, 19, 2651–2664. [Google Scholar] [CrossRef] [PubMed]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Gustav, M. Beitraege zur Optik trueber Medien. Ann. Physik 1908, 25, 377. [Google Scholar]
- Barrera, R.G.; Garcıa-Valenzuela, A. Coherent reflectance in a system of random Mie scatterers and its relation to the effective-medium approach. J. Opt. Soc. Am. A 2003, 20, 296–311. [Google Scholar] [CrossRef] [PubMed]
- García-Valenzuela, A.; Barrera, R.G.; Sánchez-Pérez, C.; Reyes-Coronado, A.; Méndez, E.R. Coherent reflection of light from a turbid suspension of particles in an internal-reflection configuration: Theory versus experiment. Opt. Express 2005, 13, 6723–6737. [Google Scholar] [CrossRef] [PubMed]
- Van de Hulst, H.C. Light scattering by small particles. Q. J. R. Meteorol. Soc. 1958, 84, 198–199. [Google Scholar] [CrossRef]
- Sánchez-Alvarez, A.; Rodríguez-Quiroz, O.; Quintanilla-Villanueva, G.E.; Rodríguez-Delgado, M.M.; Villarreal-Chiu, J.F.; Silva-Hernández, O.J.; Luna-Moreno, D. Development of a Portable Optomechatronic System to Obtain the Characterization of Transparent Materials and Dielectric Thin Films. Optics 2024, 5, 595–610. [Google Scholar] [CrossRef]
- Macleod, H.A. Thin-film optical filters. In Thin-Film Optical Filters, 4th ed.; CRC Press: Boca Raton, FL, USA, 2010; pp. 1–782. [Google Scholar]
- SCHOTT. 2025. Available online: https://www.schott.com/pt-br/special-selection-tools/interactive-abbe-diagram (accessed on 27 May 2025).
- Refractive Index of Au (Gold)—Johnson n.d. Available online: https://refractiveindex.info/?shelf=main&book=Au&page=Johnson (accessed on 27 May 2025).
- Refractive Index of H2O, D2O (Water, Heavy Water, Ice)—Hale n.d. Available online: https://refractiveindex.info/?shelf=main&book=H2O&page=Hale (accessed on 30 June 2025).
- Refractive Index of PLASTICS—PS n.d. Available online: https://refractiveindex.info/?shelf=3d&book=plastics&page=ps (accessed on 30 June 2025).
- Quintanilla-Villanueva, G.E.; Rodríguez-Quiroz, O.; Sánchez-Álvarez, A.; Rodríguez-Delgado, J.M.; Villarreal-Chiu, J.F.; Luna-Moreno, D.; Rodríguez-Delgado, M.M. An Innovative Enzymatic Surface Plasmon Resonance-Based Biosensor Designed for Precise Detection of Glycine Amino Acid. Biosensors 2025, 15, 81. [Google Scholar] [CrossRef] [PubMed]
- Malyuskin, O. Microplastic detection in soil and water using resonance microwave spectroscopy: A feasibility study. IEEE Sens. J. 2020, 20, 14817–14826. [Google Scholar] [CrossRef]
- Res-Tec-DE. 2025. Available online: http://www.res-tec.de/downloads.html (accessed on 27 May 2025).
- Lowan, A. Tables of Scattering Functions for Spherical Particles; Applied Math Series 4; National Bureau of Standards: Washington, DC, USA, 1948.
- Gumprecht, R.O.; Sliepcevich, C.M. Tables of Light-Scattering Functions for Spherical Particles; Engineering Research Institute, University of Michigan: Ann Arbor, MI, USA, 1951. [Google Scholar]
- Goldberg, B. New Computation of the Mie Scattering Functions for Spherical Particles. J. Opt. Soc. Am. 1953, 43, 1221. [Google Scholar] [CrossRef]
- Matzler, C. MATLAB Functions for Mie Scattering and Absorption; Institute of Applied Physics, University of Bern: Bern, Switzerland, 2002. [Google Scholar]
- Mie Scattering Calculator. 2025. Available online: https://omlc.org/calc/mie_calc.html (accessed on 27 May 2025).
- Ma, D.; Tuersun, P.; Cheng, L.; Zheng, Y.; Abulaiti, R. PyMieLab_V1.0: A software for calculating the light scattering and absorption of spherical particles. Heliyon 2022, 8, e11469. [Google Scholar] [CrossRef] [PubMed]



| (Equation (4)) | (Equation (5) or Equation (15)) | |||
|---|---|---|---|---|
| % PS | ||||
| 0.00 | 1.331400 | 0 | 1.331400 | 0 |
| 0.02 | 1.331450 | 1.3816 × 10−7 | 1.331402 | 6.5749 × 10−6 |
| 0.05 | 1.331524 | 3.4548 × 10−7 | 1.331404 | 1.6437 × 10−5 |
| 0.50 | 1.332644 | 3.4656 × 10−6 | 1.331440 | 1.6437 × 10−4 |
| 1.00 | 1.333893 | 6.9550 × 10−6 | 1.331480 | 3.2874 × 10−4 |
| (Equations (16) and (17)) | ||
|---|---|---|
| 0.00 | 1.331400 | 0 |
| 0.05 | 1.331403 | 1.6437 × 10−5 |
| 0.17 | 1.331414 | 5.5886 × 10−5 |
| 0.52 | 1.331442 | 1.7095 × 10−4 |
| 0.95 | 1.331476 | 3.1231 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Quiroz, O.; Luna-Moreno, D.; Sánchez-Álvarez, A.; Quintanilla-Villanueva, G.E.; Silva-Hernández, O.J.; Rodríguez-Delgado, M.M.; Villarreal-Chiu, J.F. Measurement of the Effective Refractive Index of Suspensions Containing 5 µm Diameter Spherical Polystyrene Microparticles by Surface Plasmon Resonance and Scattering. Chemosensors 2025, 13, 257. https://doi.org/10.3390/chemosensors13070257
Rodríguez-Quiroz O, Luna-Moreno D, Sánchez-Álvarez A, Quintanilla-Villanueva GE, Silva-Hernández OJ, Rodríguez-Delgado MM, Villarreal-Chiu JF. Measurement of the Effective Refractive Index of Suspensions Containing 5 µm Diameter Spherical Polystyrene Microparticles by Surface Plasmon Resonance and Scattering. Chemosensors. 2025; 13(7):257. https://doi.org/10.3390/chemosensors13070257
Chicago/Turabian StyleRodríguez-Quiroz, Osvaldo, Donato Luna-Moreno, Araceli Sánchez-Álvarez, Gabriela Elizabeth Quintanilla-Villanueva, Oscar Javier Silva-Hernández, Melissa Marlene Rodríguez-Delgado, and Juan Francisco Villarreal-Chiu. 2025. "Measurement of the Effective Refractive Index of Suspensions Containing 5 µm Diameter Spherical Polystyrene Microparticles by Surface Plasmon Resonance and Scattering" Chemosensors 13, no. 7: 257. https://doi.org/10.3390/chemosensors13070257
APA StyleRodríguez-Quiroz, O., Luna-Moreno, D., Sánchez-Álvarez, A., Quintanilla-Villanueva, G. E., Silva-Hernández, O. J., Rodríguez-Delgado, M. M., & Villarreal-Chiu, J. F. (2025). Measurement of the Effective Refractive Index of Suspensions Containing 5 µm Diameter Spherical Polystyrene Microparticles by Surface Plasmon Resonance and Scattering. Chemosensors, 13(7), 257. https://doi.org/10.3390/chemosensors13070257






