Many Objective Optimization of a Magnetic Micro–Electro–Mechanical (MEMS) Micromirror with Bounded MP-NSGA Algorithm
Abstract
:1. Introduction
- (i)
- The electrostatic excitation, based on an electric field which causes the controlled displacement of a movable component or the deformation of an elastic membrane;
- (ii)
- The thermal excitation, which exploits the difference between the thermal expansion coefficients featuring two elastic materials when subject to a temperature gradient;
- (iii)
- The magnetic excitation, based on the Lorentz force acting on a loop of current placed in an external magnetic field.
2. Materials and Methods
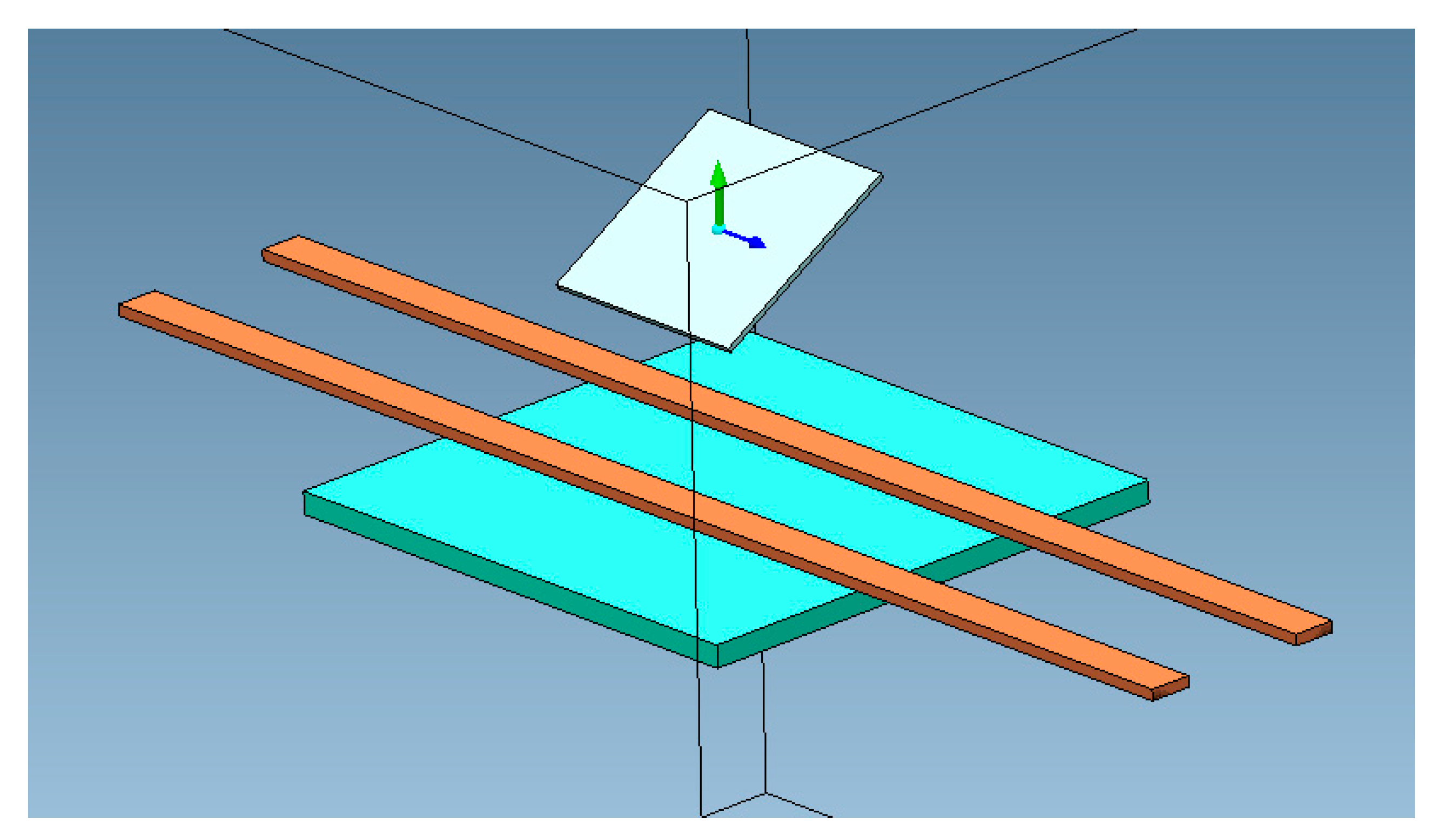
2.1. The Magnetic Micromirror
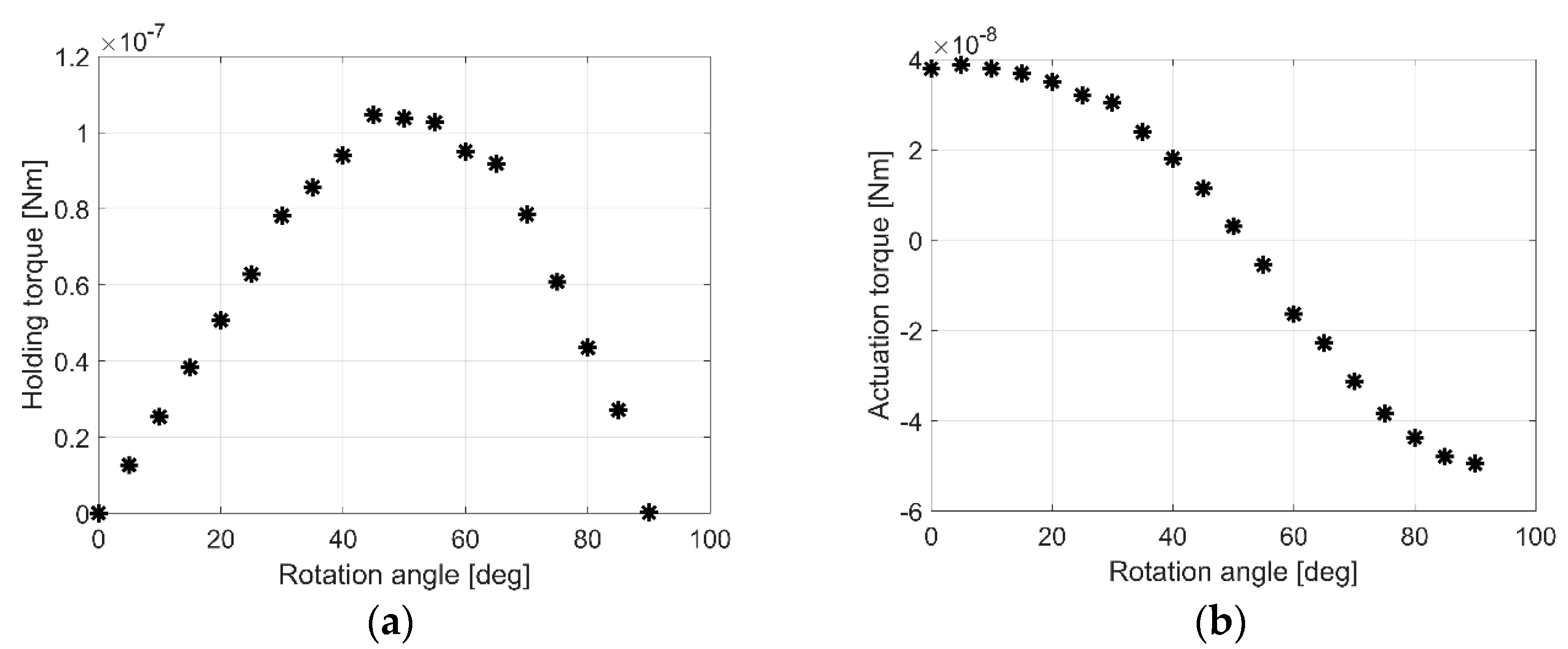
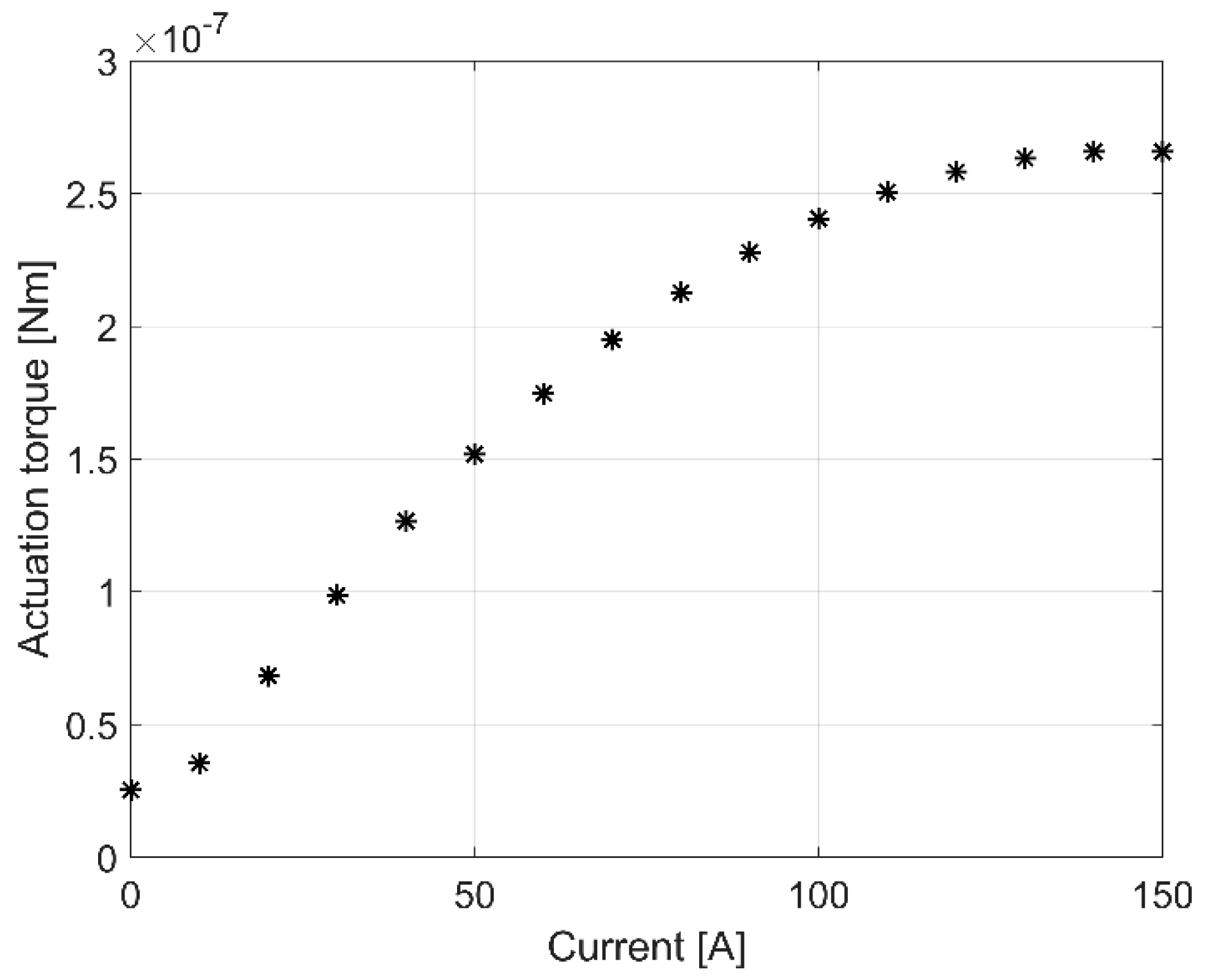
2.2. Field Analysis
2.3. Optimization Problem
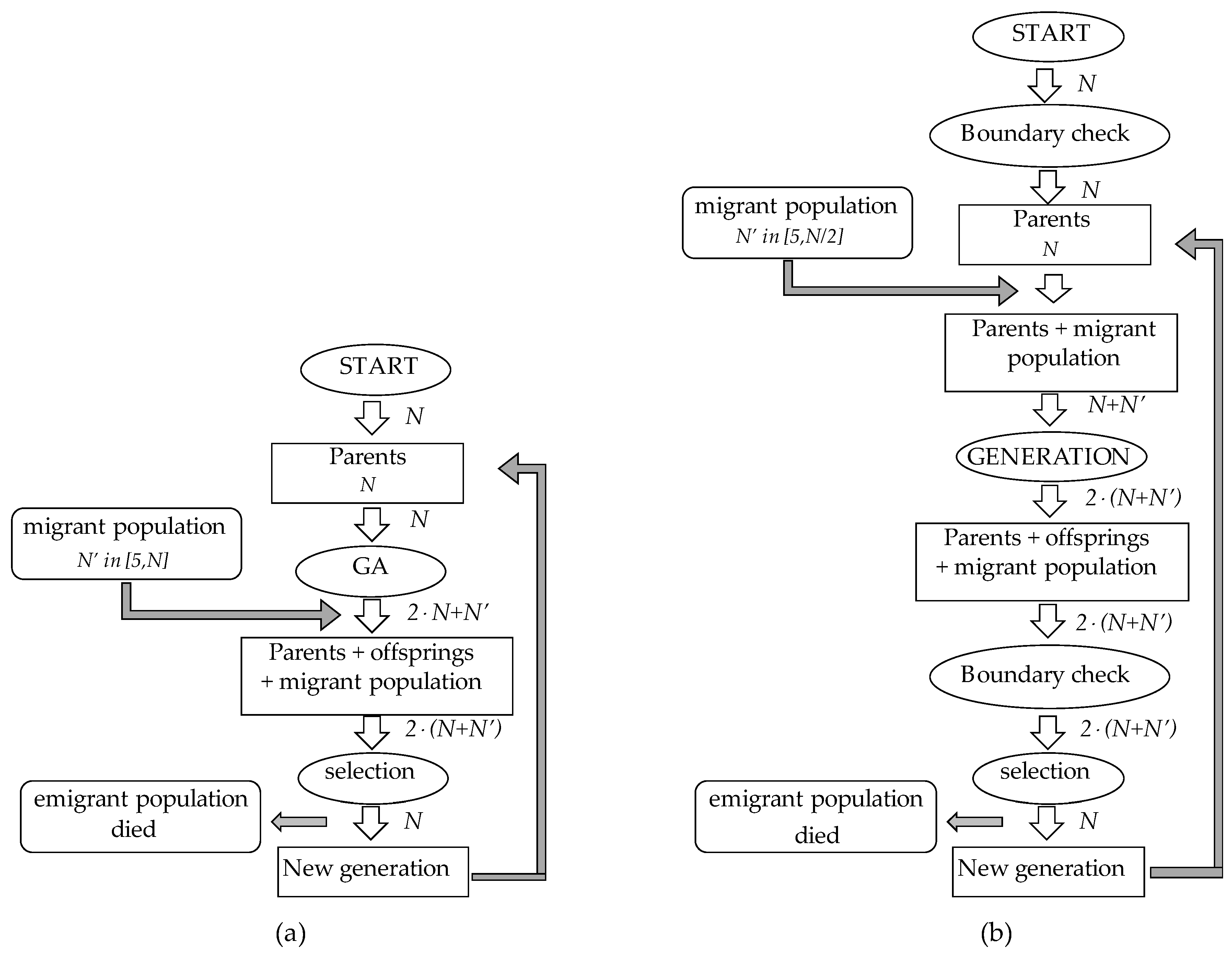
2.4. Optimization Algorithms
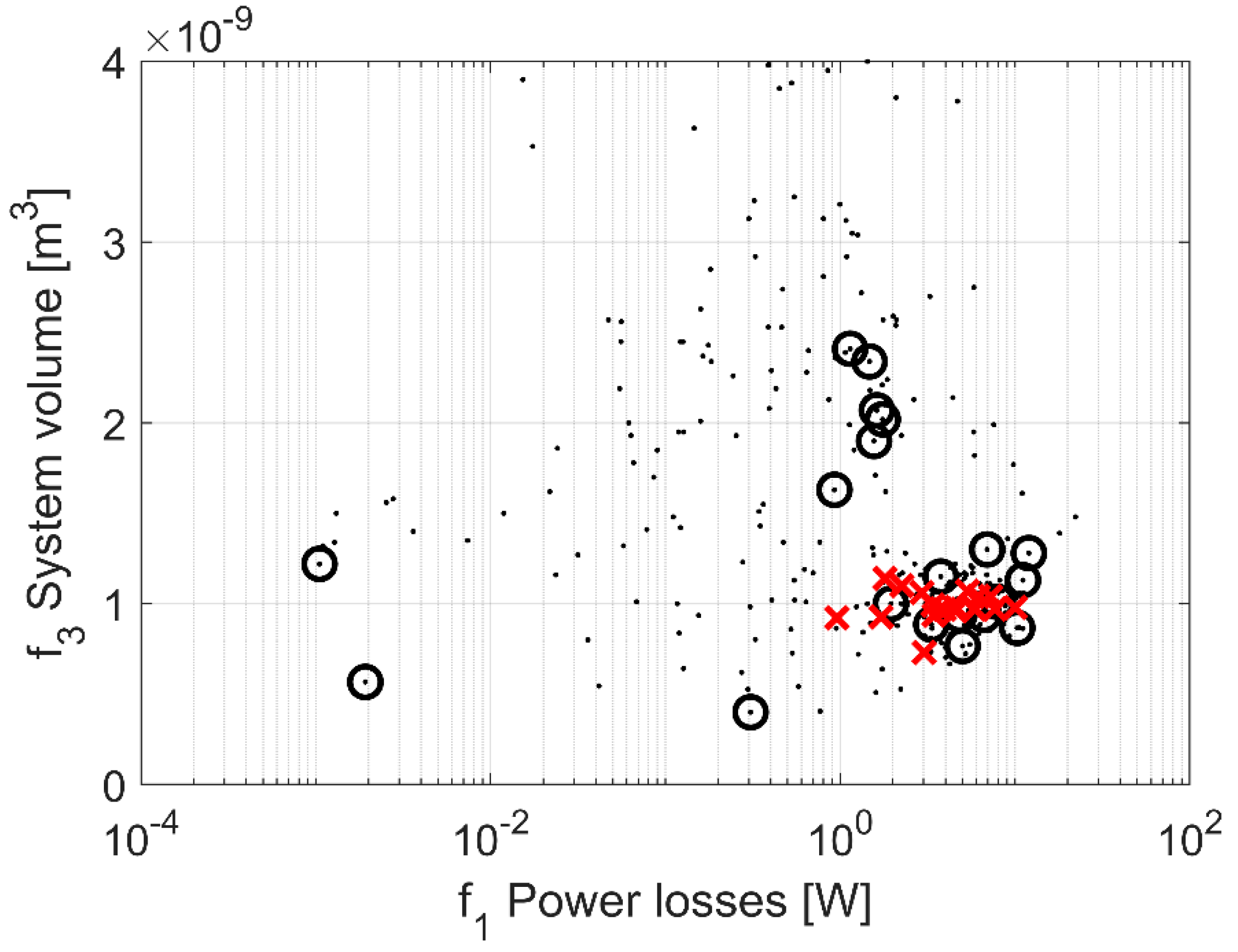
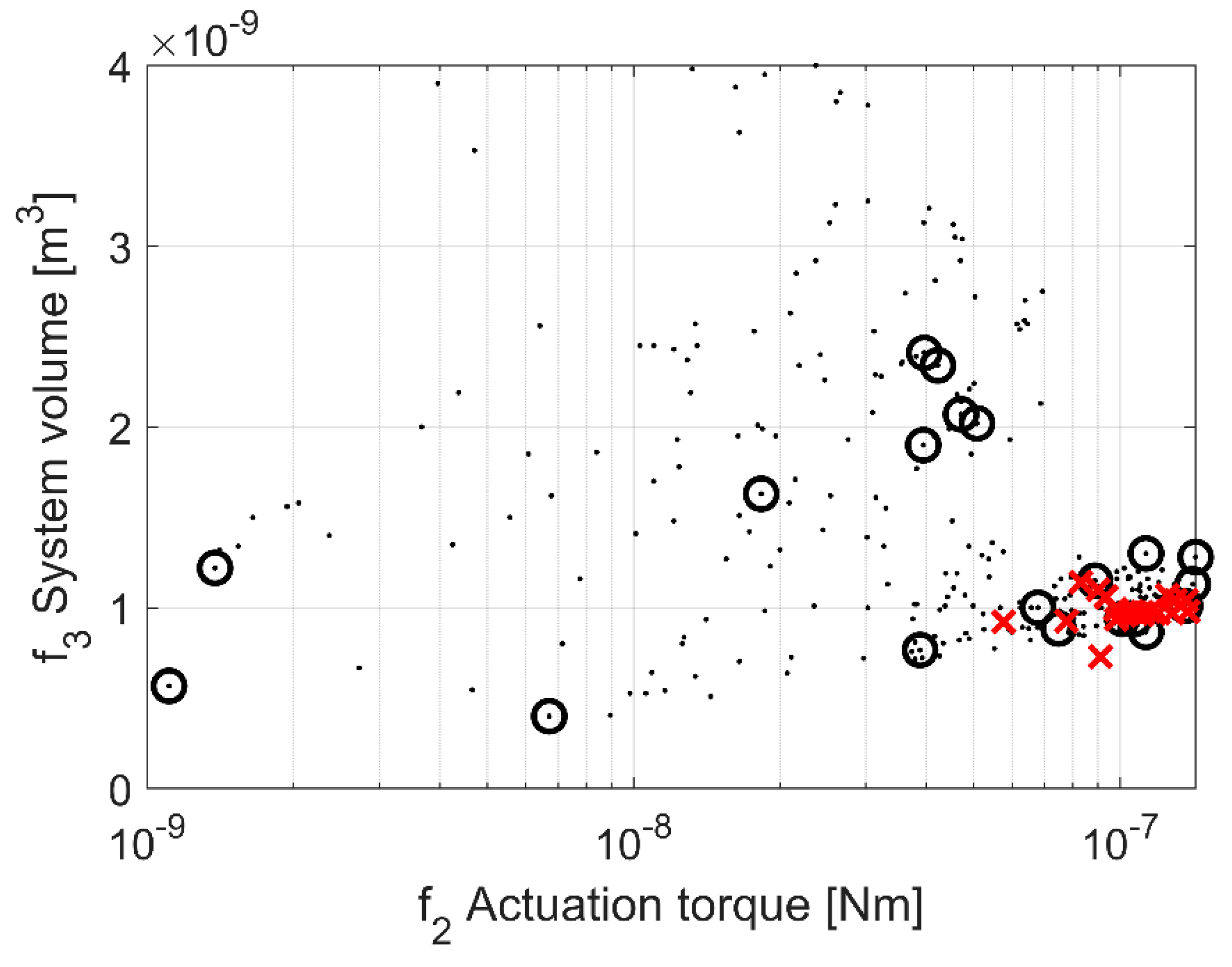
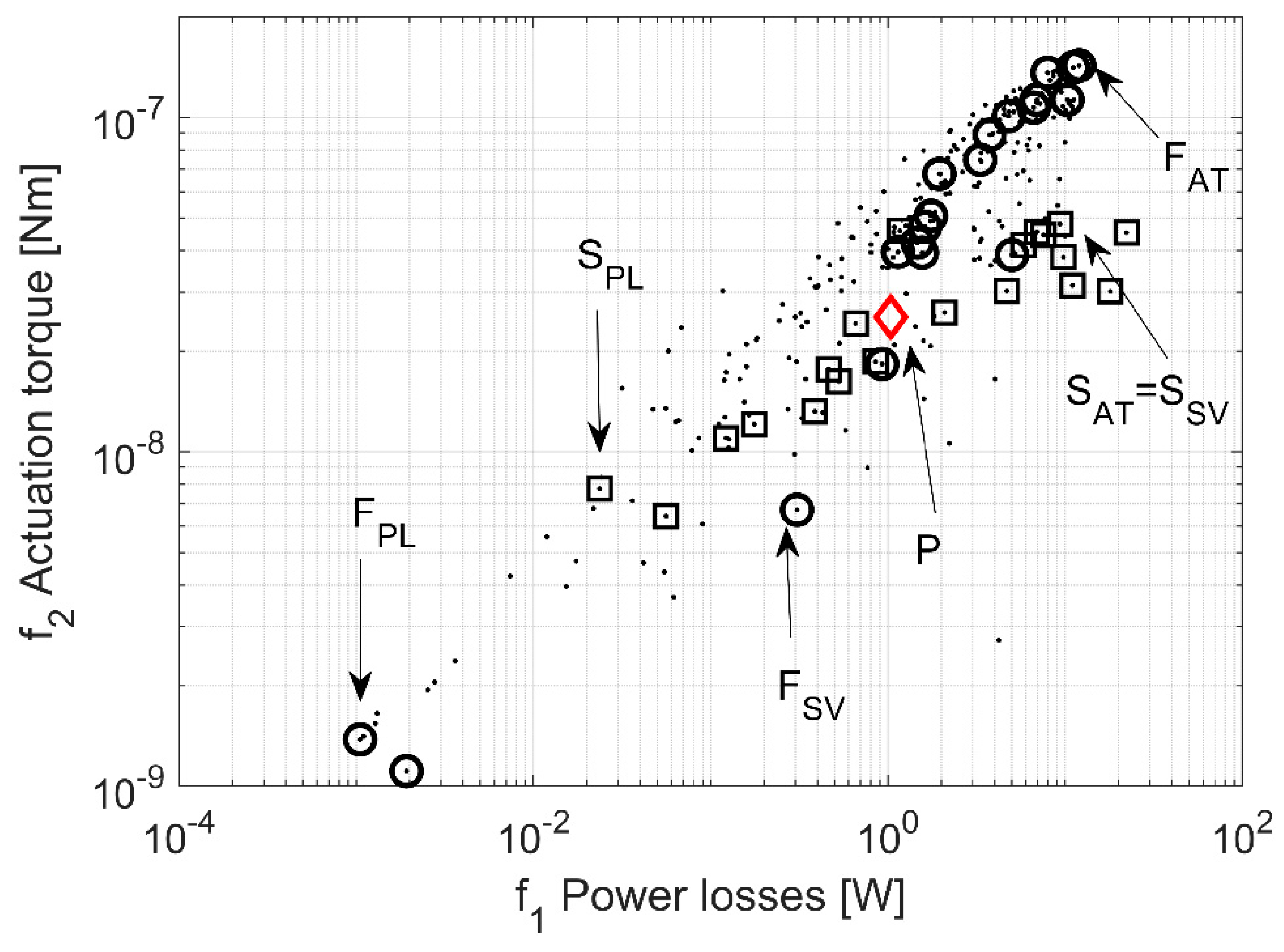
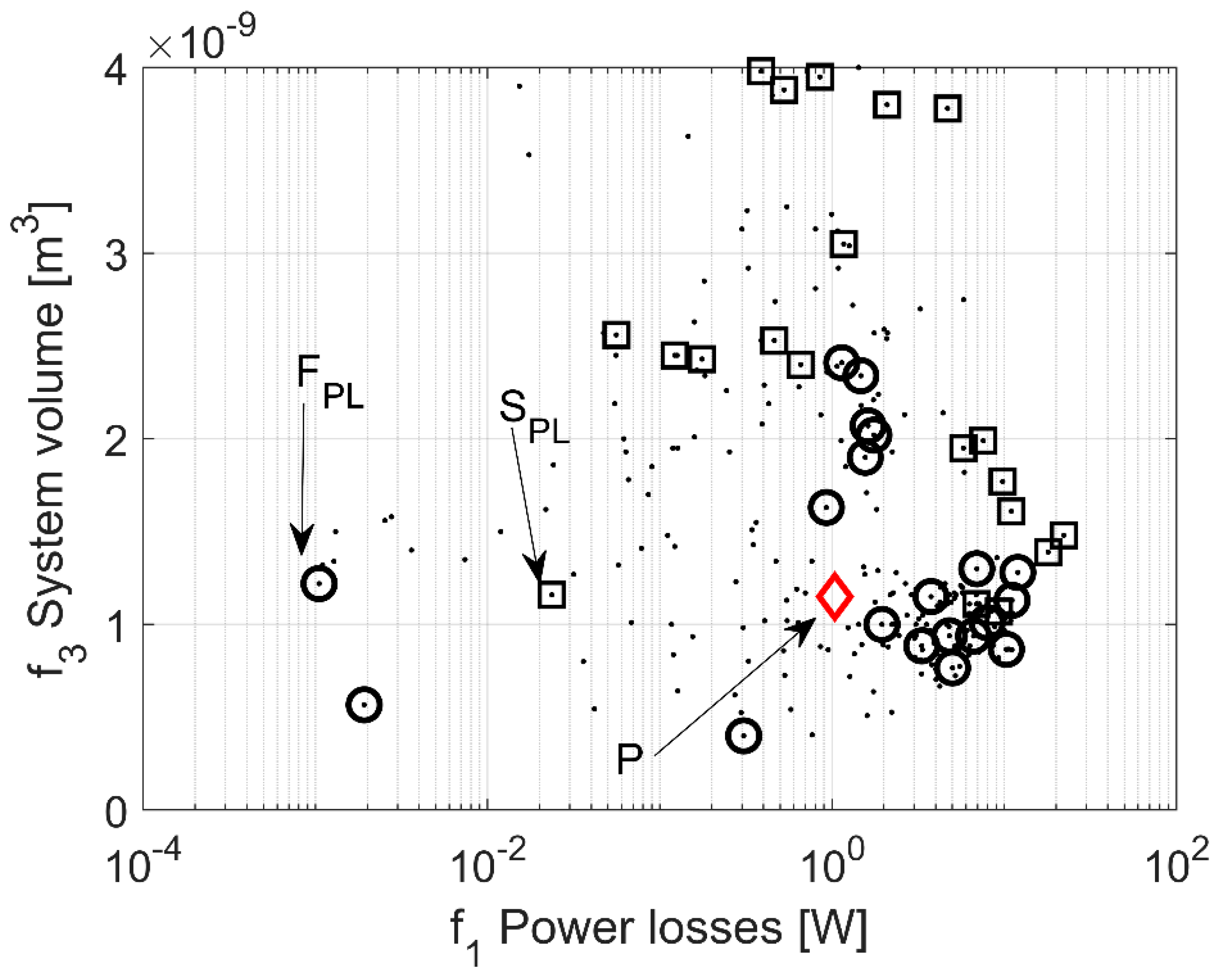
3. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Jones, T.B.; Nenadic, N.G. Electromechanics and MEMS; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; ISBN 978-0-521-76483-4. [Google Scholar]
- Nathanson, H.C.; Newell, W.E.; Wickstrom, R.A.; Davis, J.R. The resonant gate transistor. IEEE Trans. Electron Devices 1967, 14, 117–133. [Google Scholar] [CrossRef]
- Pelesko, J.A.; Bernstein, D.H. Modeling MEMS and NEMS; Chapman & Hall/CRC: Boca Raton, FL, USA, 2003; ISBN 978-1-58488-306-7. [Google Scholar]
- Di Barba, P.; Mognaschi, M.E.; Venini, P.; Wiak, S. Biogeography-inspired multiobjective optimization for helping MEMS synthesis. Arch. Electr. Eng. 2017, 66. [Google Scholar] [CrossRef]
- Di Barba, P.; Liu, B.; Mognaschi, M.E.; Venini, P.; Wiak, S. Multiphysics field analysis and evolutionary optimization: Design of an electro-thermo-elastic microactuator. Int. J. Appl. Electromagn. Mech. 2017, 54, 433–448. [Google Scholar] [CrossRef] [Green Version]
- Zega, V.; Frangi, A.; Guercilena, A.; Gattere, G. Analysis of Frequency Stability and Thermoelastic Effects for Slotted Tuning Fork MEMS Resonators. Sensors 2018, 18, 2157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zozulya, V.V.; Saez, A. A high-order theory of a thermoelastic beams and its application to the MEMS/NEMS analysis and simulations. Arch. Appl. Mech. 2016, 86, 1255–1272. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Luo, A.; Hu, Y.; Li, X.; Wang, F. Micro electrostatic energy harvester with both broad bandwidth and high normalized power density. Appl. Energy 2018, 212, 362–371. [Google Scholar] [CrossRef]
- Velosa-Moncada, L.; Aguilera-Cortés, L.; González-Palacios, M.; Raskin, J.-P.; Herrera-May, A. Design of a Novel MEMS Microgripper with Rotatory Electrostatic Comb-Drive Actuators for Biomedical Applications. Sensors 2018, 18, 1664. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di Barba, P.; Gotszalk, T.; Majstrzyk, W.; Mognaschi, M.; Orłowska, K.; Wiak, S.; Sierakowski, A. Optimal Design of Electromagnetically Actuated MEMS Cantilevers. Sensors 2018, 18, 2533. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di Barba, P.; Wiak, S. MEMS: Field Models and Optimal Design; Lecture Notes in Electrical Engineering; Springer International Publishing: Cham, Switzerland, 2020; Volume 573, ISBN 978-3-030-21495-1. [Google Scholar]
- de Oliveira Hansen, R.; Mátéfi-Tempfli, M.; Safonovs, R.; Adam, J.; Chemnitz, S.; Reimer, T.; Wagner, B.; Benecke, W.; Mátéfi-Tempfli, S. Magnetic films for electromagnetic actuation in MEMS switches. Microsyst. Technol. 2018, 24, 1987–1994. [Google Scholar] [CrossRef]
- Karami Mohammadi, A.; Ali, N.A. Effect of High Electrostatic Actuation on Thermoelastic Damping in Thin Rectangular Microplate Resonators. J. Theor. Appl. Mech. 2015, 53, 317. [Google Scholar] [CrossRef] [Green Version]
- Majstrzyk, W.; Mognaschi, M.E.; Orłowska, K.; Di Barba, P.; Sierakowski, A.; Dobrowolski, R.; Grabiec, P.; Gotszalk, T. Electromagnetic cantilever reference for the calibration of optical nanodisplacement systems. Sens. Actuators A Phys. 2018, 282, 149–156. [Google Scholar] [CrossRef]
- Cauchi, M.; Grech, I.; Mallia, B.; Mollicone, P.; Sammut, N. Analytical, Numerical and Experimental Study of a Horizontal Electrothermal MEMS Microgripper for the Deformability Characterisation of Human Red Blood Cells. Micromachines 2018, 9, 108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, J.; Liu, X.; Shi, Q.; He, T.; Sun, Z.; Guo, X.; Liu, W.; Sulaiman, O.B.; Dong, B.; Lee, C. Development Trends and Perspectives of Future Sensors and MEMS/NEMS. Micromachines 2019, 11, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ouakad, H.M. Electrostatic fringing-fields effects on the structural behavior of MEMS shallow arches. Microsyst. Technol. 2018, 24, 1391–1399. [Google Scholar] [CrossRef]
- Di Barba, P.; Fattorusso, L.; Versaci, M. Electrostatic field in terms of geometric curvature in membrane MEMS devices. Commun. Appl. Ind. Math. 2017, 8, 165–184. [Google Scholar] [CrossRef] [Green Version]
- Rahaman, A.; Ishfaque, A.; Jung, H.; Kim, B. Bio-Inspired Rectangular Shaped Piezoelectric MEMS Directional Microphone. IEEE Sens. J. 2019, 19, 88–96. [Google Scholar] [CrossRef]
- Versaci, M.; Angiulli, G.; Fattorusso, L.; Jannelli, A. On the uniqueness of the solution for a semi-linear elliptic boundary value problem of the membrane MEMS device for reconstructing the membrane profile in absence of ghost solutions. Int. J. Non-Linear Mech. 2019, 109, 24–31. [Google Scholar] [CrossRef]
- Angiulli, G.; Jannelli, A.; Morabito, F.C.; Versaci, M. Reconstructing the membrane detection of a 1D electrostatic-driven MEMS device by the shooting method: Convergence analysis and ghost solutions identification. Comp. Appl. Math. 2018, 37, 4484–4498. [Google Scholar] [CrossRef]
- Javaheri, H.; Ghanati, P.; Azizi, S. A Case Study on the Numerical Solution and Reduced Order Model of MEMS. Sens. Imaging 2018, 19, 3. [Google Scholar] [CrossRef]
- Vinyas, M.; Kattimani, S.C. Investigation of the effect of BaTiO3/CoFe2O4 particle arrangement on the static response of magneto-electro-thermo-elastic plates. Compos. Struct. 2018, 185, 51–64. [Google Scholar] [CrossRef]
- Imai, S.; Tsukioka, T. A magnetic MEMS actuator using a permanent magnet and magnetic fluid enclosed in a cavity sandwiched by polymer diaphragms. Precis. Eng. 2014, 38, 548–554. [Google Scholar] [CrossRef]
- Feng, J.; Liu, C.; Zhang, W.; Hao, S. Static and Dynamic Mechanical Behaviors of Electrostatic MEMS Resonator with Surface Processing Error. Micromachines 2018, 9, 34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mashinchi Joubari, M.; Asghari, R. Analytical Solution For Nnonlinear Vibration Of Micro-electromechanical System (mems) By Frequency-amplitude Formulation Method. J. Math. Comput. Sci. 2012, 4, 371–379. [Google Scholar] [CrossRef]
- Di Barba, P.D.; Fattorusso, L.; Versaci, M. A 2D Non-Linear Second-Order Differential Model for Electrostatic Circular Membrane MEMS Devices: A Result of Existence and Uniqueness. Mathematics 2019, 7, 1193. [Google Scholar] [CrossRef] [Green Version]
- Versaci, M.; Morabito, F.C. Membrane Micro Electro-Mechanical Systems for Industrial Applications. In Handbook of Research on Advanced Mechatronic Systems and Intelligent Robotics; Habib, M.K., Ed.; IGI Global: Hershey, PA, USA, 2020; pp. 139–175. ISBN 978-1-79980-137-5. [Google Scholar]
- Fattorusso, L.; Versaci, M. A New One-Dimensional Electrostatic Model for Membrane MEMS Devices. In Proceedings of the Lecture Notes in Engineering and Computer Science, London, UK, 4–6 July 2018; p. 2235. [Google Scholar]
- Fattorusso, L.; Versaci, M. A New Mathematical Model for a Membrane MEMS Device. In Transactions on Engineering Technologies; Ao, S.-I., Gelman, L., Kim, H.K., Eds.; Springer Singapore: Singapore, 2019; pp. 1–17. ISBN 978-981-329-530-8. [Google Scholar]
- Daeichin, M.; Ozdogan, M.; Towfighian, S.; Miles, R. Dynamic response of a tunable MEMS accelerometer based on repulsive force. Sens. Actuators A Phys. 2019, 289, 34–43. [Google Scholar] [CrossRef]
- Morabito, E.C.; Versaci, M. A fuzzy neural approach to localizing holes in conducting plates. IEEE Trans. Magn. 2001, 37, 3534–3537. [Google Scholar] [CrossRef]
- Angiulli, G.; Versaci, M. A Neuro-Fuzzy Network for the Design of Circular and Triangular Equilateral Microstrip Antennas. Int. J. Infrared Millim. Waves 2002, 23, 1513–1520. [Google Scholar] [CrossRef]
- Guckel, H. Progress in magnetic microactuators. Microsyst. Technol. 1998, 5, 59–61. [Google Scholar] [CrossRef]
- Guckel, H.; Earles, T.; Klein, J.; Zook, D.; Ohnstein, T. Electromagnetic Linear Actuators With Inductive Position Sensing For Micro Relay, Micro Valve And Precision Positioning Applications. In Proceedings of the International Solid-State Sensors and Actuators Conference-TRANSDUCERS ’95, Stockholm, Sweden, 25–29 June 1995; Volume 1, pp. 324–327. [Google Scholar]
- Delinchant, B.; Rakotoarison, H.L.; Ardon, V.; Chadebec, O.; Cugat, O. Gradient based optimization of semi-numerical models with symbolic sensitivity: Application to a simple ferromagnetic MEMS switch device. Int. J. Appl. Electromagn. Mech. 2009, 30, 189–200. [Google Scholar] [CrossRef] [Green Version]
- Di Barba, P.; Wiak, S. Evolutionary Computing and Optimal Design of MEMS. IEEE/ASME Trans. Mechatron. 2015, 20, 1660–1667. [Google Scholar] [CrossRef]
- Di Barba, P.; Savini, A.; Wiak, S. Higher-order multiobjective design of MEMS. Int. J. Appl. Electromagn. Mech. 2017, 53, S239–S247. [Google Scholar] [CrossRef]
- MagNet. Available online: https://www.mentor.com/products/mechanical/magnet/magnet/ (accessed on 20 July 2020).
- Di Barba, P.; Mognaschi, M.E.; Rezaei, N.; Lowther, D.A.; Rahman, T. Many-objective shape optimisation of IPM motors for electric vehicle traction. Int. J. Appl. Electromagn. Mech. 2019, 60, S149–S162. [Google Scholar] [CrossRef]
- Di Barba, P. Multiobjective Shape Design in Electricity and Magnetism; Lecture Notes in Electrical Engineering; Springer: Doredrecht, The Netherlands; New York, NY, USA, 2010; ISBN 978-90-481-3079-5. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms, 1st ed.; Wiley-Interscience Series in Systems and Optimization; John Wiley & Sons: Chichester, UK; New York, NY, USA, 2001; ISBN 0-471-87339-X. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Lahanas, M.; Schreibmann, E.; Milickovic, N.; Baltas, D. Evolutionary Multi-Criterion Optimization. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 632, p. 70. ISBN 978-3-540-01869-8. [Google Scholar]
- Nourbakhsh, A.; Safikhani, H.; Derakhshan, S. The comparison of multi-objective particle swarm optimization and NSGA II algorithm: Applications in centrifugal pumps. Eng. Optim. 2011, 43, 1095–1113. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q. Multiobjective Optimization Problems with Complicated Pareto Sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Sieni, E.; Di Barba, P.; Forzan, M. Migration NSGA: Method to improve a non-elitist searching of Pareto front, with application in magnetics. Inverse Probl. Sci. Eng. 2016, 24, 543–566. [Google Scholar] [CrossRef]
- Bertani, R.; Forzan, M.; Sgarbossa, P.; Sieni, E.; Di Barba, P.; Spizzo, F.; Del Bianco, L. Multi-objective Design of a Magnetic Fluid Hyperthermia Device. In Proceedings of the Industrial Electronics Society, IECON 2015-41th Annual Conference of the IEEE, Yokohama, Japan, 9–12 November 2015. [Google Scholar]
- Di Barba, P.; Dughiero, F.; Mognaschi, M.E.; Sieni, E. Multi-objective optimization of an electrode pair for electrochemotherapy: M-NSGA and µ-BIMO comparison. Int. J. Appl. Electromagn. Mech. 2019, 60, S163–S172. [Google Scholar] [CrossRef]
- Di Barba, P.; Dughiero, F.; Forzan, M.; Sieni, E. Self-adaptive NGSA algorithm and optimal design of inductors for magneto-fluid hyperthermia. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2017, 36, 535–545. [Google Scholar] [CrossRef]
- Sieni, E.; Di Barba, P.; Dughiero, F.; Forzan, M. Self-adaptive migration NSGA and optimal design of inductors for magneto-fluid hyperthermia. Eng. Comput. 2018, 35, 1727–1746. [Google Scholar] [CrossRef]
- Di Barba, P.; Dughiero, F.; Forzan, M.; Sieni, E. SELF-adaptive Migration-NSGA algorithm: An application in uncertainty-tolerant magnetic field synthesis for MFH inductor design. Int. J. Appl. Electromagn. Mech. 2018, 56, 17–32. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. Normal-Boundary Intersection: A New Method for Generating the Pareto Surface in Nonlinear Multicriteria Optimization Problems. SIAM J. Optim. 1998, 8, 631–657. [Google Scholar] [CrossRef] [Green Version]



| Design Variable | Minimum | Maximum | Constraint | Threshold |
|---|---|---|---|---|
| x1 | 50 µm | 150 µm | Holding torque | >10−8 Nm |
| x2 | 1 mm | 2 mm | ||
| x3 | 25 µm | 75 µm | Actuation torque | >10−9 Nm |
| x4 | 25 µm | 75 µm | ||
| x5 | 100 µm | 300 µm | Current density | <5 × 109 Am−2 |
| x6 | 300 µm | 900 µm | ||
| x7 | 0 A | 150 A |
| MP-NSGA | NSGA-III | ||||
|---|---|---|---|---|---|
| f1 | f2 | f3 | f1 | f2 | f3 |
| 1.91 × 10−3 | 1.11 × 10−9 | 5.67 × 10−10 | 10 | 1.38 × 10−7 | 9.8 × 10−10 |
| 0.31 | 6.71 × 10−9 | 4.00 × 10−10 | 1.8 | 8.31 × 10−8 | 1.14 × 10−9 |
| 1.05 × 10−3 | 1.38 × 10−9 | 1.22 × 10−9 | 3.39 | 9.79 × 10−8 | 9.92 × 10−10 |
| 12.0 | 1.43 × 10−7 | 1.28 × 10−9 | 7.68 | 1.28 × 10−7 | 9.71 × 10−10 |
| 1.14 | 3.96 × 10−8 | 2.41 × 10−9 | 7.27 | 1.37 × 10−7 | 1.04 × 10−9 |
| 7.96 | 1.36 × 10−7 | 1.01 × 10−9 | 1.72 | 7.76 × 10−8 | 9.25 × 10−10 |
| 3.76 | 8.88 × 10−8 | 1.15 × 10−9 | 3.44 | 9.82 × 10−8 | 9.37 × 10−10 |
| 10.3 | 1.13 × 10−7 | 8.66 × 10−10 | 4.59 | 1.11 × 10−7 | 9.61 × 10−10 |
| 6.93 | 1.13 × 10−7 | 1.30 × 10−9 | 5.91 | 1.2 × 10−7 | 9.71 × 10−10 |
| 5.01 | 3.88 × 10−8 | 7.66 × 10−10 | 6.14 | 1.3 × 10−7 | 1.04 × 10−9 |
| 11.1 | 1.41 × 10−7 | 1.13 × 10−9 | 2.94 | 9.36 × 10−8 | 1.06 × 10−9 |
| 1.75 | 5.08 × 10−8 | 2.02 × 10−9 | 4.59 | 1.11 × 10−7 | 9.74 × 10−10 |
| 4.81 | 1.01 × 10−7 | 9.39 × 10−10 | 5.35 | 1.25 × 10−7 | 1.07 × 10−9 |
| 1.62 | 4.71 × 10−8 | 2.07 × 10−9 | 3.03 | 9.11 × 10−8 | 7.29 × 10−10 |
| 6.64 | 1.07 × 10−7 | 9.38 × 10−10 | 4.59 | 1.15 × 10−7 | 9.80 × 10−10 |
| 0.97 | 1.83 × 10−8 | 1.63 × 10−9 | 5.90 | 1.20 × 10−7 | 9.71 × 10−10 |
| 1.95 | 6.78 × 10−8 | 1.00 × 10−9 | 2.26 | 9.02 × 10−8 | 1.10 × 10−9 |
| 1.47 | 4.22 × 10−8 | 2.34 × 10−9 | 3.76 | 1.04 × 10−7 | 9.71 × 10−10 |
| 1.56 | 3.94 × 10−8 | 1.90 × 10−9 | 0.96 | 5.76 × 10−8 | 9.22 × 10−10 |
| 3.32 | 7.47 × 10−8 | 8.85 × 10−10 | 3.95 | 1.08 × 10−7 | 9.69 × 10−10 |
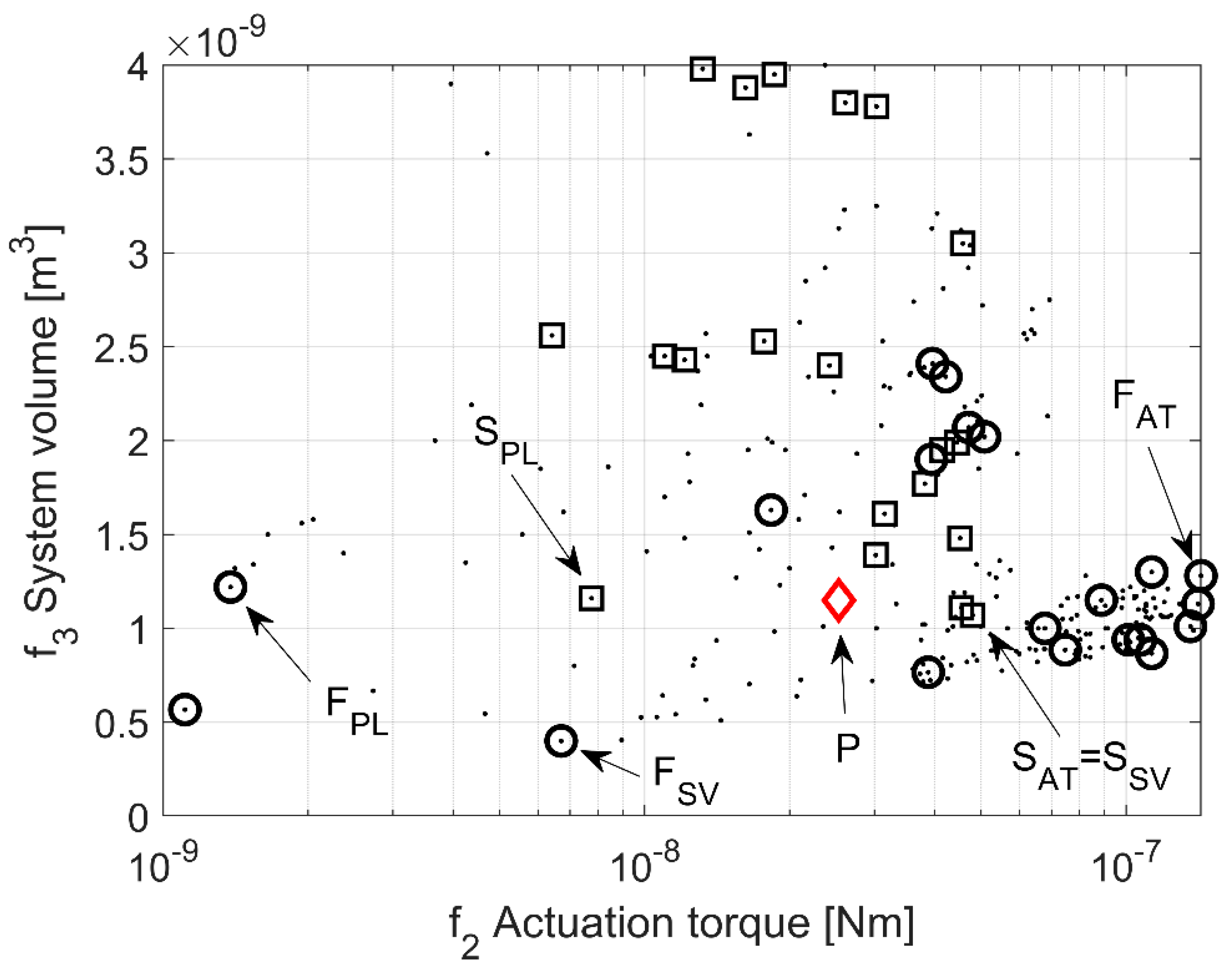
| Design Variable | P | SPL | FPL | Objective Function | P | SPL | FPL |
|---|---|---|---|---|---|---|---|
| x1 [µm] | 100 | 144 | 140 | f1 power losses [W] | 1.04 | 2.36 × 10−2 | 1.05 × 10−3 |
| x2 [mm] | 1.2 | 1.17 | 1.24 | ||||
| x3 [µm] | 50 | 33.8 | 28.9 | f2 actuation torque [Nm] | 2.53 × 10−8 | 7.76 × 10−9 | 1.38 × 10−9 |
| x4 [µm] | 50 | 34.6 | 29.2 | ||||
| x5 [µm] | 200 | 178 | 175 | f3 system volume [m3] | 1.15 × 10−9 | 1.16 × 10−9 | 1.22 × 10−9 |
| x6 [µm] | 600 | 532 | 485 | ||||
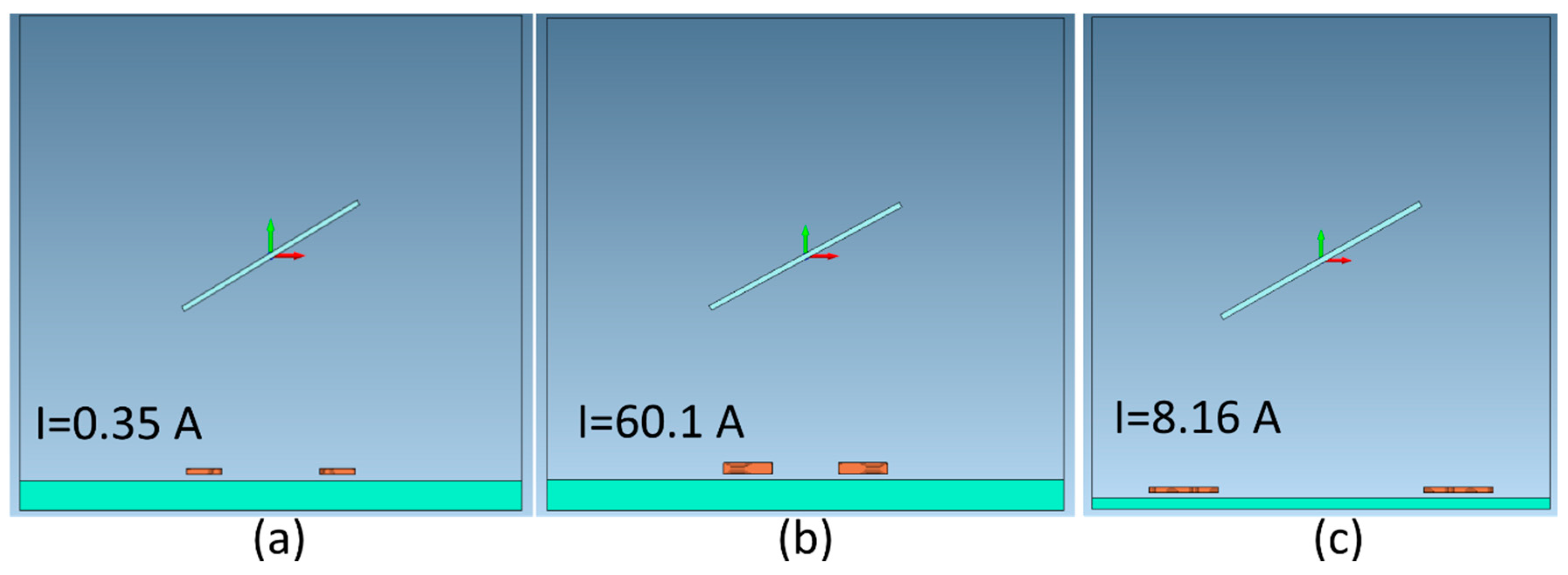
| x7, current [A] | 10 | 1.89 | 0.35 | ||||
| Design Variable | SAT = SSV | FAT | FSV | Objective Function | SAT = SSV | FAT | FSV |
|---|---|---|---|---|---|---|---|
| x1 [µm] | 134 | 150 | 50 | f1 power losses [W] | 9.34 | 12 | 0.31 |
| x2 [mm] | 1.02 | 1.18 | 1 | ||||
| x3 [µm] | 45.9 | 25 | 25 | f2 actuation torque [Nm] | 4.8 × 10−8 | 1.43 × 10−7 | 6.71 × 10−9 |
| x4 [µm] | 75 | 55 | 25 | ||||
| x5 [µm] | 156 | 222 | 300 | f3 system volume [m3] | 1.07 × 10−9 | 1.28 × 10−9 | 4 × 10−10 |
| x6 [µm] | 827 | 300 | 900 | ||||
| x7, current [A] | 55.6 | 60.1 | 8.16 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Barba, P.; Mognaschi, M.E.; Sieni, E. Many Objective Optimization of a Magnetic Micro–Electro–Mechanical (MEMS) Micromirror with Bounded MP-NSGA Algorithm. Mathematics 2020, 8, 1509. https://doi.org/10.3390/math8091509
Di Barba P, Mognaschi ME, Sieni E. Many Objective Optimization of a Magnetic Micro–Electro–Mechanical (MEMS) Micromirror with Bounded MP-NSGA Algorithm. Mathematics. 2020; 8(9):1509. https://doi.org/10.3390/math8091509
Chicago/Turabian StyleDi Barba, Paolo, Maria Evelina Mognaschi, and Elisabetta Sieni. 2020. "Many Objective Optimization of a Magnetic Micro–Electro–Mechanical (MEMS) Micromirror with Bounded MP-NSGA Algorithm" Mathematics 8, no. 9: 1509. https://doi.org/10.3390/math8091509
APA StyleDi Barba, P., Mognaschi, M. E., & Sieni, E. (2020). Many Objective Optimization of a Magnetic Micro–Electro–Mechanical (MEMS) Micromirror with Bounded MP-NSGA Algorithm. Mathematics, 8(9), 1509. https://doi.org/10.3390/math8091509







