An Analysis of a KNN Perturbation Operator: An Application to the Binarization of Continuous Metaheuristics

Abstract

The optimization methods and, in particular, metaheuristics must be constantly improved to reduce execution times, improve the results, and thus be able to address broader instances. In particular, addressing combinatorial optimization problems is critical in the areas of operational research and engineering. In this work, a perturbation operator is proposed which uses the k-nearest neighbors technique, and this is studied with the aim of improving the diversification and intensification properties of metaheuristic algorithms in their binary version. Random operators are designed to study the contribution of the perturbation operator. To verify the proposal, large instances of the well-known set covering problem are studied. Box plots, convergence charts, and the Wilcoxon statistical test are used to determine the operator contribution. Furthermore, a comparison is made using metaheuristic techniques that use general binarization mechanisms such as transfer functions or db-scan as binarization methods. The results obtained indicate that the KNN perturbation operator improves significantly the results.

1. Introduction

In many areas of the industry, it is necessary to make decisions that are increasingly complex given the scarcity and cost of resources. The amount of elements that are considered today means that these decisions are made on a large number of assessments which constitute combinatorial optimization problems (COPs) to find a result that, on the one hand, is feasible and, on the other hand, satisfactory. In the industry, there are several areas where this situation occurs such as automatic learning [1], transport [2], biology [3], logistics [4], civil engineering [5], sustainability [6], among others. Among the optimization problems are the so-called NP-hard problems, which are difficult to solve. Various techniques can be applied to solve these problems, ranging from the application of exact techniques to the use of approximate techniques. Within the latter, we find the metaheuristics which allow us to tackle large problems and find good solutions, which is not necessarily optimal, but in a reasonable computing time. Metaheuristics are an active line of research in the areas of computer science and operational research that allow us to obtain robust algorithms associated with the solution of COPs.

The need to find better results has allowed the development of new lines of research, where the hybridization stands out, to obtain more robust methods on the one hand in relation to the quality of the solution and on the other hand in improving the times of convergence. In hybridization there are four lines of work: The first corresponds to the combination of heuristics with mathematical programming [7], the second to the combination of different heuristic methods [8], the third line corresponds to the combination between simulation and heuristic methods [9], and finally the fourth line corresponds to the combination between heuristics and machine learning. This last line is an emerging area of interest for researchers where this combination (heuristics-machine learning) can occur in such a way that metaheuristics help machine learning algorithms to improve their results ([10,11]) or it can also occur in the reverse direction, where machine learning techniques help to obtain more robust metaheuristic algorithms (for example, in [12]). In Section 2.1, the different ways of hybridization are presented in detail.

In this work, in order to improve the diversification and intensification properties, and taking into account the different lines of research presented above, the k-nearest neighbors algorithm is applied to a perturbation operator. The contributions of this work are presented below.

• Inspired by the work in [13], an improvement is proposed to the binarization technique that uses transfer functions, developed in [14], with the objective of metaheuristics which were defined to function in continuous spaces, efficiently solve COPs. This article includes the K-nearest neighbor technique to improve the diversification and intensification properties of a specific metaheuristic. Unlike in [13], in which the perturbation operator is integrated with the k-means clustering technique, in this article the perturbation operator is integrated with transfer functions, and these functions perform the binarization of the continuous metaheuristics. For this work, the Cuckoo Search (CS) metaheuristic was used. This algorithm was chosen due to its ease in parameter tuning, in addition to the existence of basic theoretical models of convergence.
• Unlike in [13], in which the multidimensional knapsack problem was tackled, this article addresses the set covering problem (SCP). This combinatorial problem has been widely studied and, because of that, instances of different difficulties are available which facilitate our analysis. In this work, we have chosen to use large size instances in order to adequately evaluate the contribution of the KNNperturbation operator.
• For a suitable evaluation of our KNN perturbation operator, we first use a parameter estimation methodology proposed in [15] with the goal to find the best metaheuristic configurations. Later, experiments are carried out to get insight into the contribution of the KNN operator. Finally, our hybrid algorithm is compared to the state-of-the-art general binarization methods. The numerical results show that our proposal achieves highly competitive results.

The rest of the work is presented as follows. In Section 2, a state-of-the-art of integrating metaheuristics with machine learning is developed. Then, in the same section, the different binarization methods are summary. Later, in Section 3, the optimization set covering problem is explained. Then, in Section 4, the detail of the perturbation operator and the algorithm that solves SCP is explained. After that, the results obtained are detailed in Section 5. Finally, in Section 6, the conclusions and new research lines are developed.

2. Related Work

In the industry there are a series of problems that must be solved, and in this sense the optimization allows to give solution to some of them. Within the optimization techniques are the metaheuristics which in recent years have gained much ground, especially in those areas where the exact techniques do not have a good performance.

Among the most used metaheuristics are the last generation calls [16] where they are found: Harmony Search [17], Artificial Bee Colony [18], Biogeography-based, Cuckoo Search [19], Gravitational Search Algorithm [20], Teaching–learning-Based [21], Krill Herd [22], and Social spider optimization [23].

The metaheuristics have been used to solve important problems in several productive areas such as engineering, bioinformatics, communications, operational research, and geophysics, among others [24].

The metaheuristics, unlike exact techniques, do not perform a complete search of the search space, so it is of utmost importance to use the right techniques to obtain good results.

2.1. Hybridizing Metaheuristics with Machine Learning

In the process of finding good solutions, important auxiliary data are generated such as as trajectories, movements, solutions, fitness, among others. These data allow the researchers use machine learning (ML) techniques with the aim of improving results. The use of ML in metaheuristics occurs on three main fronts:

• The first front is to apply ML at the level of the problem to be solved. This first front considers obtaining expert knowledge about the characteristics of the data of the problem under consideration. The problem model can be reformulated or it can be broken down to achieve a more efficient and effective solution. The good knowledge of the characteristics allows to design efficient metaheuristics and to understand the behavior of the algorithms. The benefits are varied, ranging from allowing the selection of an appropriate metaheuristic for each type of problem [25] to the possibility of finding an appropriate configuration of parameters [26]. For the knowledge of the ML characteristics it has several methods that can be used: neural networks [27], Bayesian networks [28], regression trees [26], support vector regression [29], Gaussian process [30], ridge regression [25], and random forest [30].
• The second front is to apply ML at the level of the components of metaheuristics. On this front, ML can be used to find suitable search components (or to find a good configuration of parameter values the latter in sin is an optimization problem. ML can be used to find good initial solutions which allows to improve the quality of the solutions and reduce processing costs since currently the initial solutions are randomly generated and of not very good quality [31]. Another participation of ML is in the design of the search operators: constructive, unary, binary, indirect, intensification, and diversification. Furthermore, ML can be present in the important task of finding a good configuration of parameters as this activity has direct impact on the performance of the algorithm [32]. Usually, the assignment of parameters is done by applying the technique of trial and error, which undoubtedly causes a loss of resources, especially time [33]. The number of parameters can vary between one metaheuristic and another, which makes experience an important factor.
  In general there are two major groups of parameters: those where the values are given before the execution of the algorithm known as static or offline parameters and there are also the parameters where the values are assigned during the execution of the algorithm also known as online or dynamic parameter setting. In the case of the offline parameters, the following ML methodologies can be used: unsupervised learning, supervised learning, and surrogate-based optimization. For the case of sustainable wall design, the k-means unsupervised learning technique was used in [34] to allow algorithms that work naturally in continuous spaces to solve a combinatorial wall design problem. In the allocation of resources, the db-scan technique was used in [35], to solve the multidimensional knapsack problem. For the case of online parameter value assignment, where parameters are changed during the execution of the algorithm, the knowledge obtained during the search can serve as information to dynamically change the values of the parameters during its execution using ML methodologies, as they are Sequential learning approach, Classification/regression approach and Clustering approach. In [36], an algorithm has been proposed in order to carry out an intelligent initiation of algorithms based on populations. In this article, clustering techniques are used for the initiation. The results indicated that the proposed intelligent sampling has a significant impact, as it improves the performance of the algorithms with which it has been integrated. The integration of the k-nearest neighbors technique with a quantum cuckoo search algorithm was proposed in [37]. In this case, the proposed hybrid algorithm was applied to the multidimensional knapsack problem. The results showed that the hybrid algorithm is more robust than the original version.
• A third front is the choice of the best algorithm within a portfolio arranged for a certain problem. There are several metaheuristics to solve complex problems which may have common characteristics among them. For this reason, we can think of selecting an adequate metaheuristic to solve a problem with certain characteristics. We know that there is not a single metaheuristic that can solve a wide variety of problems, so the use of an alternative is to select from a portfolio of algorithms [38]. ML is a good tool for an adequate selection of the algorithm [39]. In this case, we can distinguish between offline learning where information is gathered from a series of instances in a previous form with the purpose of replicating new instances considering three approaches: classification, regression, and clustering. On the other hand, there is the online approach, which has the potential to be adaptive. Additionally, there are some hybrid approaches [40]. In [41], a cooperative strategy was implemented with the aim of land mine detection. The results of the strategy show good detection precision and robustness to environmental changes and data sets.

2.2. Related Binarization Work

There is a group of problems that work in discrete spaces and others particularly in binary spaces. However, some algorithms that were built to work in continuous spaces, such as Cuckoo Search (CS) and Particle Swarm Optimization (PSO) are required to work in discrete spaces.

In [42], the author makes an exhaustive review of the existing binarization methods where he identifies two big groups: one called two-step binarization and a second group called continuousbinary operator transformation. Within the first group the most used techniques are Transfer FunctionBinarization and Angle Modulation-Rule.

• Transfer Function-Binarization. This two-step binarization technique is widely used due to its low implementation cost. In the first step, transfer functions (TF) are used which produce values between 0 and 1 and then in the second step convert these values into binary using rules that allow to leave as value 0 or 1.
  There are two groups of transfer functions which are associated with the form of the function, which can be either S or V. A TF takes values of ${\mathbb{R}}^n$ and generates transition probability values of ${\left[0.1\right]}^n$. These were used to allow PSO to work with binary problems by relating the speed of particles to a transition probability. In PSO a particle is a solution which in each iteration has a position and velocity which is given by the difference of position between iterations. On the other hand, there are several rules to convert these values to binary among these are Complement, Static probability, Elitist, Elitist Roulette, or Monte Carlo.
  This technique has been used to solve feature selection problem [43,44], knapsack problem [45], and set covering problem [2].
• Angle Modulation-Rule. This binary technique has as a first step the use of Angle Modulation was used for phase and frequency modulation of the signal in the telecommunications industry [46]. It belongs to the family of four-parameter trigonometric functions by which it controls the frequency and displacement of the trigonometric function.

  $$g_i\left(x_j\right)=sin(2\pi (x_j-a_i)b_{i}cos\left(2\pi (x_j-a_i)c_i\right))+d_i$$

  (1)
  In PSO, binary heuristic optimization applied to a set of reference functions was used for the first time [47].
  Consider an n-dimensional binary problem, and let $X=(x_1,x_2,...x_n)$ be a solution. First of all, we define a four-dimensional search space. In this space, each dimension corresponds to a coefficient of Equation  (1). As a first stage, using the four-dimensional space, we get a function. Specifically, from every tuple $(a_i,b_i,c_i,d_i)$ in this space, we get a $g_i$. This $g_i$ corresponds to a trigonometric function.
  In the second stage, binarization, for each element $x_j$, the rule  (2) is applied and getting an n-dimensional binary solution.

  $$b_{ij}=\left\{\begin{array}{cc}1& \mathrm{if} g_i\left(x_j\right)\ge 0\\ 0& \mathrm{otherwise}\end{array}\right.$$

  (2)
  Then, for each initial 4-dimensional solution $(a_i,b_i,c_i,d_i)$, we obtain a binary n-dimensional solution $(b_{i1},b_{i2},...,b_{in})$ that is a feasible solution of our n-binary problem. In [48], the authors successfully applied to network reconfiguration problems multi-user detection in multi-carrier wireless broadband system [49], the antenna position problem [50], and N-queens problems [51].

The second group of binarization techniques, the most used techniques are quantum binary and set-based approaches.

• Quantum binary. In reviewing the areas of quantum and evolutionary computing we can distinguish three types of algorithms [52]:
  • Quantum evolutionary algorithms: In these methods, EC algorithms are used in order to apply them in quantum computing.
  • Evolutionary-based quantum algorithms: The objective of these methods is to automate the generation of new quantum algorithms. This automation is done using evolutionary algorithms.
  • Quantum-inspired evolutionary algorithms: This category adapts concepts obtained from quantum computing in order to strengthen the EC algorithms.
  The quantum binary approach is an evolutionary algorithm that adapts the concepts of q-bits and overlap used in quantum computing applied to traditional computers.
  The position of a feasible solution is given by $X=(x_1,x_2,...,x_n)$ and a quantum bit vector q$Q=[Q_1,Q_2,...,Q_n]$ where in this approach the probability of change Q is the probability that $x_j$ takes the value 1. For each dimension, a random number between [0.1] is generated and compared to $Q_j$: if $rand<Q_j$, then $x_j=1$; otherwise, $x_j=0$. The updating mechanism of the Q vector is specific to each metaheuristic.
  This technique has been used to solve the following problems: unit commitment problem [53], hydropower generation scheduling [54], knapsack problem [55], and recognize facial expressions [56].

3. The Set Covering Problem

The classical set covering combinatorial problem (SCP) is an important NP-hard problem, which has not only theoretical importance in the field of optimization but also from a practical point of view as it has important practical applications in different areas of engineering, for example, in the vehicle routing, railroads, airline crew scheduling, microbial communities, and pattern finding [57,58,59,60].

The SCP consists of choosing a subset of possible locations at the lowest possible cost, which is given by a fixed cost of construction and implementation, so that all agents are covered from a set of possible locations that cover them.

Several algorithms have been created to solve this problem. Some of them may be exact as are exact algorithms that generally rely on the branch-and-bound and branch-and-cut methods to obtain optimal solutions [61,62]. However, this type of algorithm is faced with the time required to provide a solution which does not allow them to be used in industrial problems. As an alternative to this problem, different heuristics have been proposed [63,64].

Mathematically, the SCP is represented in the next paragraph: Consider $A=\left(a_{ij}\right)$ be an $n\times m$ zero-one matrix. Then, a column j covers a row i if $a_{ij}=1$, and a column j is related with a positive real cost $c_j$. Consider $J=\{1,...m\}$ and $I=\{1,...,n\}$ be, respectively, the columns and rows sets of A. Then, the SCP corresponds to a finding a minimum cost subset $S\subset J$ for which each row $i\in I$, at least one column $j\in J$ covers it , i.e.,

$$\mathrm{Minimize}f\left(x\right)=\sum _{j=1}^m{c}_j{x}_j$$

(3)

$$\mathrm{Subject}\mathrm{to}\sum _{j=1}^m{a}_{ij}{x}_j\ge 1,\forall i\in I,\mathrm{and}{x}_j\in \{0,1\},\forall j\in J$$

(4)

where $x_j=1$ if $j\in S$ and $x_j=0$ otherwise.

4. The Binary KNN Perturbed Algorithm

This section details the binary KNN perturbation algorithm to solve the SCP. This hybrid algorithm has 4 main operators: A solution initialization operator which is described in Section 4.1. A binarization operator which uses transfer functions to perform the binarization. This operator is detailed in Section 4.4. The perturbation operator described in Section 4.3 is based on the k-nearest neighbor technique. Finally, a repair operator in the event the solutions do not meet any of the coverage constraints. This operator is detailed in Section 4.5. Additionally, the KNN perturbation algorithm has a KNN-perturbation analysis module. The objective of this module is to collect data from the solutions obtained in the optimization process to later deliver information to the perturbation operator. The detail of this module will be developed in Section 4.2. The algorithm flow chart is shown in Figure 1.

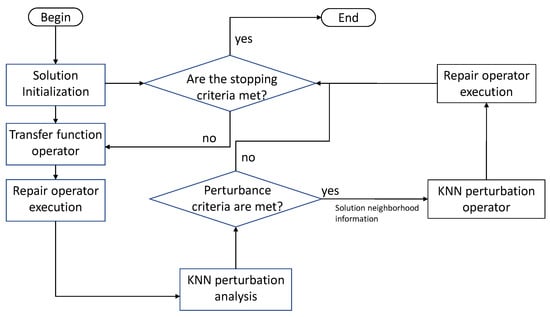
Figure 1. A KNNperturbation algorithm flow chart.

4.1. Initialization Operator

The goal of this operator is to initiate solutions. As the first stage, a column will be selected randomly through the SelRandCol() function. Once we have the first column selected, compliance with the coverage constraints is evaluated. In the case that they are not fulfilled, then the Heu() function is called, which will be detailed in Section 4.6. This function receives a list with the currently selected column or columns ($lSol$) and returns the new column $nC$ to be incorporated into the $lSol$. This Heu() function is executed until the coverage constraints are satisfied. The pseudocode for the initiation procedure is shown in Algorithm 1.

Algorithm 1 Init Operator

1: Function Init() 2: Input 3: Output  $lSol$ 4: $lSol\leftarrow$ SelRandCol() 5: while not all rows are covered by $lSol$ do 6:  $nC$ = Heu($lSol$) 7:  lSol.append($nC$) 8: end while 9: return $lSol$

4.2. KNN Perturbation Analysis Module

This module uses the data generated in the evolution of the metaheuristic algorithm and, through a measure, suggests a perturbation probability of the elements of the solution. As a measure of importance, the definition made in [65] is adapted. The objective of the measure developed in [65] corresponds to identifying the variables that are the most relevant considering a reduced number of evaluations. This approach models linear and non-linear effects and the correlation between variables.

Let K points belonging to the search space S. Then, $E{E}_i\left(X\right)$ is defined in Equation (5), where $X\in S$.

$$E{E}_i\left(X\right)=f(X_1,...,\widehat{X_i},..,X_d)-f\left(X\right)$$

(5)

where f corresponds to the objective function and $\widehat{X_i}$ is the complement of $X_i$, that is, if $X_i=1$ then $\widehat{X_i}=0$, and i represents the location of the element $X_i$ in the solution. Subsequently, for each dimension, the average ${\mu }_i$ and the standard deviation ${\sigma }_i$, defined in Equations (6) and (7) respectively, can be calculated.

$${\mu }_i=\frac{1}{K}\sum _{j=1}^K\left|E{E}_i\left(X^j\right)\right|$$

(6)

$${\sigma }_i=\sqrt{\frac{1}{K}\sum _{j=1}^K{|E{E}_i\left(X^j\right)-{\mu }_i|}^2}$$

(7)

When the $(\mu ,\sigma )$ pair is analyzed, interesting interpretations can be obtained. In the case of obtaining small values of $\mu$ and $\sigma$, it is an indicator that the input variables have a small impact on the objective function. A small value of $\mu$ and a high value of $\sigma$ suggest that the input variables have a nonlinear effect. A linear effect on the objective function is related to high values of $\mu$ and small values of $\sigma$. Finally, high values in both indicate that there are nonlinear effects or interaction with other variables.

In the methods reviewed in [65], the objective is to evaluate the exploration of the entire space. In our case, the goal is to measure the exploitation of a region around a solution to later apply a perturbation to the solution. Therefore, to achieve this goal, the previous calculus must be adapted. In this adaptation, the neighborhood concept must be incorporated. For our case, instead of calculating the indicators over the entire space, the calculation will be carried out on the k-nearest neighbors of the solution to be perturbed. The data set used to obtain the k-neighbors is generated with 25% of the best solutions obtained in each iteration. Therefore, the elements of the first quartile are being used in the estimation. For k-neighbors retrieval, we use the k-nearest neighbor algorithm (KNN).

Because, to perform the perturbation, it is necessary to obtain a value of $w_i$ between 0 and 1 for each dimension i. Therefore, in Equation (8), $w_i$ is defined. The indicators ${\mu }_i^{*}$ and ${\sigma }_i^{*}$ correspond to normalized values between 0 and 1 of ${\mu }_i$ and ${\sigma }_i$, respectively. On the other hand, $\sqrt{2}$ is added to ensure that $w_i$ takes values between 0 and 1. The detail of the $w_i$ calculation is shown in Algorithm 2.

$$w_i=\frac{\sqrt{{\mu }_i^{*}+{\sigma }_i^{*}}}{\sqrt{2}}$$

(8)

Algorithm 2 KNN perturbation analysis module

1: Function weight($lSol$) 2: Input  $lSol$ 3: Output The list of weights ($lWeight$) 4: $lWeight\leftarrow$ [] 5: $neigbours\leftarrow$ getKneighbours($lSol$) 6: for (each dimension i in $lSol$) do 7:  $w_i\leftarrow$ getweight($neighbours$) 8:  $lWeight$.append($w_i$) 9: end for 10: return  $lWeight$

4.3. KNN Perturbation Operator

The goal of this operator is to perturb the solution list when the perturbation criterion is met. This operator, in the case that the solution is found in 25% of the best solutions of that iteration, consults the KNN-perturbation analysis module, for the probability of perturbation for each element of the solution. Otherwise, that is, the solution is not found in 25% of the best solutions, the solution is randomly perturbed, where the coefficient $\nu$ is used in order to manage the force of the perturbation. The criterion used for the list of solutions to be perturbed, corresponds to a number T of iterations without the best value changing. In this particular case, the number of T was 35. The pseudocode of the perturbation operator is shown in Algorithm 3. In the pseudocode, $bSolutions$ corresponds to 25% of the best solutions and $oSolutions$ to the rest of the solutions.

Algorithm 3 KNN Perturbation operator

1: Function Perturbation($listSolutions$, $\nu$) 2: Input Input sol $listSolutions$, strength of perturbation $\nu$ 3: Output The perturbed sol $listSolutions$ 4: $bSolutions$, $oSolutions\leftarrow$ getBSols($listSolutions$) 5: for each $lSol$ in $bSolutions$ do 6:  for (each dimension i in $lSol$) do 7:   if ($w_i>$ random and i == 1) then 8:    remove element i from $sol$ 9:   end if 10:  end for 11:  $sol\leftarrow$ Repair($lSol$) 12: end for 13: for (each $lSol$ in $oSolutions$) do 14:  for (i=1 to $\nu$) do 15:   Randomly delete an item from $lSol$ 16:  end for 17:  $sol\leftarrow$ Repair($sol$) 18: end for 19: return $listSolutions$

4.4. Transfer Function Operator

As CS is an algorithm that works naturally in continuous search spaces, it is necessary to adapt it to solve the SCP. A widely used method for these situations is transfer functions (Section 2.2). In this work, the function shown in Equation (9) was used as the transfer function and the Elitist roulette discretization method shown in Equation (10), to get the binary solutions.

$$TF\left(x\right)=|tanh\left(x\right)|$$

(9)

$$x_i^d(t+1)=\left\{\begin{array}{c}Bes{t}_i^d\left(t\right),\mathrm{if} \mathrm{rand}\le TF\left(x_i^d(t+1)\right)\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

(10)

where $Bes{t}^d\left(t\right)$ corresponds to the best solution obtained by the solution d, up to the iteration t.

4.5. Repair Operator

Every time the transfer function operator or the perturbation operator is executed, there is a possibility the solution obtained does not meet the constraints of the problem. For these cases, a repair operator is used to obtain a viable solution. If there are rows that are not covered by the solution, the repair operator uses the heuristic function to choose the necessary elements. Once all the rows have been covered, the operator checks whether there are disjoint groups of columns that cover the same set of rows. In this case, we proceed to eliminate what has the highest cost. The pseudocode of the repair operator is shown in Algorithm 4.

Algorithm 4 Repair Operator

1: Function Repair($lSol)$) 2: Input Input sol $lSol$ 3: Output The repaired sol $lSo{l}_{rep}$ 4: while needRepair(lSol) == True do 5:  $lSol$.append(Heu($lSol$)) 6: end while 7: $lSo{l}_{rep}\leftarrow$ delRepeatedItem($lSol$) 8: return  $lSo{l}_{rep}$

4.6. Heuristic Function

In cases where it is necessary to repair or initialize a solution, a heuristic function is often used in order to select the most suitable candidates. In our proposal as an input parameter, the heuristic function considers the list of elements of the solution $lSol$. Therefore, with the elements of $lSol$, we obtain the set of rows $uR$ that have not been covered. Using the Equation (11), the bestRows function returns the first N rows. With this list of rows, $lRows$, and using the Equation (11), the bestCols function returns the first M columns. Finally, from the list of the selected columns, $lCols$, one of these is randomly obtained. The operation of the heuristic function is shown in Algorithm 5.

$$WeightRow\left(i\right)=\frac{1}{L_i}$$

(11)

where $L_i$ is the sum of all ones in row i

$$WeightColumn\left(j\right)=\frac{c_j}{|R\cap M_j|}$$

(12)

where $M_j$ is the set of rows covered by Col j

Algorithm 5 Heuristic function

1: Function Heuristic() 2: Input Input solution $lSol$ 3: Output The new column $nC$ 4: $lRows\leftarrow$ bestRows($lSol$, N=10) 5: $lCols\leftarrow$ bestCols($lRows$, M=5) 6: $nC\leftarrow$ getCols($lCols$) 7: return  $nC$

5. Numerical Results

This section aims to study the contribution of the KNN perturbation operator when applied to the SCP. As the first stage in Section 5.1, the methodology to perform parameter tuning is explained. Later, in Section 5.2, the contribution of the KNN perturbation operator is analyzed. Finally, in Section 5.3 our proposal is compared with other algorithms that have solved SCP in recent years. The dataset used to develop the experiments considers the instances E, F, G, and H of the OR-library (OR-Library: http://people.brunel.ac.uk/~mastjjb/jeb/orlib/scpinfo.html). The configuration of the equipment used in the execution of the experiments corresponds to an Intel Core i7-4770 with 16GB in RAM. The algorithm was programmed in Python 3.6. For the analyzes, each instance was executed 30 times and box plots, convergence graphs, and the Wilcoxon test were considered to develop the comparisons.

5.1. Parameter Settings

In this section, the methodology used in the parameter setting is described. The methodology was proposed in [15] and considers 4 measurements based on the best value, the worst value, the average value, and the average time obtained by a specific configuration. The definition of the measures are shown in the Equations (13)–(16).

• The percentage deviation of the best value resulting in ten runs compared with the best-known value:

  $$bSolution=1-\frac{KBestVal-BestVal}{KBestVal}$$

  (13)
• The percentage deviation of the worst value resulting in ten runs compared to the best-known value:

  $$wSolution=1-\frac{KBestVal-WorstVal}{KBestVal}$$

  (14)
• The average percentage deviation value resulting in ten runs compared with the best-known value:

  $$aSolution=1-\frac{KBestVal-AverageVal}{KBestVal}$$

  (15)
• The convergence time in each experiment is standardized using Equation (16).

  $$nTime=1-\frac{AvgConvTime-minTime}{maxTime-minTime}$$

  (16)

The different explored configurations were obtained from the Range column in Table 1. For each configuration, problems E1, F1, G1, and H1 were considered, and each one of them was executed 10 times. Subsequently, the four previously defined measurements are obtained for each configuration. These measurements allow to generate a radar plot and calculate its area for each configuration. The configuration that gets the largest area corresponds to the selected setting. In the case of CS, the selected configuration is shown in the Value column of Table 1.

Table 1. Parameter configuration for the CS algorithm.

Parameters	Description	Value	Range
$\nu$	Perturbation operator coefficient	25%	[20, 25, 30]
N	Number of Nest	20	[20, 30,40]
K	Neighbours for the perturbation	15	[10, 15,20]
$\gamma$	Step Length	0.01	0.01
$\kappa$	Levy distribution parameter	1.5	1.5
Iterations	Maximum iterations	1000	[800, 900, 1000]

5.2. Perturbation Operator Analysis

This section aims to describe the experiments that evaluate the contribution of the KNN perturbation operator in the final result of the optimization. Once the experiments are detailed, the results will be presented and analyzed. To evaluate the contribution of the KNN perturbation operator, two algorithms were designed. In the first one, the KNN perturbation operator is replaced by a random perturbation operator. This random operator also uses a perturbation coefficient $\nu$ but does not consider the information provided by the KNN perturbation analysis module. The perturbation is executed in a random way, in the same way, that the $oSolutions$ are perturbed in Algorithm 3. For this random perturbation operator, 2 values of $\nu$, 25, and 50 were used and its algorithms are denoted by $rand.25$, and $rand.50$, respectively. The first value used, is the same one used by the KNN perturbation operator.

The second algorithm used to understand the contribution of the perturbation operator corresponds to an algorithm that does not use a perturbation operator. That is, it is equivalent to the design in Figure 1; however, in this case, the solutions will never be perturbed. This algorithm will be denoted by non-perturbed.

For the analysis of the results, a comparative table, Table 2, is generated where the best value and the average obtained from the 30 executions in the different algorithms, and for each of the instances are compared. Moreover, in Figure 2 and Figure 3, box plots have been generated by type of instance. The objective of these box plots is to make a statistical and visual comparison between the results obtained by the different algorithms. Finally, in Figure 4 and Figure 5, the convergence charts of the different algorithms by type of instance are shown.

Table 2. Comparison between not perturbed, random and KNN perturbation operators.

Instance	Best Known	$\mathit{R}\mathit{a}\mathit{n}\mathit{d}$.25 (Best)	$\mathit{R}\mathit{a}\mathit{n}\mathit{d}$.50 (Best)	Non Perturbed (Best)	KNN Perturbed (Best)	$\mathit{R}\mathit{a}\mathit{n}\mathit{d}$.25 (Avg)	$\mathit{R}\mathit{a}\mathit{n}\mathit{d}$.50 (avg)	Non Perturbed (Avg)	KNN (Avg)
E.1	29	30	30	31	29	30.6	30.9	31.8	29.4
E.2	30	31	31	31	30	31.8	32.1	32.1	30.2
E.3	27	28	29	29	27	28.7	29.5	29.7	27.6
E.4	28	29	29	29	28	29.6	29.5	29.8	28.7
E.5	28	28	28	28	28	28.7	28.8	29.1	28.4
F.1	14	15	15	16	14	15.8	15.7	16.4	14.6
F.2	15	15	15	15	15	15.7	16.1	15.9	15.2
F.3	14	16	15	16	14	16.5	15.9	16.7	14.7
F.4	14	15	16	16	14	15.4	16.5	16.7	14.8
F.5	13	15	15	15	13	15.3	15.8	15.6	13.9
G.1	176	179	180	182	176	180.1	181.2	183.2	177.2
G.2	154	158	158	160	155	159.7	159.4	161.1	156.6
G.3	166	171	172	171	168	172.4	173.2	172.3	169.2
G.4	168	171	171	171	170	171.9	172.1	171.9	170.2
G.5	168	171	171	172	168	172.1	172.0	173.2	168.6
H.1	63	65	65	66	64	66.1	66.4	66.8	64.6
H.2	63	65	65	65	64	65.8	65.9	66.1	64.8
H.3	59	62	63	63	60	62.4	63.8	64.2	60.7
H.4	58	60	60	60	59	61.3	61.2	61.1	59.4
H.5	55	58	58	58	55	59.2	59.4	59.4	55.2
Average	67.10	69.10	69.30	69.80	67.55	69.96	70.27	70.66	68.20
Wilcoxon p-value						1.2 × ${10}^{-4}$	1.1 × ${10}^{-5}$	2.7 × ${10}^{-6}$

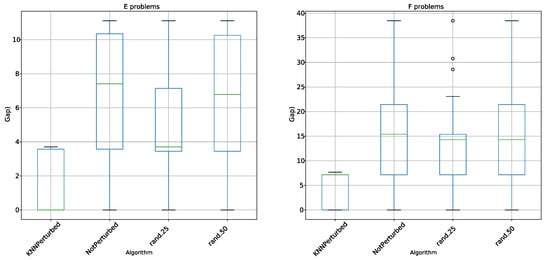
Figure 2. Box plots comparison between non-perturbed, random perturbed, and KNN perturbed operators for E y F instances.

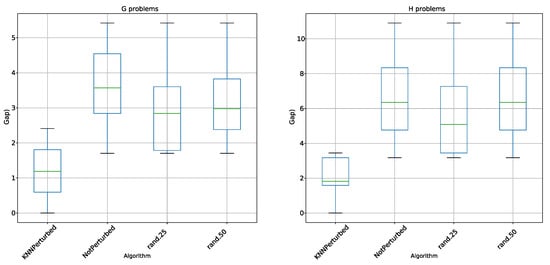
Figure 3. Box plots comparison between non-perturbed, random perturbed, and KNN perturbed operators for G y H instances.

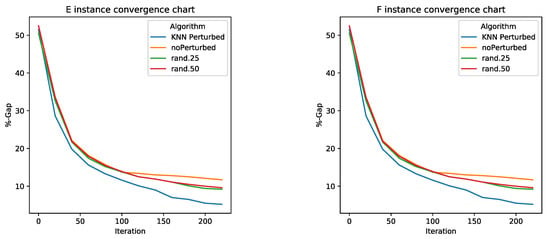
Figure 4. Convergence chart for E and F instances.

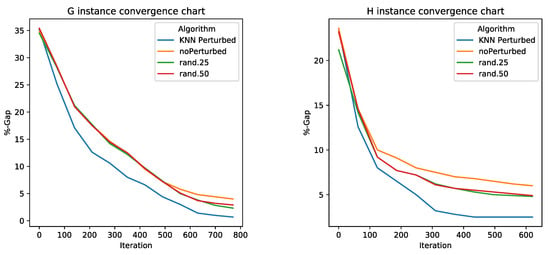
Figure 5. Convergence chart for G and F instances.

In Table 2, it is observed for the indicator best value that KNN perturbed algorithm was the one that obtained the best values in all instances. Rand.25 and rand.50 got similar values, and the non-perturbed algorithm got the worst values. In the case of the average indicator, the result is similar to the previous one. Again, the KNN perturbed algorithm obtained the best results, subsequently followed by rand.25, with non-perturbed being the one that once again obtained the worst value. The Wilcoxon test indicates that the difference between the algorithms is statistically significant. In the case of the box plots shown in Figure 2 and Figure 3, KNN perturbed obtains the best interquartile range values, with values closer to 0 in all instance types, when comparing it with the other algorithms. In addition, almost in all cases IQR (IQR = Q3–Q1) is smaller than in the case of the other algorithms, except in instances E and F in which it has values are very similar to rand.25. Finally, in Figure 4 and Figure 5, the convergence curves for the 4 types of instances studied are compared. In the 4 types, we observe that the shape of the convergence charts stabilizes in the same number of iterations for the different algorithms. However, in the first iterations, KNN perturbed is separated from the other algorithms, obtaining GAPslower than the rest, and this difference is maintained during the complete execution of the optimization.

In summary, it is observed that the KNN perturbed operator contributes to the final result. This contribution makes it possible to obtain consistently better results, as well as a decrease in the dispersion of the values when comparing these with the other proposed algorithms. Regarding convergence, it is observed that the KNN perturbed operator contributes in an important way in the initial iterations of the optimization process.

5.3. Comparisons

This section aims to evaluate the KNN perturbed algorithm against other algorithms that have efficiently solved the SCP. For this, we select three algorithms. The first is the Binary Black Hole Algorithm (BBH) [66]. BBH uses a transfer function as a binarization method. In particular, the function used was $\frac{1}{1+e^{\frac{-x_i^d(t+1)}{3}}}$. The maximum number of iterations allowed for BBH was 4000 and the implementation was done in Java. The second algorithm [66], corresponds to a Binary Cuckoo Search algorithm (BCS). The BCS also uses transfer functions, $\frac{1}{1+e^{-x_i^d(t+1)}}$, as a method of binarization. The algorithm was developed in Java and the maximum number of iterations allowed was 4000. Finally, the last algorithm used in the comparison [2] executes the binarization through the concept of clustering. Through the db-scan clustering technique, the solutions are grouped to generate binarization. The algorithm was developed in Python and the maximum number of iterations was 800.

The results are shown in Table 3. When analyzing the best value indicator, we observed that KNN perturbed was superior in 15 of the 20 instances when compared to BBH. When contrasting with BCS, we see that KNN perturbed was superior in 11 instances and BCS in none. Finally, the comparison with db-scan-CS showed similar results. KNN perturbed outperformed db-scan-CS in 4 instances. The latter was superior in 1 instance. When comparing the final average between KNN perturbed and db-scan-CS, these are practically the same. The Wilcoxon test indicates that the difference is significant in the cases of BBH and BCS and is not significant for db-scan.

Table 3. Comparison between db-scan-CS, BBH, BCS, and KNN-perturbation algorithms.

Instance	Best Known	db-Scan-CS (Best)	BBH (Best)	BCS (Best)	KNN (Perturbed) (Best)	db-Scan-CS (Avg)	BBH (Avg)	BCS (Avg)	KNN (Perturbed) (Avg)	Time (s)
E.1	29	29	29	29	29	29.0	30.0	30.0	29.4	17.6
E.2	30	30	31	31	30	30.1	31.0	32.0	30.2	19.1
E.3	27	27	28	28	27	27.5	28.0	29.0	27.6	18.6
E.4	28	28	29	30	28	28.1	29.0	31.0	28.7	20.1
E.5	28	28	28	28	28	28.3	28.0	30.0	28.4	18.2
F.1	14	14	14	14	14	14.1	15.0	14.0	14.6	17.8
F.2	15	15	15	15	15	15.4	16.0	17.0	15.2	17.9
F.3	14	14	16	15	14	14.4	16.0	16.0	14.7	19.4
F.4	14	14	15	15	14	14.4	16.0	15.0	14.8	19.8
F.5	13	14	14	14	13	13.4	15.0	15.0	13.9	18.4
G.1	176	176	179	176	176	176.8	181.0	177.0	177.2	116.2
G.2	154	157	158	156	155	156.8	160.0	157.0	156.6	114.7
G.3	166	169	169	169	168	168.9	169.0	170.0	169.2	113.1
G.4	168	169	170	170	170	170.1	171.0	171.0	170.2	110.6
G.5	168	169	170	170	168	169.6	169.1	171.0	168.6	117.9
H.1	63	64	66	64	64	64.5	67.0	64.0	64.6	104.2
H.2	63	64	67	64	64	64.3	68.0	64.0	64.8	107.5
H.3	59	60	65	61	60	60.6	65.0	63.0	60.7	95.6
H.4	58	59	63	59	59	59.8	64.0	60.0	59.4	102.1
H.5	55	55	62	56	55	55.2	62.0	57.0	55.2	92.1
Average	67.1	67.8	69.4	68.2	67.6	68.1	70.0	69.2	68.2	63.05
Wilcoxon p-value		0.157	0.0005	0.0017		0.14	0.0001	0.0011

When analyzing the average indicator, we observe that the difference in favor of KNN perturbed with respect to BCS and BBH is maintained. In the case of BBH, KNN perturbed was higher in 18 instances and BHH in 2. The Wilcoxon test indicates that the difference is statistically significant. In the comparison with BCS, KNN perturbed was superior in 17 instances and BCS in 3. The Wilcoxon test also indicates that the difference is significant. In the comparison between db-scan-CS and KNN perturbed, the average indicator shows very similar results between them. Db-scan-CS obtains a better result in 15 instances and KNN perturbed in 5. However, due to the proximity of the results, the Wilcoxon test indicates that the difference is not statistically significant.

Additionally, we have incorporated Table 4 in order to develop a better understanding of the comparisons. In the Average Gap column of Table 4, the value corresponds to the average of the Gaps calculated for each instance. Subsequently, in the Gap ratio column, the gap ratio of each algorithm is calculated using KNN perturbation algorithm as a basis for comparison.

Table 4. GAP ratio respect to KNN-perturbation algorithm.

Problems	Algorithm	Avg Gap	Gap Ratio
E instances	db-scan-CS	0.2	0.43
	BBH	0.8	4.0
	BCS	2.0	10
	KNN-perturbation	0.46	1.00
F instances	db-scan-CS	0.4	0.625
	BBH	1.6	2.5
	BCS	1.4	2.19
	KNN-perturbation	0.64	1.00
G instances	db-scan-CS	2.04	1.04
	BBH	3.62	1.85
	BCS	2.8	1.43
	KNN-perturbation	1.96	1.00
H instances	db-scan-CS	1.28	0.96
	BBH	5.6	4.18
	BCS	2.0	1.50
	KNN-perturbation	1.34	1.00

We noted the following patterns.

• KNN perturbation in the 4 types of problems outperforms BBH and BCS. These techniques use transfer functions as a method of binarization, the same methods used by KNN perturbation.
• KNN perturbation outperforms db-scan-CS only on instance G. In all other instances, db-scan-CS performs better. db-scan-CS uses a binarization mechanism based on db-scan which adapts iteration to iteration. However, the difference is not statistically significant.

6. Conclusions

In this work, we have used the K-nearest neighborhood technique in a perturbation operator, in order to tackle combinatorial problems effectively. The cuckoo search algorithm was selected for the development of the experiments. Two random operators were designed in order to determine the contribution of the KNN perturbed operator in the optimization result. From the experiments, it was concluded that the KNN perturbed operator contributes to improving the quality and dispersion of the solutions, in addition to obtaining better convergences. Additionally, a comparison was made with other algorithms that have tackled the SCP efficiently. From the comparison, it is concluded that our proposal improves the results of the algorithms that use the same binarization mechanism (Transfer functions). In the comparison with algorithms that use db-scan clustering techniques as a binarization method, we observed that the results were very close to each other.

As lines of future work, we observe that there is an opportunity in the dynamic handling of metaheuristics parameters. Here, we intuit that the integration of dynamic programming techniques or reinforcement learning is a line that can contribute to improving the quality and convergence of the metaheuristics algorithms. Another interesting line is the use of machine learning techniques for the selection of algorithms or parameterizations of algorithms. Appealing to the no-free-launch-theorem, having a group of algorithms or algorithm parameterizations together with a selection method of these, based on the historical behavior of the different algorithms, could contribute to improving the quality of the solutions obtained.