Abstract
In this paper, we presented a modification of the extragradient method to solve pseudomonotone equilibrium problems involving the Lipschitz-type condition in a real Hilbert space. The method uses an inertial effect and a formula for stepsize evaluation, that is updated for each iteration based on some previous iterations. The key advantage of the algorithm is that it is achieved without previous knowledge of the Lipschitz-type constants and also without any line search procedure. A weak convergence theorem for the proposed method is well established by assuming mild cost bifunction conditions. Many numerical experiments are presented to explain the computational performance of the method and to equate them with others.
1. Introduction
An equilibrium problem (EP) consider various mathematical problems as a special case i.e., the variational inequality problems (VIP), the optimization problems, the fixed point problems, the complementarity problems, Nash equilibrium of non-cooperative games, the saddle point and the vector minimization problem (see [1,2,3] for more details). To the best of our knowledge the term “equilibrium problem” was initially established in 1992 by Muu and Oettli [2] and has been further developed by Blum and Oettli [1]. The problem of equilibrium is also considered as the Ky Fan inequality [4]. It is interesting and useful to develop new iterative schemes and study their convergence analysis. Many methods have been well-established to figure out the solution of an equilibrium problem (1) in finite and infinite-dimensional spaces. Some of these algorithms involve projection methods [5,6,7,8], the proximal point methods [9,10], the extragradient methods with or without line searches [11,12,13,14,15,16,17,18], the methods using the inertial effect [19,20,21,22] and other methods in [23,24,25,26,27,28].
The proximal point method (PPM) is one of the well-established methods to deal with equilibrium problems. Martinet [29] initially developed this strategy for the case of monotone variational inequality problems, and afterwards, they extended it to monotone operators by Rockafellar [30]. Moudafi [9] presented the proximal point method to solve monotone equilibrium. Konnov [31] also proposed another modification of the proximal point method, with weaker assumptions to deal with equilibrium problems involving monotone bifunction. Normally, the proximal point method applies to monotone equilibrium problems. Then, each regularized sub-problem converts into strongly monotone and accordingly its unique solution exists. Another well-known technique is the auxiliary problem principle, i.e., formulate a new equivalent problem that is usually simpler and easier to figure out compared to the initial problem. This idea was originally initiated by Cohen [32] for solving optimization problems and thereafter applied to variational inequality problems [33]. In addition, Mastroeni [34] extended the auxiliary problem principle to solve equilibrium problems involving a strongly monotone bifunction.
Next, we consider a well-known two-step extragradient method [35]. Tran et al. [36] and Flam et al. [10] used the auxiliary problem principle and extend the extragradient method in [35] for monotone equilibriums problems. The first drawback of the extragradient method is to compute two projections on the feasible set C to achieve the next iteration. So, in the case, when the computation of a projection on a constraint set C is difficult to compute, then it is hard to solve two minimal distance problems. A fact that could affect the performance and applicability of the method. To overcome this situation, Censor et al. introduced a subgradient extragradient method [37] wherein the second projection in the extragradient method is replaced by a specific half-plane projection that can be computed easily and efficiently. An iterative sequence developed due to extragradient-like methods essentially needs a stepsize that depends upon the Lipschitz-type constants of a cost bifunction. The prior information of such constants imposes some restrictions on implementing these methods because these Lipschitz-type constants are normally not known or hard to compute.
In this paper, we are introducing a new algorithm to solve the pseudomonotone equilibrium problem (1) incorporating the Lipschitz-type condition (2) on a bifunction in a real Hilbert space. The algorithm can be viewed as a combination of Algorithm 1 in [16] with inertial effects. The stepsize used in the proposed scheme is not fixed but updated on the basis of the previous iterations using an explicit formula. Under certain mild conditions, a weak convergence theorem is established which ensures that the sequence of iterations converges towards a solution to the problem of equilibrium. We are also examine the computational performance of the new method on various test problems in comparison to Algorithm 1 in [16].
The rest of this paper is arranged in the following way: in Section 2, we provide some definitions and necessary results that will be needed throughout this article. Section 3 contains our algorithm and the weak convergence theorem. Section 4 sets out the numerical experiments to show the computational performance of our proposed method on different test problems.
2. Preliminaries
We use C to be a closed, convex subset of the real Hilbert space The notion and denote the inner product and induced norm on the Hilbert space, respectively. The notion is the solution set of an equilibrium problem over C and q represent any arbitrary element of
Definition 1 ([1]). Let C be a nonempty, close and convex subset of and be a bifunction such that for all The equilibrium problem for the bifunction f on C is formulated as follows:
Definition 2 ([38]). The metric projection of x onto a closed, convex subset C of is defined as follows:
Now, we recall classical concepts of monotonicity of nonlinear operators (see [39,40]).
Definition 3.
An operator is said to be
- (1)
- strongly monotone on C if
- (2)
- monotone on C if
- (3)
- strongly pseudomonotone on C if
- (4)
- pseudomonotone on C if
- (5)
- L-Lipschitz continuous on C if there exists a constant such that
Now, we consider different notions of the bifunction monotonicity (see [1,41]).
Definition 4.
A bifunction on C for is said to be
- (1)
- strongly monotone if
- (2)
- monotone if
- (3)
- strongly pseudomonotone if
- (4)
- pseudomonotone if
Remark 1.
It is clear to see that the following consequences are as follows:
Let a bifunction satisfy the Lipschitz-type condition [34] on C if there are such that
The normal cone of C at is defined by
Let is a convex function and subdifferential of g at is defined as follows:
Lemma 1 ( [42]). Let be a convex, sub-differentiable and lower semi-continuous function on where C to be a nonempty, convex and closed subset of a Hilbert space An element is said to be a minimizer of a function g if and only if while and are serve as the sub-differential of g on x and the normal cone of C at x, respectively.
Lemma 2 ([43]). For every and , then the following relation is true:
Lemma 3 ([44]). Let , and be sequences in such that
and also with such that for all Then the following relations are hold.
- (i)
- with
- (ii)
Lemma 4 ([45]). Let be a sequence in and such that the following conditions hold.
- (i)
- For each exists;
- (ii)
- All sequentially weak cluster point of lies in C.
Then, weakly converges to a point in
3. Main Results
In this section, we present an inertial method to solve pseudomonotone equilibrium problem involving the Lipschitz-type bifunction condition. The detailed method is described below.
Assumption 1.
Let a bifunction satisfy the following conditions:
- (A1)
- and also f is pseudomonotone on C;
- (A2)
- f satisfies the Lipschitz-type condition on through positive constants and ;
- (A3)
- for every and satisfying ;
- (A4)
- needs to be convex and subdifferentiable on C for each fixed
Remark 2.
It is noted that represent a half-space and From value of we have
By using Lemma 1, we obtain
Thus, there exists and such that
Thus, we have
Since then for all Therefore, we have
The above implies that
This shows that for every
Lemma 5.
If in Algorithm 1 then
| Algorithm 1 Inertial Explicit Extragradient Algorithm for Pseudomonotone EP |
|
Proof.
By definition of and Lemma 1, we have
Thus, there exists and such that
Thus, we have
Given that and implies that
Due to and using subdifferential definition, we obtain
By and condition (A1) implies that for all . □
Lemma 6.
Let is a bifunction satisfying the conditions(A1)-(A4). Let we have
Proof.
By value of and using Lemma 1, we have
Thus, for there exists such that
Therefore, we have
Since then for all This implies that
Due to we have
By substituting in (8), we get
Since then and it implies that due to pseudomonotonicity of a bifunction Thus, from (9) we get
From the definition of we get
which after multiplying both sides by , gives that
Since and by the definition of we have
Thus, above implies that
Due to and with definition of subdifferential, we have
Substituting in expression (13), we have
We have the following facts:
From the above two facts and expression (16), we obtain
□
Theorem 1.
Let sequences and generated by Algorithm 1 are converges weakly to the solution q of the problem (EP) where
Proof.
From Lemma 6, we have
From the definition of and using Lemma 2, we obtain
Due to the definition of we have which is used to obtain the last inequality. From the value of we obtain
By the definition of and using Cauchy inequality, we get
Next, we substitute
We have compute
Next, we need to compute
Since from our hypothesis, we have
Since then there exist such that
Thus, expression (27) implies that
The sequence is nonincreasing for . From definition of we have
From we have
The expression (31) implies that for we have
By letting in (34) implies that This implies that
Moreover, by Lemma 3 with expression (23) and implies that
We also have
Next, need to show that Using Lemma 6 for we have
Further, it implies that
The above discussion implies that the sequences , and are bounded and for every and the limit of and exists. Next, we determining that the set of all sequentially weak limit point of the sequence belongs to To confirm this, consider element z to be sequentially weak limit point of the sequence which yields a subsequence of that weakly converge to Thus, the sequence also converges weakly to due to Next, the remaining part is to prove that element z belongs to the solution set By (8), the definition of and (15), we have
where y is an any element in It follows from expressions (36), (40), (42) and the boundedness of that the right-hand side of the last inequality tends to zero. Using condition (A3) and we have
Since and implies This shows that Thus Lemma 4, provides that and weakly converge to q as ☐
Note:
Let consider the cost bifunction in the following way
where is an operator. Then, the problem (1) is translated into the variational inequality problem and the value of Lipschitz constant is From the value of in the Algorithm 1 and expression (44), we have
The value of translate into
Let consider that F meets the following conditions:
- (F1)
- F satisfy the following condition on C for some positive constant
- (F2)
- The solution set and F is pseudomonotone operator on C;
- (F3)
- for every and satisfying
Corollary 1.
Suppose that follows the requirement(F1)-(F3). Assume and are the sequences formed in the following way:
- (i)
- Choose and nondecreasing sequence Set
- (ii)
- Let and are known for Computewhere and
- (iii)
- Moreover, assume thatand revise the stepsize as follows:
Then, the sequence and converge weakly to the solution q of
4. Numerical Experiments
For numerical experiments, we analyzed four examples by allowing different dimensions to see the effectiveness of our proposed method. We used the Matlab Quadprog program (https://www.mathworks.com/help/optim/ug/quadprog.html) to solve optimization problems and computed on a (Matlab R2018b) PC Intel(R) Core(TM)i5-6200 CPU @ 2.30GHz 2.40GHz, RAM 8.00 GB.
Example 1.
Assume that there have been n companies that manufacture the same commodities and this model taken as extension of the Nash-Cournot Oligopolistic equilibrium model [36]. Let x correspond to a vector in which every element indicates the amount of the commodity generated by the company i. So, in this case the price function P has been taken the form as where and is the sum of total commodity generated by all companies. The profit function for each firm i is defined by where is the value of tax and fee for producing Suppose that is the set of strategies belongs to each firm i and the strategy scheme for the whole model take the form as In particular, each organization desires to attain its optimum return by considering that the resulting amount of production is an input parameter and is dependent on the engagement of all the other parties. The methodology frequently managed to work on this type of model primarily concentrates on the well-known Nash equilibrium principle. A point is an equilibrium point of the above-discussed model if
while the vector represent the vector get from by taking with Finally, we take with and the problem of finding the Nash equilibrium point of the model can be taken as follows:
It follows from [36,46], the bifunction could be taken in the following form
while is defined as
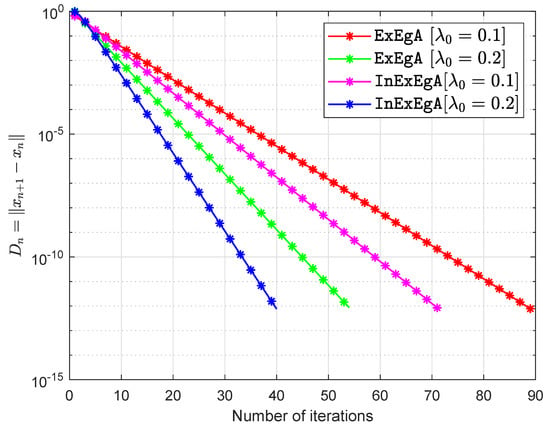
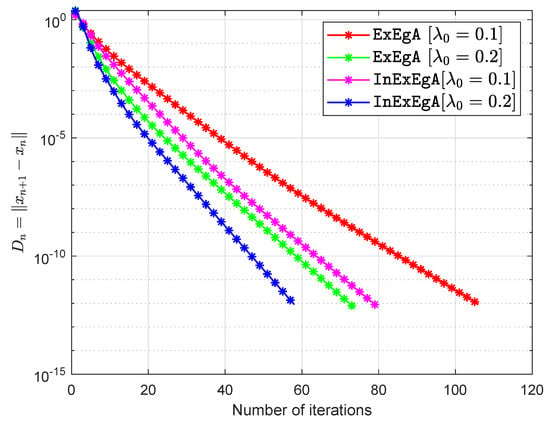
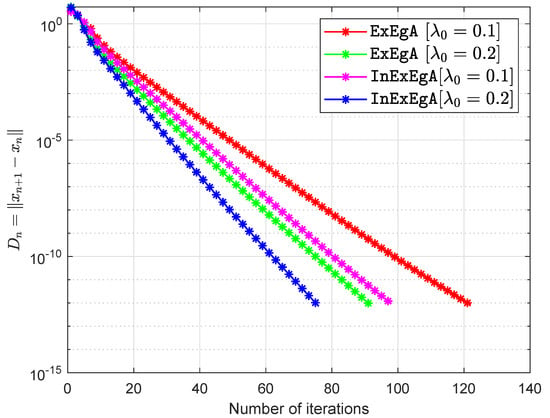
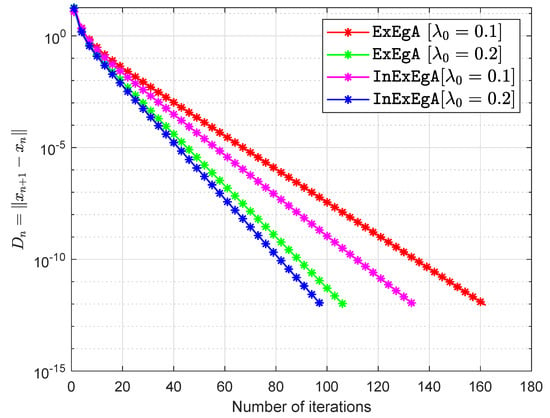
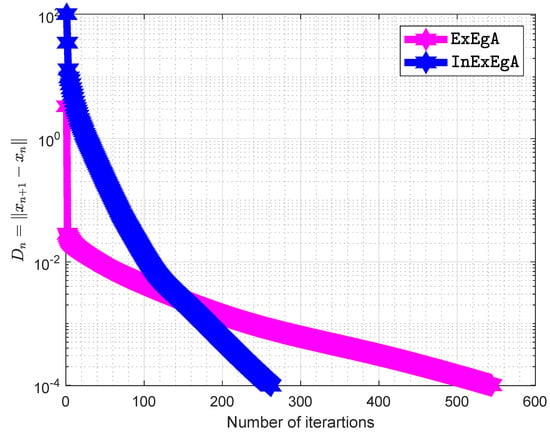
The matrices are being taken arbitrary (Choosing two diagonal matrices randomly and with entries from and respectively. Two random orthogonal matrices and are able to generate a positive semidefinite matrix and negative semidefinite matrix Finally, set and ) and vector q entries taken from interval (for more details see [36,47]). The starting points are and with . Figure 1, Figure 2, Figure 3 and Figure 4 and Table 1 demonstrates the numerical performance of Algorithm 1 (InExEgA) comparison with Algorithm 1 (ExEgA) in [16] relative to number of iterations.

Figure 1.
Algorithm 1 comparison with Algorithm 1 in [16] in term of iterations when

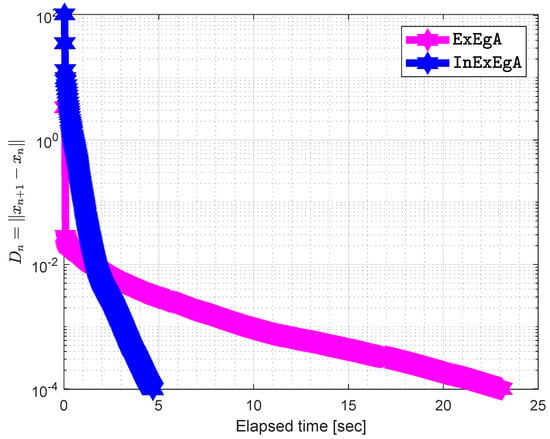
Figure 2.
Algorithm 1 comparison with Algorithm 1 in [16] in term of iterations when

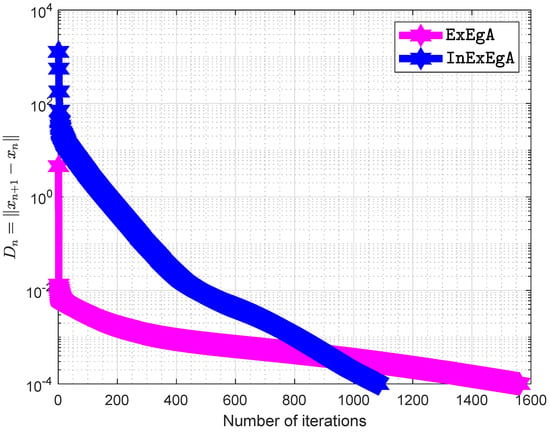
Figure 3.
Algorithm 1 comparison with Algorithm 1 in [16] in term of iterations when

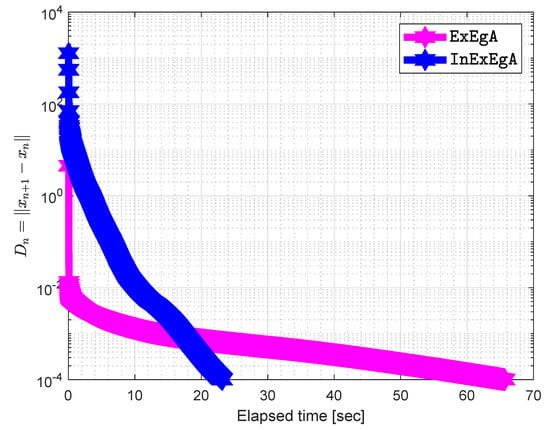
Figure 4.
Algorithm 1 comparison with Algorithm 1 in [16] in term of iterations when
Example 2.
Consider the following problem of fractional programming as in [48]:
subject to where and
It is easy to verify that Q is symmetric and positive definite in and consequently g is pseudoconvex on C. We minimize g over by using both algorithms with bifunction on to with unknown Lipschitz constants where
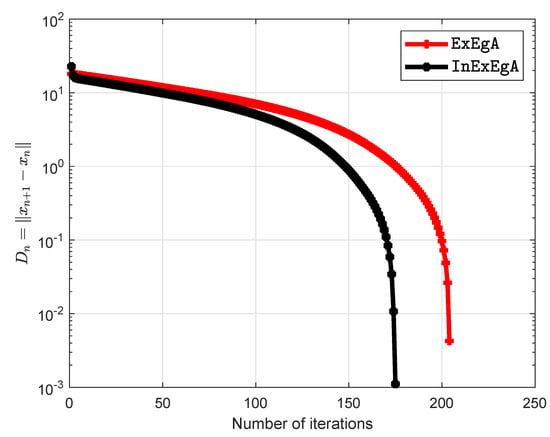
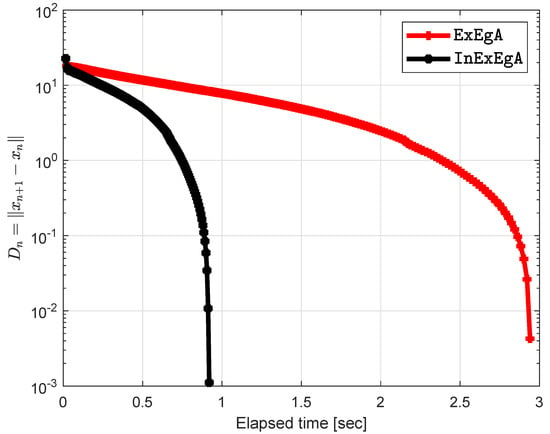
This problem has a unique solution Choose initial points are and . Figure 5 and Figure 6 demonstrates the numerical performance of Algorithm 1 (InExEgA) comparison with Algorithm 1 (ExEgA) in [16] in term of number of iterations and elapsed time respectively.

Figure 5.
Algorithm 1 comparison with Algorithm 1 in [16] and number of iterations are 204 and 175 respectively.

Figure 6.
Algorithm 1 comparison with Algorithm 1 in [16] and elapsed time in seconds are 2.9404 and 0.9194 respectively.
Example 3.
Let the bifunction f define on the convex set C as
where B is an matrix, S is an skew-symmetric matrix, D is an diagonal matrix, whose diagonal entries are nonnegative. The feasible set is closed and convex and defined as
while A is an matrix and b is a nonnegative vector. It is clear that bifunction f is monotone and its Lipschitz-type constants are The initial points are and with . Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 and Table 2 demonstrates the numerical performance of Algorithm 1 comparison with Algorithm 1 in [16] in term of number of iterations and elapsed time in seconds.

Figure 7.
Algorithm 1 comparison with Algorithm 1 in [16] when

Figure 8.
Algorithm 1 comparison with Algorithm 1 in [16] when

Figure 9.
Algorithm 1 comparison with Algorithm 1 in [16] when

Figure 10.
Algorithm 1 comparison with Algorithm 1 in [16] when

Figure 11.
Algorithm 1 comparison with Algorithm 1 in [16] when

Figure 12.
Algorithm 1 comparison with Algorithm 1 in [16] when
Example 4.
Consider a bifunction defined by
with unknown Lipschitz constants and and
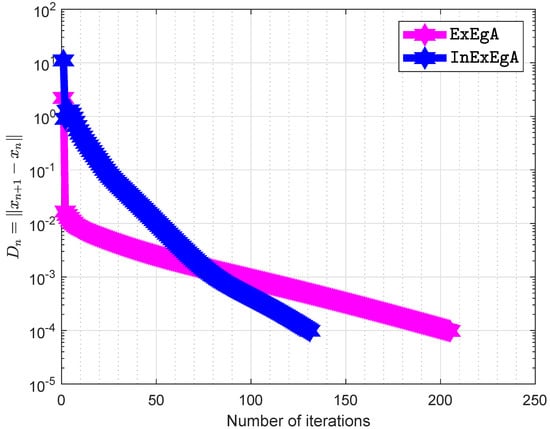
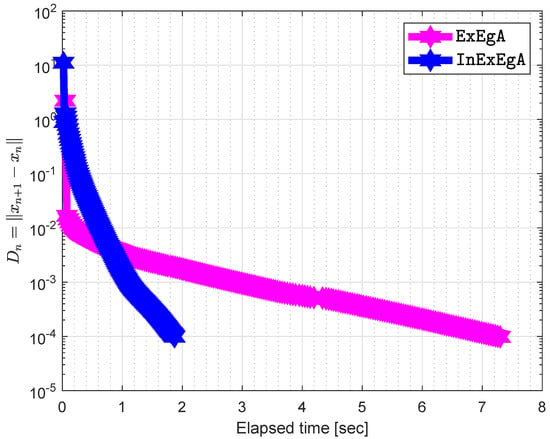
The initial values are and with . Figure 13 and Figure 14 demonstrates the numerical performance of Algorithm 1 comparison with Algorithm 1 in [16].

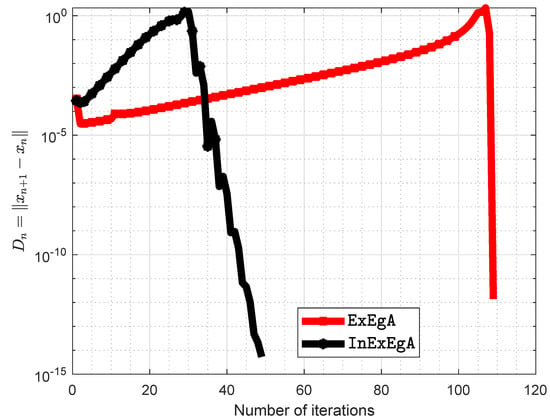
Figure 13.
Algorithm 1 comparison with Algorithm 1 in [16] and number of iterations are 108 and 49 respectively.

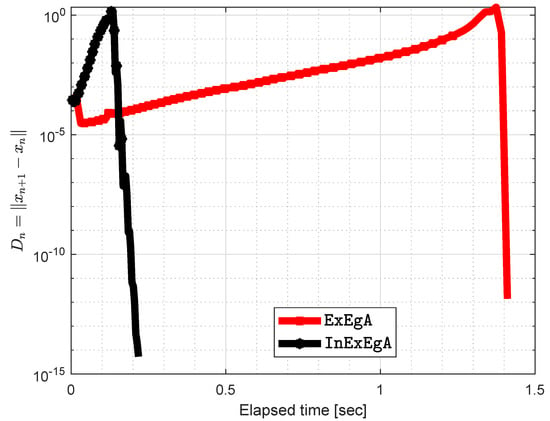
Figure 14.
Algorithm 1 comparison with Algorithm 1 in [16] and elapsed time in seconds are 1.3294 and 0.1701 respectively.
5. Conclusions
The paper proposed an inertial extragradient-like approach to addressing the problem of equilibrium of a pseudomonotone bifunction with a Lipschitz-like condition. A stepsize rule has been presented that does not depend on the Lipschitz-type constant information. Several experimental studies have been reported to demonstrate the numerical behavior of our method and compare it with other methods. Such numerical experiments indicate that inertial influences normally extend the performance of iterative sequences in this sense.
Author Contributions
Conceptualization, P.Y., H.u.R. and P.K.; Methodology, P.Y., H.u.R., P.K. and A.H.I.; Investigation, H.u.R., P.K. and A.H.I.; Writing–original draft preparation, P.Y., H.u.R., P.K. and A.H.I.; Writing–review and editing, P.Y., H.u.R. and P.K.; Visualization, P.Y., P.K. and A.H.I.; Software, H.u.R, P.K. and A.H.I.; Supervision, P.K.; Funding Acquisition, P.K. All authors have read and agree to the published version of the manuscript.
Funding
This project was supported by Center of Excellence in Theoretical and Computational Science (TaCS-CoE), Faculty of Science, KMUTT. The first author was financially supported by the Research Professional Development Project Under the scholarship of Rajabhat Rajanagarindra University (RRU). The third and the fourth authors were supported by “the Petchra Pra Jom Klao Ph.D. Research Scholarship” from King Mongkut’s University of Technology Thonburi Grant Nos. 16/2561 and 16/2018, respectively).
Acknowledgments
The author has received support from ”Petchra Pra Jom Klao Ph.D. Research Scholarship from King Mongkut’s University of Technology Thonburi”. We are very grateful to the editor and the anonymous referees for their valuable and useful comments, which helps in improving the quality of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Blum, E. From optimization and variational inequalities to equilibrium problems. Math. Student 1994, 63, 123–145. [Google Scholar]
- Muu, L.D.; Oettli, W. Convergence of an adaptive penalty scheme for finding constrained equilibria. Nonlinear Anal. Theory Methods Appl. 1992, 18, 1159–1166. [Google Scholar] [CrossRef]
- Facchinei, F.; Pang, J.S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Fan, K. A Minimax Inequality and Applications, Inequalities III; Shisha, O., Ed.; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Hieu, D.V. Projected subgradient algorithms on systems of equilibrium problems. Optim. Lett. 2017, 12, 551–566. [Google Scholar] [CrossRef]
- Scheimberg, S.; Santos, P. A relaxed projection method for finite-dimensional equilibrium problems. Optimization 2011, 60, 1193–1208. [Google Scholar] [CrossRef]
- Muu, L.D.; Quoc, T.D. Regularization Algorithms for Solving Monotone Ky Fan Inequalities with Application to a Nash-Cournot Equilibrium Model. J. Optim. Theory Appl. 2009, 142, 185–204. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Argyros, I.K.; Deebani, W.; Kumam, W. Inertial Extra-Gradient Method for Solving a Family of Strongly Pseudomonotone Equilibrium Problems in Real Hilbert Spaces with Application in Variational Inequality Problem. Symmetry 2020, 12, 503. [Google Scholar] [CrossRef]
- Moudafi, A. Proximal point algorithm extended to equilibrium problems. J. Nat. Geometry 1999, 15, 91–100. [Google Scholar]
- Flåm, S.D.; Antipin, A.S. Equilibrium programming using proximal-like algorithms. Math. Progr. 1996, 78, 29–41. [Google Scholar] [CrossRef]
- Quoc, T.D.; Anh, P.N.; Muu, L.D. Dual extragradient algorithms extended to equilibrium problems. J. Glob. Optim. 2011, 52, 139–159. [Google Scholar] [CrossRef]
- Lyashko, S.I.; Semenov, V.V. A New Two-Step Proximal Algorithm of Solving the Problem of Equilibrium Programming. In Optimization and Its Applications in Control and Data Sciences; Springer International Publishing: Berlin, Germany, 2016; pp. 315–325. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Cho, Y.J.; Yordsorn, P. Weak convergence of explicit extragradient algorithms for solving equilibirum problems. J. Inequalities Appl. 2019, 2019. [Google Scholar] [CrossRef]
- Anh, P.N.; Hai, T.N.; Tuan, P.M. On ergodic algorithms for equilibrium problems. J. Glob. Optim. 2015, 64, 179–195. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Argyros, I.K.; Shutaywi, M.; Shah, Z. Optimization Based Methods for Solving the Equilibrium Problems with Applications in Variational Inequality Problems and Solution of Nash Equilibrium Models. Mathematics 2020, 8, 822. [Google Scholar] [CrossRef]
- Hieu, D.V.; Quy, P.K.; Vy, L.V. Explicit iterative algorithms for solving equilibrium problems. Calcolo 2019, 56. [Google Scholar] [CrossRef]
- Hieu, D.V. New extragradient method for a class of equilibrium problems in Hilbert spaces. Appl. Anal. 2017, 97, 811–824. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Je Cho, Y.; Suleiman, Y.I.; Kumam, W. Modified Popov’s explicit iterative algorithms for solving pseudomonotone equilibrium problems. Optim. Methods Softw. 2020, 1–32. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Abubakar, A.B.; Cho, Y.J. The extragradient algorithm with inertial effects extended to equilibrium problems. Comput. Appl. Math. 2020, 39. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Kumam, W.; Shutaywi, M.; Jirakitpuwapat, W. The Inertial Sub-Gradient Extra-Gradient Method for a Class of Pseudo-Monotone Equilibrium Problems. Symmetry 2020, 12, 463. [Google Scholar] [CrossRef]
- Hieu, D.V. Convergence analysis of a new algorithm for strongly pseudomontone equilibrium problems. Numer. Algorithms 2017, 77, 983–1001. [Google Scholar] [CrossRef]
- Hieu, D.V.; Strodiot, J.J. Strong convergence theorems for equilibrium problems and fixed point problems in Banach spaces. J. Fixed Point Theory Appl. 2018, 20. [Google Scholar] [CrossRef]
- ur Rehman, H.; Kumam, P.; Argyros, I.K.; Alreshidi, N.A.; Kumam, W.; Jirakitpuwapat, W. A Self-Adaptive Extra-Gradient Methods for a Family of Pseudomonotone Equilibrium Programming with Application in Different Classes of Variational Inequality Problems. Symmetry 2020, 12, 523. [Google Scholar] [CrossRef]
- Hieu, D.V.; Gibali, A. Strong convergence of inertial algorithms for solving equilibrium problems. Optim. Lett. 2019. [Google Scholar] [CrossRef]
- Abubakar, J.; Kumam, P.; ur Rehman, H.; Ibrahim, A.H. Inertial Iterative Schemes with Variable Step Sizes for Variational Inequality Problem Involving Pseudomonotone Operator. Mathematics 2020, 8, 609. [Google Scholar] [CrossRef]
- Abubakar, J.; Sombut, K.; ur Rehman, H.; Ibrahim, A.H. An Accelerated Subgradient Extragradient Algorithm for Strongly Pseudomonotone Variational Inequality Problems. Thai J. Math. 2019, 18, 166–187. [Google Scholar]
- ur Rehman, H.; Kumam, P.; Shutaywi, M.; Alreshidi, N.A.; Kumam, W. Inertial Optimization Based Two-Step Methods for Solving Equilibrium Problems with Applications in Variational Inequality Problems and Growth Control Equilibrium Models. Energies 2020, 13, 3292. [Google Scholar] [CrossRef]
- Iusem, A.N.; Sosa, W. On the proximal point method for equilibrium problems in Hilbert spaces. Optimization 2010, 59, 1259–1274. [Google Scholar] [CrossRef]
- Martinet, B. Brève communication. Régularisation d’inéquations variationnelles par approximations successives. Revue Française D’inf. Rech. Opérationnelle. Série Rouge 1970, 4, 154–158. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 1976, 14, 877–898. [Google Scholar] [CrossRef]
- Konnov, I. Application of the Proximal Point Method to Nonmonotone Equilibrium Problems. J. Optim. Theory Appl. 2003, 119, 317–333. [Google Scholar] [CrossRef]
- Cohen, G. Auxiliary problem principle and decomposition of optimization problems. J. Optim. Theory Appl. 1980, 32, 277–305. [Google Scholar] [CrossRef]
- Cohen, G. Auxiliary problem principle extended to variational inequalities. J. Optim. Theory Appl. 1988, 59, 325–333. [Google Scholar] [CrossRef]
- Mastroeni, G. On Auxiliary Principle for Equilibrium Problems. In Nonconvex Optimization and Its Applications; Springer: Berlin, Germany, 2003; pp. 289–298. [Google Scholar] [CrossRef]
- Korpelevich, G. The extragradient method for finding saddle points and other problems. Matecon 1976, 12, 747–756. [Google Scholar]
- Quoc Tran, D.; Le Dung, M.N.V.H. Extragradient algorithms extended to equilibrium problems. Optimization 2008, 57, 749–776. [Google Scholar] [CrossRef]
- Censor, Y.; Gibali, A.; Reich, S. The Subgradient Extragradient Method for Solving Variational Inequalities in Hilbert Space. J. Optim. Theory Appl. 2010, 148, 318–335. [Google Scholar] [CrossRef] [PubMed]
- Goebel, K.; Reich, S. Uniform convexity, Hyperbolic Geometry, and Nonexpansive Mappings. 1984. Available online: https://www.researchgate.net/publication/248772020_Uniform_Convexity_Hyperbolic_Geometry_and_Nonexpansive_Mappings (accessed on 10 June 2020).
- Minty, G.J. Monotone (nonlinear) operators in Hilbert space. Duke Math. J. 1962, 29, 341–346. [Google Scholar] [CrossRef]
- Karamardian, S.; Schaible, S. Seven kinds of monotone maps. J. Optim. Theory Appl. 1990, 66, 37–46. [Google Scholar] [CrossRef]
- Bianchi, M.; Schaible, S. Generalized monotone bifunctions and equilibrium problems. J. Optim. Theory Appl. 1996, 90, 31–43. [Google Scholar] [CrossRef]
- Tiel, J.V. Convex Analysis: An Introductory Text, 1st ed.; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Heinz, H.; Bauschke, P.L.C.A. Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd ed.; CMS Books in Mathematics; Springer: Berlin, Germany, 2017. [Google Scholar]
- Attouch, F.A.H. An Inertial Proximal Method for Maximal Monotone Operators via Discretization of a Nonlinear Oscillator with Damping. Set-Valued Var. Anal. 2001, 9, 3–11. [Google Scholar] [CrossRef]
- Opial, Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Amer. Math. Soc. 1967, 73, 591–598. [Google Scholar] [CrossRef]
- Hieu, D.V. Parallel extragradient-proximal methods for split equilibrium problems. Math. Modell. Anal. 2016, 21, 478–501. [Google Scholar] [CrossRef]
- ur Rehman, H.; Pakkaranang, N.; Hussain, A.; Wairojjana, N. A modified extra-gradient method for a family of strongly pseudomonotone equilibrium problems in real Hilbert spaces. J. Math. Comput. Sci. 2020, 22, 38–48. [Google Scholar] [CrossRef]
- Hu, X.; Wang, J. Solving Pseudomonotone Variational Inequalities and Pseudoconvex Optimization Problems Using the Projection Neural Network. IEEE Trans. Neural Netw. 2006, 17, 1487–1499. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
