An Accelerated Diagonally Structured CG Algorithm for Nonlinear Least Squares and Inverse Kinematics
Abstract
1. Introduction
- This work proposes a novel SCG method that incorporates a structured diagonal approximation of the second-order term of the Hessian, combined with an acceleration scheme.
- The resulting search directions are proven to satisfy the sufficient descent condition.
- The proposed method is shown to have global convergence properties, relying on a strong Wolfe line search strategy and mild assumptions.
- Numerical experiments are conducted on a broad scale to evaluate the performance of the proposed method against existing methods.
- To illustrate its practical use, the SCG algorithm is implemented to solve the inverse kinematics of a robotic problem with 4DOF.
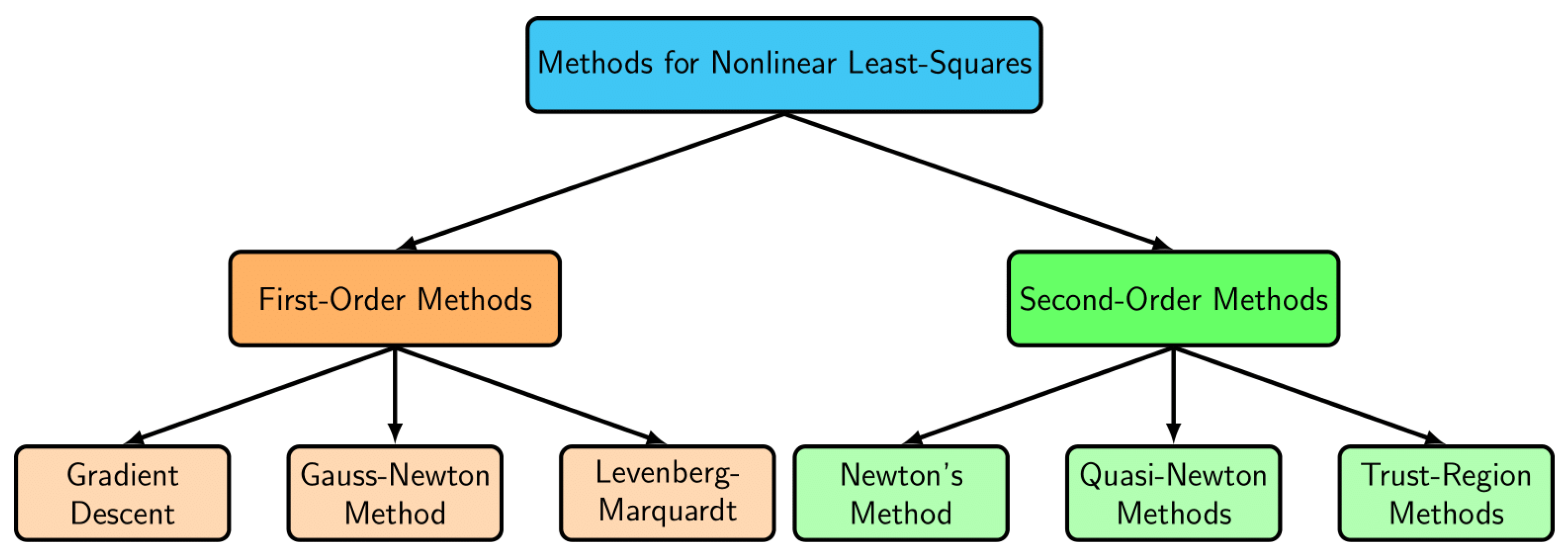
2. Formulation of the Diagonally Structured Conjugate Gradient with Acceleration Scheme
2.1. The Diagonally Structured CG Coefficient
2.2. The Acceleration Scheme
3. Global Convergence Analysis
| Algorithm 1: Diagonally Structured Conjugate Gradient with Acceleration (DSCGA) |
Step 1: Select the starting point from the domain of f. Set and . Scalars , and . Compute , , and . Step 2: If , stop; otherwise, proceed to Step 3. Step 4: Calculate , , and . Step 5: Evaluate and rescale the search direction . Update , where . Else set . Step 6: Compute and with and . Form , with Step 7: Compute using Equation (14). Step 8: Evaluate Step 9: Update and return to Step 2. |
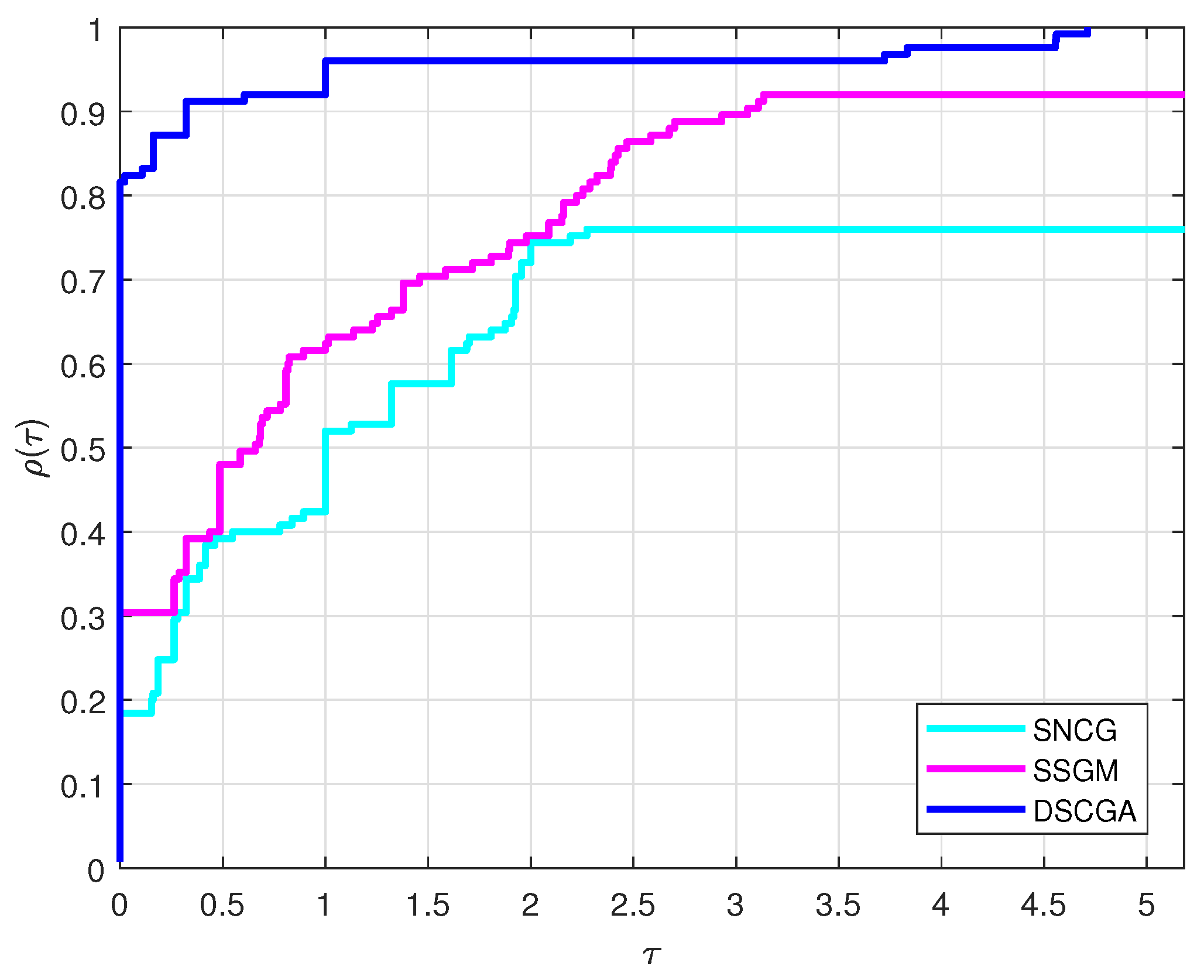
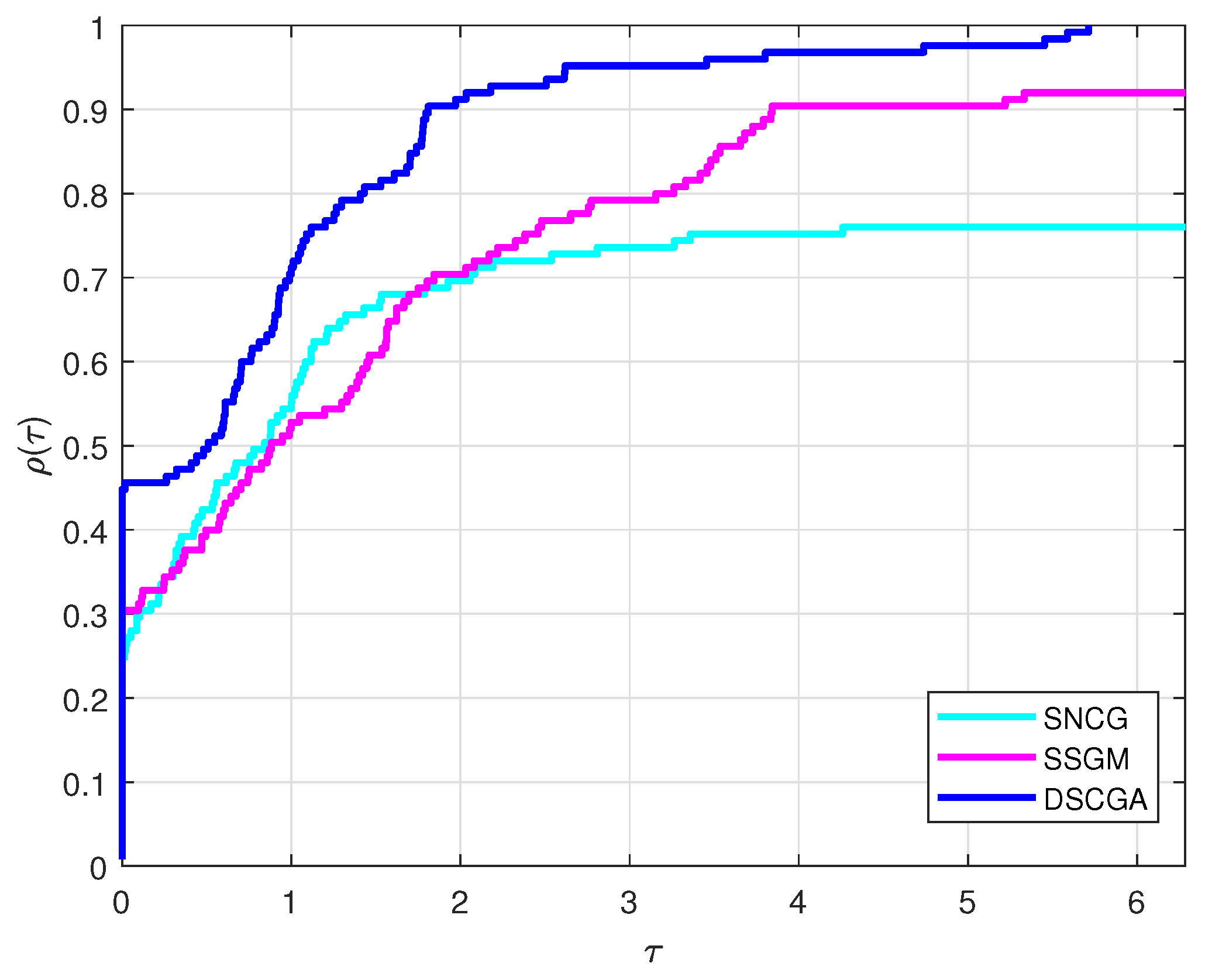
4. Numerical Results
- The algorithm ran for over 1000 iterations.
- More than 5000 evaluations of the function were performed.
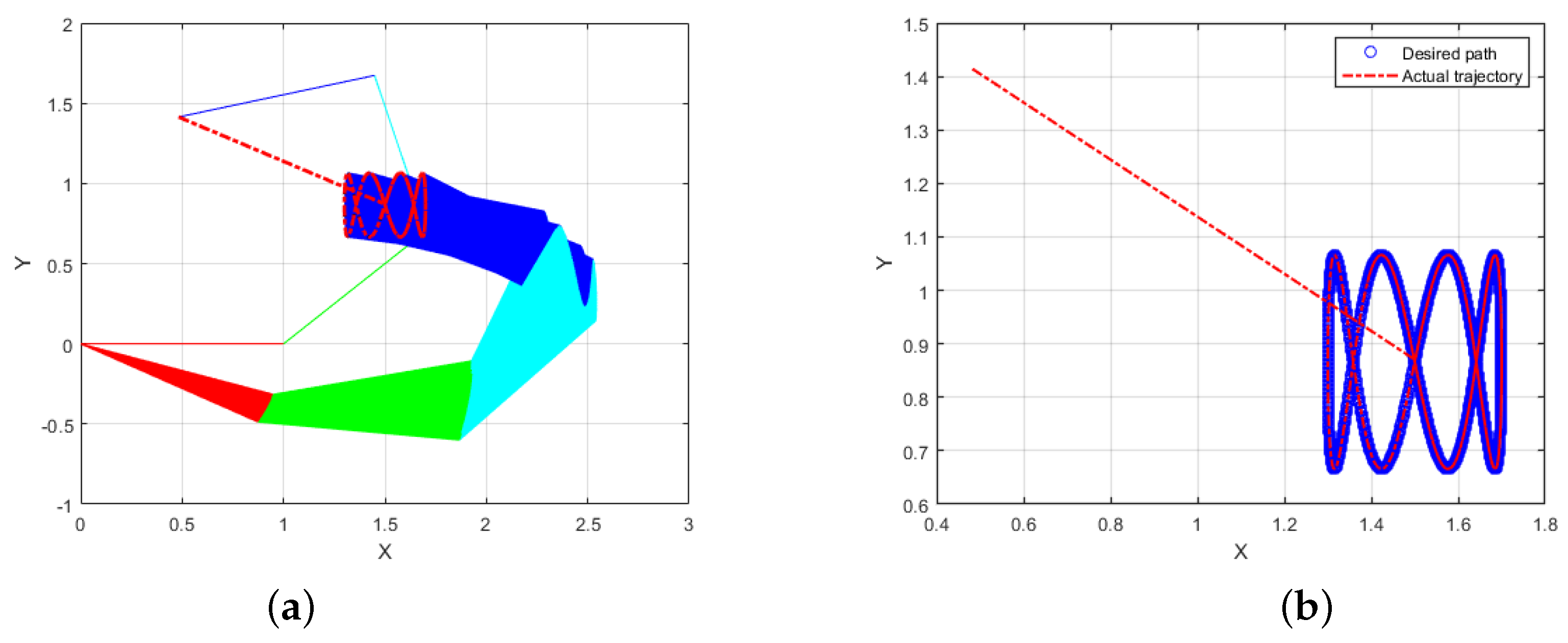
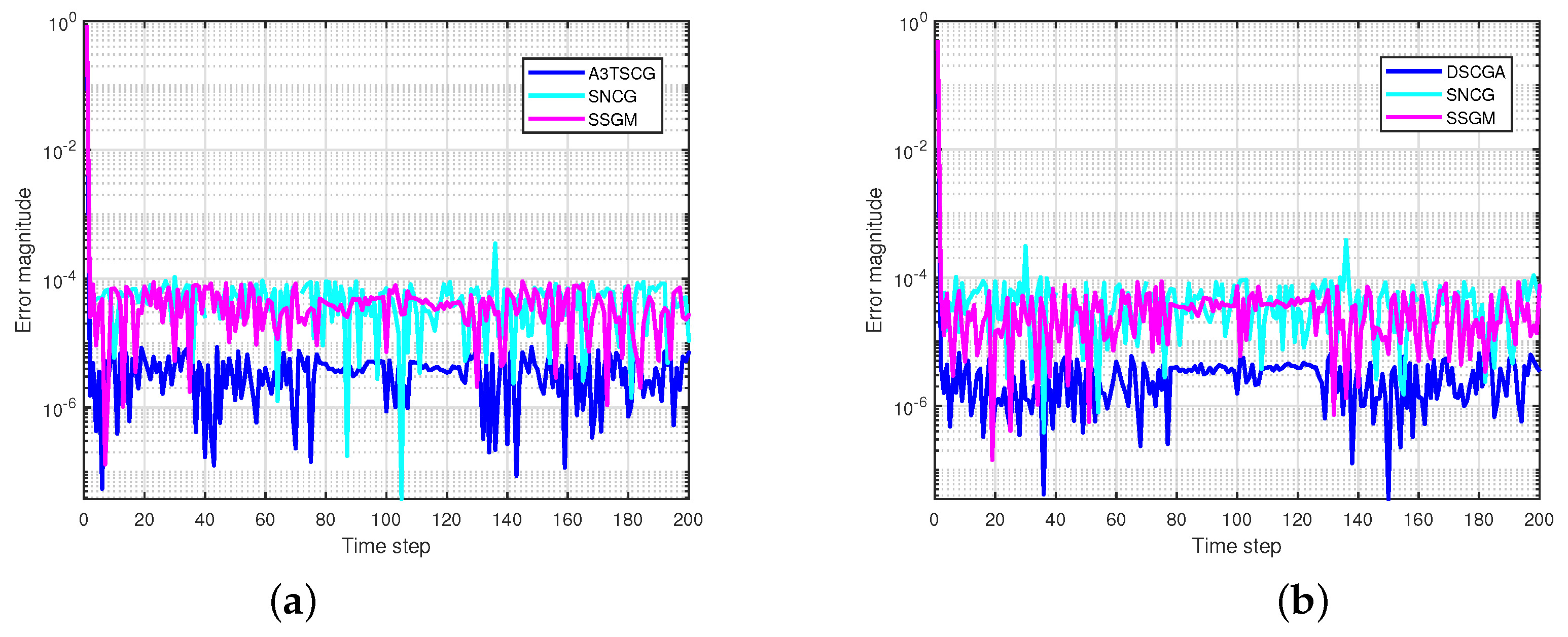
5. Applications in Inverse Kinematics
- The initial joint angular vector is at the starting time .
- The length of the links is represented by , where .
- The task should take seconds in total.
| Algorithm 2: Solution of the 4DOF Model Using the DSCGA Method |
Step 1: Inputs: , , , g, and Step 2: For to , repeat ; Step 3: Compute ; Step 4: Calculate using the DSCGA , as detailed in Algorithm 1; Step 5: Set ; Step 6: Return: |
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NLS | Nonlinear least squares |
| CG | Conjugate gradient |
| SCG | Structured conjugate gradient |
| DSCGA | Diagonally structured conjugate gradient with acceleration |
| SQN | Structured Quasi-Newton |
| 4DOF | Four degrees of freedom |
| SD | Steepest descent |
| GN | Gauss–Newton |
| LM | Levenberg–Marquard |
| NM | Newton’s method |
| QN | Quasi-Newton |
| TR | Trust-region |
| HS | Hestenes–Stiefel |
| PRP | Polak–Ribiere–Polyak |
| LS | Liu–Storey |
| BB | Barzilai–Borwein |
| SNCG | Scaled conjugate gradient |
| SSGM | Structured spectral gradient method |
References
- Yunus, R.B.; El-Saeed, A.R.; Zainuddin, N.; Daud, H. A structured RMIL conjugate gradient-based strategy for nonlinear least squares with applications in image restoration problems. AIMS Math. 2025, 10, 14893–14916. [Google Scholar] [CrossRef]
- Yahaya, M.M.; Kumam, P.; Awwal, A.M.; Chaipunya, P.; Aji, S.; Salisu, S. A new generalized quasi-newton algorithm based on structured diagonal hessian approximation for solving nonlinear least-squares problems with application to 3dof planar robot arm manipulator. IEEE Access 2022, 10, 10816–10826. [Google Scholar] [CrossRef]
- Salihu, N.; Kumam, P.; Awwal, A.M.; Arzuka, I.; Seangwattana, T. A structured Fletcher-Revees spectral conjugate gradient method for unconstrained optimization with application in robotic model. In Operations Research Forum; Springer: Berlin/Heidelberg, Germany, 2023; Volume 4, p. 81. [Google Scholar]
- Henn, S. A Levenberg–Marquardt scheme for nonlinear image registration. BIT Numer. Math. 2003, 43, 743–759. [Google Scholar] [CrossRef]
- Chen, Z.; Shao, H.; Liu, P.; Li, G.; Rong, X. An efficient hybrid conjugate gradient method with an adaptive strategy and applications in image restoration problems. Appl. Numer. Math. 2024, 204, 362–379. [Google Scholar] [CrossRef]
- Diphofu, T.; Kaelo, P. A modified extended Fletcher–Reeves conjugate gradient method with an application in image restoration. Int. J. Comput. Math. 2025, 102, 830–845. [Google Scholar] [CrossRef]
- Wang, L.; Wu, H.; Luo, C.; Xie, Y. A novel preconditioned modified conjugate gradient method for vehicle–bridge moving force identification. In Structures; Elsevier: Amsterdam, The Netherlands, 2025; Volume 73, p. 108322. [Google Scholar]
- Ciaburro, G.; Iannace, G. Modeling acoustic metamaterials based on reused buttons using data fitting with neural network. J. Acoust. Soc. Am. 2021, 150, 51–63. [Google Scholar] [CrossRef]
- Yahaya, M.M.; Kumam, P.; Chaipunya, P.; Awwal, A.M.; Wang, L. On diagonally structured scheme for nonlinear least squares and data-fitting problems. RAIRO Oper. Res. 2024, 58, 2887–2905. [Google Scholar] [CrossRef]
- Passi, R.M. Use of nonlinear least squares in meteorological applications. J. Appl. Meteorol. (1962–1982) 1977, 16, 827–832. [Google Scholar] [CrossRef][Green Version]
- Omesa, A.U.; Ibrahim, S.M.; Yunus, R.B.; Moghrabi, I.A.; Waziri, M.Y.; Sambas, A. A brief survey of line search methods for optimization problems. Results Control Optim. 2025, 19, 100550. [Google Scholar] [CrossRef]
- Ibrahim, S.M.; Muhammad, L.; Yunus, R.B.; Waziri, M.Y.; Kamaruddin, S.b.A.; Sambas, A.; Zainuddin, N.; Jameel, A.F. The global convergence of some self-scaling conjugate gradient methods for monotone nonlinear equations with application to 3DOF arm robot model. PLoS ONE 2025, 20, e0317318. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, G. An accelerated descent CG algorithm with clustering the eigenvalues for large-scale nonconvex unconstrained optimization and its application in image restoration problems. J. Comput. Appl. Math. 2024, 437, 115454. [Google Scholar] [CrossRef]
- Liu, P.; Li, J.; Shao, H.; Shao, F.; Liu, M. An accelerated Dai–Yuan conjugate gradient projection method with the optimal choice. Eng. Optim. 2025, 1–29. [Google Scholar] [CrossRef]
- Wu, X.; Ye, X.; Han, D. A family of accelerated hybrid conjugate gradient method for unconstrained optimization and image restoration. J. Appl. Math. Comput. 2024, 70, 2677–2699. [Google Scholar] [CrossRef]
- Nosrati, M.; Amini, K. A new structured spectral conjugate gradient method for nonlinear least squares problems. Numer. Algorithms 2024, 97, 897–914. [Google Scholar] [CrossRef]
- Mo, Z.; Ouyang, C.; Pham, H.; Yuan, G. A stochastic recursive gradient algorithm with inertial extrapolation for non-convex problems and machine learning. Int. J. Mach. Learn. Cybern. 2025, 16, 4545–4559. [Google Scholar] [CrossRef]
- Mohammad, H.; Sulaiman, I.M.; Mamat, M. Two diagonal conjugate gradient like methods for unconstrained optimization. J. Ind. Manag. Optim. 2024, 20, 170–187. [Google Scholar] [CrossRef]
- Hestenes, M.; Stiefel, E. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Inst. Stand. Technol. 1952, 49, 409–435. [Google Scholar] [CrossRef]
- Polak, B.; Ribiere, G. Note on the convergence of conjugate direction methods. Math. Model. Numer. Anal. 1969, 16, 35–43. [Google Scholar]
- Polyak, B.T. The conjugate gradient method in extreme problems. USSR Comput. Math. Math. Phys. 1969, 9, 94–112. [Google Scholar] [CrossRef]
- Liu, Y.; Storey, C. Efficient generalized conjugate gradient algorithms, part 1: Theory. J. Optim. Theory Appl. 1991, 69, 129–137. [Google Scholar] [CrossRef]
- Hager, W.; Zhang, H. A survey of nonlinear conjugate gradient methods. Pac. J. Optim. 2006, 2, 35–58. [Google Scholar]
- Sun, W.; Yuan, Y.X. Optimization Theory and Methods: Nonlinear Programming; Springer Science: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Mohammad, H.; Waziri, M.Y.; Santos, S.A. A brief survey of methods for solving nonlinear least-squares problems. Numer. Algebra Control Optim. 2019, 9, 1–13. [Google Scholar] [CrossRef]
- Dennis, J.; Martinez, H.J.; Tapia, R.A. Convergence Theory for the Structured BFGS Secant Method with an Application to Nonlinear Least Squares. J. Optim. Theory Appl. 1989, 61, 161–178. [Google Scholar] [CrossRef]
- Kobayashi, M.; Narushima, Y.; Yabe, H. Nonlinear Conjugate Gradient Methods with Structured Secant Condition for Nonlinear Least Squares Problems. J. Comput. Appl. Math. 2010, 234, 375–397. [Google Scholar] [CrossRef]
- Hanke, M.; Nagy, J.G.; Vogel, C. Quasi-Newton approach to nonnegative image restorations. Linear Algebra Appl. 2000, 316, 223–236. [Google Scholar] [CrossRef][Green Version]
- Hochbruck, M.; Hönig, M. On the convergence of a regularizing Levenberg–Marquardt scheme for nonlinear ill-posed problems. Numer. Math. 2010, 115, 71–79. [Google Scholar] [CrossRef]
- Pes, F.; Rodriguez, G. A doubly relaxed minimal-norm Gauss–Newton method for underdetermined nonlinear least-squares problems. Appl. Numer. Math. 2022, 171, 233–248. [Google Scholar] [CrossRef]
- Huynh, D.Q.; Hwang, F.N. An accelerated structured quasi-Newton method with a diagonal second-order Hessian approximation for nonlinear least squares problems. J. Comput. Appl. Math. 2024, 442, 115718. [Google Scholar] [CrossRef]
- Mohammad, H.; Santos, S.A. A Structured Diagonal Hessian Approximation Method with Evaluation Complexity Analysis for Nonlinear Least Squares. Comput. Appl. Math. 2018, 37, 6619–6653. [Google Scholar] [CrossRef]
- Dehghani, R.; Mahdavi-Amiri, R. Scaled nonlinear conjugate gradient methods for nonlinear least squares problems. Numer. Algorithms 2018, 82, 1–20. [Google Scholar] [CrossRef]
- Yunus, R.B.; Zainuddin, N.; Daud, H.; Kannan, R.; Karim, S.A.A.; Yahaya, M.M. A Modified Structured Spectral HS Method for Nonlinear Least Squares Problems and Applications in Robot Arm Control. Mathematics 2023, 11, 3215. [Google Scholar] [CrossRef]
- Yahaya, M.M.; Kumam, P.; Chaipunya, P.; Seangwattana, T. Structured Adaptive Spectral-Based Algorithms for Nonlinear Least Squares Problems with Robotic Arm Modelling Applications. Comput. Appl. Math. 2023, 42, 320. [Google Scholar] [CrossRef]
- Yunus, R.B.; Zainuddin, N.; Daud, H.; Kannan, R.; Yahaya, M.M.; Al-Yaari, A. An Improved Accelerated 3-Term Conjugate Gradient Algorithm with Second-Order Hessian Approximation for Nonlinear Least-Squares Optimization. J. Math. Comput. Sci. 2025, 36, 263–274. [Google Scholar] [CrossRef]
- Andrei, N. Accelerated conjugate gradient algorithm with finite difference Hessian/vector product approximation for unconstrained optimization. J. Comput. Appl. Math. 2009, 230, 570–582. [Google Scholar] [CrossRef]
- Zoutendijk, G. Nonlinear Programming, Computational Methods. In Integer and Nonlinear Programming; Abadie, J., Ed.; North-Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Muhammad, H.; Waziri, M.Y. Structured two-point step size gradient methods for nonlinear least squares. J. Optim. Theory Appl. 2019, 181, 298–317. [Google Scholar] [CrossRef]
- Cruz, W.L.; Martínez, J.; Raydan, M. Spectral residual method without gradient information for solving large-scale nonlinear systems of equations. Math. Comput. 2006, 75, 1429–1448. [Google Scholar] [CrossRef]
- Moré, J.J.; Garbow, B.S.; Hillstrom, K.E. Testing unconstrained optimization software. ACM Trans. Math. Softw. 1981, 7, 17–41. [Google Scholar] [CrossRef]
- Liu, J.; Li, S. A projection method for convex constrained monotone nonlinear equations with applications. Comput. Math. Appl. 2015, 70, 2442–2453. [Google Scholar] [CrossRef]
- Lukšan, L.; Vlček, J. Test Problems for Unconstrained Optimization; Technical Report 897; Institute of Computer Science Academy of Sciences of the Czech Republic: Praha, Czech Republic, 2003. [Google Scholar]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef]
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]
- Yunus, R.B.; Zainuddin, N.; Daud, H.; Kannan, R.; Yahaya, M.M.; Karim, S.A.A. New CG-Based Algorithms With Second-Order Curvature Information for NLS Problems and a 4DOF Arm Robot Model. IEEE Access 2024, 12, 61086–61103. [Google Scholar] [CrossRef]




| No. | FUNCTION | No. | FUNCTION |
|---|---|---|---|
| 1. | PENALTY FUNCTION 1 | 13. | EXPONENTIAL FUNCTION 2 |
| 2. | VARIABLY DIMENSIONED | 14. | SINGULAR FUNCTION 2 |
| 3. | TRIGONOMETRIC FUNCTION | 15. | EXT. FREUDENSTEIN AND ROTH |
| 4. | DISCRETE BOUNDARY-VALUE | 16. | EXT. POWELL SINGULAR FUNCTION |
| 5. | LINEAR FULL RANK | 17. | FUNCTION 21 |
| 6. | PROBLEM 202 | 18. | BROYDEN TRIDIAGONAL FUNCTION |
| 7. | PROBLEM 206 | 19. | EXTENDED HIMMELBLAU |
| 8. | PROBLEM 212 | 20. | FUNCTION 27 |
| 9. | RAYDAN 1 | 21. | TRILOG FUNCTION |
| 10. | RAYDAN 2 | 22. | ZERO JACOBIAN FUNCTION |
| 11. | SINE FUNCTION 2 | 23. | EXPONENTIAL FUNCTION |
| 12. | EXPONENTIAL FUNCTION 1 | 24. | FUNCTION 18 |
| 25. | BROWN ALMOST FUNCTION |
| METHODS | SNCG | SSGM | DSCGA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FUNCS | DIM | It | Fe | Ge | TIME | It | Fe | Ge | TIME | It | Fe | Ge | TIME |
| 1. | 3000 | 4 | 7 | 10 | 0.1762 | 3 | 5 | 8 | 0.0183 | 2 | 5 | 7 | 0.2012 |
| 6000 | 4 | 7 | 10 | 0.0674 | 3 | 5 | 8 | 0.0195 | 2 | 5 | 7 | 0.0798 | |
| 9000 | 4 | 7 | 10 | 0.0482 | 3 | 5 | 8 | 0.0237 | 3 | 5 | 7 | 0.0630 | |
| 12,000 | 4 | 7 | 10 | 0.0413 | 3 | 5 | 8 | 0.0197 | 3 | 5 | 7 | 0.0315 | |
| 15,000 | 4 | 7 | 10 | 0.0324 | 3 | 5 | 8 | 0.0279 | 3 | 5 | 7 | 0.0956 | |
| 2. | 3000 | ⋆ | ⋆ | ⋆ | ⋆ | 138 | 153 | 215 | 0.78824 | 16 | 18 | 49 | 0.2485 |
| 6000 | ⋆ | ⋆ | ⋆ | ⋆ | 133 | 185 | 250 | 1.0024 | 25 | 32 | 76 | 0.7239 | |
| 9000 | ⋆ | ⋆ | ⋆ | ⋆ | 154 | 261 | 263 | 2.8126 | 70 | 71 | 71 | 0.0698 | |
| 12,000 | ⋆ | ⋆ | ⋆ | ⋆ | 177 | 321 | 323 | 3.9750 | 32 | 95 | 97 | 0.2875 | |
| 15,000 | ⋆ | ⋆ | ⋆ | ⋆ | 183 | 387 | 350 | 5.2280 | 22 | 49 | 67 | 1.6995 | |
| 3. | 3000 | 50 | 446 | 151 | 0.4861 | 71 | 114 | 214 | 0.6545 | 45 | 47 | 136 | 0.4324 |
| 6000 | 60 | 578 | 181 | 1.2966 | 82 | 146 | 247 | 2.3541 | 35 | 52 | 106 | 1.0266 | |
| 9000 | 48 | 253 | 145 | 0.8607 | 97 | 175 | 292 | 4.0113 | 73 | 94 | 220 | 2.623 | |
| 12,000 | 66 | 765 | 199 | 4.1457 | 106 | 184 | 319 | 4.6306 | 67 | 90 | 202 | 2.8439 | |
| 15,000 | 84 | 454 | 253 | 4.1474 | 98 | 185 | 295 | 5.9078 | 61 | 85 | 184 | 2.1456 | |
| 4. | 3000 | 5 | 25 | 22 | 0.1225 | 5 | 23 | 40 | 0.0923 | 2 | 6 | 7 | 0.0667 |
| 6000 | 7 | 35 | 16 | 0.0753 | 7 | 35 | 25 | 0.0896 | 2 | 6 | 7 | 0.1102 | |
| 9000 | 11 | 37 | 4 | 0.0377 | 9 | 6 | 14 | 0.0256 | 3 | 8 | 8 | 0.1157 | |
| 12,000 | 15 | 39 | 4 | 0.0349 | 11 | 35 | 25 | 0.0954 | 4 | 11 | 16 | 0.0555 | |
| 15,000 | 20 | 46 | 4 | 0.0711 | 13 | 59 | 40 | 0.1001 | 5 | 26 | 18 | 0.0598 | |
| 5. | 3000 | 2 | 5 | 7 | 0.0514 | 2 | 5 | 7 | 0.0073 | 2 | 5 | 7 | 0.0139 |
| 6000 | 2 | 5 | 7 | 0.0385 | 2 | 5 | 7 | 0.0092 | 2 | 5 | 7 | 0.0175 | |
| 9000 | 2 | 5 | 7 | 0.0165 | 2 | 5 | 7 | 0.0133 | 2 | 5 | 7 | 0.0428 | |
| 12,000 | 2 | 5 | 7 | 0.0176 | 2 | 5 | 7 | 0.0191 | 2 | 5 | 7 | 0.0425 | |
| 15,000 | 2 | 5 | 7 | 0.2577 | 2 | 5 | 7 | 0.0251 | 2 | 5 | 7 | 0.0817 | |
| 6. | 3000 | 4 | 9 | 13 | 0.00804 | 5 | 13 | 16 | 0.0126 | 5 | 11 | 16 | 0.0275 |
| 6000 | 4 | 9 | 13 | 0.02215 | 5 | 13 | 16 | 0.040159 | 5 | 11 | 16 | 0.0439 | |
| 9000 | 4 | 9 | 13 | 0.0261 | 5 | 13 | 16 | 0.0329 | 5 | 11 | 16 | 0.0509 | |
| 12,000 | 4 | 9 | 13 | 0.0331 | 5 | 13 | 16 | 0.0427 | 5 | 11 | 16 | 0.1295 | |
| 15,000 | 4 | 9 | 13 | 0.0484 | 5 | 13 | 16 | 0.0593 | 5 | 11 | 16 | 0.1678 | |
| 7. | 3000 | 6 | 13 | 19 | 0.0222 | 6 | 16 | 19 | 0.2530 | 5 | 12 | 16 | 0.0760 |
| 6000 | 6 | 13 | 19 | 0.1060 | 6 | 16 | 19 | 0.5337 | 5 | 12 | 16 | 0.0500 | |
| 9000 | 6 | 13 | 19 | 0.0659 | 6 | 16 | 19 | 0.6334 | 5 | 12 | 16 | 0.0667 | |
| 12,000 | 6 | 13 | 19 | 0.0603 | 6 | 16 | 19 | 0.6633 | 5 | 12 | 16 | 0.1283 | |
| 15,000 | 6 | 13 | 19 | 0.1582 | 6 | 16 | 19 | 0.0774 | 5 | 12 | 16 | 0.1472 | |
| 8. | 3000 | 10 | 21 | 31 | 0.0577 | 7 | 11 | 22 | 0.1155 | 4 | 9 | 13 | 0.0431 |
| 6000 | 10 | 21 | 31 | 0.0898 | 7 | 11 | 22 | 0.1234 | 4 | 9 | 13 | 0.0774 | |
| 9000 | 10 | 21 | 31 | 0.22631 | 7 | 11 | 22 | 0.2435 | 4 | 9 | 13 | 0.2239 | |
| 12,000 | 10 | 21 | 31 | 0.2282 | 7 | 11 | 22 | 0.2355 | 4 | 9 | 13 | 0.1138 | |
| 15,000 | 10 | 21 | 31 | 0.2192 | 7 | 11 | 22 | 0.3259 | 4 | 9 | 13 | 0.3342 | |
| 9. | 3000 | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | 5 | 5 | 16 | 0.0641 |
| 6000 | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | 5 | 5 | 16 | 0.2054 | |
| 9000 | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | 7 | 18 | 22 | 0.0152 | |
| 12,000 | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | 7 | 18 | 22 | 0.0199 | |
| 15,000 | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | 7 | 18 | 22 | 0.0357 | |
| 10. | 3000 | 5 | 11 | 16 | 0.0404 | 4 | 9 | 13 | 0.0095 | 4 | 9 | 13 | 0.0161 |
| 6000 | 5 | 11 | 16 | 0.0224 | 4 | 9 | 13 | 0.0191 | 4 | 9 | 13 | 0.0312 | |
| 9000 | 5 | 11 | 16 | 0.0328 | 4 | 9 | 13 | 0.0214 | 4 | 9 | 13 | 0.0465 | |
| 12,000 | 5 | 11 | 16 | 0.0505 | 4 | 9 | 13 | 0.0317 | 4 | 9 | 13 | 0.0914 | |
| 15,000 | 5 | 11 | 16 | 0.0494 | 4 | 9 | 13 | 0.0465 | 4 | 9 | 13 | 0.0957 | |
| 11. | 3000 | 2 | 3 | 4 | 0.0332 | 1 | 3 | 4 | 0.0173 | 1 | 3 | 4 | 0.0146 |
| 6000 | 2 | 3 | 4 | 0.0259 | 1 | 3 | 4 | 0.0119 | 1 | 3 | 4 | 0.0407 | |
| 9000 | 2 | 3 | 4 | 0.0251 | 1 | 3 | 4 | 0.0187 | 1 | 3 | 4 | 0.0494 | |
| 12,000 | 2 | 3 | 4 | 0.0247 | 1 | 3 | 4 | 0.0247 | 1 | 3 | 4 | 0.0094 | |
| 15,000 | 2 | 3 | 4 | 0.0255 | 1 | 3 | 4 | 0.0408 | 1 | 3 | 4 | 0.0249 | |
| 12. | 3000 | ⋆ | ⋆ | ⋆ | ⋆ | 4 | 7 | 8 | 0.0563 | 7 | 13 | 17 | 0.503 |
| 6000 | ⋆ | ⋆ | ⋆ | ⋆ | 5 | 10 | 9 | 0.0192 | 6 | 14 | 16 | 0.0115 | |
| 9000 | ⋆ | ⋆ | ⋆ | ⋆ | 5 | 10 | 9 | 0.0280 | 13 | 25 | 34 | 0.3499 | |
| 12,000 | ⋆ | ⋆ | ⋆ | ⋆ | 7 | 12 | 13 | 0.0332 | 16 | 35 | 46 | 0.4575 | |
| 15,000 | ⋆ | ⋆ | ⋆ | ⋆ | 8 | 15 | 14 | 0.0680 | 18 | 38 | 55 | 0.0261 | |
| 13. | 3000 | ⋆ | ⋆ | ⋆ | ⋆ | 83 | 444 | 250 | 0.2925 | 13 | 34 | 40 | 0.3015 |
| 6000 | ⋆ | ⋆ | ⋆ | ⋆ | 67 | 357 | 202 | 0.3742 | 15 | 31 | 46 | 0.6974 | |
| 9000 | ⋆ | ⋆ | ⋆ | ⋆ | 79 | 421 | 238 | 0.5503 | 46 | 43 | 49 | 0.8374 | |
| 12,000 | ⋆ | ⋆ | ⋆ | ⋆ | 37 | 259 | 112 | 0.0935 | 21 | 37 | 64 | 0.3054 | |
| 15,000 | ⋆ | ⋆ | ⋆ | ⋆ | 61 | 327 | 184 | 0.3767 | 50 | 64 | 51 | 0.3524 | |
| 14. | 3000 | 5 | 12 | 16 | 0.0465 | 7 | 17 | 22 | 0.1774 | 5 | 12 | 16 | 0.0259 |
| 6000 | 5 | 12 | 16 | 0.0272 | 7 | 17 | 22 | 0.3432 | 5 | 12 | 16 | 0.0509 | |
| 9000 | 5 | 12 | 16 | 0.0343 | 7 | 17 | 22 | 0.4903 | 5 | 12 | 16 | 0.0657 | |
| 12,000 | 5 | 12 | 16 | 0.0409 | 7 | 17 | 22 | 0.0525 | 5 | 12 | 16 | 0.0755 | |
| 15,000 | 5 | 12 | 16 | 0.1378 | 7 | 17 | 22 | 0.7693 | 5 | 12 | 16 | 0.1830 |
| METHODS | SNCG | SSGM | DSCGA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FUNCS | DIM | It | Fe | Ge | TIME | It | Fe | Ge | TIME | It | Fe | Ge | TIME |
| 15. | 3000 | ⋆ | ⋆ | ⋆ | ⋆ | 26 | 69 | 79 | 0.0637 | 10 | 17 | 31 | 0.0905 |
| 6000 | ⋆ | ⋆ | ⋆ | ⋆ | 26 | 69 | 79 | 0.3639 | 10 | 17 | 31 | 0.2584 | |
| 9000 | ⋆ | ⋆ | ⋆ | ⋆ | 26 | 69 | 79 | 0.2277 | 10 | 23 | 31 | 0.4727 | |
| 12,000 | ⋆ | ⋆ | ⋆ | ⋆ | 26 | 69 | 79 | 0.2571 | 13 | 34 | 40 | 0.6318 | |
| 15,000 | ⋆ | ⋆ | ⋆ | ⋆ | 26 | 69 | 79 | 0.3489 | 14 | 38 | 41 | 0.4181 | |
| 16. | 3000 | 19 | 149 | 58 | 0.1235 | 5 | 18 | 16 | 0.2524 | 10 | 12 | 13 | 0.0617 |
| 6000 | 19 | 149 | 58 | 0.1494 | 5 | 18 | 16 | 0.6322 | 10 | 12 | 13 | 0.3435 | |
| 9000 | 19 | 149 | 58 | 0.2219 | 5 | 18 | 16 | 0.4866 | 10 | 12 | 13 | 0.1647 | |
| 12,000 | 19 | 149 | 58 | 0.4396 | 5 | 18 | 16 | 0.5401 | 10 | 12 | 13 | 0.2115 | |
| 15,000 | 19 | 149 | 58 | 0.4359 | 5 | 18 | 16 | 0.6261 | 10 | 12 | 13 | 0.4103 | |
| 17. | 3000 | 67 | 432 | 202 | 0.5096 | 59 | 276 | 178 | 0.4913 | 66 | 428 | 199 | 0.8889 |
| 6000 | 67 | 432 | 202 | 0.9914 | 59 | 276 | 178 | 0.8029 | 66 | 428 | 199 | 1.2145 | |
| 9000 | 67 | 432 | 202 | 1.9478 | 59 | 276 | 178 | 0.89849 | 66 | 428 | 199 | 1.8835 | |
| 12,000 | 67 | 432 | 202 | 1.8094 | 59 | 276 | 178 | 1.4494 | 66 | 428 | 199 | 2.3523 | |
| 15,000 | 67 | 432 | 202 | 2.0496 | 59 | 276 | 178 | 1.4754 | 66 | 428 | 199 | 2.5114 | |
| 18. | 3000 | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | 23 | 101 | 109 | 2.4467 |
| 6000 | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | 39 | 245 | 116 | 2.8094 | |
| 9000 | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | 40 | 256 | 117 | 2.8123 | |
| 12,000 | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | 41 | 255 | 117 | 2.8332 | |
| 15,000 | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | ⋆ | 50 | 331 | 152 | 2.6772 | |
| 19. | 3000 | 52 | 335 | 157 | 0.31743 | 67 | 357 | 202 | 0.2436 | 17 | 114 | 52 | 0.14464 |
| 6000 | 52 | 335 | 157 | 0.2549 | 83 | 444 | 250 | 0.4514 | 17 | 114 | 52 | 0.4019 | |
| 9000 | 52 | 335 | 157 | 0.4769 | 85 | 452 | 256 | 0.8718 | 17 | 114 | 52 | 0.2591 | |
| 12,000 | 52 | 335 | 157 | 0.4952 | 76 | 399 | 229 | 0.6840 | 17 | 114 | 52 | 0.3423 | |
| 15,000 | 52 | 335 | 157 | 0.9069 | 89 | 473 | 268 | 0.9816 | 17 | 114 | 52 | 0.3721 | |
| 20. | 3000 | 31 | 242 | 94 | 0.1337 | 61 | 327 | 184 | 0.2679 | 8 | 67 | 24 | 0.0534 |
| 6000 | 32 | 246 | 97 | 0.2033 | 34 | 246 | 103 | 0.2648 | 8 | 68 | 25 | 0.1076 | |
| 9000 | 32 | 244 | 97 | 0.4123 | 43 | 300 | 130 | 0.5784 | 8 | 68 | 25 | 0.1785 | |
| 12,000 | 26 | 216 | 79 | 0.4675 | 42 | 347 | 127 | 0.9517 | 8 | 68 | 25 | 0.2726 | |
| 15,000 | 31 | 229 | 94 | 0.8068 | 34 | 218 | 103 | 0.5337 | 8 | 68 | 25 | 0.2123 | |
| 21. | 3000 | 5 | 12 | 16 | 0.0460 | 7 | 17 | 22 | 0.2688 | 5 | 12 | 16 | 0.0427 |
| 6000 | 5 | 12 | 16 | 0.0338 | 7 | 17 | 22 | 0.4862 | 5 | 12 | 16 | 0.2084 | |
| 9000 | 5 | 12 | 16 | 0.0505 | 7 | 17 | 22 | 0.0599 | 5 | 12 | 16 | 0.1205 | |
| 12,000 | 5 | 12 | 16 | 0.0634 | 7 | 17 | 22 | 0.1868 | 5 | 12 | 16 | 0.0967 | |
| 15,000 | 5 | 12 | 16 | 0.0723 | 7 | 17 | 22 | 0.1079 | 5 | 12 | 16 | 0.1268 | |
| 22. | 3000 | 34 | 241 | 103 | 0.1115 | 40 | 266 | 121 | 0.1011 | 9 | 49 | 28 | 0.0387 |
| 6000 | 32 | 227 | 97 | 0.1781 | 42 | 283 | 127 | 0.2281 | 7 | 43 | 22 | 0.0766 | |
| 9000 | 29 | 222 | 88 | 0.3336 | 39 | 282 | 118 | 0.6486 | 6 | 44 | 19 | 0.0174 | |
| 12,000 | 24 | 171 | 73 | 0.5712 | 41 | 273 | 124 | 0.7159 | 11 | 66 | 34 | 0.3608 | |
| 15,000 | 29 | 230 | 88 | 0.5215 | 42 | 305 | 127 | 0.6488 | 9 | 56 | 28 | 0.3549 | |
| 23. | 3000 | 26 | 120 | 79 | 0.2191 | 62 | 223 | 384 | 0.6480 | 28 | 272 | 85 | 0.3291 |
| 6000 | 19 | 54 | 58 | 0.1244 | 62 | 223 | 384 | 0.6481 | 13 | 105 | 40 | 0.2024 | |
| 9000 | 20 | 58 | 61 | 0.15792 | 158 | 498 | 475 | 1.4069 | 18 | 173 | 55 | 0.4258 | |
| 12,000 | 25 | 168 | 76 | 0.4151 | 52 | 310 | 157 | 0.8004 | 14 | 103 | 43 | 0.5185 | |
| 15,000 | 26 | 231 | 79 | 0.6274 | 46 | 385 | 139 | 1.1442 | 14 | 81 | 43 | 0.3717 | |
| 24. | 3000 | 2 | 3 | 3 | 0.0380 | 1 | 2 | 2 | 0.0360 | 1 | 1 | 1 | 0.0042 |
| 6000 | 2 | 3 | 3 | 0.0031 | 1 | 2 | 2 | 0.0249 | 1 | 1 | 1 | 0.0024 | |
| 9000 | 2 | 3 | 3 | 0.0034 | 1 | 2 | 2 | 0.0391 | 1 | 1 | 1 | 0.0033 | |
| 12,000 | 2 | 3 | 3 | 0.0037 | 1 | 2 | 2 | 0.0485 | 1 | 1 | 1 | 0.0055 | |
| 15,000 | 2 | 3 | 3 | 0.0193 | 1 | 2 | 2 | 0.0486 | 1 | 1 | 1 | 0.0075 | |
| 25. | 3000 | 17 | 29 | 37 | 0.0300 | 21 | 79 | 64 | 0.0510 | 13 | 21 | 22 | 0.0276 |
| 6000 | 17 | 31 | 39 | 0.0391 | 23 | 86 | 70 | 0.1759 | 13 | 22 | 22 | 0.0530 | |
| 9000 | 17 | 32 | 39 | 0.058212 | 23 | 87 | 70 | 0.2089 | 14 | 24 | 22 | 0.0811 | |
| 12,000 | 18 | 33 | 40 | 0.0698 | 24 | 91 | 73 | 0.4886 | 15 | 27 | 22 | 0.0381 | |
| 15,000 | 19 | 33 | 40 | 0.1273 | 23 | 88 | 70 | 0.3694 | 17 | 29 | 29 | 0.4467 |
| Methods | DSCGA | SNCG | SSGM | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NI | Time (s) | Re | NI | Time (s) | Re | NI | Time (s) | Re | |
| Problem 26 | 52 | 0.299 | 77 | 0.824 | 81 | 0.496 | |||
| Methods | DSCGA | SNCG | SSGM | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NI | Time (s) | Re | Ni | Time (s) | Re | NI | Time (s) | Re | |
| Problem 27 | 58 | 0.433 | 76 | 0.469 | 89 | 0.604 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yunus, R.B.; Ben Ghorbal, A.; Zainuddin, N.; Ibrahim, S.M. An Accelerated Diagonally Structured CG Algorithm for Nonlinear Least Squares and Inverse Kinematics. Mathematics 2025, 13, 2766. https://doi.org/10.3390/math13172766
Yunus RB, Ben Ghorbal A, Zainuddin N, Ibrahim SM. An Accelerated Diagonally Structured CG Algorithm for Nonlinear Least Squares and Inverse Kinematics. Mathematics. 2025; 13(17):2766. https://doi.org/10.3390/math13172766
Chicago/Turabian StyleYunus, Rabiu Bashir, Anis Ben Ghorbal, Nooraini Zainuddin, and Sulaiman Mohammed Ibrahim. 2025. "An Accelerated Diagonally Structured CG Algorithm for Nonlinear Least Squares and Inverse Kinematics" Mathematics 13, no. 17: 2766. https://doi.org/10.3390/math13172766
APA StyleYunus, R. B., Ben Ghorbal, A., Zainuddin, N., & Ibrahim, S. M. (2025). An Accelerated Diagonally Structured CG Algorithm for Nonlinear Least Squares and Inverse Kinematics. Mathematics, 13(17), 2766. https://doi.org/10.3390/math13172766





