Mathematical Modeling of Gas-Solid Two-Phase Flows: Problems, Achievements and Perspectives (A Review)
Abstract
:1. Introduction
2. Main Problems and Specific Features of Two-Phase Flow Modeling
2.1. Main Problems of Two-Phase Flow Modeling
2.2. Specific Features of Two-Phase Flow Modeling
2.2.1. Multiscale Physics of Two-Phase Flow
2.2.2. Multiplicity of Forces Acting on Particles
2.2.3. Multiplicity of Modeling Parameters
2.2.4. Multiplicity of Collision Processes
2.2.5. Multiplicity of Phase and Chemical Transformations
2.2.6. Multiplicity of Dimensionless Parameters
3. Main Characteristics of Two-Phase Flows
3.1. Particle Concentrations
3.1.1. One-Way Coupling
3.1.2. Two-Way Coupling
3.1.3. Four-Way Coupling
3.2. Particles’ Dynamic Relaxation Time
3.3. Stokes Numbers
3.3.1. Stokes Number in Time-Averaged Motion
3.3.2. Stokes Number in Large-Scale Fluctuation Motions
3.3.3. Stokes Number in Small-Scale Fluctuation Motions
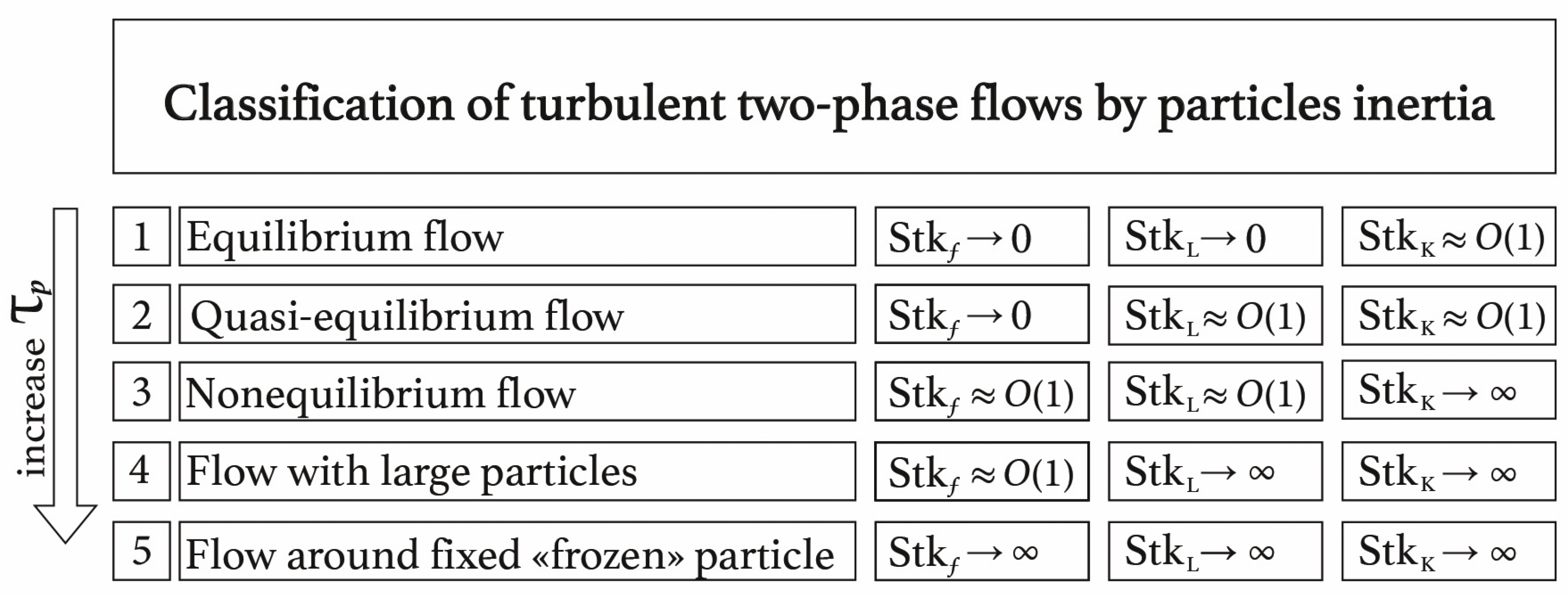
3.4. Classification of Turbulent Two-Phase Flows According to Particle Inertia
4. Lagrangian and Eulerian Modeling of Two-Phase Flows
4.1. Reasons for Considering of the Two-Phase Nature of Tornados
4.2. Lagrangian Modeling
4.3. Eulerian Modeling
4.4. Advantages and Limitations of Lagrangian and Eulerian Modeling
4.5. Description of the Gas Flow Carrying the Particles
4.5.1. Actual Equations
4.5.2. Time-Averaged Equations
4.5.3. Equations for the Reynolds Stresses
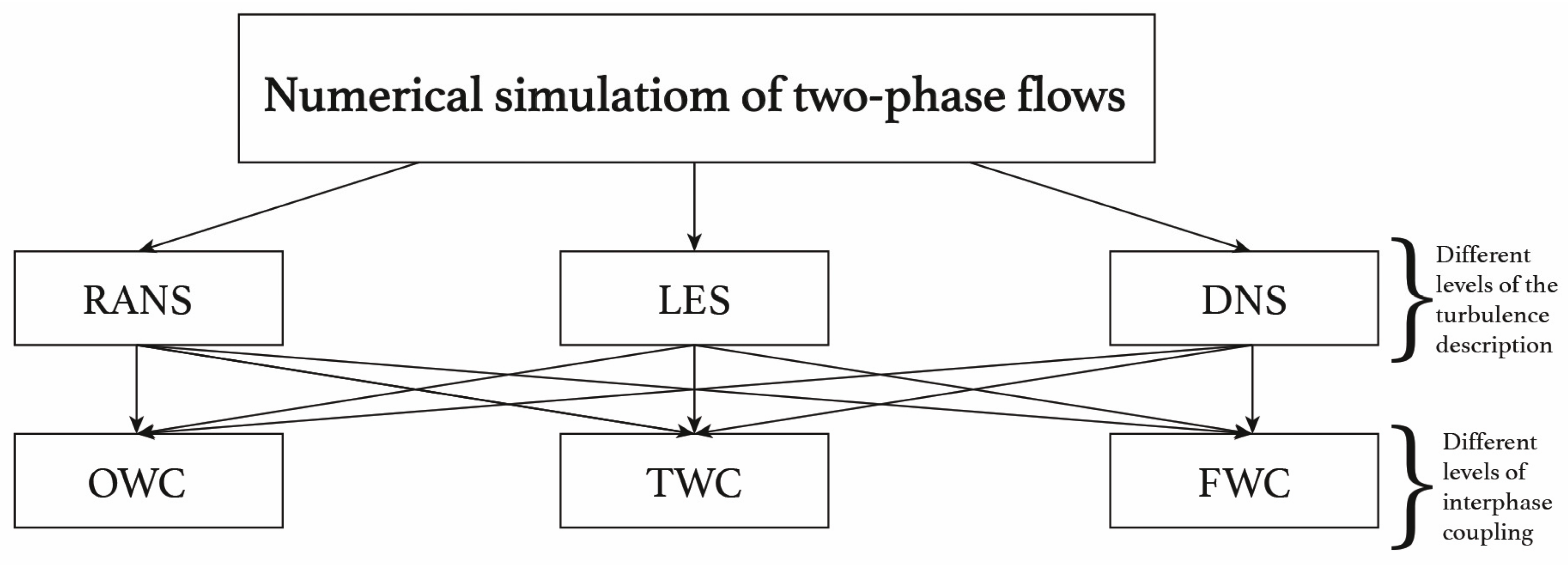
5. Methods of Numerically Modeling Two-Phase Flows
5.1. Particle-Resolved DNS
5.2. Particle Point Methods
5.3. Direct Numerical Simulation
5.4. Large Eddy Simulation
6. Conclusions
- (1)
- The development of mathematical modeling methods for two-phase flows with relatively large particles (non-equilibrium flows) that only interact with large energy-carrying vortices and are characterized by dynamic slippage (velocity difference) in relation to average motion.
- (2)
- The development of mathematical modeling methods for two-phase flows with large particles, which form turbulent wakes behind them. With the increase in particle concentration, these turbulent wakes will interfere with each other, and the particles will undergo collisions.
- (3)
- The development of mathematical modeling methods for two-phase flows containing particles of different sizes (polydisperse particles). Such flows are of interest to practicing engineers. Particles of different sizes will have different velocities and different effects on gas flow and tend to collide with each other at lower concentrations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| particle diameter, m | |
| Kolmogorov length scale, m | |
| particle radius vector, m | |
| vector of actual velocity of gas, m/s | |
| vector of actual velocity of particle, m/s | |
| , , | actual velocity components of gas, m/s |
| , , | actual velocity components of particle, m/s |
| , , | time-averaged velocity components of gas, m/s |
| , , | time-averaged velocity components of particle, m/s |
| , , | fluctuation velocity components of gas, m/s |
| , , | fluctuation velocity components of particle, m/s |
| kinematic viscosity of gas, m2/s | |
| coefficient of thermal diffusivity, m2/s | |
| time, s | |
| dynamic relaxation time of particle, s | |
| heat relaxation time of particle, s | |
| Kolmogorov time scale, s | |
| characteristic time of gas in time-averaged motion, s | |
| Lagrangian integral time scale, s | |
| particle interaction time with energy-containing velocity fluctuations, s | |
| particle interaction time with energy-containing temperature fluctuations, s | |
| actual temperature of gas, K | |
| actual temperature of particle, K | |
| time-averaged temperature of gas, K | |
| time-averaged temperature of particle, K | |
| fluctuation temperature of gas, K | |
| fluctuation temperature of particle, K | |
| dynamic viscosity of gas, kg/(ms) | |
| gas density, kg/m3 | |
| particle density, kg/m3 | |
| actual pressure of the gas, Pa | |
| time-averaged pressure of the gas, Pa | |
| fluctuation pressure of the gas, Pa | |
| isobaric heat capacity of gas, J/(kg K) | |
| heat capacity of material of particle, J/(kg K) | |
| actual volumetric concentration of the particles | |
| time-averaged volumetric concentration of the particles | |
| fluctuation volumetric concentration of the particles | |
| time-averaged mass concentration of the particles | |
| particles Reynolds number | |
| Reynolds number determined via Taylor turbulence scale | |
| frictional Reynolds number | |
| Stokes number in time-averaged motion | |
| Stokes number in large-scale fluctuation motion | |
| Stokes number in small-scale fluctuation motion | |
| Superscripts | |
| fluctuation value | |
| time-averaged value | |
| Subscripts | |
| particle | |
| f | fluid (gas) |
References
- Crowe, C.; Sommerfeld, M.; Tsuji, Y. (Eds.) Multiphase Flows with Droplets and Particles; CRC Press: Boca Raton, FL, USA, 1998; 471p. [Google Scholar]
- Varaksin, A.Y. Turbulent Particle-Laden Gas Flows; Springer: New York, NY, USA, 2007; 210p. [Google Scholar]
- Michaelides, E.E.; Crowe, C.T.; Schwarzkopf, J.D. (Eds.) Multiphase Flow Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; 1396p. [Google Scholar]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. Tornado; Begell House: New York, NY, USA, 2015; 394p. [Google Scholar]
- Elghobashi, S. Direct numerical simulation of turbulent flows laden with droplets of bubbles. Annu. Rev. Fluid Mech. 2019, 51, 217–244. [Google Scholar] [CrossRef] [Green Version]
- Varaksin, A.Y. Collisions in Particle-Laden Gas Flows; Begell House: New York, NY, USA, 2013; 370p. [Google Scholar]
- Varaksin, A.Y. Two-phase flows with solid particles, droplets, and bubbles: Problems and research results (review). High Temp. 2020, 58, 595–614. [Google Scholar] [CrossRef]
- Elghobashi, S. Particle-laden turbulent flows. Appl. Sci. Res. 1991, 48, 301–314. [Google Scholar] [CrossRef]
- Elghobashi, S. On predicting particle-laden turbulent flows. Appl. Sci. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Tsuji, Y.; Morikawa, Y. LDV Measurements of an air-solid two-phase flow in a horizontal pipe. J. Fluid Mech. 1982, 120, 385–409. [Google Scholar] [CrossRef]
- Tsuji, Y.; Morikawa, Y.; Shiomi, H. LDV measurements of an air-solid two-phase flow in a vertical pipe. J. Fluid Mech. 1984, 139, 417–434. [Google Scholar] [CrossRef]
- Rogers, C.B.; Eaton, J.K. The behavior of small particles in a vertical turbulent boundary layer in air. Int. J. Multiph. Flow 1990, 16, 819–834. [Google Scholar] [CrossRef]
- Kulick, J.D.; Fessler, J.R.; Eaton, J.K. Particle response and turbulence modification in fully developed channel flow. J. Fluid Mech. 1994, 277, 109–134. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Polezhaev, Y.V.; Polyakov, A.F. Effect of particle concentration on fluctuating velocity of the disperse phase for turbulent pipe flow. Int. J. Heat Fluid Flow 2000, 21, 562–567. [Google Scholar] [CrossRef]
- Saffman, P.G.; Turner, J.S. On the collision of drops in turbulent cloud. J. Fluid Mech. 1956, 1, 16–30. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.-P.; Wexler, A.S.; Zhou, Y. On the collision rate of small particles in isotropic turbulence. I. Zero-inertia case. Phys. Fluids 1998, 10, 2647–2651. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.-P.; Wexler, A.S.; Zhou, Y. Statistical mechanical description and modelling of turbulent collision of inertial particles. J. Fluid Mech. 2000, 415, 117–153. [Google Scholar] [CrossRef] [Green Version]
- Varaksin, A.Y. Collision of particles and droplets in turbulent two-phase flows. High Temp. 2019, 57, 555–572. [Google Scholar] [CrossRef]
- Squires, K.D.; Eaton, J.K. Particle response and turbulence modification in isotropic turbulence. Phys. Fluids A 1990, 2, 1191–1203. [Google Scholar] [CrossRef]
- Squires, K.D.; Eaton, J.K. Preferential concentration of particles by turbulence. Phys. Fluids A 1991, 3, 1169–1178. [Google Scholar] [CrossRef]
- Fessler, J.R.; Kulick, J.D.; Eaton, J.K. Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 1994, 6, 3742–3749. [Google Scholar] [CrossRef]
- Rouson, D.W.I.; Eaton, J.K. On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 2001, 428, 149–169. [Google Scholar] [CrossRef]
- Osiptsov, A.N. Investigation of regions of unbounded growth of the particle concentration in disperse flows. Fluid Dyn. 1984, 19, 378–385. [Google Scholar] [CrossRef]
- Volkov, A.N.; Tsirkunov, Y.M.; Oesterle, B. Numerical simulation of a supersonic gas-solid flow over a blunt body: The role of inter-particle collisions and two-way coupling effects. Int. J. Multiph. Flow 2005, 31, 1244–1275. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. Tornado-like gas-solid flow. AIP Conf. Proc. 2010, 1207, 342–347. [Google Scholar]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N.; Gorbachev, M.A. Experimental study of wall-free non-stationary vortices generation due to air unstable stratification. Int. J. Heat Mass Transf. Transf. 2012, 55, 6567–6572. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. Effect of net structures on wall-free non-stationary air heat vortices. Int. J. Heat Mass Transf. 2013, 64, 817–828. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Turbulence in two-phase flows with macro-, micro- and nanoparticles: A review. Symmetry 2022, 14, 2433. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Particle-laden and droplet-laden two-phase flows past bodies (a review). Symmetry 2023, 15, 388. [Google Scholar] [CrossRef]
- Sommerfeld, M. Analysis of collision effects for turbulent gas-particle flow in a horizontal channel. Part, I. Particle transport. Int. J. Multiph. Flow 2003, 29, 675–828. [Google Scholar] [CrossRef]
- Gavin, L.B.; Naumov, V.A.; Shor, V.V. Numerical investigation of a gas jet with heavy particles on the basis of a two-parameter model of turbulence. J. Appl. Mech. Tech. Phys. 1984, 25, 56–61. [Google Scholar] [CrossRef]
- Kondrat‘ev, L.V. Modeling of two-phase flow on the stabilized section of a pipe. In Turbulent Two-Phase Flows and Experimental Techniques (pt. 2); Academy of Sciences of the Estonian SSR: Tallinn, Estonia, 1985; pp. 144–148. (In Russian) [Google Scholar]
- Chen, C.P.; Wood, P.E. A turbulence closure model for dilute gas-particle flows. Can. J. Chem. Eng. 1985, 63, 349–360. [Google Scholar] [CrossRef]
- Volkov, E.P.; Zaichik, L.I.; Pershukov, V.A. Simulation of the Combustion of Solid Fuels; Nauka: Moscow, Russian, 1994; 320p. (In Russian) [Google Scholar]
- Melville, W.K.; Bray, K.N.C. A model of the two-phase turbulent jet. Int. J. Heat Mass Transf. 1979, 22, 647–656. [Google Scholar] [CrossRef]
- Zaichik, L.I.; Alipchenkov, V.M.; Sinaiski, E.G. Particles in Turbulent Flows; Wiley-VCH: Darmstadt, Germany, 2008; 320p. [Google Scholar]
- Buyevich, Y.A. Statistical hydrodynamics of disperse systems. Part 1. Physical background and general equations. J. Fluid Mech. 1971, 49, 489–507. [Google Scholar] [CrossRef]
- Derevich, I.V.; Zaichik, L.I. Particle deposition from a turbulent flow. Fluid Dyn. 1988, 23, 722–729. [Google Scholar] [CrossRef]
- Derevich, I.V.; Zaichik, L.I. An equation for the probability density velocity and temperature of particles in a turbulent flow modeled by a random Gaussian field. J. Appl. Math. Mech. 1990, 54, 631–636. [Google Scholar] [CrossRef]
- Zaichik, L.I. Models of turbulent momentum and heat transfer in a dispersed phase based on equations for the second and third moments of particle velocity and temperature fluctuations. J. Eng. Phys. Thermophys. 1992, 63, 976–984. [Google Scholar] [CrossRef]
- Zaichik, L.I. Modelling of the motion of particles in non-uniform turbulent flow using the equation for the probability density function. J. Appl. Math. Mech. 1997, 61, 127–133. [Google Scholar] [CrossRef]
- Swailes, D.C.; Darbyshire, K.F.F. A generalized Fokker-Plank equation for particle transport in random media. Physica A 1997, 242, 38–48. [Google Scholar] [CrossRef]
- Hyland, K.E.; McKee, S.; Reeks, M.W. Derivation of a PDF kinetic equation for the transport of particles in turbulent flows. J. Phys. A Math. Gen. 1999, 32, 6169–6190. [Google Scholar] [CrossRef]
- Zaichik, L.I. A statistical model of particle transport and heat transfer in turbulent shear flows. Phys. Fluids 1999, 11, 1521–1534. [Google Scholar] [CrossRef]
- Derevich, I.V. Statistical modelling of mass transfer in turbulent two-phase dispersed flows. 1. Model development. Int. J. Heat Mass Transf. 2000, 43, 3709–3723. [Google Scholar] [CrossRef]
- Pandya, R.V.R.; Mashayek, F. Kinetic equation for particle transport and heat transport in non-isothermal turbulent flows. AIAA Paper 2002, 41, 841–847. [Google Scholar] [CrossRef]
- Zaichik, L.I.; Oesterle, B.; Alipchenkov, V.M. On the probability density function model for the transport of particles in anisotropic turbulent flow. Phys. Fluids 2004, 16, 1956–1964. [Google Scholar] [CrossRef]
- Reeks, M.W. On a kinetic equation for the transport of particles in turbulent flows. Phys. Fluids A 1991, 3, 446–456. [Google Scholar] [CrossRef]
- Reeks, M.W. On the continuum equation for dispersed particles in nonuniform flows. Phys. Fluids A 1992, 4, 1290–1303. [Google Scholar] [CrossRef]
- Pandya, R.V.R.; Mashayek, F. Non-isotermal dispersed phase of particles in turbulent flow. J. Fluids Mech. 2003, 475, 205–245. [Google Scholar] [CrossRef]
- Pozorski, J. Derivation of the kinetic equation for dispersed particles in turbulent flows. J. Theor. Appl. Mech. 1998, 36, 31–46. [Google Scholar]
- Pozorski, J.; Minier, J.-P. Probability density function modeling of dispersed two-phase turbulent flows. Phys. Rev. E 1999, 59, 855–863. [Google Scholar] [CrossRef]
- Pialat, X.; Simonin, O.; Villedieu, P. Direct coupling between Lagrangian and Eulerian approaches in turbulent gas-solid flows. In Proceedings of the ASME 2005 Fluids Engineering Division Summer Meeting, Houston, TX, USA, 19–23 June 2005. FEDS2006-98122. [Google Scholar]
- Jones, W. Models for turbulent flows with variable density and combustion. In Prediction Methods for Turbulent Flows; Hemisphere: Washington, DC, USA, 1980; 468p. [Google Scholar]
- Derevich, I.V.; Yeroshenko, V.M.; Zaichik, L.I. Hydrodynamics and heat transfer of turbulent gas suspension flows in tubes. 1. Hydrodynamics. Int. J. Heat Mass Transf. 1989, 32, 2329–2339. [Google Scholar] [CrossRef]
- Derevich, I.V.; Yeroshenko, V.M.; Zaichik, L.I. Hydrodynamics and heat transfer of turbulent gas suspension flows in tubes. 2. Heat Transfer. Int. J. Heat Mass Transf. 1989, 32, 2341–2350. [Google Scholar] [CrossRef]
- Abramovich, G.N. The effect of solid particle or drop addition on the structure of a turbulent gas jet. Dokl. Akad. Nauk SSSR 1970, 190, 1052–1055. (In Russian) [Google Scholar]
- Abramovich, G.N.; Girshovich, T.A.; Krasheninnikov, S.Y.; Sekundov, A.N.; Smirnova, I.P. The Theory of Turbulent Jets; Nauka: Moscow, Russian, 1984; 717p. (In Russian) [Google Scholar]
- Varaksin, A.Y. Effect of particles on carrier gas flow turbulence. High Temp. 2015, 53, 423–444. [Google Scholar] [CrossRef]
- Eaton, J.K.; Fessler, J.R. Preferential concentration of particles by turbulence. Int. J. Multiph. Flow 1994, 20, 169–209. [Google Scholar] [CrossRef]
- Fessler, J.R.; Eaton, J.K. Particle response in a planar sudden expansion flow. Exp. Therm. Fluid Sci. 1997, 15, 413–423. [Google Scholar] [CrossRef]
- Fessler, J.R.; Eaton, J.K. Turbulence modification by particles in a backward-facing step flow. J. Fluid Mech. 1999, 394, 97–117. [Google Scholar] [CrossRef]
- Yuan, Z.; Michaelides, E.E. Turbulence modulation in particulate flows–a theoretical approarch. Int. J. Multiph. Flow 1992, 18, 779–785. [Google Scholar] [CrossRef]
- Yarin, L.P.; Hetsroni, G. Turbulence intensity in dilute two-phase flows–3. The particles-turbulence interaction in dilute two-phase flow. Int. J. Multiph. Flow 1994, 20, 27–44. [Google Scholar] [CrossRef]
- Zaichik, L.I.; Varaksin, A.Y. Effect of the wake behind large particles on the turbulence intensity of carrier flow. High Temp. 1999, 37, 655–658. [Google Scholar]
- Elghobashi, S.E.; Abou-Arab, T.W. A two-equation turbulence model for two-phase flows. Phys. Fluids 1983, 26, 931–938. [Google Scholar] [CrossRef]
- Rizk, M.A.; Elghobashi, S.E. A two-equation turbulence model for dispersed dilute confined two-phase flows. Int. J. Multiph. Flow 1989, 15, 119–134. [Google Scholar] [CrossRef]
- Mostafa, A.A.; Mongia, H.C. On the interaction of particles and turbulent fluid flow. Int. J. Heat Mass Transf. 1988, 31, 2063–2075. [Google Scholar] [CrossRef]
- Berlemont, A.; Grancher, M.-S.; Gousbet, G. On the Lagrangian simulation of turbulence influence on droplet evaporation. Int. J. Heat Mass Transf. 1991, 34, 2805–2812. [Google Scholar] [CrossRef]
- Burton, T.M.; Eaton, J. Fully resolved simulations of particle-turbulence interaction. J. Fluid Mech. 2005, 545, 67–111. [Google Scholar] [CrossRef]
- Picano, F.; Breugem, W.P.; Brandt, L. Turbulent channel flow of dense suspensions of neutrally-buoyant spheres. J. Fluid Mech. 2015, 764, 463–487. [Google Scholar] [CrossRef] [Green Version]
- ten Cate, A.; Derksen, J.J.; Portela, L.M.; van den Akker, H.E.A. Fully resolved simulations of colliding monodisperse spheres in forced isotropic turbulence. J. Fluid Mech. 2004, 539, 233–271. [Google Scholar] [CrossRef] [Green Version]
- Takagi, S.; Oguz, H.N.; Zhang, Z.; Prosperetti, A. Physalis: A new method for particle simulation: Part ii: Two-dimensional Navier-Stokes flow around cylinders. J. Comput. Phys. 2003, 187, 371–390. [Google Scholar] [CrossRef]
- Riley, J.J.; Patterson Jr, G.S. Diffusion experiments with numerically integrated isotropic turbulence. Phys. Fluids 1974, 17, 292–297. [Google Scholar] [CrossRef]
- Yeung, P.K.; Pope, S.B. An algorithm for tracking fluid particles in numerical simulation of homogeneous turbulence. J. Comput. Phys. 1988, 79, 373–416. [Google Scholar] [CrossRef]
- Balachandar, S.; Maxey, M.R. Methods for evaluating fluid velocities in spectral simulations of turbulence. J. Comput. Phys. 1989, 83, 96–125. [Google Scholar] [CrossRef]
- McLaughlin, J.B. Aerosol particle deposition in numerically simulated channel flow. Phys. Fluids 1989, A1, 1211–1224. [Google Scholar] [CrossRef]
- Kontomaris, K.; Hanratty, T.J.; McLaughlin, J.B. An algorithm for tracking fluid particles in a spectral simulation of turbulent channel flow. J. Comput. Phys. 1992, 103, 231–242. [Google Scholar] [CrossRef]
- Marchioli, C.; Soldati, A.; Kuerten, J.G.M.; Arcen, B.; Taniere, A.; Goldensoph, G.; Squires, K.D.; Cargnelutti, M.F.; Portela, L.M. Statistics of particle dispersion in direct numerical simulations of wallbounded turbulence: Results of an international collaborative benchmark test. Int. J. Multiph. Flow 2008, 34, 879–893. [Google Scholar] [CrossRef] [Green Version]
- Marchioli, C.; Giusti, A.; Salvetti, M.V.; Soldati, A. Direct numerical simulation of particle wall transfer and deposition in upward turbulent pipe flow. Int. J. Multiph. Flow 2003, 29, 1017–1038. [Google Scholar] [CrossRef]
- van Esch, B.P.M.; Kuerten, J.G.M. Direct numerical simulation of the motion of particles in rotating pipe flow. J. Turbul. 2008, 9, N4. [Google Scholar] [CrossRef]
- Picano, F.; Sardina, G.; Casciola, C.M. Spatial development of particle-laden turbulent pipe flow. Phys. Fluids 2009, 21, 093305. [Google Scholar] [CrossRef]
- Elghobashi, S.; Truesdell, G.C. Direct simulation of particle dispersion in a decaying isotropic turbulence. J. Fluid Mech. 1992, 242, 655–700. [Google Scholar] [CrossRef]
- Boivin, M.; Simonin, O.; Squires, K.D. Direct numerical simulation of turbulence modulation by particles in homogeneous turbulence. J. Fluid Mech. 1998, 375, 235–263. [Google Scholar] [CrossRef] [Green Version]
- Eaton, J.K. Two-way coupled turbulence simulations of gas-particle flows using point-particle tracking. Int. J. Multiph. Flow 2009, 35, 792–800. [Google Scholar] [CrossRef]
- Kuerten, J.G.M.; Vreman, A.W. Effect of droplet interaction on droplet-laden turbulent channel flow. Phys. Fluids 2015, 27, 053304. [Google Scholar] [CrossRef] [Green Version]
- Russo, E.; Kuerten, J.G.M.; van der Geld, C.W.M.; Geurts, B.J. Water droplet condensation and evaporation in turbulent channel flow. J. Fluid Mech. 2014, 749, 666–700. [Google Scholar] [CrossRef]
- Pan, Y.; Banerjee, S. Numerical simulation of particle interactions with wall turbulence. Phys. Fluids 1996, 8, 2733–2755. [Google Scholar] [CrossRef]
- Zhao, L.H.; Andersson, H.I.; Gillissen, J.J.J. Turbulence modulation and drag reduction by spherical particles. Phys. Fluids 2010, 22, 081702. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.H.; Andersson, H.I.; Gillissen, J.J.J. Interphasial energy transfer and particle dissipation in particle-laden wall turbulence. J. Fluid Mech. 2013, 715, 32–59. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Lee, C. Modification of particle-laden near-wall turbulence; effect of Stokes number. Phys. Fluids 2015, 27, 023303. [Google Scholar] [CrossRef] [Green Version]
- Letournel, R.; Laurent, F.; Massot, M.; Vie, A. Modulation of homogeneous and isotropic turbulence by sub-Kolmogorov particles: Impact of particle field heterogeneity. Int. J. Multiph. Flow 2020, 125, 103233. [Google Scholar] [CrossRef]
- Yu, Z.; Xia, Y.; Lin, J. Modulation of turbulence intensity by heavy finite-size particles in upward channel flow. J. Fluid Mech. 2021, 913, A3. [Google Scholar] [CrossRef]
- Vreman, A.W. Turbulence characteristics of particle-laden pipe flow. J. Fluid Mech. 2007, 584, 235–279. [Google Scholar] [CrossRef]
- Vreman, A.W. Turbulence attenuation in particle-laden flow in smooth and rough channels. J. Fluid Mech. 2015, 773, 103–136. [Google Scholar] [CrossRef] [Green Version]
- Mallouppas, G.; George, W.K.; van Wachem, B.G.M. Dissipation and inter-scale transfer in fully coupled particle and fluid motions in homogeneous isotropic forced turbulence. Int. J. Heat Fluid Flow 2017, 67, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Bardina, J.; Ferziger, J.H.; Reynolds, W.C. Improved Turbulence Models Based on LES of Homogeneous Incompressible Turbulent Flows; Technical Report No. TF-19; Stanford, Depart. Mech. Eng.: Stanford, CA, USA, 1984. [Google Scholar]
- Clark, R.A.; Ferziger, J.H.; Reynolds, W.C. Evaluation of subgrid-scale models using an accurately simulated turbulent flow. J. Fluid Mech. 1979, 91, 1–16. [Google Scholar] [CrossRef]
- Stolz, S.; Adams, N.A.; Kleiser, L. An approximate deconvolution model for large-eddy simulation with application to incompressible wall-bounded flows. Phys. Fluids 2001, 13, 997–1015. [Google Scholar] [CrossRef]
- Deardorff, J.W.; Peskin, R.L. Lagrangian statistics from numerically integrated turbulent shear flow. Phys. Fluids 1970, 13, 584–595. [Google Scholar] [CrossRef]
- Uijttewaal, W.S.J.; Oliemans, R.V.A. Particle dispersion and deposition in direct numerical and large eddy simulation of vertical pipe flows. Phys. Fluids 1996, 8, 2590–2604. [Google Scholar] [CrossRef]
- Wang, Q.; Squires, K.D. Large eddy simulation of particle deposition in a vertical turbulent channel flow. Int. J. Multiph. Flow 1996, 22, 667–683. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 1991, A3, 1760–1765. [Google Scholar] [CrossRef]
- Boivin, M.; Simonin, O.; Squires, K.D. On the prediction of gas-solid flows with two-way coupling using large eddy simulation. Phys. Fluids 2000, 12, 2080–2090. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, Y.; Potthoff, M.; Tanaka, T.; Kajishima, T.; Tsuji, Y. Large-eddy simulation of turbulent gas-particle flow in a vertical channel: Effect of considering inter-particle collisions. J. Fluid Mech. 2001, 442, 303–334. [Google Scholar] [CrossRef] [Green Version]
- Vreman, A.W.; Geurts, B.J.; Deen, N.G.; Kuipers, J.A.M.; Kuerten, J.G.M. Two- and four-way coupled Euler-Lagrangian large-eddy simulation of turbulent particle-laden channel flow. Flow Turbul. Combust. 2009, 82, 47–71. [Google Scholar] [CrossRef] [Green Version]
- Mallouppas, G.; van Wachem, B. Large eddy simulations of turbulent particle-laden channel flow. Int. J. Multiph. Flow 2013, 54, 65–75. [Google Scholar] [CrossRef] [Green Version]
- Breuer, M.; Alletto, M. Efficient simulation of particle-laden turbulent flows with high mass loadings using LES. Int. J. Heat Fluid Flow 2012, 35, 2–12. [Google Scholar] [CrossRef]
- Pozorski, J.; Apte, S.V. Filtered particle tracking in isotropic turbulence and stochastic modeling of subgrid-scale dispersion. Int. J. Multiph. Flow 2009, 35, 118–128. [Google Scholar] [CrossRef]
- Alletto, M.; Breuer, M. Prediction of turbulent particle-laden flow in horizontal smooth and rough pipes inducing secondary flow. Int. J. Multiph. flow 2013, 55, 80–98. [Google Scholar] [CrossRef]
- Breuer, M.; Almohammed, N. Modeling and simulation of particle agglomeration in turbulent flows using a hard-sphere model with deterministic collision detection and enhanced structure models. Int. J. Multiph. Flow 2015, 73, 171–206. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Approximate calculation of convective heat transfer near hypersonic aircraft surface. J. Enhanc. Heat Transf. 2018, 25, 181–193. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. The Qualitative and Quantitative Study of Radiation Sources with a Model Configuration of the Electrode System. Symmetry 2021, 13, 927. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Estimation of the neutron generation in the combined magneto-inertial fusion scheme. Phys. Scr. 2021, 96, 125613. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Numerical Simulation of Pulsed Jets of a High-Current Pulsed Surface Discharge. Comput. Therm. Sci. 2021, 13, 45–56. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Calculation of heat transfer and drag coefficients for aircraft geometric models. Appl. Sci. 2022, 12, 11011. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Frolko, P.A. Numerical simulation of the coaxial magneto-plasma accelerator and non-axisymmetric radio frequency discharge. J. Phys. Conf. Ser. 2017, 830, 012049. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. The Adaptive Composite Block-Structured Grid Calculation of the Gas-Dynamic Characteristics of an Aircraft Moving in a Gas Environment. Mathematics 2022, 10, 2130. [Google Scholar] [CrossRef]
- Engler, M.; Kockmann, N.; Kiefer, T.; Woias, P. Numerical and experimental investigations on liquid mixing in static micromixers. Chem. Eng. J. 2004, 101, 315. [Google Scholar] [CrossRef]
- Lobasov, A.; Minakov, A. Analyzing mixing quality in a T-shaped micromixer for different fluids properties through numerical simulation. Chem. Eng. Process 2018, 124, 11. [Google Scholar] [CrossRef] [Green Version]
- Mariotti, A.; Galletti, C.; Brunazzi, E.; Salvetti, M.V. Unsteady flow regimes in arrow-shaped micro-mixers with different tilting angles. Phys. Fluids 2021, 33, 012008. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varaksin, A.Y.; Ryzhkov, S.V. Mathematical Modeling of Gas-Solid Two-Phase Flows: Problems, Achievements and Perspectives (A Review). Mathematics 2023, 11, 3290. https://doi.org/10.3390/math11153290
Varaksin AY, Ryzhkov SV. Mathematical Modeling of Gas-Solid Two-Phase Flows: Problems, Achievements and Perspectives (A Review). Mathematics. 2023; 11(15):3290. https://doi.org/10.3390/math11153290
Chicago/Turabian StyleVaraksin, Aleksey Yu., and Sergei V. Ryzhkov. 2023. "Mathematical Modeling of Gas-Solid Two-Phase Flows: Problems, Achievements and Perspectives (A Review)" Mathematics 11, no. 15: 3290. https://doi.org/10.3390/math11153290
APA StyleVaraksin, A. Y., & Ryzhkov, S. V. (2023). Mathematical Modeling of Gas-Solid Two-Phase Flows: Problems, Achievements and Perspectives (A Review). Mathematics, 11(15), 3290. https://doi.org/10.3390/math11153290





