Eulerian-Eulerian Modeling of the Features of Mean and Fluctuational Flow Structure and Dispersed Phase Motion in Axisymmetric Round Two-Phase Jets

Abstract

The features of the local mean and fluctuational flow structure, carrier phase turbulence and the propagation of the dispersed phase in the bubbly and droplet-laden isothermal round polydispersed jets were numerically simulated. The dynamics of the polydispersed phase is predicted using the Eulerian–Eulerian two-fluid approach. Turbulence of the carrier phase is described using the second-moment closure while taking into account the presence of the dispersed phase. The numerical analysis was performed in a wide range of variation of dispersed phase diameter at the inlet and particle-to-fluid density ratio (from gas flow laden with water droplets to carrier fluid flow laden with gas bubbles). An increase in the concentration of air bubbles and their size leads to jet expansion (as compared to a single-phase jet up to 40%), which indicates an increase in the intensity of the process of turbulent mixing with the surrounding space. However, this makes the gas-droplet jet narrower (up to 15%) and with a longer range in comparison with a single-phase flow. The addition of finely dispersed liquid droplets to an air jet suppresses gas phase turbulence (up to 15%). In a bubbly jet, it is found that small bubbles (Stk < 0.1) accumulate near the jet axis in the initial cross-sections, while concentration of the large ones (Stk > 0.2) along the jet axis decreases rapidly. In the gas-droplet jet, the effect of dispersed phase accumulation is also observed in the initial cross-section, and then its concentration decreases gradually along the jet axis. For gas bubbles (Stk < 0.1), small turbulence attenuation (up to 6%) is shown.

1. Introduction

Two-phase bubbly and gas-droplet turbulent free round jets are widely used in energy, chemical, and pharmaceutical industries, etc. For example, this includes the processes of intensifying mass transfer between gas bubbles and liquid flow and the transportation of various liquids with air bubbles in pipelines; atomization of liquid fuel in injectors of internal combustion engines or gas turbines; and spreading dangerous viral infections, such as COVID-19, through droplets of liquids containing the virus during coughing and sneezing.

The motion and dispersion of gas bubbles or liquid droplets in jets of a carrier fluid (liquid or gas) is accompanied by a large number of complex phenomena: interfacial dynamic interaction, change in the size of droplets or bubbles due to coalescence or break up, and suppression or generation of turbulence in the carrier medium by the presence of dispersed phase. The study of the local turbulent structure and propagation of the dispersed phase in bubbly and droplet-laden jets is required to design the modern technological equipment. When developing mathematical models of two-phase bubbly flows, it is very important to describe interfacial interaction correctly (see reference lists in monographs [1,2] and reviews [3,4]). This is possible with exact consideration of the contribution of carrier liquid phase turbulence in terms describing the interfacial interaction [5].

For the first time, probably, the bubbly and gas-droplet free axisymmetric jets were experimentally and theoretically studied in [6,7,8], respectively. Later, the approach of [7,8] was developed in [9,10] for isothermal two-phase jets. The next step in modeling the two-phase jets was the application of the k–ε-model, considering or neglecting the presence of a dispersed phase for the bubbly [6], gas-dispersed [11,12], and gas-droplet jets [13,14,15,16]. Data were obtained on the average velocity of drops and gas, fluctuations in the carrier phase velocity, the turbulent kinetic energy of the gas phase, the volume fraction of the dispersed phase in the gas jet, and the particle size and gas temperature distributions.

However, the conclusions in these works often contradict each other. For example, it was shown in [13] that the use of the Eulerian–Lagrangian (EL) approach is promising for describing the gas-droplet jets. The Eulerian–Eulerian (EE) description has an advantage over the EL method when compared with the measurement data and calculation time in [14]. The EE description is used to describe the transport processes in the carrier and dispersed phases. In the EL method, the carrier phase is described in Eulerian variables, while the dispersed phase is modeled using the Lagrangian approach. Turbulence in [11,12,13,14] is described by the isotropic two-equation k–ε model. A gas-droplet spray with and without droplet vaporization was measured in detail and simulated numerically in [16]. The Eulerian–Lagrangian approach was used to study the spray numerically. However, it was experimentally shown in [17] that there is significant anisotropy of the components of velocity fluctuations in gaseous and dispersed phases in a solid particles laden jet with solid particles. The EL approach was used in [18,19] to simulate the droplet-laden spray. The algebraic RSM [18] and RSM or SMC (the second-moment closure) were used in [18,19] to model the carrier phase turbulence. The spray structure was studied using the PIV measurements and numerical simulation. The detached eddy simulation and RSM methods were used to model the gas flow in [19].

It was experimentally shown in [20,21,22,23,24,25] that an increase in the fraction of gas bubbles leads to significant turbulence of a two-phase jet. Here, W_b and W are the volumetric flow rates of gas phase and carrier liquid, respectively, m³/s. Optical diagnostics of bubbly turbulent air-water jets was performed in [23,24]. A panoramic technique gives a possibility to measure simultaneously the instantaneous characteristics of both fluid and gas bubbles with a high spatial resolution. To determine the bubble shape in images, a neural network was developed in [24]. The local flow structure and turbulence attenuation in the upward bubbly jet were studied in [25] using Planar Laser-Induced Fluorescence (PLIF) and Particle Image Velocimetry (PIV).

The disadvantages of using isotropic k–ε models for modeling such flows are mentioned above, even taking the corrections used in predictions of free round or slot jet [26]. The methods of Large Eddy Simulation (LES) [27,28,29] and Direct Numerical Simulation (DNS) [30,31] provide fundamentally different possibilities to describe such flows. However, this requires the use of high-performance supercomputers, which limits the possibility of their application to describe flows for engineering applications. One of the ways to partially take into account anisotropy of components of the Reynolds stress tensor is to use more complicated turbulence models, such as the SMC. When using the SMC approach to describe gas turbulence, it is possible to avoid application of the hypothesis of carrier phase isotropic viscosity. The literature contains a number of works on the description of bubbly [32,33] and droplet-laden [18,19,34,35,36] free turbulent two-phase jets using the SMC model. Some of them [33,36] were published by the authors of this paper.

To date, the theory of applying the EE and EL models to describe two-phase turbulent flows has been developed (see, for example, monographs [1,2,3,37,38,39] and comprehensive reviews [4,40,41,42,43,44,45,46,47]). However, in general, all these studies refer to gas-dispersed flows with heavy particles. The theory of turbulent flows with drops and gas bubbles is developed to a much lesser extent. The reviews of the droplets’ dispersion, mixing, evaporation, and combustion in turbulent gas flows are given in [4,48]. All of abovementioned books and reviews study the sprays with droplet evaporation and combustion with solid particle-laden free round or slot jets.

A thorough validation of several dispersion models for gas-dispersed (laden with solid particles) and gas-droplets free round jets was carried out in [18]. The development of the mathematical model taking into account the effect of lift (Saffman) and turbulent dispersion forces was the main aim of [22]. The numerical study of the effect of diameter or volume fraction on flow structure and turbulence of bubbly and droplet-laden jets was not investigated in these papers, though. The authors of this paper did not find previous papers concerned with the study of arbitrary-density particles from gas flow laden with water droplets to carrier fluid flow laden with gas bubbles in a two-phase free round jet. However, we have tried to find some common features of such flow types. The authors did not find papers on the simulation of free round bubbly and droplet-laden turbulent jets, either.

To the authors’ best knowledge, there are a few papers concerned with the measurements and numerical simulations of the flow characteristics in submerged bubbly and gas-droplet free jets. This work is aimed at numerical simulation of the influence of the mean Stokes number and the fraction of the dispersed phase on the turbulent flow structure and dispersed phase propagation in the bubbly and gas-droplet free round jets. The range of initial parameters studied in our paper corresponds to those widely used in various practical applications. Similar publications are available [49], but they deal with the upward two-phase flow in a duct. The model of [49] covers the entire range of variation in the ratio of densities of the dispersed and continuous phases. The paper is the fundamental piece of research and it did not have a direct practical application. The authors think that this research has grounds for possible practical application, such as for intensification of mixing processes in chemical and biological reactors and for various spraying systems.

2. Mathematical Model

The problem of two-phase bubbly and gas-droplet free round jet dynamics is numerically solved. The system of Reynolds-averaged Navier–Stokes (RANS) equations is written by taking into account the effect of particles on the transport processes in the carrier phase. The Eulerian two-fluid approach is used to describe the dynamics of a two-phase flow. This flow is schematically shown in Figure 1. The carrier phase turbulence is described by the elliptical SMC model [50], written by taking into account air bubbles [32] or liquid droplets [35]. Fluctuations of the dispersed phase velocity components were calculated with the help of the kinetic equations given in [38]. The paper does not take into account the effect of droplet evaporation on the transport processes and carrier phase turbulence. The carrier phase (liquid) is considered as an incompressible flow, and the dispersed phase (air bubbles) serves as a compressible medium with its own pressure [32,33].

2.1. Bubbly Free Round Jet

2.1.1. Carrier Phase (Liquid)

The mathematical model of the bubbly flows is based on the EE approach [32,33]. The expressions for interfacial forces in [33] included only the averaged velocity of the carrier phase and did not consider the effect of the actual velocity of the gas phase. This is the main difference between this model and the other ones [32,33]. Here, we have taken the effect of actual gas velocity, the so-called gas velocity seen by the particle [18,51]. The carrier phase velocity seen by the droplet (gas bubble) position differs from the average velocity of the carrier phase, which is determined directly from RANS, by the value of the drift velocity [51]. The system of governing equations takes this form [33]:

$$\begin{array}{l}\nabla \cdot \left({\Phi }_l\rho \mathit{U}\right)=0,\\ \nabla \cdot \left({\Phi }_l\rho \mathit{U}\mathit{U}\right)={\Phi }_l\left(-\nabla P+\rho \mathit{g}\right)+\nabla \cdot \left({\Phi }_l\rho {\mathsf{\tau }}_V\right)-\nabla \cdot \left({\Phi }_l\rho 〈\mathit{u}\mathbf{\prime }\mathit{u}\mathbf{\prime }〉+{\displaystyle \sum _{k=1}^N{\mathsf{\sigma }}_k^{BI}}\right)+\\ +\left(P-P_{in}\right)\nabla \cdot {\Phi }_l+{\displaystyle \sum _{k=1}^N{\mathit{M}}_{lk}}\\ {\Phi }_l+\Phi \equiv 1\end{array},$$

(1)

Here and below, the index k is partially omitted to reduce the notation cumbersomeness. A bold variable indicates the vector parameter; $\Phi ={\displaystyle \sum _{k=1}^N{\Phi }_k}$; N is number of bubble groups; U_i (U_x ≡ U, U_r ≡ V), ${u^{\prime }}_i$ ($u^{\prime }{}_x\equiv u^{\prime },u^{\prime }{}_r\equiv v^{\prime }$) are components of the average carrier phase velocity and its fluctuations; P and $P_{in}=P_b=P-0.5\rho {\Phi }_l│{\mathit{U}}_R{│}^2$ are pressures in the liquid phase and on the surface of a spherical bubble, respectively [1,32]; ${\mathsf{\sigma }}_k^{BI}$ is the effect of bubbles of the k-th group on the tensor of averaged Reynolds stresses in the liquid phase [1]; τ_V and $〈\mathit{u}\prime \mathit{u}\prime 〉$ are tensors of viscous stresses and Reynolds stresses in the carrier phase, respectively; ${\mathit{M}}_l={\displaystyle \sum _{k=1}^B{\mathit{M}}_{lk}}=-{\mathit{M}}_b$ is interfacial interaction, detailed in [33]; g is the gravity acceleration vector; ${\mathrm{Re}}_{bk}=\left|{\mathit{U}}_{Rk}\right|d_k/\nu$ is the Reynolds number of a bubble from the k-th group; and ${\mathit{U}}_{Rk}={\mathit{U}}_S-{\mathit{U}}_{bk}$ is the average slip velocity. ${\mathit{U}}_S=\mathit{U}+〈{\mathit{u}}_S^{\prime }〉$; $〈{\mathit{u}}_S^{\prime }〉$ is the drift velocity between the liquid and particles [49].

The initial diameter of gas bubbles in this work varies within d = 0.2–2 mm. In the δ-approximation method, a polydisperse ensemble of particles is modeled by a system of monodisperse groups (modes or fractions); for this purpose, the continuous function of the distribution density over the mass (size) of the dispersed phase particles is approximated by the sum of a few δ-functions [51].

$$P\left(m\right)={\displaystyle \sum _{k=1}^B{N}_k\delta \left(m-m_k\right),}$$

where m_k = M_k/N_k is the mass of a particle of the k-th group, determined as the ratio of mass concentration of particles of the k-th group M_k to their numerical concentration N_k, and B is the number of particle fractions into which the continuous size spectrum is divided (in this work B = 4) and $N_k=6{\Phi }_k/\left(\pi d_k^6\right)$ is numerical concentration (m⁻³).

2.1.2. Dispersed Phase (Gas Bubbles)

The system of non-stationary equations for the k-th group of bubbles takes the following form [33]:

$$\begin{array}{l}\frac{\mathsf{\partial }{\rho }_b}{\mathsf{\partial }t}+\nabla \cdot \left({\Phi }_{bk}{\rho }_{bk}{\mathit{U}}_{bk}\right)=0,\\ \frac{\mathrm{D}\left({\Phi }_{bk}{\rho }_{bk}{\mathit{U}}_{bk}\right)}{\mathrm{D}t}={\Phi }_{bk}\left(-\nabla \cdot P-\frac{D_{bk}}{{\tau }_k}\nabla \cdot \left({\Phi }_{bk}{\rho }_{bk}\right)+{\rho }_b\mathit{g}\right)-\nabla \cdot \left({\Phi }_{bk}{\rho }_{bk}E〈\mathit{u}\prime \mathit{u}\prime 〉\right)+{\displaystyle \sum _{k=1}^N{\mathit{M}}_{bk}}.\end{array}$$

(2)

Here, $\frac{\mathrm{D}\varphi }{\mathrm{D}t}=\frac{\mathsf{\partial }\varphi }{\mathsf{\partial }t}+\mathit{U}\cdot \nabla \cdot \varphi$ is the total derivative, ϕ is the variable, τ is the relaxation time of gas bubbles written, and $D_{bk}={\Omega }_L〈\mathit{u}\prime \mathit{u}\prime 〉$ is the tensor of turbulent diffusion of the k-th fraction of bubbles or droplets [49,51].

$$E=\frac{\left(1-A\right)\left(1-A\Omega \right)}{\left(1+\Omega \right)},$$

(3)

Expression (3) is valid for the case of low-inertia gas bubbles at A > 1 [49]. $A=\left(1+C_{VM}\right){\rho }_0/\left(1+C_{VM}{\rho }_0\right)$ is the added mass parameter [49], ρ₀ = ρ/ρ_b, Ω = τ/T_L [38], where T_L = 0.3k/ε [38].

Non-stationary and convective transfer of the dispersed phase is described by the terms on the left side of the equation of the motion of the bubbles of the k-th group (2). The first term on the right side characterizes dispersed phase transfer due to pressure gradient, turbulent diffusion, and gravity force; the second term characterizes transfer caused by turbulent migration (turbophoresis) under the action of a turbulent stress gradient in the dispersed and carrier phases; and the last term describes the interfacial interaction.

The equation for numerical concentration of bubbles (the number of particles per unit volume) is written taking into account the approach [51]. It differs from the corresponding equations in [51] by the absence of terms that take into account the action of inertial, lifting, and near-wall forces, which are considered in this work in the form of individual force factors in Equation (2) (see [51]):

$$\begin{gathered} \frac{\mathsf{\partial }{N}_k}{\mathsf{\partial }{x}_j}+\frac{\mathsf{\partial }\left(U_{b,j}{N}_k\right)}{\mathsf{\partial }{x}_j}=\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}\left[\frac{1}{1+n}\left(D_T\frac{\mathsf{\partial }{N}_k}{\mathsf{\partial }{x}_j}+N_k\frac{\mathsf{\partial }\left(q_k{D}_T\right)}{\mathsf{\partial }{x}_j}\right)\right]+S_k^N, \\ \frac{\mathsf{\partial }{M}_k}{\mathsf{\partial }{x}_j}+\frac{\mathsf{\partial }\left(U_{b,j}{M}_k\right)}{\mathsf{\partial }{x}_j}=\frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}\left[\frac{1}{1+n}\left(D_T\frac{\mathsf{\partial }{M}_k}{\mathsf{\partial }{x}_j}+M_k\frac{\mathsf{\partial }\left(q_k{D}_T\right)}{\mathsf{\partial }{x}_j}\right)\right]+S_k^M. \end{gathered}$$

(4)

Here, $m\equiv {\displaystyle \sum _{k=1}^B{m}_k}$, $N\equiv {\displaystyle \sum _{k=1}^B{N}_k}$, $M\equiv {\displaystyle \sum _{k=1}^B{M}_k}$ are the mass of all particles, numerical and mass concentrations of air bubbles, and $n=\Phi {\rho }_b/\left[\left(1-\Phi \right)\rho \right]$. The terms on the left side of Equation (4) describe a change in the numerical concentration of bubbles of the k-th group due to the action of convective transfer. On the right side, the first term describes the turbulent diffusion and migration (turbophoresis) of bubbles. The last terms on the right side of Equation (4) denote the sources (sinks) of numerical and mass concentrations of gas bubbles due to break up and coagulation. The model of [52] is used to take into account the process of break up and the coalescence of bubbles. The bubble diameter varies both along the length and the radius of a jet due to break up and coalescence. All predictions presented in this paper were made for four δ-functions, similarly to [51,52]. Since the initial dispersed phase distribution in this work is not based on known experimental results, the share of bubbles in each fraction is 25% of their total number. The interfacial interaction is determined taking into account the action of the aerodynamic drag, the effect of the added mass, the forces of gravity and Archimedes, the Saffman force (lift force), and turbulent migration (turbophoresis) and diffusion of bubbles [33,53].

2.2. Gas-Droplet Jet

2.2.1. Carrier Phase (Gas)

When looking for a solution for the carrier phase, two-dimensional stationary axisymmetric RANS equations are used, which are written taking into account the influence of particles on the transport processes in the gas phase [38,39]. The break up and coalescence of droplets in the flow are not considered [36,40]. The gas-droplet flow is an incompressible medium with one pressure (P = P_in). The set of governing equations takes form (1). The function of Rosin–Rammler size distribution is used in this work to model a polydispersed two-phase flow at the inlet section. The mass fraction of droplets m_L with a diameter greater than d is calculated by the formula [39]:

$$m_L=\exp \left[-{\left(d/d_e\right)}^2\right],$$

where d_e is the average size of particles. The initial average Sauter droplet diameter is d₁ = 5–100 µm.

2.2.2. Dispersed Phase (Liquid Droplets)

The governing equations have the form [36]:

$$\begin{array}{l}\frac{\mathsf{\partial }\left({\rho }_L\Phi U_{Lj}\right)}{\mathsf{\partial }{x}_j}=0,\\ \frac{\mathsf{\partial }\left({\rho }_L\Phi U_{Lj}{U}_{Li}\right)}{\mathsf{\partial }{x}_j}+\frac{\mathsf{\partial }\left({\rho }_L\Phi 〈u_{Li}{u}_{Lj}〉\right)}{\mathsf{\partial }{x}_j}=\Phi \left(U_i-U_{Li}\right)\frac{{\rho }_L}{\tau }+\Phi {\rho }_{L}g-\frac{1}{\tau }\frac{\mathsf{\partial }\left({\rho }_L{D}_{Lij}\Phi \right)}{\mathsf{\partial }{x}_j}-\frac{\mathsf{\partial }\left(\Phi P\right)}{\mathsf{\partial }{x}_i}.\end{array}$$

(5)

Here, D_Lij is the tensor of dispersed phase turbulent diffusion [38], and ρ_L is the density of liquid droplet material. The system of Equation (5) takes into account a change in the amplitude of fluctuations of the dispersed phase velocity and concentration both in the longitudinal and transverse directions. The significantly non-isotropic character of amplitudes of turbulent fluctuations of particle velocity is considered. These equations do not take into account the Magnus and Saffman forces and the added mass effect because of the smallness of these force factors in comparison with those taken into account in this work. The radial movement of droplets is caused by momentum convection, viscous friction force, turbophoresis force (turbulent migration) due to inhomogeneity of the dispersed phase turbulent energy, and the turbulent diffusion of the dispersed phase associated with gradient of the volume fraction of droplets. The coefficients of turbulent diffusion of the dispersed phase in the momentum equations of System (5) are caused by the chaotic motion of droplets and their entrainment by energy-intensive vortices of the carrier phase, and are determined by the model of [38].

The system of Equations (1)–(4) for the bubbly jet and (1) and (5) for the gas-droplet jet is supplemented by equations for calculating the second moments of fluctuations in the dispersed phase velocity $〈{\mathit{u}}_L^{\prime }{\mathit{u}}_L^{\prime }〉$, given in [38]. The second moments of velocity fluctuations of a dispersed admixture in the longitudinal and transverse directions take into account the involvement of particles in turbulence due to the action of viscous forces, convective and diffusion transfers, and an increase in the intensity of the pulsating motion of the dispersed phase in the longitudinal direction initiated by generation of turbulence from the average motion.

2.3. SMC Model of Carrier Phase Turbulence for Bubbly and Gas-Droplet Flows

The Reynolds stress transport model was used to describe the liquid phase turbulence [50]:

$$\begin{array}{l}\nabla \left({\Phi }_l\mathit{U}〈\mathit{u}\prime \mathit{u}\prime 〉\right)=\nabla \cdot \left({\Phi }_l{D}_d\right)+{\Phi }_l\left(P_d+{\varphi }_d-\epsilon \right)+S_k,\\ \nabla \left({\Phi }_l\mathit{U}\epsilon \right)={\Phi }_l\frac{\epsilon }{k}\left[\left(C_{\epsilon 1}P-C_{\epsilon 2}\tilde{\epsilon }\right)+\nabla \left(C_{\epsilon 3}〈\mathit{u}\mathbf{\prime }\mathit{u}\mathbf{\prime }〉\right)\nabla \epsilon \right]+S_{\epsilon },\\ \tilde{\epsilon }=\epsilon -2\nu {\left[\nabla \cdot \left(\sqrt{k}\right)\right]}^2.\end{array}$$

(6)

Here, $2k=〈\mathit{u}\mathbf{\prime }\mathit{u}\mathbf{\prime }〉$ is the kinetic energy of turbulence (KET) of the carrier phase (liquid or gas). The turbulence model [50] was initially developed for the single-phase free round jet. Authors have modified it for the simulation of two-phase bubbly and droplet-laden free round jets. Authors have also modified them for the two-phase bubbly [33] and gas-droplet [36] free round jets. The developed models were validated against the experimental results of the previous papers (bubbly jet [33]) and the measured data presented by authors of [36]. The difference lies only in the last terms on the right side of (6). The last terms S_k and S_ε on the right sides of the first two equations of System (6) determine additional generation [32] and dissipation [51] of liquid turbulence in a bubbly free jet and additional dissipation of turbulence in a gas-droplet free jet [35,38].

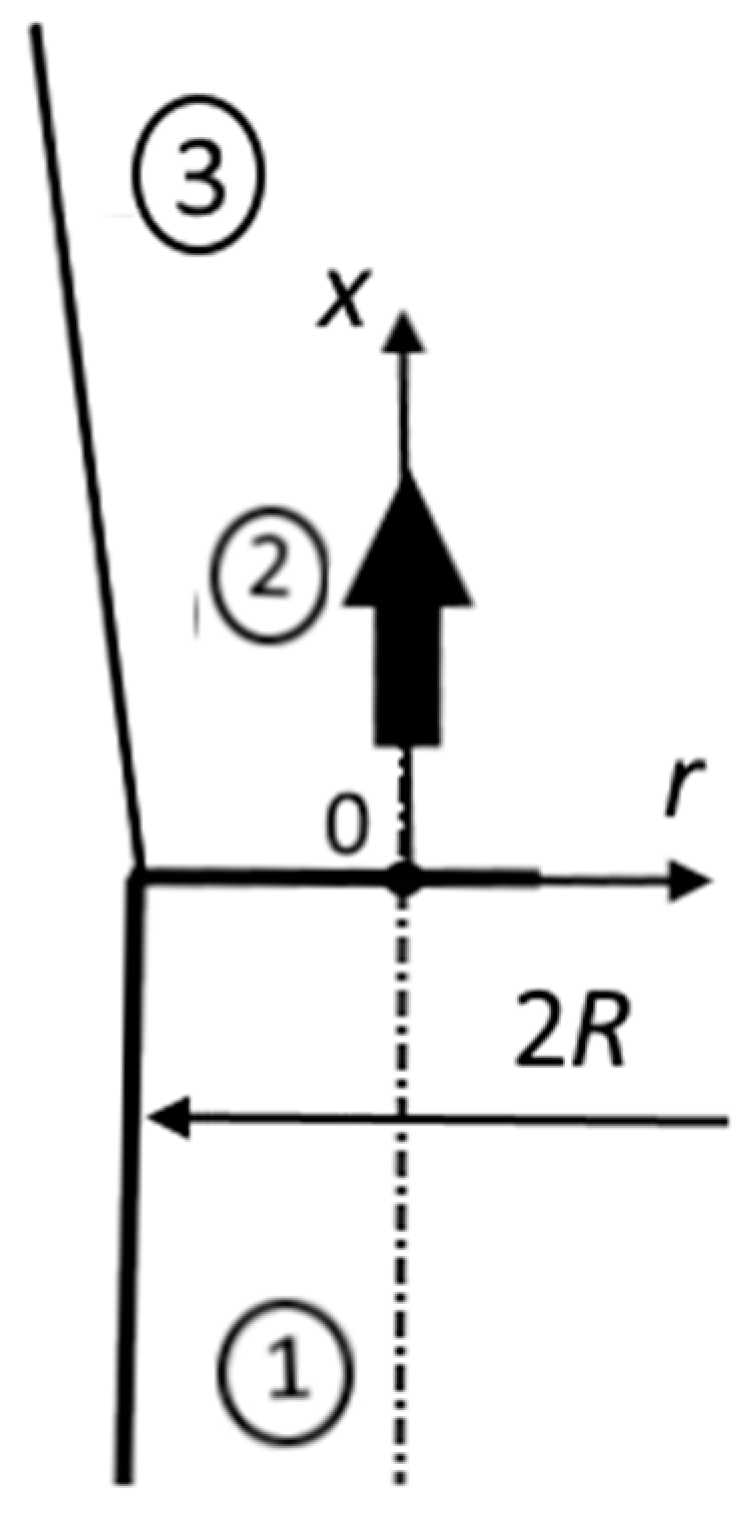
3. Numerical Implementation

The finite volume method on staggered grids was applied to obtain the numerical solution. For the convective terms of differential equations, the QUICK procedure of the third order of accuracy was used. The central difference scheme was used for diffusion terms. It has the second order of accuracy. To discretize time derivatives, the implicit Euler scheme of the first order of accuracy was applied. The pressure field was corrected according to finite volume SIMPLEC procedure. An uneven computational grid was utilized (thickening of the computational nodes in the areas of the pipe edge and the jet axis) (see Figure 2). In the radial direction, we used coordinate transformation so that the computational plane remained rectangular as the submerged jet expanded [33,36]. The radial coordinate was transformed so that the computational domain became rectangular [36]. In the inlet cross-section, uniform distribution of all parameters of a two-phase flow was specified. The symmetry conditions were set on the jet axis for both phases. On the outer boundary of the computational domain, the boundary conditions were set in the form of zero derivatives of the desired parameters in the axial direction. To perform simulations, the authors used their own in-house code.

The computational domain had the form of a cylinder. The length of the computational domain was 60R and its size in the radial direction was 25R. All calculations were carried out utilizing a grid (“basic”) with 100 × 412 control volumes (CV) in radial and axial directions. Additionally, calculations were carried out using the grids with 50 × 200 (“coarse”) and 150 × 600 (“fine”) CV. The time step was ∆t = 0.1 ms.

Comparison of calculation results for two-phase jets (averaged phase velocities and volumetric concentrations of the dispersed phase) obtained for the “basic” and “fine” grids showed that the maximum difference in the value of average velocities of the carrier fluid (liquid and gas) and the volume fraction of droplets or bubbles does not exceed 0.2% (see

Table 1. Axial velocity of the liquid U₀ and volume fraction Φ₀ on the bubbly jet axis for two stations on different grids for Re = 10⁴, 2R = 20 mm, T = T_b = 293 K, d = 1 mm, β = 5%.

Grid	x/(2R) = 10
	U0, m/s	Φ0, %
“coarse” 50 × 200	0.400	3.35
“basic” 100 × 412	0.44100	3.412
“fine” 150 × 600	0.44101	3.4122

and

Table 2. Axial velocity of gas U₀ and droplet volume fraction Φ₀ on the droplet-laden jet axis for two stations on different grids for Re = 10⁴, 2R = 20 mm, T = T_b = 293 K, d = 20 μm, M_L1 = 5%.

Grid	x/(2R) = 10
	U0, m/s	Φ0, %
“coarse” 50 × 200	7.318	3.95
“basic” 100 × 412	7.101	4.002
“fine” 150 × 600	7.0995	4.003

). The maximum error is $e_{\max }=\underset{i=1, N}{\max }\left|{\varphi }_i^n-{\varphi }_i^{n-1}\right|\le {10}^{-6}$, where N is the total number of cells, subscript i is the specific CV, and superscript n is the iteration level.

4. Comparison with Data from Other Works

4.1. Comparisons with Measurement Results for a Single-Phase Gas Jet

Comparisons were made with respect to the averaged and turbulent characteristics of an axisymmetric single-phase jet [54,55]. Good agreement was obtained with the measurements of [54,55] (the difference did not exceed 10–15%).

4.2. Comparison with Measurement Data for Two-Phase Submerged Gas-Dispersed, Gas-Droplet and Bubbly Jets

Previously, the authors of this work compared the numerical results obtained by this model with the measurement data of [6] for an isothermal upward bubbly jet. For a gas-droplet jet, the results were compared with experimental data obtained for an isothermal turbulent axisymmetric gas-droplet jet [36]. The results of these comparisons are presented in our previous publications [33,36] for the bubbly and gas-droplet jets, respectively, and are not shown here. Thus, a thorough verification of the developed model was previously carried out to calculate the dynamics of motion and propagation of the dispersed phase (gas bubbles and liquid drops) in a vertical submerged round jet.

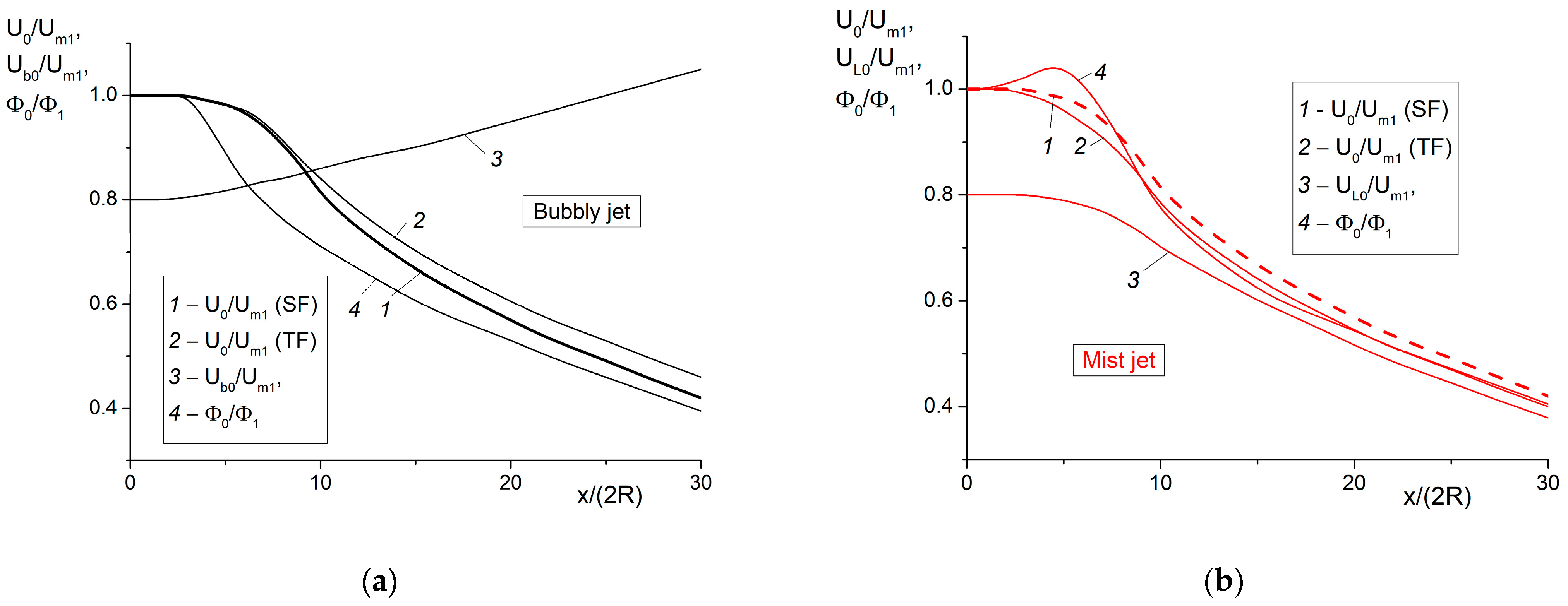
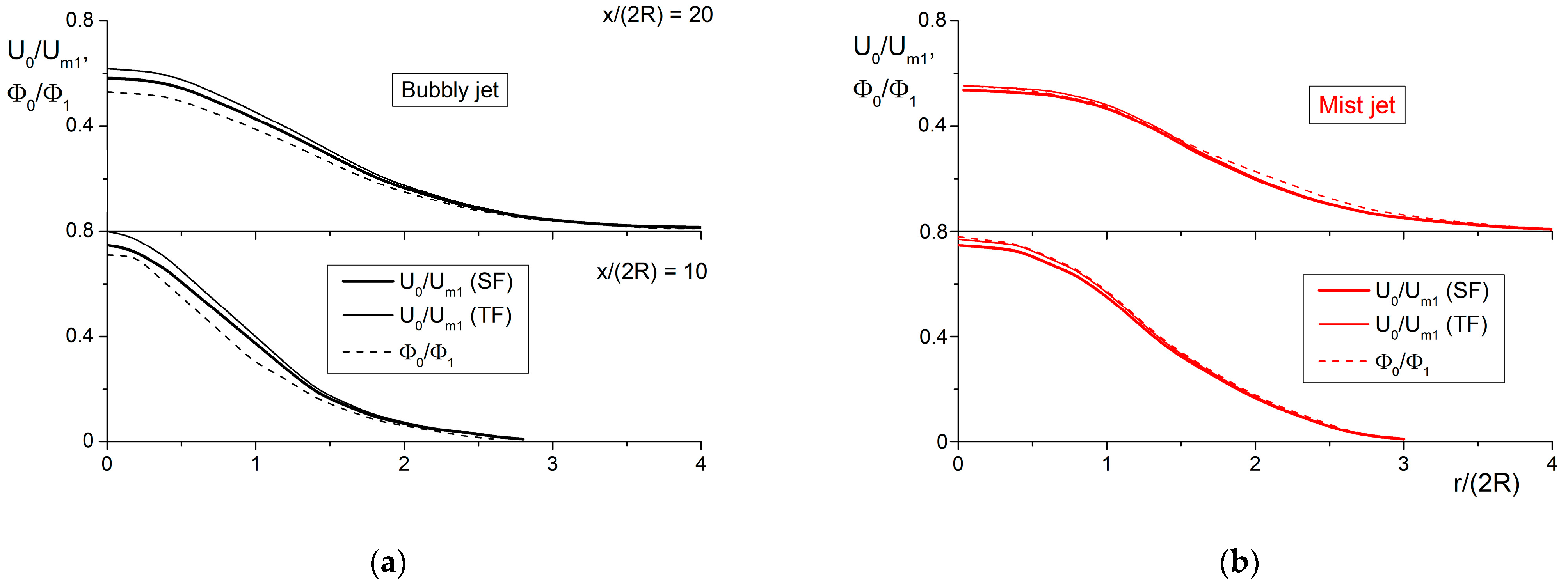
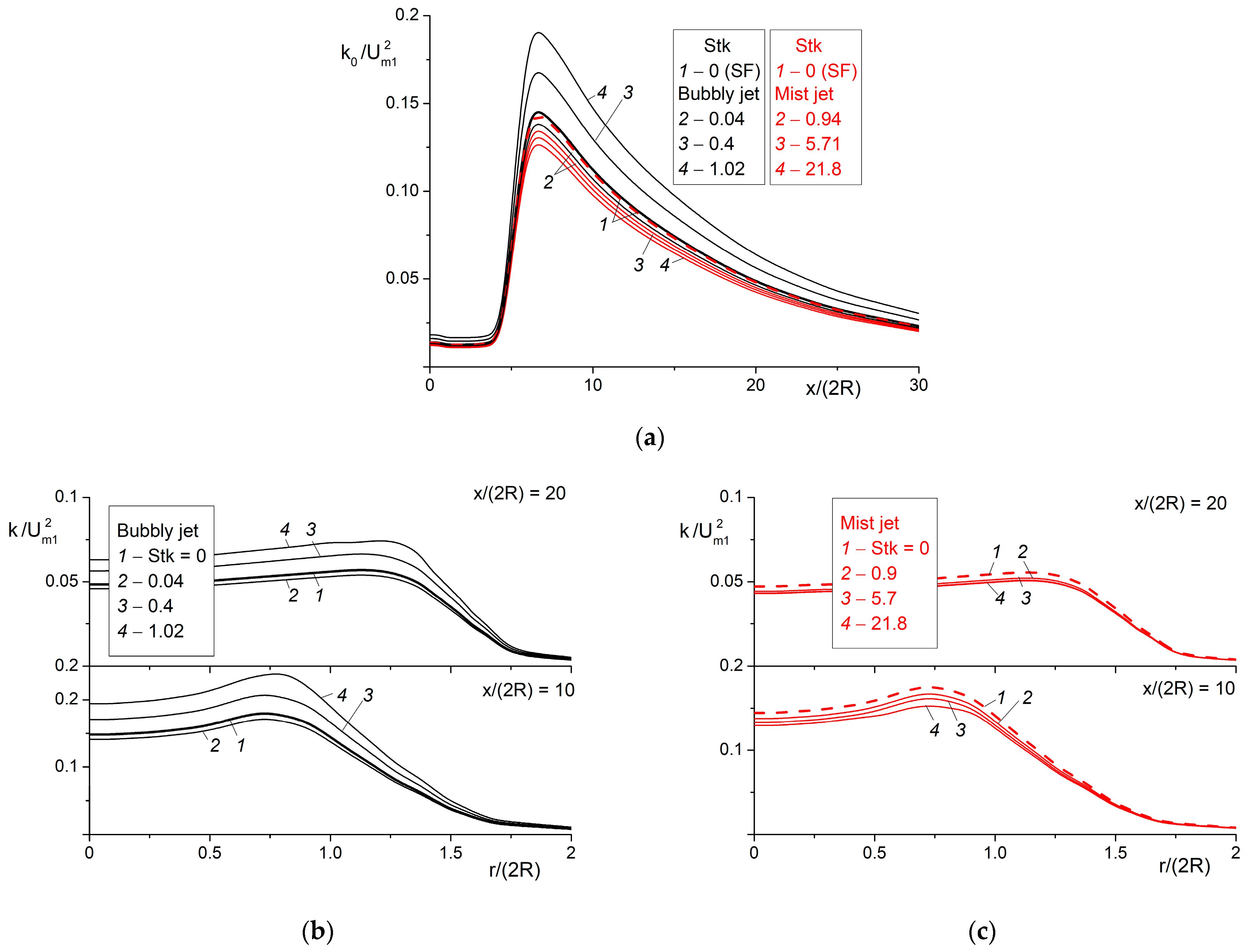
5. The Results of Numerical Simulation and Analysis

All numerical calculations were carried out for an upward isothermal flow of the following mixtures: (1) water and polydisperse air bubbles (bubbly jet), and (2) water droplets and air (gas-droplet jet). The inner diameter of the pipe from which the submerged jet flows out was 2R = 20 mm. The average mass velocity of liquid (water) was U_m1 = 0.5 m/s, and the gas (air) flow rate was U_m1 = 8 m/s. The Reynolds number of the carrier phase for the bubble and gas-droplet jets was Re = 2RU_m1/ν = 10⁴. Simulations are performed on the same geometry and Reynolds numbers for both bubbly and gas-droplet free round jets. The initial velocity of air bubbles was U_b1 = 0.8U_m1. Their average diameter in the inlet cross-section varied within d = 0.1–2 mm, and the gas volumetric flow rate ratio was β = 0–10%. The initial mass concentration of water droplets varied within M_L1 = 0–0.1; their average diameter was d = 5–100 µm. A fully developed flow was obtained at the pipe edge for a single-phase flow. The temperatures of the two-phase flow at the pipe edge and the temperatures of liquid in the quiescent environment were T₁ = T_b1 = T_L1 = T_f = 293 K.

One of the main parameters characterizing the behavior of particles in the flow is the Stokes number of the average motion, which is the ratio of time of dynamic relaxation to characteristic turbulent macroscale Stk = τ/τ_f. The ratio of the pipe radius to the average mass velocity at its edge τ_f = R/U_m1 was taken as a turbulent macroscale [56]. Here, $\tau =\frac{4d\left(1+0.5{\rho }_0\right)}{3C_D\left|{\mathit{U}}_{{}^R}\right|{\rho }_0}$ is the relaxation time of the gas bubble [49,51], C_D is the drag coefficient [49,51], $\tau ={\rho }_L{d}^2/\left(18\mu W\right)$ is the time of droplet relaxation, $W=1+0.15{\mathrm{Re}}_L^{0.687}$, and ${\mathrm{Re}}_L=\left|{\mathit{U}}_S-{\mathit{U}}_L\right|d_1/\nu$ is the Reynolds number of the dispersed phase. The ratio of the bubble or droplet diameter to the minimum Kolmogorov scale of turbulence in the near-wall region of the pipe outlet has the form [56]: $d/\eta ={\left(\frac{18\cdot \mathrm{Stk}\cdot \rho }{{\rho }_L\cdot {\mathrm{Re}}_L}\right)}^{0.5}\cdot \frac{{\mathrm{Re}}_{\tau }}{{\eta }_W^{+}}$, where ${\mathrm{Re}}_{\tau }=u_{*}R/\nu$ and ${\eta }_W^{+}\approx 1.6$ [56]. The Kolmogorov geometric ${\eta }_K=2R\cdot {\mathrm{Re}}_1^{-3/4}$ and time ${\tau }_K={\eta }_K^2/\nu$ scales were determined by formulas of [57]. Here, ${\mathrm{Re}}_1=2R\cdot 〈u_{01}^{\prime }〉/\nu$, $〈u_{01}^{\prime }〉$ is the gas velocity fluctuations on the pipe axis tion, and Stk_K = τ/τ_K is the Stokes number during the pulsating motion.

The Stokes numbers for bubbly and gas-droplet jets plotted from the flow parameters at the pipe edge are presented in

Table 3. Parameters of bubbly and gas-droplet jets determined on the inlet conditions.

Bubbly Round Jet
d, mm	τ, ms	τf, ms	DR = ρ/ρb	Reb	Stk	d/η	StkK
0.1	0.33	0.02	825	116	0.02	499	8 × 10−4
0.2	0.88			231	0.04	1343	2 × 10−3
0.3	1.55			347	0.08	2365	4 × 10−3
0.5	3.13			578	0.2	3519	6 × 10−3
1	8.01			1156	0.4	4777	8 × 10−3
2	20.31			2312	1	12,230	0.02
Droplet-Laden Round Jet
d, µm	τ, ms	τf, ms	DR = ρ/ρL	ReL	Stk	d/η	StkK
5	0.08	1.3 × 10−3	1.2 × 10−3	3 × 10−3	0.06	103	3 × 10−3
10	0.3			0.01	0.2	147	0.01
20	1.19			0.07	0.9	434	0.05
30	2.6			0.33	2.1	660	0.1
50	7.14			0.48	5.7	1408	0.3
100	27.3			0.72	21.8	2257	1.1

. Thus, the study was carried out at a change in the diameters of dispersed phase d, ratios of densities of the carrier and dispersed phases DR, turbulent macroscales τ_f, Reynolds numbers of the dispersed phase Re_L, Stokes numbers of the averaged Stk and fluctuating Stk_K movements, and ratios of the dispersed phase diameter to the minimum Kolmogorov scale d/η, but at close times of dispersed phase dynamic relaxation τ.

5.1. Flow Structure

The distribution of the jet half-width along its length with variation of the Stokes number (diameter of the dispersed phase) is shown in Figure 3 for the bubbly and gas-droplet jets. Here, $r_{0.5}^U$ is the distance from the jet axis, where the velocity of the carrier phase (liquid or gas) is equal to half its value on the jet axis (U = 0.5U₀) in the corresponding cross-section and U₀ is the carrier phase velocity on the jet centerline. The calculation for a single-phase air jet almost coincides with that for a liquid jet and is not shown in this figure. The length of the initial section of a single-phase liquid jet is x/(2R) ≈ 4.8. The addition of air bubbles reduces the length of the initial section in the bubbly jet and an increase in its width, and this effect becomes more evident with an increase in the Stokes number. For single-phase axisymmetric turbulent jets, the length of initial section is x/(2R) = 5–6 [54,55]. For a two-phase jet, the length of the initial section of the jet is x/(2R) ≈ 2.5 at β = 5% and d = 2 mm, and it decreases by 55%, approximately. An increase in the jet width indicates flow turbulence indirectly [33,54]. However, for the smallest bubble diameter at Stk = 0.04 and d₁ = 0.2 mm, the jet width decreases as in a gas-droplet flow. This confirms the data of many works (e.g., monographs [37,38,39]) on the suppression of the carrier phase turbulence by adding finely dispersed low-inertia elements (particles, droplets, or bubbles).

In contrast to the bubbly jet, the width of the gas-droplet jet decreases (up to 15% in comparison with a single-phase air jet) and this effect increases with an increasing Stokes number. This indicates the suppression of carrier phase turbulence and deterioration of the process of turbulent mixing with the surrounding space. These conclusions agree with the data for gas-dispersed [12,58,59,60] and gas-droplet jets [36]. With an increase in the Stokes number, an increase in the length of the initial section (up to 20%) is observed.

Distributions of axial average velocities of the carrier U₀/U_m1 (lines 1 and 2) and the dispersed U_b0/U_m1 (air bubbles) and U_L0/U_m1 (droplets) phases (3) and volume concentration of the dispersed phase Φ₀/Φ₁ (4) along the axis of the two-phase jet are presented in Figure 4. The parameters of the two-phase jet are related to the corresponding values in the inlet cross-section. The abbreviations “SF” and “TF” denote single-phase and two-phase flows, respectively. Let us note that in the inlet cross-section, the average velocity of the dispersed phase is 20% lower than the corresponding value for the carrier medium U_bm1 = U_Lm1 = 0.8U_m1. The carrier phase velocity (2) in the upward bubbly jet is higher than the corresponding value for the single-phase liquid jet (1). This relates to entrainment of the carrier liquid by gas bubbles (4) in the upward flow, since the interfacial force causes additional acceleration of the flow. The presence of droplets (3), whose velocity is lower than the corresponding value for the carrier gas phase (2) due to the action of gravity, leads to the fact that the force of interfacial interaction causes additional slight deceleration.

The effect of dispersed admixture pinching is observed in the initial section and Φ₀/Φ₁ > 1 when finely dispersed particles are added to the flow Stk = 0.94. The mass fraction of the dispersed phase then decreases gradually, which is consistent with the results of many works both with solid particles [12,37,58,59,60] and with liquid droplets [36]. An increase in the mass fraction of small particles in the axial region of the jet is explained by a change in the turbulent energy of gas in the axial and radial directions in the initial section of the two-phase jet [12,37]. We should note that a decrease in the volume fraction of the dispersed phase along the jet axis is more intense than a decrease in phase velocities.

Distributions of the carrier average axial velocity U/U₀ (lines 1), volumetric concentration of bubbles or particles Φ₀/Φ₁ (2), and average longitudinal velocities of the dispersed U_b/U_b0 (air bubbles) and U_L/U_L0 (droplets) (3) phases over a cross-section of the two-phase jet are presented in Figure 5. Here, U₀, U_b0, and U_L0 are axial average velocities of the carrier phase, gas bubbles, and water droplets on the jet axis in the current cross-section, respectively. Only the profiles of streamwise phase velocities are shown in Figure 4a, whereas Figure 4b demonstrates only the profiles of axial velocity of the carrier phase and volumetric concentration of the dispersed phase. The Reichardt profile [61] (dashed line 4) for a self-similar section of a single-phase submerged jet is also shown in Figure 5:

$$\frac{U}{U_0}=\exp \left[-{\left(\frac{1}{C_m\sqrt{2}}\frac{r}{x}\right)}^2\right],$$

where C_m = 0.071–0.08 is the coefficient of single-phase jet expansion [54], C_m = 0.075 (see [23,26]). The volume fraction of bubbles, droplets, and phase velocities lie below the Reichardt distribution [61]. The largest difference from the Reichardt profile reaches 80% at r/x = 0.1. Therefore, we can conclude that application of the self-similarity hypothesis [54] when calculating the parameters of two-phase bubble and gas-droplet jets in the considered cross-section is limited. This correlates with our previous papers [33,36].

The radial profiles of axial velocity (continues lines) and volume fraction (dashed lines) in bubbly (a) and droplet-laden (b) jets are presented in Figure 6. The difference between the distributions of parameters in bubbly and gas-droplets jets is quite noticeable. In the gas-droplet free round jets, the velocity of the gas phase and the volume fraction are very close to each other, which simplifies the engineering analysis of such flows. The gas velocity in a two-phase jet also differs slightly from that in the single-phase jet. In the bubbly jet, the fluid (liquid) velocity is higher than the corresponding value for the single-phase fluid jet (about 6%). The greatest difference (up to 10%) is observed between the distributions of velocity and the volume fraction of air bubbles.

A bubbly jet is characterized by a local maximum in the distribution of concentration for small bubbles (Stk < 0.08 and d₁ < 0.3 mm) and Φ_0,max = 1.1 (see Figure 7). For a gas-droplet jet, it was found that initially, with an increase in the averaged Stokes number (droplet diameter), a pronounced maximum of droplet concentration for bubble and gas-droplet jets appears on the jet axis and Φ_0,max = 1.18. Here, ${\Phi }_{0,\max }={\Phi }_{0,\max }^{TF}/{\Phi }_1$ and ${\Phi }_{0,\max }^{TF}$ is the maximum of bubble and droplet volume fraction on the axis. This is explained by an increase in the role of turbulent migratory transfer (turbophoresis force) [12,37,59,60]. It should be noted that directions of turbophoresis force action differ for the bubble and gas-drop flows. In the bubble flow, bubbles migrate from an area with a low carrier phase turbulence to a zone with its high level [49]. In a gas-droplet jet, the opposite is true: droplets are transferred from a region of high turbulence to a zone with a low level of kinetic energy of turbulence. If the Stokes number of the dispersed phase increases further, a monotonous decrease in dispersed phase concentration is observed for the bubble and gas-drop jets due to an increase in the role of turbulent dispersion.

5.2. Turbulence

Distributions of the carrier phase KET in the free round bubbly (black lines) and gas-droplets (red lines) jets at different values of the mean Stokes number Stk along the jet axis (a), in the radial direction at two-stations x/(2R) = 10, and 20 for bubbly (b) and mist (c) jets are shown in Figure 8. The turbulent energy of the gas phase was calculated for an axisymmetric jet using the formula: $2k=u\prime +v\prime +w\prime \approx u\prime +2v\prime$, and a sharp increase in the level of carrier phase (liquid) turbulence can be seen both in the single-phase and in bubbly and gas-droplet jets after the initial zone. Positions of the turbulence level maximum in the single- and two-phase jets almost coincide and are located at x/(2R) ≈ 7–8. Further, as the single- and two-phase jets propagate, the level of turbulence along the jet axis decreases significantly. This is due to their mixing with the surrounding quiescent environment and a decrease in concentration of bubbles and liquid droplets.

The level of KET of the carrier phase in the bubbly jet becomes significantly higher compared to the single-phase fluid jet (up to 25%). The value of turbulence in two-phase jets far from the inlet cross-section approaches the turbulence level for the single-phase jet (see Figure 8). Numerical calculations show that when gas bubbles are added to the carrier fluid (liquid), additional generation of turbulence takes place, which qualitatively agrees with the measurement data [21,23,25] and our previous predictions [33]. This confirms the data in Figure 3, which shows the expansion of a turbulent fluid (liquid) jet when air bubbles are added, except for the case of the smallest air bubbles, when turbulence is suppressed similar to the gas-droplet jets [36].

The kinetic energy of gas turbulence in the droplet-laden jet decreases compared to the corresponding value of a single-phase jet (up to 12%). This effect increases with an increase in the concentration of droplets and their diameters. This mechanism begins to dominate at large distances from the pipe outlet (x/(2R) > 20) for the two-phase jets, and the turbulence level approaches the corresponding value for a single-phase flow. The maximum value of KET is obtained in the mixing layer of the jet for both bubbly and gas-droplet free round jets (see Figure 8b,c). At the outer edge of the jet, the value of turbulence in two-phase jets coincides approximately with the corresponding value in a single-phase fluid jet.

The effect of the addition of finely dispersed droplets on a change in the maximum value of turbulence kinetic energy $K_{0,\max }=k_{0,\max }^{TF}/k_{0,\max }^{SF}$ on the axis of the two-phase bubble and the gas-droplet jets with varying dispersed phase concentration is shown in Figure 9. Here, $k_{0,\max }^{TF}$ and $k_{0,\max }^{SF}$ are the maximum KET values in two-phase and single-phase jets, respectively. Turbulence intensification in a free round bubbly jet with the addition of gas bubbles is observed with an increase in the Stokes number, and it reaches 20% at Stk = 1 (d₁ = 2 mm). The only exceptions are the smallest bubbles at Stk < 0.08 (d₁ < 0.3 mm), which are characterized by slight suppression of the turbulence level up to 10%. With an increase in volume fraction of gas bubbles, the level of turbulence of liquid increases (up to 20% as compared to the single-phase flow) due to the separation of the carrier fluid (liquid) flow around air bubbles. This leads to intensification of jet mixing with the surrounding environment. The KET of gas phase decreases in a gas-droplet jet (up to 10%) as compared with the one in the single-phase fluid jet. The additional dissipation increases with an increase in the droplet diameter and their mass fraction. This is mainly caused by the involvement of particles in the pulsating motion. The stronger suppression of turbulence with an enlargement of the mass fraction of particles is observed. The process of jet mixing with the environment becomes worse and this makes the jet narrower and gives it a longer range.

6. Comparison with Experimental Data for a Gas-Droplet Jet with Evaporating Droplets

Measurements of [62] were used for comparative analysis. The methods of Phase Doppler Interferometry/Planar Laser-Induced Fluorescence were applied to perform experiments in an upward air jet with evaporating acetone droplets. The diameter of a pipe from which the two-phase flow was blown out was 2R = 9.8 mm, and its length to the nozzle edge was 75 mm (the pipe length was x/(2R) = 7.7). The velocity of the co-current air flow was 3 m/s, and the level of turbulence there was Tu ≈ 2%. The mass flow rate of air was g = 2.25 g/s, and its temperature was T₁ = 275 K. The Reynolds number of the flow was Re = 15,800. The mass concentration of acetone droplets was M_L1 = 5% and concentration of its vapors was M_V1 = 4.3%. The initial Sauter diameter of particles was d₃₂ = 13.2 µm. The measurements of [62] were carried out for four fractions of droplets: d₁ < 5 µm (the authors of [62] used particles of this fraction as the tracers to determine the gas phase parameters), d₁ = 10–20 µm, 20–30, and 30–40. At that, the equations of energy in gas and dispersed phases as well as the equation of vapor diffusion into a binary gas-vapor mixture were added and numerically solved.

Distributions of the averaged axial phase velocities and the rates of their fluctuations over the jet cross-section are presented in Figure 10. For greater clarity, Figure 10 show comparisons only for the fraction of the largest particles. The averaged axial velocities of droplets and gas hardly differ from each other, which is characteristic of both our calculations and the measurements of [62] (see Figure 10a). This can be explained by the small inertia of particles. Attenuation of the axial velocity of particles due to their inertia is slower than that of the gas velocity, which leads to the fact that the gas velocity is slightly lower than the droplet velocity at x/(2R) = 20 and 25.

The results of a comparative analysis on the distribution of intensity of the axial and radial velocity fluctuations of the gaseous and dispersed phases are shown in Figure 10b,c, respectively. The intensity of axial fluctuations of the gas phase is higher than that of the droplet phase for all distances from the nozzle edge, despite the fact that the opposite pattern is observed in the initial cross-section. We can see significant anisotropy of fluctuations of the gas and dispersed phase velocities over the jet cross-section. This agrees with the data of our previous calculations [33,36] and the data of other works on two-phase round jets [17,58,59,60]. Radial fluctuations of the dispersed phase velocity over the jet cross-section are much smaller than those of gas fluctuations (see Figure 10c). This is due to the involvement of fine particles in the fluctuation motion of gas.

7. Conclusions

The motion and scattering of a dispersed phase of an arbitrary density in a free round turbulent jet are numerically studied. The dispersed phase dynamics are calculated using the Eulerian–Eulerian approach. The polydispersed distribution of gas bubble size is modeled by a set of monodisperse groups by the sum of δ-functions. The size distribution of droplets in the initial section is modeled by the Rosin–Rammler expression. The model takes into account the interphase momentum transfer, bubble break-up, and coalescence processes. The velocity fluctuations of the dispersed phase are determined using a system of kinetic equations.

An increase in the concentration of air bubbles and their size leads to jet expansion (as compared to a single-phase jet up to 40%), which indicates an increase in the intensity of the process of turbulent mixing with the surrounding space. However, this makes the gas-droplet jet narrower (up to 15%) and with a longer range in comparison with a single-phase flow. When air bubbles are added, liquid turbulence increases significantly (up to 30%). The addition of finely dispersed liquid droplets to an air jet suppresses gas phase turbulence (up to 15%). In a bubbly jet, it is found that small bubbles (Stk < 0.1) accumulate near the jet axis in the initial cross-sections, while concentration of the large ones (Stk > 0.2) along the jet axis decreases rapidly. In the gas-droplet jet, the effect of dispersed phase accumulation is also observed in the initial cross-section, and then its concentration decreases gradually along the jet axis. The turbulence level in a bubbly jet increases noticeably in comparison with a single-phase jet (up to 25%). The value of the kinetic energy of gas turbulence in a gas-droplet jet drops compared to the corresponding value in a single-phase jet (up to 12%).

8. Unresolved Problems

The results and main conclusion of this paper show a significant progress in the development of numerical models and experimental techniques of free round jets with a wide range of density-to-diameter ratios in the dispersed and carrier phases, but a few important problems in this area still have not been solved. This section is certainly incomplete. Undoubtedly, choosing unsolved problems is partially subjective, and has been motivated by the personal research interests of the authors. First of all, these are the effects of interaction between the dispersed phase (bubbles and droplets) and interaction between the carrier phase turbulence and the dispersed phase. Secondly, there is a comparison of heat transfer rates in these two-phase round jets and finding common and different points.