Abstract
Statistical process control (SPC) charts are commonly used to monitor quality characteristics in manufacturing processes. When monitoring two or more related quality characteristics simultaneously, multivariate control charts are often employed. Like univariate control charts, control chart pattern recognition (CCPR) plays a crucial role in multivariate SPC. The presence of non-random patterns in control charts indicates that a process is influenced by one or more assignable causes and that corrective actions should be taken. In this study, we developed a deep learning-based classification model for recognizing control chart patterns in multivariate processes. To address the problem of the insufficient representation of one-dimensional (1D) data, we explore the advantages of using two-dimensional (2D) image data obtained from a threshold-free recurrence plot. A multi-channel deep convolutional neural network (MCDCNN) model was developed to incorporate both 1D and 2D representations of control chart data. This model was tested on multivariate processes with different covariance matrices and compared with other traditional algorithms. Moreover, the effects of imbalanced datasets and dataset size on classification performance were analyzed. Simulation studies revealed that the developed MCDCNN model outperforms other techniques in identifying multivariate non-random patterns. For the most significant one, our proposed MCDCNN method achieved a 10% improvement over traditional methods. The overall results suggest that the developed MCDCNN model can be beneficial for intelligent SPC.
MSC:
37M10
1. Introduction
Shewhart control charts are the most widely used tools in statistical process control (SPC). The primary objective of a control chart is to determine whether a process is performing as expected or if there are any non-random patterns resulting from assignable causes. Among the various types of control charts, the commonly used univariate control charts are designed to monitor and control a single process variable or characteristic over time. They are typically used to monitor and control various aspects of the process, such as means, standard deviations, fraction nonconforming, and defect rates.
With advancements in data acquisition techniques, it has become common practice to monitor multiple correlated characteristics simultaneously. A widely adopted tool for monitoring and controlling multivariate processes is the Hotelling chart, which focuses on tracking the mean vector of the processes [1].
The Hotelling chart is briefly introduced as follows. Boldface lowercase letters indicate vectors, and boldface uppercase letters represent matrices in this context. The chart is based on the assumption that correlated characteristics are measured simultaneously, following a multivariate normal distribution with a mean vector and a covariance matrix .
Suppose that the random vectors , each of which represents the quality characteristics to be monitored, are observed over time. These vectors represent sample mean vectors from a sample of size . The well-known control chart is based on a measure of distance to the target mean vector () of the process. The statistic used in the chart for the th sample can be expressed as follows:
The upper limit of the control chart is where is the upper percentage point of the distribution with degrees of freedom. When monitoring the mean vector by using the chart, it is assumed that the covariance matrix remains constant as . When the in-control mean vector and covariance matrix are unknown, they are often replaced by the sample estimators and , respectively. The test statistic for the th sample can be expressed as follows:
The control procedure mentioned above is commonly referred to as the Hotelling multivariate control chart [1].
When implementing control charts, a process is considered out of control if any plotted points fall outside the control limits or exhibit a discernible non-random pattern [1]. In industrial processes, various non-random patterns may emerge, signaling out-of-control conditions such as trends, sudden shifts, mixtures, cycles, and systematic variations. A comprehensive description of these non-random patterns can be found in the Western Electric Handbook [2].
Non-random control chart patterns can provide useful insights regarding areas for potential process improvements. It is widely recognized that particular non-random patterns on a control chart are often linked to specific sets of assignable causes [2]. The early detection and diagnosis of control chart patterns is critical. Researchers generally agree that recognizing non-random patterns can assist the detection of out-of-control processes in a timely manner [3,4,5], which can narrow down the list of potential assignable causes that must be investigated, ultimately reducing the time and effort required for diagnostic searches.
Control chart pattern recognition (CCPR) is a significant challenge in SPC. It relies heavily on the expertise and experience of analysts to detect non-random patterns, which introduces a greater risk of human error in decision-making. Many supplementary tests (known as zone tests or run tests) have been proposed to detect whether assignable cause variation exists and to determine whether a process requires further investigation [2,6]. The main disadvantage of these tests is that, although they can detect abnormalities that represent out-of-control conditions, they do not reveal which non-random pattern may have occurred. Consequently, the non-random pattern and assignable cause do not have a one-to-one correspondence [4]. Several patterns might be associated with a specific test. Furthermore, performing supplementary tests might increase the risk of false alarms [1]. The aforementioned reasons therefore highlight the need for the development of machine learning (ML)-based control chart pattern recognition.
Studies on CCPR have primarily focused on univariate charts; limited attention has been given to multivariate control chart patterns. Similar to univariate charts, multivariate control charts are designed to identify general shifts instead of non-random patterns. Therefore, the conventional chart is inadequate for identifying patterns in multivariate processes.
Mason et al. [7] have noted that multivariate control charts might exhibit non-random patterns and have proposed several visual methods to identify these patterns on the chart. A trend can be characterized as a continuous movement of values in one direction. Distinct groupings of values signify a sudden shift. When values cluster above the zero line, this indicates a mixture pattern. The presence of repeated U shapes occurring with short periods represents a cycle. Their research findings emphasize that CCPR is a crucial task in multivariate process control. Figure 1 presents some examples of patterns that might occur in a multivariate process.
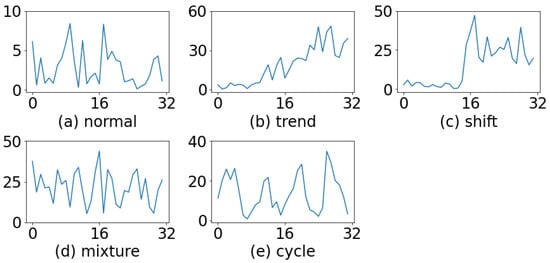
Figure 1.
Typical patterns shown on control chart.
When applying CCPR, the following two methods can be used: (1) the online real-time method, which involves continuous classification of data within a window, and (2) the activation of the pattern classification model when an abnormality is detected in the process by the judgment mechanism, such as the use of supplementary rules [2,6]. Notable studies related to the first approach include those conducted by Hwarng and Hubele [3] and Cheng [4], while representative studies of the second approach are the works of Pham and Wani [5] and Hassan et al. [8]. Previous studies often assumed that the shift pattern occurs near the middle of the window [5,8] or at some fixed positions [9], while other patterns appear from the first point in the window. These assumptions limit the diversity of data in the training dataset and affect the accuracy of classification in practical applications.
Hachicha and Ghorbel [10] conducted a review of more than 120 papers on CCPR and stated that past researchers had trained models in a static mode but had applied them in a dynamic manner. They emphasized the need for future work to address the issue of pattern misalignment in time, which had not been adequately considered in prior studies. The problem of misalignment is illustrated in Figure 2, in which the observed pattern is not temporally aligned with the learned pattern. In this figure, the dotted box represents an analysis window, and misalignment is evident. This misalignment can result in the pattern observed in the analysis window being marginally different from the pattern in the training dataset, thereby leading to incorrect classification.
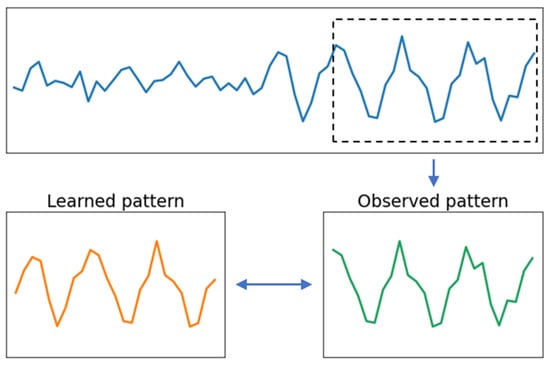
Figure 2.
Example of temporal pattern misalignment.
In the feature-based approach to CCPR, the pattern locations in the analysis window are typically assumed to be consistent between the training and testing datasets when developing discriminative features. This assumption oversimplifies the CCPR task and might lead to an overestimation of the classification accuracy rate. The same problem can also arise in models that use raw data as inputs.
Based on the review results of previous studies, we have observed that there are still research gaps in current studies. To meet the requirements of practical applications, it is crucial to consider the diversity and dynamic changes of non-random patterns. Classification models should be capable of extracting diverse features from different types of data.
Additionally, the difficulty of data collection in practical applications needs to be considered. The sample sizes of various non-random patterns may not be equal during the data collection phase, which can lead to an imbalanced dataset. Therefore, it is necessary to evaluate the performance of a classification model under the condition of unequal sample sizes in each class.
This study proposes the use of a multi-channel deep convolutional neural network (MCDCNN) architecture [11,12,13] that combines one-dimensional (1D) raw data and two-dimensional (2D) texture image data to create feature diversity. The purpose is to reduce the sensitivity of the classification model to the misalignments of the pattern in time while improving the accuracy of the classification model. A threshold-free recurrence plot (RP) [14] was constructed to obtain a 2D representation. Additionally, a new pattern generator was proposed to generate a highly diverse dataset. This diversity aims to enhance the classification model’s robustness in dealing with the dynamic nature of non-random patterns. The effectiveness of the proposed approach was investigated by applying it to multivariate processes with diverse covariance matrices and varying numbers of quality characteristics.
The rest of this paper is organized as follows. Section 2 provides information about related work on ML-based CCPR. Section 3 describes the proposed methods, including the RP plot, data generation method, and MCDCNN model for multivariate CCPR. Section 4 describes the experimental settings, simulated datasets, performance metrics and presents the experimental results. Finally, Section 5 summarizes the findings of this study and provides suggestions for future research.
2. Related Work
This section presents a literature review on topics relevant to the present study, including the identification and classification of control chart patterns and the use of 2D texture image transformation methods for analyzing time series data.
In recent years, numerous studies have investigated the usefulness of ML techniques for the identification of non-random patterns on a control chart. The primary goal is to enhance classification accuracy and provide a complementary tool to traditional control charts [15]. The adoption of ML-based classification models aims to emulate the analysis methods used by engineers. With the emergence of the industrial internet of things and artificial intelligence, collecting process data and utilizing intelligent decision-making models for analysis has become more feasible. Consequently, the demand for intelligent detection and diagnosis systems has increased over time [16].
Hachicha and Ghorbel [10] conducted an extensive analysis of existing research on the identification of control chart patterns. The approaches used for classification include rule-based methods [17,18], decision tree (DT) [5,19], artificial neural network (ANN) [4,20,21], and support vector machine (SVM) [22,23]. Previous studies have utilized either raw data as input vectors for the classification models [4,20] or hand-crafted features [5,9,19,24,25].
Previous studies have primarily focused on identifying single patterns. However, researchers have begun to investigate data that exhibit multiple basic pattern features, which are referred to as concurrent patterns [21,23,26,27]. The occurrence of concurrent patterns suggests that the manufacturing process is simultaneously influenced by several assignable causes. In a recent study, García et al. [28] conducted a comprehensive review of the research on concurrent patterns.
Although some researchers have employed ML techniques for multivariate process control, their focus has primarily been on identifying process mean shifts [29,30,31,32,33] or diagnosing sources of variability [34]. Some studies have used ML methods to develop approaches for detecting changes in multivariate process variance [35]. However, none of the mentioned studies were designed specifically to identify non-random patterns in multivariate processes. Few studies have explored non-random patterns in multivariate processes. Cheng and Cheng [36] developed a multivariate non-random pattern classification model using artificial neural networks (ANN) and support vector regression (SVR). However, their consideration of covariance matrices was limited to those with equi-correlation. Moreover, they assumed that all patterns except for the shift pattern begin at the first point within the window. While this assumption has been commonly used in previous research, it is impractical and may restrict the model’s generalizability.
Beshah and Muluneh [37] proposed a neural network-based approach to classify multivariate control chart patterns. They developed a classifier by using univariate data and assumed that the autocorrelation of multivariate data can be removed using a time series analysis method. After the autocorrelation was removed, a set of statistics was generated, and the standardized statistics were employed as the input vector for the developed classifier. It appears that the authors presumed that their classifier built using univariate data could be applied to classify the standardized statistics.
CCPR has been addressed with conventional ML techniques, such as SVM, multilayer perceptron neural networks and decision trees. However, the prevailing approach has shifted towards deep learning methods, with a particular focus on convolutional neural networks (CNNs) [15,38,39,40,41,42,43,44]. The reason for adopting the CNN approach in CCPR is the ability of deep learning models to learn discriminative features directly from the data.
Zan et al. [15] investigated six patterns using a window size of 32. This research examined five different periods for cycles to overcome the restrictive assumptions made in previous studies. The non-random patterns consistently began at the first point within the window in both the training and test datasets.
In [38], a window size of 32 was utilized. The shift pattern was assumed to occur between points 11 and 21 within the window. For other non-random patterns present in both the training and test datasets, the starting position of patterns was consistently fixed at the first point of the window.
In [39], Miao and Yang utilized a CNN network but first transformed the one-dimensional data into statistical characteristics and shape features, which were subsequently employed as inputs for the CNN. In their research, non-random patterns consistently appeared at the first position within the window. The positions where these patterns appeared remained fixed in both the training and test datasets.
In [40], the shift pattern appeared in three different positions within the window, whereas the other non-random patterns consistently appeared at a fixed position (the first point) within the window. These positions where non-random patterns emerged remained unchanged across both the training and test datasets.
Yu et al. [41] proposed the use of a stacked denoising autoencoder (SDAE) method to develop a classification system for process patterns. This research considered normal pattern and seven types of abnormal patterns resulting from changes in the process mean and standard deviation. The window size used in this study was 64, and the occurrence of abnormal patterns was approximately in the middle of the window. Importantly, these positions were kept consistent in both the training and test datasets.
Fuqua and Razzaghi [42] proposed a method called the cost-sensitive convolutional neural network to establish a classification system for non-random patterns in control charts. This research considered the impact of imbalanced datasets on classification results. They addressed both binary classification and multi-class classification problems. For binary classification, they treated normal data and a specific type of non-random data as a combination to construct a specific model. For multi-class classification, they considered normal pattern and multiple types of non-random patterns in the dataset. Since this study dealt with imbalanced data classification, they employed performance metrics such as accuracy rate, recall, precision, and F-score. Although the results of this study showed that the performance of the cost-sensitive convolutional neural network method outperformed that of other deep learning algorithms in building classification models, it should be noted that the comparisons were limited to specific combinations of non-random pattern parameters, and that the performance of their method across all non-random pattern parameter combinations could not be determined.
Zan et al. [43] employed the bidirectional long short-term memory network (Bi-LSTM) algorithm to develop a classification system for non-random patterns in control charts. They utilized a window size of 25, while the dataset consisted of a normal pattern and eight different non-random patterns. While considering multiple occurrence positions for certain types of non-random patterns, they maintained consistent position settings across both the training and test datasets.
Cheng et al. [44] utilized CNN to establish a classification model for non-random patterns in control charts. What sets this research apart from previous studies is the consideration of the pattern misalignment issue mentioned by Hachicha and Ghorbel [10]. This study allowed non-random patterns to appear at multiple positions within the window. Their research results demonstrate that CNN possesses the characteristic of translation invariance, enabling it to tolerate slight pattern misalignment issues.
The deep learning-based time series classification methods can be divided into 1D [45] and 2D schemes [46,47]. In the 1D scheme, raw data are used as the inputs and directly fed into the CNN model. The CNN model learns and extracts relevant features from the raw data to perform classification tasks. On the other hand, in the 2D scheme, the time series data are transformed into 2D forms before being fed into the subsequent CNN network. This transformation process converts the time series into an image-like representation. In comparison with the 1D scheme, the 2D scheme can potentially yield better classification accuracy, but at the expense of a more complex transformation process and increased network complexity.
Wang and Oates [46] proposed two methods for converting 1D time series data into 2D images, the two methods are the Gramian Angular Field (GAF) and the Markov Transition Field (MTF). After converting 1D data into 2D images, they employed a CNN to construct a time series data classifier. They compared the performances of different classification models on 12 datasets from UCR, and their findings indicate that higher classification accuracy was achieved when combining GAF and MTF images into a single image as the input for a CNN than when using GAF or MTF images alone.
Wang and Oates [48] divided GAF into two encoding methods: the Gramian Angular Summation Field (GASF) and the Gramian Angular Difference Field (GADF), used to convert time series data into 2D image data. GASF, GADF and MTF images were used as inputs for the three channels of a CNN. They compared their method to other algorithms using 20 datasets from UCR. Their research results showed that their proposed method outperforms most existing methods.
Martínez-Arellano et al. [49] presented a novel approach based on signal imaging and deep learning for tool wear classification. In their method, the GASF was used to automatically encode raw signals into images.
The recurrence plot proposed by Eckmann et al. [50] is also a common method for encoding 1D time series data into 2D images. Hatami et al. [47] proposed converting 1D time series data into 2D texture images using the RP method, and the application of CNN to establish a classification system. Their research results show that this method can improve the classification accuracy of time series data. They found that representing time series data with texture images can obtain different feature types not available in 1D time series data. They compared different methods using 20 datasets in UCR. The results show that the RPCNN method they proposed outperforms GAF-MTF.
Although the RP method is frequently used to analyze time series data, RP representations are rarely utilized to obtain features in previous studies on CCPR. While the RP method has been applied to a specific control chart pattern dataset in some studies [47,51], extensive feasibility studies have not been conducted. Chen and Shi [51] have indicated that the major disadvantage of RP representations is the loss of directional information for non-random patterns, particularly trend and shift patterns. Therefore, it is expected that a combination of 1D time series and 2D image encoding may be more effective.
Table 1 summarizes the key information of some recent relevant works. These recent works are not included in the survey study conducted by Hachicha and Ghorbel [10]. In the rightmost column of Table 1, the “fixed” label indicates that the shift pattern appears in the middle position of the window, while other non-random patterns appear in the first position of the window. Unless otherwise stated, the training dataset and the test dataset adopt the same position setting. The aforementioned configuration has been commonly used in the majority of previous studies. Analyzing Table 1 reveals that there are some research gaps in the existing studies when applying the CCPR model in practical applications. From Table 1, it can be observed that most of the previous studies assumed fixed positions of non-random patterns within the window, without considering the issue of pattern misalignment.

Table 1.
Summary of relevant works.
Because CCPR studies assume that only a portion of the observations is analyzed at a time, the position of non-random patterns appearing in the analysis window (or moving window) becomes a crucial factor affecting the correct classification. In previous studies, the position of non-random patterns occurrences was often oversimplified.
If the position of non-random patterns appearing in the window is fixed at the first point, it would make the patterns easier to distinguish, but it would also lead to an optimistic overestimation of classification accuracy. Additionally, in most studies, the position of non-random patterns in the window is set the same during both the training and testing phases, which further contributes to an overestimation of classification performance.
To meet the requirements of practical applications, it is necessary to consider a more diverse range of occurrence positions for non-random patterns in both the training and test datasets. Additionally, the diversity in the dataset needs to be increased. This also implies that the classification model should be capable of learning more diverse features from the data.
3. Methodology
This section outlines the two primary steps of the methodology, namely, the 2D image encoding using recurrence plot and the classification using MCDCNN. Additionally, to facilitate comparison, a brief overview of traditional classifiers is also presented.
3.1. Recurrence Plot
The recurrence plot is a technique created to visualize time series data [50]. The first step in obtaining the recurrence plot is to reconstruct the phase space of the time series. Given the original time series data as , and as the length of the time series, the phase space after reconstruction can be expressed as:
where is the embedded dimensions, and is the delay time. The subsequent is referred to as the state in the phase space, and is also known as trajectory. Each subsequence corresponds to a point in the phase space trajectory.
where , is a threshold distance, is the Euclidean norm. Here is a Heaviside step function that returns unity for positive argument and has value 0 for negative argument. In this approach, if two extracted trajectories and are sufficiently close to each other, the value of is set to 1; otherwise, it is set to 0. RP Plot is a graphical representation of the matrix R. The total number of states , determines the size of the recurrence plot. Equation (4) generates an image. Depending on whether or not a threshold was selected, the resulting image could be binary or grayscale. Because of the predefined distance, Equation (4) is regarded as binary. To extract additional information from the RP images, the un-threshold technique [14,52] is utilized in this study. The matrix can be defined as follows:
A detailed procedure for creating an unthresholded image from time series data is presented in Figure 3. We adhere to the procedure outlined in the work of Hatami et al. [47].
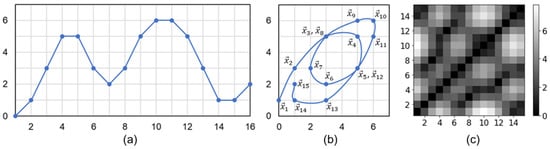
Figure 3.
The steps of coding time series data using recurrence plot: (a) a time series with length ; (b) the 2D phase space trajectory is constructed from by the time delay embedding (τ = 1), states in the phase space are shown with bold dots: : (, ), : (, ),, : (, ). (c) the recurrence plot is a square matrix with , .
Figure 4 illustrates a time series along with its unthresholded and thresholded recurrence plots. Figure 4a presents the raw data, while Figure 4b displays the unthresholded RP. Figure 4c illustrates the thresholded RP with a black point percentage of 20. In the context of recurrence plots, the black point percentage denotes the threshold that determines the intensity of the points plotted in the recurrence matrix. This percentage directly influences the contrast and clarity of the recurrence plot. A higher black point percentage will yield darker and more discernible black points, facilitating the identification of recurring patterns. Conversely, a lower black point percentage will generate lighter black points, potentially making it more challenging to discern recurrent structures.

Figure 4.
Example of unthresholded and thresholded recurrence plots with : (a) a time series of length ; (b) the unthresholded RP; (c) the thresholded RP with a black point percentage of 20.
3.2. Multi-Channel Deep Convolutional Neural Network
This section begins with a concise overview of the principles and the main operations of CNN. Following this, we provide a detailed description of the architecture of the multi-channel CNN model that we proposed in this study for classifying patterns on multivariate control charts.
CNNs have been widely used in the field of computer vision [53,54,55]. However, recent studies have shown that CNNs can also be applied to time series classification tasks [45,56], known as one-dimensional convolutional neural networks (1D CNNs).
In CNN architecture, there are three main layers: the convolution layer, the pooling layer, and one or more fully connected layers. Among these, the convolution layer plays a crucial role as it performs feature extraction through a combination of linear and nonlinear operations, involving convolution operations and activation functions.
The convolution layer, activation layer, and pooling layer are commonly grouped together as the convolution block. In CNN networks, these blocks are utilized to extract features, while fully connected layers are employed for the classification task. This integrated approach enables the creation of an end-to-end classifier that reduces the need for traditional feature engineering.
In the convolution block, the 1D convolution layer is utilized to extract feature maps. Different numbers of 1D convolution filters of the same size are applied in each layer, with deeper convolution blocks having more convolutional filters. The distance between two consecutive filter positions is referred to as the stride, which is commonly set to 1. To prevent the loss of spatial dimensions, zero padding is typically employed during the convolution operation. When applying a convolution layer, the hyperparameters that need to be determined include the filter size and the number of filters.
The output of the convolution operation is then passed through a nonlinear activation function. Commonly used activation functions include the identity, sigmoid, hyperbolic tangent, and rectified linear unit (ReLU) functions. The pooling layer performs a nonlinear form of downsampling. There are different types of pooling, with the most commonly used type being max pooling, which has a size of 1 × 2 and a stride of 2. The pooling layer helps reduce the dimensionality of the feature map, resulting in translation invariance for small offsets and deformations.
The output feature map of the final convolutional or pooling layer is typically flattened, resulting in a 1D vector that is connected to one or more fully connected layers. The number of neurons in these layers is commonly determined through experimentation. In classification tasks, the last layer of the network is composed of a number of neurons equal to the number of classes, with the softmax function being the preferred choice for activation. This function normalizes the output values from the last fully connected layer, producing class probabilities ranging between 0 and 1, with all values summing up to 1. The resulting probabilities represent the likelihood of each class, and the maximum probability value corresponds to the predicted class label.
During the training process, the network determines the weights of the filters and the fully connected layers to decrease the discrepancy between the actual class label of a sample in the training set and the network’s predicted value. The most critical elements of training are the loss function and the optimization algorithm.
Gradient descent is a widely used optimization algorithm that is used to iteratively update the learnable parameters (such as the weights of the filter and the weights of the fully connected layer) within a network in order to minimize loss. Some of the most common optimization algorithms include stochastic gradient descent (SGD), root mean square prop (RMSprop), and adaptive moment estimation (Adam) [57]. For multi-class classification tasks, categorical cross-entropy loss function is commonly used.
MCDCNN is an extension of the traditional CNN that can process input data with multiple channels [11,12,13]. The primary idea behind the MCDDNN model is to combine the features extracted from various channels. Each channel can focus on a particular aspect of the input data, enabling the network to learn more diverse and meaningful features. The channels can be considered as different views of the input, allowing the model to extract complementary information. For instance, in the context of images, different channels could represent different color channels (e.g., red, green, and blue) or additional information. This approach allows the model to utilize more comprehensive information and attain improved classification accuracy.
The architecture of an MCDCNN is similar to a standard CNN, but the input data have multiple channels instead of a single channel. Each convolutional layer in an MCDCNN operates on all input channels independently and computes separate feature maps. These feature maps are then combined through concatenation before being passed to the fully connected layer in the network. This study utilizes two channels: the first channel processes 1D raw time series data, while the second channel handles time series images encoded through the RP transform. The model architecture used in the experiments is depicted in Figure 5.
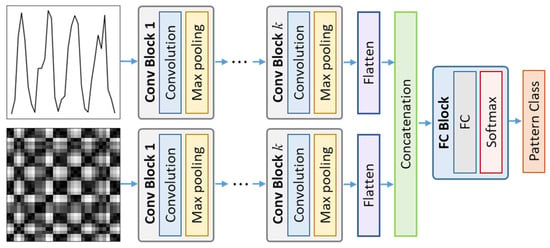
Figure 5.
The architecture of the MCDCNN model used in the experiments.
3.3. Traditional Machine Learning Algorithms
In order to conduct a thorough comparison, we have selected three commonly used machine learning algorithms suitable for analyzing time series data as our baseline models. These algorithms include support vector machine (SVM), random forest (RF), and time series forest (TSF). The following subsections offer a concise summary of each of these algorithms.
3.3.1. Support Vector Machine
SVM is a supervised learning technique that can be applied to both regression and classification problems [58]. The SVM algorithms used for classification and regression are commonly referred to as support vector classification (SVC) and support vector regression (SVR), respectively. This section introduces the underlying principles of SVC. SVC is based on the margin maximization principle. It performs structural risk minimization, which improves the complexity of the classifier with the aim of achieving excellent generalization performance. This technique uses various kernel functions to project nonlinear separable samples onto a separate higher dimensional space.
The SVC algorithm performs classification by creating an optimal hyperplane that divides the data into categories in a higher dimensional space. SVC was initially designed for binary classification. It can be extended to handle multi-class classification tasks through the use of the one-vs-one or one-vs-rest (OVR) method [59]. OVR is a heuristic technique that transforms a multi-class dataset into multiple binary classification problems. In the one-vs-one strategy, each pair of classes is split into a separate binary classification problem. To achieve optimal classification performance, it is crucial to appropriately select the parameters of the SVC classifier, such as the kernel width and the regularization constant .
3.3.2. Random Forest
Breiman [60] proposed the RF algorithm as a machine learning method that can address classification and regression problems by utilizing ensemble learning, which combines multiple classifiers to solve complex problems. The RF algorithm generates multiple decision trees by using bootstrap samples from a training dataset, while also employing a random feature selection technique. In this technique, a subset of available features is randomly chosen as the splitting variable in each node of the decision tree. The RF algorithm aggregates the outputs of all generated trees to produce a final prediction. Majority voting is used for classification tasks, while averaging is used for regression, to achieve the final prediction.
To optimize the performance of random forest models, it is crucial to select appropriate values for several hyperparameters. One important parameter is the number of features randomly chosen to split each node. Breiman [60] has recommended setting this value to one-third of the total number of predictors for regression and the square root of the number of features for classification. Another significant hyperparameter is the number of trees in the ensemble. Generally, the number of trees is increased until the model performance stabilizes. The final key hyperparameter is the maximum depth of the decision trees used in the ensemble. While a deeper tree may improve accuracy, it can also increase the risk of overfitting.
3.3.3. Time Series Forest
Deng et al. [61] introduced the TSF algorithm for classifying time series data. Unlike other algorithms that consider the entire time series, TSF focuses on intervals, or sub-series. To train an individual tree, the algorithm selects random intervals, where is the length of the time series. The mean, standard deviation, and slope of each interval are calculated and used as features, resulting in features for each tree. This interval representation of the time series is used for classification, with the final result being based on a majority vote of all the trees in the forest. The two important parameters of the algorithm are the number of trees in the forest and the minimum length of the intervals.
3.4. Generation of Datasets in Multivariate Processes
To build effective classification models, machine learning requires a large amount of training data. In practice, gathering non-random patterns is expensive. This is because the production process is mostly in a normal state and non-random data is rare. If non-random patterns can be represented mathematically, the simulation method is commonly used to generate the necessary dataset [4,62].
In the remainder of this section, we provide a description of the generation of simulated data. A -dimensional multivariate normal process can be simulated by generating pseudo-random variates from a multivariate normal distribution whose mean vector is and covariance matrix is a matrix. For simplicity, it is assumed without loss of generality that the in-control process mean vector is . It is also assumed that the in-control covariance matrix is known. A normal (or random) pattern will be generated by a general form expressed as follows:
where is the quality characteristics observed at time , represents a known process mean of the data series when the process is in control, is the random noise at time . When a non-pattern occurs, a second component, , is introduced to the process mean of the variable associated with an assignable cause. The quantity denotes a special disturbance at time . By manipulating the value of , a non-pattern can then be simulated. For example, when the first and third variables have non-random patterns (which can be of the same type or different types), then the mean vector will be represented as . In this study, four common non-random patterns on control charts were considered, namely, trends, sudden shifts, mixtures and cycles [7].
This study utilizes the formulas proposed by Cheng et al. [44] to generate the four aforementioned types of . What sets it apart from previous studies [5,9] is that the formulas they proposed includes an additional parameter , which is used to control the starting point of non-random patterns within the window.
In this study, the simulation was implemented using NumPy library for Python [63]. The specific function employed was “random.multivariate_normal()”. For simplicity, all variables were scaled such that each process variable has a mean of zero and a variance of one. With this approach, the covariance matrix is referred to as the correlation form [1]; that is, the main diagonal elements are all one and the off-diagonal elements represent the pairwise correlation () between the process variables. Each off-diagonal element ranges from and , inclusive.
Figure 6 illustrates the data variations that occur on the multivariate control chart when individual variables exhibit non-random patterns. This example includes three variables, and the correlation coefficient between each pair of variables is 0.7. Figure 6a represents the data with a trend in Variable 1, Figure 6b represents the normal data for Variable 2, Figure 6c represents the data with a trend in Variable 3, and Figure 6d illustrates the data variations observed on the control chart.
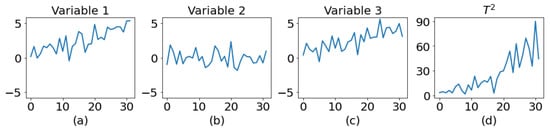
Figure 6.
Data variations on the multivariate control chart caused by non-random patterns in individual variables. (a) A trend in variable 1; (b) random variation in variable 2; (c) a trend in variable 3; (d) a trend on control chart.
4. Discussion
4.1. Experimental Settings
This section presents the comprehensive experiments conducted to confirm the effectiveness and benefits of MCDCNN. Additionally, we evaluate the performance of our approach by comparing it with several classification models.
The first two experiments aim to assess the performance of MCDCNN and other classification models on diverse datasets with varying covariance matrices. The second experiment also evaluates the capability of various classification models in the presence of multiple sources of assignable causes in the process. The third experiment is designed to investigate the impact of dataset size on classification performance. The fourth experiment examines how imbalanced datasets affect classification performance. Finally, the fifth experiment uses a covariance matrix estimated from real-world data to illustrate the effectiveness of the MCDCNN model. Through these experiments, it will be demonstrated that the innovative approach of combining 1D raw data with 2D image data and using them as inputs for MCDCNN will help it to learn more diverse dynamic features of non-random pattern data. It exhibits robustness against misalignment in time of non-random patterns and offers solutions to the challenges encountered in practical applications.
The remaining part of this section outlines the different experimental setups used in this study, which include (1) the input vectors utilized for various classification algorithms; (2) the dataset size and parameters for each pattern type; (3) the performance metrics used; (4) the settings of the CNN architecture; (5) the method used for determining the hyperparameters of the various algorithms; and (6) the software libraries employed by the various algorithms.
In the present application, selecting an appropriate window size is a crucial step. To achieve efficient calculations, it is desirable to reduce the window size as rapid computation is essential for process control. However, preliminary studies indicate that a window that is too small may result in a higher type I error due to insufficient data representation. Conversely, a large window size may require a longer computation time. After experimentation, a window size of 32 was chosen for this study. As a result, 32 statistics were computed as components of the input vector for CNN-based models. The 2D RP image size for MCDCNN was set to .
The total number of samples in the training, validation, and test sets was 3000, 1000, and 3000, respectively. The validation dataset provides an unbiased evaluation of a model fit on the training dataset while tuning the model’s hyperparameters. Table 2 shows the parameters for each pattern considered in this study. The parameters are stated in units of standard deviation.

Table 2.
Parameters used for simulating control chart patterns.
Despite the existence of several other performance measures, all the models were compared based on their classification accuracy in this study because it has been a widely used measure in the research of CCPR [10]. Conventional average run lengths (ARLs) are insufficient in describing the performance characteristics of a CCPR approach. The CCPR approach is designed to classify multiple patterns simultaneously, rather than addressing a general out-of-control situation. In order to have a direct comparison with other work, we select classification accuracy as the performance measure. Classification accuracy is a simple and useful metric on balanced classification problems, where the distribution of samples in the training dataset across the classes is equal. When dealing with imbalanced datasets, accuracy is no longer an adequate measure, since it does not distinguish between the numbers of correctly classified instances of different classes, leading to incorrect conclusions. In imbalanced classification scenarios, the score is a commonly used metric that combines precision and recall to provide a more comprehensive understanding of a model’s performance [64].
Precision measures the proportion of correctly predicted positive instances among all instances that are predicted as positive. It is calculated as:
where TP is the number of true positives (correctly predicted positive instances) and FP is the number of false positives (incorrectly predicted positive instances).
Recall measures the proportion of correctly predicted positive instances among all positive instances. It is calculated as:
where FN is the number of false negatives (positive instances that were not correctly predicted as positive).
score is the harmonic mean of precision and recall, and provides a single score that balances both metrics. It is calculated as:
When evaluating multi-class classification models, we can calculate these metrics for each class separately, and then calculate a macro or micro average of these metrics across all classes.
The micro-average recall, precision, and score are computed as follows:
The micro-average metrics treat all instances equally and provide a more representative evaluation of the overall performance of the model. These metrics are particularly useful when the dataset is imbalanced. On the other hand, the macro-average approach calculates the metrics for each class separately and then averages them, which can introduce bias towards classes with more instances. In the current application, the performance evaluation is based on the micro-average method. This decision is made because we need to treat every non-random pattern alarm equally.
Except for SVC, the performance of the other models was based on ten runs because these algorithms were not deterministic. All of the experiments were executed on a machine with an Intel Core i7-8700 3.20 GHz CPU and 32.0 GB RAM.
The 1D CNN and MCDCNN were implemented in Keras [57] with the TensorFlow backend. The RF and SVC algorithms were implemented in Python using scikit-learn v1.1.3 [59]. The TSF algorithm was implemented in sktime—a scikit-learn compatible Python library for machine learning with time series [65].
It is well known that the hyperparameters of the machine learning algorithms have a great impact on the experimental results. In this study, we chose hyperparameters after a series of experiments. For RF model, the number of features used for each decision split was set to the square root of the number of input features, i.e., the window size 32. We did not restrict the maximum depth of each tree. The number of trees was evaluated over a range of values. We increased the tree number until no further improvement was seen.
For SVC, the best combination of and is often selected by a grid search with exponentially growing sequences of and . In this study we fixed the kernel function as a radial basis function (RBF).
Choosing the appropriate hyperparameters for CNN networks can be challenging. In this study, the focus was on determining the size and number of filters, as well as the number of neurons in the fully connected layer for the network architecture. Regarding the training process, the batch size was the main parameter determined. The proposed architecture consists of two to three convolution layers and one fully connected layer. ReLU activation function was applied to all layers except for the output layer, which used the SoftMax layer. To mitigate overfitting, the dropout technique was employed, with the dropout rate set to different values.
The grid search method was employed to determine the size and number of filters while keeping the training parameters fixed. The filter size was chosen from {3, 5, 7, 9}, and the number of filters in each layer was selected from {16, 32, 64, 128}.
For the CNN-based models, training was performed by minimizing the categorical cross-entropy using Adam algorithm. The batch sizes have an impact on the classification performance. We experimented with different batch sizes to see how they would affect the classification results. The batch sizes were chosen from {16, 32, 64, 128, 256} based on their performance on the validation set.
The CNN-based models were trained up to 50 epochs with a learning rate of . To avoid overfitting, an early stopping procedure was employed; specifically, the loss value of the validation set was monitored in each epoch and the training procedure was halted if training yielded no improvements within the previous three epochs.
In order to address the temporal misalignment issue raised by Hachicha and Ghorbel [10], this study removed the limitations on the starting point that were present in previous research. For ease of presentation, let and . and are used to define the possible values of . Through the configuration of the parameter, we will be able to demonstrate that the innovative approach of combining 1D raw data and 2D image data in MCDCNN can effectively address the problem of misalignment in time for non-random patterns.
4.2. Results
4.2.1. Experiment 1
Consider a multivariate process with in-control covariance matrix expressed as:
This symmetric, positive definite matrix is randomly generated using the “make_spd_matrix” function of the scikit-learn package [59]. The first variable in this matrix is the source of assignable cause and is negatively correlated with the other variables.
Here are the descriptions of the optimal hyperparameter settings for each model. For RF, the n_estimator parameter was set to 800. An RBF kernel was employed in the SVC, and the optimal performance was attained by setting the values of and to 8 and , respectively. TSF was configured with 400 trees and a minimum interval length of 8.
The MCDCNN architecture comprises two channels. In channel 1, 1D raw data are utilized as inputs, while channel 2 employs 2D RP images as inputs. Each channel within MCDCNN consists of an equal number of convolutional layers and parameters but possesses independent weights. Initially, the model learns features from each channel separately. Subsequently, the information from all channels is merged into a comprehensive feature representation in the final layer. Finally, the learned features are passed through a fully connected hidden layer for classification purposes. The architectures for 1D CNN and MCDCNN are presented in Table 3 and Table 4, respectively. The batch size for both models was set to 128.

Table 3.
1D CNN architecture.

Table 4.
MCDCNN architecture.
Table 5 presents a comparison of means and standard deviations for various models with . The average accuracies of RF, TSF, SVC, and 1D CNN are 94.15%, 91.86%, 95.57%, and 95.83%, respectively. Notably, our proposed MCDCNN model achieves the highest accuracy among all the models, which is 97.24%

Table 5.
Results of experiment 1, for the training and testing processes.
To investigate the effect of on the classification performance, we conducted an experiment with for the training dataset and for the test dataset. The following are the best hyperparameter settings based on the experimental results. The parameter n_estimator of RF was set to 700. The best performance of SVC was achieved when it was used with an RBF kernel with the parameters and set to 16.0 and , respectively. The number of trees was set to 400 for TSF, and the minimum length of interval was set to 8. For 1D CNN and MCDCNN, the same architectures as presented in Table 4 and Table 5 were adopted without further tuning. The batch size for both CNN-based models was set to 128.
The obtained results are shown in Table 6. Again, MCDCNN achieves significantly better results than other models. Comparing the results of Table 5 and Table 6, it can be observed that, as the change of increases, the classification accuracy drops sharply. However, the proposed CNN is less affected by the variation of . The MCDCNN model, based on 1D raw data and 2D images, can achieve an average accuracy of 96.67%, reflecting the potential of CNN using 1D and 2D features.

Table 6.
Results of experiment 1, for the training process and for the testing process.
The classification accuracy of the models considered in this experiment shows the same trend as the previously discussed experiment. It is worth noting that TSF provides stable results even when varies. This may be attributed to its nature of extracting features from random intervals. Therefore, the TSF algorithm is less affected by changes in .
To further analyze and compare the classification accuracy of different classification models, a confusion matrix is utilized to display the classification accuracy of various models for different patterns. The diagonal elements of the confusion matrix represent the number of cases where the predicted label matches the true label, while the off-diagonal elements correspond to cases that are misclassified by the classifier.
Figure 7 illustrates the confusion matrices obtained from the test dataset’s classification outcomes for the SVC, 1D CNN, and MCDCNN algorithms when was used for both training and testing phases. In general, the MCDCNN algorithm performs better than the other two models, except for the cycle. On the other hand, Figure 8 shows the confusion matrices for during the training process and during the testing process. The results indicate that the MCDCNN algorithm outperforms all other classification models for all patterns.

Figure 7.
Confusion matrices for different classification models when for the training and testing processes.

Figure 8.
Confusion matrices for different classification models when during the training process and during the testing process.
4.2.2. Experiment 2
This experiment considers a covariance matrix estimated from real world data [66], which has been studied in [67,68]. This example concerns the testing of ballistic missiles, where four () related thrust measurements are recorded for each test firing. The covariance matrix was estimated from 40 measurements, and its representation in a correlational form () is as follows:
In this matrix, all variables are positively correlated with other variables. It is assumed that the first variable in this matrix denotes the source of the assignable cause.
According to the experimental results, the following are the best system settings. The number of trees in the RF model was set to 400. For TSF, the number of trees was set to 900. The minimum interval length was set to 8. The parameters and for SVC were set to 8.0 and , respectively. Both 1D CNN and MCDCNN employed the same architectures as those listed in Table 3 and Table 4, respectively, without undergoing any additional tuning. Each CNN-based model used a batch size of 512 during the training phase.
Table 7 presents the classification results of various models where during the training and testing processes. As shown in Table 7, the MCDCNN model achieves much better performance than all the other models in terms of testing accuracy. The MCDCNN model outperforms SVC significantly with an accuracy of 97.26% compared with 95.20%.

Table 7.
Results of experiment 2, the first variable represents the source of the assignable cause, for the training and testing processes.
To better illustrate the advantages of the CNN-based models, we consider the case where for the training process and for the testing process. The following are the best hyperparameter settings based on the experimental results. For the RF model, the number of trees was set to 600. For TSF, the number of trees was set to 800, and the minimum length of the interval was set to 8. For SVC, the parameters and were set to 32.0 and , respectively. A batch size of 512 was utilized for training each CNN-based model. The test results of the five competing models are presented in Table 8. As shown in Table 8, the performance of the classification model deteriorates when varies. When the values of in the training dataset differ from those in the test dataset, the classification accuracies of RF and SVC show a sharp decline. The CNN-based models, on the other hand, are less affected by variations in . Again, the MCDCNN model outperforms all the other models, as demonstrated in Table 8. From Table 8, it can be seen that the MCDCNN model has achieved the highest accuracy of 96.81%. The average accuracy of the 1D CNN is 93.39%. These results indicate that the MCDCNN model significantly improves the classification accuracy of 1D CNN. The SVC model achieves an accuracy rate of 91.47%. When compared with the SVC model, the 1D CNN model outperforms the SVC model. The TSF model has an accuracy of 91.59%, which is comparable to the SVC model. It is also worth noting that TSF produces consistent results even when varies. The RF model exhibits the lowest classification accuracy among the five models, with an accuracy of 88.14%.

Table 8.
Results of experiment 2, the first variable represents the source of the assignable cause, for the training process and for the testing process.
It is possible that multiple variables may change simultaneously. Therefore, we further considered the case where the first and third variables are sources of non-random variation. According to the experimental results, the following are the best system settings. The number of trees in the RF model was set to 500. For TSF, the number of trees was set to 900, and the minimum interval length was set to 8. The parameters and for SVC were set to 1.0 and , respectively. Both 1D CNN and MCDCNN utilized the architectures outlined in Table 4 and Table 5, respectively, without undergoing any additional tuning. Each CNN-based model used a batch size of 256 during the training phase. Table 9 presents the classification results of various models for during the training and testing phases.

Table 9.
Results of experiment 2, the first and third variables represent the sources of the assignable cause, for the training and testing processes.
Table 10 displays the results for the case where for the training process and for the testing process. The optimal hyperparameter settings, as determined by the experimental results, are as follows. For the RF model, the number of trees was set to 400. The number of trees was set to 600 for TSF. The minimum length of interval was set to 8. For SVC, the parameters and were set to 4.0 and , respectively. The 1D CNN and MCDCNN employed identical architectures as those listed in Table 3 and Table 4, respectively, without any further tuning. A batch size of 256 was utilized for training each CNN-based model.

Table 10.
Results of experiment 2, the first and third variables represent the sources of the assignable cause, for the training process and for the testing process.
Comparing Table 7 and Table 8 with Table 9 and Table 10 reveals a significant change in the performance of the classifier when two positively correlated variables are changed simultaneously. This is primarily due to the fact that, when such variables change together, the value of increases compared with a situation in which only one variable is changed. This results in a more prominent and apparent change in the pattern. Figure 9 presents a visual representation of the changes in the statistics of shift pattern and cycle under two different conditions, which effectively illustrates the phenomenon mentioned earlier.
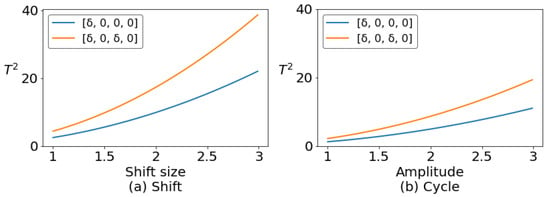
Figure 9.
The variation of statistics when multiple variables changed at the same time.
4.2.3. Experiment 3
The impact of dataset size on CNN classification performance is widely recognized. This experiment aimed to examine the impact of dataset size on classification performance using the covariance matrix . We trained all the algorithms using six different sizes of training dataset (1500, 3000, 4500, 6000, 7500, and 9000), referred to as . The subscript denotes the multiple of the original dataset size.
The following are the optimal hyperparameter settings for each model. For the RF model, the number of trees was set to 600. For TSF, the number of trees was set to 0. The minimum length of interval was set to 8. As for SVC, the parameters and were set to 1.0 and , respectively. The architectures presented in Table 3 and Table 4 were utilized for both 1D CNN and MCDCNN, without any additional adjustments. Throughout the training process of each CNN-based model, a batch size of 256 was employed.
Figure 10a displays the impact of the training dataset size on the classification accuracy under the condition that is used for both training and testing phases. The horizontal axis represents the size of the training dataset, and as it increases, all five machine learning models exhibit improved performance. Figure 10a illustrates that, regardless of the method employed, the classification accuracy rate does not improve significantly when the dataset size goes beyond . The MCDCNN method demonstrates the best classification performance, while TSF performs the worst. Figure 10b depicts the effect of the training dataset size on the classification accuracy when is used for the training process and is used for the testing process.
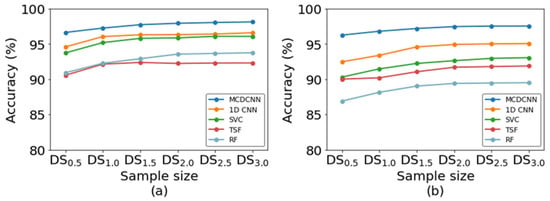
Figure 10.
The impact of the training dataset size on the classification accuracy. (a) is used for both training and testing processes; (b) is used for the training process and is used for the testing process.
4.2.4. Experiment 4
It is widely recognized that imbalanced datasets have a significant impact on the classification performance of machine learning algorithms. Imbalanced datasets contain unequal numbers of instances in each category. In SPC, this may be due to the natural distribution of non-random patterns. For instance, some patterns may be less common than others, resulting in an imbalanced dataset. The issue with training a model on an imbalanced dataset is that the model tends to be biased towards the majority class. While this study used simulated data, an experiment was designed to explore the influence of imbalanced datasets in practical applications.
In order to create an imbalanced scenario, the original sample size of the normal pattern was maintained while one of the non-random patterns was reduced to 20% of its original size, yielding a sample size of 120 with 40 samples per parameter. The remaining three non-random patterns were assigned random sizes of 40%, 60%, and 80% of their original sizes. As a result, the ratio of the number of normal pattern data to the total number of non-random pattern data in this experiment was 1:2.
For both 1D CNN and MCDCNN, the architectures outlined in Table 3 and Table 4 were employed without any modifications. During the training of each CNN-based model, a batch size of 256 was used. Table 11 presents the results for different settings, with each setting repeated 10 times to allow each pattern to be randomly assigned at 40%, 60%, and 80%. In imbalanced settings, we computed the recall, precision, and score. In this scenario, we considered the case where for the training process and for the testing process.

Table 11.
Results of experiment 4, for the training process and for the testing process.
As shown in Table 11, our proposed method outperforms 1D CNN in handling imbalanced data. The MCDCNN learns the features in 1D raw data and 2D image data, it produces more accurate models as reflected by the higher scores shown in Table 11. Further analysis reveals that, when there is a significant imbalance in the amount of data among different categories, the performance of the category with less data will be heavily affected, except in the case of the mixture pattern, which is less susceptible to imbalanced data.
4.2.5. Experiment 5
To demonstrate and validate the effectiveness of the proposed MCDCNN method in learning dynamic characteristics of non-random patterns and its application to online analysis, we employ real-world data obtained from a detergent manufacturing company, as described in the work of Niaki and Abbasi [68]. The data were obtained from the sulfonation process, and three correlated parameters, namely color, free oil percentage, and acidity percentage, are of high importance. The data obtained from 10 days were used to estimate the mean vector and covariance matrix. The mean vector of these data is
The covariance matrix is
The estimated mean vector and covariance matrix were used to generate non-random data for illustrative purposes.
This experiment uses a moving window approach to demonstrate and compare the performance of different models through online analysis. The size of the moving window is set to 32. At each step, the window advances to include a new observation and discard an old one. This method ensures a constant number of observations within the window.
Figure 11 presents the results of various models in detecting and classifying trend patterns. For the purpose of explanation and comparison, we made adjustments to the data, with the non-random pattern starting from the 33rd observation. As seen in Figure 11, the MCDCNN correctly identifies the non-random pattern as a trend pattern in the 15th analysis window (composed of observations from the 15th to the 46th data point). The 1D CNN model, on the other hand, detects the trend pattern in the 18th window. The SVC, TSF, and RF models detect the trend pattern in the 21st, 20th, and 21st windows, respectively. It is evident that the MCDCNN model outperforms the 1D CNN model and traditional machine learning models. These results align with the findings from previous experiments.
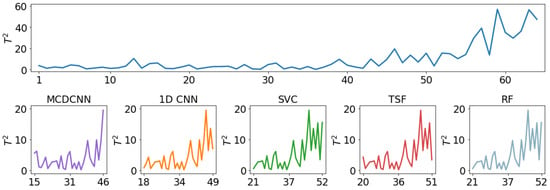
Figure 11.
The results of various models in detecting and classifying the trend pattern.
Figure 12 displays the results of various models in detecting and classifying the shift pattern. The MCDCNN, 1D CNN, SVC, TSF, and RF models identify the shift pattern in the 16th, 22nd, 23rd, 23rd, and 25th windows, respectively. Based on these results, it is evident that the MCDCNN model is still capable of detecting the shift pattern earlier than the other models.
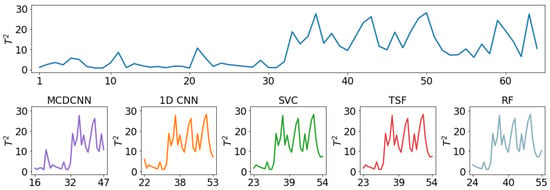
Figure 12.
The results of various models in detecting and classifying the shift pattern.
The experimental results presented above reveal several important findings. Firstly, the simulation results indicate that the proposed MCDCNN model performs better than other methods and achieves the highest accuracy on the test dataset. This suggests that incorporating both 1D and 2D features of control chart patterns could result in improved performance, as shown by the comparison between MCDCNN and 1D CNN. Although the use of 2D texture images may lead to longer computational time, this is unlikely to be a significant issue in real-world applications, as the data analysis for a window can be completed within 0.02 s using the aforementioned software and hardware.
Secondly, the results indicate that the CNN-based models and TSF method are less sensitive to the position of than are other methods. Conversely, the RF and SVC models exhibit a decline in performance if the values of in the training dataset differ from those in the test dataset.
5. Conclusions
This study developed a multi-channel CNN-based approach for CCPR in multivariate processes. We conducted a comparative analysis using various covariance matrices and demonstrated that the multi-channel CNN approach outperforms other methods.
The novel contribution of this study lies in the integration of 1D raw time series data and 2D time series imaging data using a multichannel CNN method. To evaluate the performance of various classifiers, we estimated the average classification accuracy and F1 score. Extensive comparisons revealed that the CNN-based models outperform traditional ML classifiers. The superiority of the MCDCNN implies that learning both 1D and 2D features of control chart patterns may lead to better performance.
This study also addressed the dynamic nature of control chart patterns by examining various pattern starting points within an analysis window. According to the results, both 1D CNN and the proposed MCDCNN are found to be less affected by misalignment issues. In addition, we considered the issue of imbalanced data, which arises from quantitative differences between various pattern classes. By evaluating the metric, we found that the proposed MCDCNN outperforms other classification models on imbalanced datasets. Overall, the results suggest that the proposed MCDCNN is a promising tool for CCPR in multivariate processes. The proposed method can advance intelligent SPC methods.
The datasets in this study were generated through simulations, which resulted in several limitations. Consequently, it is crucial to identify key areas for future research. First, we assumed that the data of each category in the training set has been labelled correctly. This assumption is not unrealistic, because in practice, the categories can be judged by experienced human experts. However, future research might consider developing an appropriate unsupervised learning algorithm that can be used to initially group the collected data before it is reevaluated by human experts to reduce the burden of labor. Additional work can also include investigating the impact on classification accuracy when a small amount of data is misclassified.
Collecting non-random pattern data is extremely costly, and more importantly, the number of samples for normal patterns is usually much larger than that of non-random patterns. This leads to the problem of imbalanced data across different classes. Future research can explore suitable data augmentation methods for multivariate data, with the goal of balancing the data across different classes and achieve improved classification accuracy. Exploring the effectiveness of the proposed method for datasets with a larger number of variables could be considered as a topic for future research to further demonstrate its capabilities. Finally, investigating concurrent control chart patterns would also be an interesting area of study for future research.
Author Contributions
Conceptualization, C.-S.C.; methodology, C.-S.C. and P.-W.C.; software, C.-S.C., P.-W.C., Y.-C.H. and Y.-T.W.; formal analysis, C.-S.C., P.-W.C., Y.-C.H. and Y.-T.W.; investigation, C.-S.C. and P.-W.C.; data curation, P.-W.C., Y.-C.H. and Y.-T.W.; writing—original draft preparation, C.-S.C., P.-W.C., Y.-C.H. and Y.-T.W.; writing—review and editing, C.-S.C., P.-W.C., Y.-C.H. and Y.-T.W.; supervision, C.-S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the National Science and Technology Council, R.O.C. (grant number NSTC 111-2221-E-155-028-).
Data Availability Statement
All data generated in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest regarding the publication of this manuscript.
References
- Montgomery, D.C. Introduction to Statistical Quality Control, 8th ed.; John Wiley & Sons: New York, NY, USA, 2020. [Google Scholar]
- Western Electric. Statistical Quality Control Handbook; Western Electric Company: Indianapolis, IN, USA, 1956. [Google Scholar]
- Hwarng, H.B.; Hubele, N.F. Back-propagation pattern recognizers for control charts: Methodology and performance. Comput. Ind. Eng. 1993, 24, 219–235. [Google Scholar] [CrossRef]
- Cheng, C.S. A neural network approach for the analysis of control chart patterns. Int. J. Prod. Res. 1997, 35, 667–697. [Google Scholar] [CrossRef]
- Pham, D.T.; Wani, M.A. Feature-based control chart pattern recognition. Int. J. Prod. Res. 1997, 35, 1875–1890. [Google Scholar] [CrossRef]
- Nelson, L.S. The Shewhart control chart—Tests for special causes. J. Qual. Technol. 1984, 16, 237–239. [Google Scholar] [CrossRef]
- Mason, R.L.; Chou, Y.M.; Sullivan, J.H.; Stoumbos, Z.G.; Young, J.C. Systematic patterns in T2 charts. J. Qual. Technol. 2003, 35, 47–58. [Google Scholar] [CrossRef]
- Hassan, A.; Baksh, M.S.N.; Shaharoun, A.M.; Jamaluddin, H. Improved SPC chart pattern recognition using statistical features. Int. J. Prod. Res. 2003, 41, 1587–1603. [Google Scholar] [CrossRef]
- Gauri, S.K.; Chakraborty, S. Recognition of control chart patterns using improved selection of features. Comput. Ind. Eng. 2009, 56, 1577–1588. [Google Scholar] [CrossRef]
- Hachicha, W.; Ghorbel, A. A survey of control chart pattern recognition literature (1991–2010) based on a new conceptual classification scheme. Comput. Ind. Eng. 2012, 63, 204–222. [Google Scholar] [CrossRef]
- Barros, P.; Magg, S.; Weber, C.; Wermter, S. A multichannel convolutional neural network for hand posture recognition. In Artificial Neural Networks and Machine Learning—ICANN 2014; Wermter, S., Weber, C., Duch, W., Honkela, T., Koprinkova-Hristova, P., Magg, S., Palm, G., Villa, A.E.P., Eds.; Springer: Cham, Switzerland, 2014; pp. 403–410. [Google Scholar]
- Yang, J.B.; Nguyen, M.N.; San, P.P.; Li, X.L.; Krishnaswamy, S. Deep convolutional neural networks on multichannel time series for human activity recognition. In Proceedings of the 24th International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Exploiting multi-channels deep convolutional neural networks for multivariate time series classification. Front. Comput. Sci. 2016, 10, 96–112. [Google Scholar] [CrossRef]
- Sipers, A.; Borm, P.; Peeters, R. On the unique reconstruction of a signal from its unthresholded recurrence plot. Phys. Lett. A 2011, 375, 2309–2321. [Google Scholar] [CrossRef]
- Zan, T.; Liu, Z.; Wang, H.; Wang, M.; Gao, X. Control chart pattern recognition using the convolutional neural network. J. Intell. Manuf. 2020, 31, 703–716. [Google Scholar] [CrossRef]
- Reis, M.S.; Gins, G. Industrial process monitoring in the big data/industry 4.0 era: From detection, to diagnosis, to prognosis. Processes 2017, 5, 35. [Google Scholar] [CrossRef]
- Evans, J.R.; Lindsay, W.M. A framework for expert system development in statistical quality control. Comput. Ind. Eng. 1988, 14, 335–343. [Google Scholar] [CrossRef]
- Cheng, C.S.; Hubele, N.F. Design of a knowledge-based expert system for statistical process control. Comput. Ind. Eng. 1992, 22, 501–517. [Google Scholar] [CrossRef]
- Bag, M.; Gauri, S.K.; Chakraborty, S. An expert system for control chart pattern recognition. Int. J. Adv. Manuf. Syst. 2012, 62, 291–301. [Google Scholar] [CrossRef]
- Pham, D.T.; Oztemel, E. Control chart pattern recognition using neural networks. J. Syst. Eng. 1992, 2, 256–262. [Google Scholar]
- Guh, R.S.; Tannock, J.D.T. Recognition of control chart concurrent patterns using a neural network approach. Int. J. Prod. Res. 1999, 37, 1743–1765. [Google Scholar] [CrossRef]
- Ranaee, V.; Ebrahimzadeh, A.; Ghaderi, R. Application of the PSO-SVM model for recognition of control chart patterns. ISA Trans. 2010, 49, 577–586. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, Y.; Wang, R.; Cheng, W. Recognition of mixture control chart patterns based on fusion feature reduction and fireworks algorithm-optimized MSVM. Pattern Anal. Appl. 2020, 23, 15–26. [Google Scholar] [CrossRef]
- Ranaee, V.; Ebrahimzadeh, A. Control chart pattern recognition using neural networks and efficient features: A comparative study. Pattern Anal. Appl. 2013, 16, 321–332. [Google Scholar] [CrossRef]
- Addeh, A.; Khormali, A.; Golilarz, N.A. Control chart pattern recognition using RBF neural network with new training algorithm and practical features. ISA Trans. 2018, 79, 202–216. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Lu, S.; Lam, S. A hybrid system for SPC concurrent pattern recognition. Adv. Eng. Inform. 2007, 21, 303–310. [Google Scholar] [CrossRef]
- Yang, W.A.; Zhou, W.; Liao, W.; Gou, Y. Identification and quantification of concurrent control chart patterns using extreme-point symmetric mode decomposition and extreme learning machines. Neurocomputing 2015, 147, 260–270. [Google Scholar] [CrossRef]
- García, E.; Peñabaena-Niebles, R.; Jubiz-Diaz, M.; Perez-Tafur, A. Concurrent control chart pattern recognition: A systematic review. Mathematics 2022, 10, 934. [Google Scholar] [CrossRef]
- Wang, T.Y.; Chen, L.H. Mean shifts detection and classification in multivariate process: A neural-fuzzy approach. J. Intell. Manuf. 2002, 13, 211–221. [Google Scholar] [CrossRef]
- Low, C.; Hsu, C.M.; Yu, F.J. Analysis of variations in a multi-variate process using neural networks. Int. J. Adv. Manuf. Technol. 2003, 22, 911–921. [Google Scholar] [CrossRef]
- Sun, R.; Tsung, F. A kernel-distance-based multivariate control chart using support vector methods. Int. J. Prod. Res. 2003, 41, 2975–2989. [Google Scholar] [CrossRef]
- Chen, L.H.; Wang, T.Y. Artificial neural networks to classify mean shifts from multivariate χ2 chart signals. Comput. Ind. Eng. 2004, 47, 195–205. [Google Scholar] [CrossRef]
- Guh, R.S. On-line identification and quantification of mean shifts in bivariate processes using a neural network-based approach. Qual. Reliab. Eng. Int. 2007, 23, 367–385. [Google Scholar] [CrossRef]
- Cheng, C.S.; Cheng, H.P. Identifying the source of variance shifts in the multivariate process using neural networks and support vector machines. Expert Syst. Appl. 2008, 35, 198–206. [Google Scholar] [CrossRef]
- Cheng, C.S.; Cheng, H.P. Using neural networks to detect the bivariate process variance shifts pattern. Comput. Ind. Eng. 2011, 60, 269–278. [Google Scholar] [CrossRef]
- Cheng, H.P.; Cheng, C.S. A support vector machine for recognizing control chart patterns in multivariate processes. In Proceedings of the 5th Asian Network for Quality Congress, Incheon, Republic of Korea, 17–18 October 2007. [Google Scholar]
- Beshah, B.; Muluneh, A. Control chart pattern recognition of multivariate auto-correlated processes using artificial neural network. Zede J. 2017, 35, 47–57. [Google Scholar]
- Hong, Z.; Li, Y.; Zeng, Z. Convolutional neural network for control chart patterns recognition. In Proceedings of the CSAE 2019: 3rd International Conference on Computer Science and Application Engineering, Sanya, China, 22–24 October 2019. [Google Scholar]
- Miao, Z.; Yang, M. Control chart pattern recognition based on convolution neural network. In Smart Innovations in Communication and Computational Sciences; Advances in Intelligent Systems and Computing (AISC) 670; Panigrahi, B., Trivedi, M., Mishra, K., Tiwari, S., Singh, P., Eds.; Springer: Singapore, 2019; pp. 97–104. [Google Scholar]
- Xu, J.; Lv, H.; Zhung, Z.; Lu, Z.; Zou, D.; Qin, W. Control chart pattern recognition method based on improved one-dimensional convolutional neural network. IFAC Pap. 2019, 52, 1537–1542. [Google Scholar] [CrossRef]
- Yu, J.; Zheng, X.; Wang, S. A deep autoencoder feature learning method for process pattern recognition. J. Process. Control. 2019, 79, 1–15. [Google Scholar] [CrossRef]
- Fuqua, D.; Razzaghi, T. A cost-sensitive convolution neural network learning for control chart pattern recognition. Expert Syst. Appl. 2020, 150, 113275. [Google Scholar] [CrossRef]
- Zan, T.; Liu, Z.; Su, Z.; Wang, M.; Gao, X.; Chen, D. Statistical process control with intelligence based on the deep learning model. Appl. Sci. 2020, 10, 308. [Google Scholar] [CrossRef]
- Cheng, C.S.; Ho, Y.; Chiu, T.C. End-to-end control chart pattern classification using a 1D convolutional neural network and transfer learning. Processes 2021, 9, 1484. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Wang, Z.; Oates, T. Encoding time series as images for visual inspection and classification using tiled convolutional neural networks. In Proceedings of the Workshops at the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–26 January 2015. [Google Scholar]
- Hatami, N.; Gavet, Y.; Debayle, J. Classification of time-series images using deep convolutional neural networks. arXiv 2017, arXiv:1710.00886. [Google Scholar]
- Wang, Z.; Oates, T. Imaging time-series to improve classification and imputation. arXiv 2015, arXiv:1506.00327. [Google Scholar]
- Martínez-Arellano, G.; Terrazas, G.; Ratchev, S. Tool wear classification using time series imaging and deep learning. Int. J. Adv. Manuf. Technol. 2019, 104, 3647–3662. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Kamphorst, S.O.; Ruelle, D. Recurrence plots of dynamical systems. Europhys. Lett. 1987, 4, 973–977. [Google Scholar] [CrossRef]
- Chen, W.; Shi, K. A deep learning framework for time series classification using relative position matrix and convolutional neural network. Neurocomputing 2019, 359, 384–394. [Google Scholar] [CrossRef]
- Faria, F.A.; Almeida, J.; Alberton, B.; Morellato, L.P.C.; Torres, R.S. Fusion of time series representations for plant recognition in phenology studies. Pattern Recognit. Lett. 2016, 83, 205–214. [Google Scholar] [CrossRef]
- Al-Saffar, A.A.M.; Tao, H.; Talab, M.A. Review of deep convolution neural network in image classification. In Proceedings of the 2017 International Conference on Radar, Antenna, Microwave, Electronics, and Telecommunications (ICRAMET), Jakarta, Indonesia, 23–24 October 2017; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017. [Google Scholar]
- Aloysius, N.; Geetha, M. A review on deep convolutional neural networks. In Proceedings of the 2017 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 6–8 April 2017; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017. [Google Scholar]
- Ajit, A.; Acharya, K.; Samanta, A. A review of convolutional neural networks. In Proceedings of the 2020 International Conference on Emerging Trends in Information Technology and Engineering (ic-ETITE), Vellore, India, 24–25 February 2020; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2020. [Google Scholar]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef]
- Chollet, F. Others, Keras. 2015. Available online: https://github.com/fchollet/keras (accessed on 24 April 2023).
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Breiman, L. Random forests. Mach. Leran. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Deng, H.; Runger, G.; Tuv, E.; Vladimir, M. A time series forest for classification and feature extraction. Inf. Sci. 2013, 239, 142–153. [Google Scholar] [CrossRef]
- Guh, R.S.; Hsieh, Y.C. A neural network based model for abnormal pattern recognition of control charts. Comput. Ind. Eng. 1999, 36, 97–108. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Löning, M.; Bagnall, A.; Ganesh, S.; Kazakov, V.; Lines, J.; Király, F.J. Sktime: A unified interface for machine learning with time series. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Jackson, J.E. Principal components and factor analysis: Part I—Principal components. J. Qual. Technol. 1980, 12, 201–213. [Google Scholar] [CrossRef]
- Doganaksoy, N.; Faltin, F.W.; Tucker, W.T. Identification of out of control quality characteristics in a multivariate manufacturing environment. Commun. Stat. Theory Methods 1991, 20, 2775–2790. [Google Scholar] [CrossRef]
- Niaki, S.T.A.; Abbasi, B. Fault diagnosis in multivariate control charts using artificial neural networks. Qual. Reliab. Eng. Int. 2005, 21, 825–840. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).