Abstract
Mathematical modeling is the most important tool for constructing the theory of concentrated tornado-like vortices. A review and analysis of computational and theoretical works devoted to the study of the generation and dynamics of air tornado-like vortices has been conducted. Models with various levels of complexity are considered: a simple analytical model based on the Bernoulli equation, an analytical model based on the vorticity equation, a new class of analytical solutions of the Navier–Stokes equations for a wide class of vortex flows, and thermodynamic models. The approaches developed to date for the numerical simulation of tornado-like vortices are described and analyzed. Considerable attention is paid to developed approaches that take into account the two-phase nature of tornadoes. The final part is devoted to the analysis of modern ideas about the tornado, concerning its structure and dynamics (up to the breakup) and the conditions for its occurrence (tornadogenesis). Mathematical modeling data are necessary for interpreting the available field measurements while also serving as the basis for planning the physical modeling of tornado-like vortices in the laboratory.
Keywords:
concentrated vortices; analytical model; thermodynamic model; numerical simulation; physical modeling MSC:
00A72; 76B47; 76Txx; 82D05
1. Introduction
One of the most common states of a moving continuous medium is vortex motion. Among the colossal variety of different vortex structures, concentrated vortices stand out [1]. Concentrated vortices are compact spatial regions characterized by high vorticity values, which are surrounded by a flow with significantly lower vorticity (or with zero in the case of an ideal fluid). Concentrated vortices are widespread in Earth’s atmosphere [2,3,4] and in the Sun [5,6,7].
The main problems with studying destructive atmospheric vortices (including tornadoes) are as follows: (1) assessment of the probability of the occurrence of a vortex structure at a given point in space at a given time, (2) prediction of the development of an already arisen element, and (3) investigation of the possibilities of the weakening and destruction (decay) of the vortex structure as well as changes in the path of its propagation [8,9].
Mathematical modeling is the most important tool for constructing the theory of concentrated tornado-like vortices. The results of the calculations are necessary for the interpretation of the available field measurements [10,11,12,13] and also serve as a reliable basis for planning the physical modeling of tornado-like vortices in laboratory conditions [14,15,16,17,18,19,20,21,22,23,24,25].
The subject of this review is the methods of mathematical modeling of the structure and dynamics of vertically oriented concentrated tornado-like vortices, which are analogs of vortex formations observed in nature (“dust devils”, water tornadoes, fire tornadoes, etc.). The main purpose of mathematical modeling is to ascertain the main characteristics of vortices that determine their destructive potential (azimuthal velocity and corresponding pressure drop, geometric dimensions of the vortex, etc.) at all stages of their life cycle (from generation to decay). In the review, significant emphasis is given to the consideration of works devoted to the development of analytical and simplified methods of mathematical modeling that allow for the obtainment of accurate solutions. Despite their rapid development, computational fluid dynamics (CFD) methods are quite effective since they allow us to isolate the main physical mechanisms and focus on their detailed consideration.
The review is constructed as follows. Section 2 contains a description of analytical models of tornado-like vortices with various levels of complexity. The results of numerical studies of tornado-like vortices are described and analyzed in Section 3. This section highlights the importance of taking into account the multiphase nature (in this particular case, the two-phase nature) of the tornado. Lastly, Section 4 is devoted to a short description of modern ideas about the tornado. In conclusion, some directions for further improvement of the theory of tornado-like vortices are formulated.
2. Mathematical Modeling: Analytical Simulation
Among the simplest classes of tornado-like vortex models are those based on the Bernoulli equation. Note that even such simple models can accurately describe the basic properties of real tornadoes, namely, the thickening of the funnel with distance from the ground and an increase in azimuthal (tangential) velocity as the funnel approaches the ground.
2.1. Simple Analytical Models
The simplest model of a tornado is a vortex flow with a vertical axis of symmetry and a fixed core (or funnel) [26]. Figure 1 shows a diagram of the vortex under consideration. The axis is the axis of symmetry of the tornado; corresponds to the surface of the Earth. The horizontal axis shows the distance from the axis of symmetry of the tornado. At , the boundary between a stationary funnel and rotating air is .
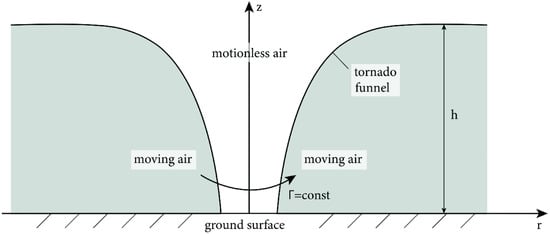
Figure 1.
Scheme of the flow [26].
It is assumed that the density of air in the core is lower than the density of moving air. The speed of rotation of the air increases toward the surface of the funnel and reaches a maximum on the surface of the Earth.
The Bernoulli equations for rotating air and for the stationary air () of the core (funnel) are written as
where for and ; .
The simplest solution is obtained for the case of incompressible air, i.e., and . This assumption is not strict because it is true for most real tornadoes. Next, we assume the constancy of the circulation of moving air along any circle located around the core (funnel), i.e., .
We subtract (1) from (2), taking into account the equality of pressures on the surface of the funnel from the rotating and stationary air. Then, for the velocity of air on the surface of the funnel , we obtain
where the subscript denotes the surface of the funnel. In a more concise form, expression (3) has the form . From this relation and the condition of constant circulation, it is easy to obtain
Equation (4) gives the shape of the funnel. For , ; a larger value corresponds to a wider funnel with a larger area of destruction.
On the surface of the Earth (), we give and . Here, and are the values of the azimuthal air velocity and the radius of the funnel on the Earth’s surface. Equation (4) gives the widening of the funnel with increasing distance from the ground, which is in qualitative agreement with most real tornadoes.
In the work [27], a new class of analytical solutions of the Navier–Stokes equations is obtained, which allows for the prediction of the characteristics of complex vortex flows. One of the simplest solutions of the Euler and Navier–Stokes equations is for a plane vortex sink (vortex source). In [27], this solution is generalized for the case when axial flow is superimposed on axisymmetric vortex sinks. A new solution (more precisely, a family of solutions) for a viscous incompressible fluid, taking into account the superimposed shear longitudinal flow, significantly expands the scope of its use, allowing one to build pictures of various vortex flows, including tornadoes.
In [27], a stationary vortex flow in which the velocity does not depend on the axial coordinate is considered. In this case, the Navier–Stokes equations for the radial velocity projection and the azimuthal velocity projection become independent of the equation for the axial velocity projection . For axisymmetric distributions and ( may depend on ), the continuity equation is reduced to the form . Hence, we obtain that . For the sink (source), we have , where is the gas flow rate through a cylindrical surface of unit length .
Transformations of the equation of motion for the azimuthal velocity projection lead it to the following form:
where , and is the length scale. The general solution (5) has the form , where the first term of the right-hand side represents solid-state rotation () and the second term denotes a potential vortex. In [27], we are limited to considering only a particular solution (). In this case, , where is the circulation along the circle and . In further analysis, a dimensionless parameter was used: the Reynolds vortex number . The flow in the plane , determined by the corresponding projections of the velocity vector (), is a well-known vortex sink (vortex source) at ().
The purpose of the analysis conducted in [27] is to obtain a generalized solution for vortex flow by superimposing on it an axial (longitudinal) flow. Note that the axial flow () independent of the coordinate does not affect the continuity equation and the equations of motion for radial and azimuthal velocity projections.
The equation of motion for the axial velocity projection is written in [27] as
where . The axisymmetric solution (6) has the form , where and are constants.
To account for the nonzero longitudinal pressure gradient (), a term is added, where is a dimensionless parameter characterizing the longitudinal pressure gradient and having the form . Thus, the solution for takes the form , where . The third term on the right side is the contribution of the longitudinal pressure gradient.
For a flow in an unbounded space (), is the velocity on the axis at or at infinity at and . Thus, is a free parameter characterizing a homogeneous part of the axial velocity profile. Other parameters, namely, and , characterize the inhomogeneous shear of the axial velocity due to the longitudinal pressure gradient and radial advection, respectively.
As a result, the velocity field is determined by the following relations:
Expressions in (7) are a generalized solution for a vortex sink [27]. These relations satisfy the Navier–Stokes equations and contain five dimensionless parameters: , , , , and . The first two expressions are well-known solutions for the classical vortex sink. The third expression is a solution for the case of the superposition of axial flow on a vortex sink.
Further, in [27], by integrating the equation for the streamline using (7), the following expressions are obtained:
where , , , and the vortex parameter (twist parameter) .
The velocity field is identical to the axisymmetric surfaces of the flow (8), differing only in the shift along . The projections of curved streamlines on the plane are logarithmic spirals, as follows from (9). The plane vortex sink is a special case obtained from (8) and (9) at .
To visualize the flow pattern, which is necessary for comparison with experimental results, in [27], the stream function is used. The radial and axial projections of the gas velocity are related to the stream function as
Using (7) as well as (8) and (9), in [27], an expression is obtained for a dimensionless stream function in the form , where .
The pressure distribution for the resulting family of solutions has the form [27] . It follows that the pressure reaches a minimum at . For most practical applications, ; therefore, the minimum pressure is mainly associated with the presence of vortex motion. The decrease in pressure reflects the so-called cyclostrophic balance, i.e., the mutual counteraction of centrifugal force and radial pressure gradient. Also, the pressure may decrease or increase in the axial direction, depending on the sign .
Solutions in [27] describe a wide range of different vortex flows, including tornadoes. Solution (7) makes it possible to analyze the formation of a tornado near the surface, as well as to interpret the effect of a sharp expansion of the funnel at a certain height from the ground.
Figure 2a shows the meridional streamlines in the area where the tornado funnel is expanding [27]. Figure 2b illustrates the formation of a tornado near the Earth’s surface [27]. Current lines are constructed for the following conditions: , , , , and for Figure 2a and , , , and for Figure 2b. The specified parameter values were chosen to satisfy the condition at for streamlines approaching the Earth and for crosslinking the flow characteristics shown in Figure 2a,b.

Figure 2.
Meridional streamlines (a) at the place of funnel widening and (b) near the ground surface [27].
In [28], a mathematical model describing the process of formation of intense atmospheric vortices of the tornado type due to instability is constructed. The instability condition is an increase in the vertical component of the air velocity in the direction of the Earth’s surface or an increase in the concentration of suspended particles. Such conditions can be realized in some cases in thunderclouds in the atmosphere and over the dusty or snow-covered surface of the Earth. The initial stage of tornado development is being studied in research [28].
When writing equations of geophysical hydrodynamics, taking into account the presence of solid (or liquid) suspended particles having a density in the air with a density , the assumption of a linear relationship between turbulent friction and the speed of motion ( is the proportionality coefficient) was used. So, the density of the mixture of air and particles was equal . It should be noted that in order to conduct an analytical study, the vertical component of the velocity in [28] was considered to be known from observations.
Then, in [28], an equation was constructed for the vertical component of vorticity: . To do this, it is necessary to differentiate the equation for by and the equation for by and then subtract the first equation from the second (from the obtained) equation.
As a result, an equation is obtained for the vertical component of vorticity [28]:
Here, is the Jacobian of the functions and , written as , , and is the latitudinal variation of the first and second Coriolis parameters; is the radius of the Earth.
Further, in [28], an analysis of the equation obtained above for the vertical component of vorticity was conducted. For this, Equation (11) was presented in the form
The first term of the right side of Equation (12) in atmospheric physics is called the convergence of flows. Available observational data [29,30] indicate that it is the convergence of flows that dominates the initial stage of the vortex development. With the use of the continuity equation, the convergence of flows can be expressed in terms of the vertical velocity gradient, representing (12) in the following form:
where is the initial (at ) value of vertical vorticity.
Integrate (14) in time from 0 to . As a result, we obtain [28]
where is the vertical component of the velocity, taking into account the gravitational subsidence of suspended particles, i.e., .
Expression (15) clearly shows that the growth of vorticity in tornadoes can occur exponentially, which is characteristic of explosive instability [28]. In the absence of convergence, Equation (11) takes the following simple form, , where is the right side of Equation (11), i.e., there is no explosive instability. The presence in the equations of motion of a coefficient of friction with a frequency dimension, which has a physical meaning of momentum loss in the collision of particles moving at different velocities, leads to exponential attenuation of vorticity over time.
From the analysis of Equation (15), it follows that explosive instability for vortices with a vertical axis of rotation is realized under the condition [28]
In [28], it is noted that there is no vertical velocity component in the troposphere under normal conditions. Vertical velocity appears when the air flow moves around mountains and hills and when air flows collide (for example, cold and dry air from Canada and warm and humid air from the Gulf of Mexico over the territory of the United States). In addition, as a result of convection, secondary movements occur over a highly overheated surface, and the formation of thunderclouds may occur, under which rapid vertical flows are observed. Precipitation does not occur in the front part of the thundercloud due to large wind speed gradients, and there are updrafts that lead to the formation of a cloud shape in the form of an anvil. Precipitation is formed in the central and rear parts of the thunderstorm cloud, contributing to the emergence of vertical air flows directed downward.
Under a mature thunderstorm cloud, the convergence of wind speed is of the order of s−1. The vertical velocity profile can be represented as a parabola with a maximum in the middle of the thickness layer , i.e., .
The concentration of suspended particles usually increases as it approaches the underlying surface, i.e., . It follows from (16) and the parabolic vertical velocity profile that in this case, the condition of vortex instability takes the form .
We will carry out transformation (15) taking into account (14) and the parabolic vertical velocity profile and under the assumptions , . As a result, we obtain the formula [28], suitable for calculating the vertical distribution of vorticity :
In [28], some calculations are performed using the vorticity dependence obtained above on the vertical coordinate and time. Calculations of the dependence of the vorticity on the vertical coordinate in the area under the thundercloud were performed. Calculations were carried out at s−1, m/s (downward movement), km, , and s−1. The results of calculations showed that a very strong vortex is formed in the lower part of the storm cloud, the rotating trunk of which falls below the cloud but does not reach the surface of the Earth. A similar pattern is characteristic of a tornado, which is defined as a rapidly rotating air funnel in contact with both the surface of the Earth and a cloud.
A similar vortex, but with the throat pointing upwards, can also be calculated using Formula (17) in the region , setting (upward movement). Calculations of the ascending vortex were performed according to Formula (17) of the dependence of the vorticity on the vertical coordinate above the underlying surface. Calculations were performed at s−1, m/s (upward movement), km, , and s−1. The results showed that the ascending vortex grows with time, rising upwards. The value of vorticity above the underlying surface is lower than under a thundercloud due to stronger friction near the Earth’s surface (with all other parameters equal).
Similar tornadoes, each in the form of a funnel with a base on the ground and a trunk rising to the clouds, have been repeatedly observed. A fully developed tornado is obtained by closing two vortices [28]: one coming from a cloud and a surface one, both in the area of constriction . The binding for the accepted parabolic velocity profile takes place at . A significant role in the formation of the vortex according to (17) should be played by the concentration gradient of suspended particles , which is very significant to account for.
2.2. Thermodynamic Models
All of the hydrodynamic models of tornado-like flows described above did not directly take into account the most important “thermodynamic” factor: convective instability of the atmosphere due to the implementation of high-temperature gradients in the surface layer. The following are simple thermodynamic models of tornadoes that take into account the most important mechanism for generating atmospheric vortices.
One of the first mathematical models (Gutman’s model) of tornado-like vortices was proposed in [31]. The strength of this model is an attempt to take into account the stratification of the atmosphere depending on a specific synoptic situation. Here are just two basic equations (the equation of thermodynamics of moist air and the equation for vertical velocity) of the original system of equations for a tornado [31]:
where and are deviations of temperature and pressure from the corresponding values and at a great distance from the tornado, is wet–adiabatic gradient at temperature and pressure , is gas constant for air, and and are coefficients of turbulent thermal conductivity and turbulent viscosity, respectively.
During the process of solving the above system of equations, the principal role should be played by the term located on the right-hand side of (18) and proportional to (in the case of ()) the intensity of the convective instability energy conversion. As noted in [31], the left part of (19) contains terms that are negligible and not taken into account in the analysis of most meteorological processes, namely, . These terms take into account the heat consumption for the expansion or compression of air when its pressure changes and becomes commensurate with other terms of the equation for typical values of pressure drop ( mbar) on the axis of the tornado.
Note also that the equation of cyclostrophic balance is used for azimuthal velocity. As boundary conditions on the tornado axis (), the radial and azimuthal velocities as well as the radial gradients of vertical velocity and temperature deviation () from the equilibrium value are assumed to be equal to zero: , . At a great distance from the vortex (), all disturbances should attenuate, as a result of which the gas-dynamic (radial, azimuthal, and vertical components of velocity) and thermodynamic (pressure and temperature deviation) parameters should tend to zero:, , , , and .
The intensity of rotation in [31] was set by selecting the value of circulation in a circle of a sufficiently large radius centered on the axis of the tornado. In order to obtain an analytical solution to the problem, it was assumed that , , , and , assuming values for these parameters of the averages for the entire stratified unstable () layer of the atmosphere “penetrated” by a tornado. Further, in order to reduce the initial system to a system of ordinary differential equations in [31], a variable is replaced by a variable . Here, is an arbitrary constant value.
In Ref. [31], as mentioned above, rotation in the parent cloud (tornado-cyclone) was set and not found in the course of solving the problem. From the solving of a system of equations, formulas for calculating the main characteristics of a tornado are obtained. To calculate the parameters of the tornado, the following circulation value was taken [32]: m2/s. For the remaining dimensional values, the most probable values were taken: m2/s, K/m, β = 30 °C, and m/s2.
With the above values taken into account, m/s was found for the maximum azimuthal velocity at m. The pressure in a tornado is always lower than the pressure in the ambient air. For the tornado axis, where the pressure is lowest, mbar was obtained. The angular velocity is zero at the periphery, reaching its maximum in the center of the tornado rad/s.
The resulting solution showed that the vertical velocity, generally increasing with height, has a negative component near the axis of rotation at all heights. This is due to a strong drop in pressure in the tornado and the lack of air flow from below (the inflow of air from the sides is slowed down by centrifugal force). The presence of a negative component leads to the appearance of a “compensatory” descending jet in the lower part of the tornado. With height, the velocity and width of the descending flow decrease in absolute magnitude and vanish at the next value of the vertical coordinate m. It can be seen that the velocity of the descending flow is proportional to the square of the circulation (), while the maximum azimuthal velocity (see above) is proportional only to the circulation in the first degree ().
Conclusions [31] showed that to simulate a tornado-like vortex, it is necessary first to calculate the rotating parent cloud (tornado-cyclone) and then solve the problem of the emergence of a tornado from a tornado-cyclone due to unstable stratification. Note that the solution [31] admits two limiting cases: (1) in a stably stratified atmosphere, the resulting solution vanishes, since convective instability is a necessary condition for the occurrence of a tornado, and (2) in the absence of rotation, the found solution turns into known expressions describing an upward convective flow over an overheated surface.
Model [31] received further development in the works [33,34,35] and others. In [33,34], a different solution of the nonlinear differential equation obtained in [31] has been found. According to this solution, a descending current surrounded by an ascending flow takes place in the central part of the tornado.
In [35], it is shown that the downward flow on the vortex axis occurs when the vertical pressure gradient is taken into account in the equation for the vertical velocity , i.e., . In this work, two layers of the atmosphere were considered: (1) the lower one with unstable stratification (; is the height of this layer) and (2) the upper one with stable stratification (). These layers were formed by setting a temperature gradient that decreases with height. The following boundary conditions different from [31] were assumed on the tornado axis (): , . At a great distance from the vortex (), conditions other than [31] were set in the form , , , and . Note that unlike [31], a condition is also set for the attenuation of all disturbances at high altitudes () as , , and . As for the initial conditions, at rest () is set, and at the moment of time , rotation () is set at the periphery of the vortex.
As a result of the calculations performed in [35] at km, the following characteristic parameters of a tornado-like vortex were found: (1) the diameter of the vortex was about 1 km (the boundary was determined using the condition: ), (2) the maximum value of the azimuthal velocity was m/s ( m, min), (3) the maximum value of the vertical velocity was m/s (, m, min), (4) the maximum pressure drop reached hPa (, , min), (5) the maximum heating was °C (, m, min), and (6) the maximum cooling in the lower part of the vortex was several degrees.
The main drawback of the model [35] is an extremely rough description of turbulent friction. The coefficient of turbulent shear viscosity was assumed to be m2/s, which is probably much less than the real values. As a result, the calculated vortex practically did not weaken (even after the incident 120 min after the start of the count).
In [36], some boundary and initial conditions were changed. In this work, for the development of a non-rotating convective “pipe” at the initial moment of time (), an initial temperature perturbation was set . In order to give an initial twist at a sufficient distance from the axis of the vortex ( m), the initial value of the azimuthal velocity ( m/s) was set, independent of height, and maintained unchanged for several time steps. Thus, in [36], a vortex developing from an ascending convective flow swirled at the periphery was calculated. The study showed that the stability of the numerical scheme strongly depended on the set values of the coefficient of turbulent viscosity , the convection parameter , and the thickness of the surface boundary layer included in the boundary condition (on the Earth’s surface) for vertical velocity. As rightly noted in [37], the main idea of the studies described above—to obtain a powerful tornado-like vortex from relatively weak convective currents arising over overheated surfaces—is questionable.
In [38], a simple hydrodynamic model of tornado-like vortices (Kurgansky’s model) is proposed, developing Gutman’s thermodynamic approach [31] and its subsequent modifications [35,36]. The analysis based on [38] contains the equation of thermodynamics of moist air, which is linearized with respect to deviations of temperature and pressure from the values of and in the atmosphere surrounding the vortex, depending only on altitude . In [38], a vortex solution is obtained in the approximation of the weak compressibility of atmospheric air in the dynamic sense. The main equation is solved together with the equations of motion and the continuity equation in the Boussinesq approximation. The transformation of the equation for the vertical component of velocity, taken on the axis of symmetry (), and the equations for the radial component of velocity (cyclostrophic balance) make it possible to receive on the right side of the final equation the convective available potential energy (see, for example, [39,40]). Traditionally, it is called (convective available potential energy). As a result, in [39], we come to the following special case of the equation:
where is the maximum azimuthal velocity in the vortex, taken at the level of free convection (); is the corresponding velocity of upward motion in the center of the vortex.
A formula similar to (21) was obtained from general considerations (without detailing the three-dimensional structure of the vortex) in a review [41] for the case of a compressible atmosphere. Consideration of the vortex structure is necessary to establish a connection and . For dry convective vortices and when refusing to use the cyclostrophic balance equation, an analog of Formula (21) was obtained in Refs. [42,43].
Let us make one important remark. When the term is neglected in the right part (21), a formula is obtained for the “thermodynamic velocity limit” [41,44,45,46,47], determined by the hydrostatic pressure deficit in the center of the vortex. Since the vertical velocity vanishes at , the term describes the pressure deficit in the center of the vortex caused by the Bernoulli effect in the downward-tapering vortex core. The sum on the right side (21) is equal to the pressure deficit maintained by the conditions of cyclostrophic balance.
One of the well-known problems of studying tornadoes is the prediction by Formula (21) of significantly lower maximum velocity values in a tornado at values known from observations of . In [38], an attempt is made to solve this problem by considering two (supercritical and subcritical) vortices and a detailed analysis of the vertical helicity flow in the constructed “composite” vortex. For this purpose, the helicity balance condition is used. It is suggested that the helicity is generated by the buoyancy force in the main (subcritical) vortex updraft due to the correlation of buoyancy and vertical vorticity. Further, the helicity is transmitted downwards, where it dissipates due to turbulent viscosity, first in the vortex decay region and finally in the surface boundary layer (during the interaction of a supercritical vortex with the Earth’s surface).
In conclusion, we note that estimates and conclusions performed in [38] have a double meaning. Firstly, they indicate, in accordance with the observational data, that at a given value of the convective available potential energy (), the generation of atmospheric vortices of various intensities is possible (). Secondly, in contrast, a vortex (tornado) of a given intensity () can form at different values of convective potential energy ().
In [48], an approach (Renno’s model) is proposed that develops the ideas of Shuleikin [49] and considers natural convection as a heat engine—a device that turns the heat accumulated in the lower layer of the atmosphere into mechanical work. The analysis is performed in the approximation of the Carnot cycle, which has maximum thermodynamic efficiency and is limited by hot and cold adiabats as well as hot and cold isotherms. Since the work produced by a heat engine in one cycle is equal to the total mechanical energy due to convective instability, we write [48]
where is the total convective available potential energy received by a heat engine in one cycle in a reversible process and converted into mechanical energy. It includes the available energy converted into kinetic energy by both (ascending and descending) flows, i.e., .
As a result of the application of the first law of thermodynamics, the following relation is obtained for estimating the vertical velocity of the air flow: , where is the dimensionless coefficient of mechanical energy dissipation. It can be concluded that the larger values of correspond to smaller values of vertical velocities.
In [50,51], a simple thermodynamic model was developed to describe the intensity of “dust devils” and water tornadoes, respectively. The developed theoretical approach is based on the concept of thermodynamic “efficiency” (by analogy with a heat engine) of atmospheric vortices, defined as
where and is the amount of heat at the entrance and exit from the vortex (heat engine), respectively; is entropy. Thermodynamic efficiency can be represented in the following form: , where and are the entropy-averaged temperatures of the heat source and sink, respectively. In [48], an assumption was made that the temperature of the “dust devil” heat source is equal to the average temperature of the near-surface air.
The use of the first law of thermodynamics [50] allowed us to obtain an equation for the pressure loss in the radial direction across the “dust devil”. Further, in [50], assuming that the cyclostrophic balance condition and the equation of state of an ideal gas are fulfilled, expressions for determining the maximum tangential (azimuthal) velocity and vertical velocity are obtained. In [51], close (to [50]) relations for calculating the velocity components for water tornadoes are derived, differing in the presence of terms responsible for the latent heat of vaporization. Based on the obtained ratios, estimates of pressure drops along with tangential and vertical velocities were made, which correlate well with real measurements of the parameters of “dust devils” [52,53] and water tornadoes [54,55,56,57].
For anyone interested in thermodynamic models of tornadoes based on , we can recommend a relatively recently published paper [58]. It provides a brief overview of three main varieties of mathematical models of this kind: (1) models based on the balance of entropy [48] and their modifications, (2) models based on two height scales [59] arising from a mismatch between latent heating and radiative cooling profiles, and (3) models based on zero buoyancy [60].
There are works [61,62,63,64] where it is shown that intense atmospheric vortices (called macrovortices in these studies), including tornadoes, can occur due to the presence of mesovortices in the atmosphere. Mesovortices are vortices whose scales are much smaller than the external scales of the phenomenon under consideration (in this case, a tornado). It is shown in [61,62] that it is possible to transfer the energy of turbulent air movement along the hierarchy of scales: from mesovortices to macrovortices, occurring at a certain ratio of the energy of these vortices, i.e., . In this study, the possibility of generating intense macrovortices due to the initial energy of mesovortices was demonstrated for the first time in a numerical simulation of an axisymmetric vortex in a one-dimensional incompressible nonstratified atmosphere. It is revealed that in the case of the energy of the mesovortices running out, the reverse process of energy leaving into the mesoscale begins.
The mechanisms of the origin of the initial field of mesovortices can be different: the formation of coherent structures of a 50–500 m scale in the surface layer of the atmosphere [65]; vortices in floating turbulent jets caused by both natural and anthropogenic factors [66]; anomalies of the average monthly temperature [67]; and, of course, the destruction of global vortices, for example, tropical cyclones [68].
In [63,64], a numerical model of tornado development in a three-dimensional compressible dry adiabatic atmosphere from a cloud of mesovortices was implemented. At the initial moment of time, the vertical and radial components of the velocity were absent; a weak calm cyclonic wind with an amplitude of 1.5 m/s was set. As a result of numerical modeling, the features of the formation of the vertical radial circulation and spiral structure characteristic of tornadoes are studied. In general, the mushroom-shaped structure of the tornado formed in about one minute. The simulated vortex structure persisted for several minutes (the velocity varied in the range of 43–35 m/s) and then gradually faded to 12 m/s for half an hour, which is typical for tornadoes of low and medium intensity.
It is noted in [63] that the hypothesis of a dry adiabatic atmosphere does not allow for modeling the slow processes of accumulation of the energy necessary for the generation of tornadoes for mesovortices. To do this, it is necessary to take into account the influx of energy due to the heating of the underlying surface by solar radiation, the heat of phase transformations, and other factors.
3. Mathematical Modeling: Numerical Simulation
Despite the obvious difficulties in setting up correct boundary and initial conditions, there is a colossal amount of numerical calculations for tornado-like flows.
3.1. Main Trends of Numerical Modeling
All numerical studies of tornado-like vortices can be conditionally divided into three classes.
The first class of studies is devoted to solving axisymmetric Navier–Stokes equations in a two-dimensional cylindrical coordinate system. However, in [69], where the structure and dynamics of axisymmetric tornado-like vortices were studied, the following was shown. In the case of sudden expansion and the beginning of “wandering” (precession) of the vortex before its decay, its structure ceases to be axisymmetric. Therefore, the studied flow cannot be adequately described by an axisymmetric mathematical model.
The second class of studies is devoted to solving full-scale three-dimensional equations and comparing the obtained results with the characteristics of real natural vortices.
The third class of flows is devoted to solving three-dimensional laboratory-scale equations and comparing the obtained results with the characteristics of model tornadoes (laboratory-simulated tornadoes).
Below, we consider and analyze some of the results of these studies.
3.2. Early Numerical Studies
The study [70] is a pioneering work that considers the process of tornado formation due to convective instability near the Earth’s surface (modeling “from below”). In Refs. [70,71], the method of “stream function—vorticity” was used for numerical research. For this, the original system of equations consisting of three Navier–Stokes equations for the radial , azimuthal , and vertical components of the velocity vector and the continuity equation, written in the cylindrical coordinate system, was converted to the next form:
where is the Jacobian.
Transformations of the original system of equations to the system of Equations (24)–(26) were made using known relations: , , , and . Equations (24)–(26) make up a system of three equations with three variables: the stream function , circulation , and the azimuthal component of the vorticity . The boundary and initial conditions for solving the system of Equations (24)–(26) were selected in accordance with the conditions of the experiments [14]. The boundary conditions were as follows: (1) on the axis of symmetry (, , and ), (2) on the lower wall of the chamber (, , and ), (3) on the upper wall of the chamber (, , and ), (4) on the side wall of the chamber (, , and ), and (5) in the entrance section (, , and ). The following are the initial conditions (): and , being solution (26) at and for all and except and , where the circulation is given ().
The results of numerical calculations made it possible to obtain the development of fields , , and in time when varying the incoming flow constructed using the radial velocity of the Reynolds number (), the angle of rotation of the guide blades (), and the viscosity ( m2/s).
As a result of the analysis of the data obtained, the following conclusions were made [70]: (1) the size of the vortex core is mainly a function of the twist parameter, (2) the size of the kernel does not depend on the Reynolds number at large values of the latter, (3) the size of the kernel ceases to depend on viscosity when it reaches small values (molecular viscosity values), and (4) the areas of the practically stationary core and the non-rotating external flow are separated by a thin layer with a high vortex.
In [71], it is noted that the most important parameter determining the structure of the vortex is the twist parameter. The results of calculations for different values of the twist parameter () at the Reynolds number (by radial velocity) of the order made it possible to draw the following conclusions: (1) when , the flow breaks away from the lower surface due to a negative pressure gradient; (2) when , the separation of the flow, still taking place, deflects the vector of vortices around the angular region, thus preventing the formation of a concentrated vortex at short distances from the surface; (3) when , the flow is detached from the lower surface, and convergence (convergence) does not occur, generating a large vortex and vertical velocity in the angular region; the decay of the vortex occurs above this region, with the propagation of inertial waves of large amplitude downstream; and (4) when the downward flow reaches the lower surface, the vortex moves very close to the surface.
In [72], a numerical simulation of a non-stationary three-dimensional flow in a vortex chamber [14] was performed. At the initial moment of time, the parameters of the axisymmetric non-rotating flow were calculated, where air enters through the sides below and exits through the upper part of the chamber. The distributions of the three components (radial, azimuthal, and vertical) of the velocity and pressure vector in the meridional section and their development over time were obtained. It is shown that when superimposed on the upward current of rotation at the lower levels, the structure of the flow changes from “single-cell” (upward flow everywhere) to “double-cell” (updraft surrounding the central downward flow).
In [73], a simple model of the flow in a vortex chamber is proposed. Assumptions are made about the weak dependence of the main characteristics of the flow in height, which is consistent with the data from the experiments. This allows for the integration procedure at a vertical coordinate, which makes it possible to first reduce the three-dimensional equations to two-dimensional ones and take into account the assumption of axisymmetric to one-dimensional equations. The performed calculations showed that features of the dynamics of the vortex such as the development of the downward flow and the expansion of the core are the result of the pressure distribution at the top of the chamber. The dependence of the vertical velocity and pressure distributions on the twist parameter are analyzed. The presence of two modes was revealed: turbulent and laminar at high and low twisting parameters, respectively. An explanation is given why the pressure in a turbulent vortex is much higher than in a non-turbulent one with the same twist parameter () and volume flow rate ().
In [74], numerical investigations of vortices observed in experiments [14,16] were continued. As a result of the calculations, stationary fields of all components of the velocity vector , , and , vertical vorticity , stream function , and pressure were obtained for different values of the twist parameter () and viscosity ( m2/s). It was found that at a relatively low twist parameter, the vortex is concentrated and laminar. In this case, the radial incoming air flow reaches the axis of the chamber, and the vertical velocity takes positive values everywhere. An increase in the twist parameter leads to the destruction of the vortex with a free critical point on the axis. Below this point, the flow is strictly ascending and laminar, while immediately adjacent to it, a region of weak descending and highly turbulent flow is formed. It should be noted that at high altitudes, the flow becomes ascending again. A further increase in the twist parameter leads to the displacement of the critical point towards the lower wall of the chamber, and the flow becomes descending and turbulent along the entire axis and acquires a biconical structure. The highest twist parameter values correspond to the flow characterized by a wide inner region occupying a significant part of the entire vortex chamber. Secondary vortices develop near the boundary of ascending and descending flows, where large gradients of the main parameters (all velocity components and vertical vorticity) occur. It was found that an increase in viscosity from the laminar (molecular) value to the turbulent one intensifies mixing processes. This delays the formation of the inner region and reduces the gradients of the main parameters at the boundary of ascending and descending flows.
Studies [75,76,77,78,79] are dedicated to the analysis of the dynamics of tornado-like flows. The analysis is conducted using the large eddy simulation (LES) method.
In [75], the possible role of turbulence in the interaction of tornadoes with the Earth’s surface is studied. The influence of secondary helical vortices developing around the main vortex on its kinematics is analyzed. It is found that these intense vortices have higher intensity and lead to the appearance of velocity fluctuations, the magnitude of which is about 1/3 relative to the averaged velocity.
In [76], three-dimensional modeling of the non-stationary interaction of a tornado-like vortex with a surface is carried out. The influence of the main physical parameters (circulation, horizontal convergence, effective roughness, vortex speed, and structure of the inflow) on the parameters of the “corner flow” (the region where the central vortex reaches the Earth’s surface) is considered. It is shown that the main parameter determining the dynamics of the corner flow is the radial inflow of fluid in the wall layer with low angular momentum relative to the moment that occurs in the main vortex above it.
The influence of compressibility (Mach number) of the tornado-like flow on its characteristics is studied in [77]. The conclusion is drawn about the insignificant influence of compressibility on the dynamics of the vortex. In [78,79], an investigation is made regarding the possibilities of intensifying quasi-stationary and non-stationary turbulent vortices. The key role of the corner flow twist parameter in the intensification (increase in azimuthal velocity and decrease in pressure) of the vortex in the surface area is revealed.
In [80,81,82], a turbulent LES model was developed and verified using laboratory experimental data. The Navier–Stokes equations (Reynolds-averaged) were used for the vertical and radial velocity components in the following form:
where and are terms responsible for diffusion.
To visualize the calculated vortex structures, 10 μm tracer particles were used. Variation of the swirl parameter () led to the realization of four main types of vortices: (1) single vortex (), (2) vortex breakdown with the formation of a recirculation bubble (), (3) vortex touch-down (), and (4) multi-vortex structures ().
3.3. Two-Phase Nature of Tornado
The study of the features of the motion of the dispersed phase (cloud drops, raindrops, particles, and fragments) in tornado-like vortices is of considerable interest due to several reasons.
The first reason is that the presence of a dispersed phase in the form of drops, soil particles, and fragments visualizes (makes visible) atmospheric vortices [3]. Tracer particles of low inertia are used for the physical modeling of vortex structures in laboratory conditions [83,84,85]. Figure 3 shows a typical frame with a fixed laboratory vortex. The vortex funnel and debris cloud, visualized by low inertia and large particles, respectively, are clearly seen in this photograph. Even when conducting numerical studies, a technique is used that consists of the introduction of low-inertia particles, following the streamlines of the carrier air to visualize the calculated flow patterns [82].
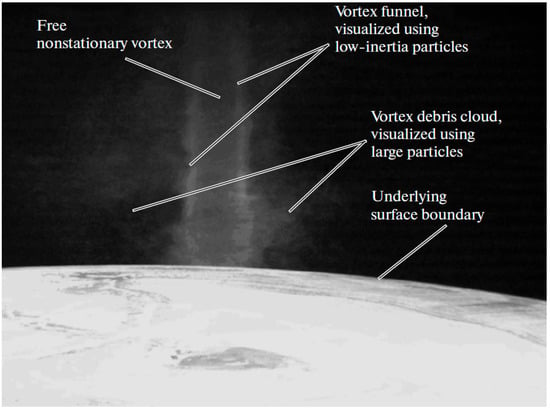
Figure 3.
Typical frame with a fixed laboratory-simulated vortex [85].
The second reason is that the possibility of measuring the velocity of the dispersed phase opens the way to studying the dynamics of the vortex structure. The above applies both to laboratory conditions [86] and natural vortices. It is known that the simplest video recording of atmospheric vortices can provide useful information by measuring the velocity of debris of various masses.
The third reason is that the latent heats of phase transformations (primarily condensation and evaporation) during the formation (disappearance) of droplets have a significant effect on the generation process, dynamics, and stability of tornado-like vortices [3].
The fourth reason is the reverse effect of the dispersed phase on the behavior of the vortex structure. There are numerous works showing that, at certain concentrations, the dispersed phase can have a significant effect on the characteristics of an atmospheric vortex and its behavior (up to decay) [87,88,89,90].
The fifth reason is that the presence of fragments and other dispersed inclusions can make a decisive contribution to the negative consequences (destruction and casualties) of a tornado [3].
Below are the results of works that consider some aspects of the two-phase nature of vortex structures, namely, phase transformations and features of particle motion along with their reverse effect on the characteristics of carrier air.
3.4. Processes of Evaporation and Condensation
A pioneering study that considers the process of tornado formation due to rotation in a thundercloud (modeled “from above”) is [91]. This study developed a three-dimensional model of a thundercloud, which is based on compressible gas equations that take into account the Coriolis force. The model considers the content of water vapor, cloud droplets and raindrops, condensation and evaporation processes, and the corresponding latent heat of phase transformations.
Additional transport equations for all unknown quantities , which are the potential temperature (), the concentrations of water vapor , cloud droplets , and raindrops , were presented in the following generalized form:
where is the terms defined by “microphysical” processes and is terms determined by the intensity of turbulent transfer. Expressions for and in [91] were represented as
where , is the latent heat of vaporization, is the ratio of the components of the saturation mixture, and is the rate of condensation or evaporation of cloud droplets . Terms , , and are the rates of auto-recalculation, accumulation, and evaporation of raindrops, respectively; is the rate of winding of raindrops.
In [91], a number of assumptions were made in which the “turbulent” terms in (29) and were represented as follows:
where is the coefficient of turbulent viscosity; strokes denote the fluctuation values of the parameters.
As a result of numerical calculations, a number of interesting results were obtained: (1) flow bifurcation is initiated by a high concentration of water droplets realized in the central part of the developing updraft, (2) updrafts are supported by an influx of moist surface air while rain falls between them, and (3) all of the above leads to the realization of self-sustaining convection in the cloud under consideration.
In [92], a three-dimensional simulation was performed that followed the study of tornadogenesis processes within a storm supercell. Within 40 min, the generation and decay of two tornadoes were recorded. The lifetime of each tornado was approximately 10 min. The maximum speed in the surface region exceeded 60 m/s for both tornadoes. Conclusions were made: (1) the tornadogenesis is initiated by the growth of rotation in the area above the cloud base; (2) the intensification of rotation leads to a decrease in pressure, an increase in forces caused by vertical pressure gradients, and the generation of an intense ascending current at this level; (3) the ascending current leads to a rapid increase in the convergence of air in the subcloud layer; (4) this leads to an increase in the vertical vorticity in the convergent flow, generating a tornado; (5) the weakening (dissipation) of the tornado begins with a decrease in forces caused by pressure gradients in the vertical direction; and (6) the tornado dissolves due to the loss of its source of positive vertical vorticity.
In [93], the process of generating a tornado-like vortex within a storm supercell was studied. For modeling, a computer system previously created at the University of Colorado to calculate cloud dynamics was used. The system includes a number of blocks, one of which is a block of “microphysical” processes, which allow one to calculate the processes of formation and growth of liquid (droplets) and solid (ice) particles as well as the features of their dynamics. To initiate the convection of air masses in the cloud at the initial time in the center of the calculation cell, a thermal “bubble” of rectangular shape was formed (height: 3 km and length: 10 km). The temperature of the “bubble” was 1.5 K, and the water vapor content was 2 g/kg higher than the corresponding values in the surrounding space. The calculations performed with high spatial resolution made it possible to obtain and analyze the dynamics of the fields of various components of the air velocity vector as well as the pressure and water vapor content in selective vertical and horizontal sections. Calculations have shown that after 90 min on the edge (direction “east–southeast”) of the storm supercell, a “pipe” of low pressure is formed in the region of high gradients of vertical velocity in the horizontal direction, which begins its spread towards the Earth’s surface. Thus begins the formation of a strong vortex in the subcloudal layer. Therefore, in [92,93], it was clearly shown that the initial stage of tornado formation proceeds for many tens of minutes.
Let us note another work [94], numerous results of which demonstrate the possibilities of numerical modeling of the dynamics of downward air flows. It used a mathematical model similar to [93]. It is shown that both the intensity and duration of the tornado depend on the thermodynamic characteristics of the rotating downward flow, depending on the surrounding humidity of the surface layer and the nature of atmospheric precipitation in the rain curtain. Model tornadoes were more intense and long-lived in the case of relatively warm rotating downward flows, contributing to a strong convergence of angular momentum in the surface layer. Warmer downward flows are formed in conditions of high relative humidity and in conditions of relatively low precipitation concentration.
The importance of considering possible phase transformations on the dynamics of tornado-like atmospheric vortices was discussed in [95,96,97].
In [95], a system of equations describing the flow of moist air inside a tornado funnel was constructed, allowing for an analytical solution for the quasi-stationary case (without considering the processes of tornado initiation and dissipation) using two small parameters of the problem: (1) the specific humidity of air (the ratio of the mass of water vapor to the mass of moist air) and (2) the ratio of the tornado funnel radius to its height, . This work considers the processes of energy and mass transfer as stationary in a developed tornado, and the flow is considered in a rotating cylinder, the walls of which consist of hailstones and water droplets. Condensation of moisture from the air occurs on the surface of this cylinder. The walls of the tornado funnel are considered impermeable, and condensation occurs in a thin layer (compared to the radius of the tornado) on the inner surface of the cylinder. It is assumed that the walls of the funnel consist of hailstones, water droplets, and other objects sucked up by the tornado. It is also assumed that the parameters of the walls remain unchanged during the entire time the tornado exists.
In the absence of data on the mass transfer coefficient from the flow of moist air to the walls of the tornado funnel, the diffusion equation for humidity (water vapor) was written in an approximate form:
where is the velocity along the axis of the tornado funnel and is the coefficient of turbulent diffusion of moisture in the tornado funnel. Taking into account the boundary condition , solution (32) was obtained in the following form in [95]:
As a result, the solutions obtained in [95] introduced another important criterion for the existence of tornadoes: the critical vertical humidity gradient , which determines the conditions for the onset of the updraft. In [96,97], modifications were made to the flow model of [95].
To numerically describe the hydrodynamics of a two-phase flow and heat and mass transfer processes taking into account condensation inside the tornado vortex, transport equations for averaged quantities were used with coefficients of turbulent viscosity, diffusion, and thermal conductivity constant for the entire computational domain. Water droplets formed due to bulk condensation were considered only in the equations of energy and diffusion by introducing corresponding source terms. According to observational estimates presented in [98], the thermal power of a tornado of average intensity can reach GW. Calculations were performed for two power values of GW and GW for small ( m) and large ( m) vortex radii. The results confirmed that the energy of water vapor condensation is sufficient to provide the observed tornado lifespan.
3.5. Disperse Phase Motion in Tornado-like Flows
In [99], the characteristics of the movement of solid particles with different inertial properties in a “dust devil” were studied based on numerical simulations using the LES method and the Lagrangian trajectory approach. The motion of dust particles (density 2560 kg/m3) of three different sizes (100 μm, 200 μm, and 300 μm) was calculated in a previously calculated non-stationary velocity field of the air vortex. During the calculations, trajectories of 20,000 particles of each size, which were injected in equal portions (400 particles) into the lower part of the vortex every 0.1 s, were analyzed. As a result, the spatial arrangement of all introduced dust particles in the “dust devil” after 5 s was obtained. The following conclusions were made: (1) the particle arrangement in space is significantly non-uniform; (2) the smallest small-inertial particles rise to a height of 25 m or more, and their spatial arrangement is the most uniform; (3) the decrease in vertical air velocity with increasing distance from the surface and the increase in particles inertia lead to a significant decrease in the maximum lift of larger particles; and (4) the non-uniform distribution of larger particles in space is due to lower values of their velocities caused by centrifugal forces.
In [100], the behavior of trajectories and concentration fields of particles in the axisymmetric flow of viscous incompressible fluid, modeling the interaction of a vertical vortex filament thread with a horizontal plane, was investigated based on numerical calculations. For the description of the motion of the carrying gas phase, a self-similar solution of the Navier–Stokes equations obtained by Gol’dshtik [101] was used. The parameters of the dispersed phase, including concentration, were calculated using a complete Lagrangian approach along the selected trajectories. The influence of particles on the parameters of the carrying gas was not taken into account, as the volume and mass concentration of particles were assumed to be small [90,102].
As a result of the calculations in [100], the possibility of multiple intersections of particle streamlines and the formation of “folds” in the concentration field of the dispersed phase were demonstrated. For heavy particles (exceeding the carrying phase in density), the formation of a “bowl-shaped” accumulation surface of the dispersed phase and a zone of particle deposition near the base of the vortex were observed (Figure 4). In the case of taking into account the force of gravity (), the edge of the bowl-shaped accumulation surface of particles is twisted into a spiral around a circle. The position of this circle is determined by the zero balance of hydrodynamic (drag force), gravitational (gravity), and inertial (centrifugal force) forces acting on particles in the vortex flow.

Figure 4.
Typical (a) ascending and (b) descending trajectories of particles [100].
In works [103,104], a two-fluid tornado model is developed. The first (primary) fluid is water vapor that condenses during a sharp pressure jump. The second (secondary) fluid is composed of solid particles picked up by the vortex. It should be noted that there is no proper description of the mathematical model used in [103,104], but the results of numerical modeling of the life cycle of a tornado and the effects of a tornado on a car and a small house moving along a highway are presented.
In article [105], mathematical modeling of tornado-like vortices was conducted using the LES method. The features of the vortex throwing “projectiles” of two types were studied: a wooden board weighing 14 kg and a car weighing 1810 kg. Statistical distributions of the maximum values of the horizontal velocity components of these “projectiles” were obtained.
Article [106] presents a detailed analysis of the influence of solid, low-inertia fragments on tornado characteristics. Modeling was performed based on the Euler–Euler (two-fluid) model, which assumes the use of one type of equation to describe the continuous and dispersed phases within the framework of the mechanics of interpenetrating media with the account of the particles’ backward influence (in English-language publications, such calculations are called “two-way coupling”).
Three dimensionless parameters that determine the dynamics of fragments in the tornado were found: (1) the parameter of the twist of the corner flow, determining the “type” (structure) of the tornado, (, , and are the characteristic radius of the core above the area of angular flow, the moment of rotation at a considerable distance from the core, and the loss of the flow’s rotational momentum in the “surface-corner-core” area, respectively); (2) a parameter that is a measure of the relative importance of “centrifugation” of fragments and is determined as the ratio of the radial acceleration in the angular flow to the acceleration of free fall, , where is the characteristic azimuthal velocity; and (3) a parameter that is a measure of the ease of lifting fragments and is determined as the ratio of the characteristic velocity of the tornado and the settling (swirling) velocity of the fragments, .
First, the tornado parameters were calculated in the absence of particles and then with particles. The calculations included the particle size, which was varied ( μm), phase density ratio (), and some surface characteristics. It was found that the sand cloud (tornado cascade) reaches a quasi-stationary state when the mass of suspended particles becomes equal to the mass of those deposited. As a result of the calculations, the main characteristics (formation time, total mass of fragments, height of the cascade, maximum tangential velocity of the vortex as a whole, etc.) of the vortex and tornado cascade were obtained. The following conclusions were drawn: (1) intense exchange of momentum between air and suspended sand particles that make up the tornado cascade led to a decrease in the maximum vortex velocity; (2) the accumulation of low-inertia fragments near the corner flow in the surface layer has a significant effect on the strength of the tornado; and (3) with an increase in the inertia of the particles, the time of formation of the tornado cascade, the total mass of the particles involved, and the geometric dimensions of the cascade decrease significantly.
4. Latest Results
The formation of strong tornadoes, according to the generally accepted opinion, mostly begins with the generation of so-called supercells. Supercells are characterized by strong rotation at the middle level [107]. The formation of small and weaker tornadoes that occur in North America is not accompanied by strong circulation at the middle level. Such tornadoes have been named “non-supercell tornadoes” [108] or “nonsupercyclonic” tornadoes [109].
4.1. Dynamics of the Cyclostrophic Balance
As shown in [110], the compression of a developing surface cyclone occurs only when surface friction is taken into account. The cyclostrophic balance between the pressure gradient and the centrifugal force, which exists without surface friction, is disturbed (Figure 5). The pressure gradient (directed inward towards the axis) becomes greater than the centrifugal force (directed outward). This disturbs the cyclostrophic balance and leads to a strong radial inflow of air. Therefore, air parcels penetrate much closer to the axis than to the equilibrium radius of cyclostrophic balance. To satisfy the continuity equation (mass conservation), the radial inflow must turn as it approaches the axis. It rises rapidly at high speed. The axial helical jet can be regarded as the upward continuation of the surface boundary layer. The “new” cyclostrophic balance maintains very low pressure at the axis.
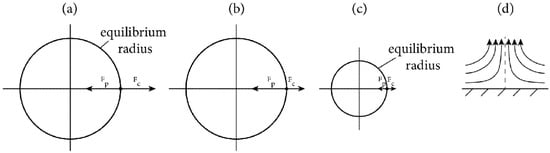
Figure 5.
Scheme of the intensification of the upward flow with the friction force taken into account: (a) an initial cyclostrophic balance, (b) a decrease in centrifugal force due to friction and decrease in air velocity, (c) a new cyclostrophic balance, and (d) an intensification of radial air inflow and upward movement. Here, is the pressure gradient force, and is the centrifugal force. The velocity and friction force vectors are not given.
In [111,112], it is proposed to use a certain fictitious force that creates false (artificial) horizontal vorticity. However, [113] notes that in meteorology, the laws of mass, energy, momentum, angular momentum, and entropy conservation must be inviolable. In [113], it is shown that rapid tornado genesis in modeling can be associated with a combination of the following factors: (1) excessively strong convective initiation in a very unstable atmosphere, which leads to too-strong low-level updraft at the beginning of the supercell’s life; (2) the use of a lower boundary condition of semi-slip; (3) the absence of perturbations to excite significant turbulence, which leads to too-strong friction force and too-large shear in a too-thin layer near the ground [114]; and (4) the use of omnipresent, all-pervading external force to maintain a stable horizontally homogeneous medium—this force introduces additional degrees of freedom that allow the restrictions of the Taylor–Proudman theorem to be bypassed but leads to changes in the dynamics within the storm.
A possible mechanism for rapid tornado genesis in mathematical modeling can be described as follows. As a result of factor 4, the external force is balanced by three forces in the surrounding environment. This balance is concentrated at the ground by factors 2 and 3. Inside the storm, friction and the Coriolis force no longer balance the external force, so it creates strong horizontal vorticity in the shallow surface layer. The tilt and stretching of this vorticity (if it occurs along the flow) by the upward flow, according to factor 1, will create significant vertical vorticity at low heights.
Examples of the formation of vortices in high-temperature substances and under the action of a strong magnetic field, as well as under conditions of fast plasma processes, are possible [115,116,117,118].
The above-described tornado genesis mechanism is consistent with the results of natural measurements of the development of a tornado mesocyclone during the PECAN field experiment conducted in 2015, in South Dakota, which used an extensive network of stationary and mobile observation systems for low-level convective jets [119].
4.2. Main Mechanisms of Tornadogenesis
To date, much is known about the environmental conditions necessary for supercell tornado genesis. At the same time, the dynamics of ground-level vorticity in the process of tornado genesis itself are still not sufficiently studied.
In the literature, a very large number of seemingly contradictory mechanisms responsible for high values of ground-level vertical vorticity can be found. All of these mechanisms can be divided into two main classes [120].
The first mechanism class is based on the upward tilt of horizontal vorticity generated primarily baroclinically in the downdraft. This mechanism is referred to as the “downdraft mechanism”. Recent works [121,122,123,124,125] represent this approach.
The second mechanism class is based on the upward tilt of horizontal vorticity near the ground (Figure 6 and Figure 7), which is created by a strong horizontal gradient in the updraft (the “in-and-up mechanism”). Recent works [126,127,128,129,130,131,132,133] illustrate this approach well. In addition, we note that different vortices can form under different conditions [134,135,136,137,138,139,140,141].

Figure 6.
Scheme of generation of horizontal vorticity and its inclination by ascending flows near the Earth’s surface: (a) generation of horizontal vorticity by a horizontal buoyancy gradient, (b) generation of ascending flows by a horizontal buoyancy gradient, and (c) inclination of initially horizontal vortex filaments by a surrounding vertical flow.

Figure 7.
Mechanism of wall-free non-stationary air vortex generation [130]: (a) photo of laboratory non-stationary vortex (image size is 155 × 200 mm) and (b) scheme of vortex formation. The numbers denote (1, 2) source vortex filaments, (3) convergence and twisting of water filaments, (4) wall-free non-stationary vortex, and (5) edge of the underlying surface.
In Ref. [120], it is clearly shown that both downdraft and updraft mechanisms play an important role in tornadogenesis. It is known that pre-tornadic maxima of vertical vorticity are generated primarily by the downdraft mechanism, while the dynamics of a fully developed tornado vortex are controlled by the updraft mechanism. This paper makes an important conclusion that there is a transition between these two mechanisms, which occurs during tornadogenesis. This transition is a result of the axisymmetrization of the pre-tornadic vortex “blob” and its intensification by vertical stretching. These processes facilitate the development of corner flow, the presence of which promotes the generation of vertical vorticity by tilting horizontal vorticity near the ground (i.e., through the in-and-up mechanism). Plasma vortexes are the subject of a separate study and require special consideration [142,143,144,145].
In conclusion, we mention works [119,146,147] in which the authors tried to take into account the influence of both mechanisms (downdraft mechanism and in-and-up mechanism) on tornado generation and dynamics in their calculations.
4.3. Main Factors of Tornadogenesis
The downdraft mechanism and in-and-up mechanism are needed to start the process of tornadogenesis. The role of both of these mechanisms is not yet fully understood. Since only the ascending mechanism can lead to the transformation of the horizontal vorticity into a vertical one, a transition between these mechanisms is likely to take place. The presence of a downward mechanism is necessary for the rapid intensification of a tornado and is necessary throughout the life of a tornado until its collapse.
Here, we summarize some factors facilitating tornado appearance (generation). The four major circumstances affecting the generation of the ascending air flow are as follows (see Figure 8):

Figure 8.
Main factors affecting the generation of the ascending air flow and formation of the tornado funnel.
(i) The presence of warm and, consequently, relatively light air near the underlying surface, which tends upwards;
(ii) A possible presence in the warm air of sand (soil) particles or drops (in the case of a waterspout), lifted from the surface, which often have a greater (compared to the air) temperature, resulting in additional heating of air;
(iii) The presence of (due to various reasons) rotation (vorticity) of the warm air, which generates low-pressure regions at the center of the developing ascending flow, thus facilitating the condensation of water vapor in the air and the release of heat;
(iiii) Intensified condensation of the water vapor in the warm ascending air, when it is lifted and interacts with cold air, facilitating its further heating and making it lighter.
Evidently, there exist four major factors affecting the formation of the tornado funnel; they are as follows (see Figure 8):
(1) The presence of cold and, consequently, relatively heavy air at the top, tending to descend to the underlying surface;
(2) The presence in the cold air of water drops, making it heavier (enhancing the effective density);
(3) The presence of rotation (vorticity) of the cold air, generating a low-pressure region at the center of the developing funnel, which facilitates further concentration of drops, their coagulation, and higher effective density of the descending cold air;
(4) Intensified evaporation of drops in the cold air, which interacts with the warm air near the surface, facilitating its further cooling and making it heavier.
All of the above physical mechanisms should be reflected in modern numerical models of tornados. In terms of aerodynamics, a tornado is an analog of a tube carrying warm air upwards, rather than cold air downwards. This is evident, since the flow rate of the carried heated air greatly exceeds the flow rate of the cold air. The flow rate of the warm air, defined by the geometry (above all, by the cross-sectional area) of the carrying channel and the vertical velocity component, is one of the characteristics determining the tornado force. The vertical gradient of air temperature that characterizes the degree of atmosphere instability determines the speed of the ascending flows. The largest vertical temperature gradients are implemented in low clouds (cumulonimbus clouds); therefore, the most violent tornados develop under such conditions, as a rule. The movement of the tornado funnel together with the cloud facilitates further involvement of new portions of warm air and is a factor increasing the tornado stability.
5. Conclusions
A review of works devoted to the mathematical modeling of air tornado-like vortices has been made. Analytical models of various levels of complexity created to date (based on the Bernoulli, Navier–Stokes, and vorticity equations) and the possibility of numerical modeling are described. The results of computational and theoretical studies of the conditions of formation, dynamics, and main characteristics of vertical concentrated vortices are given and analyzed. Special attention is paid to features taking into account the two-phase nature (phase transitions, the movement of particles in vertical vortices, and the particles’ back effect on the characteristics) of tornado-like vortices.
It can be concluded that the main problems of modeling tornado-like vortices, related to predicting the probability of their occurrence, development, and control, largely remain unsolved.
Apparently, further progress in building the theory of concentrated tornado-like vortices will be determined by the following:
- (1)
- The ability to plan laboratory studies of the conditions for the generation, stability, and control of significantly non-stationary concentrated vortices;
- (2)
- The ability to improve measurements of the characteristics of real natural vortex structures;
- (3)
- The ability to develop mathematical models that adequately describe the structure and dynamics of both laboratory and natural non-stationary vortices throughout their life cycle (from generation to decay).
Author Contributions
Conceptualization, A.Y.V.; formal analysis, S.V.R.; data curation, A.Y.V.; writing—original draft preparation, A.Y.V.; writing—review and editing, S.V.R.; visualization, A.Y.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
The authors express their sincere gratitude to Varaksina V.A. for her great help in editing the figures and preparing the graphic materials of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| distance from the axis of symmetry of the vortex, m | |
| universal gas constant, J/(kg K); Earth radius, m | |
| distance from the surface of the Earth, m | |
| , , | velocity components in a cylindrical coordinate system (), m/s |
| , , | velocity components in Cartesian coordinates (), m/s |
| , , | fluctuation velocity components in a cylindrical coordinate system (), m/s |
| particle gravitational settling rate, m/s | |
| debris gravitational settling rate, m/s | |
| pressure of moving air, Pa | |
| pressure of fixed air, Pa | |
| density of moving air, kg/m3 | |
| density of fixed air, kg/m3 | |
| dispersed phase density, kg/m3 | |
| kinematic viscosity, m2/s | |
| turbulent viscosity, m2/s | |
| turbulent thermal diffusivity, m2/s | |
| circulation, m2/s | |
| gravitational acceleration, m/s2 | |
| stream function, m3/s | |
| azimuthal component of vorticity, s−1 | |
| vertical vorticity component, s−1 | |
| first Coriolis parameter, s−1 | |
| second Coriolis parameter, s−1 | |
| temperature, K | |
| averaged (by entropy) temperature of the heat source, K | |
| averaged (by entropy) temperature of heat sink, K | |
| potential temperature, K | |
| wet adiabatic gradient, K/m | |
| mesovortex energy, J | |
| macrovortex energy, J | |
| isobaric heat capacity of air, J/(kg K) | |
| entropy, J/K | |
| volumetric concentration of the dispersed phase | |
| ratio of the densities of the gas and dispersed phases | |
| spin parameter | |
| dimensionless dissipation coefficient | |
| dimensionless dissipation coefficient | |
| thermodynamic efficiency of the “dust devil” | |
| dimensionless current function | |
| radial Reynolds number | |
| vortex Reynolds number | |
| Froude number | |
| Superscripts | |
| deviation from the mean | |
| average (over time) value | |
| Subscripts | |
| air | |
| still air, in the core of the vortex | |
| particles | |
| funnel surface | |
| on the surface of the Earth, in the center, the initial moment of time | |
| at an infinite distance from the center | |
| in the surrounding atmosphere | |
| maximum value | |
References
- Alekseenko, S.; Kuibin, P.; Okulov, V. Theory of Concentrated Vortices: An Introduction; Spinger: Berlin/Heidelberg, Germany, 2007; 506p. [Google Scholar]
- Bluestein, H.B. Severe Convective Storms and Tornadoes: Observations and Dynamics; Spinger Science & Business Media: Berlin/Heidelberg, Germany, 2013; 456p. [Google Scholar]
- Rotunno, R. The fluid dynamics of tornadoes. Annu. Rev. Fluid Mech. 2013, 45, 59–84. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. Tornado; Begell House: New York, NY, USA, 2015; 394p. [Google Scholar]
- Finley, A.J.; Brun, A.S.; Carlsson, M.; Szydlarski, M.; Hansteen, V.; Shoda, M. Stirring the base of the solar wind: On heat transfer and vortex formation. Astron. Astrophys. 2022, 665, A118. [Google Scholar] [CrossRef]
- Barczynski, K.; Schmieder, B.; Peat, A.W.; Labrosse, N.; Mein, P.; Mein, N. Spectro-imagery of an active tornado-like prominence: Formation and evolution. Astron. Astrophys. 2021, 653, A94. [Google Scholar] [CrossRef]
- Vasheghani Farahani, S.; Ghanbari, E.; Ghaffari, G.; Safari, H. Torsional wave propagation in solar tornadoes. Astron. Astrophys. 2017, 599, A19. [Google Scholar] [CrossRef][Green Version]
- Agee, E.; Taylor, L. Historical analysis of U.S. tornado fatalities (1808–2017): Population, science and technology. Weather Clim. Soc. 2019, 11, 355–368. [Google Scholar] [CrossRef]
- Anderson-Frey, A.K. Tornado fatalities: An environmental perspective. Weather Forecast. 2019, 34, 1999–2015. [Google Scholar] [CrossRef]
- Alexander, C.R.; Wurman, J. The 30 May 1998 Spencer, South Dakota, storm. Part I: The structural evolution and environment of the tornadoes. Mon. Weather Rev. 2005, 133, 72–96. [Google Scholar] [CrossRef]
- Wurman, J.; Alexander, C.R. The 30 May 1998 Spencer, South Dakota, storm. Part II: Comparison of observed damage and radar-derived winds in the tornadoes. Mon. Weather Rev. 2005, 133, 97–119. [Google Scholar] [CrossRef]
- Kosiba, K.A.; Wurman, J.; Richardson, Y.; Markowski, P.; Robinson, P.; Marquis, J.N. Genesis of the Goshen County, Wyoming, tornado on 5 June 2009 during VORTEX2. Mon. Weather Rev. 2013, 141, 1157–1182. [Google Scholar] [CrossRef]
- Trapp, R.J.; Kosiba, K.A.; Marquis, J.N.; Kumjian, M.R.; Nesbitt, S.W.; Wurman, J.; Salio, P.; Grover, M.A.; Robinson, P.; Hence, D.A. Multi-platform and multiple-doppler radar observations of a supercell thunderstorm in South America during RELAMPAGO. Mon. Weather Rev. 2020, 148, 3225–3241. [Google Scholar] [CrossRef]
- Ying, S.J.; Chang, C.C. Exploratory model study of tornado-like vortex dynamics. J. Atmos. Sci. 1970, 27, 3–14. [Google Scholar] [CrossRef]
- Wan, C.A.; Chang, C.C. Measurement of the velocity field in a simulated tornado-like vortex using a three-dimensional velocity probe. J. Atmos. Sci. 1972, 29, 116–127. [Google Scholar] [CrossRef]
- Ward, N.B. The exploration of certain features of tornado dynamics using laboratory model. J. Atmos. Sci. 1972, 29, 1194–1204. [Google Scholar] [CrossRef]
- Fizjarrald, D.E. A laboratory simulation of convective vortices. J. Atmos. Sci. 1973, 30, 894–902. [Google Scholar] [CrossRef]
- Church, C.R.; Snow, J.T.; Agee, E.M. Tornado vortex simulation at Purdue University. Bull. Amer. Meteorol. Soc. 1977, 58, 900–908. [Google Scholar] [CrossRef]
- Baker, G.; Church, C.R. Measurements of core radii and peak velocities in modeled atmospheric vortices. J. Atmos. Sci. 1979, 36, 2413–2424. [Google Scholar] [CrossRef]
- Snow, J.T.; Church, C.R.; Barnhart, B.J. An investigation of the surface pressure fields beneath simulated tornado cyclones. J. Atmos. Sci. 1980, 37, 1013–1025. [Google Scholar] [CrossRef]
- Kuai, L.; Haan, F.L.; Gallus, W.A.; Sarkar, P.P. CFD simulations of the flow field of a laboratory-simulated tornado for parameter sensitivity studies and comparison with field measurements. Wind Struct. 2008, 11, 75–96. [Google Scholar] [CrossRef]
- Haan, F.L.; Sarkar, P.P.; Gallus, W.A. Design, construction and performance of a large tornado simulator for wind engineering applications. Eng. Struct. 2008, 30, 1146–1159. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N.; Taekin, S.I. The possibility of physical simulation of air tornados under laboratory conditions. High Temp. 2008, 46, 888–891. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Taekin, S.I.; Kopeitsev, V.N. The generation of free concentrated air vortexes under laboratory conditions. High Temp. 2009, 47, 78–82. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. The parameters of unstable stratification of air leading to generation of free vortexes. High Temp. 2010, 48, 251–255. [Google Scholar] [CrossRef]
- Yih, C.-S. Tornado-like flows. Phys. Fluids 2007, 19, 076601–1–076601-6. [Google Scholar] [CrossRef]
- Shtern, V.; Borissov, A.; Hussain, F. Vortex-sinks with axial flows: Solution and applications. Phys. Fluids 1997, 9, 2941–2959. [Google Scholar] [CrossRef]
- Arsen’ev, S.A.; Nikolaevskii, V.N.; Shelkovnikov, N.K. Eddy instability and origination of whirlwinds and tornadoes. Mosc. Univ. Phys. Bull. 2000, 55, 57–61. [Google Scholar]
- Khrgian, A.K. Atmospheric Physics; Gidrometeoizdat: Leningrad, Russia, 1978; 318p. (In Russian) [Google Scholar]
- Shuleikin, V.V. Calculation of Development, Movement, and Attenuation of Tropical Storms and Major Waves Produced by Hurricanes; Gidrometeoizdat: Leningrad, Russia, 1978; 96p. (In Russian) [Google Scholar]
- Gutman, L.N. Theoretical model of a tornado. Izv. Akad. Nauk SSSR Ser. Geofiz 1957, 79–93. (In Russian) [Google Scholar]
- Lewis, W.; Perkins, P.J. Recorded pressure distribution in the outer portion of a tornado vortex. Mon. Weather Rev. 1953, 81, 379–385. [Google Scholar] [CrossRef]
- Kuo, H.L. On the dynamics of convective atmospheric vortices. J. Atmos. Sci. 1966, 23, 25–42. [Google Scholar] [CrossRef]
- Kuo, H.L. Note on the similarity solutions of the vortex equations in an unstably stratified atmosphere. J. Atmos. Sci. 1967, 24, 95–97. [Google Scholar] [CrossRef]
- Mal’bakhov, V.M.; Gutman, L.N. Nonstationary problem about meso-scale atmospheric vortices with vertical axis. Izv. Akad. Nauk SSSR Fiz. Atmos. Okeana 1968, 4, 586–598. (In Russian) [Google Scholar]
- Mal’bakhov, V.M. Investigation of tornado structure. Izv. Akad. Nauk SSSR Fiz. Atmos. Okeana 1972, 8, 17–28. (In Russian) [Google Scholar]
- Arsen’ev, S.A.; Babkin, V.A.; Gubar’, A.Y.; Nikolaevskiy, V.N. Theory of Mesoscale Turbulence: Vortices of the Atmosphere and Ocean; Inst. Komp’yut. Issled.: Izhevsk, Russia, 2010; 308p. (In Russian) [Google Scholar]
- Kurganskii, M.V. A simple hydrodynamic model of tornado-like vortices. Izv. Atmos. Oceanic Phys. 2015, 51, 292–298. [Google Scholar] [CrossRef]
- Holton, J.R. An Introduction to Dynamic Meteorology; Academic Press: San Diego, CA, USA, 1992; 507p. [Google Scholar]
- Ambaum, M.H.P. Thermal Physics of the Atmosphere; Wiley-Blackwell: Chichester, UK, 2010; 256p. [Google Scholar]
- Davies-Jones, R. A review of supercell and tornado dynamics. Atmos. Res. 2015, 158, 274–291. [Google Scholar] [CrossRef]
- Kurgansky, M.V. A simple model of dry convective helical vortices (with applications to the atmospheric dust devil. Dyn. Atmos. Oceans 2005, 40, 151–162. [Google Scholar] [CrossRef]
- Kurgansky, M.V. Simple models of helical baroclinic vortices. Proc. IUTAM 2013, 7, 193–202. [Google Scholar] [CrossRef]
- Davies-Jones, R.P.; Kessler, E. Tornadoes. In Weather and Climate Modification; Hess, W.N., Ed.; Jon Wiley and Sons: New York, NY, USA, 1974; pp. 552–595. [Google Scholar]
- Lewellen, W.S. Theoretical Models of the Tornado Vortex. In Weather and Climate Modification, Proceedings of the A Simposium on Tornadoes Assessment of Knowledge and Implications for Man, Lubbock, TX, USA, 22–24 June 1976; Hess, W.N., Ed.; Texas Tech. Univ.: Lubbock, TX, USA, 1976; pp. 107–143. [Google Scholar]
- Snow, J.T.; Pauley, R.L. On the thermodynamic method for estimating tornado windspeeds. J. Clim. Appl. Meteorol. 1984, 23, 1465–1468. [Google Scholar] [CrossRef]
- Fiedler, B.H.; Rotunno, R. A theory for the maximum windspeeds in tornado-like vortices. J. Atmos. Sci. 1986, 43, 2328–2340. [Google Scholar] [CrossRef]
- Renno, N.O.; Ingersoll, A.P. Natural convection as a heat engine: A theory for CAPE. J. Atmos. Sci. 1996, 53, 572–585. [Google Scholar] [CrossRef]
- Shuleikin, V.V. Sea Physics; Nauka: Moscow, Russia, 1990. (In Russian) [Google Scholar]
- Renno, N.O.; Burkett, M.L.; Larkin, M.P. A simple thermodynamical theory for dust devils. J. Atmos. Sci. 1998, 55, 3244–3252. [Google Scholar] [CrossRef]
- Renno, N.O. A simple theory for waterspouts. J. Atmos. Sci. 2001, 58, 927–932. [Google Scholar] [CrossRef]
- Sinclair, P.C. General characteristics of dust devils. J. Appl. Meteorol. 1969, 8, 32–45. [Google Scholar] [CrossRef]
- Sinclair, P.C. The lower structure of dust devils. J. Atmos. Sci. 1973, 30, 1599–1619. [Google Scholar] [CrossRef]
- Golden, J.H. The life cycle of Florida Keys’ waterspouts. J. Appl. Meteorol. 1974, 13, 676–692. [Google Scholar] [CrossRef]
- Golden, J.H. Scale-interaction implications for the waterspout life cycle. II. J. Appl. Meteorol. 1974, 13, 693–709. [Google Scholar] [CrossRef]
- Simpson, J.; Morton, B.R.; McCumber, M.C.; Penc, R.S. Observations and mechanisms of GATE waterspouts. J. Atmos. Sci. 1986, 43, 753–782. [Google Scholar] [CrossRef]
- Golden, J.H.; Bluestein, H.B. The NOAA-National Geographic Society waterspout expedition (1993). Bull. Amer. Meteorol. Soc. 1994, 75, 2281–2288. [Google Scholar] [CrossRef]
- Romps, D.M. Clausius-Clapeyron scaling of CAPE from analytical solutions to RCE. J. Atmos. Sci. 2016, 73, 3719–3737. [Google Scholar] [CrossRef]
- Mapes, B.E. Water’s two height scales: The moist adiabat and the radiative troposphere. Quart. J. Roy. Meteorol. Soc. 2001, 127, 2353–2366. [Google Scholar] [CrossRef]
- Singh, M.S.; O’Gorman, P.A. Influence of entrainment on the thermal stratification in simulations of radiative-convective equilibrium. Geophys. Res. Lett. 2013, 40, 4398–4403. [Google Scholar] [CrossRef]
- Arsen’ev, S.A.; Gubar’, A.Y.; Nikolaevskiy, V.N. Self-organization of tornado and hurricanes in atmospheric currents with meso-scale eddies. Dokl. Earth Sci. 2004, 396, 588–593. [Google Scholar]
- Arsen’ev, S.A.; Gubar’, A.Y.; Shelkovnikov, N.K. Generation of typhoons and hurricanes by a mesoscale turbulence. Mosc. Univ. Phys. Bull. 2007, 62, 113–117. [Google Scholar] [CrossRef]
- Gubar’, A.Y.; Avetisyan, A.I.; Babkova, V.V. Tornado rise: 3D numerical model in mesoscale turbulence theory of Nikolaevskiy. Dokl. Earth Sci. 2008, 419, 467–472. [Google Scholar] [CrossRef]
- Nikolaevskiy, V.N.; Gubar’, A.Y. Vortices and tornado in mesoscale turbulence theory: A numerical pattern of 3D tornado rise. Geofiz. Issled. 2014, 15, 65–82. (In Russian) [Google Scholar]
- Koprov, B.M.; Koprov, V.M.; Makarova, T.I.; Golitsyn, G.S. Coherent structures in the atmospheric surface layer under stable and unstable conditions. Bound.-Later Meteorol. 2004, 111, 19–32. [Google Scholar] [CrossRef]
- Golitsyn, G.S.; Gostintsev, Y.A.; Solodovnik, A.S. Turbulent floating jet in a stratified atmosphere. J. Appl. Mech. Tech. Phys. 1989, 30, 566–577. [Google Scholar] [CrossRef]
- Etkin, D.A. Beyond the year 2000, more tornadoes in Western Canada—Implifications from the historical record. Nat. Hazards 1995, 12, 19–27. [Google Scholar] [CrossRef]
- Golitsyn, G.S. Statistics and energetics of tropical cyclones. Dokl. Earth Sci. 1997, 354, 633–636. [Google Scholar]
- Nolan, D.S.; Farrell, B.F. The structure and dynamics of tornado-like vortices. J. Atmos. Sci. 1999, 56, 2908–2936. [Google Scholar] [CrossRef]
- Rotunno, R. Numerical simulation of a laboratory vortex. J. Atmos. Sci. 1977, 34, 1942–1956. [Google Scholar] [CrossRef]
- Rotunno, R. A study in tornado like vortex dynamics. J. Atmos. Sci. 1979, 36, 140–155. [Google Scholar] [CrossRef]
- Rotunno, R. An investigation of a three dimensional asymmetric vortex. J. Atmos. Sci. 1984, 41, 283–298. [Google Scholar] [CrossRef]
- Gall, R.L. Internal dynamics of tornado-like vortices. J. Atmos. Sci. 1982, 39, 2721–2736. [Google Scholar] [CrossRef]
- Walko, R.; Gall, R.L. Some effects of momentum diffusion on axisymmetric vortices. J. Atmos. Sci. 1986, 43, 2137–2148. [Google Scholar] [CrossRef]
- Lewellen, W.S.; Lewellen, D.C.; Sykes, R.I. Large-eddy simulation of a tornado’s interaction with the surface. J. Atmos. Sci. 1997, 54, 581–605. [Google Scholar] [CrossRef]
- Lewellen, D.C.; Lewellen, W.S.; Xia, J. The influence of a local swirl ration on tornado intensification near the surface. J. Atmos. Sci. 2000, 57, 527–544. [Google Scholar] [CrossRef]
- Xia, J.; Lewellen, W.S.; Lewellen, D.C. Influence of Mach number on tornado corner flow dynamics. J. Atmos. Sci. 2003, 60, 2820–2825. [Google Scholar] [CrossRef]
- Lewellen, D.C.; Lewellen, W.S. Near-surface intensification of tornado vortices. J. Atmos. Sci. 2007, 64, 2176–2194. [Google Scholar] [CrossRef]
- Lewellen, D.C.; Lewellen, W.S. Near-surface vortex intensification through corner flow collapse. J. Atmos. Sci. 2007, 64, 2195–2209. [Google Scholar] [CrossRef]
- Ishihara, T.; Oh, S.; Tokuyama, Y.A. Numerical study on flow fields of tornado-like vortices using the LES turbulence model. J. Wind Eng. Ind. Aerodyn. 2011, 99, 239–248. [Google Scholar] [CrossRef]
- Ishihara, T.; Liu, Z.Q. Numerical study on dynamics of a tornado-like vortex with touching down by using the LES turbulence model. Wind Struct. 2014, 19, 89–111. [Google Scholar] [CrossRef][Green Version]
- Liu, Z.Q.; Ishihara, T. Numerical study of turbulent flow fields and the similarity of tornado vortices using large-eddy simulations. J. Wind Eng. Ind. Aerodyn. 2015, 145, 42–60. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. The possibilities of visualization in the case of simulation of air tornados. High Temp. 2010, 48, 588–592. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N.; Gorbachev, M.A. Physical simulation of air tornados: Some dimensionless parameters. High Temp. 2011, 49, 310–313. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Protasov, M.V.; Teplitskii, Y.S. About choice of particle parameters for visualization and diagnostics of free concentrated air vortices. High Temp. 2014, 52, 554–559. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. Effect of net structures on wall-free non-stationary air heat vortices. Int. J. Heat Mass Transf. 2013, 64, 817–828. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Zaichik, L.I. The effect of a fine divided impurity on the turbulence intensity of a carrier flow in a pipe. High Temp. 1998, 36, 983–986. [Google Scholar]
- Zaichik, L.I.; Varaksin, A.Y. Effect of the wake behind large particles on the turbulence intensity of carrier flow. High Temp. 1999, 37, 655–658. [Google Scholar]
- Varaksin, A.Y.; Ryzhkov, S.V. Vortex flows with particles and droplets (a review). Symmetry 2022, 14, 2016. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Turbulence in two-phase flows with macro-, micro- and nanoparticles: A review. Symmetry 2022, 14, 2433. [Google Scholar] [CrossRef]
- Klemp, J.B.; Wilhelmson, R.B. The simulation of three-dimensional convective storm dynamics. J. Atmos. Sci. 1978, 35, 1070–1096. [Google Scholar] [CrossRef]
- Wicker, L.J.; Wilhelmson, R.B. Simulation and analysis of tornado development and decay within a three-dimensional supercell thunderstorm. J. Atmos. Sci. 1995, 52, 2675–2703. [Google Scholar] [CrossRef]
- Grasso, L.D.; Cotton, W.R. Numerical simulation of a tornado vortex. J. Atmos. Sci. 1995, 52, 1192–1203. [Google Scholar] [CrossRef]
- Markowski, P.M.; Straka, J.M.; Rasmussen, E.N. Tornadogenesis resulting from the transport of circulation by a downdraft: Idealized numerical simulations. J. Atmos. Sci. 2003, 60, 795–823. [Google Scholar] [CrossRef]
- Sinkevich, O.A. A model of the flow in tornado vortex in a view of phase transitions. High Temp. 1996, 34, 922–927. [Google Scholar]
- Sinkevich, O.A.; Chikunov, S.E. Numerical simulation of two-phase flow in a tornado funnel. High Temp. 2002, 40, 604–612. [Google Scholar] [CrossRef]
- Smirnov, E.P. A numerical study of hydrodynamics and heat and mass transfer of a two-phase flow in an atmospheric tornado-forming cloud and a tornado model. High Temp. 2016, 54, 281–288. [Google Scholar] [CrossRef]
- Kushin, V.V. Smerch (Tornado); Energoatomizdat: Moscow, Russia, 1993. (In Russian) [Google Scholar]
- Gu, Z.; Zhao, Y.; Li, Y.; Yu, Y.; Feng, X. Numerical simulation of dust lifting within dust devils—Simulation of an intense vortex. J. Atmos. Sci. 2006, 63, 2630–2641. [Google Scholar] [CrossRef]
- Lebedeva, N.A.; Osiptsov, A.N. Structure of inertial-admixture accumulation zones in a tornado-like flow. Fluid Dyn. 2009, 44, 68–79. [Google Scholar] [CrossRef]
- Gol’dshtik, M.A. A paradoxical solution of the Navier-Stokes equations. Prikl. Mat. Mekh. 1960, 24, 610–624. (In Russian) [Google Scholar] [CrossRef]
- Varaksin, A.Y. Effect of macro-, micro- and nanoparticles on turbulence in a carrier gas. Dokl. Phys. 2021, 66, 72–75. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Z.; Gong, Z.; Chen, F.; Peng, Q. Physically based modeling and animation of tornado. J. Zhejiang Univ. Sci. A 2006, 7, 1099–1106. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Z.; Gong, Z.; Peng, Q. Real time simulation of a tornado. Vis. Comput. 2007, 23, 559–567. [Google Scholar] [CrossRef]
- Maruyama, T. Simulation of flying debris using a numerically generated tornado-like vortex. J. Wind Eng. Ind. Aerodyn. 2011, 99, 249–256. [Google Scholar] [CrossRef]
- Lewellen, D.C.; Gong, B.; Lewellen, W.S. Effect of finescale debris on near-surface tornado dynamics. J. Atmos. Sci. 2008, 65, 3247–3262. [Google Scholar] [CrossRef]
- Davies-Jones, R.P. Tornado dynamics. In Thunderstorm Morphology and Dynamics, 2nd ed.; Kessler, E., Ed.; University of Oklahoma Press: Norman, OK, USA, 1986; pp. 197–236. [Google Scholar]
- Wakimoto, R.; Wilson, J.W. Non-supercell tornadoes. Mon. Weather Rev. 1989, 117, 1113–1140. [Google Scholar] [CrossRef]
- Brady, R.H.; Szoke, E.J. A case study of non-mesocyclone tornado development in northeast Colorado: Similarities to waterspout formation. Mon. Weather Rev. 1989, 117, 843–856. [Google Scholar] [CrossRef]
- Davies-Jones, R. Can a descending rain curtain in a supercell instigate tornadogenesis barotropically? Atmos. Res. 2008, 65, 2469–2497. [Google Scholar] [CrossRef][Green Version]
- Roberts, B.; Xue, M.; Schenkman, A.D.; Dawson, D.T. The role of surface drag in tornadogenesis within an idealized supercell simulation. J. Atmos. Sci. 2016, 73, 3371–3395. [Google Scholar] [CrossRef]
- Roberts, B.; Xue, M.; Dawson, D.T. The effect of surface drag strength on mesocyclone intensification and tornadogenesis in idealized supercell simulations. J. Atmos. Sci. 2020, 77, 1699–1721. [Google Scholar] [CrossRef]
- Davies-Jones, R. Invented forces in supercell models. J. Atmos. Sci. 2021, 78, 2927–2939. [Google Scholar] [CrossRef]
- Markowski, P.M.; Bryan, G. LES of laminar flow in the PBL: A potential problem for convective storm simulations. Mon. Weather Rev. 2016, 144, 1841–1850. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Numerical simulation of the interaction of a magneto-inertial fusion target with plasma and laser drivers. High Temp. 2022, 60, S7–S15. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Thermophysical Parameter Estimation of a Neutron Source Based on the Action of Broadband Radiation on a Cylindrical Target. Fusion Sci. Technol. 2023, 79, 399–406. [Google Scholar] [CrossRef]
- Ryzhkov, S.V. The behavior of a magnetized plasma under the action of laser with high pulse energy. Probl. At. Sci. Technol. 2010, 4, 105–110. [Google Scholar]
- Kuzenov, V.V.; Ryzhkov, S.V. Evaluation of hydrodynamic instabilities in inertial confinement fusion target in a magnetic field. Probl. At. Sci. Technol. 2013, 4, 103–107. [Google Scholar]
- Flournoy, M.D.; Coniglio, M.C. Origins of vorticity in a simulated tornadic mesovortex observed during PECAN on 6 July 2015. Mon. Weather Rev. 2019, 147, 107–134. [Google Scholar] [CrossRef]
- Fischer, J.; Dahl, J.M.L. Transition of near-ground vorticity dynamics during tornadogenesis. J. Atmos. Sci. 2022, 79, 467–483. [Google Scholar] [CrossRef]
- Parker, M.D.; Wicker, L.J. Imported and storm-generated near-ground vertical vorticity in a simulated supercell. J. Atmos. Sci. 2014, 71, 3027–3051. [Google Scholar]
- Dahl, J.M.L. Near-ground rotation in simulated supercells: On the robustness of the baroclinic mechanism. Mon. Weather Rev. 2015, 143, 4929–4942. [Google Scholar] [CrossRef]
- Parker, M.D.; Dahl, J.M.L. Production of near-surface vertical vorticity by idealized downdrafts. Mon. Weather Rev. 2015, 143, 2795–2816. [Google Scholar] [CrossRef]
- Markowski, P.M. An idealized numerical simulation investigation of the effects of surface drag on the development of near-surface vertical vorticity in supercell thunderstorms. J. Atmos. Sci. 2016, 73, 4349–4385. [Google Scholar] [CrossRef]
- Fischer, J.; Dahl, J.M.L. The relative importance of updraft and cold pool characteristics in supercell tornadogenesis using highly idealized simulations. J. Atmos. Sci. 2020, 77, 4089–4107. [Google Scholar] [CrossRef]
- Mashiko, W.; Niino, H.; Kato, T. Numerical simulation of tornadogenesis in an outer-rainband minisupercell of Typhoon Shanshan on 17 September 2006. Mon. Weather Rev. 2009, 137, 4238–4260. [Google Scholar] [CrossRef]
- Mashiko, W. A numerical study of the 6 May 2012 Tsukuba City supercell tornado. Part II: Mechanisms of tornadogenesis. Mon. Weather Rev. 2016, 144, 3077–3098. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Yu; Varaksin, A. Simulation of Parameters of Plasma Dynamics of a Magneto Plasma Compressor. Appl. Sci. 2023, 13, 5538. [Google Scholar] [CrossRef]
- Rotunno, R.; Markowski, P.M.; Bryan, G.H. “Near ground” vertical vorticity in supercell thunderstorm models. J. Atmos. Sci. 2017, 74, 1757–1766. [Google Scholar] [CrossRef]
- Yokota, S.; Niino, H.; Seko, H.; Kunii, M.; Yamauchi, H. Important factors for tornadogenesis as revealed by high-resolution ensemble forecasts of the Tsukuba supercell tornado of 6 May 2012 in Japan. Mon. Weather Rev. 2018, 146, 1109–1132. [Google Scholar] [CrossRef]
- Tao, T.; Tamura, T. Numerical study of the 6 May 2012 Tsukuba supercell tornado: Vorticity sources responsible for tornadogenesis. Mon. Weather Rev. 2020, 148, 1205–1228. [Google Scholar] [CrossRef]
- Boyer, C.H.; Dahl, J.M.L. The mechanisms responsible for large near-surface vertical vorticity within simulated supercells and quasi-linear storms. Mon. Weather Rev. 2020, 148, 4281–4297. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Mochalov, A.A. A double screw spiral as a possible mechanism of wall-free nonstationary air vortex generation. Dokl. Phys. 2019, 64, 301–303. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. The adaptive composite block-structured grid calculation of the gas-dynamic characteristics of an aircraft moving in a gas environment. Mathematics 2022, 10, 2130. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Approximate calculation of convective heat transfer near hypersonic aircraft surface. J. Enhanc. Heat Transf. 2018, 25, 181–193. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Numerical simulation of pulsed jets of a high-current pulsed surface discharge. Comput. Therm. Sci. 2021, 13, 45–56. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Calculation of heat transfer and drag coefficients for aircraft geometric models. Appl. Sci. 2022, 12, 11011. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Particle-laden and droplet-laden two-phase flows past bodies (a Review). Symmetry 2023, 15, 388. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. The qualitative and quantitative study of radiation sources with a model configuration of the electrode system. Symmetry 2021, 13, 927. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Estimation of the neutron generation in the combined magneto-inertial fusion scheme. Phys. Scripta. 2021, 96, 125613. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Frolko, P.A. Numerical simulation of the coaxial magneto-plasma accelerator and non-axisymmetric radio frequency discharge. J. Phys. Conf. Ser. 2017, 830, 012049. [Google Scholar] [CrossRef]
- Mozgovoy, A.G.; Romadanov, I.V.; Ryzhkov, S.V. Formation of a compact toroid for enhanced efficiency. Phys. Plasmas 2014, 21, 022501. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Computational and Experimental Modeling in Magnetoplasma Aerodynamics and High-Speed Gas and Plasma Flows (A Review). Aerospace 2023, 10, 662. [Google Scholar]
- Ryzhkov, S.V. Magneto-Inertial Fusion and Powerful Plasma Installations (A Review). Appl. Sci. 2023, 13, 6658. [Google Scholar] [CrossRef]
- Kuzenov, V.V.; Ryzhkov, S.V. Calculation of plasma dynamic parameters of the magneto-inertial fusion target with combined exposure. Phys. Plasmas 2019, 26, 092704. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Mathematical Modeling of Gas-Solid Two-Phase Flows: Problems, Achievements and Perspectives (A Review). Mathematics 2023, 11, 3290. [Google Scholar] [CrossRef]
- Markowski, P.M.; Richardson, Y.P. The influence of environmental low-level shear and cold pools on tornadogenesis: Insights from idealized simulations. J. Atmos. Sci. 2014, 71, 243–275. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).