Extremal Analysis of Flooding Risk and Its Catastrophe Bond Pricing
Abstract
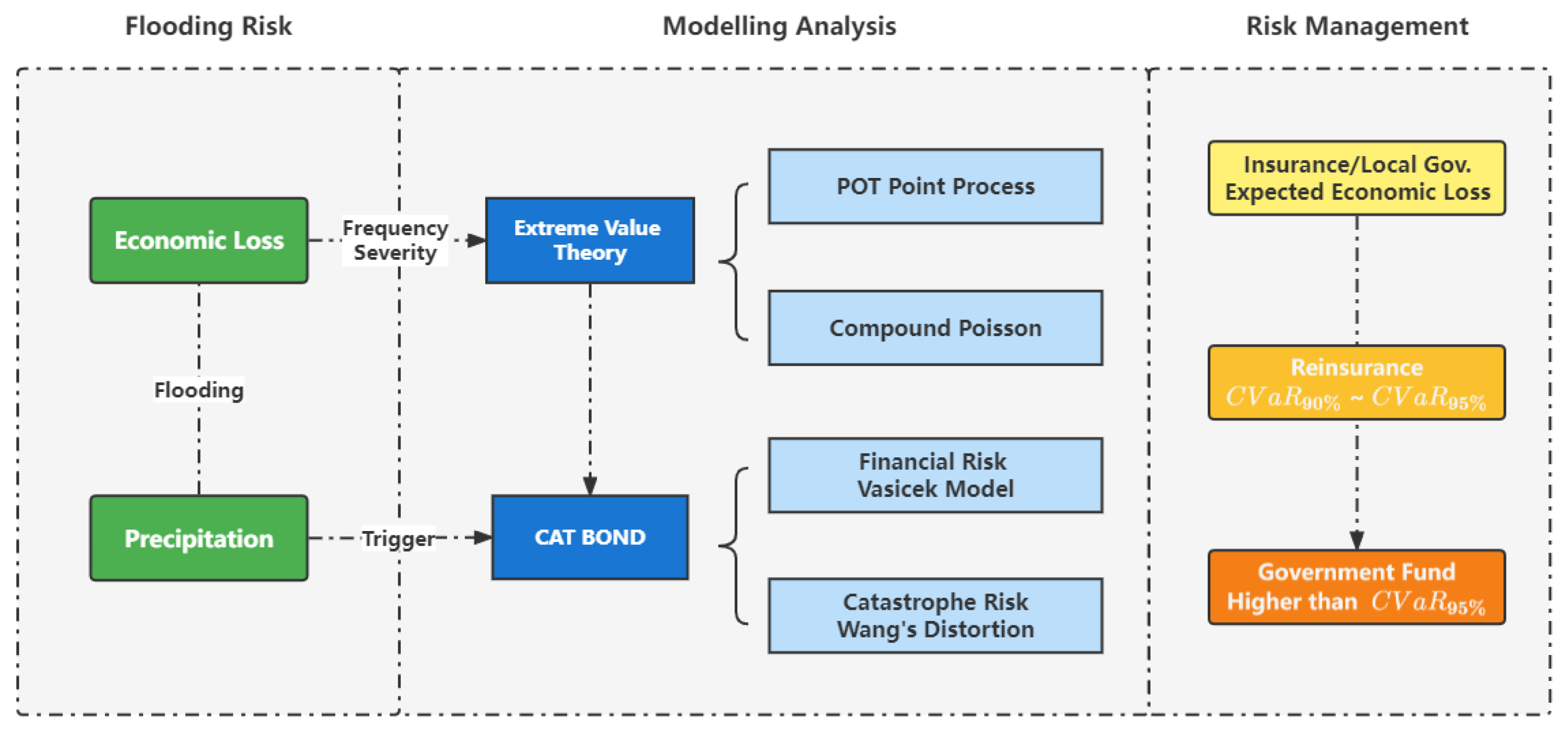
1. Introduction
2. Data Preprocessing of Flooding Economic Losses and Precipitations
3. Main Results
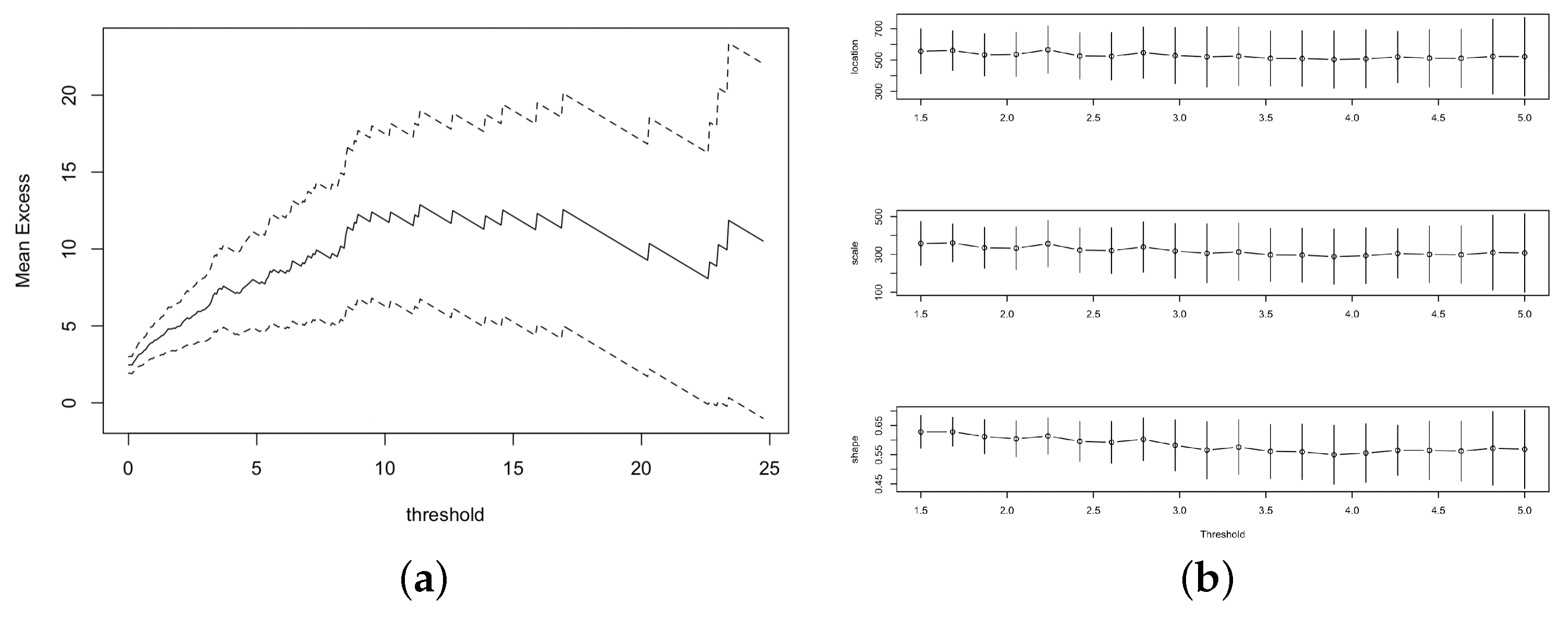
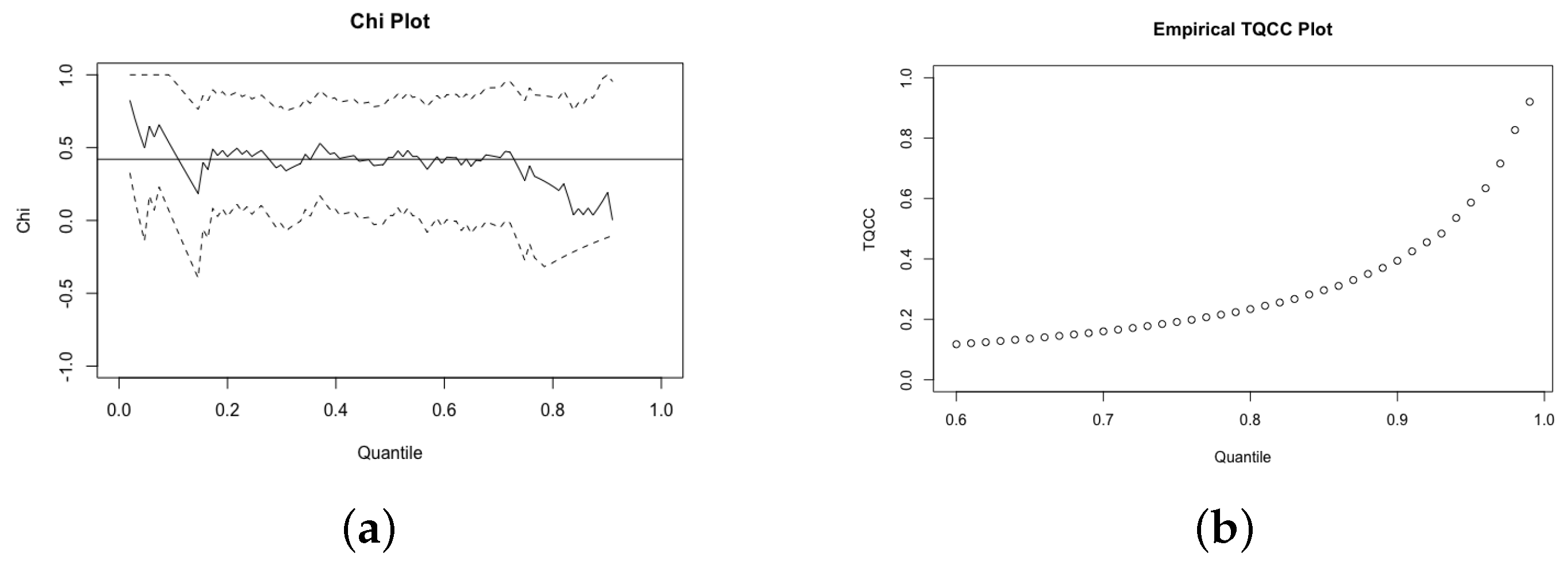
3.1. Extreme Analysis of Flooding Economic Losses and Precipitations
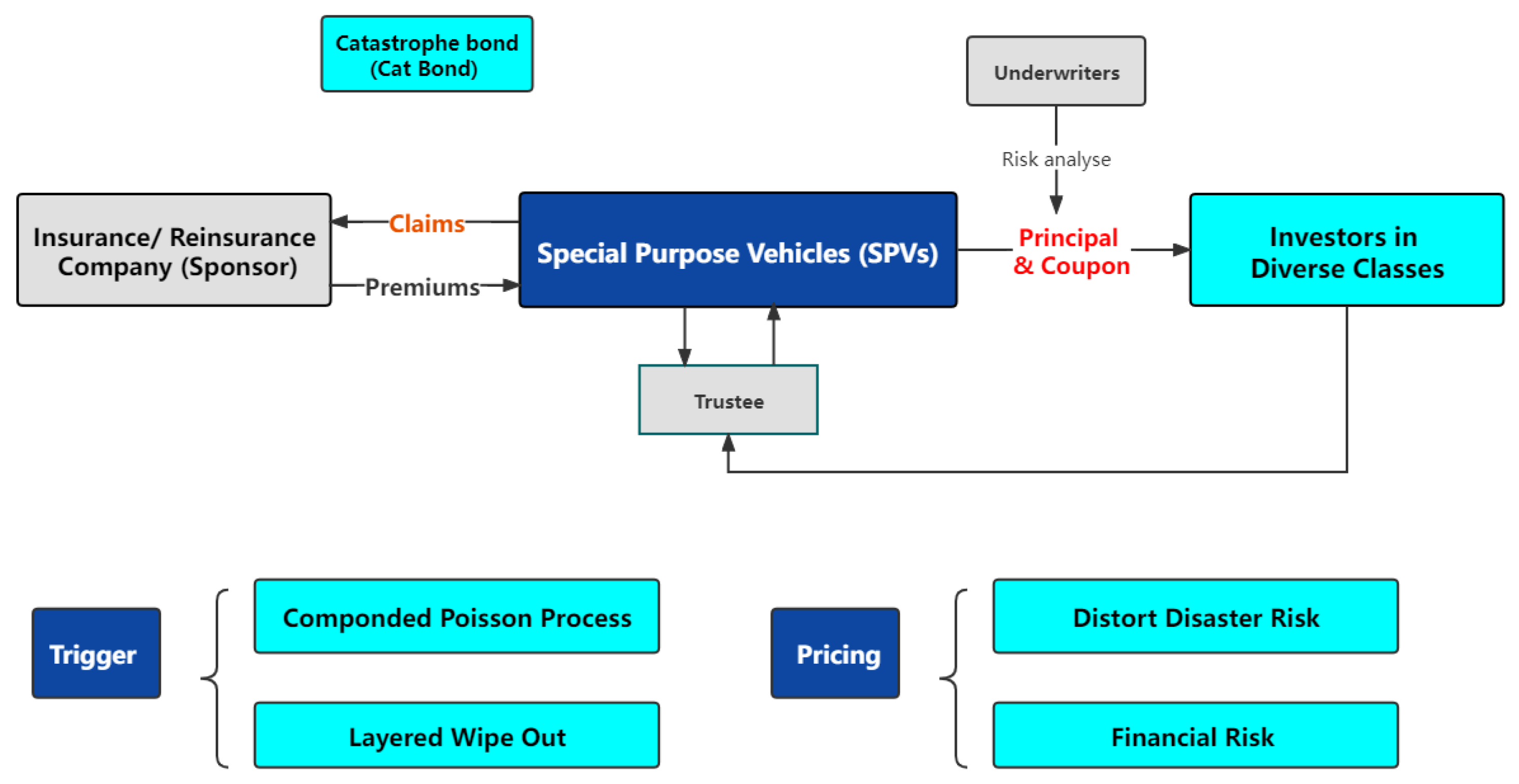
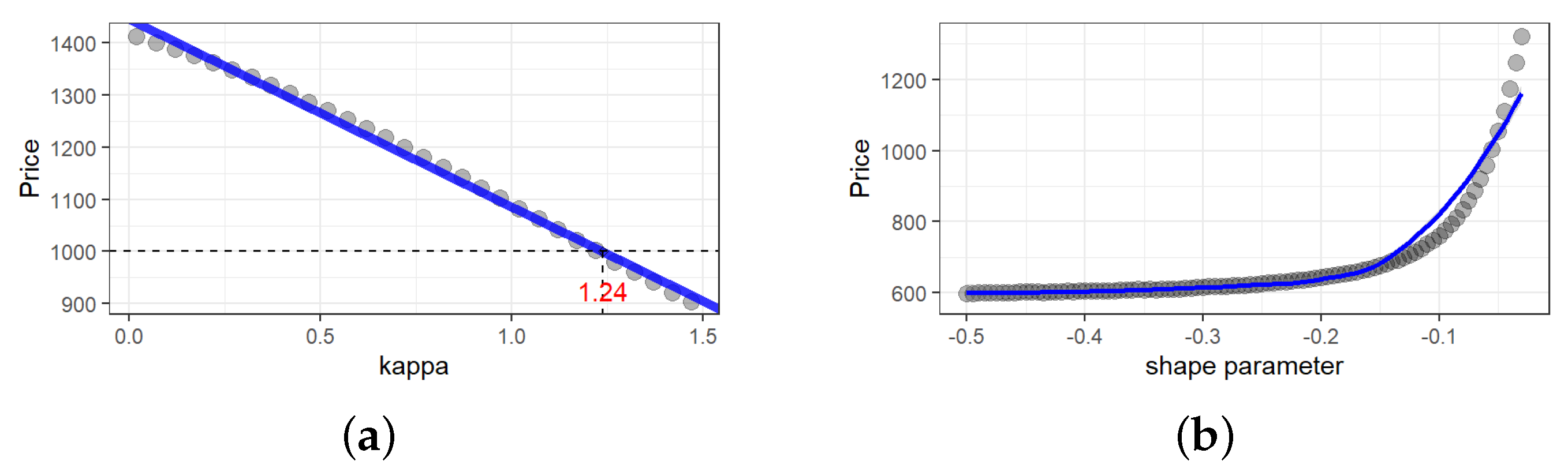
3.2. Design of Flooding Catastrophic Bonds
4. Conclusions and Extension Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Extreme Value Theory
Appendix B. A Pricing Scheme of Catastrophe Bonds
- (i)
- The aggregate amount of loss due to natural disasters, e.g., floods;
- (ii)
- The number of large floods, which considers both magnitude and frequency as belowwhere u is a high threshold and is the number of exceedances over the threshold observed in .
References
- Chen, J.; Liu, G.; Yang, L.; Shao, Q.; Wang, H. Pricing and simulation for extreme flood catastrophe bonds. Water Resour. Manag. 2013, 27, 3713–3725. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Huang, J.; Pinskwar, I.; Su, B.; Szwed, M.; Jiang, T. Climate variability and floods in China—A review. Earth-Sci. Rev. 2020, 211, 103434. [Google Scholar] [CrossRef]
- Tang, Q.; Yuan, Z. CAT bond pricing: A product probability measure with POT risk characterization. ASTIN Bull. 2019, 49, 457–490. [Google Scholar] [CrossRef]
- Falk, M.; Hüsler, J.; Reiss, R.D. Extreme Value theory. In Laws of Small Numbers: Extremes and Rare Events; Springer: Basel, Switzerland, 2011; pp. 25–101. [Google Scholar]
- Cirillo, P.; Taleb, N.N. Tail risk of contagious diseases. Nat. Phys. 2020, 16, 606–613. [Google Scholar] [CrossRef]
- Embrechts, P.; Klüppelberg, C.; Mikosch, T. Modelling Extremal Events: For insurance and Finance; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Liu, W.; Wu, J.; Tang, R.; Ye, M.; Yang, J. Daily precipitation threshold for rainstorm and flood disaster in the mainland of China: An economic loss perspective. Sustainability 2020, 12, 407. [Google Scholar] [CrossRef]
- Towler, E.; Llewellyn, D.; Prein, A.; Gilleland, E. Extreme-value analysis for the characterization of extremes in Water Resources: A generalized workflow and case study on New Mexico monsoon precipitation. Weather Clim. Extrem. 2020, 29, 100260. [Google Scholar] [CrossRef]
- Aranda, J.A.; García-Bartual, R. Effect of seasonality on the quantiles estimation of maximum floodwater levels in a reservoir and maximum outflows. Water 2020, 12, 519. [Google Scholar] [CrossRef]
- Sun, R.; Gong, Z.; Gao, G.; Shah, A.A. Comparative analysis of multi-criteria decision-making methods for flood disaster risk in the Yangtze river delta. Int. J. Disaster Risk Reduct. 2020, 51, 101768. [Google Scholar] [CrossRef]
- Coles, S.; Heffernan, J.; Tawn, J. Dependence measures for extreme value analyses. Extremes 1999, 2, 339–365. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, Z. Extreme co-movements between infectious disease events and crude oil futures prices: From extreme value analysis perspective. Energy Econ. 2022, 110, 106054. [Google Scholar] [CrossRef]
- Evgenidis, A.; Tsagkanos, A.; Siriopoulos, C. Towards an asymmetric long-run equilibrium between economic uncertainty and the yield spread. A multi-economy view. Res. Int. Bus. Financ. 2017, 39, 267–279. [Google Scholar] [CrossRef]
- Surminski, S.; Dorta, D. Flood insurance schemes and climate adaptation in developing countries. Int. J. Disaster Risk Reduct. 2014, 7, 154–164. [Google Scholar] [CrossRef]
- Loretan, M.; Philips, P.C.B. Testing the covariance stationarity of heavy tailed time series: An overview of the theory with applications to several financial datasets. J. R. Stat. Soc. 1994, 1, 211–248. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer Series in Statistics; Springer: London, UK, 2001. [Google Scholar]
- Scarrott, C.; MacDonald, A. A review of extreme value threshold estimation and uncertainty quantification. Rev. Stat. J. 2021, 10, 33–60. [Google Scholar]
- Zhao, Y.; Gong, Z.; Wang, W.; Luo, K. The comprehensive risk evaluation on rainstorm and flood disaster losses in China mainland from 2004 to 2009: Based on the triangular grey correlation theory. Nat. Hazards 2014, 71, 1001–1016. [Google Scholar] [CrossRef]
- Wang, S.S. A class of distortion operators for pricing financial and insurance risks. J. Risk Insur. 2000, 67, 15–36. [Google Scholar] [CrossRef]
- Shao, J.; Pantelous, A.; Papaioannou, A.D. Catastrophe risk bonds with applications to earthquakes. Eur. Actuar. J. 2015, 5, 113–138. [Google Scholar] [CrossRef]
- Cui, P.; Peng, J.; Shi, P.; Tang, H.; Ouyang, C.; Zou, Q.; Liu, Q.; Lei, Y. Scientific challenges of research on natural hazards and disaster risk. Geogr. Sustain. 2021, 2, 216–223. [Google Scholar] [CrossRef]
- Ho, C.T. Measuring bank operations performance: An approach based on grey relation analysis. J. Oper. Res. Soc. 2006, 57, 337–349. [Google Scholar] [CrossRef]
- Alston, A. A Bayesian Spatial Analysis of Extreme Precipitation. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2011. [Google Scholar]
- Koh, J.; Pimont, F.; Dupuy, J.L.; Opitz, T. Spatiotemporal wildfire modeling through point processes with moderate and extreme marks. arXiv 2021, arXiv:2105.08004. [Google Scholar]
- Ibrahim, R.A.; Napitupulu, H. Multiple-trigger catastrophe bond pricing model and its simulation using numerical methods. Mathematics 2022, 10, 1363. [Google Scholar] [CrossRef]
- Wei, L.; Liu, L.; Hou, J. Pricing hybrid-triggered catastrophe bonds based on copula-EVT model. Quant. Financ. Econ. 2022, 6, 223–243. [Google Scholar] [CrossRef]
- Gilleland, E.; Katz, R.W. Extremes 2.0: An extreme value analysis package in R. J. Stat. Softw. 2016, 72, 1–39. [Google Scholar] [CrossRef]
- Wang, R.; Wei, Y. Characterizing optimal allocations in quantile-based risk sharing. Insur. Math. Econ. 2020, 93, 288–300. [Google Scholar] [CrossRef]
- Mamon, R.S. Three ways to solve for bond prices in the Vasicek model. J. Appl. Math. Decis. Sci. 2004, 8, 1–14. [Google Scholar] [CrossRef]

| Variable | Size | Min | Median | Mean | Max | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| DEL | 369 | 0.004 | 0.795 | 2.47 | 54.324 | 5.45 | 41.79 |
| MPP | 99 | 75 | 476 | 525.27 | 1426 | 0.79 | 3.63 |
| Model | Location Parameter () | Scale Parameter () | Shape Parameter () | AIC | BIC | |||
|---|---|---|---|---|---|---|---|---|
| Estimates (s.e.) | 95% CI | Estimate (s.e.) | 95% CI | Estimate (s.e.) | 95% CI | |||
| PP | 57.33 (15.60) | (26.76, 87.91) | 34.02 (13.82) | (6.92, 61.11) | 0.57 (0.10) | (0.38, 0.77) | −273.544 | −265.416 |
| GP | - | - | 2.30 (0.41) | (1.49, 3.11) | 0.61 (0.16) | (0.29, 0.93) | 545.641 | 551.060 |
| Exp | - | - | 4.91 (0.47) | (3.99, 5.82) | - | - | 577.059 | 579.769 |
| Confidence Level | VaR | CVaR | Loss Level | Loss Amount (Billion RMB) | Loss Taker |
|---|---|---|---|---|---|
| 97.5% | 13.37 | 34.22 | Third level | >22.28 | Government (CAT bond) |
| 95.0% | 8.24 | 22.28 | Second level | 14.24–22.28 | Re-insurance |
| 90.0% | 4.78 | 14.24 | First level | 4.78–14.24 | CRFCIF 1 |
| Panel A: Vasicek models (under ) | ||||||||
| Risk-free rate | Shibor | Correlation | ||||||
| 1.52 | 4.12% | 1.40% | 2.28% | 0.04 | 2.02% | 4.00% | 2.43% | 0.89 |
| Panel B: Maximum point precipitation distribution | ||||||||
| Under | Under | |||||||
| Maximum magnitude: 4187 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Cai, Z.; Liu, Y.; Ling, C. Extremal Analysis of Flooding Risk and Its Catastrophe Bond Pricing. Mathematics 2023, 11, 114. https://doi.org/10.3390/math11010114
Li J, Cai Z, Liu Y, Ling C. Extremal Analysis of Flooding Risk and Its Catastrophe Bond Pricing. Mathematics. 2023; 11(1):114. https://doi.org/10.3390/math11010114
Chicago/Turabian StyleLi, Jiayi, Zhiyan Cai, Yixuan Liu, and Chengxiu Ling. 2023. "Extremal Analysis of Flooding Risk and Its Catastrophe Bond Pricing" Mathematics 11, no. 1: 114. https://doi.org/10.3390/math11010114
APA StyleLi, J., Cai, Z., Liu, Y., & Ling, C. (2023). Extremal Analysis of Flooding Risk and Its Catastrophe Bond Pricing. Mathematics, 11(1), 114. https://doi.org/10.3390/math11010114




