Quantile Trend Regression and Its Application to Central England Temperature
Abstract
:1. Introduction
2. Methods
2.1. Baseline Model
2.2. Quantile Trend Regression
2.2.1. Basic Structure of a Quantile Regression Model
2.2.2. Modeling the QTR Dependence Structure
2.2.3. Main Result
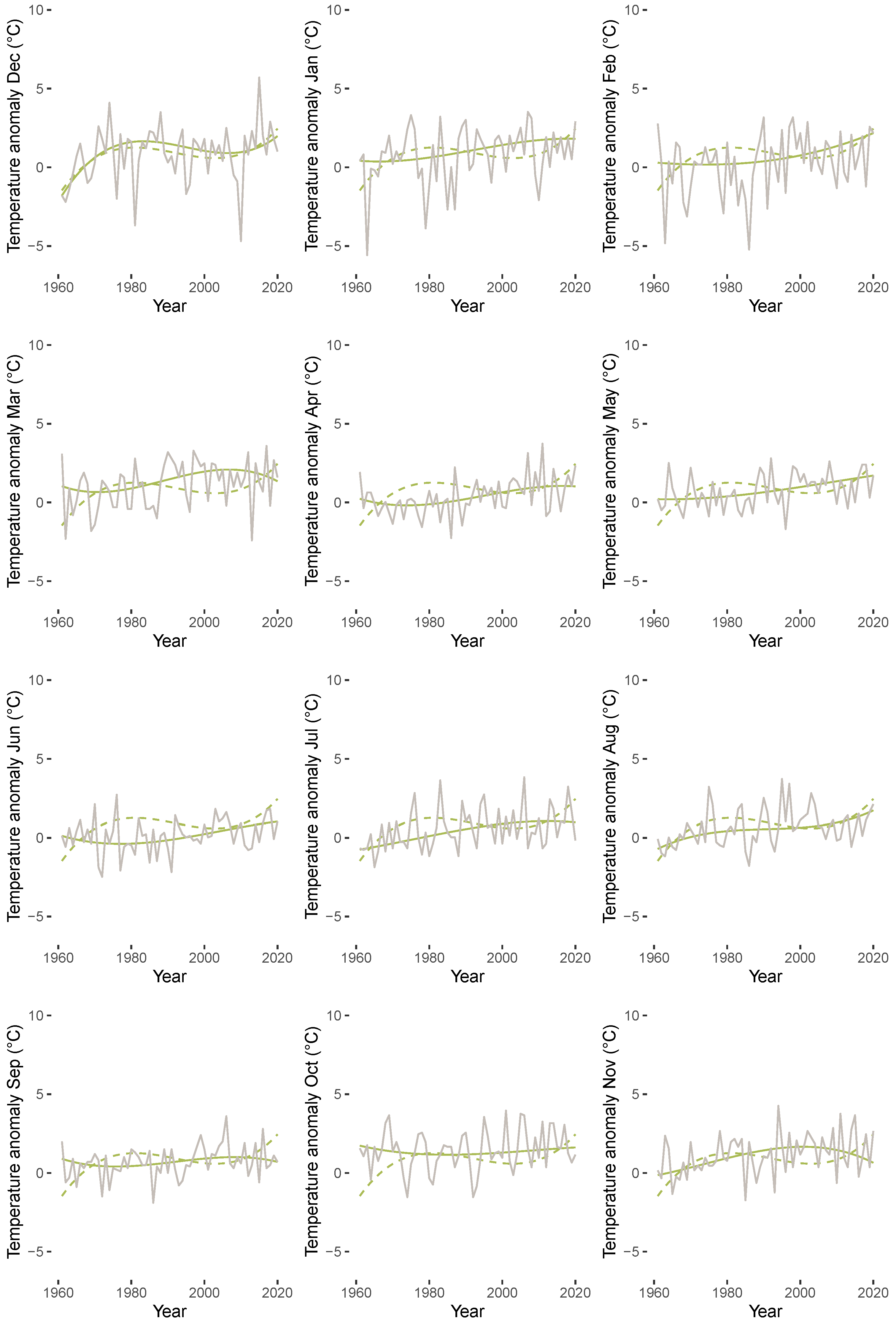
3. Data and Results
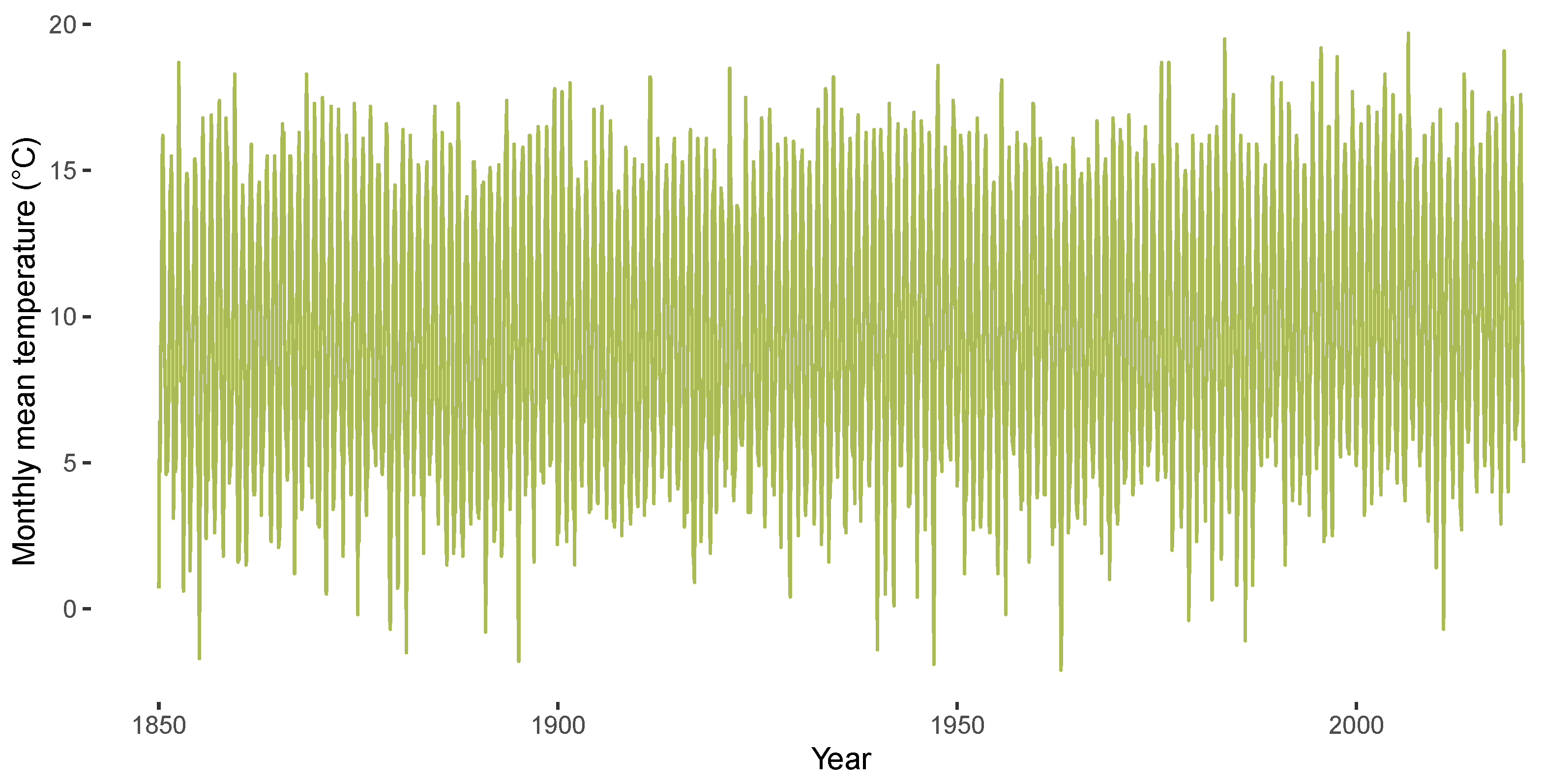
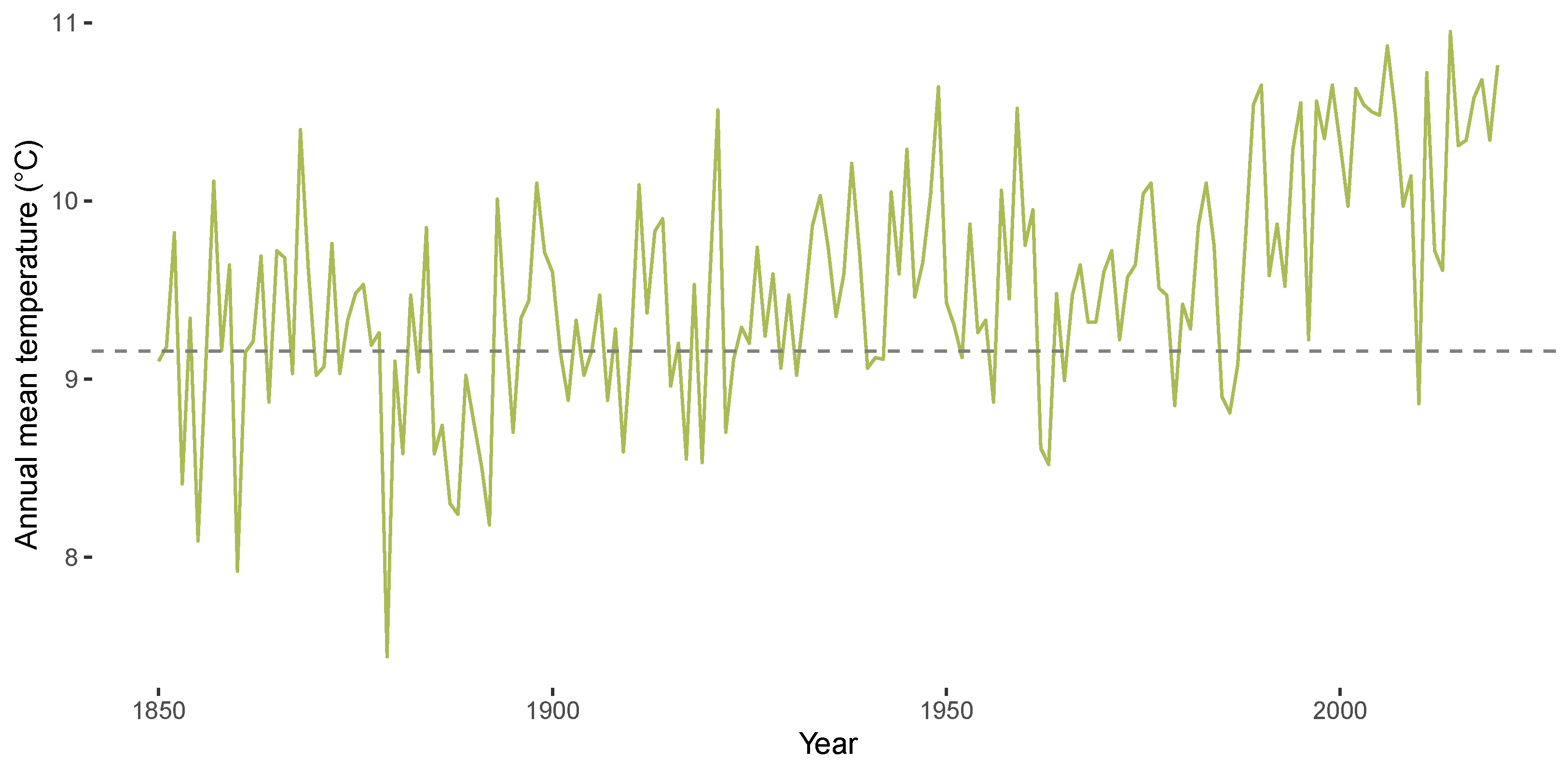
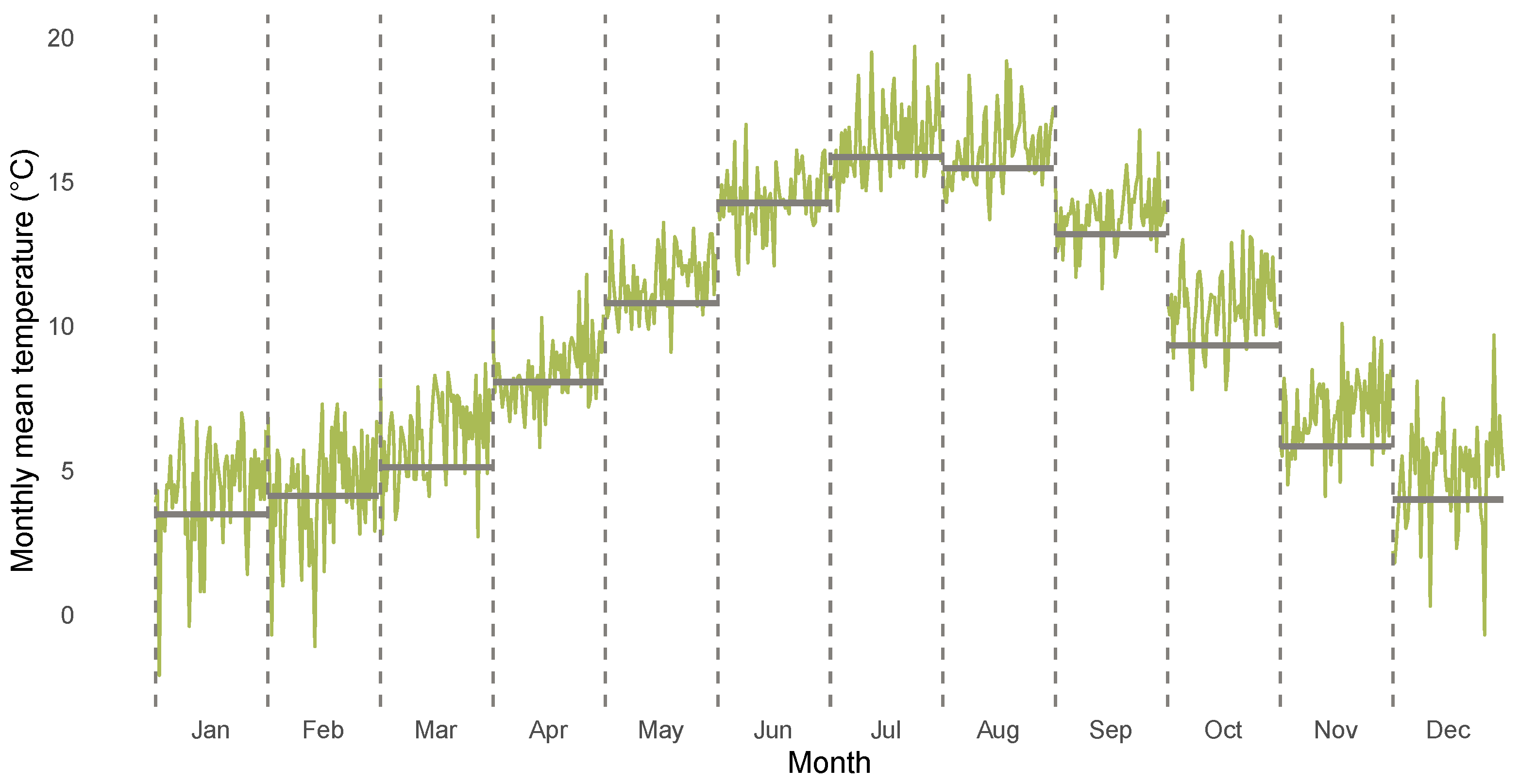
3.1. Descriptives for CET Anomalies
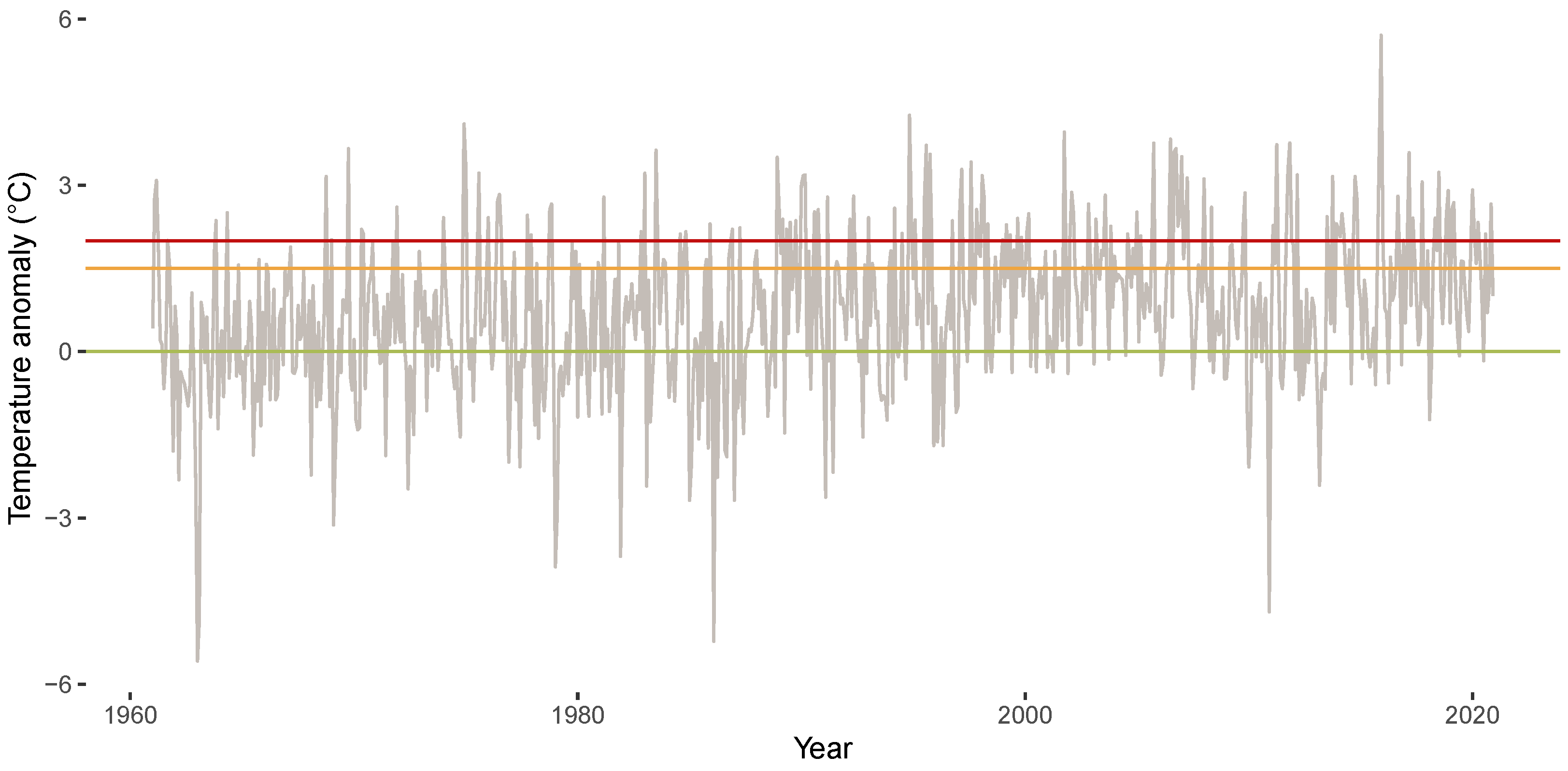
3.2. Relevance of Quantile Regression for Analyzing Anomalies
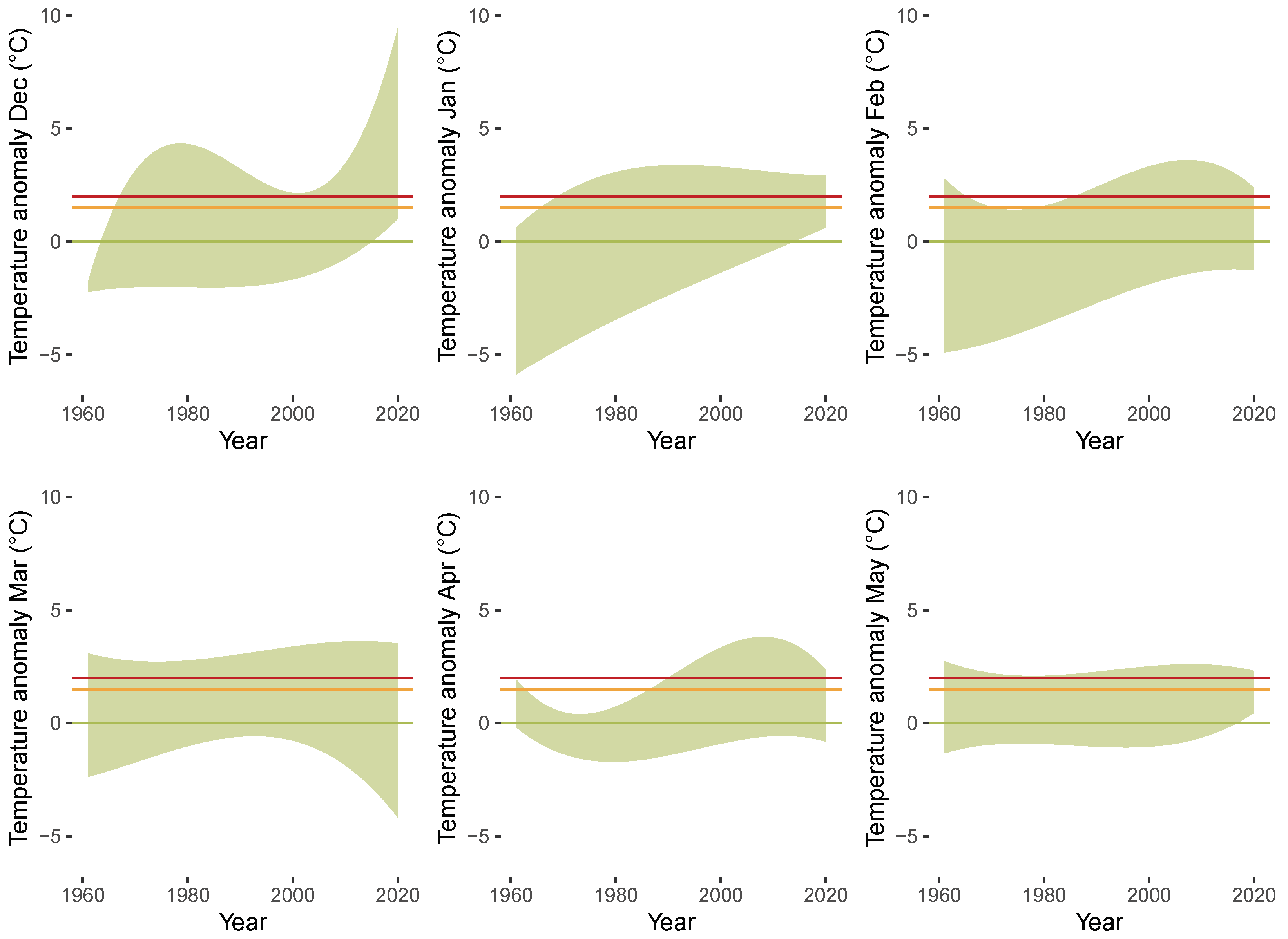
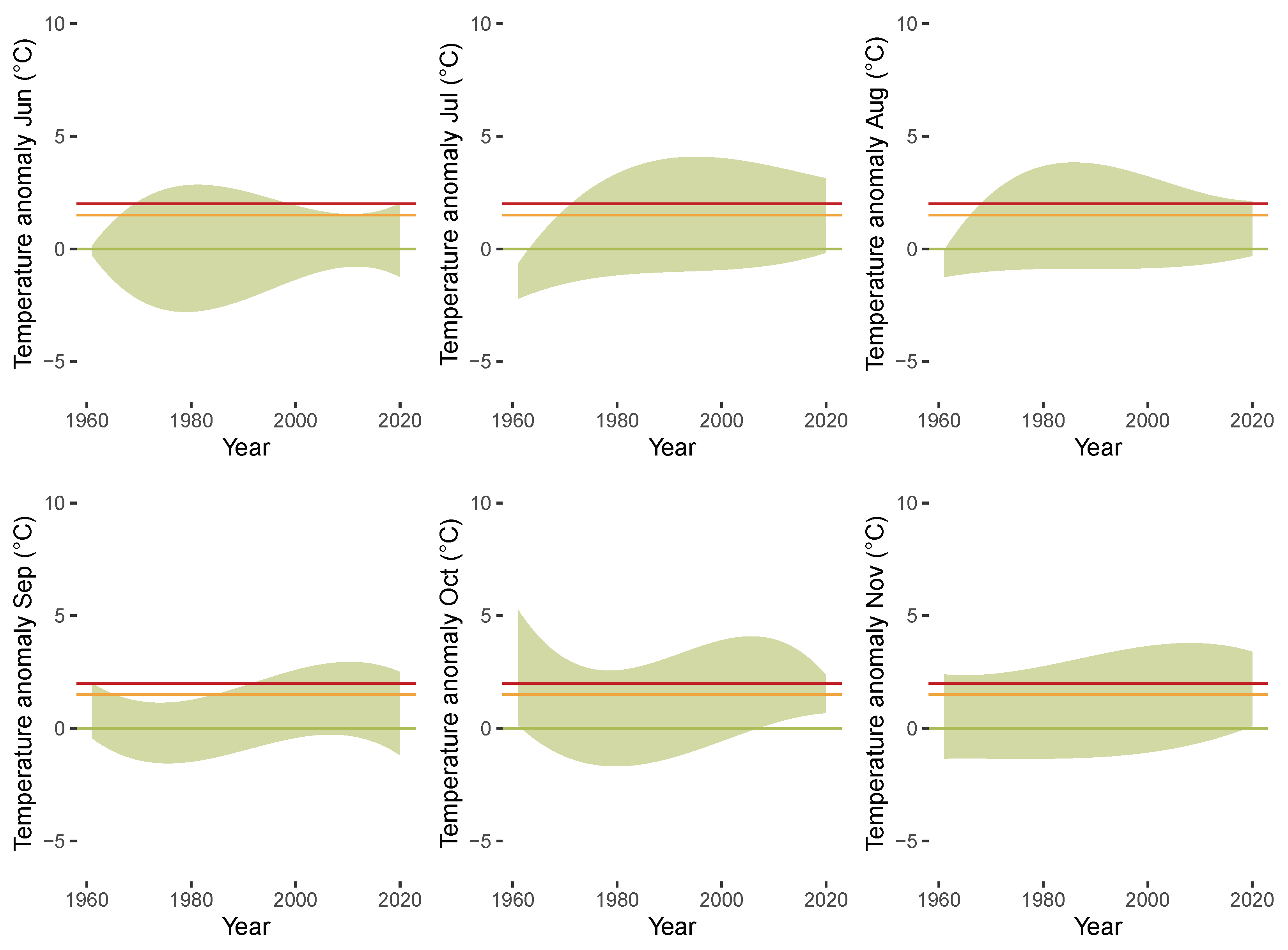
3.3. Results of QTR Estimation
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- King, A.D.; van Oldenborgh, G.J.; Karoly, D.J.; Lewis, S.C.; Cullen, H. Attribution of the record high Central England temperature of 2014 to anthropogenic influences. Environ. Res. Lett. 2015, 10, 054002. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, D.; Heaviside, C.; Vardoulakis, S.; Huntingford, C.; Masato, G.; Guillod, B.P.; Frumhoff, P.; Bowery, A.; Wallom, D.; Allen, M. Attributing human mortality during extreme heat waves to anthropogenic climate change. Environ. Res. Lett. 2016, 11, 074006. [Google Scholar] [CrossRef]
- IPCC—Intergovernmental Panel on Climate Change. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021; p. 3949. [Google Scholar]
- Vogelsang, T.J.; Franses, P.H. Are winters getting warmer? Environ. Model. Softw. 2005, 20, 1449–1455. [Google Scholar] [CrossRef]
- King, A.D. The drivers of nonlinear local temperature change under global warming. Environ. Res. Lett. 2019, 14, 064005. [Google Scholar] [CrossRef]
- Rivas, M.D.G.; Gonzalo, J. Trends in distributional characteristics: Existence of global warming. J. Econom. 2020, 214, 153–174. [Google Scholar]
- Stott, P.A.; Christidis, N.; Otto, F.E.; Sun, Y.; Vanderlinden, J.P.; van Oldenborgh, G.J.; Vautard, R.; von Storch, H.; Walton, P.; Yiou, P.; et al. Attribution of extreme weather and climate-related events. Wiley Interdiscip. Rev. Clim. Chang. 2016, 7, 23–41. [Google Scholar] [CrossRef]
- Harris, R.; Loeffler, F.; Rumm, A.; Fischer, C.; Horchler, P.; Scholz, M.; Foeckler, F.; Henle, K. Biological responses to extreme weather events are detectable but difficult to formally attribute to anthropogenic climate change. Sci. Rep. 2020, 10, 1–14. [Google Scholar] [CrossRef]
- Sibbertsen, P. Long memory versus structural breaks: An overview. Stat. Pap. 2004, 45, 465–515. [Google Scholar] [CrossRef] [Green Version]
- Gao, M.; Franzke, C. Quantile Regression–Based Spatiotemporal Analysis of Extreme Temperature Change in China. J. Clim. 2017, 30, 9897–9914. [Google Scholar] [CrossRef]
- Proietti, T.; Hillebrand, E. Seasonal changes in central England temperatures. J. R. Stat. Soc. Ser. A 2017, 180, 769–791. [Google Scholar] [CrossRef] [Green Version]
- He, C.; Kang, J.; Teräsvirta, T.; Zhang, S. The shifting seasonal mean autoregressive model and seasonality in the Central England monthly temperature series, 1772–2016. Econom. Stat. 2019, 12, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Fomby, T.B.; Vogelsang, T.J. The Application of Size-Robust Trend Statistics to Global-Warming Temperature Series. J. Clim. 2002, 15, 117–123. [Google Scholar] [CrossRef] [Green Version]
- Barbosa, S.M. Testing for Deterministic Trends in Global Sea Surface Temperature. J. Clim. 2011, 24, 2516–2522. [Google Scholar] [CrossRef] [Green Version]
- Franzke, C. Nonlinear Trends, Long-Range Dependence, and Climate Noise Properties of Surface Temperature. J. Clim. 2012, 25, 4172–4183. [Google Scholar] [CrossRef] [Green Version]
- Fatichi, S.; Barbosa, S.; Caporali, E.; Silva, M. Deterministic versus stochastic trends: Detection and challenges. J. Geophys. Res. Atmos. 2009, 114, D18121. [Google Scholar] [CrossRef] [Green Version]
- Koenker, R.; Schorfheide, F. Quantile spline models for global temperature change. Clim. Chang. 1994, 28, 395–404. [Google Scholar] [CrossRef]
- Hansen, J.E.; Lebedeff, S. Global trends of measured surface air temperature. J. Geophys. Res. 1987, 92, 13345–13372. [Google Scholar] [CrossRef] [Green Version]
- Kamarianakis, Y.; Ayuso, S.V.; Rodriguez, E.C.; Toro Velasco, M. Water temperature forecasting for Spanish rivers by means of nonlinear mixed models. J. Hydrol. Reg. Stud. 2016, 5, 226–243. [Google Scholar] [CrossRef]
- Rhines, A.; McKinnon, K.A.; Tingley, M.P.; Huybers, P. Seasonally Resolved Distributional Trends of North American Temperatures Show Contraction of Winter Variability. J. Clim. 2017, 30, 1139–1157. [Google Scholar] [CrossRef] [Green Version]
- King, A.D.; Knutti, R.; Uhe, P.; Mitchell, D.M.; Lewis, S.C.; Arblaster, J.M.; Freychet, N. On the Linearity of Local and Regional Temperature Changes from 1.5 ∘C to 2 ∘C of Global Warming. J. Climatol. 2018, 31, 7495. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E.; Maleki, M.; Devia Cortés, D. Skew-Reflected-Gompertz Information Quantifiers with Application to Sea Surface Temperature Records. Mathematics 2019, 7, 403. [Google Scholar] [CrossRef] [Green Version]
- Mudelsee, M. Trend analysis of climate time series: A review of methods. Earth-Sci. Rev. 2019, 190, 310–322. [Google Scholar] [CrossRef]
- Rial, J.; Pielke, R.; Beniston, M.; Claussen, M.; Canadell, J.; Cox, P.; Held, H.; de Noblet-Ducoudré, N.; Prinn, R.; Reynolds, J.F.; et al. Nonlinearities, Feedbacks and Critical Thresholds within the Earth’s Climate System. Clim. Chang. 2004, 65, 11–38. [Google Scholar] [CrossRef] [Green Version]
- Bassett, G.W. Breaking recent global temperature records. Clim. Chang. 1992, 21, 303–315. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G.W. Regression quantiles. Econometrica 1978, 46, 33–850. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Franzke, C. A novel method to test for significant trends in extreme values in serially dependent time series. Geophys. Res. Lett. 2013, 40, 1391–1395. [Google Scholar] [CrossRef] [Green Version]
- Colman, A. Prediction of Summer Central England Temperature from Preceding North Atlantic Winter Sea Surface Temperature. Int. J. Climatol. 1997, 17, 1285–1300. [Google Scholar] [CrossRef]
- Scrimgeour, F.; Oxley, L.; Fatai, K. Reducing carbon emissions? The relative effectiveness of different types of environmental tax: The case of New Zealand. Environ. Model. Softw. 2005, 20, 1439–1448. [Google Scholar] [CrossRef] [Green Version]
- Gardner, W.A.; Napolitano, A.; Paura, L. Cyclostationarity: Half a century of research. Signal Process. 2006, 86, 639–697. [Google Scholar] [CrossRef]
- Pagano, M. On periodic and multiple autoregressions. Ann. Stat. 1978, 1310–1317. [Google Scholar] [CrossRef]
- Davidson, J. Stochastic Limit Theory: An Introduction for Econometricians; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Yang, L.; Tschernig, R. Non- and semiparametric identification of seasonal nonlinear autoregression models. Econom. Theory 2002, 18, 1408–1448. [Google Scholar] [CrossRef] [Green Version]
- Pollard, D. Asymptotics for least absolute deviation regression estimators. Econom. Theory 1991, 7, 186–199. [Google Scholar] [CrossRef]
- Fitzenberger, B. The moving blocks bootstrap and robust inference for linear least squares and quantile regressions. J. Econom. 1998, 82, 235–287. [Google Scholar] [CrossRef]
- Koenker, R. Quantile Regression; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Oberhofer, W.; Haupt, H. Nonlinear Quantile Regression under Dependence and Heterogenity; Regensburg Discussion Contributions to Economics: Regensburg, Germany, 2003; p. 388. [Google Scholar]
- Oberhofer, W.; Haupt, H. The asymptotic distribution of the unconditional quantile estimator under dependence. Stat. Probab. Lett. 2005, 73, 243–250. [Google Scholar] [CrossRef]
- Oberhofer, W.; Haupt, H. Asymptotic theory for nonlinear quantile regression under weak dependence. Econom. Theory 2016, 32, 686–713. [Google Scholar] [CrossRef] [Green Version]
- Davidson, J. Econometric Theory; Wiley-Blackwell: Hoboken, NJ, USA, 2000. [Google Scholar]
- Huber, P. The Behavior of Maximum Likelihood Estimates under Nonstandard Conditions. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Davis Davis, CA, USA, 21 June–18 July 1965; Le Cam, L., Neyman, J., Eds.; Almquist & Wiksell: Stockholm, Sweden, 1967; pp. 221–233. [Google Scholar]
- Knight, K. Limiting distributions for L1 regression estimators under general conditions. Ann. Stat. 1998, 26, 755–770. [Google Scholar] [CrossRef]
- Jurecková, J.; Procházka, B. Regression quantiles and trimmed least squares estimator in nonlinear regression model. J. Nonparametric Stat. 1994, 3, 201–222. [Google Scholar]
- Pham, T.D.; Tran, L.T. Some mixing properties of time series models. Stoch. Process. Their Appl. 1985, 19, 297–303. [Google Scholar] [CrossRef] [Green Version]
- Roussas, G.G.; Tran, L.T.; Ioannides, D. Fixed design regression for time series: Asymptotic normality. J. Multivar. Anal. 1992, 40, 262–291. [Google Scholar] [CrossRef] [Green Version]
- Pötscher, B.; Prucha, I. Dynamic Nonlinear Econometric Models: Asymptotic Theory; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Cramér, H.; Wold, H. Some Theorems on Distribution Functions. J. Lond. Math. Soc. 1936, 1, 290–294. [Google Scholar] [CrossRef]
- Castellana, J.V.; Leadbetter, M.R. On smoothed probability density estimation for stationary processes. Stoch. Process. Their Appl. 1986, 21, 179–193. [Google Scholar] [CrossRef] [Green Version]
- Baliunas, S.; Frick, P.; Sokoloff, D.; Soon, W. Time scales and trends in the Central England temperature data (1659–1990): A wavelet analysis. Geophys. Res. Lett. 1997, 24, 1351–1354. [Google Scholar] [CrossRef]
- Harvey, D.I.; Mills, T.C. Modelling trends in central England temperatures. J. Forecast. 2003, 22, 35–47. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Koenker, R. Quantreg: Quantile Regression, R Package Version 5.86. 2021.
- Hyndman, R.; Athanasopoulos, G.; Bergmeir, C.; Caceres, G.; Chhay, L.; O’Hara-Wild, M.; Petropoulos, F.; Razbash, S.; Wang, E.; Yasmeen, F. Forecast: Forecasting Functions for Time Series and Linear Models, R Package Version 8.15. 2021.
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Auguie, B.; Antonov, A. gridExtra: Miscellaneous Functions for “Grid” Graphics, R Package Version 2.3. 2017.
- Fritsch, M.; Haupt, H. quantWarming: Data and Functions for Trend Analysis of Temperature Time Series, R Package Version 0.1.1. 2021.
- IPCC – Intergovernmental Panel on Climate Change. Global Warming of 1.5 ∘C. An IPCC Special Report on the Impacts of Global Warming of 1.5 ∘C Above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2019; p. 630. [Google Scholar]
- Fendt, L.; Ivanova, M. Why Did the IPCC Choose 2 ∘C as the Goal for Limiting Global Warming? Available online: https://climate.mit.edu/ask-mit/why-did-ipcc-choose-2deg-c-goal-limiting-global-warming (accessed on 22 June 2021).
- Taylor, A.; Stevens, H. 2C or 1.5C? How Global Climate Targets Are Set and What They Mean. Available online: https://www.washingtonpost.com/world/2021/11/10/15c-2c-climate-temperature-targets-cop26/ (accessed on 10 November 2021).
- Gil-Alana, J.; Monge, M.; Romero Rojo, M.F. Sea Surface Temperatures: Seasonal Persistence and Trends. J. Athmospheric Ocean. Technol. 2019, 36, 2257–2266. [Google Scholar] [CrossRef]
- Mudelsee, M. Statistical Analysis of Climate Extremes; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Dissanayake, P.; Flock, T.; Meier, J.; Sibbertsen, P. Modelling Short- and Long-Term Dependencies of Clustered High-Threshold Exceedances in Significant Wave Heights. Mathematics 2021, 9, 2817. [Google Scholar] [CrossRef]
- Glick, N. Breaking Records and Breaking Boards. Am. Math. Mon. 1978, 85, 2–26. [Google Scholar] [CrossRef]
- Gallardo, D.I.; Bourguignon, M.; Galarza, C.E.; Gómez, H.W. A Parametric Quantile Regression Model for Asymmetric Response Variables on the Real Line. Symmetry 2020, 12, 1938. [Google Scholar] [CrossRef]
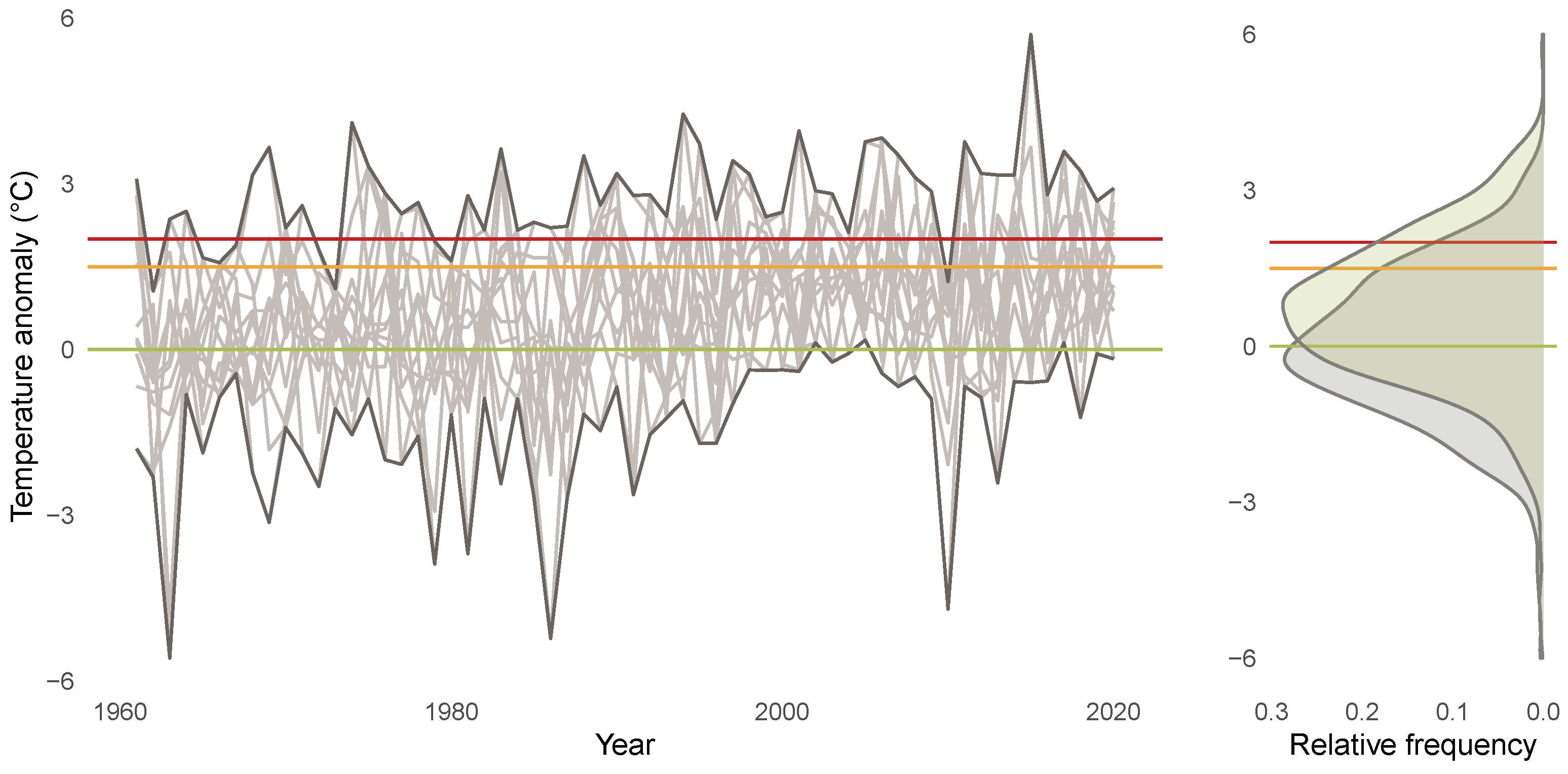
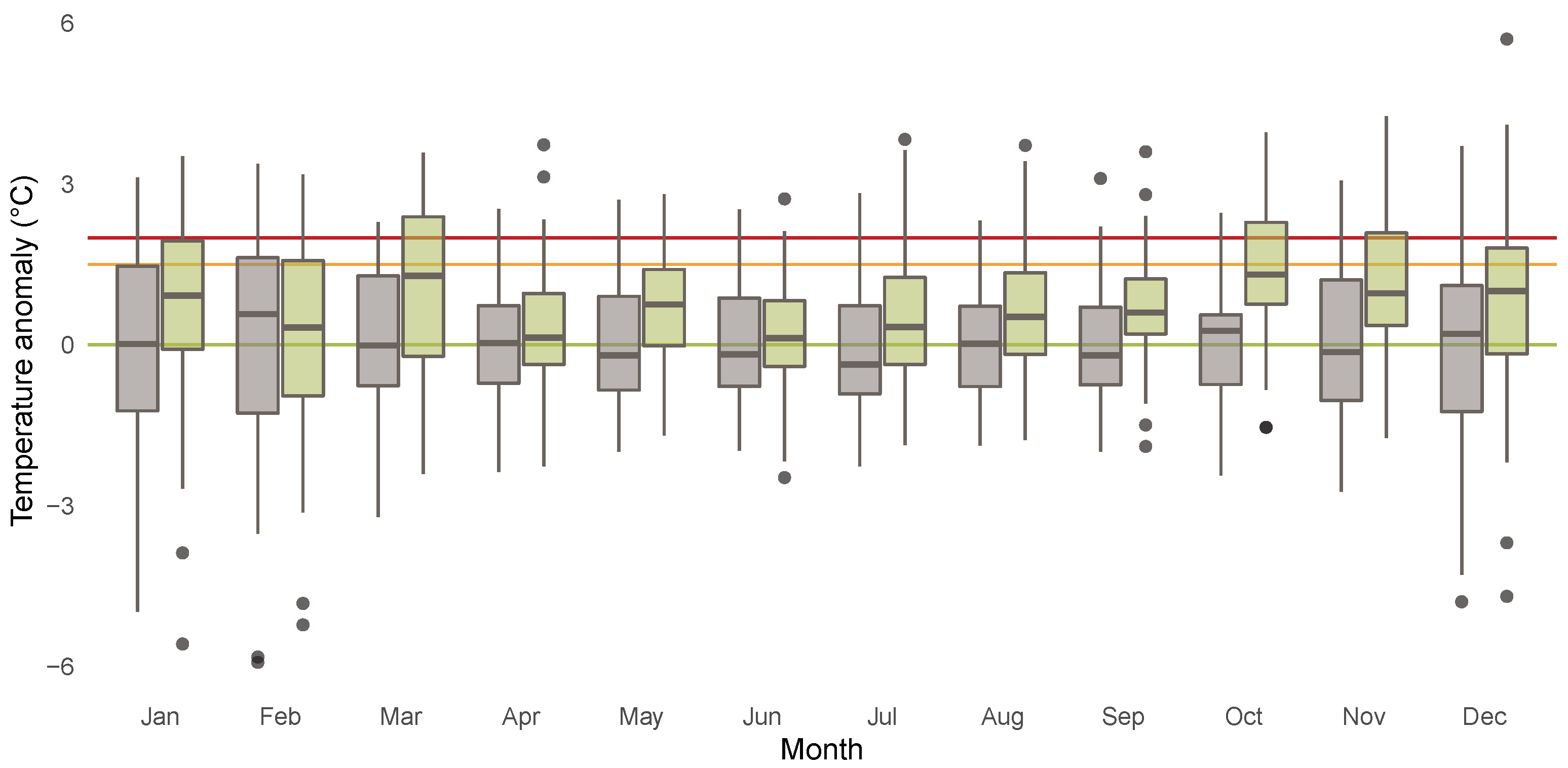
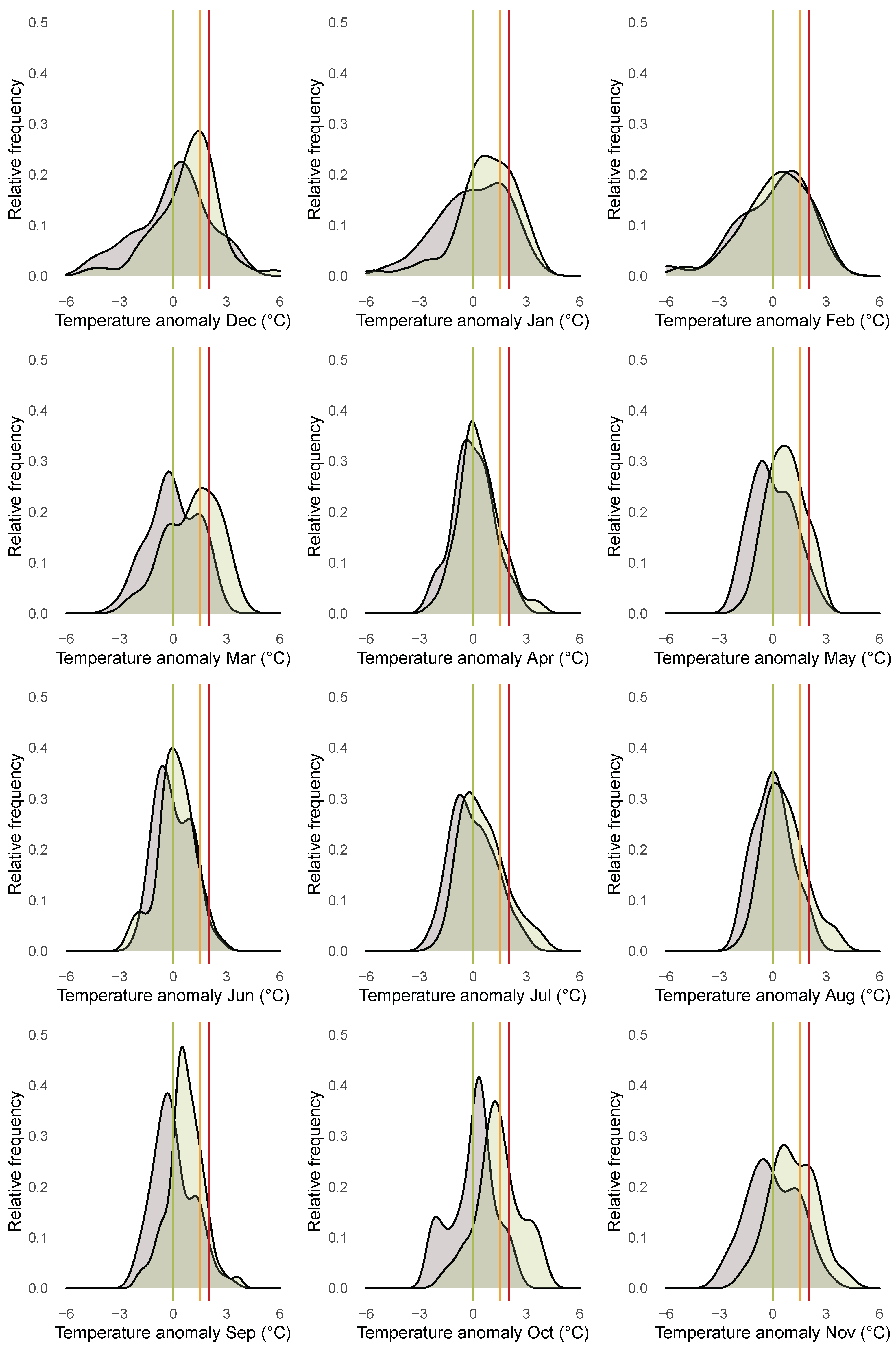
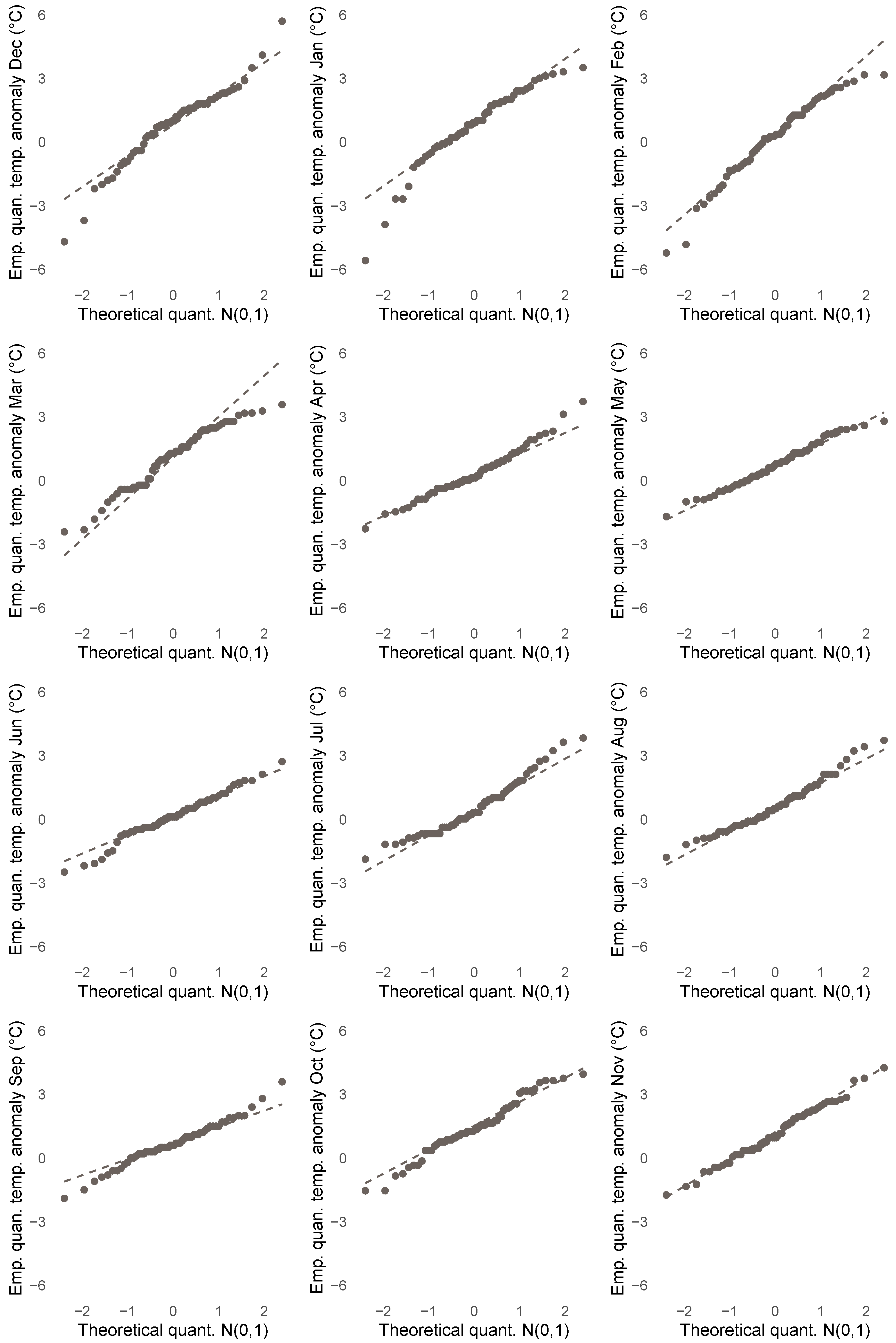
| Years | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1850–1900 | 3.48 | 4.13 | 5.11 | 8.07 | 10.79 | 14.28 | 15.87 | 15.48 | 13.20 | 9.34 | 5.84 | 3.99 | |
| 1961–2020 | 4.24 | 4.33 | 6.21 | 8.42 | 11.53 | 14.42 | 16.42 | 16.14 | 13.88 | 10.77 | 6.98 | 4.81 | |
| 1961–2020 | 0.76 | 0.20 | 1.09 | 0.35 | 0.74 | 0.15 | 0.55 | 0.66 | 0.69 | 1.43 | 1.14 | 0.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haupt, H.; Fritsch, M. Quantile Trend Regression and Its Application to Central England Temperature. Mathematics 2022, 10, 413. https://doi.org/10.3390/math10030413
Haupt H, Fritsch M. Quantile Trend Regression and Its Application to Central England Temperature. Mathematics. 2022; 10(3):413. https://doi.org/10.3390/math10030413
Chicago/Turabian StyleHaupt, Harry, and Markus Fritsch. 2022. "Quantile Trend Regression and Its Application to Central England Temperature" Mathematics 10, no. 3: 413. https://doi.org/10.3390/math10030413
APA StyleHaupt, H., & Fritsch, M. (2022). Quantile Trend Regression and Its Application to Central England Temperature. Mathematics, 10(3), 413. https://doi.org/10.3390/math10030413







