Abstract
As the necessity of location information closely related to everyday life has increased, the use of global navigation satellite systems (GNSS) has gradually increased in populated urban areas. Contrary to the high necessity and expectation of GNSS in urban areas, GNSS performance is easily degraded by multipath errors due to high-rise buildings and is very difficult to guarantee. Errors in the signals reflected by the buildings, i.e., multipath and non-line-of-sight (NLOS) errors, are the major cause of the poor accuracy in urban areas. Unlike other GNSS major error sources, the reflected signal error, which is a user-dependent error, is difficult to differentiate or model. This paper suggests training a multipath prediction model based on support vector regression to obtain a function of the elevation and azimuth angle of each satellite. To extract an unbiased multipath from the GNSS measurements, the clock error of high-elevation QZSS was estimated, and the clock offset with other constellations was also calculated. A nonlinear multipath map was generated, as a result of training with the extracted multipaths, by a Support Vector Machine, which appropriately reflected the geometry of the building near the user. The model was effective at improving the urban area positioning accuracy by 58.4% horizontally and 77.7% vertically, allowing us to achieve a 20 m accuracy level in a deep urban area, Teheran-ro, Seoul, Korea.
1. Introduction
Global navigation satellite systems (GNSS) have been used as the main navigation source in various location-based services (LBS), such as vehicle navigation [1,2] and smart phone location services, for the past 30 years, and are also expected to be used for autonomous cars [3,4] and unmanned aerial mobility (UAM) vehicles [5,6]. Its capability to provide absolute position information with only four visible satellites in any weather conditions anywhere on earth [7,8,9,10] enables it to provide position information to all fields related to location worldwide. As the necessity of position information for everyday life, such as in car navigation and smart phones, has increased, GNSS usage has gradually increased in densely populated urban areas. Contrary to the high demand and expectations for GNSS in urban areas, GNSS performance is easily degraded by multipath errors due to high-rise buildings, and robust and reliable navigation is a primary challenge for urban navigation [6]. In urban environments, satellite signals are easily blocked and/or reflected by tall buildings [11], and GNSS is not accurate or reliable due to severe multipath errors and unfavorable satellite geometry [6]. Multipath and non-line-of-sight (NLOS) signals are major error sources of GNSS in urban canyons. Although multipath and NLOS should be acknowledged as separate phenomena, they usually occur together and, thus, they are difficult to deal with separately in dense urban areas [12]. GNSS receivers perceive NLOS-type reflected signals as actual measurements [12], which might cause errors of several hundred meters.
The most usual method for reflected signal error mitigation is to increase the number of multi-GNSS signals [13,14]. Unlike other GNSS major error sources, which can be removed by differential GNSS (DGNSS) [15] or real time kinematics (RTK) [16,17], the reflected signal error, a user-dependent error, is difficult to differentiate or model. Instead, satellite elevation angle or signal strength measures, such as signal-to-noise ratio (SNR), can be used for selecting or weighting the satellites to be used for positioning. However, this multi-constellation system, with a large number of satellites, is often not effective, since the building geometry is not uniform enough to apply elevation masking in urban areas, and the strength of the signals reflected by the glass or metal parts of the buildings are often stronger than direct ones [18,19]. Three-dimensional (3D) maps [20,21] have recently been used to predict whether a satellite signal is a reflected signal, or if range correction is required to use reflected signals for positioning [22]. Shadow matching uses 3D city models to match each GNSS signal, making them directly visible in some areas and blocked in others [23]. It is designed to improve the cross-street accuracy [22], but it often causes an increase in computational load and positional inaccuracy [19] because it generates a large number of position candidates. On the other hand, a ray-tracing algorithm simulates the LOS and NLOS signal travel distance between each satellite and a receiver [24,25,26], and then calculates the multipath correction. As with shadow matching, a roughly known candidate position makes an alternate computation of the iterated position and NLOS corrections until converging with large uncertainties, which introduces multiple candidates and eventually increases the processing load [19,20,22].
To break through the chronic difficulties of GNSS, research using machine learning techniques has recently been conducted to enhance the robust and accurate performance of GNSS in the urban canyon. Since machine learning techniques are tolerant to data that are imprecise, partially incorrect, or uncertain [27], it can be a powerful tool for handling reflected signals with complex and nonlinear behavior in urban canyons. There are three ways in which machine learning can be used to enhance urban GNSS positioning: multipath/NLOS classification, reflected signal detection and mitigation, and reflected signal corrections.
First, the signal classification method separates the LOS multipath from NLOS signals using actually observed signal characteristics. A Support Vector Machine (SVM)-based algorithm has been able to classify with approximately 75% accuracy, when trained by measurement residuals, code and Doppler measures, and C/N0 [28]. When a left-handed circularly polarized (LHCP) antenna was added to a conventional right-handed circularly polarized (RHCP) antenna, various machine learning methods can be utilized for the signal classifier training of the information provided by the RHCP and LHCP antennas [29,30]. The features of the shape of the correlation function can be also used for the NLOS classification, and neural networks (NN) had a slightly better classification performance than SVM of 97.7% [31]. These methods focus only on classification itself, or employ NLOS measurement exclusion, and thus they often do not contribute significantly to improving accuracy or even reducing availability.
Second, the reflected signal detection and mitigation technique uses machine learning-based classifiers to detect reflected signals and then mitigate their effects in positioning. A multi-feature SVM signal classifier provided a weighting scheme based on the probability of the reflected signal that is superior to the traditional weighting in urban environments [32]. The change in the shape of the correlation values of NLOS signals can be trained by convolutional neural networks, and its reflected signal discrimination probability was 98%, with the positional accuracy improved by 30 m [33]. However, this method does not ultimately eliminate the reflected signal errors, but rather unweights them, so it could not be a solution to the extremely large multipath errors of hundreds of meters.
Last, the reflected signal error correction method, using machine learning, directly predicts and corrects the delay path of the reflected signal, and then uses the corrected signals for positioning. A study has been conducted to directly correct multipaths by applying the iterative properties of satellite orbits to machine learning [34]. This study shows that, by training a multipath estimation model using the multipath characteristics according to the repetitive satellite orbits of each satellite, the positioning accuracy is improved when compared to the general smoothing technique in an open sky environment. In this paper, a multipath is modeled using only the elevation and azimuth of the satellite; however, a multipath in an open sky environment is modeled, rather than an urban multipath with complex and nonlinear characteristics. The GNSS multipath modelling techniques using machine learning are summarized in Table 1.

Table 1.
Classification of the GNSS Multipath Modelling Techniques using Machine Learning.
In this paper, we introduce an SVM-based nonlinear NLOS/multipath prediction model using only the relative position information of the user and the satellite. It belongs to the third category of the machine learning-based multipath error research. It is very suitable for urban area positioning because it can directly remove the multipath error so as to be used for positioning without causing damage to availability. Moreover, the suggested nonlinear prediction model also does not require additional information, such as a 3D map or hardware modification, e.g., an LHCP antenna. As a result, it can be easily applied to most commercial receivers, even if map information is not connected. In addition, the distinction between the direct signal, multipath, and NLOS signal is not necessary for this model, so it can be generally applicable to all constellations and satellites. Since the distinction between multipath and NLOS error is meaningless for the suggested method, we collectively refer to both errors induced by these two reflected signals, i.e., LOS and NLOS signals, as multipaths in this paper.
The remainder of this paper is organized as follows. In Section 2, a mathematical model of GNSS observables and multipath errors is described that considers leveling the clock offset between different constellations. Section 3 explains the nonlinear regression-based multipath map construction methodology and discusses the map’s validity for multipath corrections. A field test was conducted in Teheran-ro, Seoul, Korea, and the results are examined in Section 4. The discussion and conclusions are presented in Section 5.
2. Mathematic Models of GNSS Observables and Multipath Error
2.1. GNSS Observables and Multipath Error
The GNSS code measurements are the ranges obtained by multiplying the traveling time of the signal when it propagates from the satellite to the receiver at the speed of light [35]. The pseudorange code measurement of the i-th satellite at time can be modeled as (1):
where d is the distance between the receiver and satellite, and B and b are the receiver and satellite clock errors, respectively. I and T denote the ionospheric and tropospheric errors, respectively. The measurement noise values of the pseudorange and multipath of both NLOS and LOS cases are represented by and . Superscript refers to the satellite PRN number.
If a rover’s position at time has been computed exactly, the multipath error that corrupts the pseudorange code observable can be calculated as shown in (2). For this computation, the distance () from the rover’s calculated position to each satellite and the estimated clock biases of the receiver () and each satellite () should be used. Pseudorange correction (PRC, ) is helpful for mitigating the atmosphere- and satellite-related errors. Reference station-free PRC corrections are effective and convenient considering the wide mobility of vehicles, and corrections from SBAS () were used in this study.
2.2. Multipath Error Extraction from GNSS Observables
If a rover’s position were calculated exactly, the distance () and the clock biases of the receiver () could also be computed accurately, and consequently the multipath error could be estimated closely to reality by Equation (2). In other words, the validity of Equation (2) is highly dependent on the positional accuracy, and it is very difficult to extract the multipath error from the GNSS observables in a seriously severe reflected signal reception environment. The distance can be relatively computed using an external reference device, whereas the clock bias cannot be accurate because it is a value coupled with the real-time position of the receiver. The mostly intuitive method is to apply the clock bias, obtained with the position computed by the least-squares method. As described in (3), the estimation error of the clock bias, , is included in the actual multipath, and the combined term is extracted:
Since is calculated by the least-squares method for all the observed satellites, no matter how small the error of the i-th satellite is, the extracted multipath inevitably includes the error due to the other satellites with large errors. The least-squares method of clock bias estimation, therefore, may degrade the multipath error extraction performance in urban area environments with severe multipaths. The core technology that extracts the pure multipath depends on how accurately the clock bias is estimated, and the estimation performance is also dependent on the multipath effect. The multipath and clock bias estimation mutually influence each other; thus, estimating clock bias using high-elevation satellites with little risk of severe multipath errors is suggested in this study.
The Quasi-Zenith Satellite System (QZSS), a dedicated regional Japanese satellite system, is a good option for reliably estimating clock bias with little anxiety of the multipath effect. It was designed to complement the visibility and performance of GPS in urban canyons. Eccentricity and inclination are designed so that users in the Asia–Pacific region are able to receive the signal from at least one of the satellites near the zenith direction with an elevation angle above 70° [36]. In addition, to effectively improve the satellite availability for the GPS + QZSS combined system [37], the QZSS clock is synchronized to GPS time, which enables us to use the clock bias estimated by the QZSS observables for the GPS multipath estimation. Since the measurements of high-elevation QZSS satellites can be reasonably assumed to be unaffected by multipath errors, receiver clock bias can be calculated as in (4):
where superscript * means a high-elevation QZSS satellite.
Now, replacing in (3) with obtained by (4) enables to extract only the pure multipath without including , as described in (5):
Figure 1a shows the GNSS signal reception environment during one hour on 1 September 2020 in Teheran-ro, Seoul, Korea. The receiver clock variation calculated by the least-squares method is described with the observed GNSS satellite geometry in Figure 1b. Since the multipath for each measurement is different, the clock bias estimated by the least square of the residuals entirely depends on which satellites are used for the estimation. As shown in Figure 1c, the receiver clock bias results estimated by the GPS least-squares method was unstable and noisy when the satellite combination was frequently changed due to signal blocking and the signal quality degradation caused by the multipath error in the urban area. On the other hand, when the receiver clock bias was calculated by measurements from a QZSS satellite located in the zenith direction, the estimate was computed very precisely.
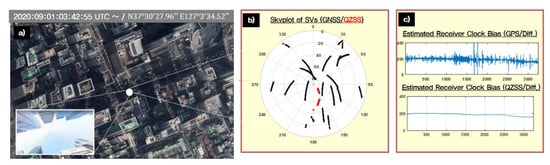
Figure 1.
(a) GNSS Signal Reception Environment; (b) GNSS Satellite Geometry; (c) Receiver Clock Bias Results Estimated by GPS Least Square and QZSS Measurement.
To estimate the multipath error of GNSS satellites other than GPS/QZSS, the clock bias of each constellation should be removed instead of the QZSS clock term, , in (5). It is necessary to compensate for the clock difference between other GNSS and GPS/QZSS in order to take advantage of the stability and reliability of the clock bias estimated by the high elevation of the QZSS satellite. A nearby reference station is able to compute the time difference between the two system, , as described in (6). Then, the multipath errors of other GNSS can be extracted by (7) using the GPS clock bias obtained from the QZSS observation and the clock difference estimated from the reference station.
3. Nonlinear Regression-Based Multipath Error Map Construction
3.1. Multipath Modeling
Signal characteristics, i.e., frequency and signal strength, are all different for each GNSS constellation and satellite; however, signals transmitted from the same transmission point travel the same straight-line path regardless of the signal type. Accordingly, signals transmitted from satellites in the same direction have the same reflected path as features near the user’s position, which is similarly assumed in the ray-tracing technique. Thus, if the line-of-sight vectors of two satellites from a user’s position are the same, both signals are highly likely to be placed in the same category among direct signals, LOS-type multipaths, and NLOS-only-type multipaths. Moreover, their multipath error amounts would be similar regardless of the multipath and signal types. Eventually, the multipath value is determined by the relative position of the satellite at a user’s position. Therefore, the multipath error () can be expressed as a function of the elevation ( and azimuth ( angle of the i-th satellites as in (8):
3.2. Nonlinear Regression
The multipath prediction model is trained based on Support Vector Regression. SVR has been widely used for various engineering problems [38,39,40,41,42]. The Support Vector Regression (SVR) algorithm is a regression technique based on the Support Vector Machine (SVM). The SVM solves binary classification problems by formulating them as convex optimization problems, which entails finding the maximum margin separating the hyperplane, while correctly classifying as many training points as possible [43]. SVM generalization to SVR is accomplished by introducing an -insensitive region around the function, called the -tube. This tube reformulates the optimization problem to find the tube that best approximates the continuous-valued function, while balancing model complexity and prediction error [44]. Training data were set as , where the input data in form a set comprising elevation and azimuth angle data, and y is the multipath extracted by (5) and (7). For the linear case, the multipath estimation model is represented by (9):
where is the dot product between and , is the weighting vector, and is the bias vector.
SVR formulates this function approximation problem as an optimization problem that attempts to find the narrowest tube centered around the surface while minimizing the prediction error, which is the distance between the predicted and the desired outputs [43]. More specifically, our goal is to find a function that has at most ε deviation from the actually obtained targets for all the training data. At the same time, it should be as flat as possible [43], which means a small . The multipath estimation model can be obtained from the optimization problems expressed in (10):
A key assumption in this formulation is that there exists a function that can approximate all input pairs (, ) with precision; however, this may not be the case, or perhaps some error allowance is desired [45]. Thus, slack variables and can be incorporated into the optimization problem to yield the following formulation (11):
where constant determines the tradeoff between flatness (a small w) and the degree to which deviations larger than ξ are tolerated, and is the number of samples. The -insensitive loss function is descried by (12):
In nonlinear cases, nonlinear function approximation can be achieved by replacing the dot product of the input vector with a nonlinear transformation of the input vectors [37]. This transformation is referred to as a kernel function and is represented by , where and are each input vectors. In this study, the Gaussian kernel given by (13) is chosen due to its ability to handle nonlinearity [46]:
By solving the optimization problem [45], the regression model is finally expressed as (14):
3.3. Multipath Map Construction
The multipath prediction model constructed by the above-described SVM-based methodology is basically based on the assumption that the reflected signal error is dependent only on the signal path. The signal path is created by the geometry of three components: a user position, the location and orientation of buildings around the user, and the signal transmission point of each observed satellite. While two components among them, the user position and building geometry, are time-invariant terms, only the signal transmission point is time variant. Even though the signal transmission point of the satellite is continuously moving, the ray from the satellite to the user is unique and constant independently of time because temporal variation of the atmospheric delay is mitigated by the fed PRC. Therefore, the signal ray from a transmission point to a user is always constant for a specific satellite and user position.
Similarly, the degree of multipath error is the same only if the line-of-sight vector to a satellite is at the user’s position because the degree of the error is the difference between the reflected signal and the direct one. The travel distances of the direct signal and the reflected signal before being reflected by the building are the same, and the path after the reflection is determined by the incidence angle of each signal. If the incidence angle even for the signal from a different satellite or constellation is the same, the total number of multipath errors observed at the user is also the same. As long as the elevation and azimuth angle are the same, the signals received from satellites of different pseudo-random noise (PRN) numbers or different constellations can be used as identical output data corresponding to input data. Therefore, the multipath can be modelled by only the geometrical direction of the satellite with respect to the user’s position, regardless of the type or constellation of the satellite, which enables the construction of a multipath map similar to a satellite skyplot. Considering the geographical location of the Asia–Pacific region as a GNSS satellite hotspot, where more than 35 satellites are observed at the same time, the ability to generate an output model for an input from multiple constellations and satellite signals is an advantage that can enhance the reliability of the model.
The advantage that the multipath model can be created and reinforced from various signal sources contributes greatly to reliable map construction when considering the actual radio reception environment in crowded urban areas. Although buildings are the main cause of the multipath errors, multipaths are also caused by vehicles and pedestrians in urban areas to a non-negligible degree. Unlike the location and influence of buildings, they are time variants and, moreover, appear almost randomly over time, which makes modeling them over time almost impossible. The reinforcement from various signals enables us to exclude time-varying results as outliers and model only time-fixed properties properly; therefore, it is possible to construct a map that appropriately models only the effects of buildings on the multipaths.
3.4. User Utilization of the Multipath Map
Once the multipath map function is properly constructed, the error-mitigated pseudorange measurements ( can be obtained by feeding the PRC with the predicted multipath by the i-th satellite elevation and azimuth angle as shown in (15):
In the ideal case, the pseudorange measurement with the mitigated error should include only measurement noise and modelling error; however, additional multipath errors due to vehicles and pedestrians passing by is likely to cause harm to the user position accuracy. In order to monitor whether an unmodelled error is included in the observation, a comparison with the Doppler measurements used in a previous study [47] is conducted. Since Doppler (dppl) is relatively less affected by the multipaths [48,49], the Doppler and time difference () of should theoretically have the same value. If the user detects that the current observable includes an unmodelled multipath with (16), the user excludes it from the available satellite set for the urban area positioning:
4. Field Test
4.1. Test Construction
All our numerical experiments were carried out on a PC with an Intel i9-10980HK CPU at 2.40 GHz and with 32 GB of physical memory. The PC runs MATLAB R2020a on a Windows 10 Pro 54-bit operating system, and the SVR models were trained using the default setting of MATLAB. A static field test was conducted in front of the Hyundai Department Store in Teheran-ro, Seoul, Korea, which is one of the areas with the poorest GNSS visibility and signal reception globally. According to the 3D building information provided by VWorld Data Center [50], operated by the Ministry of Land, Infrastructure, and Transport of South of Korea, it is surrounded by buildings with a height of about 80 m along a road 25 m away around the static test point, as shown in Figure 2. The average static position error RMS in this was reported to be 55.6 m due to the severe effect of reflected signals [51].

Figure 2.
GNSS Signal Reception Environment around Static Test Spot in Teheran-ro (Seoul, Korea).
Training data and test data were assigned to 1 h of data collected on different days, as described in Table 2. During the training data collection period, Sejong university Reference Station (RS) data were also logged to calculate the clock difference between GNSS and QZSS in the training data. Ublox-F9P receivers were used for both rover and RS multi-constellation GNSS data, i.e., GPS, GLONASS, BeiDou, GALILEO, and QZSS, as shown in Figure 3. The true position of the rover was computed by the post-processing results of the Trimble Business Center.

Table 2.
Training and Test Data Set.
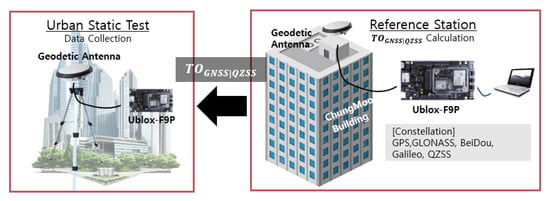
Figure 3.
GNSS Data Collection Structure.
The left skyplot of Figure 4 shows the satellite tracks observed in the training data. The trajectories observed in each training data set are different from each other, but some points intersect or overlap each other, which was expected to increase reliability. The high elevation angle of a QZSS satellite that was observed to be an average of 72 degrees enabled us to estimate the stable clock bias and extract the exact multipath without changing the reference satellite. The right skyplot shows the multipaths extracted from all the training data and leveled to the high-elevation QZSS clock bias. Although the training data were collected from various satellites and constellations at different dates and times, the multipath estimates from similar line-of-sight satellites show similar values regardless of which satellite and constellation transmitted the signals and when they were broadcast.

Figure 4.
Skyplots of Satellite Tracks (left) and Extracted Multipaths (right).
4.2. Multipath Map Construction Results
After matching the extracted multipaths to each elevation and azimuth angle in Figure 4, they were trained by the SVM, as described in Section 3.2. The nonlinear regression results can be expressed in the form of a heat map on a skyplot, as shown in Figure 5, right plot. For comparison with the existing method used for weighting the matrix generation, the linear regression results are expressed in the same way as shown in the left plot of Figure 5. Blue means that there was little multipath effect on the observables, and the color close to red indicates a large effect.
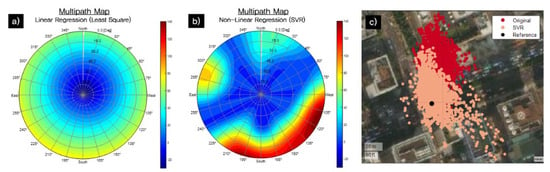
Figure 5.
Comparison of the Multipath Maps Constructed by Linear (a) and Nonlinear (b) Regression, and Horizontal Static Test Results of Nonlinear Regression (c).
The linear model could find the pattern for the elevation, but did not solve a model of the azimuth angle. On the other hand, the Support Vector Regression-based nonlinear model enabled us to model multipaths more flexibly for the azimuth angle. It predicted the multipath effect to be small for the satellites observed from the northwest direction in quadrant 2 and the northeast to southwest direction across the map, whereas the multipath on the edge of the south and west were predicted to be large. The correlation between the patterns found from the map and the actual influence will be explained in the next paragraph. Besides, while the maximum multipath was predicted to be 140 m for the nonlinear model, the maximum of 70 m was predicted by the linear model based on the least-squares method. The reason seems to be that the actual large error was regarded as an excessive error in order to minimize the errors at all points due to the original attributes of the least-squares method.
In order to intuitively show the appropriateness of the constructed multipath map, a sky view obtained by adjusting the viewpoint on Google Street View [52] was used with the satellite view image provided by Google Earth [53]. The static test site was located at the three-way intersection as shown in the left satellite image in Figure 6. The satellite image makes it easy to predict that the multipath effect on the signals broadcast from the road direction would be small. Even though this study did not use the building geometry as prior information, the geographical tendency of the multipath effect can be easily inferred from the map in Figure 5, which verifies that the map was constructed appropriately. Figure 5c clearly shows that nonlinear regression was effective enough to reduce the horizontal position bias by applying the constructed multipath map.

Figure 6.
Satellite Image of the Static Test Spot (left) and Multipath Map Overlapped with Sky View (right).
The sky view overlapped on the constructed multipath map supports the validity in more detail. The points where the multipath effects were predicted, which are painted with colors other than blue, were exactly the same as where the building is viewed from the ground. In particular, a slightly concave map in the southern part was formed, not flat in the road direction, which coincides with the building geometry, with the two buildings that were lower than those on both sides obstructing the satellite visibility less. In addition, the validity of the map is supported by the results showing that the multipath error was estimated to be larger in the direction of the lower floors than at the boundary of the buildings.
4.3. Test Data Application Results
After constructing the multipath map with the training data, the multipath prediction value ( was used like other correction data in (8) to mitigate the errors in the observed pseudorange measurements. Multipath errors caused by obstacles other than buildings were considered to be outliers and excluded from model generation; however, it is impossible to distinguish whether an unmodelled multipath was additionally included in the current measurement at the user side. Equation (16) was used as a metric to determine if there was an unmodelled multipath for each satellite. Figure 7 shows the predicted multipath values ( of the GNSS satellites and the user unmodelled error monitoring results using Doppler. In an ideal case, Doppler (dppl) and the time difference () of the error-mitigated pseudorange measurement ( should theoretically have the same value unless an unmodelled multipath error caused by moving obstacles is included. The error-mitigated pseudorange variations of GPS PRN 26 and Galileo PRN 1 were similar to their Doppler measurements, which means the constructed model was able to mitigate the multipath error of the satellites, whereas the Beidou PRN 10 satellite was excluded from the calculating position at the end of the session, despite its high elevation angle of 50°, because the difference between the pseudorange variations and Doppler measurements () were up to several meters. Series of severe unmodelled multipaths were detected on GPS PRN 14, where a difference of more than 10 m between the Doppler and pseudorange time difference existed. Since its elevation angle was about 60 degrees, if it had used the conventional elevation angle-based weighted algorithm, its weight would have been set high.

Figure 7.
Examples of Predicted Multipath ( and Unmodelled Multipath Metrics () Variation in Time.
Figure 8 and Figure 9 show the comparison of the static test results for positioning mode: original positioning, weighted positioning by linear regression, multipath-mitigated positioning by SVR, and multipath-mitigated positioning by SVR + Doppler check. Since high-rise buildings were located along the road from the northeast to the southwest, the original position results are biased to the southwest and down direction, even though all the constellations and satellites were employed for the positioning. The horizontal and vertical root mean square error (RMSE) were about 50 and 100 m, respectively, and the vertical error 95 percentile error was up to 142 m, as shown in Table 3. A conventionally used linear regression elevation-based weighting method was effective in reducing the vertical error by 67%, but it did not contribute to improving horizontal accuracy, whereas the SVR-based nonlinear model effectively reduced both horizontal and vertical errors. The overall accuracy statistics were improved by 53% horizontally and 69% vertically, and the bias error mostly disappeared. However, it was not effective to bind the excessive error in the east and down direction from 511 to 1203 epochs. Based on the fact that the nonlinear multipath map did not completely mitigate the measurement error in this session, it seems that the unmodelled multipath errors were included in it. After applying the unmodelled multipath detecting method in (16), both horizontal and vertical excessive errors were reduced to the level of other sessions. An accuracy of 20 m was achieved horizontally and vertically, which was an improvement of 58.4% horizontally and 77.7% vertically on the multi-GNSS positioning results.

Figure 8.
Horizontal (left) and Vertical (right) Static Test Results.

Figure 9.
Horizontal Position Results on Map (left) and Building Geometry (right).

Table 3.
Statistical Results Comparison of Positioning Modes.
5. Conclusions, Limitations and Future Works
This paper introduced a nonlinear multipath prediction model to remove the multipath errors, regardless of constellation or satellite PRN, in deep urban areas. Since this SVM-based nonlinear model only uses the relative direction of the satellite from a user, all kinds of signals and receivers can commonly use this model without any classification of signal or reflection types. Without any help from the prior building information, the multipath map modelled by the nonlinear regression method reflected exactly where the building is viewed from the ground.
To validate the suggested algorithm and demonstrate its performance in urban canyons, we applied the generated model to a static test in Teheran-ro, which is known for its low visibility of satellites. The model trained by 3 h of static data enabled us to improve the original position accuracy by 58.4% horizontally and 77.7% vertically, which enabled us to achieve 20 m accuracy for both directions in a street known globally for the low visibility of the navigation satellites, Teheran-ro, Seoul, Korea.
Since this model only requires a data-driven process without additional equipment or information other than GNSS observables, a similar performance is expected in other cities, as well as other spots in Seoul, with sufficient data. Moreover, it can directly remove multipath errors, meaning that it can be used for positioning without availability damage, and thus it is very suitable for urban area positioning. The fact that it can be trained and modelled by only GNSS data without additional information from a 3D map or receiver antenna modification, and that the user calculation load is not large, can increase the value of the suggested model in various fields in the future.
Based on the algorithm of the multipath construction at a single static site in this paper, our future work should include realistic scenarios for dynamic users in urban environments. Even though the azimuth and elevation angle of the satellites at the positions of users over areas of several kilometers are almost same, the direction of each nearby building varies significantly depending on the location of the users. As a result, multipath effects caused by the buildings are significantly different depending on the user position and, accordingly, dynamic multipath maps should be applied to a user. Therefore, our future work is on the construction of a dynamic multipath map and its application to the dynamic user. Since the multipath effect is significantly different depending on the user position, several multipath maps should be constructed at multiple points in order to be applied to dynamic users. Further, to identify the optimal option among multiple error maps, user position uncertainty needs to be resolved in deep areas with excessive outliers.
Author Contributions
All the authors have contributed to the presented work. The first author, Y.L., implemented the SVM-based multipath map construction and conducted the static test. B.P. suggested the original concept of the system and supervised its development and the direction of the research. All authors participated in formulating the idea and in discussing the proposed approach and results. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ministry of Science and ICT, Korea, under the Information Technology Research Center support program (IITP-2020-2018-0-01423), supervised by the Institute for Information and Communications Technology Planning and Evaluation and Unmanned Vehicles Core Technology Research and Development Program through the National Research Foundation of Korea (NRF) and Unmanned Vehicle Advanced Research Center (UVARC) funded by the Ministry of Science and ICT, the Republic of Korea (No. 2020M3C1C1A01086407).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and program codes are stored in https://github.com/wns1942/GNSS.git (accessed on 19 November 2021). All data can be obtained from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Correa-Caicedo, P.J.; Rostro-González, H.; Rodriguez-Licea, M.A.; Gutiérrez-Frías, Ó.O.; Herrera-Ramírez, C.A.; Méndez-Gurrola, I.I.; Cano-Lara, M.; Barranco-Gutiérrez, A.I. GPS Data Correction Based on Fuzzy Logic for Tracking Land Vehicles. Mathematics 2021, 9, 2818. [Google Scholar] [CrossRef]
- Buzna, Ľ.; Czimmermann, P. On the Modelling of Emergency Ambulance Trips: The Case of the Žilina Region in Slovakia. Mathematics 2021, 9, 2165. [Google Scholar] [CrossRef]
- Hussain, R.; Zeadally, S. Autonomous cars: Research results, issues, and future challenges. IEEE Commun. Surv. Tutor. 2018, 21, 1275–1313. [Google Scholar] [CrossRef]
- He, Q.; Meng, X.; Qu, R.; Xi, R. Machine Learning-Based Detection for Cyber Security Attacks on Connected and Autonomous Vehicles. Mathematics 2020, 8, 1311. [Google Scholar] [CrossRef]
- Bijjahalli, S.; Ramasamy, S.; Sabatini, R. Masking and multipath analysis for unmanned aerial vehicles in an urban environment. In Proceedings of the 2016 IEEE/AIAA 35th Digital Avionics Systems Conference (DASC), Sacramento, CA, USA, 25–29 September 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Bijjahalli, S.; Sabatini, R.; Gardi, A. GNSS performance modelling and augmentation for urban air mobility. Sensors 2019, 19, 4209. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Liu, S.; Atia, M.M.; Noureldin, A. INS/GPS/LiDAR integrated navigation system for urban and indoor environments using hybrid scan matching algorithm. Sensors 2015, 15, 23286–23302. [Google Scholar] [CrossRef]
- Gu, Y.; Hsu, L.T.; Kamijo, S. GNSS/onboard inertial sensor integration with the aid of 3-D building map for lane-level vehicle self-localization in urban canyon. IEEE Trans. Veh. Technol. 2015, 65, 4274–4287. [Google Scholar] [CrossRef]
- Yoon, H.; Seok, H.; Lim, C.; Park, B. An Online SBAS Service to Improve Drone Navigation Performance in High-Elevation Masked Areas. Sensors 2020, 20, 3047. [Google Scholar] [CrossRef]
- Lim, C.; Yoon, H.; Cho, A.; Yoo, C.-S.; Park, B. Dynamic Performance Evaluation of Various GNSS Receivers and Positioning Modes with Only One Flight Test. Electronics 2019, 8, 1518. [Google Scholar] [CrossRef]
- Rizos, C. Trends in GPS Technology & Applications. In Proceedings of the 2nd International LBS Workshop, Boston, MA, USA, 4 April 2009. [Google Scholar]
- Groves, P.D. How Does Non-Line-of-Sight Reception Differ from Multipath Interference. Inside GNSS 2013, 8, 40–42. [Google Scholar]
- Wang, L.; Groves, P.D.; Ziebart, M.K. Multi-constellation GNSS performance evaluation for urban canyons using large virtual reality city models. J. Navig. 2012, 65, 459–476. [Google Scholar] [CrossRef]
- Lisi, M. GNSS User Technology Report 2020. GEOmedia 2020, 24, 21. [Google Scholar]
- Park, B.; Kim, J.; Kee, C.; Cleveland, A.; Parsons, M.; Wolfe, D.; Kalafus, R. RRC unnecessary for DGPS messages. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 1149–1160. [Google Scholar] [CrossRef]
- Imparato, D.; El-Mowafy, A.; Rizos, C.; Wang, J. Vulnerabilities in SBAS and RTK positioning in intelligent transport systems: An overview. In Proceedings of the International Global Navigation Satellite System Association IGNSS Symposium, Sydney, Australia, 7–8 February 2018. [Google Scholar]
- Park, B.; Kee, C. The Compact Network RTK Method: An Effective Solution to Reduce GNSS Temporal and Spatial Decorrelation Error. J. Navig. 2010, 63, 343–362. [Google Scholar] [CrossRef]
- Bennett, N.; Hunter, M.; Buesnel, G. Validation of Urban Multipath Models with Record and Playback Simulation. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021. [Google Scholar]
- Groves, P.D. It’s time for 3D mapping–aided GNSS. Inside GNSS Mag. 2016, 5, 50–56. [Google Scholar]
- End Game for Urban GNSS: Google’s Use of 3D Building Models. Available online: https://insidegnss.com/end-game-for-urban-gnss-googles-use-of-3d-building-models/ (accessed on 19 November 2021).
- Dredge, S. Google Unveils 3D Cities in Google Earth and offline Google Maps for Android. The Guardian Apps Blog (6 June). Available online: http://www.theguardian.com/technology/appsblog/2012/jun/06/google-maps-3d-street-view1 (accessed on 19 November 2021).
- Adjrad, M.; Groves, P.D. Enhancing least squares GNSS positioning with 3D mapping without accurate prior knowledge. NAVIGATION J. Inst. Navig. 2017, 64, 75–91. [Google Scholar] [CrossRef]
- Groves, P.D. Shadow matching: A new GNSS positioning technique for urban canyons. J. Navig. 2011, 64, 417–430. [Google Scholar] [CrossRef]
- Obst, M.; Bauer, S.; Reisdorf, P.; Wanielik, G. Multipath detection with 3D digital maps for robust multi-constellation GNSS/INS vehicle localization in urban areas. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Madrid, Spain, 3–7 June 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Miura, S.; Hsu, L.-T.; Chen, F.; Kamijo, S. GPS error correction with pseudorange evaluation using three-dimensional maps. IEEE Trans. Intell. Transp. Syst. 2015, 16, 3104–3115. [Google Scholar] [CrossRef]
- Hsu, L.-T.; Gu, Y.; Kamijo, S. NLOS correction/exclusion for GNSS measurement using RAIM and city building models. Sensors 2015, 15, 17329–17349. [Google Scholar] [CrossRef]
- Malhotra, R. A systematic review of machine learning techniques for software fault prediction. Appl. Soft. Comput. 2015, 27, 504–518. [Google Scholar] [CrossRef]
- Hsu, L.-T. GNSS multipath detection using a machine learning approach. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Guermah, B.; El Ghazi, H.; Sadiki, T.; Guermah, H. A robust GNSS LOS/multipath signal classifier based on the fusion of information and machine learning for intelligent transportation systems. In Proceedings of the 2018 IEEE International Conference on Technology Management, Operations and Decisions (ICTMOD), Marrakech, Morocco, 21–23 November 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Park, K.; Lee, D.; Seo, J. Dual-polarized GPS antenna array algorithm to adaptively mitigate a large number of interference signals. Aerosp. Sci. Technol. 2018, 78, 387–396. [Google Scholar] [CrossRef]
- Suzuki, T.; Amano, Y. NLOS Multipath Classification of GNSS Signal Correlation Output Using Machine Learning. Sensors 2021, 21, 2503. [Google Scholar] [CrossRef] [PubMed]
- Lyu, Z.; Gao, Y. An SVM Based Weight Scheme for Improving Kinematic GNSS Positioning Accuracy with Low-Cost GNSS Receiver in Urban Environments. Sensors 2020, 20, 7265. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Kusama, K.; Amano, Y. NLOS Multipath Detection using Convolutional Neural Network. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2020), Online, 21–25 September 2020. [Google Scholar]
- Phan, Q.-H.; Tan, S.-L. Mitigation of GPS periodic multipath using nonlinear regression. In Proceedings of the 2011 19th European Signal Processing Conference, Barcelona, Spain, 29 August–2 September 2011; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Tian, Y.; Ge, M.; Neitzel, F. Variance Reduction of Sequential Monte Carlo Approach for GNSS Phase Bias Estimation. Mathematics 2020, 8, 522. [Google Scholar] [CrossRef]
- Wu, F.; Kubo, N.; Yasuda, A. A study on GPS augmentation using Japanese Quasi-Zenith satellite system. In Proceedings of the PLANS 2004. Position Location and Navigation Symposium (IEEE Cat. No. 04CH37556), Monterey, CA, USA, 26–29 April 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 347–356. [Google Scholar]
- Zhu, S.; Yue, D.; He, L.; Liu, Z.; Chen, J. Comprehensive analysis of compatibility between QZSS and GPS in Asia-Pacific region: Signal quality, RTK and PPP. Adv. Space Res. 2020, 66, 395–411. [Google Scholar] [CrossRef]
- Nabipour, N.; Karballaeezadeh, N.; Dineva, A.; Mosavi, A.; Mohammadzadeh, S.D.; Shamshirband, S. Comparative analysis of machine learning models for prediction of remaining service life of flexible pavement. Mathematics 2019, 7, 1198. [Google Scholar] [CrossRef]
- Xie, X.; Shen, J. Waterlogging Resistance Evaluation Index and Photosynthesis Characteristics Selection: Using Machine Learning Methods to Judge Poplar’s Waterlogging Resistance. Mathematics 2021, 9, 1542. [Google Scholar] [CrossRef]
- Xie, X.; Luo, K.; Yin, Z.; Wang, G. Nonlinear Combinational Dynamic Transmission Rate Model and Its Application in Global COVID-19 Epidemic Prediction and Analysis. Mathematics 2021, 9, 2307. [Google Scholar] [CrossRef]
- Diz-Mellado, E.; Rubino, S.; Fernández-García, S.; Gómez-Mármol, M.; Rivera-Gómez, C.; Galán-Marín, C. Applied Machine Learning Algorithms for Courtyards Thermal Patterns Accurate Prediction. Mathematics 2021, 9, 1142. [Google Scholar] [CrossRef]
- García, L.A.M.; Lasheras, F.S.; Nieto, P.J.G.; de Prado, L.Á.; Sánchez, A.B. Predicting Benzene Concentration Using Machine Learning and Time Series Algorithms. Mathematics 2020, 8, 2205. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar]
- Clarke, S.M.; Griebsch, J.H.; Simpson, T.W. Analysis of support vector regression for approximation of complex engineering analyses. J. Mech. Des. 2005, 127, 1077–1087. [Google Scholar] [CrossRef]
- Smola, A.J. Learing with Kernels. Ph.D. Thesis, Department of Computer Science, Technical University, Berlin, Germany, 1998. [Google Scholar]
- Lee, Y.; Park, B. Seamless Accurate Positioning in Deep Urban Area based on Mode Switching Between DGNSS and Multipath Mitigation Positioning. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Online, 21–25 September 2020. [Google Scholar]
- Kim, J.; Park, M.; Bae, Y.; Kim, O.; Kim, D.; Kim, B.; Kee, C. A low-cost, high-precision vehicle navigation system for deep urban multipath environment using TDCP measurements. Sensors 2020, 20, 3254. [Google Scholar] [CrossRef]
- Freda, P.; Angrisano, A.; Gaglione, S.; Troisi, S. Time-differenced carrier phases technique for precise GNSS velocity estimation. GPS Solut. 2015, 19, 335–341. [Google Scholar] [CrossRef]
- VWorld Data Center, Operated by the Ministry of Land, Transport and Maritime Affairs of South Korea. Available online: http://data.vworld.kr/data/v4dc_usrmain.do (accessed on 11 November 2021).
- Jeong, G.S.; Kong, S.H. GIS based advanced positioning technique for mobile GPS. J. Korean Inst. Commun. Inf. Sci. 2015, 40, 2261–2290. [Google Scholar] [CrossRef][Green Version]
- Google Maps Street View. Available online: https://www.google.com/maps/@37.5078445,127.0595055,3a,90y,338.18h,179t/data=!3m7!1e1!3m5!1srhCgHDKwyWioPJ6Q86Do5g!2e0!6shttps:%2F%2Fstreetviewpixels-pa.googleapis.com%2Fv1%2Fthumbnail%3Fpanoid%3DrhCgHDKwyWioPJ6Q86Do5g%26cb_client%3Dmaps_sv.tatile.gps%26w%3D203%26h%3D100%26yaw%3D72.211334%26pitch%3D0%26thumbfov%3D100!7i13312!8i6656 (accessed on 19 November 2021).
- Google Earth. Available online: https://earth.google.com/web/@37.50780564,127.05940105,16.35165563a,548.62225985d,35y,0h,0t,0r (accessed on 19 November 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).